Phase Compensation for Continuous Variable Quantum Key Distribution Based on Convolutional Neural Network
Abstract
:1. Introduction
2. Materials and Methods
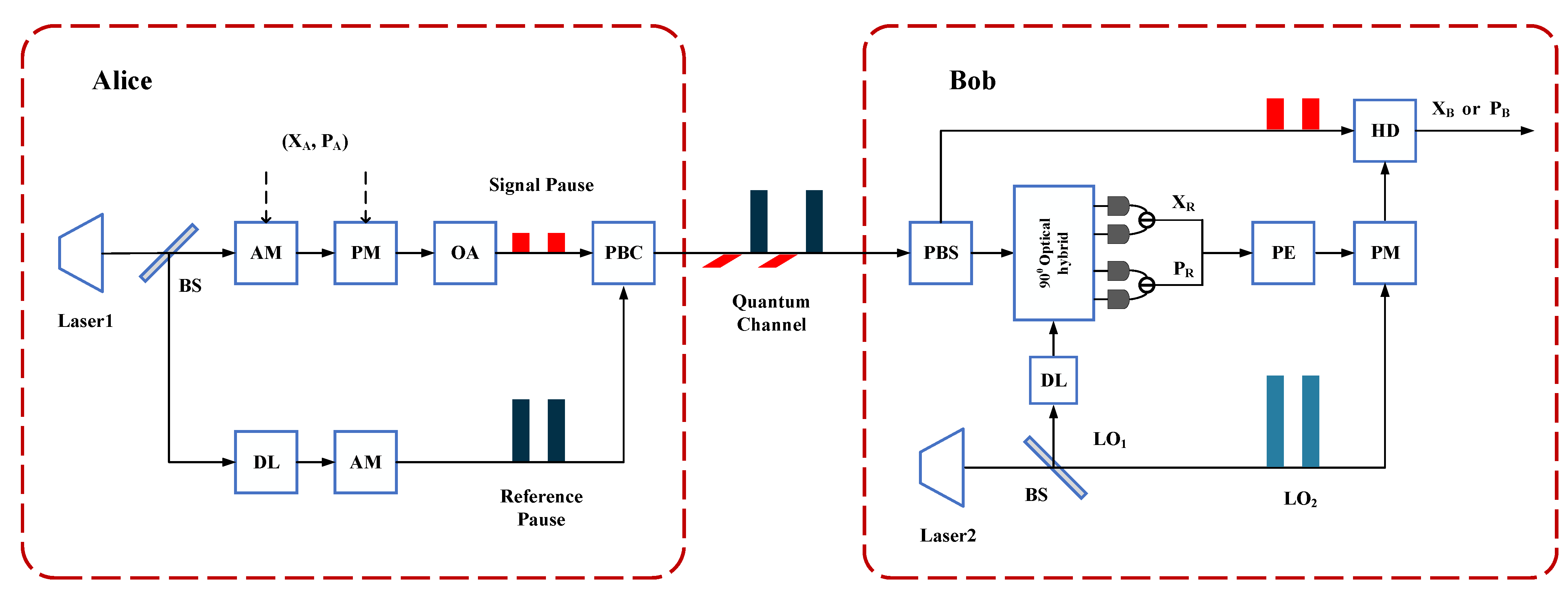
2.1. Description of LLO CV-QKD
2.2. Analysis of Phase Noise
2.3. Phase Compensation Based on CNN
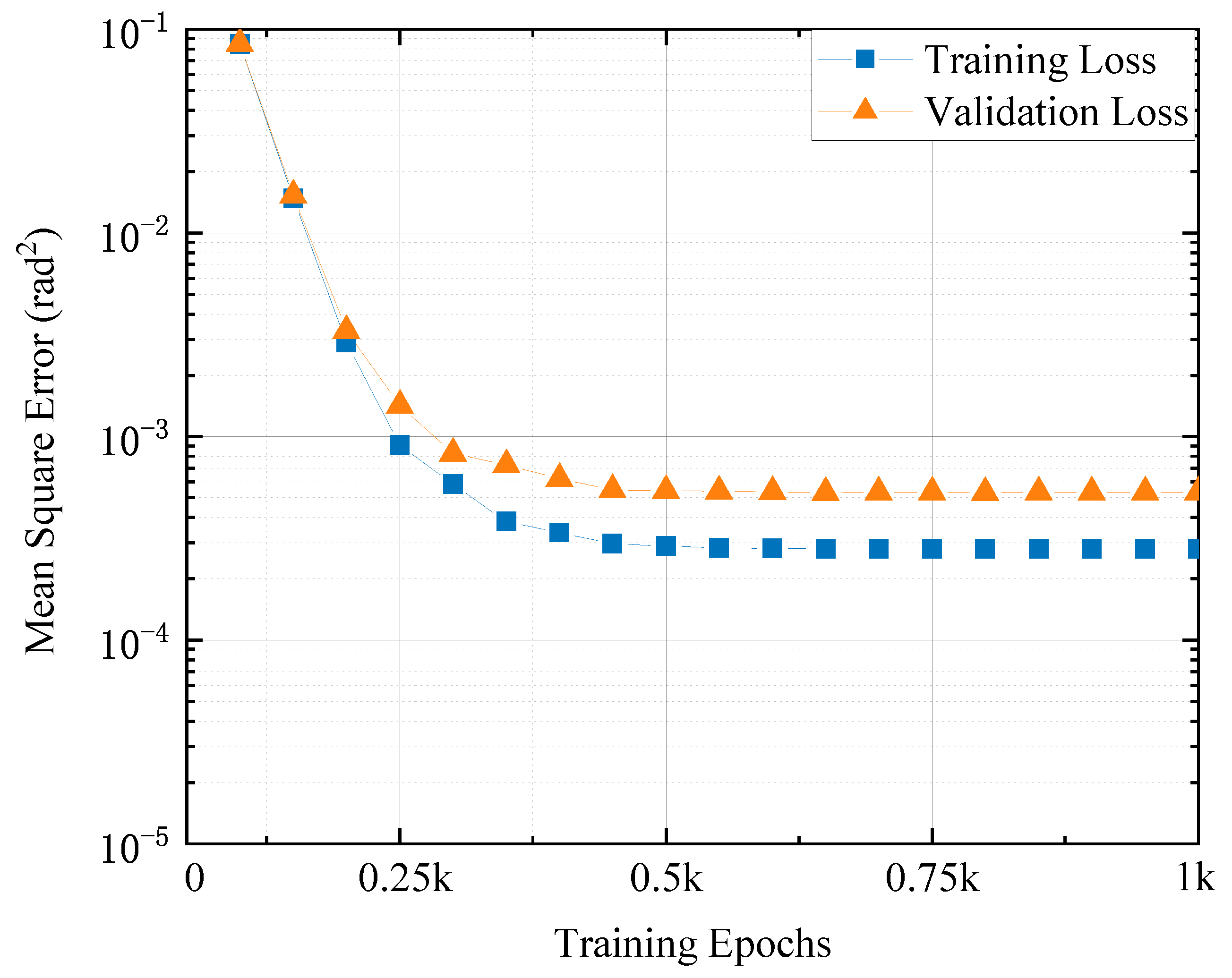
2.3.1. CNN Model
2.3.2. Phase Compensation
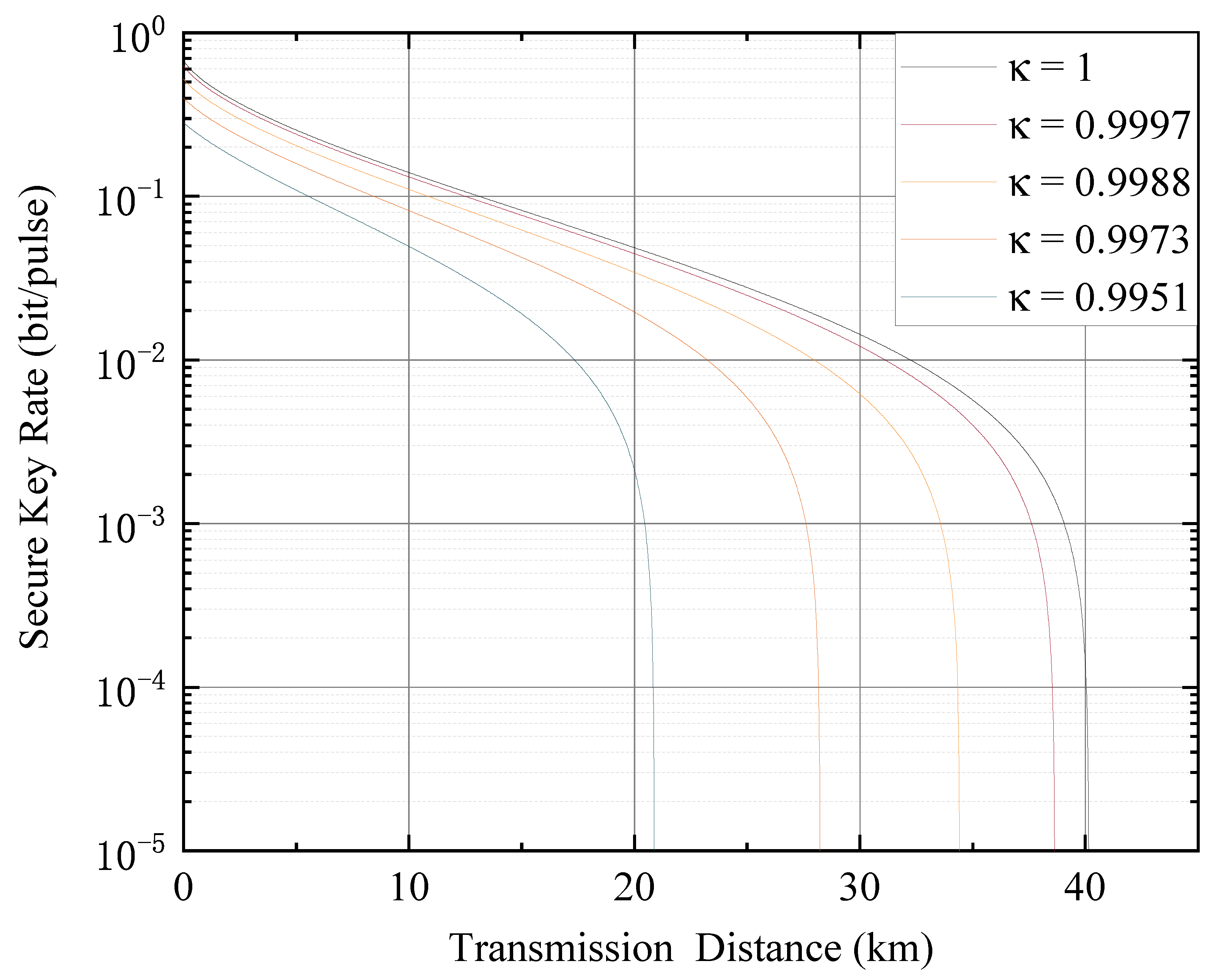
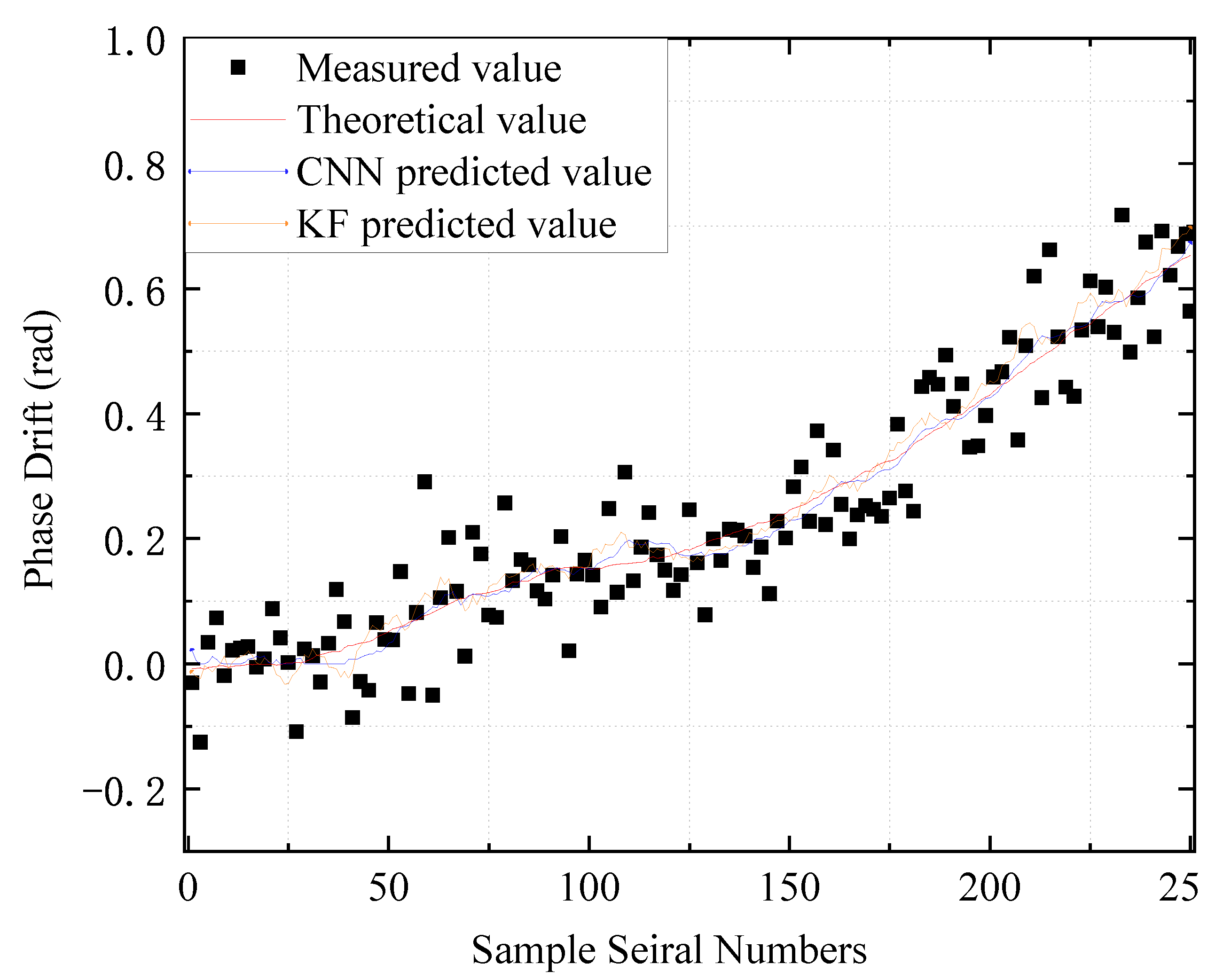
3. Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301. [Google Scholar] [CrossRef] [Green Version]
- Huang, D.; Lin, D.; Wang, C.; Liu, W.; Fang, S.; Peng, J.; Huang, P.; Zeng, G. Continuous-variable quantum key distribution with 1 Mbps secure key rate. Opt. Express 2015, 23, 17511–17519. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Huang, P.; Zhou, Y.; Liu, W.; Ma, H.; Wang, S.; Zeng, G. High key rate continuous-variable quantum key distribution with a real local oscillator. Opt. Express 2018, 26, 2794–2806. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Lv, G.; Zeng, G. Balancing continuous-variable quantum key distribution with source-tunable linear optics cloning machine. Quantum Inf. Process. 2015, 14, 4323–4338. [Google Scholar] [CrossRef]
- Li, J.; Guo, Y.; Wang, X.; Xie, C.; Zhang, L.; Huang, D. Discrete-modulated continuous-variable quantum key distribution with a machine-learning-based detector. Opt. Eng. 2018, 57, 066109. [Google Scholar] [CrossRef]
- Grosshans, F.; Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [Green Version]
- Jouguet, P.; Kunz-Jacques, S.; Diamanti, E. Preventing calibration attacks on the local oscillator in continuous-variable quantum key distribution. Phys. Rev. A 2013, 87, 062313. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Li, Y.; Mao, Y.; Guo, Y. Counteracting a Saturation Attack in Continuous-Variable Quantum Key Distribution Using an Adjustable Optical Filter Embedded in Homodyne Detector. Entropy 2022, 24, 383. [Google Scholar] [CrossRef]
- Qin, H.; Kumar, R.; Alléaume, R. Quantum hacking: Saturation attack on practical continuous-variable quantum key distribution. Phys. Rev. A 2016, 94, 012325. [Google Scholar] [CrossRef] [Green Version]
- Ma, G.L. Decomposition of the jet fragmentation function in high-energy heavy-ion collisions. Phys. Rev. C 2013, 88, 021902. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Local oscillator fluctuation opens a loophole for Eve in practical continuous-variable quantum-key-distribution systems. Phys. Rev. A 2013, 88, 022339. [Google Scholar] [CrossRef] [Green Version]
- Qi, B.; Lougovski, P.; Pooser, R.; Grice, W.; Bobrek, M. Generating the local oscillator “locally” in continuous-variable quantum key distribution based on coherent detection. Phys. Rev. X 2015, 5, 041009. [Google Scholar] [CrossRef] [Green Version]
- Soh, D.B.; Brif, C.; Coles, P.J.; Lütkenhaus, N.; Camacho, R.M.; Urayama, J.; Sarovar, M. Self-referenced continuous-variable quantum key distribution protocol. Phys. Rev. X 2015, 5, 041010. [Google Scholar] [CrossRef] [Green Version]
- Juodawlkis, P.W.; Twichell, J.C.; Wasserman, J.L.; Betts, G.E.; Williamson, R.C. Measurement of mode-locked laser timing jitter by use of phase-encoded optical sampling. Opt. Lett. 2001, 26, 289–291. [Google Scholar] [CrossRef]
- Huang, P.; Lin, D.K.; Huang, D.; Zeng, G.H. Security of continuous-variable quantum key distribution with imperfect phase compensation. Int. J. Theor. Phys. 2015, 54, 2613–2622. [Google Scholar] [CrossRef]
- Liu, W.; Huang, P.; Peng, J.; Fan, J.; Zeng, G. Integrating machine learning to achieve an automatic parameter prediction for practical continuous-variable quantum key distribution. Phys. Rev. A 2018, 97, 022316. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Y.; Huang, D. Kalman filter-based phase estimation of continuous-variable quantum key distribution without sending local oscillator. Phys. Rev. A 2019, 383, 2394–2399. [Google Scholar] [CrossRef]
- Chin, H.M.; Jain, N.; Zibar, D. Machine learning aided carrier recovery in continuous-variable quantum key distribution. Npj Quantum Inf. 2021, 7, 20. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, Y.; Zhang, L.; Ruan, X.; Huang, D. Neural Network-Powered Nonlinear Compensation Framework for High-Speed Continuous Variable Quantum Key Distribution. IEEE Photonics J. 2022, 14, 1–8. [Google Scholar] [CrossRef]
- Cavaliere, F.; Prati, E.; Poti, L.; Muhammad, I.; Catuogno, T. Secure quantum communication technologies and systems: From labs to markets. Quantum Rep. 2020, 2, 80–106. [Google Scholar] [CrossRef] [Green Version]
- Mao, Y.; Huang, W.; Zhong, H.; Wang, Y.; Qin, H.; Guo, Y.; Huang, D. Detecting quantum attacks: A machine learning based defense strategy for practical continuous-variable quantum key distribution. New J. Phys. 2020, 22, 083073. [Google Scholar] [CrossRef]
- He, Z.; Wang, Y.; Huang, D. Wavelength attack recognition based on machine learning optical spectrum analysis for the practical continuous-variable quantum key distribution system. JOSA B 2020, 37, 1689–1697. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, Y.; Huang, W.; Qin, H.; Huang, D.; Guo, Y. Hidden-Markov-model-based calibration-attack recognition for continuous-variable quantum key distribution. Phys. Rev. A 2020, 101, 062320. [Google Scholar] [CrossRef]
- Wang, T.; Huang, P.; Zhou, Y.; Liu, W.; Zeng, G. Pilot-multiplexed continuous-variable quantum key distribution with a real local oscillator. Phys. Rev. A 2018, 97, 012310. [Google Scholar] [CrossRef]
- Wang, H.; Pi, Y.; Huang, W.; Li, Y.; Shao, Y.; Yang, J.; Liu, J.; Zhang, C.; Zhang, Y.; Xu, B. High-speed Gaussian-modulated continuous-variable quantum key distribution with a local local oscillator based on pilot-tone-assisted phase compensation. Opt. Express 2020, 28, 32882–32893. [Google Scholar] [CrossRef]
- VanWiggeren, G.D.; Roy, R. Transmission of linearly polarized light through a single-mode fiber with random fluctuations of birefringence. Appl. Opt. 1999, 38, 3888–3892. [Google Scholar] [CrossRef] [Green Version]
- Biao, H.; Tiantian, M.; Yongmei, H.; Zhenming, P. Least Square Algorithm for Phase Estimation in Continuous-Variable Quantum Key Distribution. Laser Optoelectron. Prog. 2021, 58, 1127001. [Google Scholar]
- Biao, H.; Yongmei, H.; Zhenming, P. Attack and Detectionon Reference-Pulse Phase of Continuous-Variable Quantum-Key Distribution. Acta Opt. Sin. 2019, 39, 327–333. [Google Scholar]
- Huang, D.; Huang, P.; Lin, D.; Wang, C.; Zeng, G. High-speed continuous-variable quantum key distribution without sending a local oscillator. Opt. Lett. 2015, 40, 3695–3698. [Google Scholar] [CrossRef]
- Zhao, W.; Shi, R.; Huang, D. Practical security analysis of reference pulses for continuous-variable quantum key distribution. Sci. Rep. 2019, 9, 18155. [Google Scholar] [CrossRef]
- Huang, B.; Huang, Y.; Peng, Z. Tracking reference phase with a Kalman filter in continuous-variable quantum key distribution. Opt. Express 2020, 28, 28727–28739. [Google Scholar] [CrossRef]
- Liu, F.; Lin, G.; Shen, C. CRF learning with CNN features for image segmentation. Pattern Recognit. 2015, 48, 2983–2992. [Google Scholar] [CrossRef] [Green Version]
- Han, F.; Yao, J.; Zhu, H.; Wang, C. Underwater image processing and object detection based on deep CNN method. J. Sens. 2020, 2020, 6707328. [Google Scholar] [CrossRef]
- Huang, L.; He, M.; Tan, C.; Jiang, D.; Li, G.; Yu, H. Jointly network image processing: Multi-task image semantic segmentation of indoor scene based on CNN. IET Image Process. 2020, 14, 3689–3697. [Google Scholar] [CrossRef]
- Wu, H.; Huang, Q.; Wang, D.; Gao, L. A CNN-SVM combined model for pattern recognition of knee motion using mechanomyography signals. J. Electromyogr. Kinesiol. 2018, 42, 136–142. [Google Scholar] [CrossRef]
- Kwon, M.C.; Park, G.; Choi, S. Smartwatch user interface implementation using CNN-based gesture pattern recognition. Sensors 2018, 18, 2997. [Google Scholar] [CrossRef] [Green Version]
- Yin, W.; Kann, K.; Yu, M.; Schütze, H. Comparative study of CNN and RNN for natural language processing. arXiv 2017, arXiv:1702.01923. [Google Scholar]
- Li, H. Deep learning for natural language processing: Advantages and challenges. Natl. Sci. Rev. 2017, 5, 24–26. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar] [CrossRef]
- Wang, X.; Mao, D.; Li, X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2021, 173, 108518. [Google Scholar] [CrossRef]
- Qu, Z.; Djordjevic, I.B.; Neifeld, M.A. RF-subcarrier-assisted four-state continuous-variable QKD based on coherent detection. Opt. Lett. 2016, 41, 5507–5510. [Google Scholar] [CrossRef]
- Xu, B.; Tang, C.; Chen, H.; Zhang, W.; Zhu, F. Improving the maximum transmission distance of four-state continuous-variable quantum key distribution by using a noiseless linear amplifier. Phys. Rev. A 2013, 87, 062311. [Google Scholar] [CrossRef] [Green Version]
- Djordjevic, I.B. Optimized-eight-state CV-QKD protocol outperforming Gaussian modulation based protocols. IEEE Photonics J. 2019, 11, 1–10. [Google Scholar] [CrossRef]
- Qu, Z.; Djordjevic, I.B. Four-dimensionally multiplexed eight-state continuous-variable quantum key distribution over turbulent channels. IEEE Photonics J. 2017, 9, 1–8. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Z.; Li, X.; Ruan, X.; Luo, Y.; Zhang, H. Phase Compensation for Continuous Variable Quantum Key Distribution Based on Convolutional Neural Network. Photonics 2022, 9, 463. https://doi.org/10.3390/photonics9070463
Xing Z, Li X, Ruan X, Luo Y, Zhang H. Phase Compensation for Continuous Variable Quantum Key Distribution Based on Convolutional Neural Network. Photonics. 2022; 9(7):463. https://doi.org/10.3390/photonics9070463
Chicago/Turabian StyleXing, Zhuangzhuang, Xingqiao Li, Xinchao Ruan, Yong Luo, and Hang Zhang. 2022. "Phase Compensation for Continuous Variable Quantum Key Distribution Based on Convolutional Neural Network" Photonics 9, no. 7: 463. https://doi.org/10.3390/photonics9070463




