A Multichannel Superconductor-Based Photonic Crystal Optical Filter Tunable in the Visible and Telecom Windows at Cryogenic Temperature
Abstract
:1. Introduction
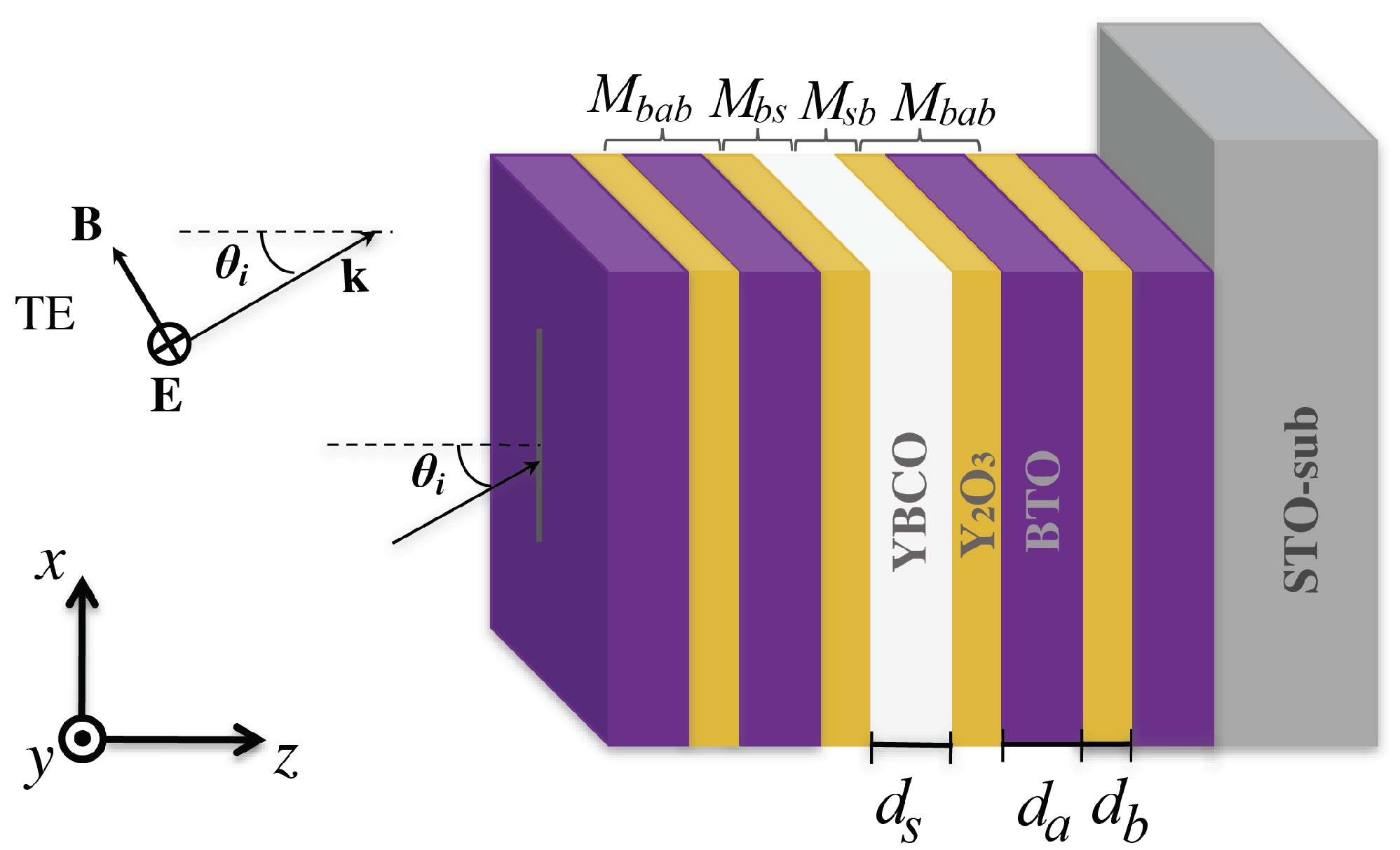
2. Theoretical Framework
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yablonovitch, E. Photonic crystals. J. Mod. Opt. 1994, 41, 173–194. [Google Scholar] [CrossRef]
- Vinet, L.; Zhedanov, A. Photonic Crystals: Physics and Technology; Springer: Milan, Italy, 2008. [Google Scholar]
- McGurn, A. Nanophotonics; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Yoshino, K.; Shimoda, Y.; Kawagishi, Y.; Nakayama, K.; Ozaki, M. Temperature tuning of the stop band in transmission spectra of liquid-crystal infiltrated synthetic opal as tunable photonic crystal. Appl. Phys. Lett. 1999, 75, 932. [Google Scholar] [CrossRef]
- Li, H.; Low, M.X.; Ako, R.T.; Bhaskaran, M.; Sriram, S.; Withayachumnankul, W.; Kuhlmey, B.T.; Atakaramians, S. Broadband Single-Mode Hybrid Photonic Crystal Waveguides for Terahertz Integration on a Chip. Adv. Mater. Technol. 2020, 5, 2000117. [Google Scholar] [CrossRef]
- Clementi, M.; Iadanza, S.; Schulz, S.A.; Urbinati, G.; Gerace, D.; O’Faloain, L.; Galli, M. Thermo-Optically Induced Transparency on a photonic chip. Light Sci. Appl. 2021, 10, 240. [Google Scholar] [CrossRef]
- Mbakop, F.K.; Tom, A.; Dadjé, A.; Vidal, A.K.C.; Djongyang, N. One-dimensional comparison of TiO2/SiO2 and Si/SiO2 photonic crystals filters for thermophotovoltaic applications in visible and infrared. Chin. J. Phys. 2020, 67, 124. [Google Scholar] [CrossRef]
- Soltani, O.; Zaghdoudi, J.; Kanzari, M. Tunable filter properties in 1D linear graded magnetized cold plasma photonic crystals based on Octonacci quasi-periodic structure. Photonics Nanostruct.-Fundam. Appl 2020, 38, 100744. [Google Scholar] [CrossRef]
- Sakata, R.; Ishizaki, K.; De Zoysa, M.; Fukuhara, S.; Inoue, T.; Tanaka, Y.; Iwata, K.; Hatsuda, R.; Yoshida, M.; Gelleta, J.; et al. Dually modulated photonic crystals enabling high-power high-beam-quality two-dimensional beam scanning lasers. Nat. Commun. 2020, 11, 3487. [Google Scholar] [CrossRef]
- Butler, S.M.; Singaravelu, P.K.J.; O’Faolain, L.; Hegarty, S.P. Long cavity photonic crystal laser in FDML operation using an akinetic reflective filter. Opt. Express 2020, 28, 38813. [Google Scholar] [CrossRef]
- Shi, C.; Yuan, J.; Luo, X.; Shi, S.; Lu, S.; Yuan, P.; Xu, W.; Chen, Z.; Yu, H. Transmission characteristics of multi-structure bandgap for lithium niobate integrated photonic crystal and waveguide. Opt. Commun. 2020, 461, 125222. [Google Scholar] [CrossRef]
- Baghbadorani, H.K.; Barvestani, J. Sensing improvement of 1D photonic crystal sensors by hybridization of defect and Bloch surface modes. Appl. Surf. Sci. 2021, 537, 147730. [Google Scholar] [CrossRef]
- Mehaney, A.; Abadla, M.M.; Elsayed, H.A. 1D porous silicon photonic crystals comprising Tamm/Fano resonance as high performing optical sensors. J. Mol. Liq. 2021, 322, 114978. [Google Scholar] [CrossRef]
- Delgado-Sanchez, J.M.; Lillo-Bravo, I. Angular dependence of photonic crystal coupled to photovoltaic solar cell. Appl. Sci. 2020, 10, 1574. [Google Scholar] [CrossRef] [Green Version]
- Zheng, W.; Luo, X.; Zhang, Y.; Ye, C.; Qin, A.; Cao, Y.; Hou, L. Efficient Low-Cost All-Flexible Microcavity Semitransparent Polymer Solar Cells Enabled by Polymer Flexible One-Dimensional Photonic Crystals. ACS Appl. Mater. Interfaces 2020, 12, 23190. [Google Scholar] [CrossRef] [PubMed]
- Aly, A.H.; Ghany, S.E.A.; Kamal, B.M.; Vigneswaran, D. Theoretical studies of hybrid multifunctional (YBa2Cu3O7-X) photonic crystals within visible and infra-red regions. Ceram. Int. 2020, 46, 365. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Aly, A.H. Theoretical Study of a Tunable Low-Temperature Photonic Crystal Sensor Using Dielectric-Superconductor Nanocomposite Layers. J. Supercond. Nov. Magn. 2020, 33, 2983. [Google Scholar] [CrossRef]
- González, L.E.; Ordoñez, J.E.; Zambrano, G.; Porras-Montenegro, N. YBa2Cu3O7/BaTiO3 1D Superconducting Photonic Crystal with Tunable Broadband Response in the Visible Range. J. Supercond. Nov. Magn. 2018, 31, 2003. [Google Scholar] [CrossRef]
- González, L.E.; Ordoñez, J.E.; Carlos, A.; Melo, L.; Mendoza, E.; Reyes, D.; Zambrano, G.; Porras-Montenegro, N.; Granada, J.C.; Gómez, M.E.; et al. Experimental realisation of tunable ferroelectric/superconductor (BTO/YBCO)N/STO 1D photonic crystals in the whole visible spectrum. Sci. Rep. 2020, 10, 13083. [Google Scholar] [CrossRef]
- Segal, N.; Keren-Zur, S.; Hendler, N.; Ellenbogen, T. Controlling light with metamaterial-based nonlinear photonic crystals. Nat. Photonics 2015, 9, 180. [Google Scholar] [CrossRef]
- Schlafmann, K.R.; White, T.J. Retention and Deformation of the Blue Phases in Liquid Crystalline Elastomers. Nat. Commun. 2021, 12, 4916. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Z.; Yang, H.; Wen, L.; Yi, Z.; Zhou, Z.; Dai, B.; Zhang, J.; Wu, X.; Wu, P. Mult-mode Surface plasmon resonance absorber base don dat-type single-layer graphene. RSC Adv. 2022, 12, 7821. [Google Scholar] [CrossRef]
- Soltani, O.; Francoeur, S.; Baraket, Z.; Kanzari, M. Tunable polychromatic filters based on semiconductor-superconductor-dielectric periodic and quasi-periodic hybrid photonic crystal. Opt. Mater. 2020, 111, 110690. [Google Scholar] [CrossRef]
- Hao, J.; Gu, K.; Xia, L.; Liu, Y.; Yang, Z.; Yang, H. Research on low-temperature blood tissues detection biosensor based on one-dimensional superconducting photonic crystal. Commun. Nonlinear Sci. Numer. Simulat. 2020, 89, 105299. [Google Scholar] [CrossRef]
- Ravanamma, R.; Reddy, K.M.; Krishnaiah, K.V.; Ravi, N. Structure and morphology of yttrium doped barium titanate ceramics for multi-layer capacitor applications. Mater. Today Proc. 2021, 46, 259. [Google Scholar] [CrossRef]
- Yang, Q.; Deng, J.; Wang, G.; Deng, Q.; Zhao, J.; Dai, Y.; Duan, P.; Cui, M.; Kong, L.; Gao, H.; et al. The physical properties and microstructure of BiFeO3/YBCO heterostructures. Vacuum 2019, 167, 313–318. [Google Scholar] [CrossRef]
- Chacón, M.; Bolaños, G.; Lopera, W.; Prieto, P. Tunneling Characteristics of Epitaxial YBa2Cu3O7-x/Y2O3/YBa2Cu3O7-x Planar Type Junctions. Phys. Supercond. 1997, 287, 711. [Google Scholar] [CrossRef]
- Li, L. Ferroelectric/superconductor heterostructure. Mater. Sci. Eng. R Rep. 2000, 29, 153. [Google Scholar] [CrossRef]
- Macleod, H.A. Thin-Film Optical Filters; Taylor & Francis: Boca Ratón, FL, USA, 2018. [Google Scholar]
- Won, R. Is it crunch time? Nat. Photonics 2015, 9, 424. [Google Scholar] [CrossRef]
- Lian, J.; Vatansever, Z.; Noshad, M.; Brandt-Pearce, M. Indoor visible light communications, networking, and applications. J. Phys. Photonics 2019, 1, 012001. [Google Scholar] [CrossRef] [Green Version]
- Haas, H.; Elmirghani, J.; White, I. Optical Wireless Communication. Philos. Trans. R. Soc. A 2020, 378, 20200051. [Google Scholar] [CrossRef] [Green Version]
- Eriksson, T.A.; Hirano, T.; Puttnam, B.J.; Rademacher, G.; Luís, R.S.; Fujiwara, M.; Namiki, R.; Awaji, Y.; Takeoka, M.; Wada, N.; et al. Wavelength división multiplexing of continuous variable quantum key distribution and 18.3 Tbit/s data channels. Commun. Phys. 2019, 2, 9. [Google Scholar] [CrossRef] [Green Version]
- Feng, C.; Ying, Z.; Zhao, Z.; Gu, J.; Pan, D.Z.; Chen, R.T. Wavelength división multiplexing (WDM) based integrated electronic-photonic switching network (EPSN) for high-speed data processing and transportation. Nanophotonics 2020, 9, 4579. [Google Scholar] [CrossRef]
- Chhipa, M.K.; Radhouene, M.; Robinson, S.; Suthar, B. Improved dropping efficiency in two-dimensional photonic crystal-based channel drop filter for coarse wavelength división multiplexing application. Opt. Eng. 2017, 56, 015107. [Google Scholar] [CrossRef]
- Sabne, A.; Panda, A.; More, V. Simplified Wavelength Division Multiplexing in Visible Light Communication by Using RGB LED as Frequency Selective Receiver. In Proceedings of the 10th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kanpur, India, 6–8 July 2019; p. 45670. [Google Scholar]
- Zhang, H.; Lu, Y.; Duan, L.; Zhao, Z.; Shi, W.; Yao, J. Intracavity absorption multiplexed sensor network based on dense wavelength division multiplexing filter. Opt. Express 2014, 22, 24546. [Google Scholar] [CrossRef] [PubMed]
- Minoli, D. Telecommunications Technology Handbook; Artech House: London, UK, 2003. [Google Scholar]
- Cavalcanti, S.B.; de Dios-Leyva, M.; Reyes-Gómez, E.; Oliveira, L.E. Photonic band structure and symmetry properties of electromagnetic modes in photonic crystals. Phys. Rev. E 2007, 75, 026607. [Google Scholar] [CrossRef] [Green Version]
- Markos, P.; Soukoulis, C. Wave Propagation: From Electrons to Photonic Crystals and Left-Handed Materials; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Deng, Y.; Cao, G.; Yang, H.; Zhou, X.; Wu, Y. Dynamic control of double plasmon-induced transparencies in aperture-coupled waveguide-cavity system. Plasmonics 2018, 13, 345. [Google Scholar] [CrossRef]
- Zheng, Z.; Luo, Y.; Yang, H.; Yi, Z.; Zhang, J.; Song, Q.; Yang, W.; Liu, C.; Wu, X.; Wu, P. Thermal tuning of teraherzt metamaterial absorber properties based on VO2. Phys. Chem. Chem. Phys. 2022, 24, 8846. [Google Scholar] [CrossRef]
- Orlando, T.; Delin, K. Foundations of Applied Superconductivity; Electrical Engineering Series; Addison-Wesley: Boston, MA, USA, 1991. [Google Scholar]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Karothu, D.P.; Dushaq, G.; Ahmed, E.; Catalano, L.; Polavaram, S.; Ferreira, R.; Li, L.; Mohamed, S.; Rasras, M.; Naumov, P. Mechanically robust amino acid crystals as fiber-optic transducers and wide bandpass filters for optical communication in the near-infrared. Nat. Commun. 2021, 12, 1326. [Google Scholar] [CrossRef]
- Wemple, S.; Didomenico, M.; Camlibel, I. Dielectric and optical properties of melt-grown BaTiO3. J. Phys. Chem. Solids 1968, 29, 1797. [Google Scholar] [CrossRef]
- Kay, H.F.; Vousden, P. Symmetry changes in barium titanate at low temperatures and their relation to its ferroelectric properties. Philos. Mag. J. Sci. 1949, 40, 1019. [Google Scholar] [CrossRef]
- Merz, W.J. The Electric and Optical Behavior of BaTiO3 Single-Domain Crystals. Phys. Rev. 1949, 76, 1221. [Google Scholar] [CrossRef]
- Nigara, Y. Measurement of the optical constants of Yttrium Oxide. Jpn. J. Appl. Phys. 1968, 7, 404. [Google Scholar] [CrossRef]
- Skorobogatiy, M.; Yang, J. Fundamentals of Photonic Crystal Guiding; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Zhang, J.; Wu, R.; Wang, M.; Fang, Z.; Lin, J.; Zhou, J.; Gao, R.; Chu, W.; Cheng, Y. High-index-contrast single-mode optical waveguides fabricated on lithium niobate by photolithography assisted chemo-mechanical etching. Jpn. J. Appl. Phys. 2020, 59, 086503. [Google Scholar] [CrossRef]
- Deng, Y.; Cao, G.; Wu, Y.; Zhou, X.; Liao, W. Theoretical description of dynamic transmission characteristics in MDM waveguide apertura-side-coupled with ring cavity. Plasmonics 2015, 10, 1537. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, L.E.; Segura-Gutierrez, L.M.; Ordoñez, J.E.; Zambrano, G.; Reina, J.H. A Multichannel Superconductor-Based Photonic Crystal Optical Filter Tunable in the Visible and Telecom Windows at Cryogenic Temperature. Photonics 2022, 9, 485. https://doi.org/10.3390/photonics9070485
González LE, Segura-Gutierrez LM, Ordoñez JE, Zambrano G, Reina JH. A Multichannel Superconductor-Based Photonic Crystal Optical Filter Tunable in the Visible and Telecom Windows at Cryogenic Temperature. Photonics. 2022; 9(7):485. https://doi.org/10.3390/photonics9070485
Chicago/Turabian StyleGonzález, Luz E., Lina M. Segura-Gutierrez, John E. Ordoñez, Gustavo Zambrano, and John H. Reina. 2022. "A Multichannel Superconductor-Based Photonic Crystal Optical Filter Tunable in the Visible and Telecom Windows at Cryogenic Temperature" Photonics 9, no. 7: 485. https://doi.org/10.3390/photonics9070485
APA StyleGonzález, L. E., Segura-Gutierrez, L. M., Ordoñez, J. E., Zambrano, G., & Reina, J. H. (2022). A Multichannel Superconductor-Based Photonic Crystal Optical Filter Tunable in the Visible and Telecom Windows at Cryogenic Temperature. Photonics, 9(7), 485. https://doi.org/10.3390/photonics9070485




