Desensitization Design Method for Freeform TMA Optical Systems Based on Initial Structure Screening
Abstract
:1. Introduction
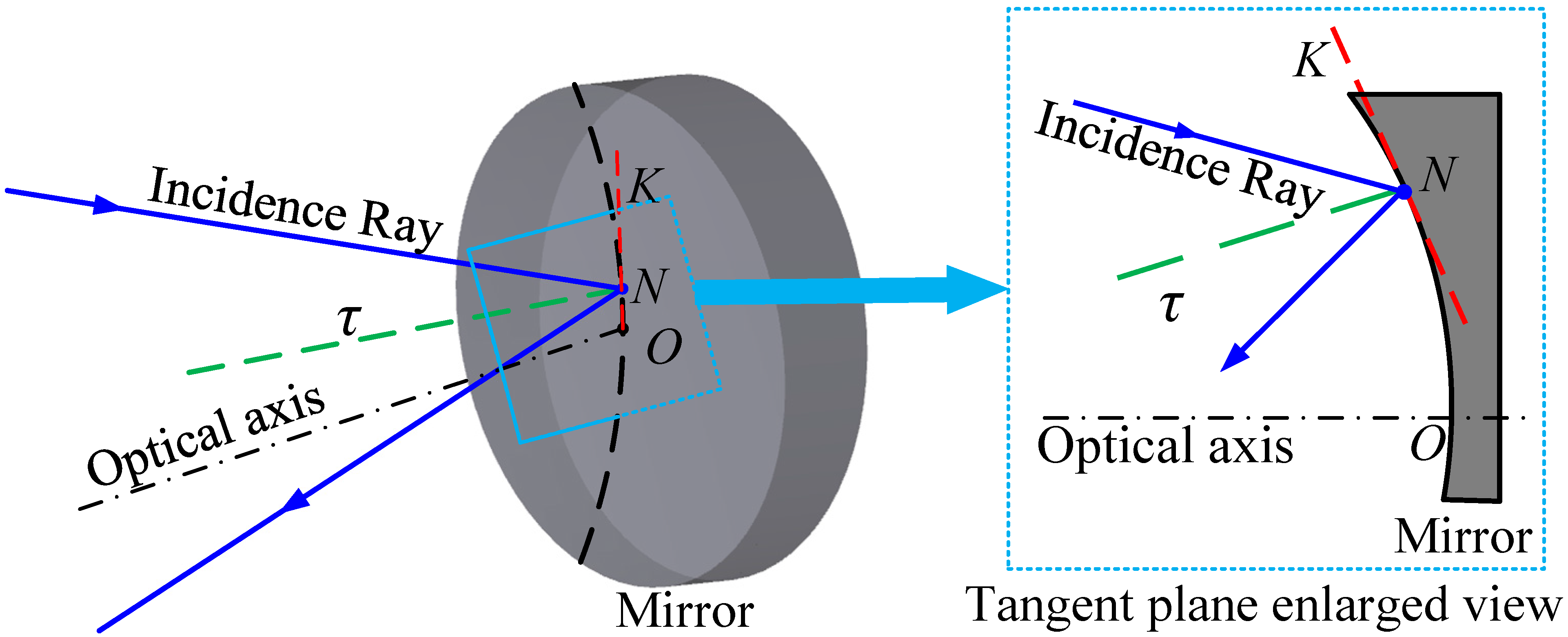
2. Error Sensitivity Evaluation Function for Freeform Surfaces
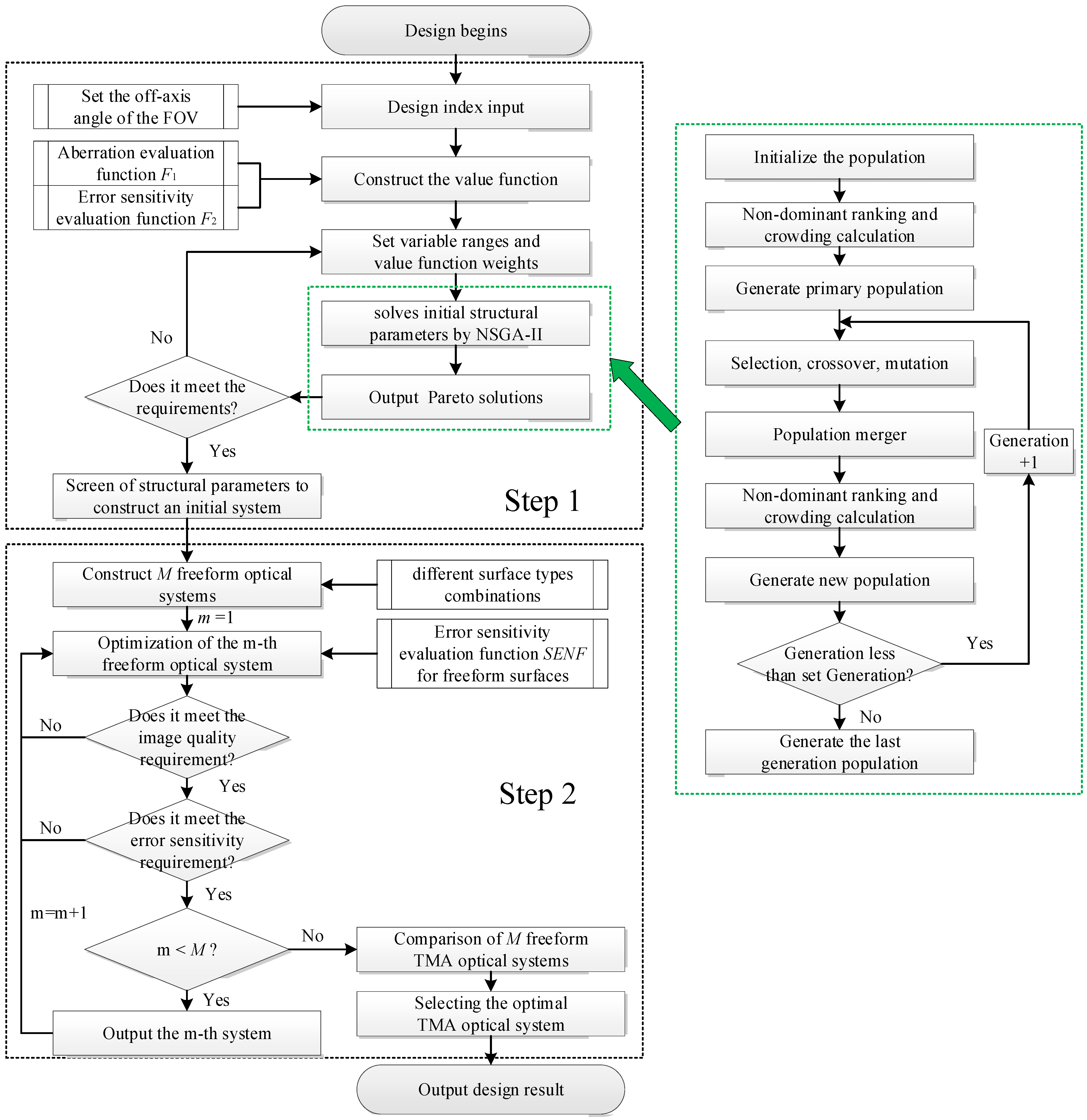
3. Design Method
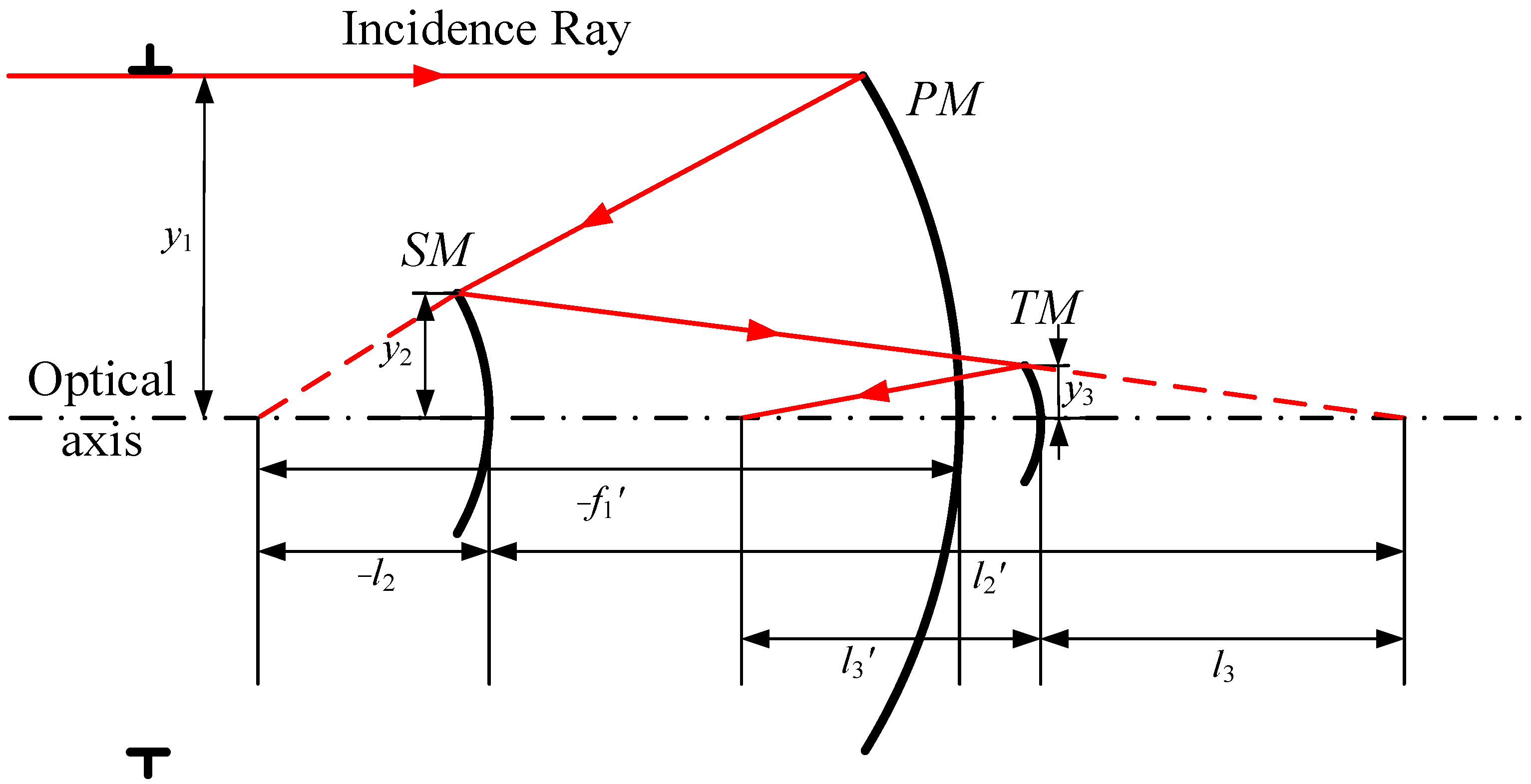
3.1. Initial Structure Construction
- (1)
- Aberration evaluation function F1
- (2)
- Error sensitivity evaluation function F2
3.2. Desensitization Design Method for Freeform Optical Systems
4. Design Example
5. Discussion
5.1. Discussion of Combined Design Methods
5.2. Discussion of Surface Type Combinations and Design Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Gong, T.; Jin, G.; Zhu, J. Design method for assembly-insensitive freeform reflective optical systems. Opt. Express 2018, 26, 27798–27811. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Wang, H.; Wang, K.; Wang, Y.; Ji, Z.; Wang, D. Off-axis three-mirror freeform telescope with a large linear field of view based on an integration mirror. Appl. Opt. 2016, 55, 8962–8970. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zheng, L.; He, X.; Wang, L.; Zhang, F.; Yu, S.; Shi, G.; Zhang, B.; Liu, Q.; Wang, T. Design and fabrication of imaging optical systems with freeform surfaces. In Proceedings of the Current Developments in Lens Design and Optical Engineering XIII, San Diego, CA, USA, 11 October 2012; p. 848607. [Google Scholar]
- Fuerschbach, K.; Rolland, J.P.; Thompson, K.P. A new family of optical systems employing φ-polynomial surfaces. Opt. Express 2011, 19, 21919–21928. [Google Scholar] [CrossRef]
- Reimers, J.; Bauer, A.; Thompson, K.P.; Rolland, J.P. Freeform spectrometer enabling increased compactness. Light Sci. Appl. 2017, 6, e17026. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Zhu, J.; Jin, G. Design of free-form imaging systems with linear field-of-view using a construction and iteration process. Opt. Express 2014, 22, 3362–3374. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Hou, W.; Zhang, X.; Jin, G. Design of a low F-number free form off-axis three-mirror system with rectangular field-of-view. J. Opt. 2015, 17, 015605. [Google Scholar]
- Meng, Q.; Wang, H.; Liang, W.; Yan, Z.; Wang, B. Design of off-axis three-mirror systems with ultrawide field of view based on an expansion process of surface freeform and field of view. Appl. Opt. 2019, 58, 609–615. [Google Scholar] [CrossRef] [PubMed]
- Thompson, K. Description of the third-order optical aberrations of near-circular pupil optical systems without symmetry. J. Opt. Soc. Am. A 2005, 22, 1389–1401. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Wang, H.; Wang, W.; Yan, Z. Desensitization design method of unobscured three-mirror anastigmatic optical systems with an adjustment-optimization-evaluation process. Appl. Opt. 2018, 57, 1472–1481. [Google Scholar] [CrossRef]
- Grey, D. Tolerance sensitivity and optimization. Appl. Opt. 1970, 9, 523–526. [Google Scholar] [CrossRef]
- Wassermann, G.D.; Wolf, E. On the Theory of Aplanatic Aspheric Systems. Proc. Phys. Soc. Sect. B 1949, 62, 2–8. [Google Scholar] [CrossRef]
- Zhu, J.; Wu, X.; Yang, T.; Jin, G. Generating optical freeform surfaces considering both coordinates and normals of discrete data points. J. Opt. Soc. Am. A 2014, 31, 2401–2408. [Google Scholar] [CrossRef] [PubMed]
- Hicks, R.A. Controlling a ray bundle with a free-form reflector. Opt. Lett. 2008, 33, 1672–1674. [Google Scholar] [CrossRef] [PubMed]
- Minano, J.C.; Benitez, P.; Lin, W.; Infante, J.; Munoz, F.; Santamaria, A. An application of the SMS method for imaging designs. Opt. Express 2009, 17, 24036–24044. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duerr, F.; Benítez, P.; Miñano, J.C.; Meuret, Y.; Thienpont, H. Analytic design method for optimal imaging: Coupling three ray sets using two free-form lens profiles. Opt. Express 2012, 20, 5576–5585. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, T.; Jin, G.; Zhu, J. Automated design of freeform imaging systems. Light Sci. Appl. 2017, 6, e17081. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Jin, G.; Zhu, J. Towards automatic freeform optics design: Coarse and fine search of the three-mirror solution space. Light Sci. Appl. 2021, 10, 65. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Zhu, J.; Hou, W.; Jin, G. Design method of freeform off-axis reflective imaging systems with a direct construction process. Opt. Express 2014, 22, 9193–9205. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Zhu, J.; Wu, X.; Jin, G. Direct design of freeform surfaces and freeform imaging systems with a point-by-point three-dimensional construction-iteration method. Opt. Express 2015, 23, 10233–10246. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, Y.; Hao, Q.; Isshiki, M. Global and local optimization for optical systems. Optik 2006, 117, 111–117. [Google Scholar] [CrossRef]
- Vasiljevic, D. Optimization of the Cook triplet with the various evolution strategies and the damped least squares. In Proceedings of the Optical Design and Analysis Software, Denver, CO, USA, 27 September 1999; p. 207. [Google Scholar]
- Sturlesi, D.; O’Shea, D.C. The search for a global minimum in optical design. In Proceedings of the Optical Engineering and Commercial Optics, San Diego, CA, USA, 22 December 1989; p. 92. [Google Scholar]
- Kuper, T.; Harris, T. A New Look at Global Optimization for Optical Design. Photonics Spectra 1992, 1, 151–160. [Google Scholar]
- Forbes, G.; Jones, A. Global Optimization in Lens Design. Opt. Photonics News 1992, 3, 23–29. [Google Scholar] [CrossRef]
- Sturlesi, D.; O’Shea, D.C. Global view of optical design space. Opt. Eng. 1991, 30, 207–218. [Google Scholar] [CrossRef]
- Isshiki, M.; Gardner, L.; Gregory, G. Automated control of manufacturing sensitivity during optimization. In Proceedings of the Optical Design and Engineering, St. Etienne, France, 18 February 2004; Volume 5249, p. 343. [Google Scholar]
- Deng, Y.; Jin, G.; Zhu, J. Design method for freeform reflective-imaging systems with low surface-figure-error sensitivity. Chin. Opt. Lett. 2019, 17, 092201. [Google Scholar] [CrossRef]
- Sasian, J.; Descour, M. Power distribution and symmetry in lens systems. Opt. Eng. 1998, 37, 1001–1005. [Google Scholar] [CrossRef]
- Qin, Z.; Wang, X.; Ren, C.; Qi, Y.; Meng, Q. Design method for reflective optical system with low tilt error sensitivity. Opt. Express 2021, 29, 43464–43479. [Google Scholar] [CrossRef]
- Ma, B.; Sharma, K.; Thompson, K.P.; Rolland, J.P. Mobile device camera design with Q-type polynomials to achieve higher production yield. Opt. Express 2013, 21, 17454–17463. [Google Scholar] [CrossRef]
- Thompson, K.P.; Schiesser, E.; Rolland, J.P. Why are freeform telescopes less alignment sensitive than a traditional unobscured TMA? In Proceedings of the Optifab 2015, Rochester, New York, USA, 11 October 2015; Volume 9633, p. 963317. [Google Scholar]
- Fuerschbach, K.; Davis, G.E.; Thompson, K.P.; Rolland, J.P. Assembly of a freeform off-axis optical system employing three φ-polynomial Zernike mirrors. Opt. Lett. 2014, 39, 2896–2899. [Google Scholar] [CrossRef]
- Wang, L.; Sasian, J. Merit figures for fast estimating tolerance sensitivity in lens systems. In Proceedings of the International Optical Design Conference 2010, 9 September 2010; Jackson Hole, WY, USA; Volume 7652, p. 76521P.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comp. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.; Gross, H.; Broemel, A.; Kirschstein, S.; Petruck, P.; Tuennermann, A. Investigation of TMA systems with different freeform surfaces. In Proceedings of the Optical Systems Design 2015: Optical Design and Engineering VI, Jena, Germany, 23 September 2015; Volume 9626, p. 96260X. [Google Scholar]

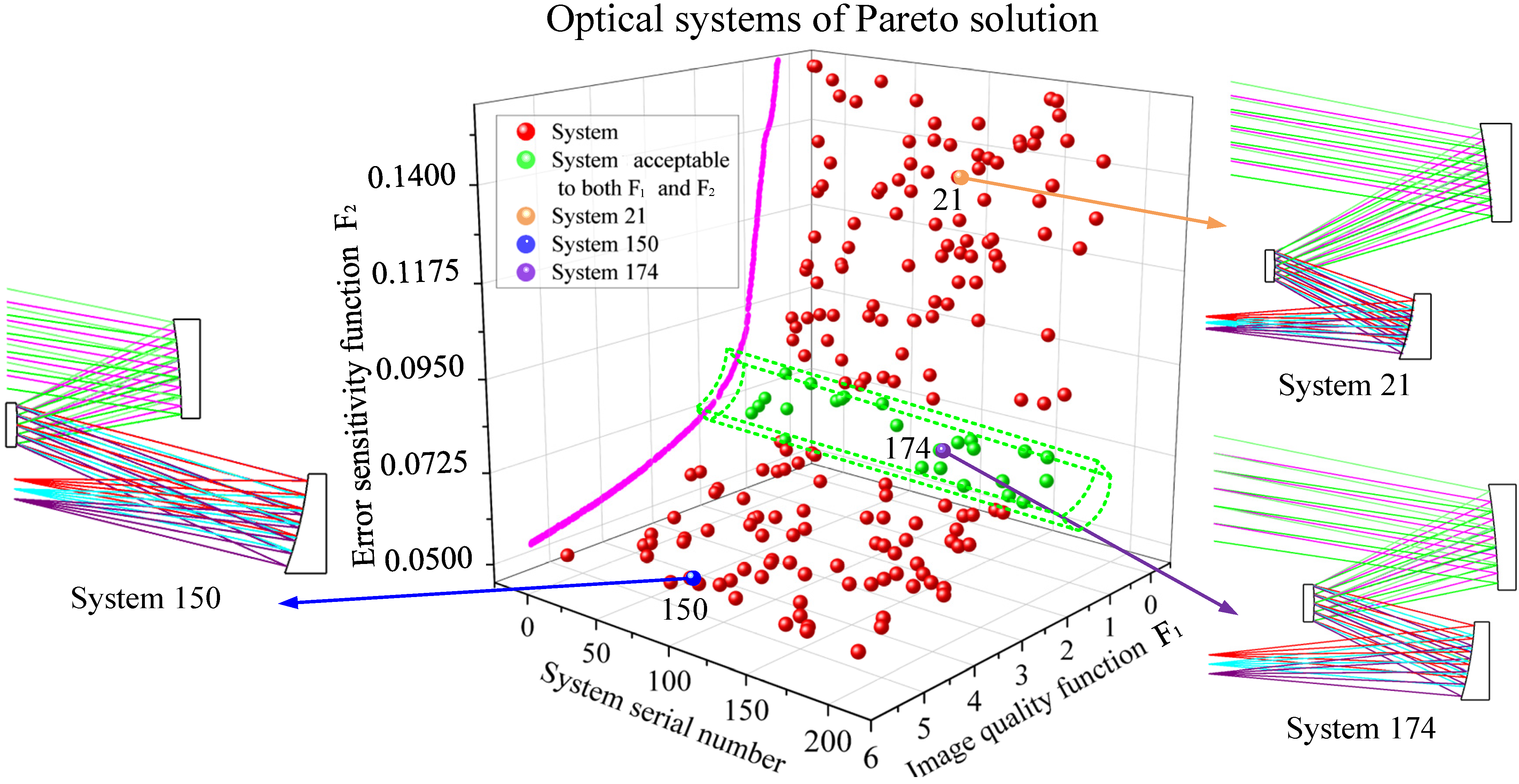

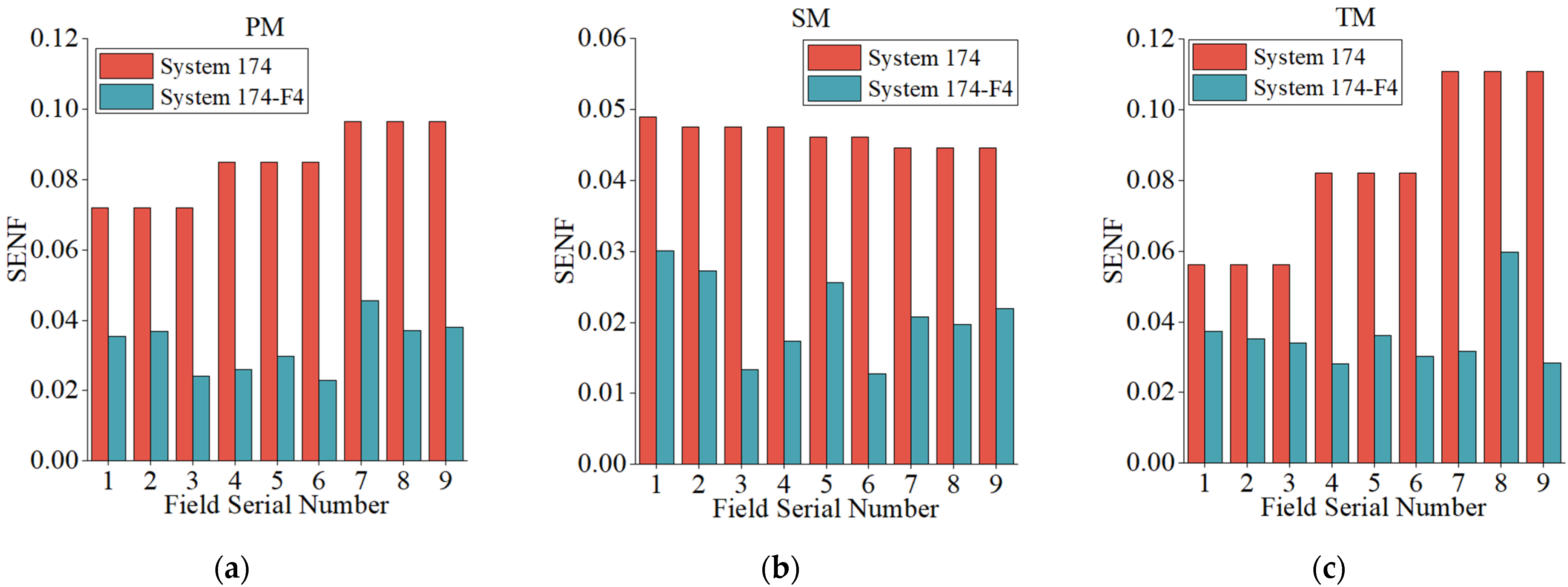
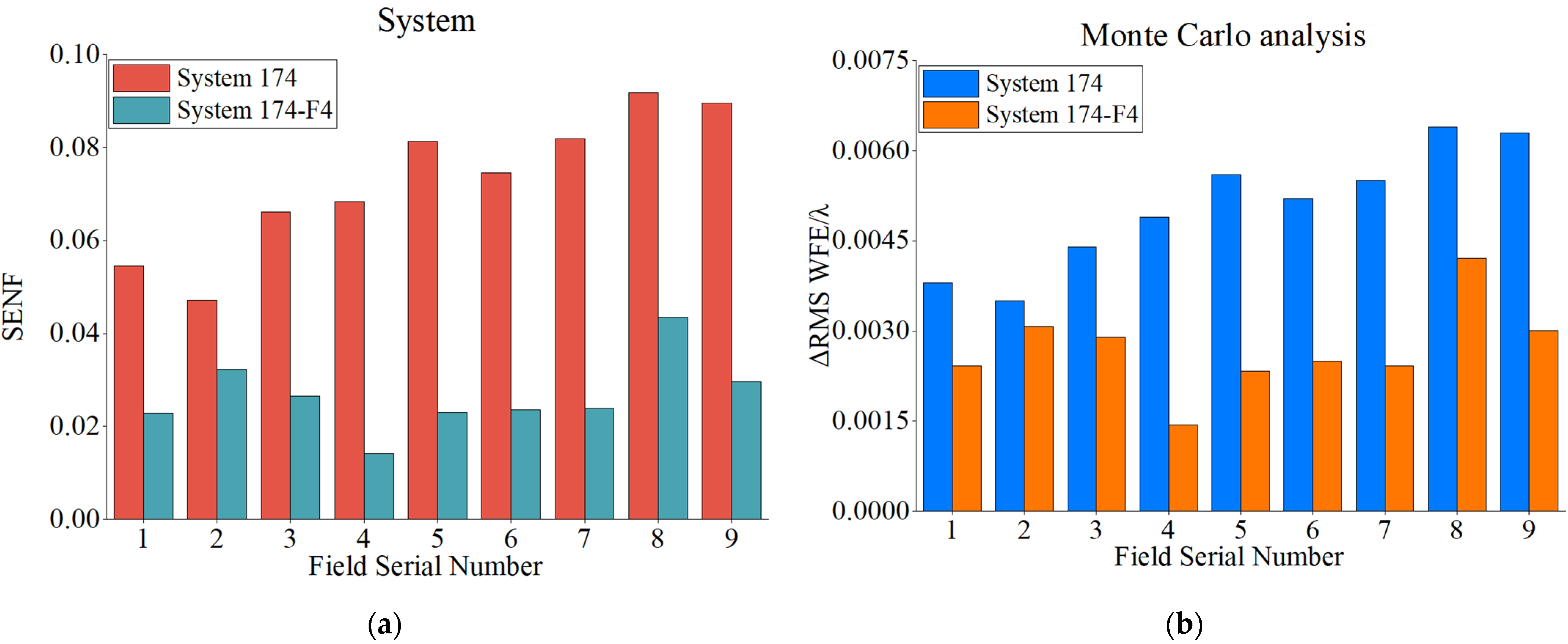
| System | α1 | α2 | β1 | β2 | e12 | e22 | e32 | F1 | F2 |
|---|---|---|---|---|---|---|---|---|---|
| 21 | 0.431 | 1.500 | 1.724 | 0.500 | −1.7066 | −0.9001 | −0.0228 | 0.3027 | 0.1247 |
| 150 | 0.500 | 1.601 | 1.999 | 0.350 | −0.6870 | −5.0000 | 0.3202 | 4.7812 | 0.0534 |
| 174 | 0.499 | 1.500 | 1.748 | 0.980 | −2.3071 | 0.0900 | 0.1430 | 1.0807 | 0.0728 |
| System | PM | SM | TM | RMS WFE/λ | SENFsystem |
|---|---|---|---|---|---|
| System 174 | Conic | Conic | Conic | 0.0645 | 0.0728 |
| System 174-F1 | XY polynomials | Fringe Zernike polynomials | Chebyshev polynomials | 0.0027 | 0.0687 |
| System 174-F2 | XY polynomials | Chebyshev polynomials | Fringe Zernike polynomials | 0.0081 | 0.0511 |
| System 174-F3 | Fringe Zernike polynomials | XY polynomials | Chebyshev polynomials | 0.0078 | 0.0477 |
| System 174-F4 | Chebyshev polynomials | Fringe Zernike polynomials | XY polynomials | 0.0026 | 0.0266 |
| System 174-F5 | Fringe Zernike polynomials | Chebyshev polynomials | XY polynomials | 0.0200 | 0.0289 |
| System 174-F6 | Chebyshev polynomials | XY polynomials | Fringe Zernike polynomials | 0.0040 | 0.0602 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Z.; Qi, Y.; Ren, C.; Wang, X.; Meng, Q. Desensitization Design Method for Freeform TMA Optical Systems Based on Initial Structure Screening. Photonics 2022, 9, 544. https://doi.org/10.3390/photonics9080544
Qin Z, Qi Y, Ren C, Wang X, Meng Q. Desensitization Design Method for Freeform TMA Optical Systems Based on Initial Structure Screening. Photonics. 2022; 9(8):544. https://doi.org/10.3390/photonics9080544
Chicago/Turabian StyleQin, Zichang, Yunsheng Qi, Chengming Ren, Xiaodong Wang, and Qingyu Meng. 2022. "Desensitization Design Method for Freeform TMA Optical Systems Based on Initial Structure Screening" Photonics 9, no. 8: 544. https://doi.org/10.3390/photonics9080544
APA StyleQin, Z., Qi, Y., Ren, C., Wang, X., & Meng, Q. (2022). Desensitization Design Method for Freeform TMA Optical Systems Based on Initial Structure Screening. Photonics, 9(8), 544. https://doi.org/10.3390/photonics9080544






