Antisymmetric Mode Cancellation for High-Q Cavities in a Double-Disk
Abstract
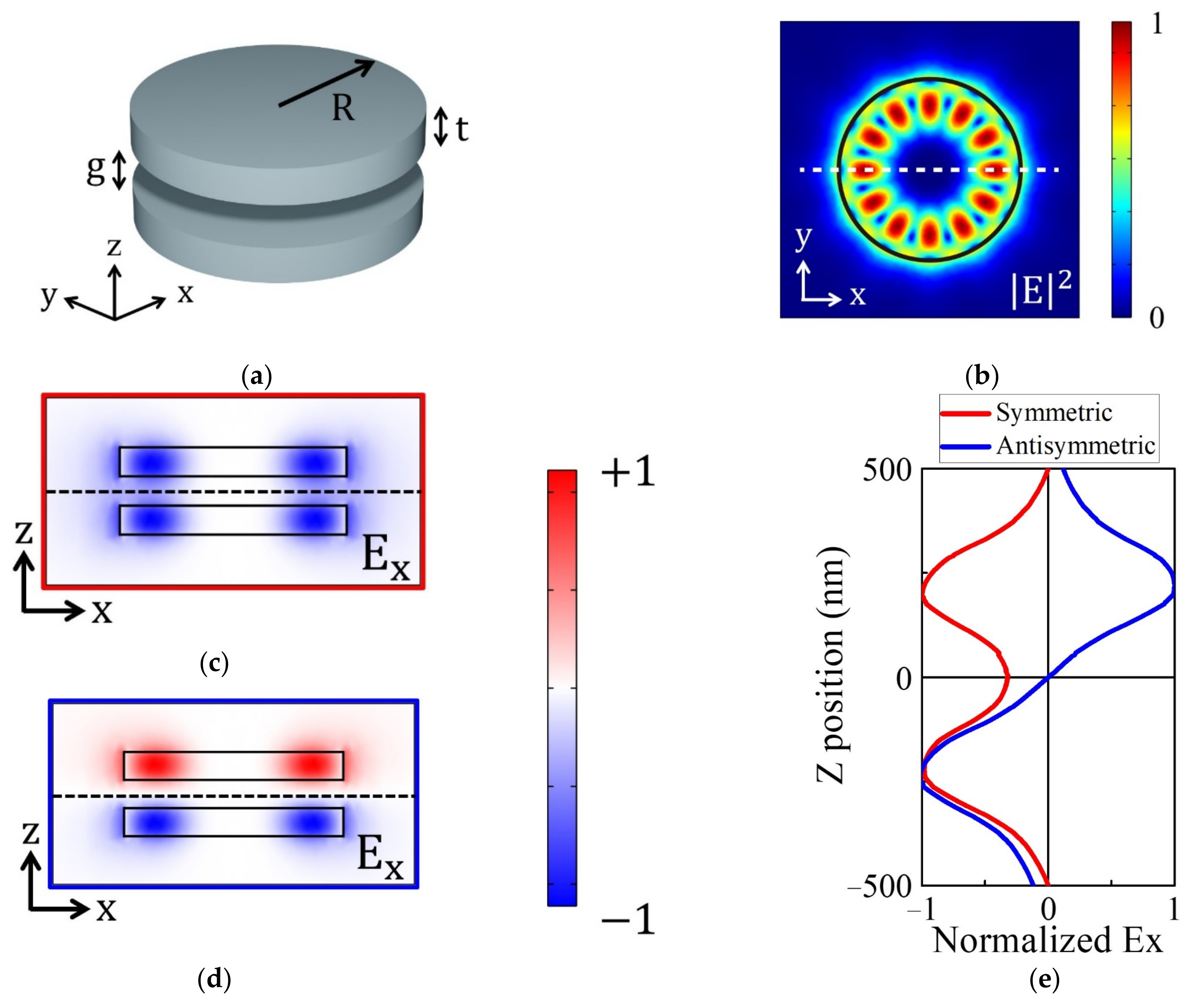
:1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akahane, Y.; Asano, T.; Song, B.S.; Noda, S. High-Q Photonic Nanocavity in a Two-Dimensional Photonic Crystal. Nature 2003, 425, 944–947. [Google Scholar] [CrossRef] [PubMed]
- Quan, Q.; Loncar, M. Deterministic Design of Wavelength Scale, Ultra-High Q Photonic Crystal Nanobeam Cavities. Opt. Express 2011, 19, 18529–18542. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Jiang, H.; Lin, Q.; Luo, R.; He, Y. High-Quality Lithium Niobate Photonic Crystal Nanocavities. Optica 2017, 4, 1251–1258. [Google Scholar] [CrossRef]
- Srinivasan, K.; Painter, O. Momentum Space Design of High-Q Photonic Crystal Optical Cavities. Opt. Express 2002, 10, 670–684. [Google Scholar] [CrossRef] [PubMed]
- Hunger, D.; Steinmetz, T.; Colombe, Y.; Deutsch, C.; Hänsch, T.W.; Reichel, J. A Fiber Fabry-Perot Cavity with High Finesse. New J. Phys. 2010, 12, 065038. [Google Scholar] [CrossRef]
- Shitikov, A.E.; Benderov, O.V.; Kondratiev, N.M.; Lobanov, V.E.; Rodin, A.V.; Bilenko, I.A. Microresonator and Laser Parameter Definition via Self-Injection Locking. Phys. Rev. Appl. 2020, 14, 064047. [Google Scholar] [CrossRef]
- Grossmann, T.; Schleede, S.; Hauser, M.; Christiansen, M.B.; Vannahme, C.; Eschenbaum, C.; Klinkhammer, S.; Beck, T.; Fuchs, J.; Nienhaus, G.U.; et al. Low-Threshold Conical Microcavity Dye Lasers. Appl. Phys. Lett. 2010, 97, 063304. [Google Scholar] [CrossRef]
- He, L.; Özdemir, Ş.K.; Yang, L. Whispering Gallery Microcavity Lasers. Laser Photon. Rev. 2013, 7, 60–82. [Google Scholar] [CrossRef]
- Bianchetti, A.; Federico, A.; Vincent, S.; Subramanian, S.; Vollmer, F. Refractometry-Based Air Pressure Sensing Using Glass Microspheres as High-Q Whispering-Gallery Mode Microresonators. Opt. Commun. 2017, 394, 152–156. [Google Scholar] [CrossRef]
- Zhu, J.; Ozdemir, S.K.; Xiao, Y.F.; Li, L.; He, L.; Chen, D.R.; Yang, L. On-Chip Single Nanoparticle Detection and Sizing by Mode Splitting in an Ultrahigh-Q Microresonator. Nat. Photonics 2010, 4, 46–49. [Google Scholar] [CrossRef]
- Little, B.E.; Chu, S.T.; Haus, H.A.; Foresi, J.; Laine, J.P. Microring Resonator Channel Dropping Filters. J. Light. Technol. 1997, 15, 998–1005. [Google Scholar] [CrossRef]
- Lee, Y.J.; Lee, D.E.; Kwon, S.H. Broadband Tunable Add/Drop Filters Based on Dielectric Double-Disk Microcavities. IEEE Photonics J. 2017, 9, 6601607. [Google Scholar] [CrossRef]
- Dusanowski, Ł.; Köck, D.; Shin, E.; Kwon, S.H.; Schneider, C.; Höfling, S. Purcell-Enhanced and Indistinguishable Single-Photon Generation from Quantum Dots Coupled to On-Chip Integrated Ring Resonators. Nano Lett. 2020, 20, 6357–6363. [Google Scholar] [CrossRef]
- Wen, Y.H.; Kuzucu, O.; Hou, T.; Lipson, M.; Gaeta, A.L. All-Optical Switching of a Single Resonance in Silicon Ring Resonators. Opt. Lett. 2011, 36, 1413–1415. [Google Scholar] [CrossRef]
- Liu, L.; Kumar, R.; Huybrechts, K.; Spuesens, T.; Roelkens, G.; Geluk, E.J.; De Vries, T.; Regreny, P.; Van Thourhout, D.; Baets, R.; et al. An Ultra-Small, Low-Power, All-Optical Flip-Flop Memory on a Silicon Chip. Nat. Photonics 2010, 4, 182–187. [Google Scholar] [CrossRef]
- Spencer, D.T.; Bauters, J.F.; Bowers, J.E.; Heck, M.J.R. Integrated Waveguide Coupled Si3N4 Resonators in the Ultrahigh-Q Regime. Optica 2014, 1, 153–157. [Google Scholar] [CrossRef]
- Liu, K.; Jin, N.; Cheng, H.; Chauhan, N.; Puckett, M.W.; Nelson, K.D.; Behunin, R.O.; Behunin, R.O.; Rakich, P.T.; Blumenthal, D.J. Ultralow 0.034 DB/m Loss Wafer-Scale Integrated Photonics Realizing 720 Million Q and 380 ΜW Threshold Brillouin Lasing. Opt. Lett. 2022, 47, 1855–1858. [Google Scholar] [CrossRef]
- Ciminelli, C.; Innone, F.; Brunetti, G.; Conteduca, D.; Dell’Olio, F.; Tatoli, T.; Armenise, M.N. Rigorous Model for the Design of Ultra-High Q-Factor Resonant Cavities. In Proceedings of the 2016 18th International Conference on Transparent Optical Networks (ICTON), Trento, Italy, 10–14 July 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, K.Y.; Oh, D.Y.; Lee, S.H.; Yang, Q.F.; Yi, X.; Shen, B.; Wang, H.; Vahala, K. Bridging Ultrahigh-Q Devices and Photonic Circuits. Nat. Photonics 2018, 12, 297–302. [Google Scholar] [CrossRef]
- Yu, D.; Humar, M.; Meserve, K.; Bailey, R.C.; Chormaic, S.N.; Vollmer, F. Whispering-Gallery-Mode Sensors for Biological and Physical Sensing. Nat. Rev. Methods Prim. 2021, 1, 82. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y.; Gong, X.; Yuan, Z.; Feng, S.; Xu, T.; Liu, T.; Chen, Y.C. Bio-Electrostatic Sensitive Droplet Lasers for Molecular Detection. Nanoscale Adv. 2020, 2, 2713–2719. [Google Scholar] [CrossRef]
- Lemieux-Leduc, C.; Guertin, R.; Bianki, M.-A.; Peter, Y.-A. All-Polymer Whispering Gallery Mode Resonators for Gas Sensing. Opt. Express 2021, 29, 8685–8697. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Guo, Z.; Zhou, Y.; Guo, J.; Liu, Z.; Li, Y.; Luo, M.; Wu, X. Optical Whispering-Gallery-Mode Microbubble Sensors. Micromachines 2022, 13, 592. [Google Scholar] [CrossRef] [PubMed]
- Capocefalo, A.; Quintiero, E.; Conti, C.; Ghofraniha, N.; Viola, I. Droplet Lasers for Smart Photonic Labels. ACS Appl. Mater. Interfaces 2021, 13, 51485–51494. [Google Scholar] [CrossRef] [PubMed]
- Nowicki-Bringuier, Y.-R.; Claudon, J.; Böckler, C.; Reitzenstein, S.; Kamp, M.; Morand, A.; Forchel, A.; Gérard, J.M. High Q Whispering Gallery Modes in GaAs/AlAs Pillar Microcavities. Opt. Express 2007, 15, 17291–17304. [Google Scholar] [CrossRef]
- Hamidi, S.R.; Daraei, A. A Nanomaterial Sensor Based on Tapered Photonic Crystal Nanometer-Scale Cavity in a Microdisk. Opt. Quantum Electron. 2020, 52, 167. [Google Scholar] [CrossRef]
- Ryu, H.Y.; Notomi, M.; Kim, G.H.; Lee, Y.H. High Quality-Factor Whispering-Gallery Mode in the Photonic Crystal Hexagonal Disk Cavity. Opt. Express 2004, 12, 1708–1719. [Google Scholar] [CrossRef]
- Gao, G.; Zhang, Y.; Zhang, H.; Wang, Y.; Huang, Q.; Xia, J. Air-Mode Photonic Crystal Ring Resonator on Silicon-on-Insulator. Sci. Rep. 2016, 6, 19999. [Google Scholar] [CrossRef]
- Fujita, M.; Baba, T. Microgear Laser. Appl. Phys. Lett. 2002, 80, 2051–2053. [Google Scholar] [CrossRef]
- Lu, X.; McClung, A.; Srinivasan, K. High-Q Slow Light and Its Localization in a Photonic Crystal Microring. Nat. Photonics 2021, 16, 66–71. [Google Scholar] [CrossRef]
- Bogdanov, A.A.; Koshelev, K.L.; Kapitanova, P.V.; Rybin, M.V.; Gladyshev, S.A.; Sadrieva, Z.F.; Samusev, K.B.; Kivshar, Y.S.; Limonov, M.F. Bound States in the Continuum and Fano Resonances in the Strong Mode Coupling Regime. Adv. Photonics 2019, 1, 016001. [Google Scholar] [CrossRef]
- Bulgakov, E.N.; Pichugin, K.N.; Sadreev, A.F. Interaction between Dielectric Particles Enhances the Q Factor. J. Phys. Conf. Ser. 2020, 1461, 012144. [Google Scholar] [CrossRef]
- Pichugin, K.; Sadreev, A.; Bulgakov, E. Ultrahigh-Q System of a Few Coaxial Disks. Nanophotonics 2021, 10, 4341–4346. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Y.; Liu, M.; Xiao, G.; Luo, Y.; Liu, H.; Li, J.; Yuan, L. High Q-Factor Hybrid Metamaterial Waveguide Multi-Fano Resonance Sensor in the Visible Wavelength Range. Nanomaterials 2021, 11, 1583. [Google Scholar] [CrossRef]
- Ghulinyan, M.; Navarro-Urrios, D.; Pitanti, A.; Lui, A.; Pucker, G.; Pavesi, L. Whispering-Gallery Modes and Light Emission from a Si-Nanocrystal-Based Single Microdisk Resonator. Opt. Express 2008, 16, 13218–13224. [Google Scholar] [CrossRef]
- Kneissl, M.; Teepe, M.; Miyashita, N.; Johnson, N.M.; Chern, G.D.; Chang, R.K. Current-Injection Spiral-Shaped Microcavity Disk Laser Diodes with Unidirectional Emission. Appl. Phys. Lett. 2004, 84, 2485–2487. [Google Scholar] [CrossRef]
- Kim, G.; Shin, J.H. Luminescent Silicon-Rich Nitride Horizontal Air-Slot Microdisk Resonators for Biosensing. IEEE Photonics Technol. Lett. 2016, 28, 2331–2334. [Google Scholar] [CrossRef]
- Park, H.G.; Kim, S.H.; Kwon, S.H.; Ju, Y.G.; Yang, J.K.; Baek, J.H.; Kim, S.B.; Lee, Y.H. Electrically Driven Single-Cell Photonic Crystal Laser. Science 2004, 305, 1444–1447. [Google Scholar] [CrossRef]
- Fujita, M.; Ushigome, R.; Baba, T. Continuous Wave Lasing in GaInAsP Microdisk Injection Laser with Threshold Current of 40 μA. Electron. Lett. 2000, 36, 790–791. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, R.; Ti, C.; Liu, Y. Tapered Optical Fiber Loops and Helices for Integrated Photonic Device Characterization and Microfluidic Roller Coasters. Optica 2016, 3, 1205–1208. [Google Scholar] [CrossRef]
- Srinivasan, K.; Borselli, M.; Johnson, T.J.; Barclay, P.E.; Painter, O.; Stintz, A.; Krishna, S. Optical Loss and Lasing Characteristics of High-Quality-Factor AlGaAs Microdisk Resonators with Embedded Quantum Dots. Appl. Phys. Lett. 2005, 86, 151106. [Google Scholar] [CrossRef]
- Zheng, Y.; Fang, Z.; Liu, S.; Cheng, Y.; Chen, X. High- Q Exterior Whispering-Gallery Modes in a Double-Layer Crystalline Microdisk Resonator. Phys. Rev. Lett. 2019, 122, 253902. [Google Scholar] [CrossRef]
- Choi, S.J.; Peng, Z.; Yang, Q.; Choi, S.J.; Dapkus, P.D. Tunable Microdisk Resonators Vertically Coupled to Bus Waveguides Using Epitaxial Regrowth and Wafer Bonding Techniques. Appl. Phys. Lett. 2004, 84, 651–653. [Google Scholar] [CrossRef]
- Li, C.; Zhou, L.; Zheng, S.; Poon, A.W. Silicon Polygonal Microdisk Resonators. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1438–1449. [Google Scholar] [CrossRef]
- Koseki, S.; Zhang, B.; De Greve, K.; Yamamoto, Y. Monolithic Integration of Quantum Dot Containing Microdisk Microcavities Coupled to Air-Suspended Waveguides. Appl. Phys. Lett. 2009, 94, 051110. [Google Scholar] [CrossRef]
- Zhukov, A.E.; Kryzhanovskaya, N.V.; Moiseev, E.I.; Maximov, M.V. Quantum-Dot Microlasers Based on Whispering Gallery Mode Resonators. Light Sci. Appl. 2021, 10, 80. [Google Scholar] [CrossRef] [PubMed]
- Moiseev, E.I.; Kryzhanovskaya, N.V.; Kudashova, Y.V.; Maximov, M.V.; Kulagina, M.M.; Troshkov, S.I.; Lipovskii, A.A.; Korpijärvi, V.M.; Karjalainen, H.; Niemi, T.; et al. Microdisk Lasers Based on GaInNAsSb/GaAsN Quantum Well Active Region. J. Phys. Conf. Ser. 2015, 643, 012040. [Google Scholar] [CrossRef]
- Wang, G.; Jiang, X.; Zhao, M.; Ma, Y.; Fan, H.; Yang, Q.; Tong, L.; Xiao, M. Microlaser Based on a Hybrid Structure of a Semiconductor Nanowire and a Silica Microdisk Cavity. Opt. Express 2012, 20, 29472–29478. [Google Scholar] [CrossRef]
- Koshelev, K.; Kruk, S.; Melik-Gaykazyan, E.; Choi, J.H.; Bogdanov, A.; Park, H.G.; Kivshar, Y. Subwavelength Dielectric Resonators for Nonlinear Nanophotonics. Science 2020, 367, 288–292. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.H.; Lee, Y.J.; Hong, S.; Kim, Y.; Kwon, S.-H. Antisymmetric Mode Cancellation for High-Q Cavities in a Double-Disk. Photonics 2022, 9, 572. https://doi.org/10.3390/photonics9080572
Hong SH, Lee YJ, Hong S, Kim Y, Kwon S-H. Antisymmetric Mode Cancellation for High-Q Cavities in a Double-Disk. Photonics. 2022; 9(8):572. https://doi.org/10.3390/photonics9080572
Chicago/Turabian StyleHong, Seung Hyeon, Young Jin Lee, Seokhyeon Hong, Youngsoo Kim, and Soon-Hong Kwon. 2022. "Antisymmetric Mode Cancellation for High-Q Cavities in a Double-Disk" Photonics 9, no. 8: 572. https://doi.org/10.3390/photonics9080572
APA StyleHong, S. H., Lee, Y. J., Hong, S., Kim, Y., & Kwon, S.-H. (2022). Antisymmetric Mode Cancellation for High-Q Cavities in a Double-Disk. Photonics, 9(8), 572. https://doi.org/10.3390/photonics9080572





