Shack–Hartmann Wavefront Sensing Based on Four-Quadrant Binary Phase Modulation
Abstract
:1. Introduction
2. Principle
2.1. Four-Quadrant Binary Phase-Modulated Shack–Hartmann Wavefront Sensor
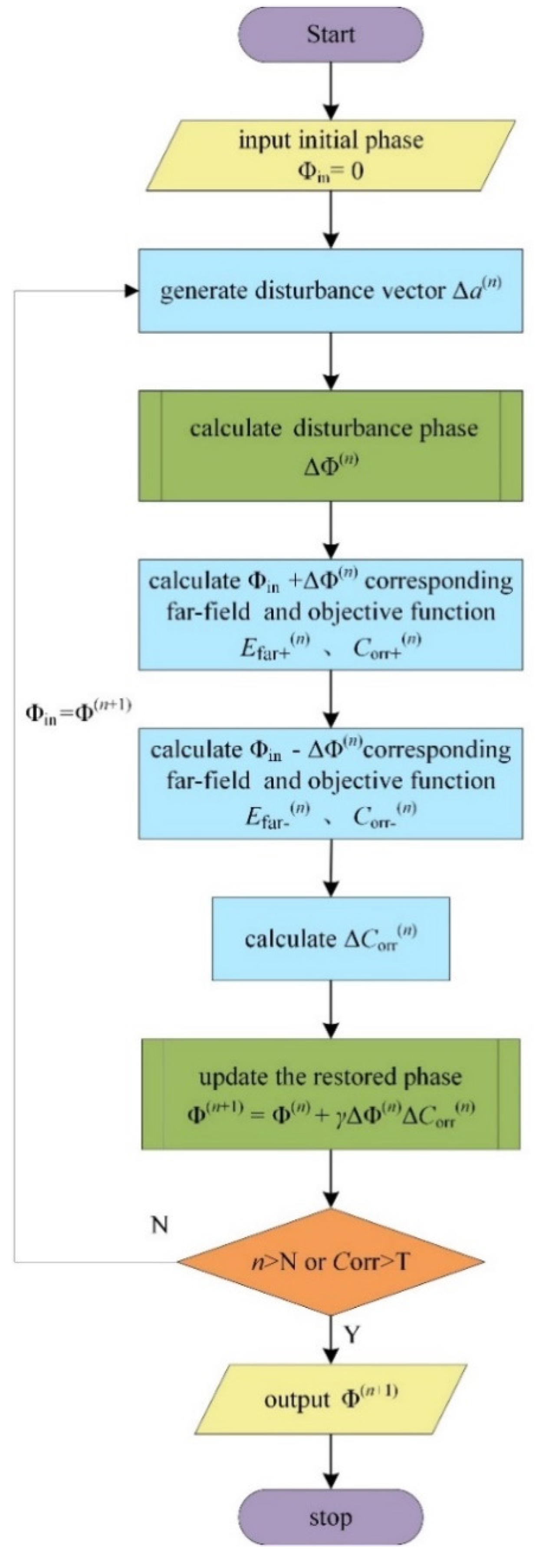
2.2. Wavefront Reconstruction Algorithm
| Algorithm 1. The procedure of the Stochastic Parallel Gradient Descent (SPGD) method |
| Require: the cost function , the gain factor γ, the certain value of , the measured far-field intensity , and the maximal number of iterations N. |
| Ensure: The optimal parameters γ. |
| Initialize the indexes = 0, = 0, n = 0; |
| Initialize the coefficients a(0) = [a1, a2, …, aM]. |
| Whilen ≥ N or Corr ≥ T do |
| 1: Randomly generated disturbance vectors Δa(n) = [Δa1(n), Δa2(n), …, ΔaM(n)]; |
| 2: Calculate the corresponding perturbation phase ; |
| 3: Calculate the far-field distribution after forward perturbation |
| ; |
| 4: Calculate the value of correlation function after forward perturbation |
| = ; |
| 5: Calculate the far-field distribution after negative perturbation |
| ; |
| 6: Calculate the value of correlation function after negative perturbation |
| = ; |
| 7: Calculate the variation amount of correlation function ; |
| 8: Calculate new phase distribution ; |
| 9: n = n + 1; |
| end while |
3. Numerical Simulation
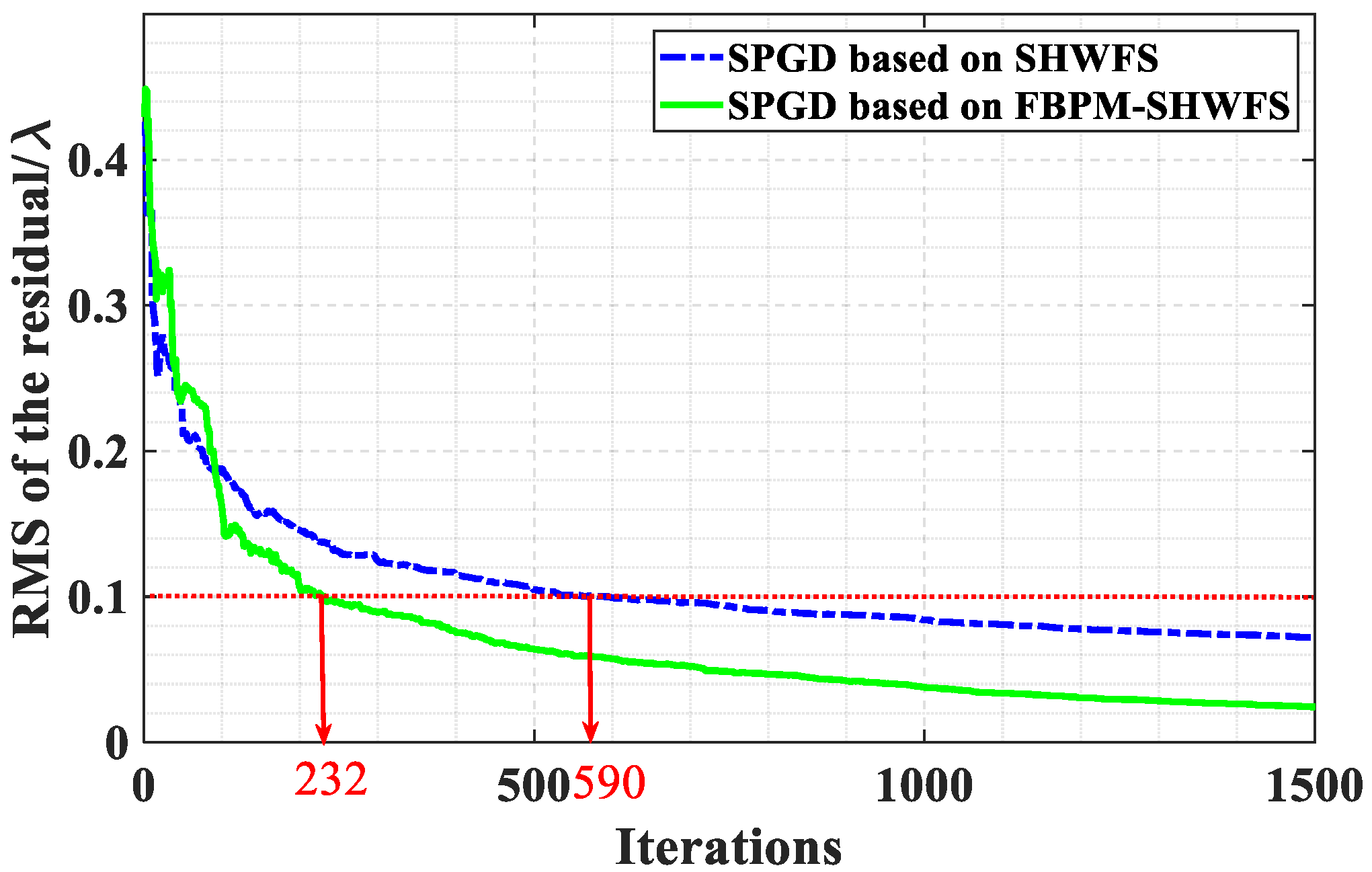
3.1. Analysis on 2 × 2 Subapertures
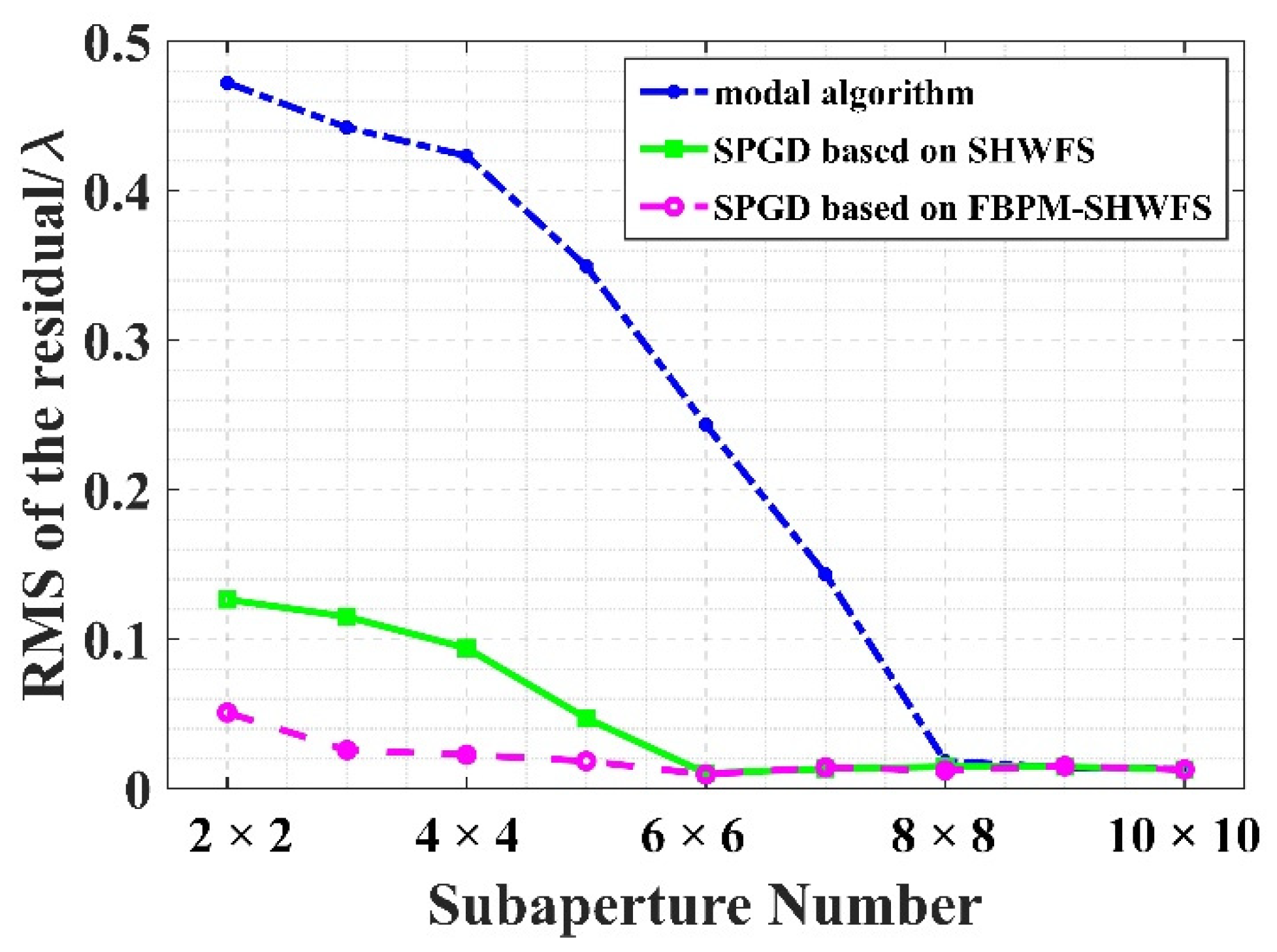
3.2. Analysis on Different Subaperture Numbers
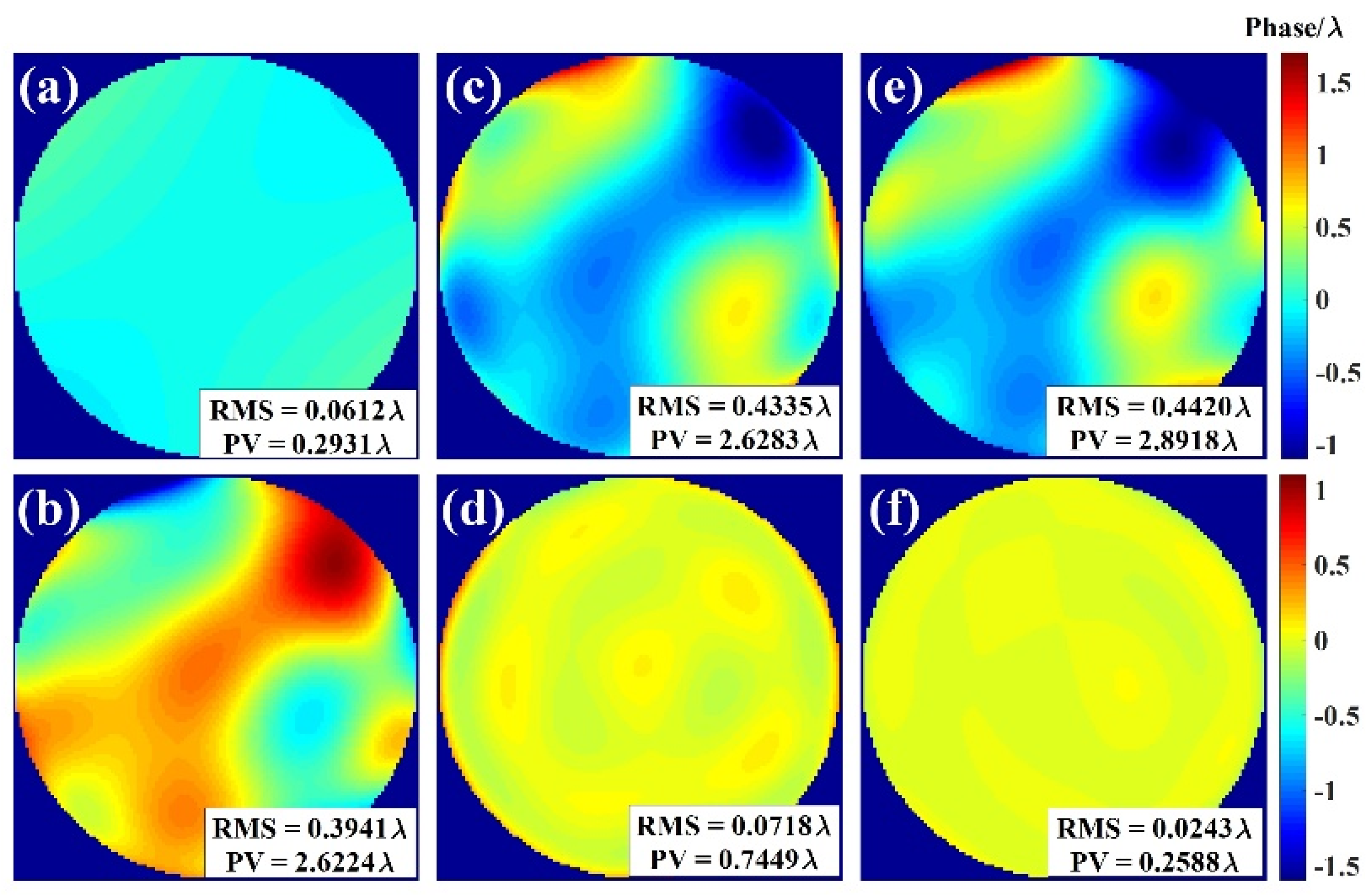
4. Experiment
4.1. Experimental Setup
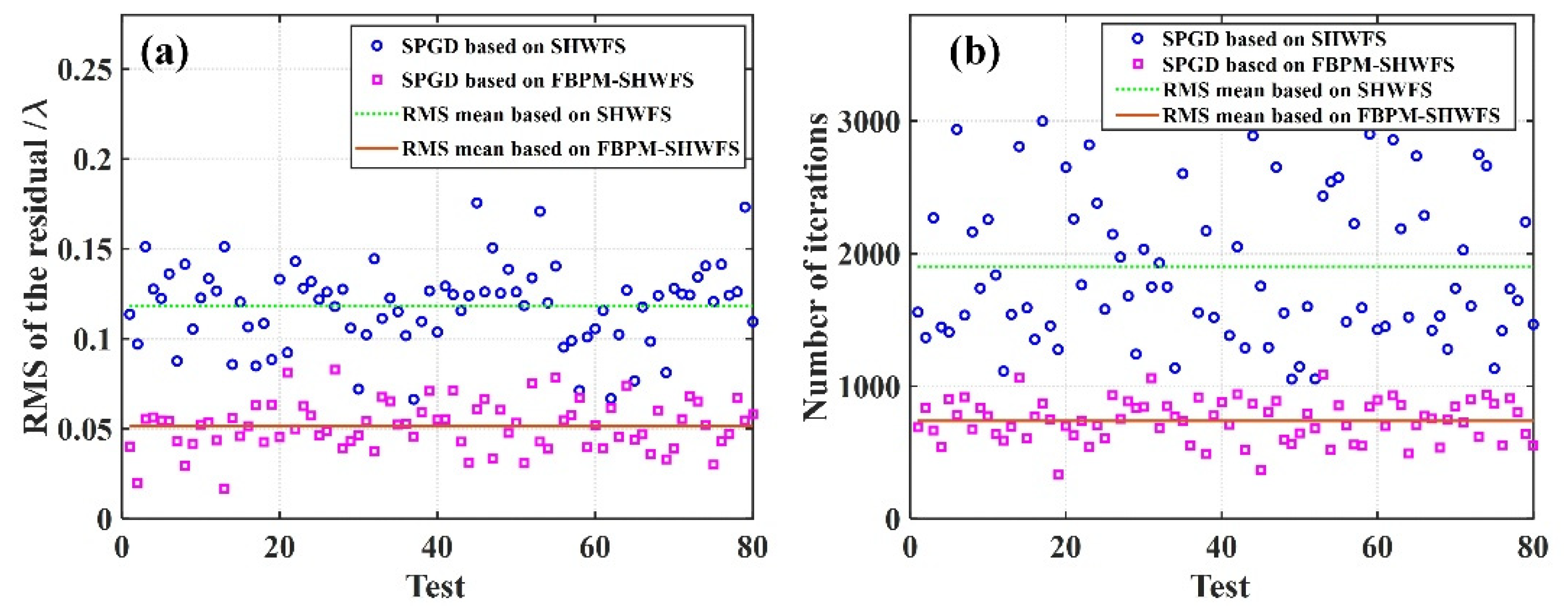
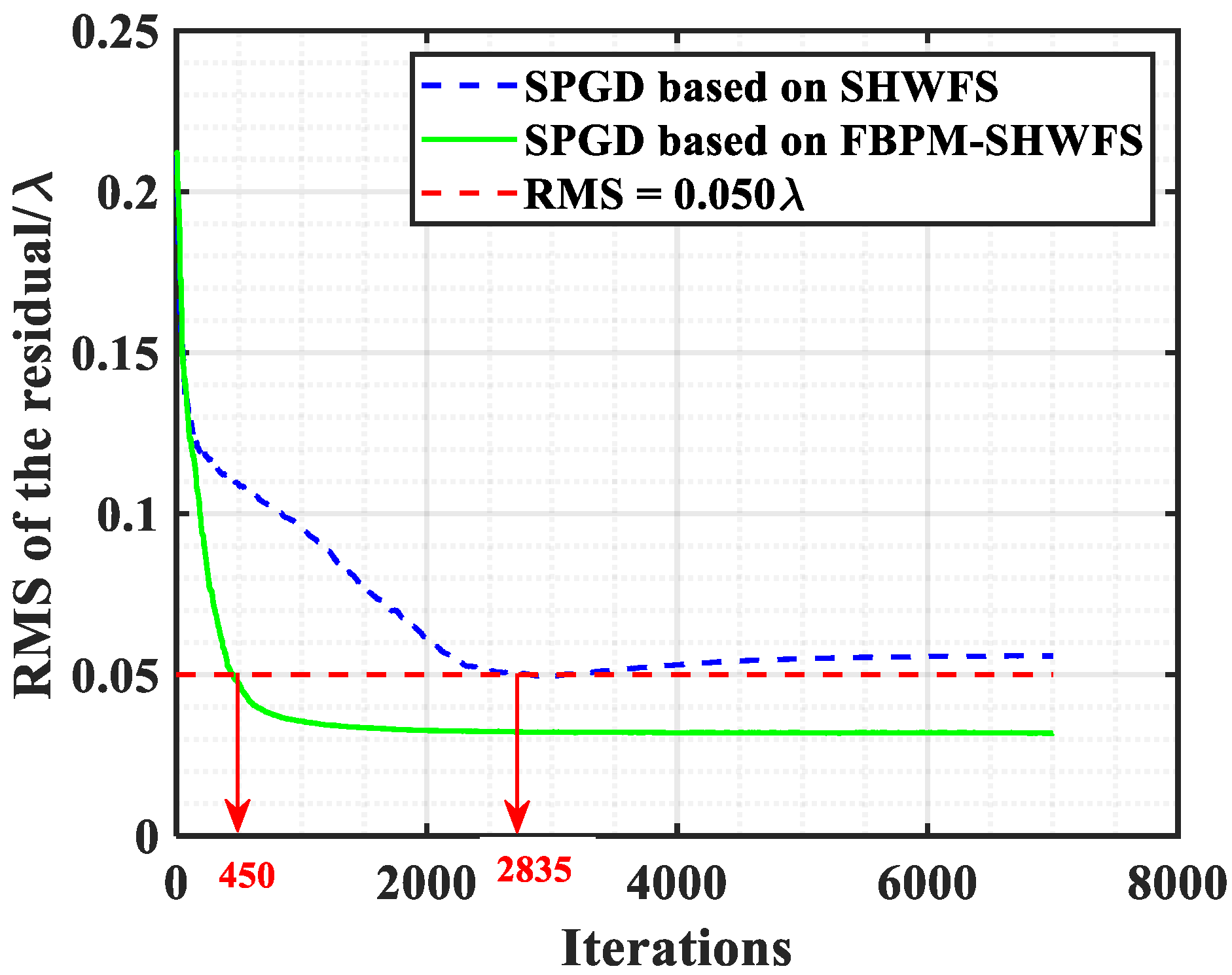
4.2. Experimental Result and Disscussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- van Dam, M.A.; Bouchez, A.H.; Mignant, D.L.; Johansson, E.M.; Wizinowich, P.L.; Campbell, R.D.; Chin, J.C.Y.; Hartman, S.K.; Lafon, R.E.; Stomski, P.J.; et al. The WM Keck observatory laser guide star adaptive optics system: Performance characterization. Publ. Astron. Soc. Pac. 2006, 118, 310–318. [Google Scholar] [CrossRef]
- Dayton, D.; Pierson, B.; Spielbusch, B.; Gonglewski, J. Atmospheric structure function measurements with a Shack–Hartmann wave-front sensor. Opt. Lett. 1992, 17, 1737–1739. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Grimm, B.; Goelz, S.; Bille, J.F. Objective measurement of wave aberrations of the human eye with the use of a Hartmann–Shack wave-front sensor. J. Opt. Soc. Am. A 1994, 11, 1949–1957. [Google Scholar]
- Dubra, A.; Sulai, Y.; Norris, J.L.; Cooper, R.F.; Dubis, A.M.; Williams, D.R.; Carroll, J. Noninvasive imaging of the human rod photoreceptor mosaic using a confocal adaptive optics scanning ophthalmoscope. Biomed. Opt. Express 2011, 2, 1864–1876. [Google Scholar] [CrossRef]
- Ji, N. Adaptive optical fluorescence microscopy. Nat. Methods 2017, 14, 374–380. [Google Scholar] [CrossRef]
- Planchon, T.A.; Rousseau, J.P.; Burgy, F.D.; Chériaux, G.; Chambaret, J.P. Adaptive wavefront correction on a 100-TW/10-Hz chirped pulse amplification laser and effect of residual wavefront on beam propagation. Opt. Commun. 2005, 252, 222–228. [Google Scholar] [CrossRef]
- Li, T.; Huang, L.; Gong, M. Wavefront sensing for a nonuniform intensity laser beam by Shack–Hartmann sensor with modified Fourier domain centroiding. Opt. Eng. 2014, 53, 044101. [Google Scholar] [CrossRef]
- Polo, A.; Kutchoukov, V.; Bociort, F.; Pereira, S.; Urbach, H. Determination of wavefront structure for a Hartmann wavefront sensor using a phase-retrieval method. Opt. Express 2012, 20, 7822–7832. [Google Scholar] [CrossRef]
- Platt, B.C.; Shack, R. History and Principles of Shack-Hartmann Wavefront Sensing. J. Refract. Surg. 2001, 17, S573–S577. [Google Scholar] [CrossRef]
- Southwell, W.H. Wave-front estimation from wave-front slope measurements. J. Opt. Soc. Am. 1980, 70, 998–1006. [Google Scholar] [CrossRef]
- Cubalchini, R. Modal wave-front estimation from phase derivative measurements. J. Opt. Soc. Am. 1979, 69, 972–977. [Google Scholar] [CrossRef]
- Fried, D.L. Least-square fitting a wave-front distortion estimate to an array of phase-difference measurements. J. Opt. Soc. Am. 1977, 67, 370–375. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Mu, Q.Q.; Li, D.Y.; Yang, C.L.; Cao, Z.L.; Hu, L.F.; Xuan, L. More Zernike modes’ open-loop measurement in the subaperture of the Shack–Hartmann wavefront sensor. Opt. Express 2016, 24, 24611–24623. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.Q.; Wang, S.; Zhao, M.M.; Zhao, W.; Dong, L.Z.; He, X.; Yang, P.; Xu, B. Wavefront reconstruction of a Shack–Hartmann sensor with insufficient lenslets based on an extreme learning machine. Appl. Opt. 2020, 59, 4768–4774. [Google Scholar] [CrossRef]
- He, Y.; Liu, Z.; Ning, Y.; Li, J.; Xu, X.; Jiang, Z. Deep learning wavefront sensing method for Shack-Hartmann sensors with sparse sub-apertures. Opt. Express 2021, 29, 17669–17682. [Google Scholar] [CrossRef]
- Feng, F.; Li, C.W.; Zhang, S.J. Wavefront Reconstruction by a Defocused Shack-Hartmann Sensor Based on Moment of Spot. Acta Opt. Sin. 2018, 38, 0628001. [Google Scholar] [CrossRef]
- Li, C.W.; Li, B.M.; Zhang, S.J. Phase retrieval using a modified Shack–Hartmann wavefront sensor with defocus. Appl. Opt. 2014, 53, 618–624. [Google Scholar] [CrossRef]
- Wang, S.; Yang, P.; Xu, B.; Dong, L.Z.; Ao, M.W. Shack-Hartmann wavefront sensing based on binary-aberration-mode filtering. Opt. Express 2015, 23, 5052–5064. [Google Scholar] [CrossRef]
- Kong, Q.F.; Wang, S.; Yang, P.; Yu, X.; Pang, B.Q.; Dong, L.Z.; Liu, Y.; Xu, B. Wavefront reconstruction based on the Fresnel zone plane with hybrid focal lengths. Opt. Commun. 2018, 425, 85–90. [Google Scholar] [CrossRef]
- Vorontsov, M.A.; Carhart, G.W.; Ricklin, J.C. Adaptive phase-distortion correction based on parallel gradient-descent optimization. Opt. Lett. 1997, 22, 907–909. [Google Scholar] [CrossRef]
- Yang, P.; Ning, Y.; Lei, X.; Xu, B.; Li, X.Y.; Dong, L.Z.; Yan, H.; Liu, W.J.; Jiang, W.H.; Liu, L. Enhancement of the beam quality of non-uniform output slab laser amplifier with a 39-actuator rectangular piezoelectric deformable mirror. Opt. Express 2010, 18, 7121–7130. [Google Scholar] [CrossRef] [PubMed]
- Vorontsov, M.A.; Sivokon, V.P. Stochastic parallel-gradient-descent technique for high-resolution wave-front phase-distortion correction. J. Opt. Soc. Am. A 1998, 15, 2745–2758. [Google Scholar] [CrossRef]
- Noll, R.J. Phase estimates from slope-type wave-front sensors. J. Opt. Soc. Am. 1978, 68, 139–140. [Google Scholar] [CrossRef]
- Lukin, V.P.; Bol’basova, L.A.; Nosov, V.V. Comparison of Kolmogorov’s and coherent turbulence. Appl. Opt. 2014, 53, B231–B236. [Google Scholar] [CrossRef] [PubMed]










| Parameters | Values |
|---|---|
| wavelength (λ) | 1064 nm |
| microlens size | 960 µm |
| focal length of the microlens | 27 mm |
| pixel size | 15 µm × 15 µm |
| Parameters | Values |
|---|---|
| wavelength (λ) | 635 nm |
| microlens size | 800 µm |
| microlens numbers | 2 × 2 |
| focal length of the microlens | 8 cm |
| diameter of aperture | 1.6 mm |
| the hosting optical system field of view | 0.57° |
| pixel size of CCD | 6.4 µm × 6.4 µm |
| pixel size of SLM | 12.5 µm × 12.5 µm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Zhao, W.; Yang, K.; Wang, S.; Yang, P.; Zeng, F.; Kong, L.; Yang, C. Shack–Hartmann Wavefront Sensing Based on Four-Quadrant Binary Phase Modulation. Photonics 2022, 9, 575. https://doi.org/10.3390/photonics9080575
Zhao M, Zhao W, Yang K, Wang S, Yang P, Zeng F, Kong L, Yang C. Shack–Hartmann Wavefront Sensing Based on Four-Quadrant Binary Phase Modulation. Photonics. 2022; 9(8):575. https://doi.org/10.3390/photonics9080575
Chicago/Turabian StyleZhao, Mengmeng, Wang Zhao, Kangjian Yang, Shuai Wang, Ping Yang, Fengjiao Zeng, Lingxi Kong, and Chao Yang. 2022. "Shack–Hartmann Wavefront Sensing Based on Four-Quadrant Binary Phase Modulation" Photonics 9, no. 8: 575. https://doi.org/10.3390/photonics9080575
APA StyleZhao, M., Zhao, W., Yang, K., Wang, S., Yang, P., Zeng, F., Kong, L., & Yang, C. (2022). Shack–Hartmann Wavefront Sensing Based on Four-Quadrant Binary Phase Modulation. Photonics, 9(8), 575. https://doi.org/10.3390/photonics9080575





