Nonreciprocity Steered with a Spinning Resonator
Abstract
:1. Introduction
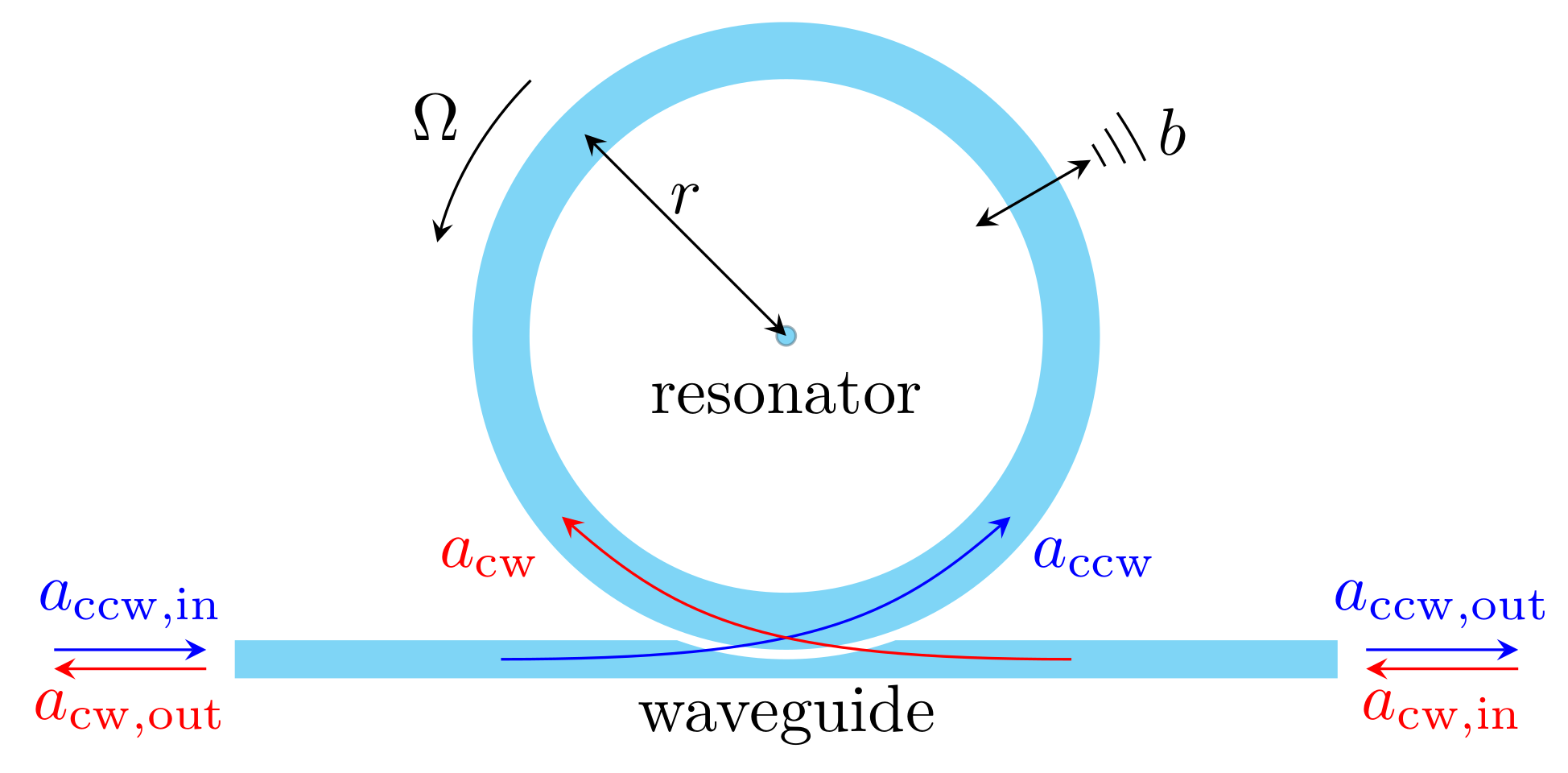
2. Model
3. Implementation of Steering Nonreciprocity
3.1. Fourier Space
3.2. Optomechanically Induced Nonreciprocity
3.3. Nonreciprocity without Optomechanical Coupling
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Caloz, C.; Alù, A.; Tretyakov, S.; Sounas, D.; Achouri, K.; Deck-Léger, Z.L. Electromagnetic Nonreciprocity. Phys. Rev. Appl. 2018, 10, 047001. [Google Scholar] [CrossRef]
- Verhagen, E.; Alù, A. Optomechanical nonreciprocity. Nat. Phys. 2017, 13, 922–924. [Google Scholar] [CrossRef]
- Rosario Hamann, A.; Müller, C.; Jerger, M.; Zanner, M.; Combes, J.; Pletyukhov, M.; Weides, M.; Stace, T.M.; Fedorov, A. Nonreciprocity Realized with Quantum Nonlinearity. Phys. Rev. Lett. 2018, 121, 123601. [Google Scholar] [CrossRef]
- Yu, Z.; Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nat. Photonics 2009, 3, 91–94. [Google Scholar] [CrossRef]
- Lira, H.; Yu, Z.; Fan, S.; Lipson, M. Electrically Driven Nonreciprocity Induced by Interband Photonic Transition on a Silicon Chip. Phys. Rev. Lett. 2012, 109, 033901. [Google Scholar] [CrossRef]
- Sounas, D.L.; Alù, A. Non-reciprocal photonics based on time modulation. Nat. Photonics 2017, 11, 774–783. [Google Scholar] [CrossRef]
- Sohn, D.B.; Kim, S.; Bahl, G. Time-reversal symmetry breaking with acoustic pumping of nanophotonic circuits. Nat. Photonics 2018, 12, 91–97. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photonics 2012, 6, 782–787. [Google Scholar] [CrossRef]
- Tzuang, L.D.; Fang, K.; Nussenzveig, P.; Fan, S.; Lipson, M. Non-reciprocal phase shift induced by an effective magnetic flux for light. Nat. Photonics 2014, 8, 701–705. [Google Scholar] [CrossRef]
- Fang, K.; Luo, J.; Metelmann, A.; Matheny, M.H.; Marquardt, F.; Clerk, A.A.; Painter, O. Generalized non-reciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering. Nat. Phys. 2017, 13, 465–471. [Google Scholar] [CrossRef]
- Hafezi, M.; Rabl, P. Optomechanically induced non-reciprocity in microring resonators. Opt. Express 2012, 20, 7672–7684. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kuzyk, M.C.; Han, K.; Wang, H.; Bahl, G. Non-reciprocal Brillouin scattering induced transparency. Nat. Phys. 2015, 11, 275–280. [Google Scholar] [CrossRef]
- Dong, C.H.; Shen, Z.; Zou, C.L.; Zhang, Y.L.; Fu, W.; Guo, G.C. Brillouin-scattering-induced transparency and non-reciprocal light storage. Nat. Commun. 2015, 6, 6193. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Zhang, Y.L.; Chen, Y.; Zou, C.L.; Xiao, Y.F.; Zou, X.B.; Sun, F.W.; Guo, G.C.; Dong, C.H. Experimental realization of optomechanically induced non-reciprocity. Nat. Photonics 2016, 10, 657. [Google Scholar] [CrossRef]
- Shen, Z.; Zhang, Y.L.; Chen, Y.; Sun, F.W.; Zou, X.B.; Guo, G.C.; Zou, C.L.; Dong, C.H. Reconfigurable optomechanical circulator and directional amplifier. Nat. Commun. 2018, 9, 1797. [Google Scholar] [CrossRef]
- Ruesink, F.; Miri, M.A.; Alù, A.; Verhagen, E. Nonreciprocity and magnetic-free isolation based on optomechanical interactions. Nat. Commun. 2016, 7, 13662. [Google Scholar] [CrossRef]
- Bernier, N.R.; Tóth, L.D.; Koottandavida, A.; Ioannou, M.A.; Malz, D.; Nunnenkamp, A.; Feofanov, A.K.; Kippenberg, T.J. Nonreciprocal reconfigurable microwave optomechanical circuit. Nat. Commun. 2017, 8, 604. [Google Scholar] [CrossRef]
- Peterson, G.A.; Lecocq, F.; Cicak, K.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Demonstration of Efficient Nonreciprocity in a Microwave Optomechanical Circuit. Phys. Rev. X 2017, 7, 031001. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Wulf, M.; Peruzzo, M.; Kalaee, M.; Dieterle, P.B.; Painter, O.; Fink, J.M. Mechanical on-chip microwave circulator. Nat. Commun. 2017, 8, 953. [Google Scholar] [CrossRef]
- Miri, M.A.; Ruesink, F.; Verhagen, E.; Alù, A. Optical Nonreciprocity Based on Optomechanical Coupling. Phys. Rev. Appl. 2017, 7, 064014. [Google Scholar] [CrossRef]
- Ruesink, F.; Mathew, J.P.; Miri, M.A.; Alù, A.; Verhagen, E. Optical circulation in a multimode optomechanical resonator. Nat. Commun. 2018, 9, 1798. [Google Scholar] [CrossRef] [PubMed]
- Kittlaus, E.A.; Otterstrom, N.T.; Kharel, P.; Gertler, S.; Rakich, P.T. Non-reciprocal interband Brillouin modulation. Nat. Photonics 2018, 12, 613–619. [Google Scholar] [CrossRef]
- Ren, L.; Xu, X.; Zhu, S.; Shi, L.; Zhang, X. Experimental Realization of on-Chip Nonreciprocal Transmission by Using the Mechanical Kerr Effect. ACS Photonics 2020, 7, 2995–3002. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, Ş.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity–time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Chang, L.; Jiang, X.; Hua, S.; Yang, C.; Wen, J.; Jiang, L.; Li, G.; Wang, G.; Xiao, M. Parity–time symmetry and variable optical isolation in active–passive-coupled microresonators. Nat. Photonics 2014, 8, 524–529. [Google Scholar] [CrossRef]
- Jin, B.; Argyropoulos, C. Nonreciprocal Transmission in Nonlinear PT-Symmetric Metamaterials Using Epsilon-Near-Zero Media Doped with Defects. Adv. Opt. Mater. 2019, 7, 1901083. [Google Scholar] [CrossRef]
- Shao, L.; Mao, W.; Maity, S.; Sinclair, N.; Hu, Y.; Yang, L.; Lončar, M. Non-reciprocal transmission of microwave acoustic waves in nonlinear parity–time symmetric resonators. Nat. Electron. 2020, 3, 267–272. [Google Scholar] [CrossRef]
- Cao, Q.T.; Wang, H.; Dong, C.H.; Jing, H.; Liu, R.S.; Chen, X.; Ge, L.; Gong, Q.; Xiao, Y.F. Experimental Demonstration of Spontaneous Chirality in a Nonlinear Microresonator. Phys. Rev. Lett. 2017, 118, 033901. [Google Scholar] [CrossRef]
- Bino, L.D.; Silver, J.M.; Woodley, M.T.M.; Stebbings, S.L.; Zhao, X.; Del’Haye, P. Microresonator isolators and circulators based on the intrinsic nonreciprocity of the Kerr effect. Optica 2018, 5, 279–282. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, Y.; Lin, G.; Niu, Y.; Xia, K.; Gong, J.; Gong, S. Thermal-motion-induced non-reciprocal quantum optical system. Nat. Photonics 2018, 12, 744–748. [Google Scholar] [CrossRef]
- Xia, K.; Nori, F.; Xiao, M. Cavity-Free Optical Isolators and Circulators Using a Chiral Cross-Kerr Nonlinearity. Phys. Rev. Lett. 2018, 121, 203602. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Tang, J.; Zhang, W.; Lu, G.; Zhang, H.; Zhang, Y.; Xia, K.; Xiao, M. On-chip chiral single-photon interface: Isolation and unidirectional emission. Phys. Rev. A 2019, 99, 043833. [Google Scholar] [CrossRef]
- Yang, P.; Xia, X.; He, H.; Li, S.; Han, X.; Zhang, P.; Li, G.; Zhang, P.; Xu, J.; Yang, Y.; et al. Realization of Nonlinear Optical Nonreciprocity on a Few-Photon Level Based on Atoms Strongly Coupled to an Asymmetric Cavity. Phys. Rev. Lett. 2019, 123, 233604. [Google Scholar] [CrossRef] [PubMed]
- Sohn, D.B.; Örsel, O.E.; Bahl, G. Electrically driven optical isolation through phonon-mediated photonic Autler–Townes splitting. Nat. Photonics 2021, 15, 822–827. [Google Scholar] [CrossRef]
- Tian, H.; Liu, J.; Siddharth, A.; Wang, R.N.; Blésin, T.; He, J.; Kippenberg, T.J.; Bhave, S.A. Magnetic-free silicon nitride integrated optical isolator. Nat. Photonics 2021, 15, 828–836. [Google Scholar] [CrossRef]
- Tang, L.; Tang, J.; Chen, M.; Nori, F.; Xiao, M.; Xia, K. Quantum Squeezing Induced Optical Nonreciprocity. Phys. Rev. Lett. 2022, 128, 083604. [Google Scholar] [CrossRef] [PubMed]
- Maayani, S.; Dahan, R.; Kligerman, Y.; Moses, E.; Hassan, A.U.; Jing, H.; Nori, F.; Christodoulides, D.N.; Carmon, T. Flying couplers above spinning resonators generate irreversible refraction. Nature 2018, 558, 569–572. [Google Scholar] [CrossRef]
- Huang, R.; Miranowicz, A.; Liao, J.Q.; Nori, F.; Jing, H. Nonreciprocal Photon Blockade. Phys. Rev. Lett. 2018, 121, 153601. [Google Scholar] [CrossRef]
- Malykin, G.B. The Sagnac effect: Correct and incorrect explanations. Physics-Uspekhi 2000, 43, 1229–1252. [Google Scholar] [CrossRef]
- Lü, H.; Jiang, Y.; Wang, Y.Z.; Jing, H. Optomechanically induced transparency in a spinning resonator. Photon. Res. 2017, 5, 367–371. [Google Scholar] [CrossRef]
- Mirza, I.M.; Ge, W.; Jing, H. Optical nonreciprocity and slow light in coupled spinning optomechanical resonators. Opt. Express 2019, 27, 25515–25530. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Özdemir, S.K.; Xu, X.W.; Zhang, L.; Kuang, L.M.; Jing, H. Nonreciprocal optical solitons in a spinning Kerr resonator. Phys. Rev. A 2021, 103, 053522. [Google Scholar] [CrossRef]
- Zhou, N.N.; Zhang, L.Q.; Yu, C.S. Mechanically controllable nonreciprocal transmission and perfect absorption of photons. Opt. Express 2022, 30, 24431–24442. [Google Scholar] [CrossRef]
- Li, B.; Huang, R.; Xu, X.; Miranowicz, A.; Jing, H. Nonreciprocal unconventional photon blockade in a spinning optomechanical system. Photon. Res. 2019, 7, 630–641. [Google Scholar] [CrossRef]
- Jing, Y.W.; Shi, H.Q.; Xu, X.W. Nonreciprocal photon blockade and directional amplification in a spinning resonator coupled to a two-level atom. Phys. Rev. A 2021, 104, 033707. [Google Scholar] [CrossRef]
- Shang, X.; Xie, H.; Lin, X.M. Nonreciprocal photon blockade in a spinning optomechanical resonator. Laser Phys. Lett. 2021, 18, 115202. [Google Scholar] [CrossRef]
- Xue, W.S.; Shen, H.Z.; Yi, X.X. Nonreciprocal conventional photon blockade in driven dissipative atom-cavity. Opt. Lett. 2020, 45, 4424–4427. [Google Scholar] [CrossRef]
- Shen, H.Z.; Wang, Q.; Wang, J.; Yi, X.X. Nonreciprocal unconventional photon blockade in a driven dissipative cavity with parametric amplification. Phys. Rev. A 2020, 101, 013826. [Google Scholar] [CrossRef]
- Yao, X.Y.; Ali, H.; Li, F.L.; Li, P.B. Nonreciprocal Phonon Blockade in a Spinning Acoustic Ring Cavity Coupled to a Two-Level System. Phys. Rev. Appl. 2022, 17, 054004. [Google Scholar] [CrossRef]
- Jiang, Y.; Maayani, S.; Carmon, T.; Nori, F.; Jing, H. Nonreciprocal Phonon Laser. Phys. Rev. Appl. 2018, 10, 064037. [Google Scholar] [CrossRef]
- Li, W.A.; Huang, G.Y.; Chen, J.P.; Chen, Y. Nonreciprocal enhancement of optomechanical second-order sidebands in a spinning resonator. Phys. Rev. A 2020, 102, 033526. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, J.Y.; Liu, W.; Xiao, Y.F. Nonreciprocal phonon laser in a spinning microwave magnomechanical system. Phys. Rev. A 2021, 103, 053501. [Google Scholar] [CrossRef]
- Xu, Y.J.; Song, J. Nonreciprocal magnon laser. Opt. Lett. 2021, 46, 5276–5279. [Google Scholar] [CrossRef]
- Jiao, Y.F.; Zhang, S.D.; Zhang, Y.L.; Miranowicz, A.; Kuang, L.M.; Jing, H. Nonreciprocal Optomechanical Entanglement against Backscattering Losses. Phys. Rev. Lett. 2020, 125, 143605. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.B.; Liu, J.S.; Zhu, A.D.; Liu, H.Y.; Yang, R.C. Nonreciprocal Transmission and Nonreciprocal Entanglement in a Spinning Microwave Magnomechanical System. Ann. Phys. 2020, 532, 2000196. [Google Scholar] [CrossRef]
- Ren, Y.L. Nonreciprocal optical–microwave entanglement in a spinning magnetic resonator. Opt. Lett. 2022, 47, 1125–1128. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.W.; Zheng, L.L.; You, C.; Hu, C.S.; Wu, Y.; Lü, X.Y. Nonreciprocal chaos in a spinning optomechanical resonator. Phys. Rev. A 2021, 104, 033522. [Google Scholar] [CrossRef]
- Schliesser, A.; Kippenberg, T.J. Cavity Optomechanics with Whispering-Gallery Mode Optical Micro-Resonators. Adv. At. Mol. Opt. Phys. 2010, 58, 207–323. [Google Scholar] [CrossRef]
- Shi, H.; Xiong, Z.; Chen, W.; Xu, J.; Wang, S.; Chen, Y. Gauge-field description of Sagnac frequency shift and mode hybridization in a rotating cavity. Opt. Express 2019, 27, 28114–28122. [Google Scholar] [CrossRef]
- Gardiner, C.; Zoller, P.; Zoller, P. Quantum Noise: A Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004. [Google Scholar]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Gardiner, C.W.; Collett, M.J. Input and output in damped quantum systems: Quantum stochastic differential equations and the master equation. Phys. Rev. A 1985, 31, 3761–3774. [Google Scholar] [CrossRef] [PubMed]
- Fabre, C.; Pinard, M.; Bourzeix, S.; Heidmann, A.; Giacobino, E.; Reynaud, S. Quantum-noise reduction using a cavity with a movable mirror. Phys. Rev. A 1994, 49, 1337–1343. [Google Scholar] [CrossRef] [PubMed]
- Verhagen, E.; Deléglise, S.; Weis, S.; Schliesser, A.; Kippenberg, T.J. Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode. Nature 2012, 482, 63–67. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, X.; Xie, H.; Lin, G.; Lin, X. Nonreciprocity Steered with a Spinning Resonator. Photonics 2022, 9, 585. https://doi.org/10.3390/photonics9080585
Shang X, Xie H, Lin G, Lin X. Nonreciprocity Steered with a Spinning Resonator. Photonics. 2022; 9(8):585. https://doi.org/10.3390/photonics9080585
Chicago/Turabian StyleShang, Xiao, Hong Xie, Gongwei Lin, and Xiumin Lin. 2022. "Nonreciprocity Steered with a Spinning Resonator" Photonics 9, no. 8: 585. https://doi.org/10.3390/photonics9080585
APA StyleShang, X., Xie, H., Lin, G., & Lin, X. (2022). Nonreciprocity Steered with a Spinning Resonator. Photonics, 9(8), 585. https://doi.org/10.3390/photonics9080585




