Holographic Encryption Applications Using Composite Orbital Angular Momentum Beams
Abstract
:1. Introduction
2. Principle and Methods
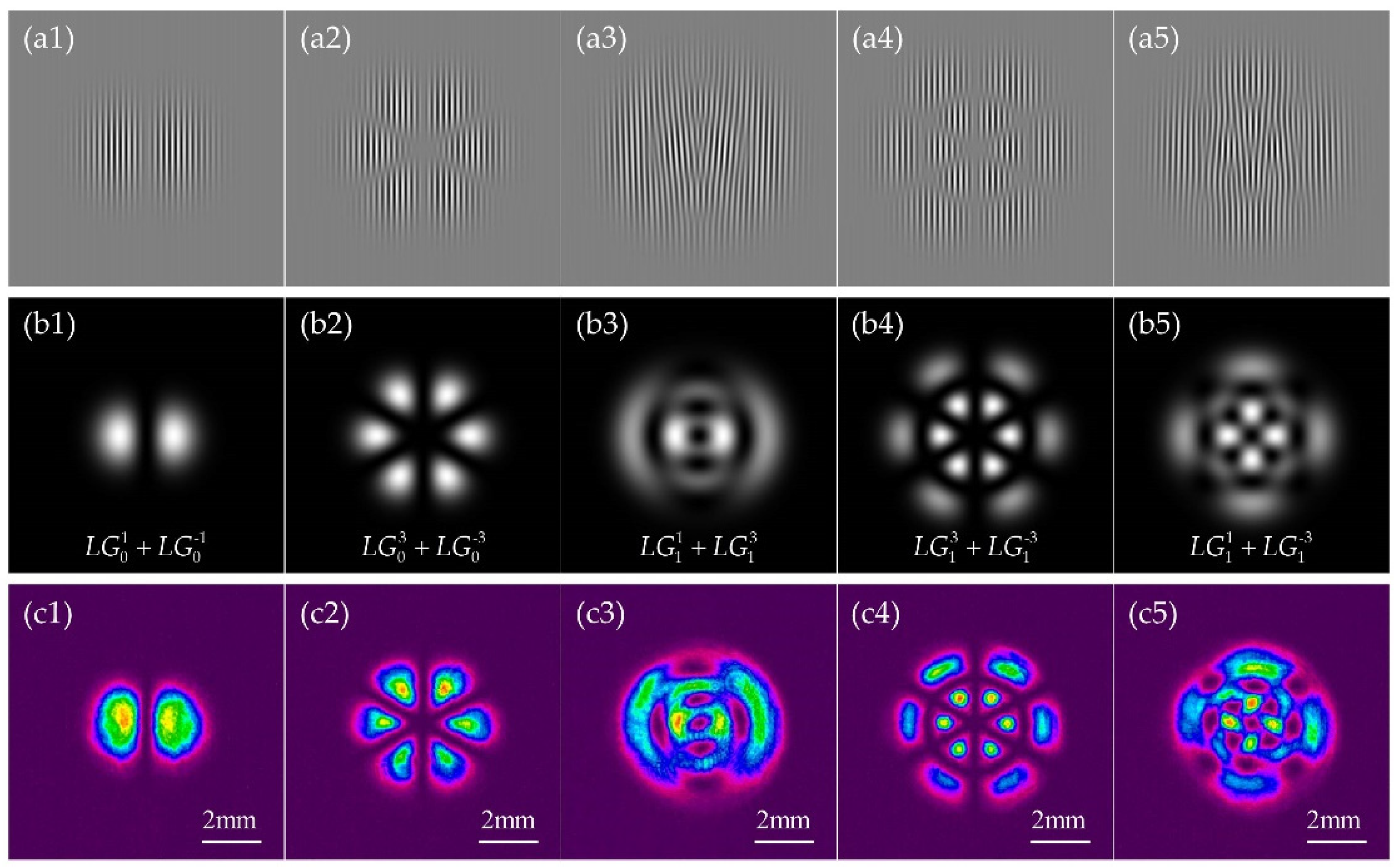
2.1. Composite-State Laguerre-Gaussian Beams
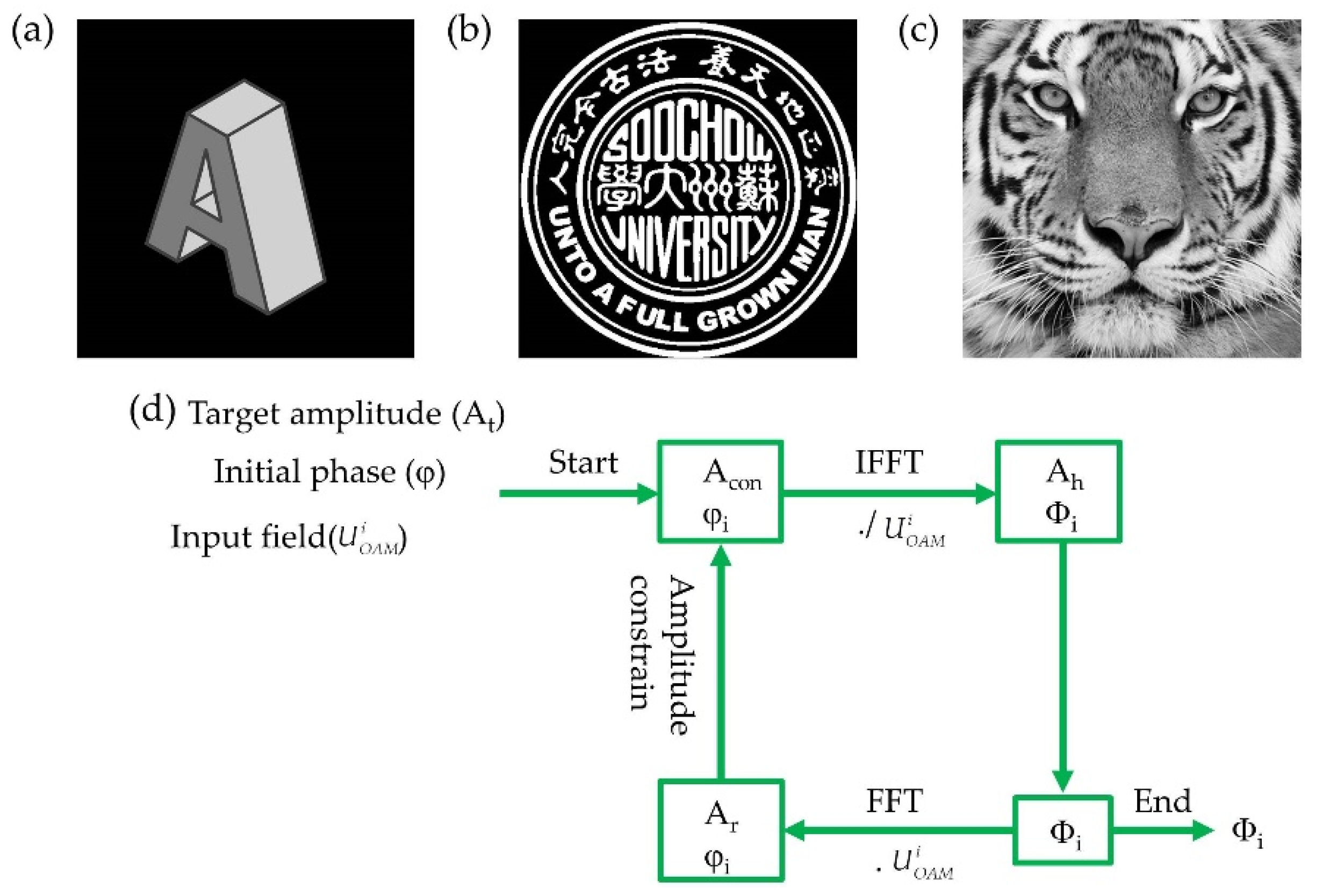
2.2. Design of the Composite-State LG Beam Hologram
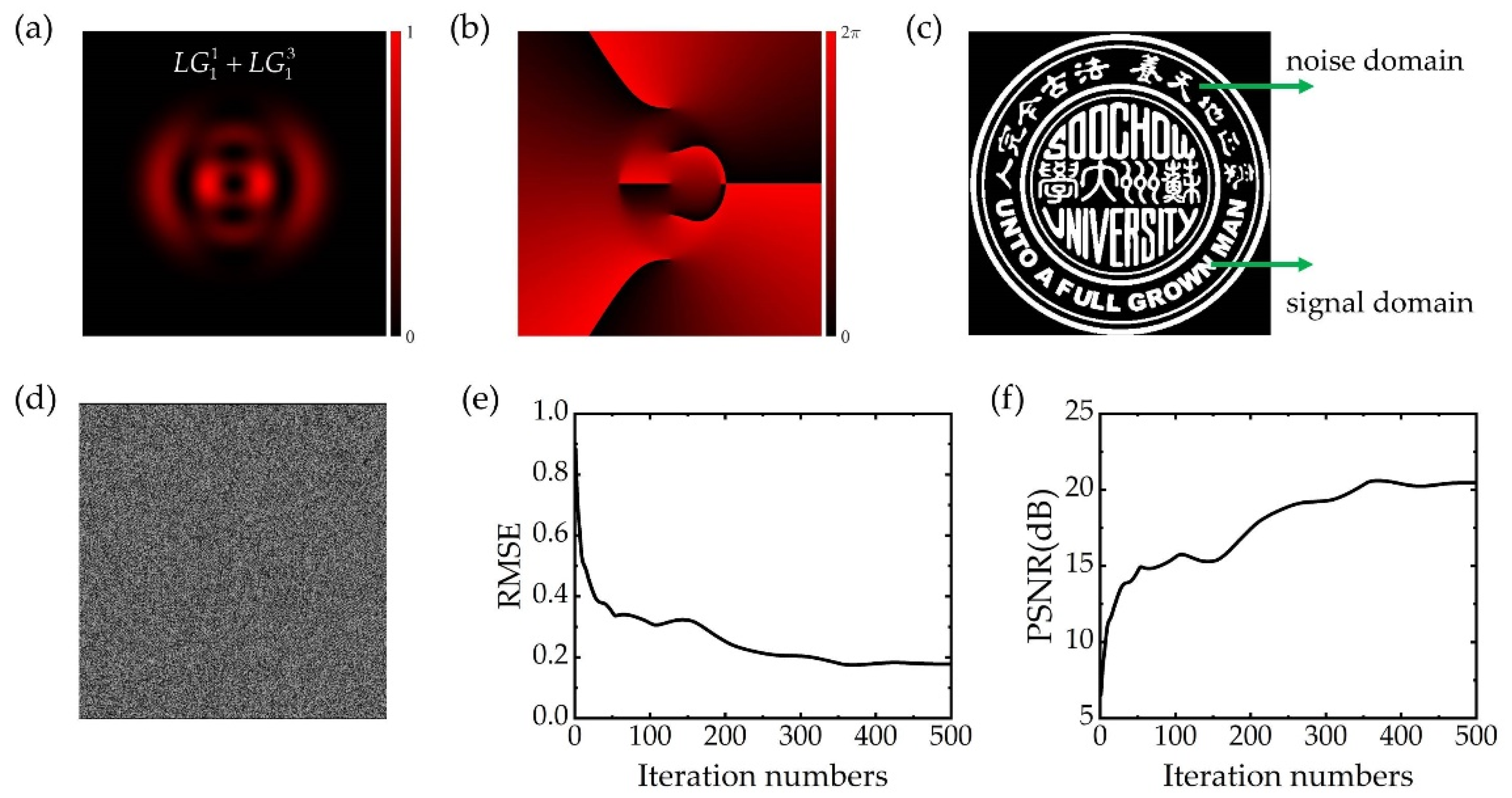
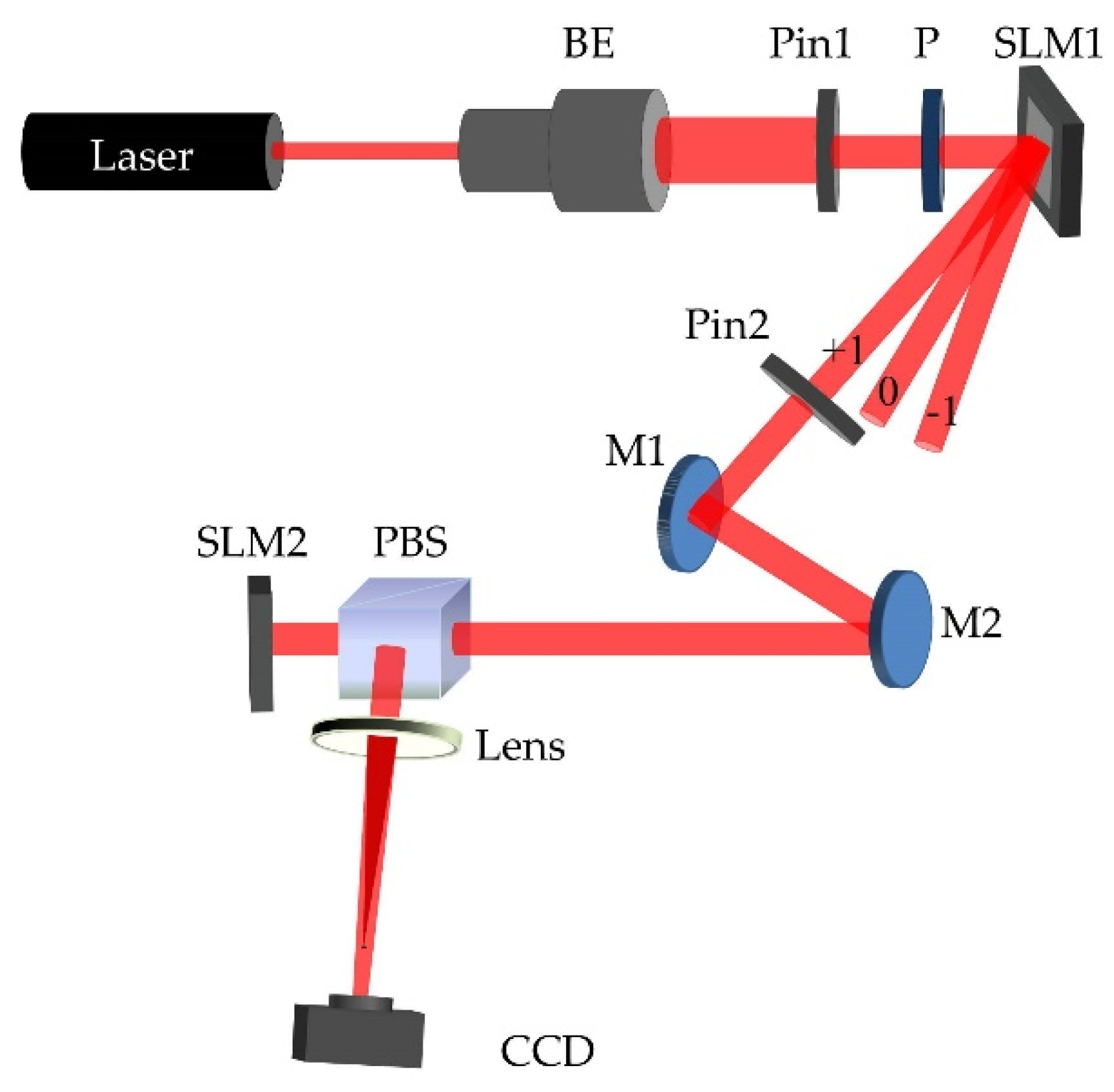
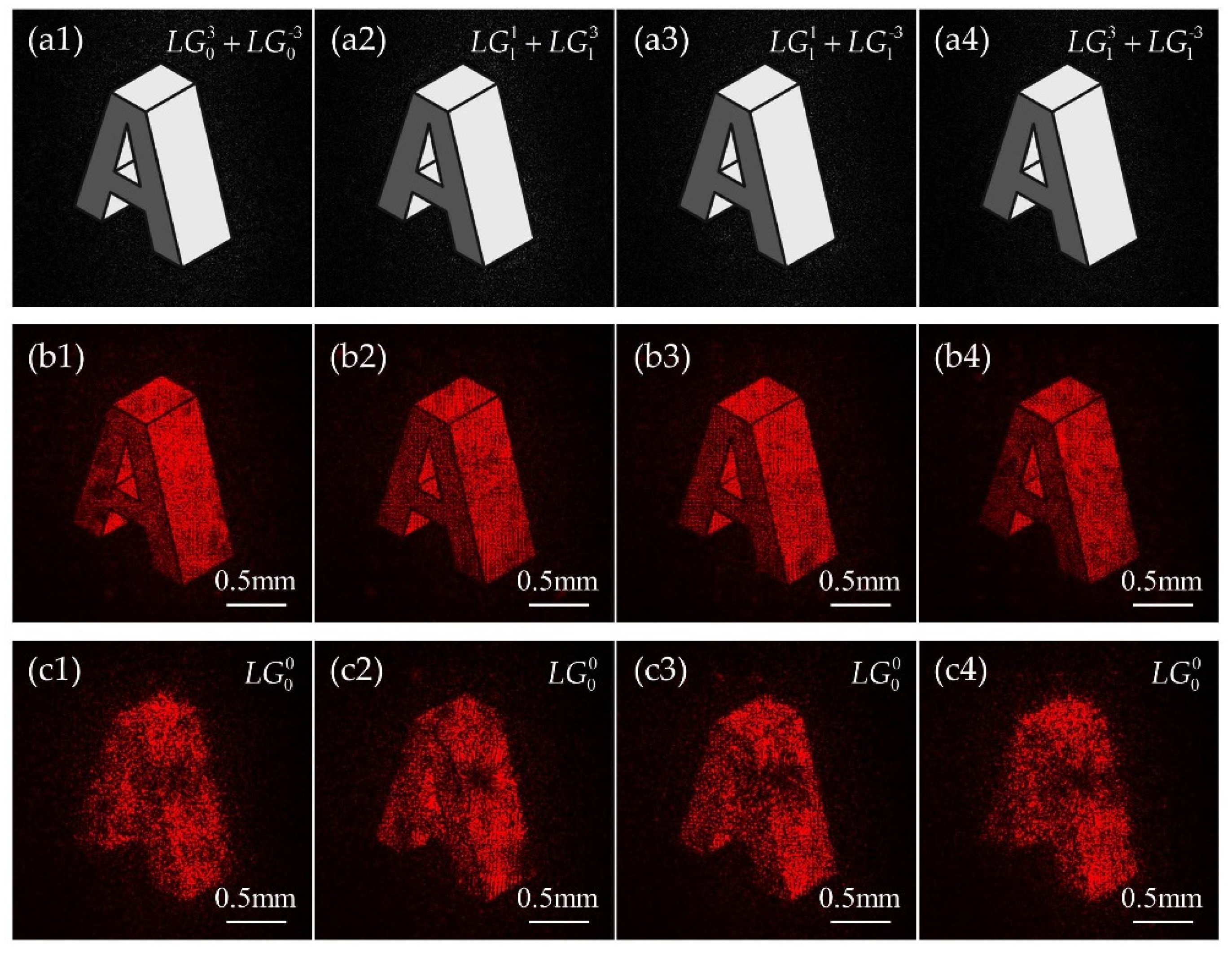
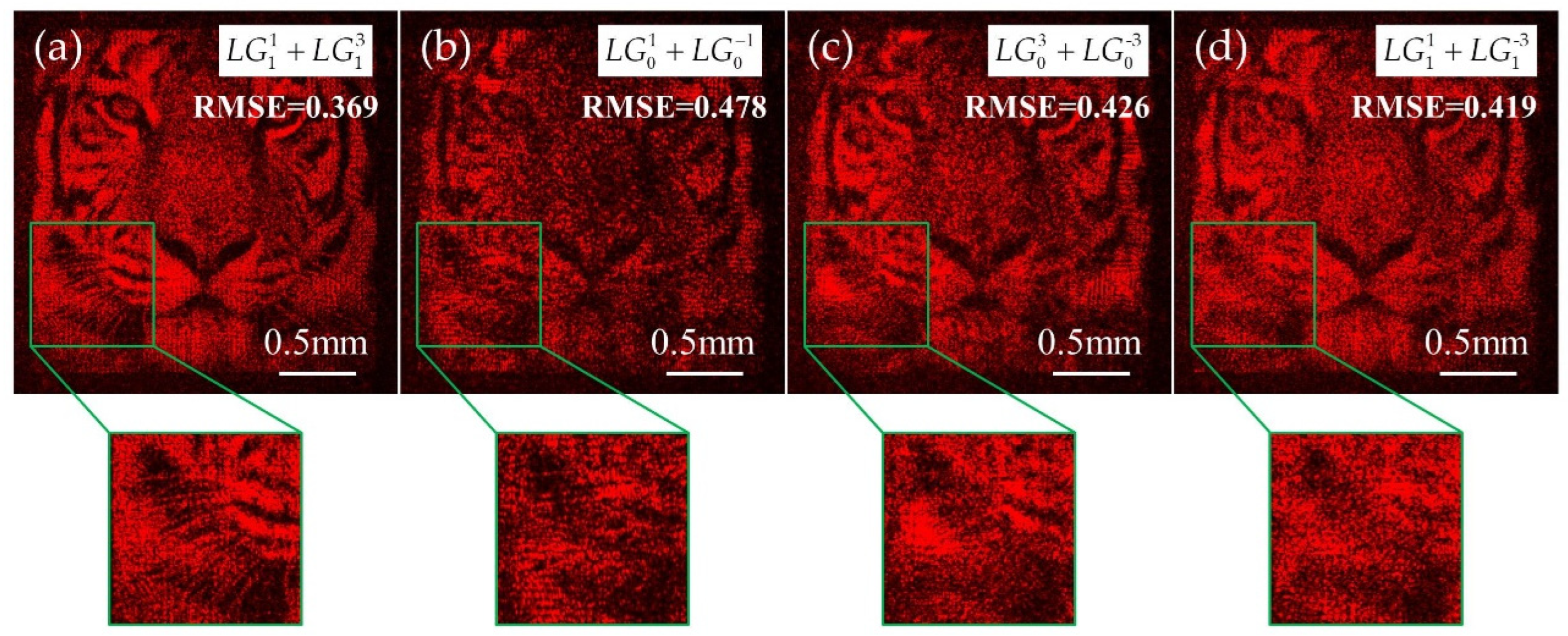
3. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dholakia, K.; Čižmár, T. Shaping the future of manipulation. Nat. Photonics 2011, 5, 335–342. [Google Scholar] [CrossRef]
- Padgett, M.; Di Leonardo, R. Holographic optical tweezers and their relevance to lab on chip devices. Lab Chip 2011, 11, 1196–1205. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Kamin, S.; Zheng, G.; Neubrech, F.; Zhang, S.; Liu, N. Addressable metasurfaces for dynamic holography and optical information encryption. Sci. Adv. 2018, 4, eaar6768. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Wang, D.; Wang, Q.; Kim, E. Full-color holographic 3D display system using off-axis color-multiplexed-hologram on single SLM. Opti. Lasers Eng. 2020, 126, 105895. [Google Scholar] [CrossRef]
- Li, X.; Chen, L.; Li, Y.; Zhang, X.; Pu, M.; Zhao, Z.; Ma, X.; Wang, Y.; Hong, M.; Luo, X. Multicolor 3D meta-holography by broadband plasmonic modulation. Sci. Adv. 2016, 2, e1601102. [Google Scholar] [CrossRef]
- Heanue, J.F.; Bashaw, M.C.; Hesselink, L. Volume holographic storage and retrieval of digital data. Science 1994, 265, 749–752. [Google Scholar] [CrossRef]
- Balthasar Mueller, J.P.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface polarization optics: Independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.F.; Wong, P.W.H.; Cheah, K.W.; et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef]
- Li, X.; Ren, H.; Chen, X.; Liu, J.; Li, Q.; Li, C.; Xue, G.; Jia, J.; Cao, L.; Sahu, A.; et al. Athermally photoreduced graphene oxides for three-dimensional holographic images. Nat. Commun. 2015, 6, 6984. [Google Scholar] [CrossRef]
- Kamali, S.M.; Arbabi, E.; Arbabi, A.; Horie, Y.; Faraji-Dana, M.; Faraon, A. Angle-Multiplexed Metasurfaces: Encoding Independent Wavefronts in a Single Metasurface under Different Illumination Angles. Phys. Rev. X 2017, 7, 041056. [Google Scholar] [CrossRef] [Green Version]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef] [PubMed]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Fang, X.; Yang, H.; Yao, W.; Wang, T.; Zhang, Y.; Gu, M.; Xiao, M. High-dimensional orbital angular momentum multiplexing nonlinear holography. Adv. Photonics 2021, 3, 015001. [Google Scholar] [CrossRef]
- Fang, X.; Wang, H.; Yang, H.; Ye, Z.; Wang, Y.; Zhang, Y.; Hu, X.; Zhu, S.; Xiao, M. Multichannel nonlinear holography in a two-dimensional nonlinear photonic crystal. Phys. Rev. A 2020, 102, 043506. [Google Scholar] [CrossRef]
- Ruffato, G.; Rossi, R.; Massari, M.; Mafakheri, E.; Capaldo, P.; Romanato, F. Design, fabrication and characterization of Computer Generated Holograms for anti-counterfeiting applications using OAM beams as light decoders. Sci. Rep. 2017, 7, 18011. [Google Scholar] [CrossRef]
- Ren, H.; Briere, G.; Fang, X.; Ni, P.; Sawant, R.; Héron, S.; Chenot, S.; Vézian, S.; Damilano, B.; Brändli, V.; et al. Metasurface orbital angular momentum holography. Nat. Commun. 2019, 10, 2986. [Google Scholar] [CrossRef]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high-security encryption. Nat. Photonics 2020, 14, 102–108. [Google Scholar] [CrossRef]
- Zhu, G.; Bai, Z.; Chen, J.; Huang, C.; Wu, L.; Fu, C.; Wang, Y. Ultra-dense perfect optical orbital angular momentum multiplexed holography. Opt. Express 2021, 29, 28452–28460. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, X.; Xiong, R.; Ma, X.; Jiang, X. Angular multiplexation of partial helical phase modes in orbital angular momentum holography. Opt. Express 2022, 30, 11110–11119. [Google Scholar] [CrossRef]
- Anguita, J.A.; Neifeld, M.A.; Vasic, B.V. Turbulence-induced channel crosstalk in an orbital angular momentum-multiplexed free-space optical link. Appl. Opt. 2008, 47, 2414–2429. [Google Scholar] [CrossRef]
- Liu, X.; Monfared, Y.E.; Pan, R.; Ma, P.; Cai, Y.; Liang, C. Experimental realization of scalar and vector perfect Laguerre–Gaussian beams. Appl. Phys. Lett. 2021, 119, 021105. [Google Scholar] [CrossRef]
- Rosales-Guzman, C.; Forbes, A. How to Shape Light with Spatial Light Modulators. SPIE 2017, SL30, 1–57. [Google Scholar]
- Forbes, A.; Dudlet, A.; McLaren, M. Geration and detection of optical modes with spatial light modulators. Adv. Opt. Photonics 2016, 8, 200–227. [Google Scholar] [CrossRef]
- Bergeron, A.; Gauvin, J.; Gagnon, F.; Gingras, D.; Arsenault, H.H.; Doucet, M. Phase calibration and applications of a liquid-crystal spatial light modulator. Appl. Opt. 1995, 34, 5133–5139. [Google Scholar] [CrossRef] [PubMed]
- Chandra, A.D.; Banerjee, A. Rapid phase calibration of a spatial light modulator using novel phase masks and optimization of its efficiency using an iterative algorithm. J. Mod. Opt. 2020, 67, 628–637. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Soifer, V.A.; Khonina, S.N. Rotation of Multimodal Gauss-Laguerre Light Beams in Free Space and in a Fiber. Opt. Las. Eng. 1998, 29, 343–350. [Google Scholar] [CrossRef]
- Baumann, S.M.; Kalb, D.M.; MacMillan, L.H.; Galvez, E.J. Propagation dynamics of optical vortices due to Gouy phase. Opt. Express 2009, 17, 9818–9827. [Google Scholar] [CrossRef]
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for the determination of phase from image and difraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Kotlyar, V.V.; Nikolski, I.V.; Soifer, V.A. Adaptive iterative algorithm for focusators synthesis. Optik 1991, 88, 17–19. [Google Scholar]
- Wu, Y.; Wang, J.; Chen, C.; Liu, C.; JIn, F.; Chen, N. Adaptive weighted Gerchberg-Saxton algorithm for generation of phase-only hologram with artifacts suppression. Opt. Express 2021, 29, 1412–1427. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Cai, Z.; Shi, L.; Zhou, F.; Guo, P.; Lu, Y.; Wu, J. A multi-plane optical see-through holographic three-dimensional display for augmented reality applications. Optik 2018, 157, 190–196. [Google Scholar] [CrossRef]
- Li, X.; Ma, H.; Yin, C.; Tang, J.; Li, H.; Tang, M.; Wang, J.; Tai, Y.; Li, X.; Wang, Y. Controllable mode transformation in perfect optical vortices. Opt. Express 2018, 26, 651–662. [Google Scholar] [CrossRef] [PubMed]
- Ruffato, G.; Massari, M.; Carli, M.; Romanato, F. Spiral phase plates with radial discontinuities for the generation of multiring orbital angular momentum beams: Fabrication, characterization, and application. Opt. Eng. 2015, 54, 111307. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Xiong, B.; Zhang, X.; Yuan, X. Holographic Encryption Applications Using Composite Orbital Angular Momentum Beams. Photonics 2022, 9, 605. https://doi.org/10.3390/photonics9090605
Zhang N, Xiong B, Zhang X, Yuan X. Holographic Encryption Applications Using Composite Orbital Angular Momentum Beams. Photonics. 2022; 9(9):605. https://doi.org/10.3390/photonics9090605
Chicago/Turabian StyleZhang, Nian, Baoxing Xiong, Xiang Zhang, and Xiao Yuan. 2022. "Holographic Encryption Applications Using Composite Orbital Angular Momentum Beams" Photonics 9, no. 9: 605. https://doi.org/10.3390/photonics9090605
APA StyleZhang, N., Xiong, B., Zhang, X., & Yuan, X. (2022). Holographic Encryption Applications Using Composite Orbital Angular Momentum Beams. Photonics, 9(9), 605. https://doi.org/10.3390/photonics9090605



