Parametric Generation of Variable Spot Arrays Based on Multi-Level Phase Modulation
Abstract
:1. Introduction
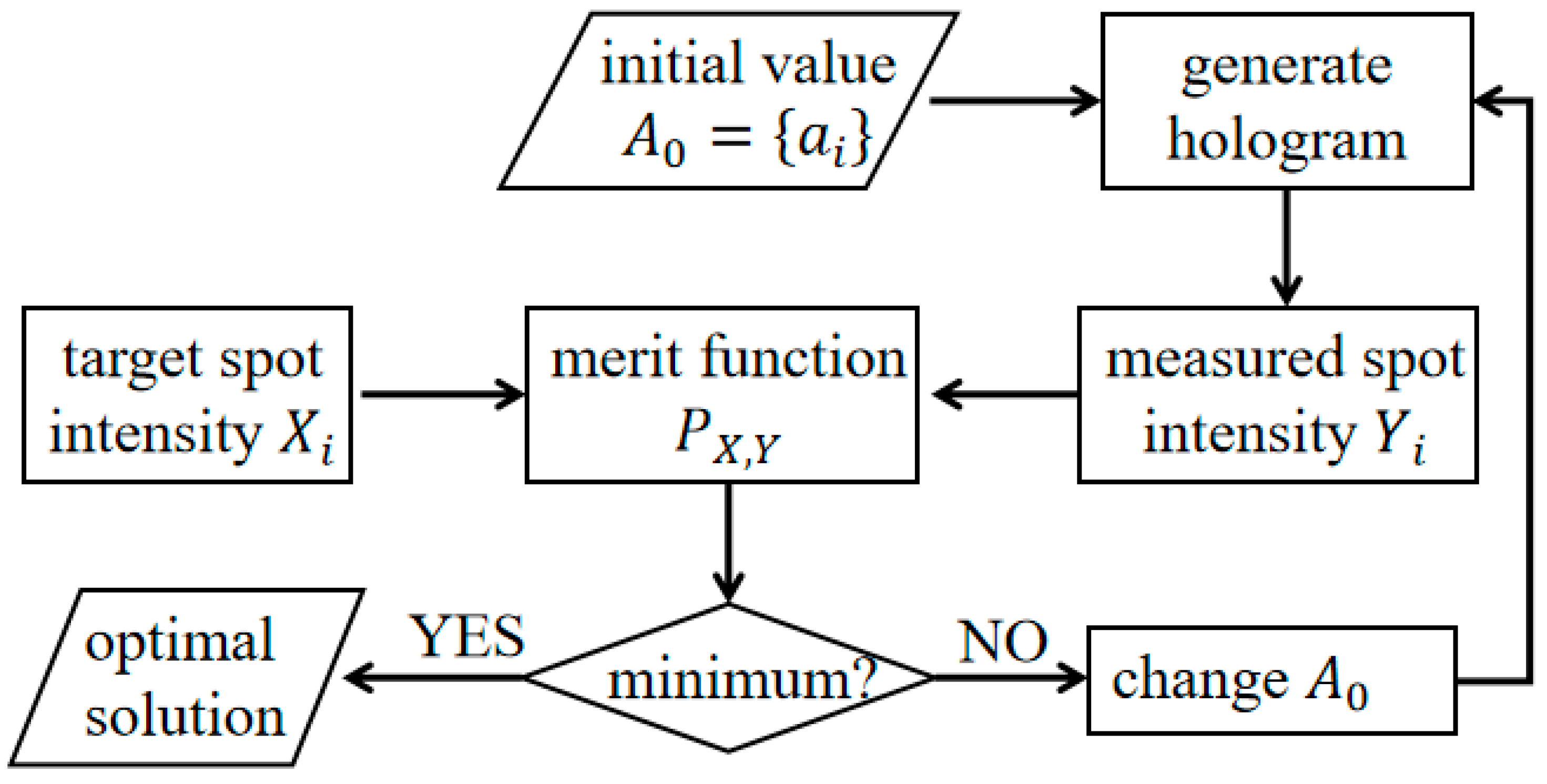
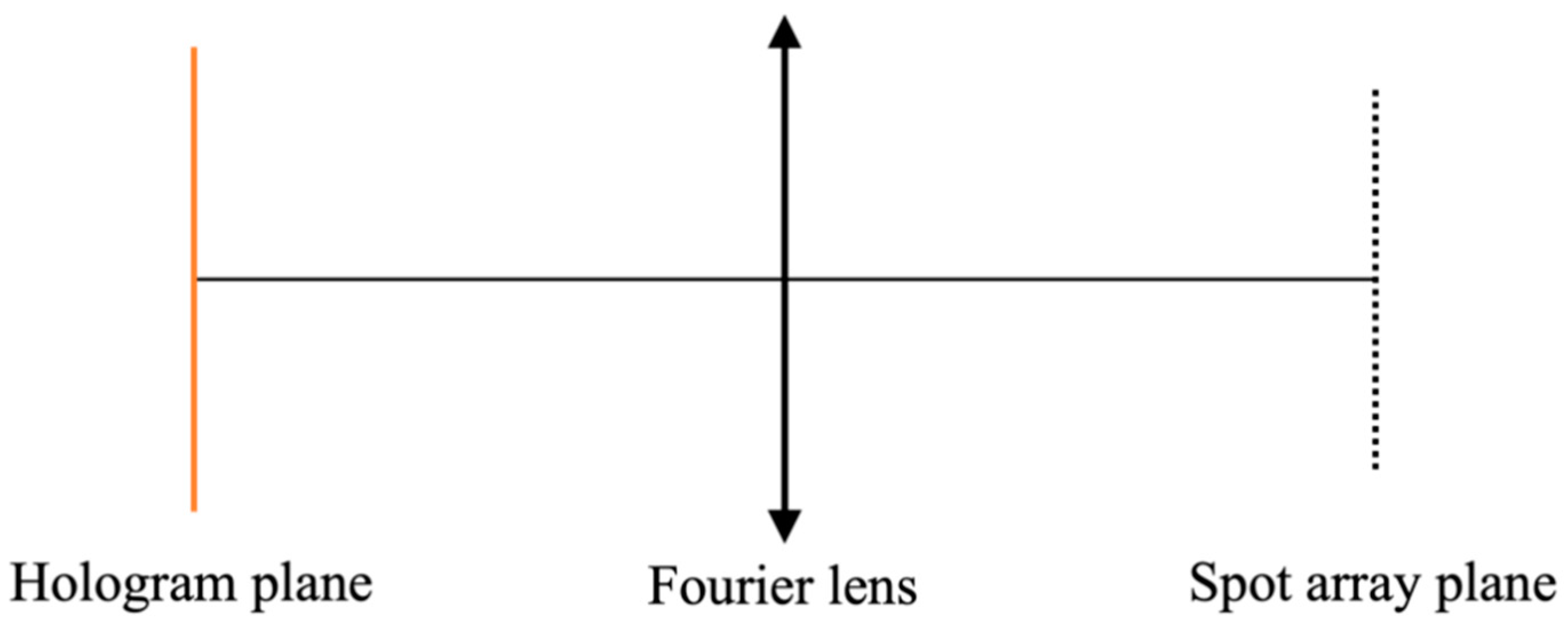
2. Methods
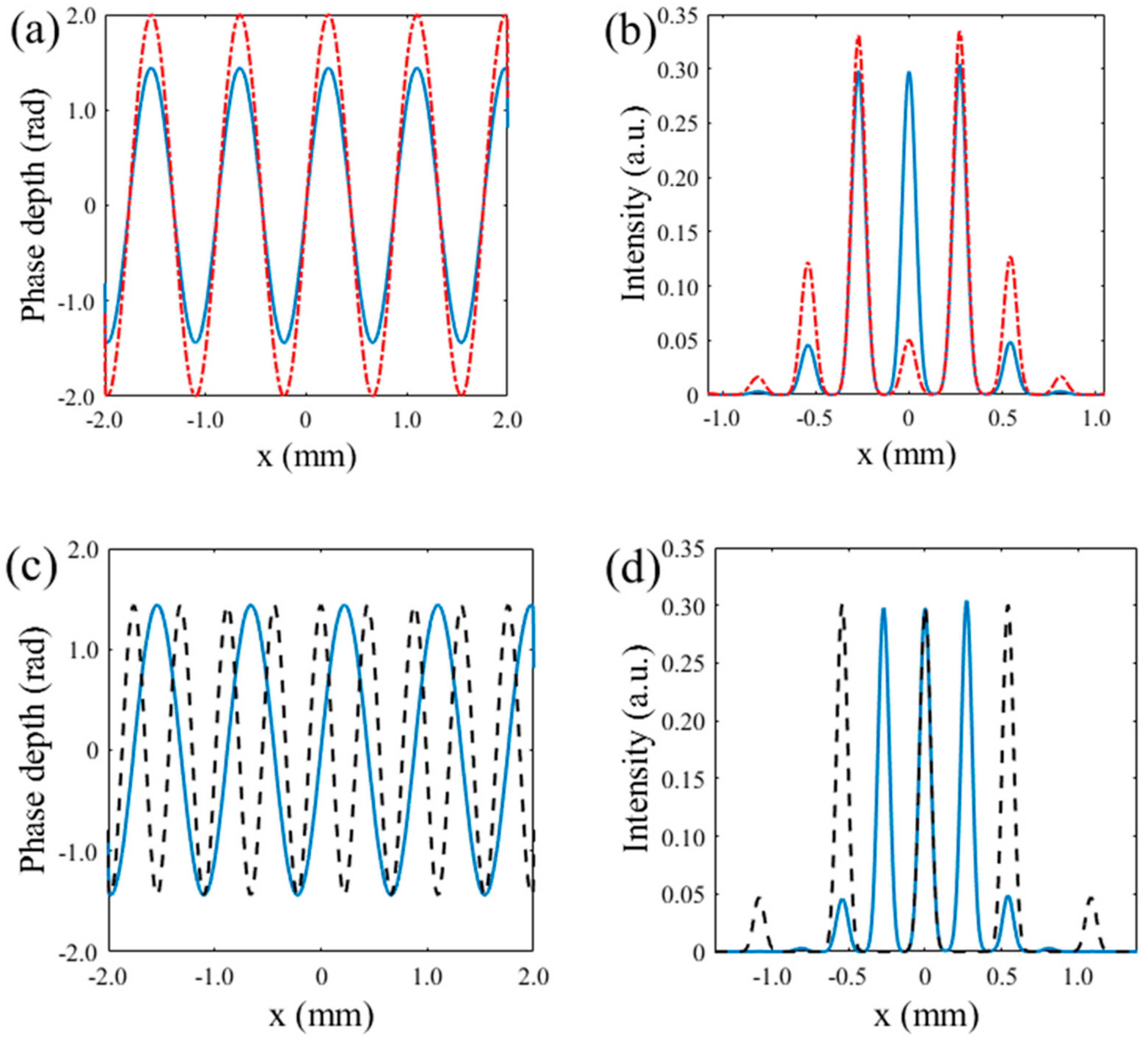
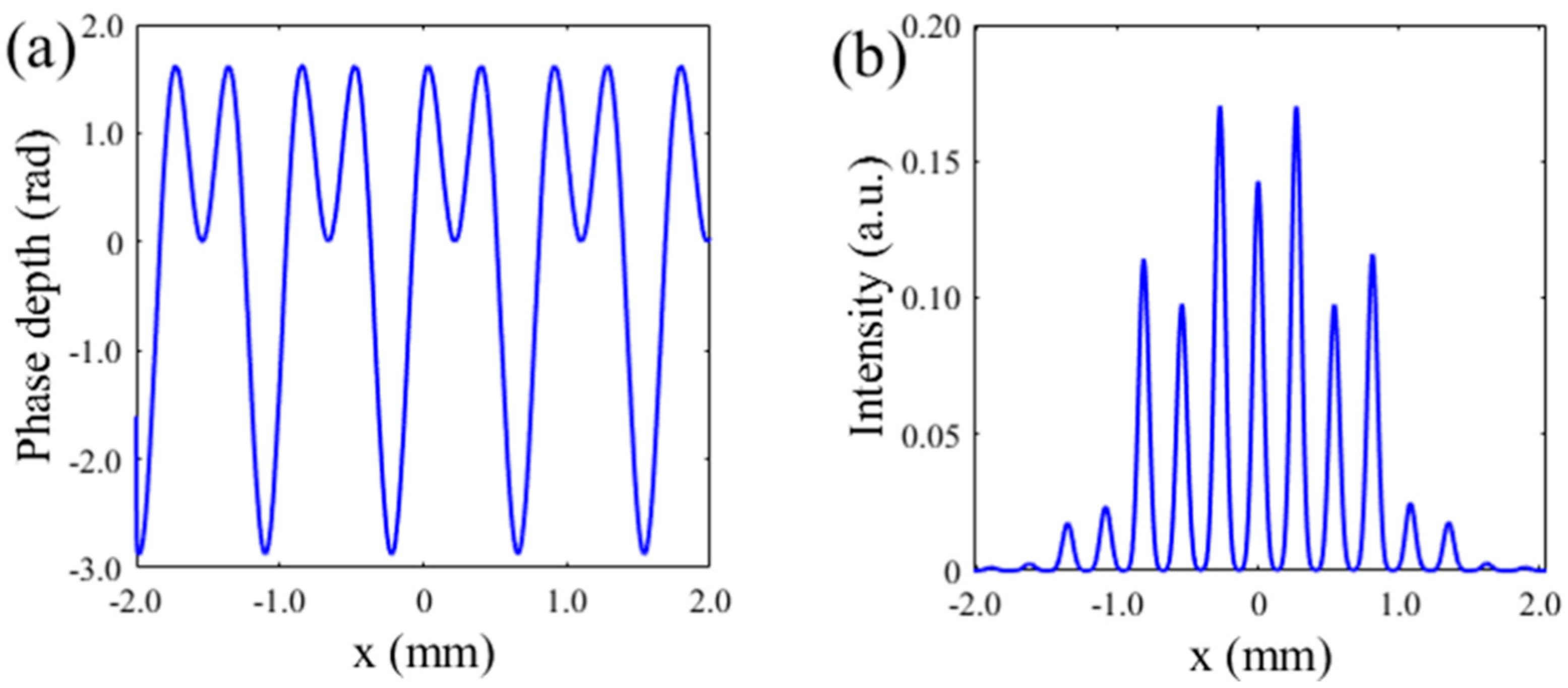
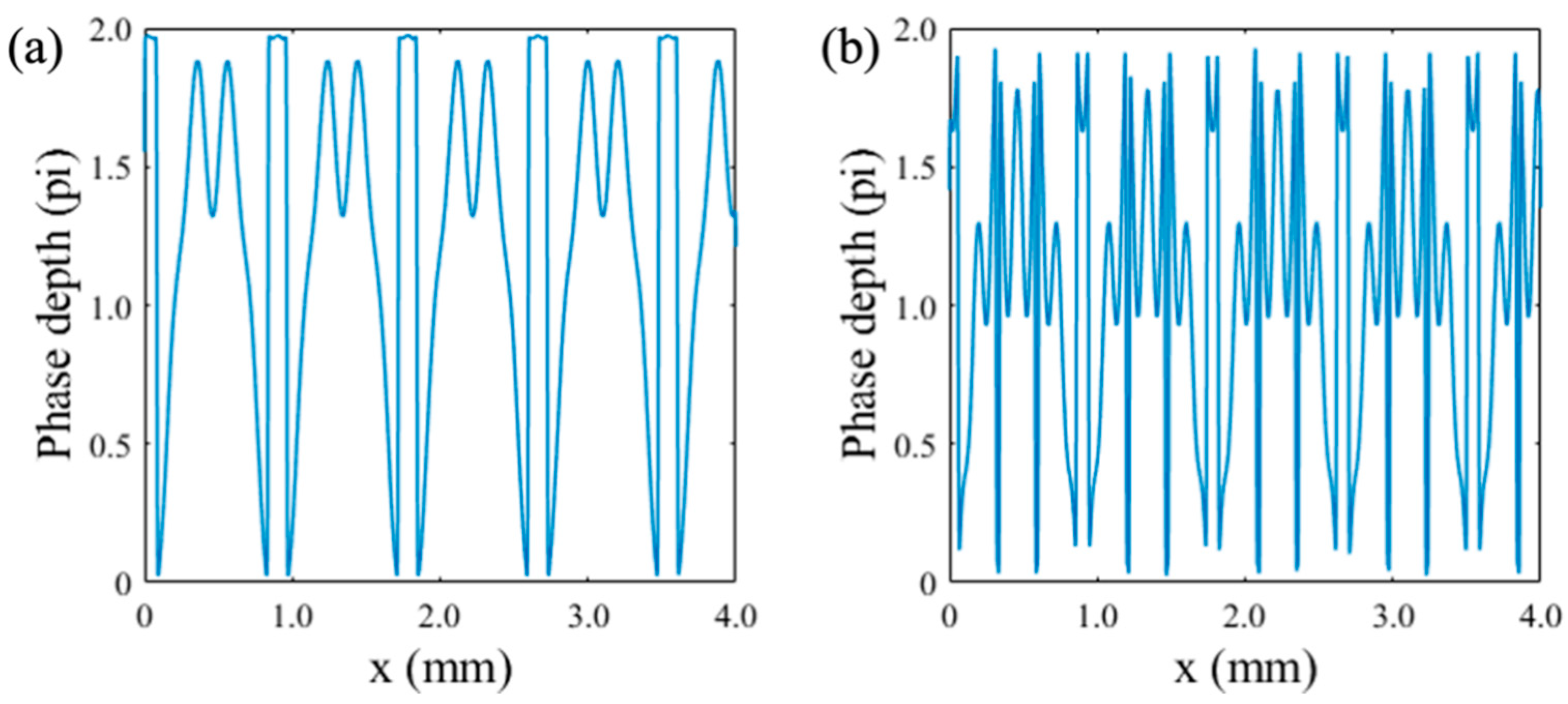
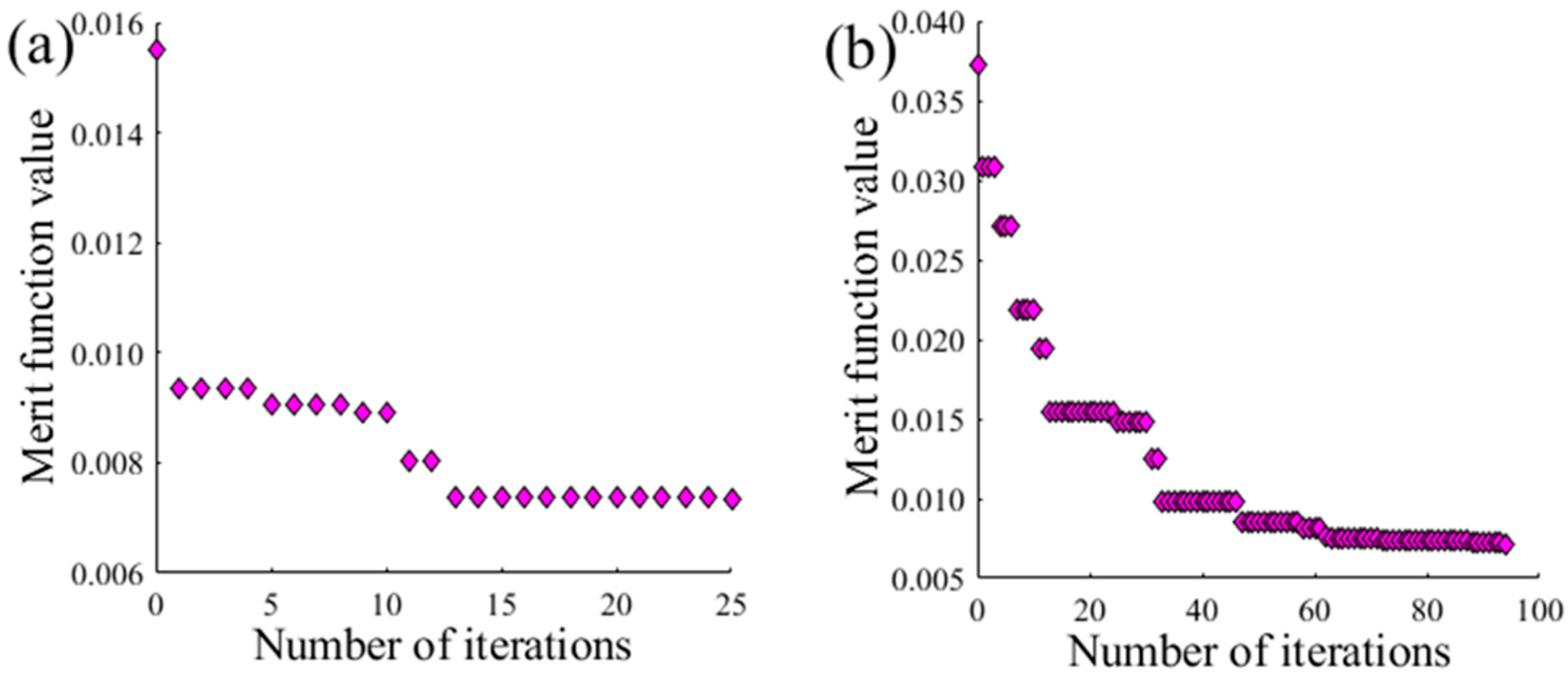
3. Simulation
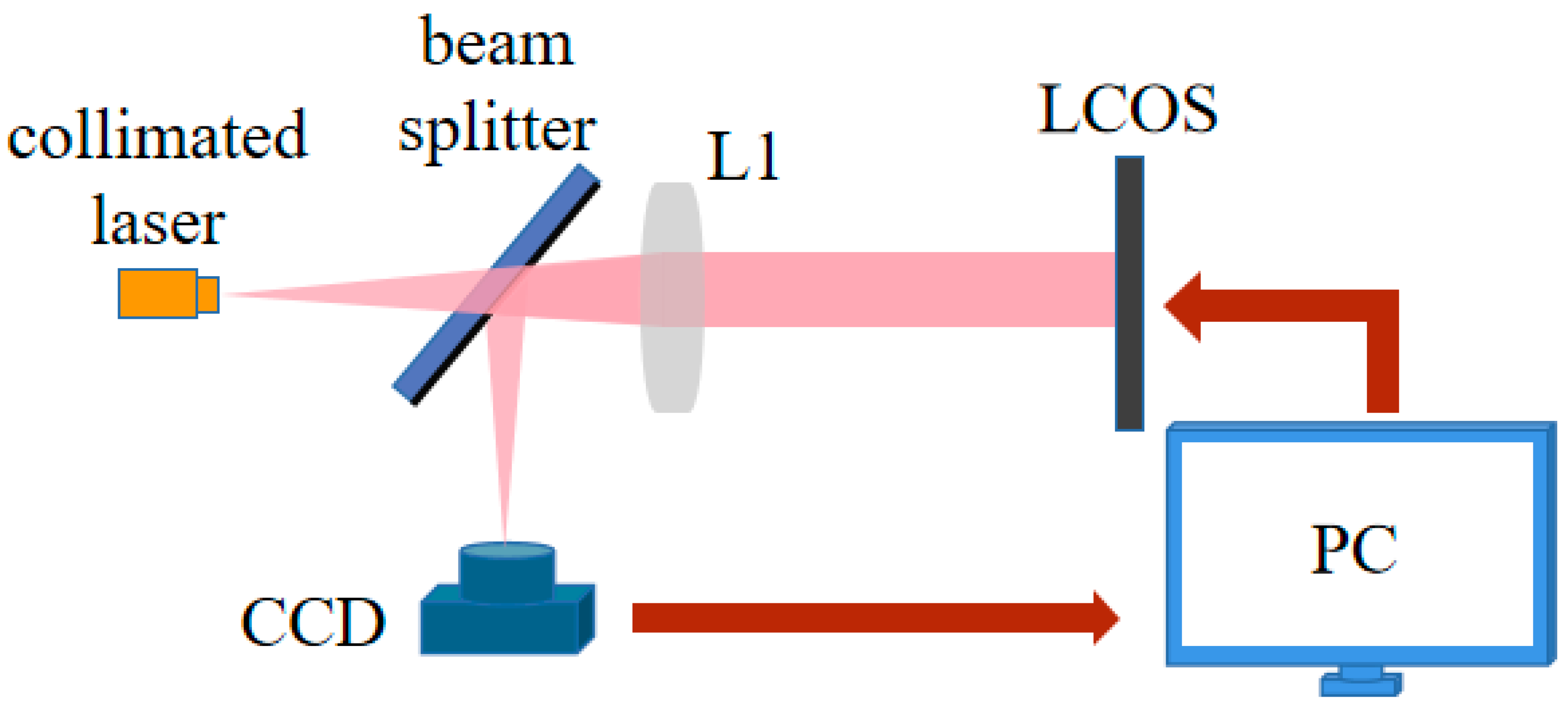
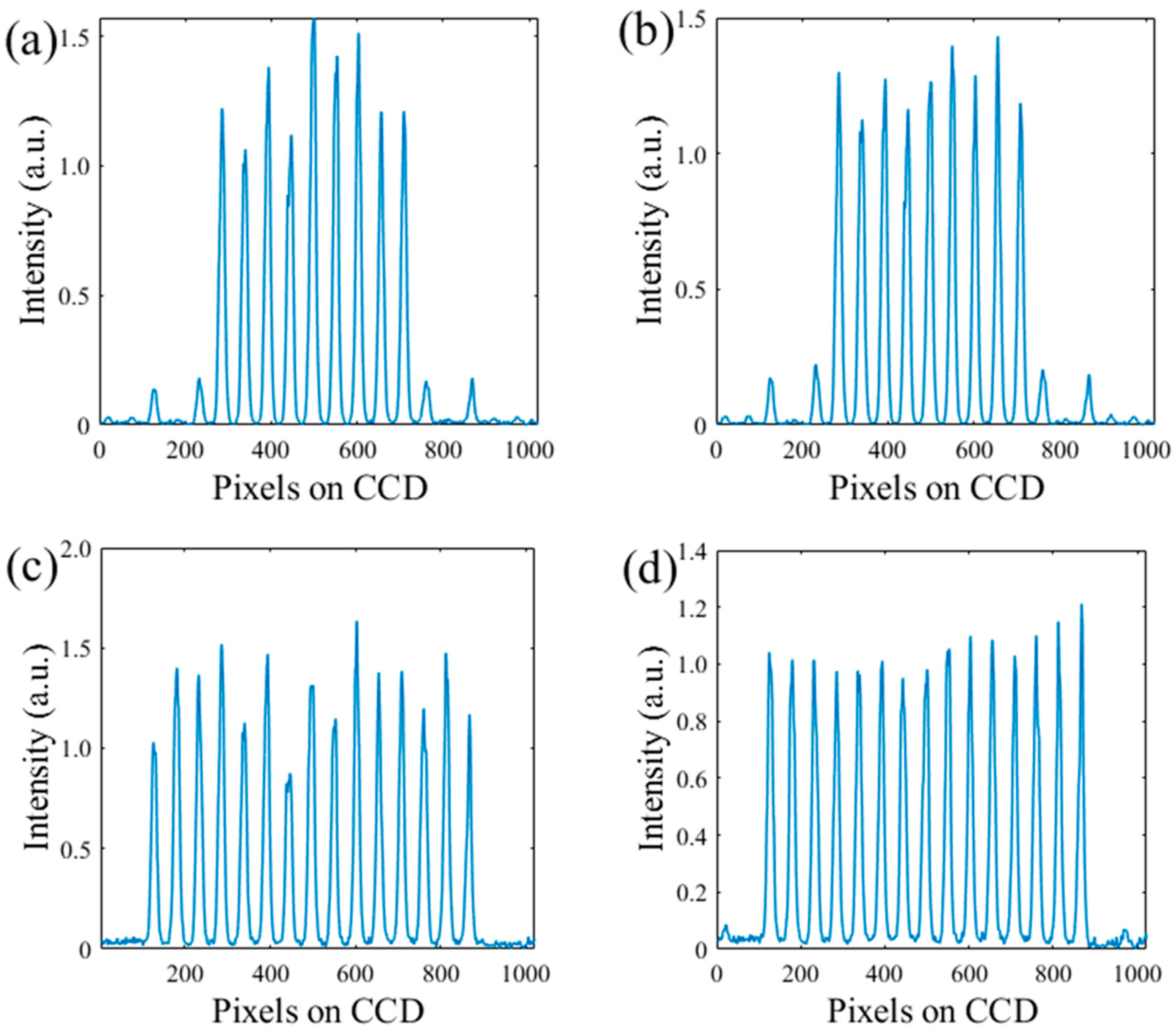
4. Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jesacher, A.; Booth, M.J. Parallel direct laser writing in three dimensions with spatially dependent aberration correction. Opt. Express 2010, 18, 21090–21099. [Google Scholar] [CrossRef] [PubMed]
- Di, C.H.; Zhou, C.H. Dynamic optical coupled system employing even-numbered Dammann gratings. Appl. Opt. 2006, 45, 1993–2000. [Google Scholar] [CrossRef]
- Gu, M.; Li, X.P.; Cao, Y.Y. Optical storage arrays: A perspective for future big data storage. Light-Sci. Appl. 2014, 3, 11. [Google Scholar] [CrossRef]
- Sacconi, L.; Froner, E.; Antolini, R.; Taghizadeh, M.R.; Choudhury, A.; Pavone, F.S. Multiphoton multifocal microscopy exploiting a diffractive optical element. Opt. Lett. 2003, 28, 1918–1920. [Google Scholar] [CrossRef] [PubMed]
- Sakakura, M.; Ishiguro, Y.; Fukuda, N.; Shimotsuma, Y.; Miura, K. Modulation of laser induced-cracks inside a LiF single crystal by fs laser irradiation at multiple points. Opt. Express 2013, 21, 26921–26928. [Google Scholar] [CrossRef] [PubMed]
- Ghebjagh, S.G.; Fischer, D.; Sinzinger, S. Multifocal multi-value phase zone plate for 3D focusing. Appl. Opt. 2019, 58, 8943–8949. [Google Scholar] [CrossRef]
- Robertson, B.; Yang, H.; Redmond, M.M.; Collings, N.; Liu, J.; Jeziorska-Chapman, A.M.; Moore, J.R.; Zhang, Z.; Crossland, W.A.; Wonfor, A.; et al. The Use of Wavefront Encoding to Reduce Crosstalk in a Multicasting Fiber Telecom Switch. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 4 March 2012; p. OM2J.6. [Google Scholar]
- Yang, H.N.; Robertson, B.; Chu, D.P. IEEE. Crosstalk Reduction in Holographic Wavelength Selective Switches Based on Phase-only LCOS Devices. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Francisco, CA, USA, 9–13 March 2014. [Google Scholar]
- Roider, C.; Piestun, R.; Jesacher, A. 3D image scanning microscopy with engineered excitation and detection (vol 4, pg 1373, 2017). Optica 2017, 4, 1559. [Google Scholar] [CrossRef]
- Kato, J.; Takeyasu, N.; Adachi, Y.; Sun, H.B.; Kawata, S. Multiple-spot parallel processing for laser micronanofabrication. Appl. Phys. Lett. 2005, 86, 3. [Google Scholar] [CrossRef]
- Anderson, T.; Segref, A.; Frisken, G.; Lorenser, D.; Ferra, H.; Frisken, S. Highly Parallelized Optical Coherence Tomography for Ocular metrology and imaging. In Proceedings of the Biophotonics Australasia Conference, Melbourne, Australia, 9–12 December 2019. [Google Scholar]
- Streibl, N.; Nolscher, U.; Jahns, J.; Walker, S. Array generation with lenslet arrays. Appl. Opt. 1991, 30, 2739–2742. [Google Scholar] [CrossRef]
- Daly, D.; Stevens, R.F.; Hutley, M.C.; Davies, N. The manufacture of microlenses by melting photoresist. Meas. Sci. Technol. 1990, 1, 759–766. [Google Scholar] [CrossRef]
- Haselbeck, S.; Schreiber, H.; Schwider, J.; Streibl, N. Microlenses fabricated by melting a photoresist on a base layer. Opt. Eng. 1993, 32, 1322–1324. [Google Scholar] [CrossRef]
- Pan, C.T.; Wu, T.T.; Chen, M.F.; Chang, Y.C.; Lee, C.J.; Huang, J.C. Hot embossing of micro-lens array on bulk metallic glass. Sens. Actuator A-Phys. 2008, 141, 422–431. [Google Scholar] [CrossRef]
- Chang, C.Y.; Yang, S.Y.; Huang, L.S.; Hsieh, K.H. Fabrication of polymer microlens arrays using capillary forming with a soft mold of micro-holes array and UV-curable polymer. Opt. Express 2006, 14, 6253–6258. [Google Scholar] [CrossRef]
- Hua, J.G.; Ren, H.; Jia, A.; Tian, Z.N.; Wang, L.; Juodkazis, S.; Chen, Q.D.; Sun, H.B. Convex silica microlens arrays via femtosecond laser writing. Opt. Lett. 2020, 45, 636–639. [Google Scholar] [CrossRef]
- Algorri, J.F.; Bennis, N.; Urruchi, V.; Morawiak, P.; Sanchez-Pena, J.M.; Jaroszewicz, L.R. Tunable liquid crystal multifocal microlens array. Sci. Rep. 2017, 7, 6. [Google Scholar] [CrossRef]
- Kuang, Z.; Perrie, W.; Liu, D.; Edwardson, S.P.; Jiang, Y.; Fearon, E.; Watkins, K.G.; Dearden, G. Ultrafast laser parallel microprocessing using high uniformity binary Dammann grating generated beam array. Appl. Surf. Sci. 2013, 273, 101–106. [Google Scholar] [CrossRef]
- Davis, J.A.; Moreno, I.; Martinez, J.L.; Hernandez, T.J.; Cottrell, D.M. Creating three-dimensional lattice patterns using programmable Dammann gratings. Appl. Opt. 2011, 50, 3653–3657. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhou, J.Y.; Chen, Q.M.; Lei, L.; Wen, K.H.; Hu, Y.M. Rapid Prototyping of a Dammann Grating in DMD-Based Maskless Lithography. IEEE Photonics J. 2019, 11, 11. [Google Scholar] [CrossRef]
- Li, Y.; Watanabe, W.; Sun, Q.; Tamaki, T.; Nishii, J.; Itoh, K. Fabrication of Dammann gratings in silica glass. Chin. Opt. Lett. 2005, 3, S57–S59. [Google Scholar]
- Krackhardt, U.; Streibl, N. Design of dammann-gratings for array generation. Opt. Commun. 1989, 74, 31–36. [Google Scholar] [CrossRef]
- Zhang, Z.C.; You, Z.; Chu, D.P. Fundamentals of phase-only liquid crystal on silicon (LCOS) devices. Light-Sci. Appl. 2014, 3, 10. [Google Scholar] [CrossRef] [Green Version]
- Chiang, K.H.F.; Wu, S.T.; Chen, S.H. Fringing field effect of the liquid-crystal-on-silicon devices. Jpn. J. Appl. Phys. Part 1—Regul. Pap. Short Notes Rev. Pap. 2002, 41, 4577–4585. [Google Scholar] [CrossRef]
- Yang, H.; Chu, D.P. Phase flicker optimisation in digital liquid crystal on silicon devices. Opt. Express 2019, 27, 24556–24567. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.N.; Chu, D.P. Phase flicker in liquid crystal on silicon devices. J. Phys. Photonics 2020, 2, 19. [Google Scholar] [CrossRef]
- Wang, C.M.; Wang, Q.D.; Mu, Q.Q.; Peng, Z.H. High-precision beam array scanning system based on Liquid Crystal Optical Phased Array and its zero-order leakage elimination. Opt. Commun. 2022, 506, 8. [Google Scholar] [CrossRef]
- Yang, H.N.; Li, K.; Chu, D.P. Liquid crystal on silicon technology and reconfigurable all-optical networks. Chin. J. Liq. Cryst. Disp. 2021, 36, 772–788. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Y.; Zhang, X.; Yang, H.; Chu, D. Parametric Generation of Variable Spot Arrays Based on Multi-Level Phase Modulation. Photonics 2022, 9, 633. https://doi.org/10.3390/photonics9090633
Lei Y, Zhang X, Yang H, Chu D. Parametric Generation of Variable Spot Arrays Based on Multi-Level Phase Modulation. Photonics. 2022; 9(9):633. https://doi.org/10.3390/photonics9090633
Chicago/Turabian StyleLei, Yi, Xi Zhang, Haining Yang, and Daping Chu. 2022. "Parametric Generation of Variable Spot Arrays Based on Multi-Level Phase Modulation" Photonics 9, no. 9: 633. https://doi.org/10.3390/photonics9090633
APA StyleLei, Y., Zhang, X., Yang, H., & Chu, D. (2022). Parametric Generation of Variable Spot Arrays Based on Multi-Level Phase Modulation. Photonics, 9(9), 633. https://doi.org/10.3390/photonics9090633





