Goos–Hänchen Lateral Displacements and Angular Deviations: When These Optical Effects Offset Each Other
Abstract
:1. Introduction
2. The Incident Beam
3. The Optical Phase

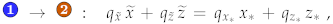

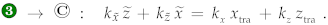
4. The Upper Transmitted Beam
 , to the reflection by the lower (dielectric/air) interface,
, to the reflection by the lower (dielectric/air) interface,  , and, finally, to the transmission through the right (dielectric/air) interface,
, and, finally, to the transmission through the right (dielectric/air) interface,  ,
,
5. GH Shifts and Angular Deviations
6. Discussions
7. Conclusions and Outlooks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Born, M.; Wolf, E. Principles of Optics; Cambridge UP: Cambridge, UK, 1999. [Google Scholar]
- Sharma, K.K. Optics: Principles and Applications; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Goos, F.; Hänchen, H. Ein neuer und fundamentaler Versuch zur Totalreflexion. Ann. Phys. 1947, 436, 333–346. [Google Scholar] [CrossRef]
- Artmann, K. Berechnung der Seitenversetzung des totalreflektierten Strahles. Ann. Phys. 1948, 437, 87–102. [Google Scholar] [CrossRef]
- Horowitz, B.R.; Tamir, T. Lateral Displacement of a Light Beam at a Dielectric Interface. JOSA 1971, 61, 586–594. [Google Scholar] [CrossRef]
- Lai, H.M.; Cheng, F.C.; Tang, W.K. Goos–Hänchen effect around and off the critical angle. JOSA A 1986, 3, 550–557. [Google Scholar] [CrossRef]
- Araújo, M.P.; De Leo, S.; Maia, G.G. Closed-form expression for the Goos-Hänchen lateral displacement. Phys. Rev. A 2016, 93, 023801. [Google Scholar] [CrossRef]
- Ra, J.W.; Bertoni, H.L.; Felsen, L.B. Reflection and transmission of beams at a dielectric interface. SIAM J. Appl. Math. 1973, 24, 396–413. [Google Scholar] [CrossRef]
- Merano, M.; Aiello, A.; ’t Hooft, G.W.; van Exter, M.P.; Eliel, E.R.; Woerdman, J.P. Observation of Goos-Hänchen Shifts in Metallic Reflection. Opt. Express 2007, 15, 15928–15934. [Google Scholar] [CrossRef]
- Kogelnik, H.; Weber, H.P. Rays, Stored Energy, and Power Flow in Dielectric Waveguides. JOSA 1974, 64, 174–185. [Google Scholar] [CrossRef]
- Prajapati, C.; Ranganathan, D. Goos-Hänchen and Imbert- Federov Shifts for Hermite-Gauss Beams. JOSA A 2012, 29, 1377–1382. [Google Scholar] [CrossRef]
- Liu, F.P.; Meng, X.J.; Xiao, J.Q.; Wang, A.L.; Yang, C.C. The Goos-Hänchen Shift of Wide-angle Seismic Reflection Wave. Sci. China Earth Sci. 2012, 55, 852–857. [Google Scholar] [CrossRef]
- De Leo, S.; Kraus, R. Incidence Angles Maximizing the Goos-Haenchen Shift in Seismic Data Analysis. Pure Appl. Geoph. 2018, 175, 2023–2044. [Google Scholar] [CrossRef]
- Madrazo, A.; Nieto-Vesperinas, M. Detection of subwavelength Goos–Hänchen shifts from near-field intensities: A numerical simulation. Opt. Lett. 1995, 20, 2445–2447. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yin, C.; Sun, J.; Li, H.; Wang, Y.; Ran, M.; Cao, Z. High-sensitivity temperature sensor using the ultrahigh order mode-enhanced Goos-Hänchen effect. Opt. Express 2013, 21, 13380–13385. [Google Scholar] [CrossRef] [PubMed]
- Nie, Y.; Li, Y.; Wu, Z.; Wang, X.; Yuan, W.; Sang, M. Detection of chemical vapor with high sensitivity by using the symmetrical metal-cladding waveguide-enhanced Goos-Hänchen shift. Opt. Express 2014, 22, 8943–8948. [Google Scholar] [CrossRef]
- Carvalho, S.A.; De Leo, S. The use of the stationary phase method as a mathematical tool to determine the path of optical beams. Am. J. Phys. 2015, 83, 249–255. [Google Scholar] [CrossRef]
- Kompanets, V.; Melnikov, A.; Chekalin, S. Goos-Hänchen shift of a mid-infrared femtosecond filament visualized by the laser coloration method. Laser Phys. Lett. 2021, 18, 015302-5. [Google Scholar] [CrossRef]
- Araújo, M.P.; De Leo, S.; Maia, G.G. Oscillatory behavior of light in the composite Goos-Hänchen shift. Phys. Rev. A 2017, 95, 053836-9. [Google Scholar] [CrossRef]
- Santana, O.; de Araujo, S.E.E. Direct measurement of the composite Goos–Hänchen shift of an optical beam. Opt. Lett. 2018, 43, 4037–4040. [Google Scholar] [CrossRef] [PubMed]
- Santana, O.; de Araujo, S.E.E. Oscillatory trajectory of an optical beam propagating in free space. Opt. Lett. 2019, 44, 646–649. [Google Scholar] [CrossRef]
- Leo, S.D.; Stefano, A. Angular deviations: From a cubic equation to a universal closed formula to determine the peak position of reflected and (upper) transmitted beams. Eur. Phys. J. Plus 2021, 136, 507–520. [Google Scholar] [CrossRef]
- Araújo, M.P.; Carvalho, S.A.; De Leo, S. The frequency crossover for the Goos-Hänchen shift. J. Mod. Opt. 2013, 60, 1772–1780. [Google Scholar] [CrossRef]
- Santana, O.J.; Carvalho, S.A.; De Leo, S.; de Araújo, L.E.E. Weak measurement of the composite Goos-Hänchen shift in the critical region. Opt. Lett. 2016, 41, 3884–3887. [Google Scholar] [CrossRef]
- Olaya, C.M.; Hayazawa, N.; Hermosa, N.; Tanaka, T. Angular Goos-Hänchen shift sensor using a gold film enhanced by surface plasmon resonance. J. Phys. Chem. A 2021, 125, 451–458. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, L.; Ang, L.K. Ultrasensitive optical temperature transducers based on surface plasmon resonance enhanced composited Goos-Hänchen and Imbert-Fedorov shifts. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 4601508-8. [Google Scholar] [CrossRef]
- Goswami, S.; Pal, M.; Nandi, A.; Panigrahi, P.K.; Ghosh, N. Simultaneous weak value amplification of angular Goos–Hänchen and Imbert–Fedorov shifts in partial reflection. Opt. Lett. 2014, 39, 6229–6232. [Google Scholar] [CrossRef] [PubMed]
- Araújo, M.; De Leo, S.; Maia, G. Optical weak measurements without removing the Goos-Haenchen phase. J. Mod. Opt. 2018, 65, 837–846. [Google Scholar] [CrossRef]
- Araújo, M.P.; De Leo, S.; Maia, G.G. Optimizing weak measurements to detect angular deviations. Ann. Phys. 2017, 529, 1600357-20. [Google Scholar] [CrossRef]
- De Leo, S.; Maia, G. Lateral shifts and angular deviations of Gaussian optical beams reflected by and transmitted through dielectric blocks: A tutorial review. J. Mod. Opt. 2019, 66, 2142–2194. [Google Scholar] [CrossRef] [Green Version]
 , forming an incidence angle, , with the normal to the first interface, . The beam transmitted through the first interface then moves in the dielectric prism towards the second (dielectric/air) interface,
, forming an incidence angle, , with the normal to the first interface, . The beam transmitted through the first interface then moves in the dielectric prism towards the second (dielectric/air) interface,  , forming an angle with the normal to the first interface, , and an angle with the normal to the second interface, . These angles are related to the incidence one by the Snell law, and , where . Once reflected by the second interface, the optical beam moves to the third (dielectric/air) interface,
, forming an angle with the normal to the first interface, , and an angle with the normal to the second interface, . These angles are related to the incidence one by the Snell law, and , where . Once reflected by the second interface, the optical beam moves to the third (dielectric/air) interface,  . Due to the geometry of the prism, the upper transmitted beam forms an angle with respect to the normal to the third interface, . The upper transmitted beam is thus detected at the camera ©. In (b), we find the coordinates systems of the incident and upper transmitted beams and of the prism interfaces.
. Due to the geometry of the prism, the upper transmitted beam forms an angle with respect to the normal to the third interface, . The upper transmitted beam is thus detected at the camera ©. In (b), we find the coordinates systems of the incident and upper transmitted beams and of the prism interfaces.
 , forming an incidence angle, , with the normal to the first interface, . The beam transmitted through the first interface then moves in the dielectric prism towards the second (dielectric/air) interface,
, forming an incidence angle, , with the normal to the first interface, . The beam transmitted through the first interface then moves in the dielectric prism towards the second (dielectric/air) interface,  , forming an angle with the normal to the first interface, , and an angle with the normal to the second interface, . These angles are related to the incidence one by the Snell law, and , where . Once reflected by the second interface, the optical beam moves to the third (dielectric/air) interface,
, forming an angle with the normal to the first interface, , and an angle with the normal to the second interface, . These angles are related to the incidence one by the Snell law, and , where . Once reflected by the second interface, the optical beam moves to the third (dielectric/air) interface,  . Due to the geometry of the prism, the upper transmitted beam forms an angle with respect to the normal to the third interface, . The upper transmitted beam is thus detected at the camera ©. In (b), we find the coordinates systems of the incident and upper transmitted beams and of the prism interfaces.
. Due to the geometry of the prism, the upper transmitted beam forms an angle with respect to the normal to the third interface, . The upper transmitted beam is thus detected at the camera ©. In (b), we find the coordinates systems of the incident and upper transmitted beams and of the prism interfaces.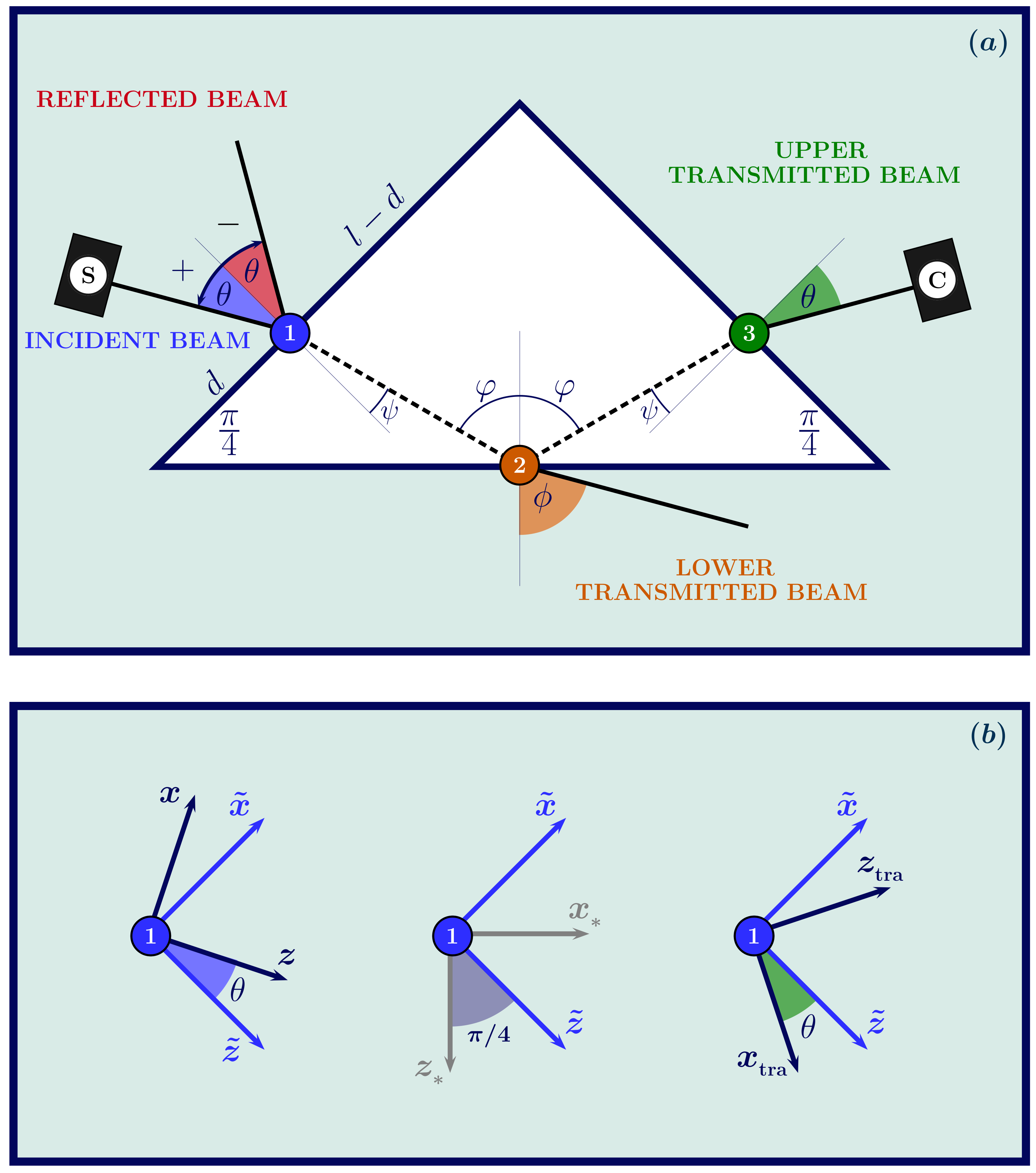
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Leo, S.; Maggio, L.; d’Ambrosio, M. Goos–Hänchen Lateral Displacements and Angular Deviations: When These Optical Effects Offset Each Other. Photonics 2022, 9, 643. https://doi.org/10.3390/photonics9090643
De Leo S, Maggio L, d’Ambrosio M. Goos–Hänchen Lateral Displacements and Angular Deviations: When These Optical Effects Offset Each Other. Photonics. 2022; 9(9):643. https://doi.org/10.3390/photonics9090643
Chicago/Turabian StyleDe Leo, Stefano, Luca Maggio, and Moreno d’Ambrosio. 2022. "Goos–Hänchen Lateral Displacements and Angular Deviations: When These Optical Effects Offset Each Other" Photonics 9, no. 9: 643. https://doi.org/10.3390/photonics9090643
APA StyleDe Leo, S., Maggio, L., & d’Ambrosio, M. (2022). Goos–Hänchen Lateral Displacements and Angular Deviations: When These Optical Effects Offset Each Other. Photonics, 9(9), 643. https://doi.org/10.3390/photonics9090643




