A Dynamic Multi-Period, Mixed-Integer Linear Programming Model for Cost Minimization of a Three-Echelon, Multi-Site and Multi-Product Construction Supply Chain
Abstract
:1. Introduction
- It merges temporal and project-based supply chains into a sustainable supply chain network with repetitive flows, large scope contracts, strategic alliances and economies of scale (through discount rates available for bulk purchase).
- It supports long-term strategic decisions on the supply chain configuration and tactical decisions on inventory control and distribution coordination and may accommodate a full spectrum of products—from engineered-to-order-products to made-to-stock products.
- It includes multidimensional binary variables that can be exploited in various problem-specific ways for introducing strategic preferences (e.g., multiple supplier sourcing), material compatibility constraints and logistics-related considerations (e.g., material kitting).
- It controls the extent of outsourcing and allows the incorporation of any logistics system by considering direct or indirect shipments from suppliers to construction sites through logistics centers or subcontractor warehouses.
- It provides a general, versatile and flexible managerial decision making tool to the general contractor who has the appropriate leverage power to act as a system integrator and manage dynamically a supply network of suppliers, subcontractors and logistics centers with multiple material flows converging to multiple sites.
- It provides artificial feedback cycles for a wide range of assumptions, enabling the decision maker to identify the most significant inputs and to negotiate with supply chain partners based on information that was not previously quantifiable.
2. Literature Review
3. Model Development
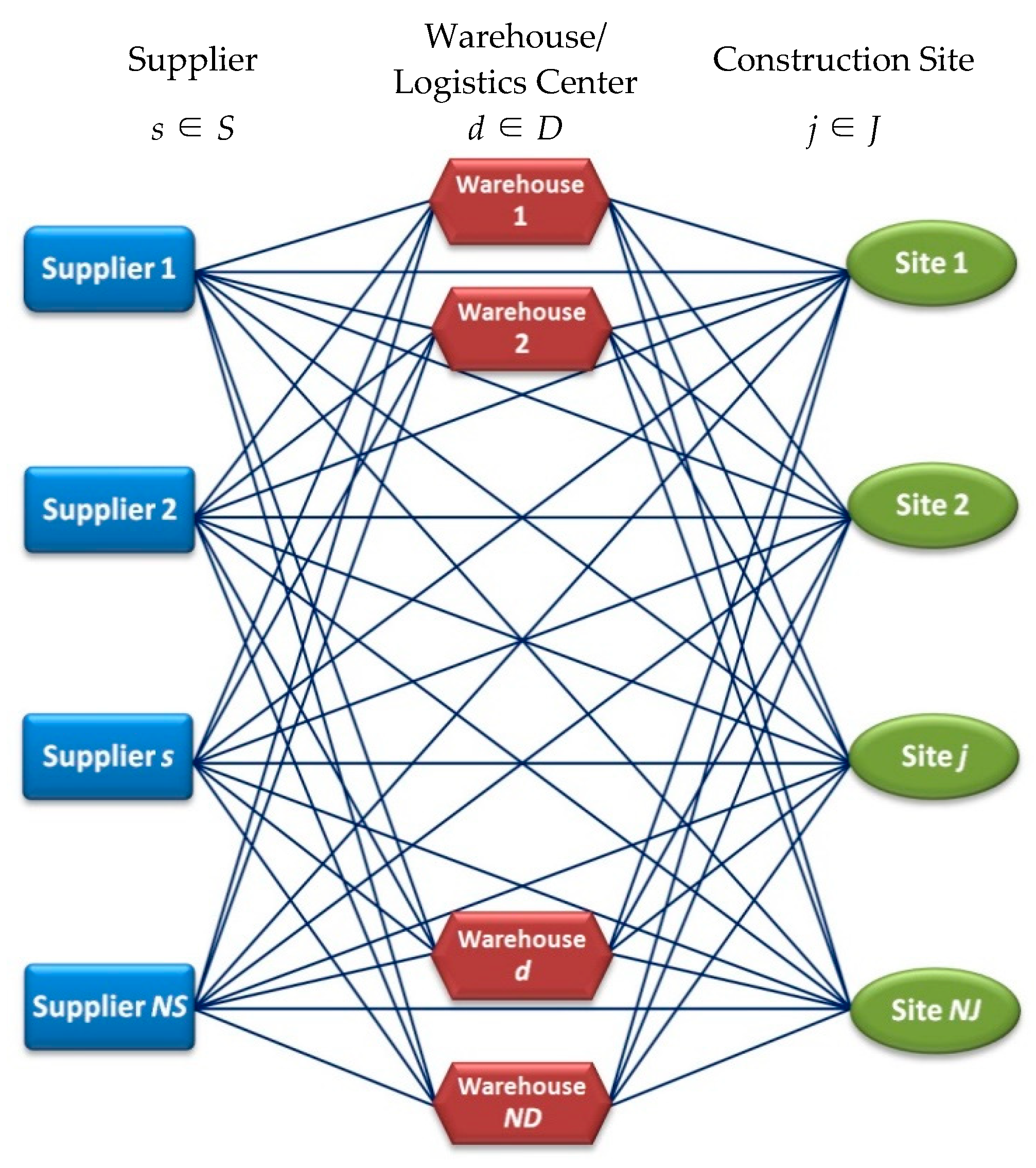
3.1. Structure and Underlying Principles
- Suppliers: suppliers of raw materials, manufacturers (plants), building merchants and manufacturing representatives. They deliver products to project sites directly or indirectly (through echelon 2) from their storage site.
- Warehouses or logistics centers: proprietary or rented storage facilities of subcontractors, referred to as warehouses for simplicity; logistics centers.
- Construction sites: locations to which construction projects are confined, usually with limited storage capacity due to physical constraints.
3.2. Assumptions and Interpretations
- The demand for construction projects over a given time horizon is a deterministic parameter. Hence, the demand of materials per time period is also known according to the project schedule and bill of material.
- The purchase prices of products are known for the overall time horizon (inflation rate is fixed) and discount rates are taken into account for bulk purchase. Cost of purchase is what suppliers charge for their products, taking into account the production cost and any costs involved in the processes of ordering products. No freight transportation costs are included, because these cost items will be studied separately.
- The holding inventory cost in this model is quantity-dependent. Fixed inventory costs are not considered in the optimization context, because they are ascribed to autonomous business entities for their constant operation regardless of which clients and supply chains they serve.
- The echelon of material production is not considered in this context, since the optimal production batches should not derive from the optimization of a CSC driven by a specific construction company; plants are part of several supply chains and serve several clients. However, the output of this model may provide valuable information to suppliers with manufacturing capacity and help them to derive an optimal production plan for their products.
- Safety stock levels are introduced in order to assure a minimum service level at the facilities of echelon 2, which should buffer against demand variations and prevent shortages in any supply chains they serve. The safety stocks usually refer to standardized products and their levels may derive from previous experience, forecasting or other descriptive analysis.
- The transportation cost consists of a fixed cost per shipment between the network nodes and a transportation quantity-dependent variable cost. For the sake of simplicity, we do not consider separate transportation costs for full or less–than–full shipments per order. However, products cannot be transported unless a minimum quantity is met for the transportation modes.
- Material unavailability/shortages are allowed to incur on-site under a known penalty cost, which is proportional to product units. The products that do not meet the demand are backordered and are not considered to be lost sales. We set a limit on the on-site material shortages to cut down the cost component arising from schedule disruption and to avoid any late project delivery.
3.3. Notation
| S | Set of suppliers indexed by |
| I | Set of products indexed by |
| J | Set of construction sites indexed by |
| D | Set of warehouses / logistics centers indexed by |
| T | Set of planning time periods indexed by |
| Demand of product at site at time period (according to each project’s bill of materials) | |
| Unit purchase cost of product from supplier | |
| Discount rate (%) for bulk purchasing of product from supplier at time period (in quantity greater than a predefined quantity, ) | |
| Variable transportation cost per unit of product shipped from network node to node at time period | |
| Variable transportation cost per unit of product shipped from network node to node at time period | |
| Variable transportation cost per unit of product shipped from network node to node at time period | |
| Fixed transportation cost per shipment from node to node at time period | |
| Fixed transportation cost per shipment from node to node at time period | |
| Fixed transportation cost per shipment from node to node at time period | |
| Maximum distribution capacity of supplier to provide product at time period | |
| Maximum number of units of product that can be shipped on one travel (loading capacity per shipment) from supplier to construction site | |
| Maximum number of units of product that can be shipped on one travel from supplier to warehouse | |
| Maximum number of units of product that can be shipped on one travel from warehouse to construction site | |
| Minimum number of units of product needed to send a shipment from supplier to construction site | |
| Minimum number of units of product needed to send a shipment from supplier to warehouse | |
| Minimum number of units of product needed to send a shipment from warehouse to construction site | |
| Variable inventory cost per unit of product at the storage facility of supplier at time period | |
| Variable inventory cost per unit of product at warehouse at time period | |
| Variable inventory cost per unit of product at construction site at time period | |
| Maximum inventory capacity (in volume) of supplier at any time period | |
| Maximum inventory capacity (in volume) of warehouse at any time period | |
| Maximum inventory capacity (in volume) of construction site at any time period | |
| Inventory space (volume) needed to hold one unit of product | |
| Initial (on-hand) inventory level of product at the storage facility of supplier | |
| Initial (on-hand) inventory level of product at warehouse | |
| Safety inventory level of product at the storage facility of supplier at any time period | |
| Safety inventory level of product at warehouse at any time period | |
| Backorder penalty cost for shortage of one unit of product at construction site | |
| Maximum shortage quantity of product allowed for backordering at construction site at time period without perturbation of the current schedule (expressed as a percentage of the demand ) | |
| Fixed cost related to the establishment of contractual relationship with supplier at time period | |
| Fixed cost related to the establishment of contractual relationship with a contractor holding a warehouse or a logistics provider (indicated by ) at time period | |
| Time period when the construction project at site is completed | |
| M | A very big positive number (infinity value) |
| Quantity of product to be purchased and transported from supplier to warehouse at time period | |
| Quantity of product to be purchased and transported from supplier to construction site at time period | |
| Quantity of product to be transported from warehouse to construction site at time period | |
| Number of shipments of product from supplier to construction site at time period | |
| Number of shipments of product from supplier to warehouse at time period | |
| Number of shipments of product from warehouse to construction site at time period | |
| Inventory level of product at the storage facility of supplier at the end of time period | |
| Inventory level of product at warehouse at the end of time period | |
| Inventory level of product at construction site at the end of time period | |
| Shortage quantity of product backordered at construction site at the end of time period | |
| 1 if supplier is selected at time period ; 0 otherwise | |
| 1 if warehouse is selected at time period ; 0 otherwise | |
| 1 if supplier is selected at time period for delivering product ; 0 otherwise | |
| 1 if warehouse is selected at time period for delivering product ; 0 otherwise | |
| 1 if supplier serves warehouse at time period ; 0 otherwise | |
| 1 if supplier serves site at time period ; 0 otherwise | |
| 1 if warehouse serves site at time period ; 0 otherwise | |
| 1 if supplier provides warehouse with product at time period ; 0 otherwise | |
| 1 if supplier provides site with product at time period ; 0 otherwise | |
| 1 if warehouse provides site with product at time period ; 0 otherwise | |
| 1 if supplier provides all sites with product in a quantity larger than at time period ; 0 otherwise | |
| 1 if supplier provides warehouse with product in a quantity larger than at time period ; 0 otherwise |
3.4. Objective Function
3.5. Constraints
3.5.1. Flow Equilibrium Constraints
3.5.2. Constraints on Storage Capacity and Inventory Holding
3.5.3. Constraints on Distribution Capacity and Transportation
3.5.4. Constraints on Quantity Discounts
3.5.5. Constraints on Shortage
3.5.6. Logical Constraints
3.5.7. General Constraints on Decision Variables
3.6. Introducing Problem-Specific Considerations to the Model
3.6.1. Case I (Material Kitting)
3.6.2. Case II (Strategic Preferences—Single-Supplier Sourcing)
3.6.3. Case III (Strategic Preferences—Multiple-Supplier Sourcing)
3.6.4. Case IV (Compatibility Issues—CSC Products)
3.6.5. Case V (Compatibility Issues—CSC Actors)
4. Computational Experience
4.1. Implementation
- translating the proposed algebraic model into a spreadsheet model,
- performing numerous zero-tests, tests with extreme input values and other logic tests to see whether the behavior of the model is as expected,
- performing numerous tests with random generated data in order to identify data sets that create a feasible solution space—i.e., satisfy simultaneously all the constraints,
- solving a feasible problem and analyzing the solution,
- conducting sensitivity analysis and multiple parameterized optimizations in order to see the impact of different data on the optimal solution.
4.2. Expected Quality of the Solution
4.3. Data Generation and Feasibility Implications
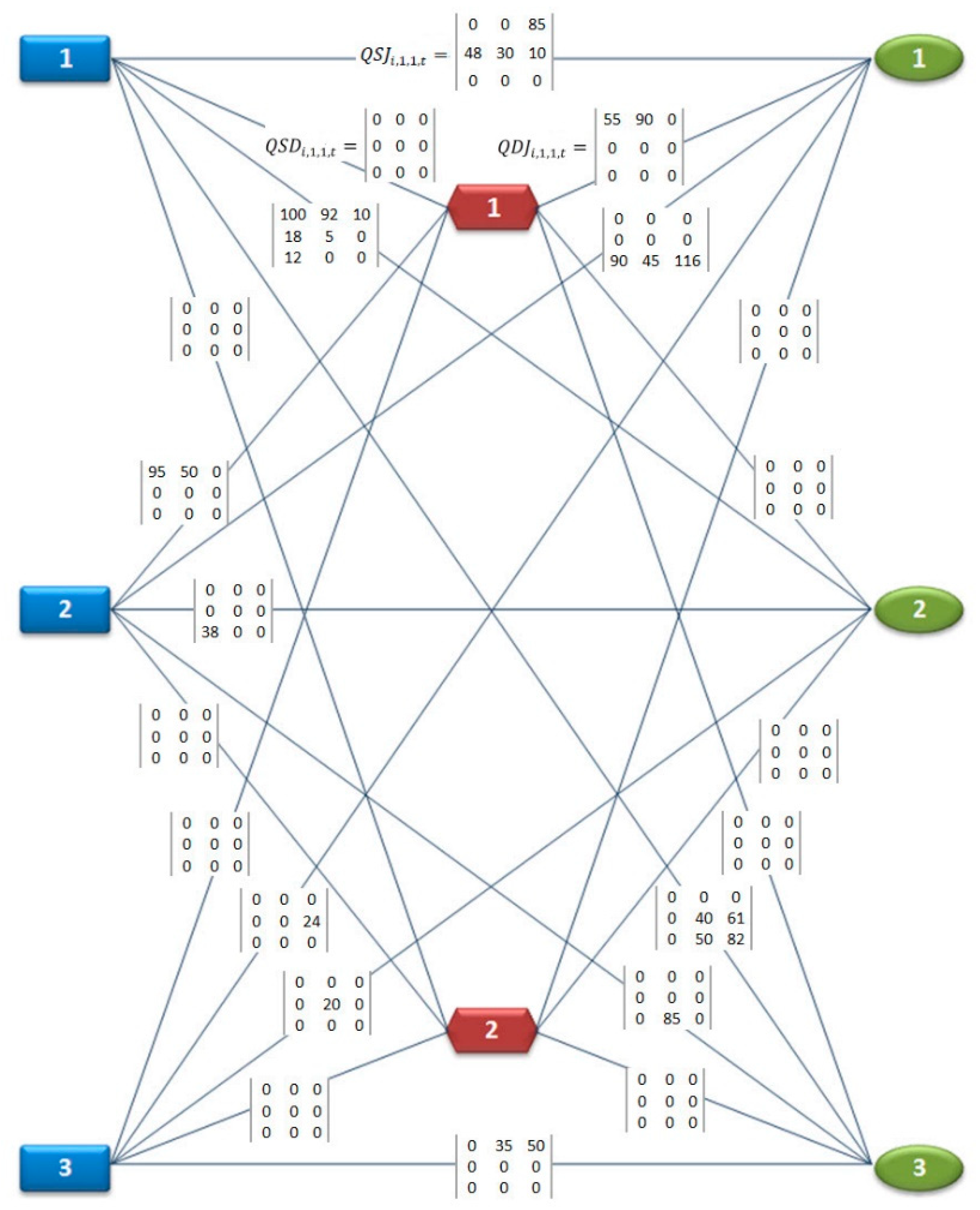
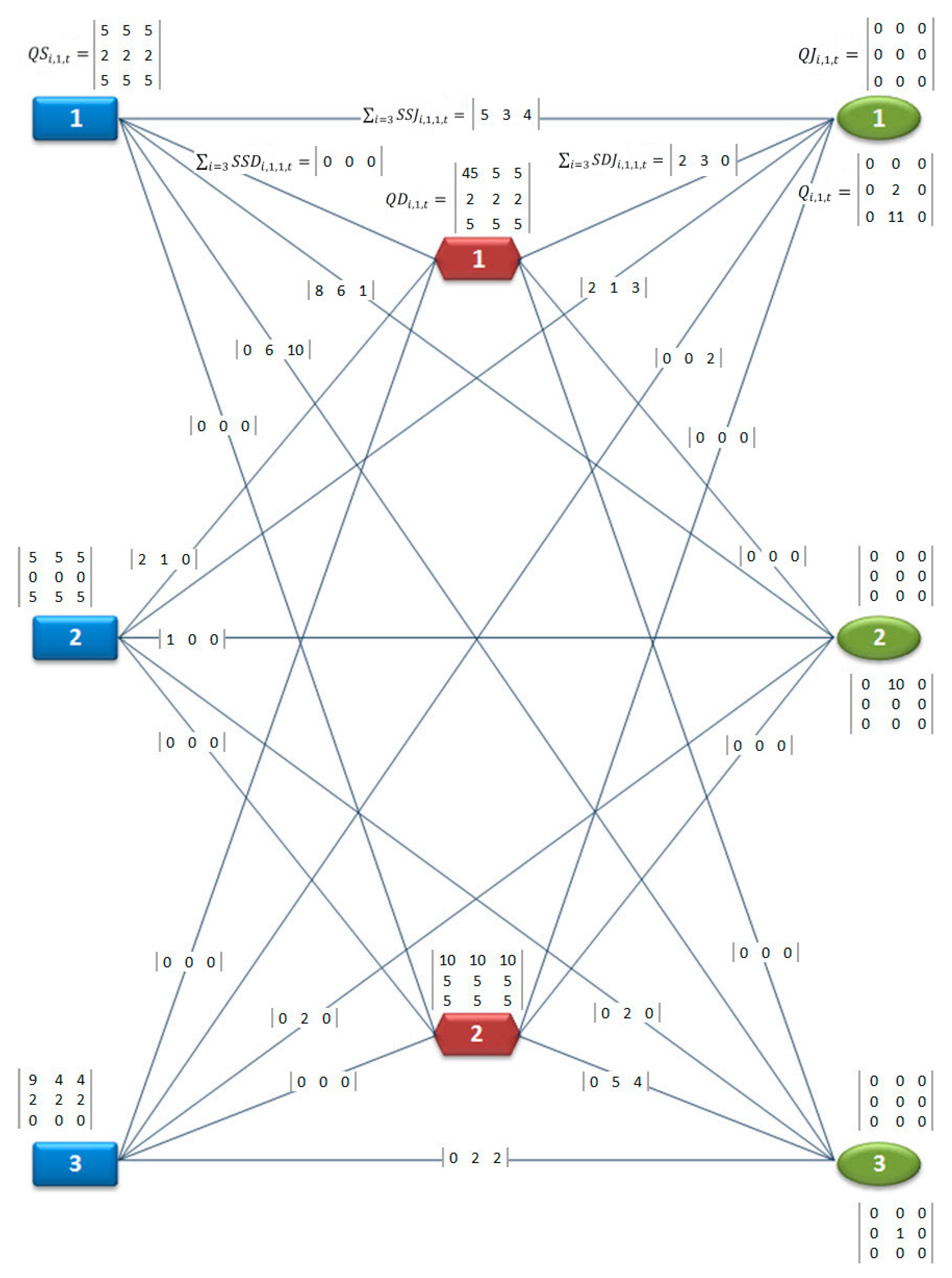
4.4. Model Solution and Analysis
4.5. Sensitivity Analysis
4.5.1. Sensitivity Reports
- Choosing a parameter to serve as a “sensitivity parameter”, defining the desirable range for its variation and invoking the related sensitivity report or graph that shows the effect on the objective function.
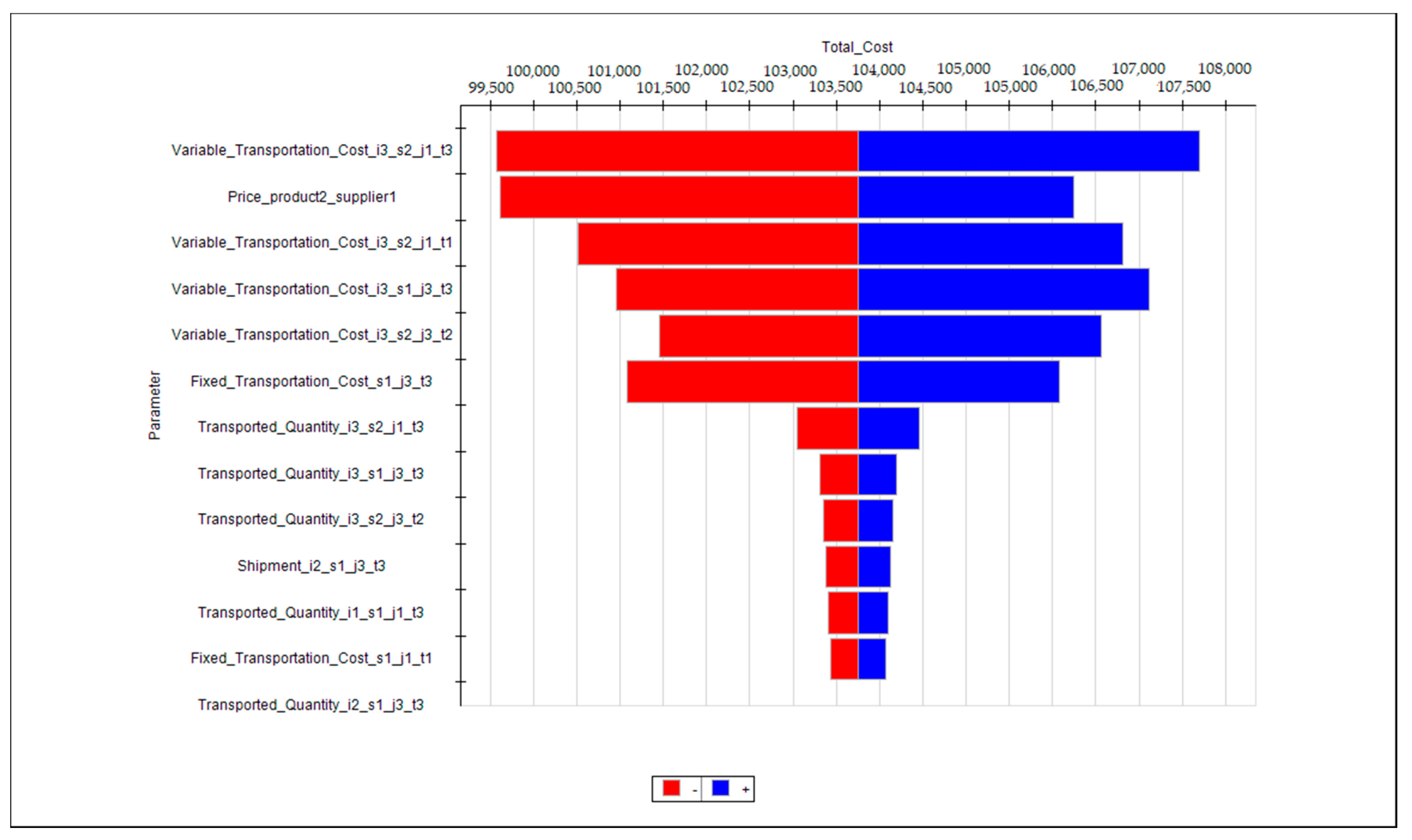
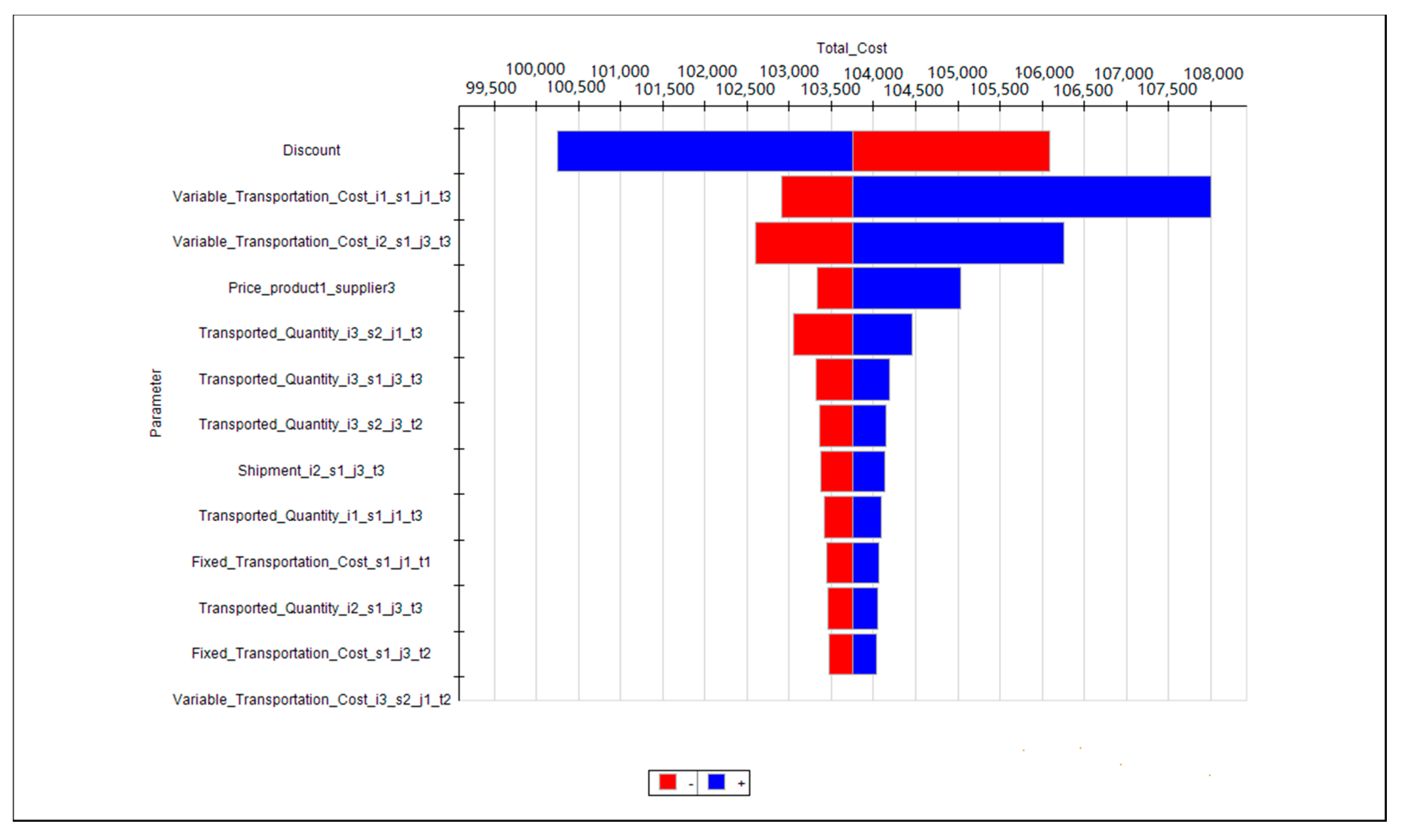
- Invoking a “tornado chart” that automatically identifies and displays the first twelve parameters with the highest impact on the selected formula—the cell of total cost. The tornado chart is generated by varying each parameter one at a time by a fixed percentage of its initial value and recording the impact on the selected cell. The tornado chart revealed that the cells with the biggest impact on the total cost are several transportation-related cost parameters, some of the purchase prices as well as some transportation-related variables. Information about the most sensitive variables is useful in exploring how the quantities that the decision-maker can control—in contrast to the problem parameters—affect the total cost. After defining some inputs of highest impact or just of interest to be “sensitivity parameters” with desirable ranges of variation, the tornado chart again ranks the most sensitive parameters, as shown in Figure 4, but now the chart bars indicate the user-determined upper and lower limits, not the percentage changes around the base-case value.
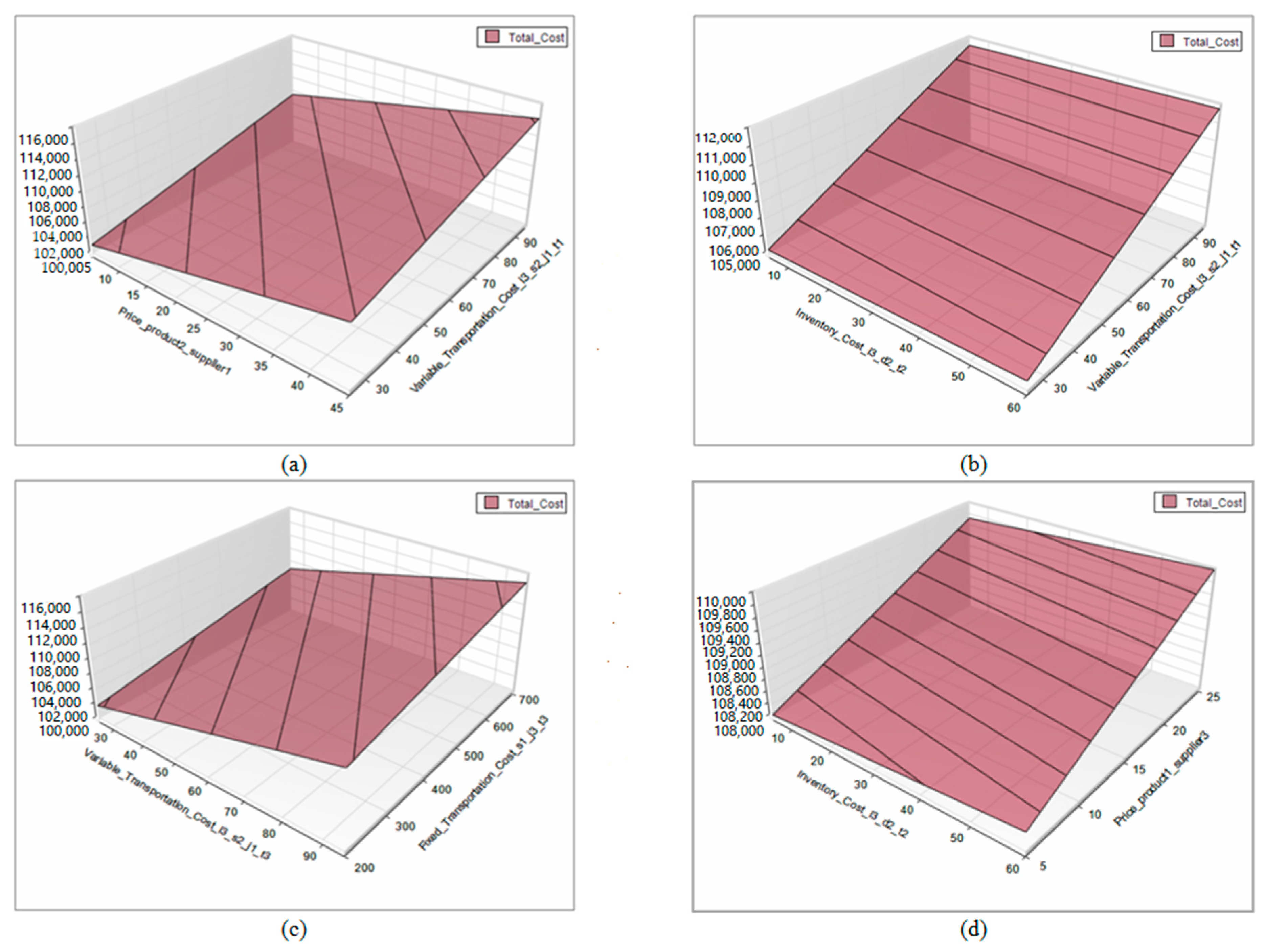
- Varying two parameters independently from their lower to upper limits over a pre-specified desirable range and for a pre-specified number of steps and getting documentation of the objective function values in tables or graphs. Such examples are presented in Table 2 and Figure 5. In the interesting case of graphical documentation, we can see the objective function as a surface in 3-dimensional space that illustrates either minor or major impacts of selected parameters and ensures the linearity assumption of the problem. The linear relationships between any parameter and the objective function are shown more explicitly in graphs than in related tables. Graphs also demonstrate easily the relative insensitivity of the objective function to some parameters, such as the unit inventory cost shown in Figure 5b,d.
- Varying simultaneously several parameters from their lower to upper limits over a pre-specified desirable range and for a pre-specified number of steps and getting documentation of the objective function values in tables. Table 3 shows the resulting values of the objective function for different combinations of the six highest-impact parameters.
4.5.2. Multiple Optimization Analysis Report
- Choosing a parameter to serve as an “optimization parameter”, defining the desirable range for its variation and invoking a multiple optimization analysis report or graph that shows the effect on the objective function.
- Invoking a “tornado chart” (Figure 6) which displays and ranks the most sensitive inputs with respect to their variation within a user-determined range or an automatic range of percentage changes around the base-case value.
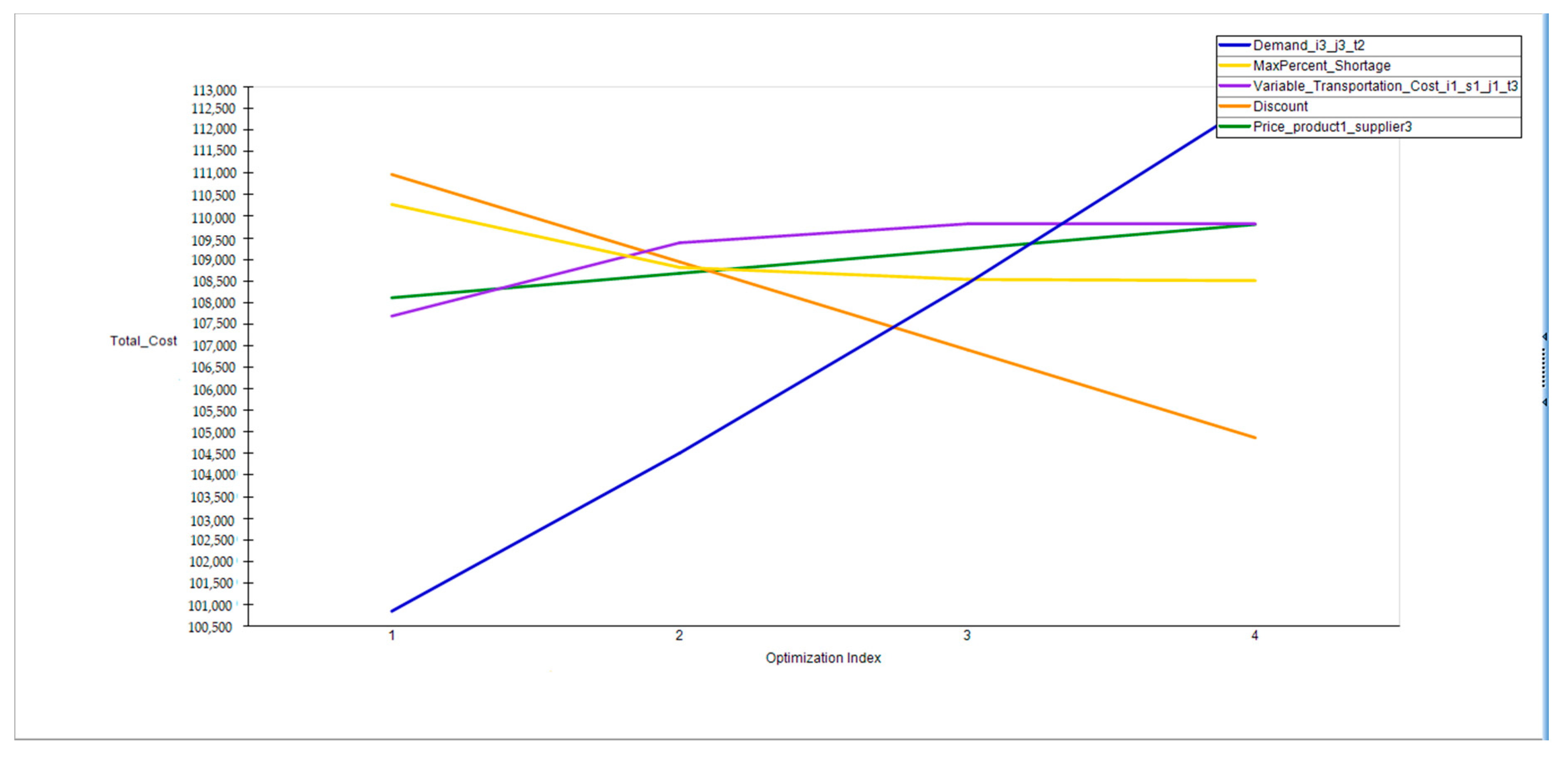
- Varying selected parameters one at a time from their lower to upper limits over a pre-specified desirable range and for a pre-specified number of runs and getting documentation of the objective function values in tables or graphs. Table 4 shows the resulting optimal values of the objective function corresponding to variations of 13 selected parameters one at a time for a number of 5 runs within their variation range (65 runs in total). Similarly, Figure 7 shows the resulting optimal values of the objective function corresponding to variations of 5 selected parameters one at a time for a number of 4 runs within their variation range (20 runs in total). The latter case of graphical representation is very useful in discerning relative sensitivities and particularly the sensitivity and insensitivity ranges of different inputs. For instance, we see that the variation of price does not influence the objective value as much as the variation of demand .
- Varying selected parameters simultaneously, from their lower to upper limits over a pre-specified desirable range and for a user-determined number of runs. The report of Table 5 displays the optimal objective values after 11 optimizations in which we varied 5 selected parameters simultaneously.
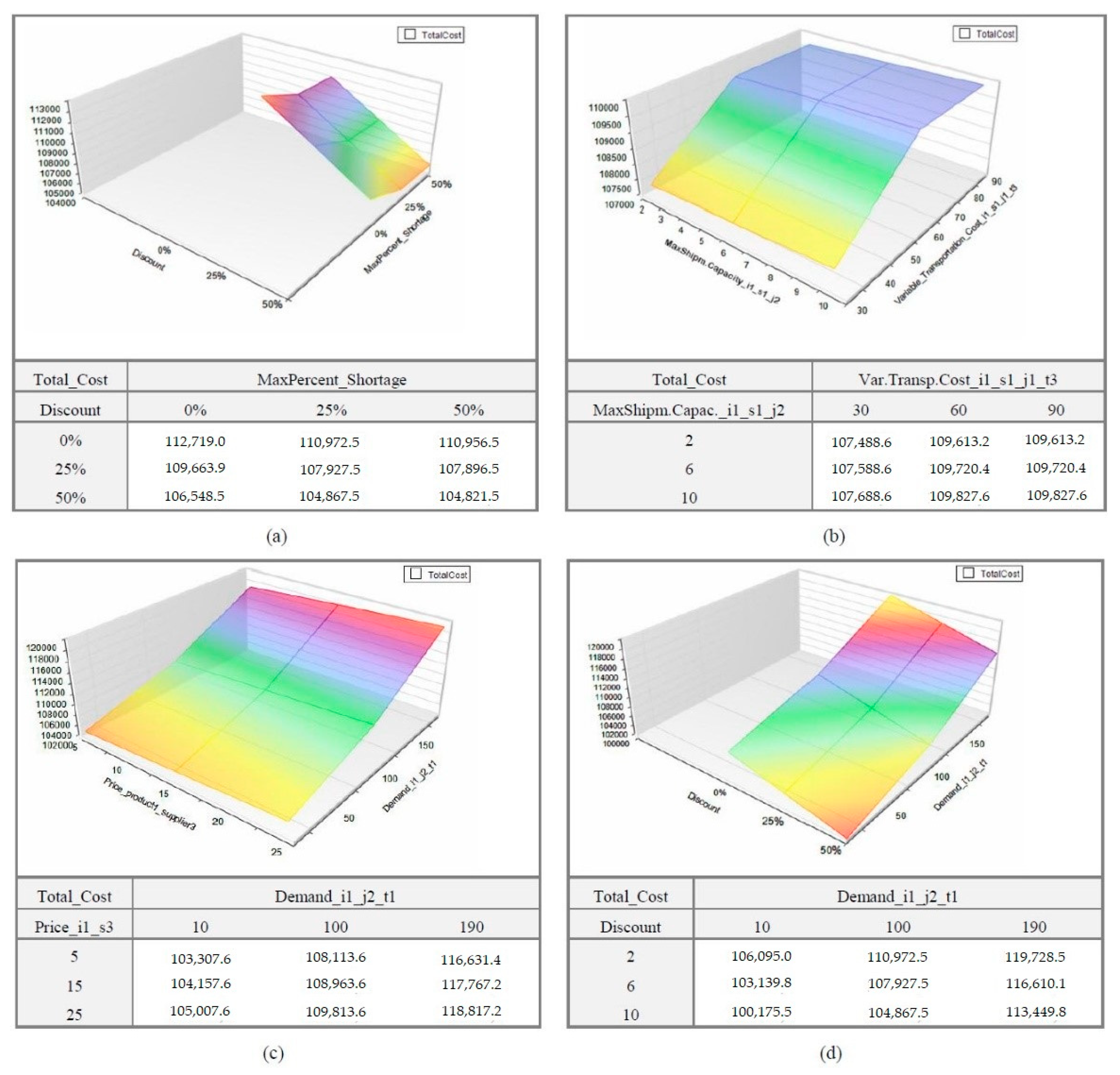
- Varying two parameters independently from their lower to upper limits over a pre-specified desirable range and for a user-determined number of runs. The related documentation may include two-dimensional tabular reports and tree-dimensional charts, as shown in Figure 8. We varied four two-parameter groups for a set of 9 runs (36 runs totally). In the charts we can see the objective function as a surface defined by 9 optimal values obtained from each optimization. Apparently, increasing the number of optimizations required for the generation of each chart results in very well-approximated surfaces. These surfaces readily illustrate the range of parameters where the optimal value of total cost remains unchanged or changes intensely.
5. Discussion and Concluding Remarks
6. Further Research
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| i = 1 | i = 2 | i = 3 | |
| j = 1 | 55 | 48 | 90 |
| j = 2 | 100 | 18 | 50 |
| j = 3 | 0 | 0 | 0 |
| i = 1 | i = 2 | i = 3 | |
| j = 1 | 90 | 32 | 56 |
| j = 2 | 102 | 25 | 0 |
| j = 3 | 35 | 41 | 135 |
| i = 1 | i = 2 | i = 3 | |
| j = 1 | 85 | 32 | 105 |
| j = 2 | 0 | 0 | 0 |
| j = 3 | 50 | 60 | 82 |
| i = 1 | i = 2 | i = 3 | |
| j = 1 | 0.2 | 0.2 | 0.2 |
| j = 2 | 0.2 | 0.2 | 0.2 |
| j = 3 | 0.2 | 0.2 | 0.2 |
| i = 1 | i = 2 | i = 3 | |
| s = 1 | 9 | 30 | 4.5 |
| s = 2 | 8.5 | – | 5 |
| s = 3 | 10 | 32 | – |
| i = 1 | i = 2 | i = 3 | |
| s = 1 | 0.2 | 0.2 | 0.2 |
| s = 2 | 0.2 | – | 0.2 |
| s = 3 | 0.2 | 0.2 | – |
| j = 1 | j = 2 | j = 3 | d = 1 | d = 2 | |
| s = 1 | 40 | 20 | 60 | 25 | 71 |
| s = 2 | 72 | 67 | 78 | 30 | 45 |
| s = 3 | 59 | 95 | 24 | 45 | 35 |
| d = 1 | 20 | 36 | 36 | – | – |
| d = 2 | 29 | 43 | 34 | – | – |
| j = 1 | j = 2 | j = 3 | d = 1 | d = 2 | |
| s = 1 | 38 | 89 | 49 | 83 | 47 |
| s = 2 | – | – | – | – | – |
| s = 3 | 79 | 45 | 95 | 47 | 45 |
| d = 1 | 50 | 53 | 48 | – | – |
| d = 2 | 95 | 48 | 43 | – | – |
| j = 1 | j = 2 | j = 3 | d = 1 | d = 2 | |
| s = 1 | 98 | 69 | 54 | 82 | 25 |
| s = 2 | 61 | 48 | 47 | 32 | 79 |
| s = 3 | – | – | – | – | – |
| d = 1 | 44 | 63 | 45 | – | – |
| d = 2 | 97 | 61 | 37 | – | – |
| j = 1 | j = 2 | j = 3 | d = 1 | d = 2 | |
| s = 1 | 447 | 289 | 467 | 340 | 419 |
| s = 2 | 654 | 698 | 520 | 536 | 598 |
| s = 3 | 600 | 490 | 267 | 498 | 340 |
| d = 1 | 300 | 329 | 400 | – | – |
| d = 2 | 780 | 290 | 679 | – | – |
| i = 1 | i = 2 | i = 3 | |
| s = 1 | 100 | 78 | 100 |
| s = 2 | 98 | – | 130 |
| s = 3 | 68 | 100 | – |
| i = 1 | i = 2 | i = 3 | |
| s = 1 | 100 | 78 | 123 |
| s = 2 | 98 | – | 130 |
| s = 3 | 68 | 100 | – |
| i = 1 | i = 2 | i = 3 | |
| s = 1 | 100 | 78 | 200 |
| s = 2 | 98 | – | 130 |
| s = 3 | 100 | 100 | – |
| i = 1 | i = 2 | i = 3 | |
| j = 1 | 30 | 60 | 25 |
| j = 2 | 25 | 50 | 20 |
| j = 3 | 25 | 50 | 20 |
| i = 1 | 3 |
| i = 2 | 2 |
| i = 3 | 1.5 |
| Start | ||
|---|---|---|
| Project 1 | t = 1 | t = 3 |
| Project 2 | t = 1 | t = 2 |
| Project 3 | t = 2 | t = 3 |
| j = 1 | j = 2 | j = 3 | d = 1 | d = 2 | |
| s = 1 | 40 | 20 | 20 | 30 | 40 |
| s = 2 | 25 | 25 | 20 | 50 | 50 |
| s = 3 | 25 | 25 | 25 | 45 | 50 |
| d = 1 | 34 | 34 | 45 | – | – |
| d = 2 | 40 | 27 | 40 | – | – |
| j = 1 | j = 2 | j = 3 | d = 1 | d = 2 | |
| s = 1 | 20 | 10 | 12 | 15 | 10 |
| s = 2 | 15 | 10 | 12 | 15 | 15 |
| s = 3 | 12 | 10 | 10 | 13 | 20 |
| d = 1 | 10 | 10 | 15 | – | – |
| d = 2 | 15 | 10 | 10 | – | – |
| j = 1 | j = 2 | j = 3 | d = 1 | d = 2 | |
| s = 1 | 10 | 10 | 8 | 14 | 10 |
| s = 2 | 1 | 1 | 1 | 1 | 1 1 |
| s = 3 | 12 | 10 | 10 | 10 | 12 |
| d = 1 | 15 | 20 | 20 | – | – |
| d = 2 | 10 | 12 | 12 | – | – |
| j = 1 | j = 2 | j = 3 | d = 1 | d = 2 | |
| s = 1 | 4 | 4 | 4 | 4 | 4 |
| s = 2 | 1 | 1 | 1 | 1 | 1 1 |
| s = 3 | 6 | 6 | 8 | 4 | 4 |
| d = 1 | 5 | 8 | 8 | – | – |
| d = 2 | 5 | 8 | 8 | – | – |
| j = 1 | j = 2 | j = 3 | d = 1 | d = 2 | |
| s = 1 | 50 | 45 | 50 | 25 | 25 |
| s = 2 | 45 | 50 | 50 | 30 | 35 |
| s = 3 | 1 | 1 | 1 | 1 | 1 1 |
| d = 1 | 50 | 40 | 40 | – | – |
| d = 2 | 35 | 48 | 50 | – | – |
| j = 1 | j = 2 | j = 3 | d = 1 | d = 2 | |
| s = 1 | 10 | 12 | 10 | 12 | 12 |
| s = 2 | 10 | 10 | 8 | 10 | 10 |
| s = 3 | 1 | 1 | 1 | 1 | 1 1 |
| d = 1 | 20 | 16 | 16 | – | – |
| d = 2 | 15 | 15 | 20 | – | – |
| i = 1 | i = 2 | i = 3 | |
| s = 1 | 24 | 10 | 19 |
| s = 2 | 23 | – | 25 |
| s = 3 | 17 | 20 | – |
| d = 1 | 2 | 11 | 5 |
| d = 2 | 9 | 8 | 32 |
| j = 1 | 14 | 15 | 10 |
| j = 2 | 10 | 26 | 30 |
| j = 3 | 7 | 15 | 17 |
| s = 1 | 800 |
| s = 2 | 290 |
| s = 3 | 550 |
| d = 1 | 600 |
| d = 2 | 943 |
| j = 1 | 167 |
| j = 2 | 325 |
| j = 3 | 300 |
| i = 1 | i = 2 | i = 3 | |
| s = 1 | 6 | 2 | 6 |
| s = 2 | 5 | – | 5 |
| s = 3 | 9 | 2 | – |
| d = 1 | 5 | 2 | 5 |
| d = 2 | 10 | 5 | 5 |
| i = 1 | i = 2 | i = 3 | |
| s = 1 | 5 | 2 | 5 |
| s = 2 | 5 | – | 5 |
| s = 3 | 4 | 2 | – |
| d = 1 | 5 | 2 | 5 |
| d = 2 | 3 | 4 | 3 |
| s = 1 | 435 |
| s = 2 | 500 |
| s = 3 | 450 |
| d = 1 | 267 |
| d = 2 | 400 |
| i = 1 | i = 2 | i = 3 | |
| s = 1 | 50 | 30 | 40 |
| s = 2 | 60 | – | 45 |
| s = 3 | 70 | 40 | – |
References
- Xue, X.; Sun, C.; Wang, Y.; Shen, Q. A Two-Level Programming Method for Collaborative Scheduling in Construction Supply Chain Management. In Cooperative Design, Visualization, and Engineering; CDVE 2007; Lecture Notes in Computer Science; Luo, Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4674, pp. 290–297. [Google Scholar] [CrossRef]
- Khalfan, M.M.A.; Maqsood, T. Supply chain capital in construction industry: Coining the term. Int. J. Manag. Proj. Bus. 2012, 5, 300–310. [Google Scholar] [CrossRef]
- De Souza, D.V.S.; Koskela, L. On Improvement in Construction Supply Chain Management. In Proceedings of the 20th Annual Conference of the International Group for Lean Construction, San Diego, CA, USA, 18–20 July 2012. [Google Scholar]
- Love, P.E.D.; Irani, Z.; Edwards, D.J. A seamless supply chain management model for construction. Supply Chain Manag. 2004, 9, 43–56. [Google Scholar] [CrossRef]
- Xue, X.; Li, X.; Shen, Q.; Wang, Y. An agent-based framework for supply chain coordination in construction. Autom. Constr. 2005, 14, 413–430. [Google Scholar] [CrossRef]
- Hai, T.; Md Yusof, A.; Ismail, S.; Wei, L. A Conceptual Study of Key Barriers in Construction Project Coordination. J. Organ. Manag. Stud. 2012, 1–14. [Google Scholar] [CrossRef]
- Koskela, L. Application of the New Production Philosophy to Construction; CIFE Technical Report n. 72; Stanford University: Stanford, CA, USA, 1992. [Google Scholar]
- Ballard, G.; Howell, G. What Kind of Production is Construction? In Proceedings of the 6th Conference of the International Group for Lean Construction, Guaruja, Brazil, 13–15 August 1998. [Google Scholar]
- O’Brien, W.J.; London, K.; Vrijhoef, R. Construction supply chain modeling: A research review and interdisciplinary research agenda. In Proceedings of the 10th Annual Conference of the International Group for Lean Construction, Gramado, Brazil, 6–8 August 2002; pp. 1–19. [Google Scholar]
- Keramati, A. Supply chain integration: A modelling classification. In Proceedings of the Eighth Annual International Symposium on Supply Chain Management, Toronto, ON, Canada, 26–28 September 2010. [Google Scholar]
- Shapiro, J.F. Modeling the Supply Chain, 2nd ed.; Cengage Learning: Boston, MA, USA, 2007; p. 624. [Google Scholar]
- Chen, D.-S.; Batson, R.G.; Dang, Y. Applied Integer Programming: Modeling and Solution; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; p. 488. [Google Scholar] [CrossRef]
- Bankvall, L.; Bygballe, L.E.; Dubois, A.; Jahre, M. Interdependence in supply chains and projects in construction. Supply Chain Manag. 2010, 15, 385–393. [Google Scholar] [CrossRef]
- Koutsokosta, A.; Katsavounis, S. Review of the Model-Based Supply Chain Management Research in the Construction Industry. Int. J. Ind. Manuf. Eng. 2015, 9, 2318–2324. [Google Scholar] [CrossRef]
- O’Brien, W.J.; Formoso, C.T.; Vrijhoef, R.; London, K.A. Construction Supply Chain Management Handbook; CRC Press: Boca Raton, FL, USA, 2008; p. 520. [Google Scholar] [CrossRef]
- Pryke, S. (Ed.) Construction Supply Chain Management: Concepts and Case Studies; Wiley-Blackwell: Oxford, UK, 2009; p. 245. [Google Scholar] [CrossRef]
- Koçtaş, Ö.; Tek, Ö.B. Construction Supply Chains: A proposal to develop a new conceptual model. In Proceedings of the International Logistics and Supply Chain Congress, Cappadocia, Kayseri, Turkey, 7–9 November 2013. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Science and Business Media: New York, NY, USA, 2006; p. 686. [Google Scholar] [CrossRef] [Green Version]
- Winston, W.L.; Albright, S.C. Practical Management Science, 6th ed.; Cengage Learning: Boston, MA, USA, 2019; p. 888. [Google Scholar]
- Baker, K.R. Optimization Modeling with Spreadsheets, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; p. 400. [Google Scholar]
- Jian-hua, C.; Wan, T. Time-cost trade-off problem in construction supply chain: A bi-level programming decision model. In Proceedings of the 2010 International Conference on Management Science and Engineering, 17th Annual Conference Proceedings, Melbourne, VIC, Australia, 24–26 November 2010; pp. 212–217. [Google Scholar] [CrossRef]
- Pan, N.-H.; Lee, M.-L.; Chen, S.-Q. Construction Material Supply Chain Process Analysis and Optimization. J. Civ. Eng. Manag. 2011, 17, 357–370. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Zhao, Y.; Chen, C.-Y. Project-driven supply chains: Integrating safety-stock and crashing decisions for recurrent projects. Ann. Oper. Res. 2012, 241. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Wei, P. Production-distribution planning of construction supply chain management under fuzzy random environment for large-scale construction projects. J. Ind. Manag. Optim. 2013, 9, 31–56. [Google Scholar] [CrossRef]
- Said, H.; El-Rayes, K. Automated multi-objective construction logistics optimization system. Autom. Constr. 2014, 43, 110–122. [Google Scholar] [CrossRef]
- Hsu, P.-Y.; Angeloudis, P.; Aurisicchio, M. Optimal logistics planning for modular construction using two-stage stochastic programming. Autom. Constr. 2018, 94, 47–61. [Google Scholar] [CrossRef]
- Feng, C.; Ma, Y.; Zhou, G.; Ni, T. Stackelberg Game Optimization for Integrated Production-Distribution-Construction System in Construction Supply Chain. Knowl. Based Syst. 2018, 157, 52–67. [Google Scholar] [CrossRef]
- Golpîra, H. Optimal Integration of the Facility Location Problem into the Multi-Project Multi-Supplier Multi-Resource Construction Supply Chain Network Design under the Vendor Managed Inventory Strategy. Expert Syst. Appl. 2019, 139. [Google Scholar] [CrossRef]
- Sobotka, A.; Czarnigowska, A.; Stefaniak, K. Logistics of construction projects. Found. Civ. Environ. Eng. 2005, 6, 203–216. [Google Scholar]
- Fengyu, Q.; Shengyue, H. The Research on the Application of Supply Chain Management in Construction. In Proceedings of the 13th International Conference on Management Science and Engineering, Lille, France, 5–7 October 2006; pp. 1191–1196. [Google Scholar]
- Hamzeh, F.R.; Tommelein, I.D.; Ballard, G.; Kaminsky, P.M. Logistics Centers to Support Project-based Production in the Construction Industry. In Proceedings of the 15th Annual Conference of the International Group for Lean Construction, East Lansing, MI, USA, 18–20 July 2007; pp. 170–180. [Google Scholar]
- Dakhli, Z.; Lafhaj, Z. Considering Materials Management in Construction: An Exploratory Study. Logistics 2018, 2, 7. [Google Scholar] [CrossRef] [Green Version]
- Guerlain, C.; Renault, S.; Ferrero, F. Understanding Construction Logistics in Urban Areas and Lowering Its Environmental Impact: A Focus on Construction Consolidation Centres. Sustainability 2019, 11, 6118. [Google Scholar] [CrossRef] [Green Version]
- Arashpour, M.; Bai, Y.; Aranda-Mena, G.; Bab-Hadiashar, A.; Hosseini, M.R.; Kalutara, P. Optimizing decisions in advanced manufacturing of prefabricated products: Theorizing supply chain configurations in off-site construction. Autom. Constr. 2017, 84, 146–153. [Google Scholar] [CrossRef]
- Powell, S.G.; Baker, K.R. Management Science: The Art of Modeling with Spreadsheets, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Frontline Systems, Inc. Frontline Solvers: User Guide, version 12.5; Frontline Systems, Inc.: Incline Village, NV, USA, 2013. [Google Scholar]
- Bradley, S.P.; Hax, A.C.; Magnanti, T.L. Applied Mathematical Programming; Addison-Wesley Publishing Company: Boston, MA, USA, 1977. [Google Scholar]
- Powell, S.G.; Batt, R.J. Spreadsheet Modeling for Insight. In Proceedings of the International Workshop on the Foundations of Spreadsheets, Rome, Italy, 30 September 2004; Elsevier Science B.V.: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Lawrence, J.A.; Pasternack, B.A. Applied Management Science: Modeling, Spreadsheet Analysis, and Communication for Decision Making, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2002; p. 768. [Google Scholar]
- Anderson, D.R.; Sweeney, D.J.; Williams, T.A.; Camm, J.D.; Cochran, J.J.; Fry, M.J.; Ohlmann, J.W. An Introduction to Management Science: Quantitative Approaches to Decision Making, 15th ed.; Cengage Learning: Boston, MA, USA, 2016; p. 912. [Google Scholar]
- Ragsdale, C. Spreadsheet Modeling and Decision Analysis: A Practical Introduction to Management Science, 8th ed.; Cengage Learning: Mason, OH, USA, 2018; p. 864. [Google Scholar]
- Geoffrion, A.M. A guided tour of recent practical advances in integer linear programming. Omega 1976, 4, 49–57. [Google Scholar] [CrossRef]
- McCarl, B.A.; Spreen, T.H. Applied Mathematical Programming Using Algebraic Systems; Texas A&M University: College Station, TX, USA, 2011; p. 567. [Google Scholar]
| Ref. | Objective/Variables | Analytical Approach | Optimization Method/Software |
|---|---|---|---|
| [1] | Maximization of profits (at an upper and lower level)/Indicative variables such as construction duration and materials lead time are mentioned | Two-level nonlinear integer programming model | Simulated annealing and discrete search algorithm/Not defined |
| [21] | Maximization of the expected profit of contracting parties/Incentive intensity (money unit per unit time) and project’s duration | Two-level programming model | Problem-specific heuristics/Not defined |
| [23] | Minimization of safety-stock and project crashing (delay cost per unit of time) for recurrent projects subject to random material delays/Safety-stock decisions in material supply chains and crashing decisions in projects | Stochastic multi-stage optimization model | Not defined/Not defined |
| [24] | Minimization of production and transportation costs (lower level) and minimization of storage, transportation, and inventory penalty costs (upper level)/Material quantities supplied from production sites to warehouses and from warehouses to concrete mixing plants | Two-level fuzzy optimization model | Artificial bee colony algorithm based on a fuzzy random simulation/MATLAB |
| [25] | Minimization of site logistics costs (by shifting noncritical activities to exploit site space for material storage) and minimization of project criticality/Noncritical activities scheduling decisions, material supply decisions, decisions on temporary facilities layout, material storage plan decisions | Multi-objective optimization model | Genetic algorithms/AMCLOS |
| [26] | Minimization of the cost required to build up inventory of modular products and complete modular projects, considering transportation, inventory, assembling and penalty costs under demand uncertainties/Optimal factory production plan of modular products (the first stage) and optimal transportation and inventory scheme of the modular products (the second stage) | Two-stage stochastic programming model | Branch and cut algorithm/IBM ILOG CPLEX Studio |
| [27] | Stackelberg game optimization to obtain an equilibrium solution for intrinsic conflicts between decision makers with multiple objectives/Optimal material distribution plan of the construction department (at the upper level) and optimal production plan of the exploitation department (at the lower level) for a large hydropower construction project | Two-level multistage programming model under a fuzzy random environment | hybrid algorithm (evolved genetic algorithm and particle swarm optimization)/MATLAB |
| [28] | Cost minimization of a three level CSC using a vendor managed inventory strategy/Resource quantities transferred from suppliers to temporal facilities and from temporal facilities to demand points; decisions for supplier selection and assignment of temporal facilities to candidate locations | Mixed-integer linear programming model | Not defined/GAMS CPLEX |
| Price_i2_s1 | Var.Transp.Cost_i3_s2_j1_t3 | |||||
|---|---|---|---|---|---|---|
| 5 | 13 | 21 | 29 | 37 | 45 | |
| 25 | 100,163.0 | 101,519.8 | 102,876.6 | 104,233.4 | 105,590.2 | 106,947.0 |
| 39 | 101,787.0 | 103,143.8 | 104,500.6 | 105,857.4 | 107,214.2 | 108,571.0 |
| 53 | 103,411.0 | 104,767.8 | 106,124.6 | 107,481.4 | 108,838.2 | 110,195.0 |
| 67 | 105,035.0 | 106,391.8 | 107,748.6 | 109,105.4 | 110,462.2 | 111,819.0 |
| 81 | 106,659.0 | 108,015.8 | 109,372.6 | 110,729.4 | 112,086.2 | 113,443.0 |
| 95 | 108,283.0 | 109,639.8 | 110,996.6 | 112,353.4 | 113,710.2 | 115,067.0 |
| Price i2_s1 | Var.Transp.Cost i3_s2_j1_t3 | Var.Transp.Cost i3_s2_j1_t1 | Var.Transp.Cost i3_s2_j3_t2 | Var.Transp.Cost i3_s1_j3_t3 | Fix.Transp.Cost s1_j3_t3 | Total_Cost |
|---|---|---|---|---|---|---|
| 5 | 25 | 25 | 20 | 20.0 | 200 | 89,170.0 |
| 9 | 32 | 32 | 26 | 27.5 | 250 | 92,915.4 |
| 13 | 39 | 39 | 32 | 35.0 | 300 | 96,660.8 |
| 17 | 46 | 46 | 38 | 42.5 | 350 | 100,406.2 |
| 21 | 53 | 53 | 44 | 50.0 | 400 | 104,151.6 |
| 25 | 60 | 60 | 50 | 57.5 | 450 | 107,897.0 |
| 29 | 67 | 67 | 56 | 65.0 | 500 | 111,642.4 |
| 33 | 74 | 74 | 62 | 72.5 | 550 | 115,387.8 |
| 37 | 81 | 81 | 68 | 80.0 | 600 | 119,133.2 |
| 41 | 88 | 88 | 74 | 87.5 | 650 | 122,878.6 |
| 45 | 95 | 95 | 80 | 95.0 | 700 | 126,624.0 |
| Optimization Parameters | Range | Total_Cost (€) | ||||
|---|---|---|---|---|---|---|
| Demand_i1_j2_t1 | 10–190 units | 103,689.6 | 105,770.8 | 108,538.6 | 112,320.0 | 117,193.4 |
| Demand_i3_j3_t2 | 10–195 units | 100,803.6 | 103,328.6 | 106,613.6 | 109,465.6 | 112,618.3 |
| Purchase_Discount | 0–50% | 110,931.5 | 109,412.4 | 107,884.0 | 106,352.8 | 104,821.5 |
| Max_Percent_Shortage | 0–50% | 110,233.8 | 108,817.6 | 108,538.6 | 116,680.6 | 108,495.6 |
| Variable_Transportation_Cost_i1_s2_d1_t1 | 20–80€ | 107,516.5 | 108,815.6 | 109,006.6 | 109,006.6 | 109,006.6 |
| Variable_Transportation_Cost_i2_s1_j3_t3 | 30–90€ | 107,336.6 | 108,251.6 | 109,166.6 | 110,081.6 | 110,859.6 |
| Variable_Transportation_Cost_i1_s1_j1_t3 | 30–90€ | 107,645.6 | 108,920.6 | 109,784.6 | 109,784.6 | 109,784.6 |
| Max _Shipment_Capacity_i1_s1_j2 | 10–60 units | 111,596.6 | 108,256.6 | 107,339.6 | 106,936.6 | 106,761.6 |
| Min _Shipment_Capacity_i1_s1_j2 | 2–10 units | 108,295.6 | 108,345.6 | 108,395.6 | 108,445.6 | 108,538.6 |
| Inventory_Capacity_d1 | 100–900 m3 | 108,565.6 | 108,538.6 | 108,538.6 | 108,538.6 | 108,538.6 |
| Distribution_Capacity_i1_s1_t1 | 40–190 units | 111,442.8 | 109,767.8 | 108,483.8 | 107,356.1 | 107,293.6 |
| Distribution_Capacity_i1_s2_t2 | 30–200 units | 109,026.0 | 108,538.6 | 108,538.6 | 108,538.6 | 108,538.6 |
| Distribution_Capacity_i3_s1_t3 | 40–300 units | 109,486.4 | 108,538.6 | 108,538.6 | 108,538.6 | 108,538.6 |
| Var.Transp.Cost i2_s1_j3_t3 | Discount | Var.Transp.Cost i1_s1_j1_t3 | Var.Transp.Cost i1_s2_d1_t1 | Max_Percent_Shortage | Total_Cost |
|---|---|---|---|---|---|
| 30 | 0% | 30 | 20 | 0% | 109,751.0 |
| 36 | 5% | 36 | 26 | 5% | 110,133.4 |
| 42 | 10% | 42 | 32 | 10% | 110,228.3 |
| 48 | 15% | 48 | 38 | 15% | 110,519.5 |
| 54 | 20% | 54 | 44 | 20% | 110,544.6 |
| 60 | 25% | 60 | 50 | 25% | 110,430.4 |
| 66 | 30% | 66 | 56 | 30% | 110,217.2 |
| 72 | 35% | 72 | 62 | 35% | 109,926.4 |
| 78 | 40% | 78 | 68 | 40% | 109,560.7 |
| 84 | 45% | 84 | 74 | 45% | 109,226.5 |
| 90 | 50% | 90 | 80 | 50% | 108,764.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koutsokosta, A.; Katsavounis, S. A Dynamic Multi-Period, Mixed-Integer Linear Programming Model for Cost Minimization of a Three-Echelon, Multi-Site and Multi-Product Construction Supply Chain. Logistics 2020, 4, 19. https://doi.org/10.3390/logistics4030019
Koutsokosta A, Katsavounis S. A Dynamic Multi-Period, Mixed-Integer Linear Programming Model for Cost Minimization of a Three-Echelon, Multi-Site and Multi-Product Construction Supply Chain. Logistics. 2020; 4(3):19. https://doi.org/10.3390/logistics4030019
Chicago/Turabian StyleKoutsokosta, Aspasia, and Stefanos Katsavounis. 2020. "A Dynamic Multi-Period, Mixed-Integer Linear Programming Model for Cost Minimization of a Three-Echelon, Multi-Site and Multi-Product Construction Supply Chain" Logistics 4, no. 3: 19. https://doi.org/10.3390/logistics4030019
APA StyleKoutsokosta, A., & Katsavounis, S. (2020). A Dynamic Multi-Period, Mixed-Integer Linear Programming Model for Cost Minimization of a Three-Echelon, Multi-Site and Multi-Product Construction Supply Chain. Logistics, 4(3), 19. https://doi.org/10.3390/logistics4030019






