Designing a Sustainable Green Closed-Loop Supply Chain under Uncertainty and Various Capacity Levels
Abstract
:1. Introduction
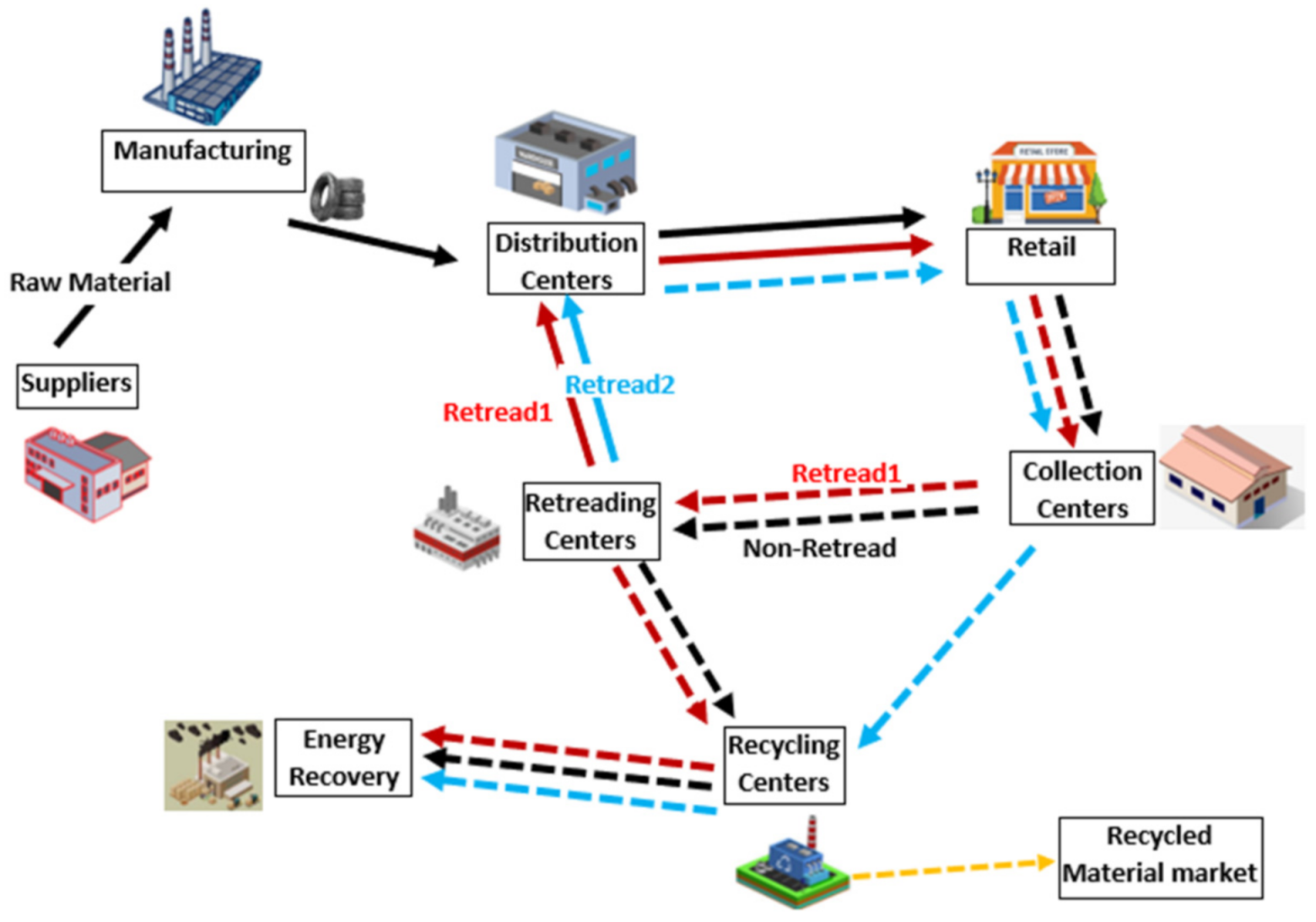
- Proposing a new sustainable, robust, multi-objective, multi-product, multi-echelon, multi-cycle, multi-capacity, green closed-loop supply-chain network by considering the real-world situation where used tires are retreaded multiple times, and the retread tires are being returned to the collection center for final processing.
- Presenting a novel Robust Fuzzy/Possibilistic Stochastics Programming (RFSP) model that controls scenario-based uncertainty (disruption risks) and fuzzy-based uncertainty (operational risks) in the network simultaneously and provide a more reliable output results for the managers and the DMs.
- Evaluating the possibility and feasibility of expanding the existing forward logistic network at different capacity levels to cope with market demand under various scenarios, and also the feasibility of establishing a new reverse logistic network at different capacity levels to cope with the return rate of EOL tires.
- Validation of the proposed model by sensitivity analysis through a case study.
2. Literature Review
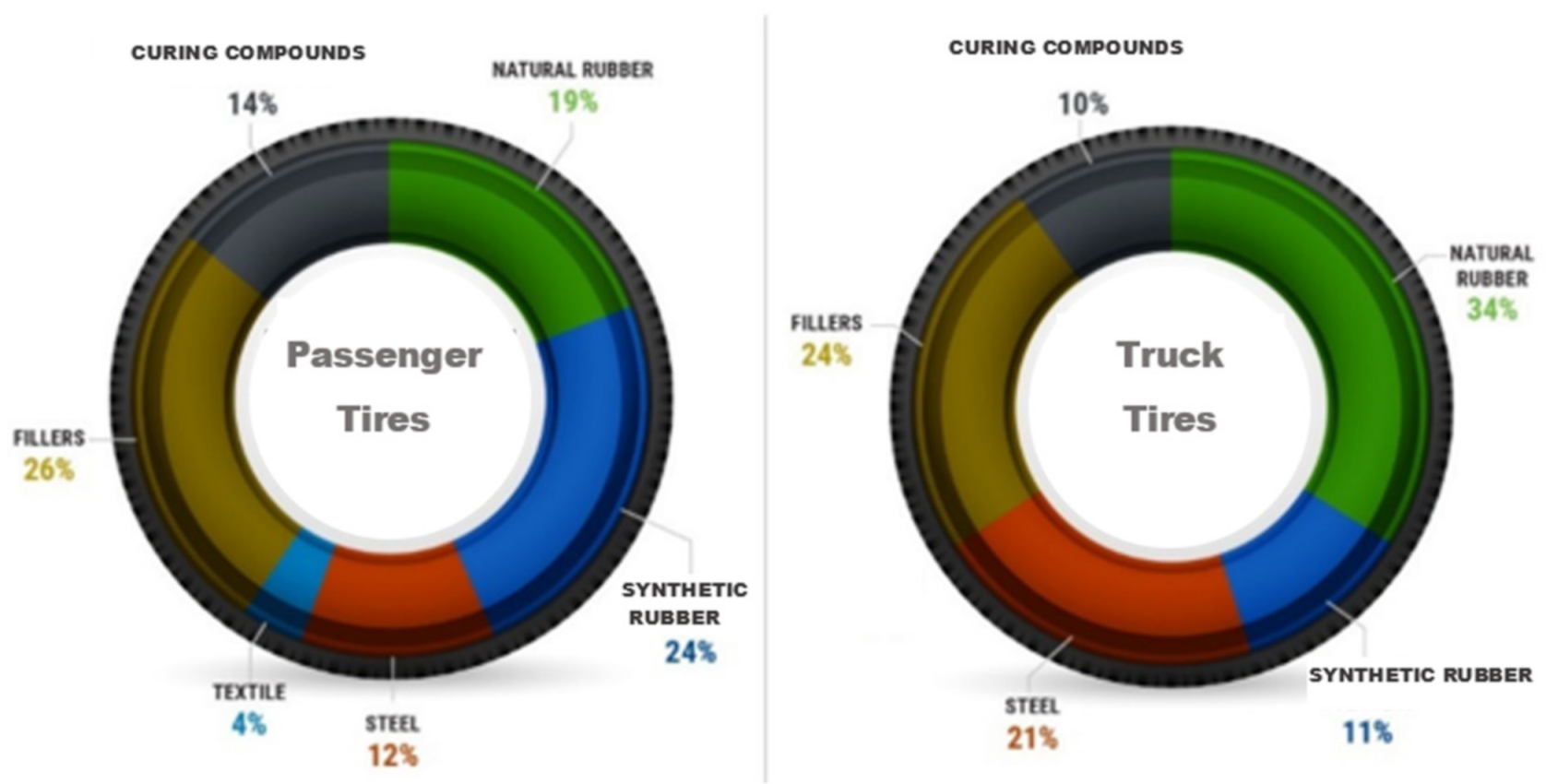
Tire Industry and Recovery Options
3. Problem Description and Formulation
3.1. Problem Assumption and Notation
- The potential location of new manufacturing centers, distribution centers, retreading centers, and recycling centers is fixed and predefined.
- Production, distribution, retreading, and recycling capacities are limited, and all are subject to capacity level U.
- Capacity of the energy recovery centers is unlimited, but it has the most negative environmental impact.
- The return, recycling, and retreading rates of new and retread tires are fuzzy.
- Raw material procurement costs and production costs are fuzzy, and their fuzzy expected value are utilized.
- Customer demand is stochastic and is expressed in different scenarios.
- Ground transportation is the only transportation method used in the network.
- There is cost associated with the collection of used tires. This provides an incentive for the end users to return the EOL tires.
- Tires can be retreaded two times, retread-1 and retread-2, and each tire will be identified how many times it has been retreaded.
- The value of the tires that were retreaded once (retread-1) is greater than the value of the tires that were retreaded two times (retread-2), and both are less than the value of the new tires.
- The demand for new tires must be satisfied, and there is a penalty for unsatisfied demand. There is no obligation to meet the demand for retread tires.
3.2. Problem Formulation
4. The Proposed Approach
4.1. Stochastic Programming
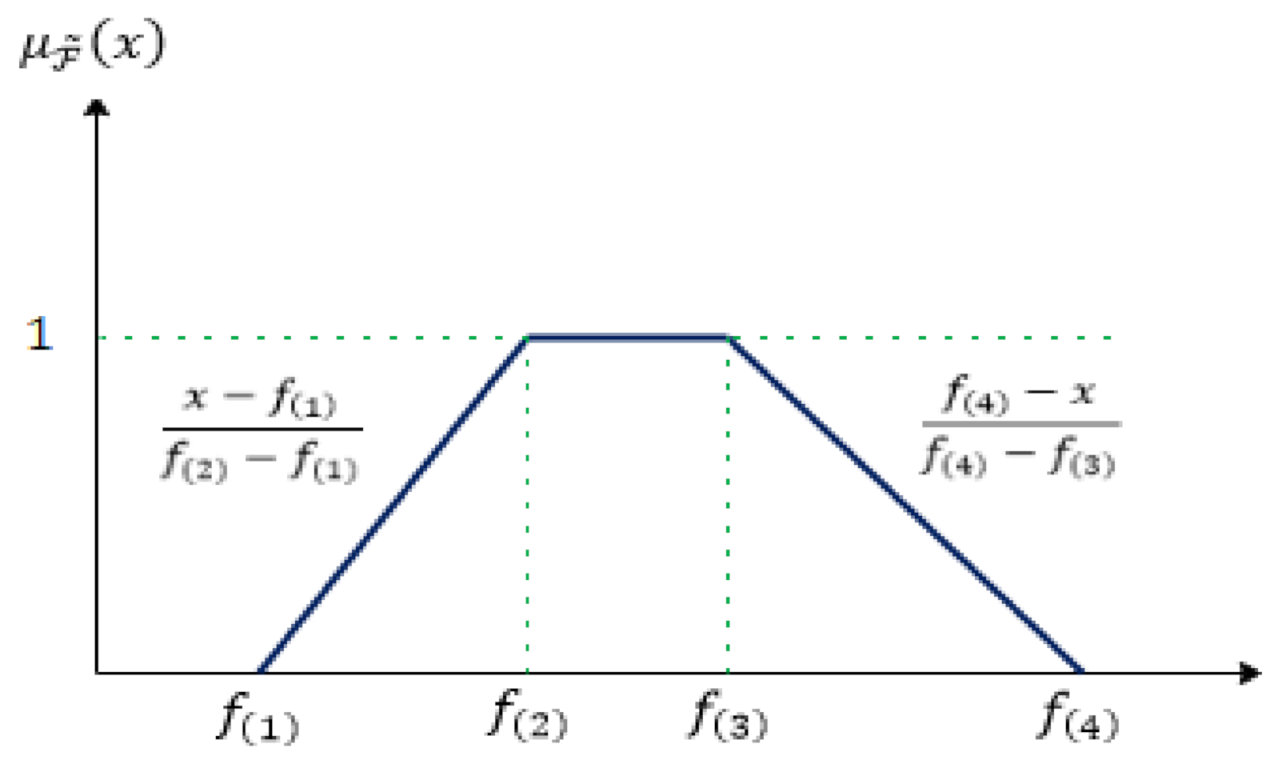
4.2. Possibilistic Programming
4.3. Robust Fuzzy/Possibilistic Stochastic Programming
4.4. Coping with Multi-Objective Functions
4.5. Epsilon Constraint
4.6. Appropriate Interval for with Lex Method
4.7. Augmented Epsilon Constraint
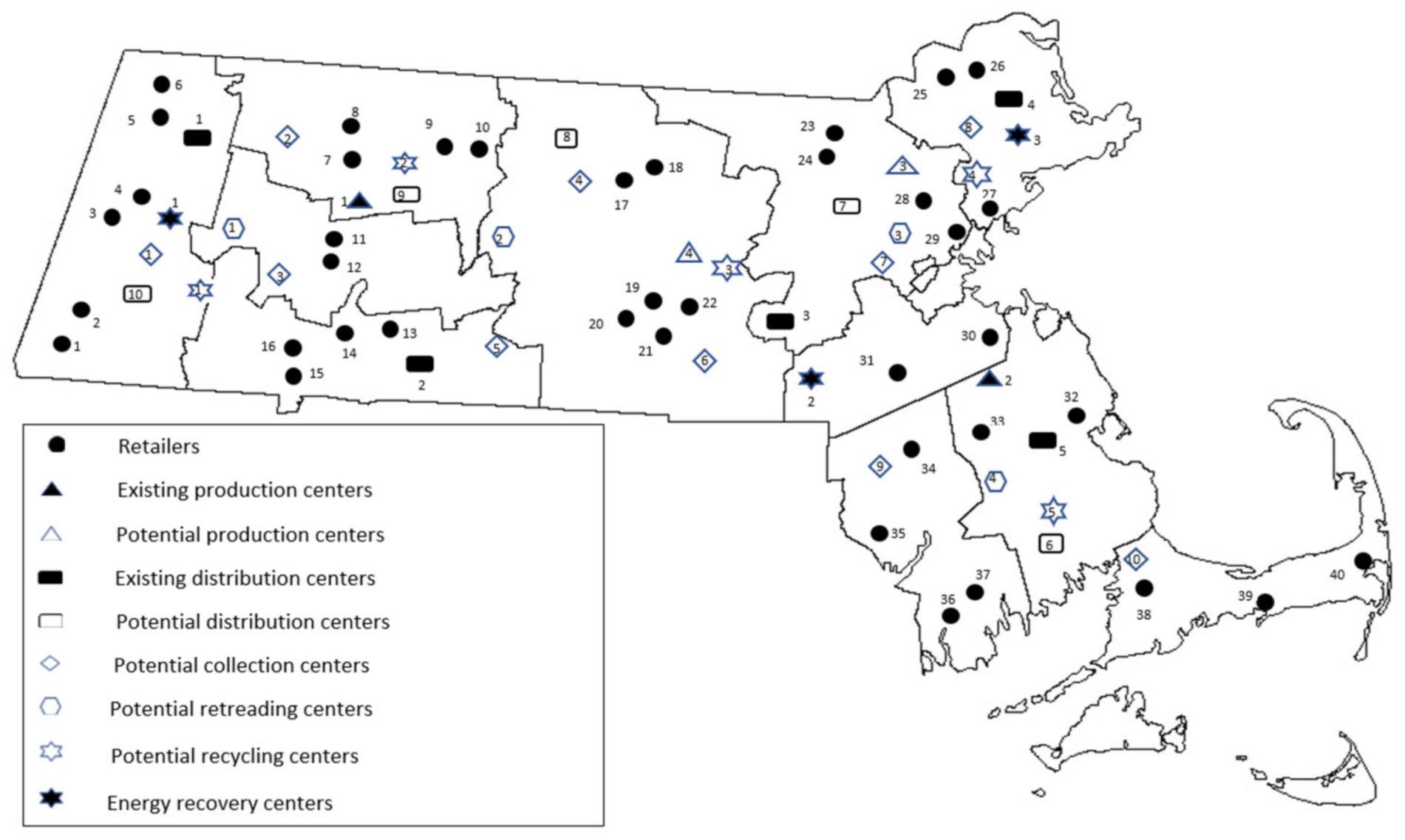
5. Computational Experiment
5.1. Computational Results and Sensitivity Analysis
5.2. The Managerial Implication
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- De Brito, M.P.; Dekker, R. A Framework for Reverse Logistics. In Reverse Logistics; Springer: Berlin, Heidelberg, 2004; pp. 3–27. [Google Scholar]
- Daugherty, P.J.; Autry, C.W.; Ellinger, A.E. Reverse logistics: The relationship between resource commitment and program performance. J. Bus. Logist. 2001, 22, 107–123. [Google Scholar] [CrossRef]
- Linton, J.; Klassen, R.; Jayaraman, V. Sustainable supply chains: An introduction. J. Oper. Manag. 2007, 25, 1075–1082. [Google Scholar] [CrossRef]
- Selbes, M.; Yilmaz, O.; Khan, A.A.; Karanfil, T. Leaching of DOC, D.N., and inorganic constituents from scrap tires. Chemosphere 2015, 139, 617–623. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Huang, C.L.; Shern, C.-C. Recycling waste tire powder for the recovery of oil spills. Resour. Conserv. Recycl. 2008, 52, 1162–1166. [Google Scholar] [CrossRef]
- Farrokh, M.; Azar, A.; Jandaghi, G.; Ahmadi, E. A novel robust fuzzy stochastic programming for closed loop supply chain network design under hybrid uncertainty. Fuzzy Sets Syst. 2018, 341, 69–91. [Google Scholar] [CrossRef]
- Yu, C.S.; Li, H.L. A robust optimization model for stochastic logistic problems. Int. J. Prod. Econ. 2000, 64, 385–397. [Google Scholar] [CrossRef]
- Pishvaee, M.S.; Torabi, S.A. A possibilistic programming approach for closed loop supply chain network design under uncertainty. Fuzzy Sets Syst. 2010, 161, 2668–2683. [Google Scholar] [CrossRef]
- Ilgin, M.A.; Gupta, S.M. Environmentally conscious manufacturing and product recovery (ECMPRO): A review of the state of the art. J. Environ. Manag. 2010, 91, 563–591. [Google Scholar] [CrossRef]
- Govindan, K.; Jafarian, A.; Khodaverdi, R.; Devika, K. Two echelon multiple vehicle location–routing problem with time windows for optimization of sustainable supply chain network of perishable food. Int. J. Prod. Econ. 2014, 15, 9–28. [Google Scholar] [CrossRef]
- Devika, K.; Jafarian, A.; Nourbakhsh, V. Designing a sustainable closed loop supply chain network based on bottom line approach: A comparative metaheuristic hybridization technique. Eur. J. Oper. Res. 2014, 253, 594–615. [Google Scholar] [CrossRef]
- Jindal, A.; Sangwan, K.S. Multi-objective fuzzy mathematical modelling of closed-loop supply chain considering economical and environmental factors. Ann. Oper. Res. 2017, 257, 95–120. [Google Scholar] [CrossRef]
- Sarkar, B.; Tayyab, M.; Kim, N.; Habib, M.S. Optimal production delivery policies for supplier and manufacturer in a constrained closed-loop supply chain for returnable transport packaging through metaheuristic approach. Comput. Ind. Eng. 2019, 135, 987–1003. [Google Scholar] [CrossRef]
- Sarkar, B.; Ullah, M.; Kim, N. Environmental and economic assessment of closed-loop supply chain with remanufacturing and returnable transport items. Comput. Ind. Eng. 2017, 111, 148–163. [Google Scholar] [CrossRef]
- Dulman, M.; Gupta, S.M. Evaluation of Maintenance and EOL Operation Performance of Sensor-Embedded Laptops. Logistics 2018, 1, 3. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Gupta, S.M. A Pricing and Acquisition Strategy for New and Remanufactured High-Technology Products. Logistics 2019, 3, 8. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Gupta, S.M. Value depreciation factors for new and remanufactured high-technology products: A case study on iPhones and iPads. Int. J. Prod. Res. 2020, 58, 7218–7249. [Google Scholar] [CrossRef]
- Aldoukhi̇, M.; Gupta, S. A robust closed loop supply chain network design under different carbon emission policies. Pamukkale University. J. Eng. Sci. 2019, 25, 1020–1032. [Google Scholar]
- Aldoukhi, M.; Gupta, S.M. Use of Maximal Covering Location Problem to Design a Closed Loop Supply Chain Network Under Product Substitution. Appl. Manag. Sci. 2020, 20, 71–96. [Google Scholar]
- Fadhel, A.W.; Gupta, S.M. Carbon Emissions and Energy Balance in the Design of a Sustainable Food Waste Network. Int. J. Ind. Eng. Oper. Manag. 2020, 2, 63–77. [Google Scholar]
- Gupta, E.V.; Mogale, D.G.; Tiwari, M.K. Optimal Control of Production and Maintenance Operations in Smart Custom Manufacturing Systems with Multiple Machines. IFAC PapersOnLine 2019, 52, 241–246. [Google Scholar] [CrossRef]
- De, M.; Giri, B.C. Modeling a closed-loop supply chain with a heterogeneous fleet under carbon emission reduction policy. Transp. Res. Part E Logist. Transp. Rev. 2020, 133, 101813. [Google Scholar] [CrossRef]
- Mogale, D.G.; Lahoti, G.; Jha, S.B.; Shukla, M.; Kamath, N.; Tiwari, M.K. Dual Market Facility Network Design under Bounded Rationality. Algorithms 2018, 11, 54. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, L.S.; Machado, R.L. Application of optimization methods in the closed-loop supply chain: A literature review. J. Comb. Optim. 2021, 41, 357–400. [Google Scholar] [CrossRef]
- Zahedi, A.; Salehi-Amiri, A.; Hajiaghaei-Keshteli, M.; Diabat, A. Designing a closed-loop supply chain network considering multi-task sales agencies and multi-mode transportation. Soft Comput. 2021, 1–33. [Google Scholar]
- Guarnieri, P.; Camara, E.; Silva, L.; Vieira, B.O. How to Assess Reverse Logistics of e-Waste Considering a Multicriteria Perspective: A Model Proposition. Logistics 2020, 4, 25. [Google Scholar] [CrossRef]
- Vieira, B.O.; Guarnieri, P.; Nofal, R.; Nofal, B. Multi-Criteria Methods Applied in the Studies of Barriers Identified in the Implementation of Reverse Logistics of E-Waste: A Research Agenda. Logistics 2020, 4, 11. [Google Scholar] [CrossRef]
- Mogale, D.G.; Kumar, S.K.; Tiwari, M.K. Green food supply chain design considering risk and post-harvest losses: A case study. Ann. Oper. Res. 2020, 295, 257–284. [Google Scholar] [CrossRef]
- Mogale, D.G.; Cheikhrouhou, N.; Tiwari, M.K. Modelling of sustainable food grain supply chain distribution system: A bi-objective approach. Int. J. Prod. Res 2019. [Google Scholar] [CrossRef] [Green Version]
- Ullah, M.; Asghar, I.; Zahid, M.; Omair, M.; AlArjani, A.; Sarkar, B. Ramification of remanufacturing in a sustainable three-echelon closed-loop supply chain management for returnable products. J. Clean. Prod. 2021, 290, 125609. [Google Scholar] [CrossRef]
- Ghadge, A.; Kara, M.; Mogale, D.G.; Choudhary, S.; Dani, S. Sustainability implementation challenges in food supply chains: A case of U.K. artisan cheese producers. Prod. Plan. Control. 2020. [Google Scholar] [CrossRef]
- Gupta, S.M.; Güngör, A.; Govindan, K.; Özceylan, E.; Can Berk, K.; Piplani, R. Responsible & sustainable manufacturing. Int. J. Prod. Res. 2020, 58, 7181–7182. [Google Scholar]
- Sazvar, Z.; Zokaee, M.; Tavakkoli-Moghaddam, R.; Al-sadat Salari, S.; Nayeri, S. Designing a sustainable closed-loop pharmaceutical supply chain in a competitive market considering demand uncertainty, manufacturer’s brand and waste management. Ann. Oper. Res. 2021, 1–32. [Google Scholar] [CrossRef]
- Meade, L.; Sarkis, J. A conceptual model for selecting and evaluating third-party reverse logistics providers. Supply Chain Manag. Int. J. 2002, 7, 283–295. [Google Scholar] [CrossRef]
- Ahmadi, A.; Amin, S. An integrated chance-constrained stochastic model for a mobile phone closed-loop supply chain network with supplier selection. J. Clean. Prod. 2019, 226, 988–1003. [Google Scholar] [CrossRef]
- Fazli-Khlaf, M.; Chaharsoohi, S.; Pishvaee, S. A new robust possibilistic programming model for reliable supply chain network design: A case study of lead- acid battery supply chain. RAIRO Oper. Res. 2019, 53, 1489–1512. [Google Scholar] [CrossRef] [Green Version]
- Sabouhi, F.; Pishvaee, M.S.; Jabalameli, M.S. Resilient Supply Chain Design under Operational and Disruption Risks Considering Quantity Discount: A Case Study of Pharmaceutical Supply Chain. Comput. Ind. Eng. 2018, 126, 657–672. [Google Scholar] [CrossRef]
- Mula, J.; Poler, R.; Garcia, J.P. MRP with flexible constraints: A fuzzy mathematical programming approach. Fuzzy Sets Syst. 2006, 157, 74–97. [Google Scholar] [CrossRef]
- Mula, J.; Poler, R.; Garcia-Sabater, J.P. Material Requirement Planning with fuzzy constraints and fuzzy coefficients. Fuzzy Sets Syst. 2007, 158, 783–793. [Google Scholar] [CrossRef]
- Pishvaee, M.S.; Razmi, J. Environmental supply chain network design using multi-objective fuzzy mathematical programming. Appl. Math. Model. 2012, 36, 3433–3446. [Google Scholar] [CrossRef]
- Pishvaee, M.S.; Torabi, S.A.; Razmi, J. Credibility-based fuzzy mathematical programming model for green logistics design under uncertainty. Comput. Ind. Eng. 2012, 62, 624–632. [Google Scholar] [CrossRef]
- Mulvey, J.M.; Vanderbei, R.J.; Zenios, S.A. Robust optimization of large-scale systems. Oper. Res. 1995, 43, 264–328. [Google Scholar] [CrossRef] [Green Version]
- Pishvaee, M.S.; Razmi, J.; Torabi, S.A. Robust possibilistic programming for socially responsible supply chain network design: A new approach. Fuzzy Sets Syst. 2012, 206, 1–20. [Google Scholar] [CrossRef]
- Mousazadeh, M.; Torabi, S.A.; Pishvaee, M.S.; Abolhassani, F. Health service network design: A robust possibilistic approach. Int. Trans. Oper. Res. 2018, 25, 337–373. [Google Scholar] [CrossRef]
- Tozanli, O.; Duman, G.M.; Kongar, E.; Gupta, S.M. Environmentally Concerned Logistics Operations in Fuzzy Environment: A Literature Survey. Logistics 2017, 1, 4. [Google Scholar] [CrossRef] [Green Version]
- Vahdat, V.; Vahdatzad, M.A. Accelerated Benders’ Decomposition for Integrated Forward/Reverse Logistics Network Design under Uncertainty. Logistics 2017, 1, 11. [Google Scholar] [CrossRef] [Green Version]
- Prakash, S.; Kumar, S.; Soni, G.; Jain, V.; Rathore, A. Closed-loop supply chain network design and modeling under risks and demand uncertainty: An integrated robust optimiza-tion approach. Ann. Oper. Res. 2020, 290, 837–864. [Google Scholar] [CrossRef]
- Yolmeh, A.; Saif, U. Closed-loop supply chain network design integrated with assembly and disassembly line balancing under uncertainty: An enhanced decomposition approach. Int. J. Prod. Res. 2020, 1–18. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Zhang, W.; Gao, G.; Zhang, H. Incentive mechanisms in a green supply chain under demand uncertainty. J. Clean. Prod. 2018, 279, 123636. [Google Scholar] [CrossRef]
- Tordecilla, R.D.; Juan, A.A.; Montoya-Torres, J.R.; Quintero-Araujo, C.L.; Panadero, J. Simulation-optimization methods for designing and assessing resilient supply chain networks under uncertainty scenarios: A review. Simul. Model. Pract. Theory 2021, 106, 102166. [Google Scholar] [CrossRef]
- Ferrer, G. The economics of tire remanufacturing. Resour. Conserv. Recycl. 1997, 19, 221–255. [Google Scholar] [CrossRef]
- Sasikumar, P.; Kannan, G.; Noorul Haq, A. A multi-echelon reverse logistics network design for product recovery—A case of truck tire remanufacturing. Int. J. Adv. Manuf. Technol. 2010, 49, 1223–1234. [Google Scholar] [CrossRef]
- Chopra, S.; Meindl, P. Supply Chain Management: Strategy, Planning and Operation; Pearson: Boston, MA, USA, 2013; Volume 232. [Google Scholar]
- Yadollahinia, M.; Teimoury, E.; Paydar, M. Tire forward and reverse supply chain design considering customer relationship management. Resour. Conserv. Recycl. 2018, 138, 215–228. [Google Scholar] [CrossRef]
- Amin, S.H.; Zhang, G.; Akhtar, P. Effects of uncertainty on a tire closed-loop supply chain network. Exp. Syst. Appl. 2017, 73, 82–91. [Google Scholar] [CrossRef] [Green Version]
- Subulan, K.; Tas, A.S.; Baykasoğlu, A. Designing an environmentally conscious tire closed-loop supply chain network with multiple recovery options using interactive fuzzy goal programming. Appl. Math. Model. 2015, 39, 2661–2702. [Google Scholar] [CrossRef]
- Derakhshan, Z.; Ghaneian, M.; Mahvi, A.; Gea, O.C.; Faramarzian, M.; Dehghani, M.; Ferrante, M. A new recycling technique for the waste tires reuse. Environ. Res. 2017, 158, 462–469. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, B.O.; North, B. A Review of Waste Tyre Gasification. J. Environ. Chem. Eng. 2017, 5, 10. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M. Hybrid optimizers to solve a tri-level programming model for a tire closed-loop supply chain network design. Appl. Soft Comput. 2018, 70, 701–722. [Google Scholar] [CrossRef]
- Pedram, A.; Yusoff, N.; Udoncy, O.; Mahat, A.; Pedram, P.; Babolola, A. Integrated forward and reverse supply chain: A tire case study. Waste Manag. 2017, 60, 460–470. [Google Scholar] [CrossRef]
- Lokesh, K.S.; Jain, P.K.; Sharma, A.K. Tactical supply chain planning for Tyre remanufacturing considering carbon tax policy. Int. J. Adv. Manuf. Technol. 2018, 97, 1505–1528. [Google Scholar]
- Lokesh, K.S.; Jain, P.K.; Sharma, A.K. A fuzzy goal programme with carbon tax for Brownfield tyre remanufacturing supply chain planning. J. Clean. Prod. 2018, 198, 737–753. [Google Scholar]
- Sahebjamnia, N.; Fathollahi-Fard, A.; Hajiaghaei-Keshteli, M. Sustainable tire closed-loop supply chain network design: Hybrid metaheuristic algorithms for large-scale networks. J. Clean. Prod. 2018, 196, 273–296. [Google Scholar] [CrossRef]
- Abdolazimi, O.; Esfandarani, M.; Salehi, M.; Shishebori, D. Robust design of a multi-objective closed-loop supply chain by integrating on-time delivery, cost, and environmental aspects, case study of a Tire Factory. J. Clean. Prod. 2020, 264, 121566. [Google Scholar] [CrossRef]
- Mehrjerdi, Y.Z.; Shafiee, M. A Resilient and sustainable closed-loop supply chain using multiple sourcing and information sharing strategies. J. Clean. Prod. 2020, 289, 125141. [Google Scholar] [CrossRef]
- Lokesh, K.S.; Jain, P.K.; Sharma, A.K. A fuzzy goal programme–based sustainable Greenfield supply network design for tyre retreading industry. Int. J. Adv. Manuf. Technol. 2020, 108, 2855–2880. [Google Scholar]
- Gupta, V.K.; Nayak, A.; Agarwal, S.; Chaudhary, M.; Tyagi, I. Removal of Ni (II) ions from water using scrap tire. J. Mol. Liq. 2014, 190, 215–222. [Google Scholar] [CrossRef]
- Derakhshan, Z.; Ehrampoush, M.H.; Faramarzian, M.; Ghaneian, M.T.; Mahvi, A.H. Waste tire chunks as a novel packing media in a fixed-bed sequence batch reactor: Volumetric removal modeling. Desalin. Water Treat. 2017, 64, 40–47. [Google Scholar] [CrossRef]
- Battista, M.; Gobetti, A.; Agnelli, S.; Ramorino, G. Post-consumer tires as a valuable resource: Review of different types of material recovery. Environ. Technol. Rev. 2021, 10, 1–25. [Google Scholar] [CrossRef]
- Conti, G.O.; Heibati, B.; Kloog, I.; Fiore, M.; Ferrante, M. A review of AirQ Models and their applications for forecasting the air pollution health outcomes. Environ. Sci. Pollut. Res. Int. 2017, 24, 6426–6445. [Google Scholar] [CrossRef]
- Sciacca, S.; Conti, G.O. Mutagens and carcinogens in drinking water. Med. J. Nutr. 2009, 2, 157–162. [Google Scholar]
- Dehghani, M.; Keshtgar, L.; Javaheri, M.R.; Derakhshan, Z.; Conti, G.O.; Zuccarello, P.; Ferrante, M. The effects of air pollutants on the mortality rate of lung cancer and leukemia. Mol. Med. 2017, 15, 3390–3397. [Google Scholar] [CrossRef] [Green Version]
- Salehi, F.; Mahootchi, M.; Husseini, S.M.M. Developing a robust stochastic model for designing a blood supply chain network in a crisis: A possible earthquake in Tehran. Ann. Oper. Res. 2019, 283, 679–703. [Google Scholar] [CrossRef]
- Kacprzyk, J.; Orlovski, S.A. Optimization Models Using Fuzzy Sets and Possibility Theory; Springer Science & Business Media: Berlin, Germany, 2013; Volume 4. [Google Scholar]
- Xu, J.; Zhou, X. Approximation based fuzzy multi-objective models with expected objectives and chance constraints: Application to earth-rock work allocation. Inf. Sci. 2013, 238, 75–95. [Google Scholar] [CrossRef]
- Zahiri, B.; Jula, P.; Tavakkoli-Moghaddam, R. Design of a pharmaceutical supply chain network under uncertainty considering perishability and substitutability of products. Inf. Sci. 2018, 423, 257–283. [Google Scholar] [CrossRef]
- Savadkoohi, E.; Mousazadeh, M.; Torabi, S.A. A possibilistic location-inventory model for multi-period perishable pharmaceutical supply chain network design. Chem. Eng. Res. Des. 2018, 138, 490–505. [Google Scholar] [CrossRef]
- Heydari, J.; Sabbaghnia, A.; Razmi, J. A dynamic bi-objective model for after disaster blood supply chain network design; a robust possibilistic programming ap-proach. J. Ind. Syst. Eng. 2018, 11, 16–28. [Google Scholar]
- Sadghiani, N.S.; Torabi, S.; Sahebjamnia, N. Retail supply chain network design under operational and disruption risks. Transp. Res. Part E Logist. Transp. Rev. 2015, 75, 95–114. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, W.-G. Multiperiod mean absolute deviation fuzzy portfolio selection model with risk control and cardinality constraints. Fuzzy Sets Syst. 2014, 255, 74–91. [Google Scholar] [CrossRef]
- Mavrotas, G. Effective implementation of the ε-constraint method in multi-objective mathematical programming problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Aghaei, J.; Amjady, N.; Shayanfar, H.A. Multi-objective electricity market clearing considering dynamic security by lexicographic optimization and augmented epsilon constraint method. Appl. Soft Comput. 2011, 11, 3846–3858. [Google Scholar] [CrossRef]



| Network Type | Supplier Selection | Multi Raw Material | Multi Product | Multi Capacity Level | Network Expansion | ||||||
| Forward | Reverse | CLSC | |||||||||
| Sasikumar et al. (2010) [52] | x | ||||||||||
| Pishvaee et al. (2012) [43] | x | ||||||||||
| Subulan et al. (2015) [56] | x | x | x | x | x | ||||||
| Jindal et al. (2016) [12] | x | x | |||||||||
| Amin et al. (2017) [55] | x | x | x | ||||||||
| Pedram et al. (2018) [60] | x | x | |||||||||
| Fazli-Khalaf et al. (2018) [36] | x | x | x | x | |||||||
| Fathollahi-Fard et al. (2018) [59] | x | x | x | ||||||||
| Sabouhi et al. (2018) [37] | x | x | x | x | x | ||||||
| Lokesh et al. (2018a) [61] | x | x | x | ||||||||
| Lokesh et al. (2018b) [62] | x | x | |||||||||
| Sahebjamnia et al. (2018) [63] | x | x | x | ||||||||
| Yadollahinia et al. (2018) [54] | x | x | |||||||||
| Ahmadi and Amin (2019) [35] | x | x | x | x | |||||||
| Mogale et al. (2019) [29] | x | ||||||||||
| De et al. (2020) [22] | x | x | |||||||||
| Abdolazimi et al. (2020) [64] | x | x | x | x | |||||||
| Mehrjerdi et al. (2020) [65] | x | x | x | x | |||||||
| Lokesh et al. (2020) [66] | x | x | x | x | |||||||
| This Paper | x | x | x | x | x | x | |||||
| Objective | Green | Uncertainty Type | Robust Optimization | Multi Cycle Network | Buyback Incentive | Penalty Cost | Case Study | ||||
| Single | Multi | Deterministic | Stochastic | Fuzzy | |||||||
| Sasikumar et al. (2010) [52] | x | x | Tire | ||||||||
| Pishvaee et al. (2012) [43] | x | x | x | x | Medical | ||||||
| Subulan et al. (2015) [56] | x | x | x | Tire | |||||||
| Jindal et al. (2016) [12] | x | x | x | ||||||||
| Amin et al. (2017) [55] | x | x | Tire | ||||||||
| Pedram et al. (2018) [60] | x | x | x | Tire | |||||||
| Fazli-Khalaf et al. (2018) [36] | x | x | x | x | Battery | ||||||
| Fathollahi-Fard et al. (2018) [59] | x | x | x | ||||||||
| Sabouhi et al. (2018) [37] | x | x | Pharma | ||||||||
| Lokesh et al. (2018a) [61] | x | x | x | Tire | |||||||
| Lokesh et al. (2018b) [62] | x | x | x | Tire | |||||||
| Sahebjamnia et al. (2018) [63] | x | x | x | Tire | |||||||
| Yadollahinia et al. (2018) [54] | x | x | x | Tire | |||||||
| Ahmadi and Amin (2019) [35] | x | x | x | Phone | |||||||
| Mogale et al. (2019) [29] | x | x | x | Grain | |||||||
| De et al. (2020) [22] | x | x | x | ||||||||
| Abdolazimi et al. (2020) [64] | x | x | x | x | Tire | ||||||
| Mehrjerdi et al. (2020) [65] | x | x | x | Tire | |||||||
| Lokesh et al. (2020) [66] | x | x | x | Tire | |||||||
| This Paper | x | x | x | x | x | x | x | x | Tire | ||
| Ξ | Set of Possible Scenarios |
| Set of raw material suppliers | |
| Set of raw materials | |
| Set of types of tires | |
| Set of existing production centers | |
| Set of potential production centers | |
| Set of existing distribution centers | |
| Set of potential distribution centers | |
| Set of customer delivery points | |
| Set of collection centers | |
| Set of recycling centers | |
| Set of retreading centers | |
| Set of energy recovery centers | |
| Set of capacity levels | |
| Parameters: Tilde symbol (∼) is to distinguish the uncertain parameters. | |
| Fixed opening cost of production center at location f at capacity level u | |
| Fixed opening cost of distribution center at location d at capacity level u | |
| Fixed opening cost of collection center at location i at capacity level u | |
| Fixed opening cost of recycling center at location j at capacity level u | |
| Fixed opening cost of retreading center at location k at capacity level u | |
| Fixed ordering cost of raw material from supplier s | |
| Unit cost of raw material m from supplier s (fuzzy) | |
| Production cost of a unit of tire p at production center f (fuzzy) | |
| Buyback price of a unit of EOL tire p from customer c | |
| Retreading cost of a unit of tire p for first time at retreading center k | |
| Retreading cost of a unit of tire p for second time at retreading center k | |
| Recyclincost of a unit of tire p at recycling center j | |
| Incineration cost of a unit of tire p at incineration center w | |
| Transportation cost for unit of raw material m from center s to center f | |
| Transportation cost for a unit of tire p from center f to d | |
| Transportation cost for a unit of tire p from center d to c | |
| Transportation cost for a unit of tire p from center c to i | |
| Transportation cost for a unit of tire p from center i to j | |
| Transportation cost for a unit of tire p from center i to k | |
| Transportation cost for a unit of tire p from center k to d | |
| Transportation cost for a unit of tire p from center k to j | |
| Transportation cost for a unit of tire p from center j to w | |
| Maximum capacity of the supplier s for material m | |
| Maximum capacity of production center f at capacity level u | |
| Binary parameter defining capacity level of existing center f | |
| Maximum cap city of distribution center d at capacity level u | |
| Binary parameter defining capacity level of existing center | |
| Maximum capacity of collection center i at capacity level u | |
| Maximum capacity of retreading center k at capacity level u | |
| Maximum capacity of recycling center j at capacity level u | |
| GHG generated at center f for producing a unit of tire p | |
| GHG generated at center j for recycling a unit of tire p | |
| GHG generated at center k for retreading a unit of tire p | |
| GHG generated at center w for incineration of a unit of tire p | |
| GHG generated for transporting a unit of material m from center s to f | |
| GHG generated for transporting a unit of tire p from center f to d | |
| GHG generated for transporting a unit of tire p from center d to c | |
| GHG generated for transporting a unit of tire p from center c to i | |
| GHG generated for transporting a unit of tire p from center i to k | |
| GHG generated for transporting a unit of tire p from center k to j | |
| GHG generated for transporting a unit of tire p from center k to d | |
| GHG generated for transporting a unit of tire p from center i to j | |
| GHG generated for transporting a unit of tire p from center j to w | |
| Quantity of material m needed to produce one unit of tire p | |
| Market demand for new tires p (scenario-based) | |
| Market demand for retread-1 tires p (scenario-based) | |
| Market demand for retread-2 tires p (scenario-based) | |
| Return rate of EOL new tire from center c (fuzzy) | |
| Return rat of EOL retread-1 tire from center c (fuzzy) | |
| Return rate of EOL retread-2 tire from center c (fuzzy) | |
| Retread rate of EOL new tires (fuzzy) | |
| Retread rate of EOL retread-1 tires (fuzzy) | |
| Recycling rate (fuzzy) | |
| Unit price of the new tire p | |
| Unit price of the retread-1 tire p | |
| Unit price of the retread-2 tire p | |
| Value of the recycled material for unit tire p | |
| Number of employees at new manuf. center at capacity u | |
| Number of employees at new dist. center at capacity u | |
| Number of employees at new retreading center k at capacity u | |
| Number of employees at new collection center i at capacity u | |
| Number of employees at new recycling center j at capacity u | |
| Variables | |
| Quantity of material m shipped form supplier s to f under scenario | |
| Total production quantity of tire p at the center f under scenario | |
| Quantity of new tire p shipped from center f to d under scenario | |
| Quantity of new tire p shipped from center d to c under scenario | |
| Quantity of retread-1 tire p shipped from center d to c under scenario | |
| Quantity of retread-2 tire p shipped from center d to c under scenario | |
| Quantity of new tire p shipped from center c to i under scenario | |
| Quantity of retread-1 tire p shipped from center c to i under scenario | |
| Quantity of retread-2 tire p shipped from center c to i under scenario | |
| Quantity of new tire p shipped from center i to k under scenario | |
| Quantity of retread-1 tire p shipped from center i to k under scenario | |
| Quantity of retread-2 tire p shipped from center i to j under scenario | |
| Quantity of retread-1 tire p shipped from center k to d under scenario | |
| Quantity of retread-2 tire p shipped from center k to d under scenario | |
| Quantity of retread-1 tire p shipped from center k to j under scenario | |
| Quantity of retread-2 tire p shipped from center k to j under scenario | |
| Total quantity of recycled tire p at recycling center j under scenario | |
| Quantity of tire p shipped from center j to w under scenario | |
| Total quantity f tire p incinerated at center w under scenario | |
| Binary variables: | |
| Indicating if center f at capacity level u opened at location or not | |
| Indicating if center d at capacity level u opened at location or not | |
| Indicating if center i at capacity level u opened or not | |
| Indicating if center k at capacity level u opened or not | |
| Indicating if center j at capacity level u opened or not | |
| Indicating if raw material is purchased from supplier s or not | |
| Scenarios () | Recession | Good | Growing |
|---|---|---|---|
| Scenario Probability | 0.20 | 0.50 | 0.30 |
| U (5000–5100) | U (5100–5300) | U (5300–5500) | |
| U (2400–2700) | U (2700–2800) | U (2800–2900) | |
| U (500–600) | U (600–700) | U (700–800) |
| Parameters | ||||
|---|---|---|---|---|
| U (0.7–0.75) | U (0.75–0.8) | U (0.80–0.85) | U (0.85–0.9) | |
| U (0.65–0.7) | U (0.7–0.75) | U (0.75–0.8) | U (0.8–0.85) | |
| U (0.55–0.6) | U (0.6–0.65) | U (0.65–0.7) | U (0.7–0.75) | |
| U (0.6–0.65) | U (0.65–0.7) | U (0.7–0.75) | U (0.75–0.8) | |
| U (0.5–0.55) | U (0.55–0.6) | U (0.6–0.65) | U (0.65–0.7) | |
| U (0.88–0.91) | U (0.91–0.93) | U (093–0.96) | U (0.96–0.99) | |
| U ($100–$110) | U ($110–$120) | U ($120–$130) | U ($130–$140) | |
| U ($9, $9.5) | U ($9.5, $10) | U ($10, $10.5) | U ($10.5, $11) | |
| U ($43, $44) | U ($44, $45) | U ($45, $46) | U ($46, $47) | |
| U ($9, $9.5) | U ($9.5–$10) | U ($10–$10.5) | U ($10.5–$11) | |
| U ($9, $9.5) | U ($9.5–$10) | U ($10–$10.5) | U ($10.5k–$11) | |
| U ($10, $10.5) | U ($10.5, $11) | U ($11, $11.5) | U ($11.5, $12) |
| Capacity Level (U) | |||
|---|---|---|---|
| Low | Medium | High | |
| U ($3M–$4M) | U ($4M–$6M) | U ($6M–$10M) | |
| U ($0.2M–$0.3M) | U ($0.3M–$0.5M) | U ($0.5M–$0.7M) | |
| U ($0.2M–$0.3M) | U ($0.3M–$0.4M) | U ($0.4M–$0.5M) | |
| U ($0.3M, $0.4M) | U ($0.4M, $0.5M) | U ($0.5M–$0.7M) | |
| U ($0.8M–$1.5M) | U ($1.5M–$2.5M) | U ($2.5M–$4M) | |
| U(200K–400K) | U (400K-600K) | U (600K–1000K) | |
| U (100K–200K) | U (200K–300K) | U (300K–400K) | |
| U (200K–400K) | U (400K–600K) | U (600K–800K) | |
| U (100K–400K) | U (400K–600K) | U (600K–800K) | |
| U (100K–400K) | U (400K–600K) | U (600K–800K) | |
| U (100–150) | U (200–300) | U (300–500) | |
| U (30–60) | U (60–100) | U (100–150) | |
| U (30–50) | U (50–70) | U (70–100) | |
| U (10–30) | U (30–50) | U (50–70) | |
| U (10–30) | U (30–50) | U (50–70) | |
| m1, U (4–6); m2, U (14–17); m3, (4–6); m4, U (9–12); m5, U (10–12) | |
| U ($1000–$1200) | |
| U ($30–$50) | |
| U ($40–$50) | |
| U ($45–$55) | |
| U ($5–$10) | |
| U ($3–$8) | |
| U (9–10) kg | |
| U (10–12) kg | |
| U (6–7) kg | |
| U (1–2) kg | |
| U ($450–$550) | |
| U ($200–$300) | |
| U ($150–$200) | |
| U ($25–$30) |
| Value of Coefficients | |
|---|---|
| Objective 1 (profit, million dollar) | 1004 |
| Objective 2 (total GHG =kg) | 324,893 |
| Objective 3 (total job opportunities) | 1600 |
| Production Centers | Production Centers 3 and 4 open at high capacity |
| Distribution Centers | Distribution Centers 6 and 7 open at low capacity Distribution Centers 8 and 9 open at medium ca-pacity Distribution Center 10 open at high capacity |
| Collection Centers | Collection Centers 1, 2, 4, 6, 8, and 9 open at low capacity |
| Retreading Centers | Retreading Center 2 open at medium capacity Retreading Centers 1 and 3 open at high capacity |
| Recycling Centers | Recycling Centers 2 and 3 open at low capacity |
| Suppliers being utilized | Suppliers 1, 3, 4, and 5 |
| (scenario variability) | 164.926 |
| (shortage) | 0 |
| 0 | |
| (confidence level of fuzzy constraints) | 𝕡1 = 1/𝕡2 = 0.5/𝕡3 = 0.5/𝕡4 = 1/𝕡5 = 1/𝕡6 = 1 |
| Value of Coefficients | |
|---|---|
| Objective 1 (profit, million dollar) | 1115 |
| Objective 2 (total GHG = kg) | 348,253 |
| Objective 3 (total job opportunities) | 1715 |
| Production Centers | Production Centers 3 and 4 open at high capacity |
| Distribution Centers | Distribution Centers 6 open at low capacityDistribution Centers 8 and 9 open at medium capacityDistribution Centers 7 and10 open at high capacity |
| Collection Centers | Collection Centers 1, 2, 4, 6, 8, and 9 open at low capacity |
| Retreading Centers | Retreading Center 2 open at medium capacityRetreading Centers1 and 3 open at high capacity |
| Recycling Centers | Recycling Centers 2 and 3 open at low capacity |
| Suppliers being utilized | Suppliers 1, 3, 4, and 5 |
| (scenario variability) | 184.695 |
| (shortage) | 107,151 |
| 0 | |
| (confidence level of fuzzy constraints) | 𝕡1 = 1/𝕡2 = 1/𝕡3 = 1/𝕡4 = 1/𝕡5 = 1/𝕡6 = 1 |
| Value of Coefficients | |
|---|---|
| Objective 1 (profit, million dollar) | 1160 |
| Objective 2 (total GHG, kg) | 358,321 |
| Objective 3 (total job opportunities) | 1980 |
| Production Centers | Production Centers 3 and 4 open at medium capacityProduction Centers 5 open at high capacity |
| Distribution Centers | Distribution Centers 6, 7, 8, 9, and 10 open at high capacity |
| Collection Centers | Collection Centers 1, 2, 4, 8, and 9 open at low capacityCollection Center 6 open at medium capacity |
| Retreading Centers | Retreading Center 2 open at low capacityRetreading Center 2 open at medium capacityRetreading Centers 1 and 3 open at high capacity |
| Recycling Centers | Recycling Centers 1, 2, 3, and 5 open at low capacity |
| Suppliers being utilized | Suppliers 1, 2, 3, 4, and 5 |
| (scenario variability) | 190.680 |
| (shortage) | 0 |
| 0 | |
| (confidence level of fuzzy constraints) | 𝕡1 = 1/𝕡2 = 0.5/𝕡3 = 0.5/𝕡4 = 1/𝕡5 = 1/𝕡6 = 1 |
| Value of Coefficients | |
|---|---|
| Objective 1 (profit, million dollar) | 998 |
| Objective 2 (total GHG =kg) | 320,563 |
| Objective 3 (total job opportunities) | 2452 |
| Production Centers | Production Centers 3 and 4 open at high capacity |
| Distribution Centers | Distribution Centers 6, 7, 8, 9, and 10 open at high capacity |
| Collection Centers | Collection Centers 1, 2, 4, 6, 8, and 9 open at high capacity |
| Retreading Centers | Retreading Centers 1, 2, 3, and 4 open at high capacity |
| Recycling Centers | Recycling Centers 1, 2, 3, 4, and 5 open at high capacity |
| Suppliers being utilized | Suppliers 1, 3, 4, and 5 |
| (scenario variability) | 168.635 |
| (shortage) | 0 |
| 0 | |
| (confidence level of fuzzy constraints) | 𝕡1 = 1/𝕡2 = 1/𝕡3 = 1/𝕡4 = 0.5/𝕡5 = 0.5/𝕡6 = 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tehrani, M.; Gupta, S.M. Designing a Sustainable Green Closed-Loop Supply Chain under Uncertainty and Various Capacity Levels. Logistics 2021, 5, 20. https://doi.org/10.3390/logistics5020020
Tehrani M, Gupta SM. Designing a Sustainable Green Closed-Loop Supply Chain under Uncertainty and Various Capacity Levels. Logistics. 2021; 5(2):20. https://doi.org/10.3390/logistics5020020
Chicago/Turabian StyleTehrani, Mohsen, and Surendra M. Gupta. 2021. "Designing a Sustainable Green Closed-Loop Supply Chain under Uncertainty and Various Capacity Levels" Logistics 5, no. 2: 20. https://doi.org/10.3390/logistics5020020
APA StyleTehrani, M., & Gupta, S. M. (2021). Designing a Sustainable Green Closed-Loop Supply Chain under Uncertainty and Various Capacity Levels. Logistics, 5(2), 20. https://doi.org/10.3390/logistics5020020






