Robot-Controlled Acupuncture—An Innovative Step towards Modernization of the Ancient Traditional Medical Treatment Method
Abstract
:1. Introduction
2. Acupuncture Point Localization
- (1)
- Symptom input: The user interacts with a chatbot on the smartphone to describe her/his symptoms.
- (2)
- Database search: According to the symptom described by the user, a TCM database is searched and symptom-related acupuncture points are retrieved.
- (3)
- Acupoint visualization: Symptom-related acupoints are visualized in an image of the human body.
2.1. Image-Based Acupoint Localization
- (i)
- The differences of face shape between different people are not considered
- (ii)
- A conversion of pixel to cun, based on the frontal face, cannot be directly applied to locating acupoints on the side of the face.
2.2. Landmark Detection
2.3. Image Deformation
2.4. 3D Morphable Model (3DMM)
2.5. Face Detection (FD) and Tracking
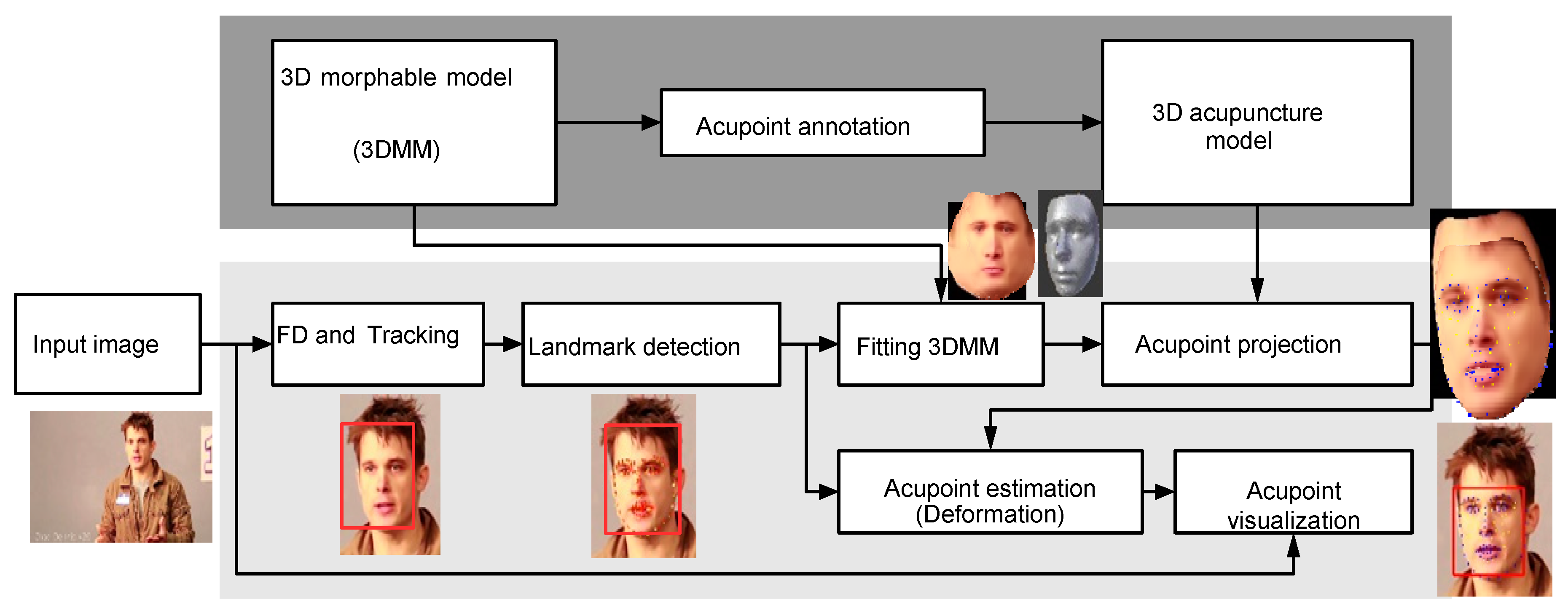
2.6. Method—Acupuncture Point Localization
2.6.1. 3D Morphable Model
2.6.2. Acupoint Annotation
2.6.3. 3D Acupuncture Model
2.6.4. Face Detection and Tracking
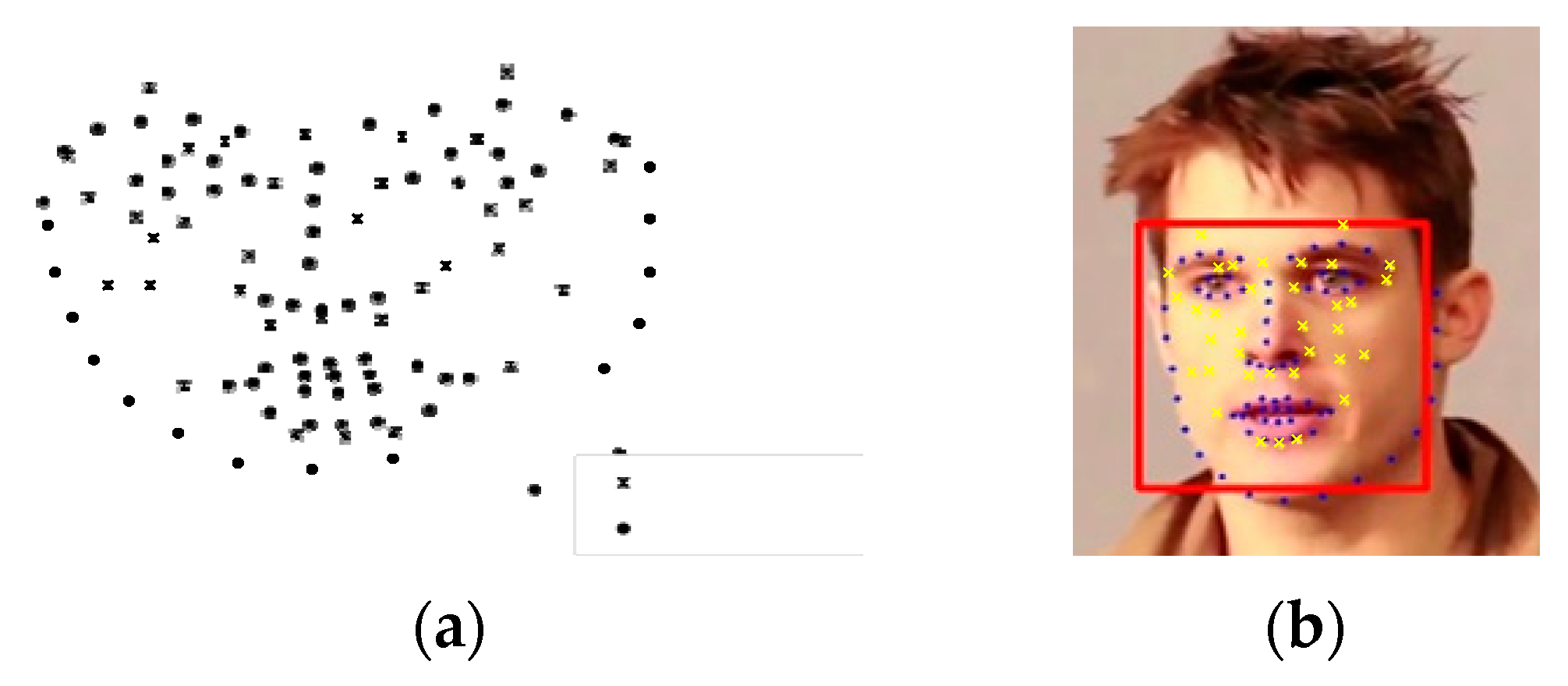
2.6.5. Landmark Detection
2.6.6. Fitting 3DMM
2.6.7. Acupoint Projection
2.6.8. Acupoint Estimation
2.6.9. Acupoint Visualization
3. Automated Acupoint Stimulation
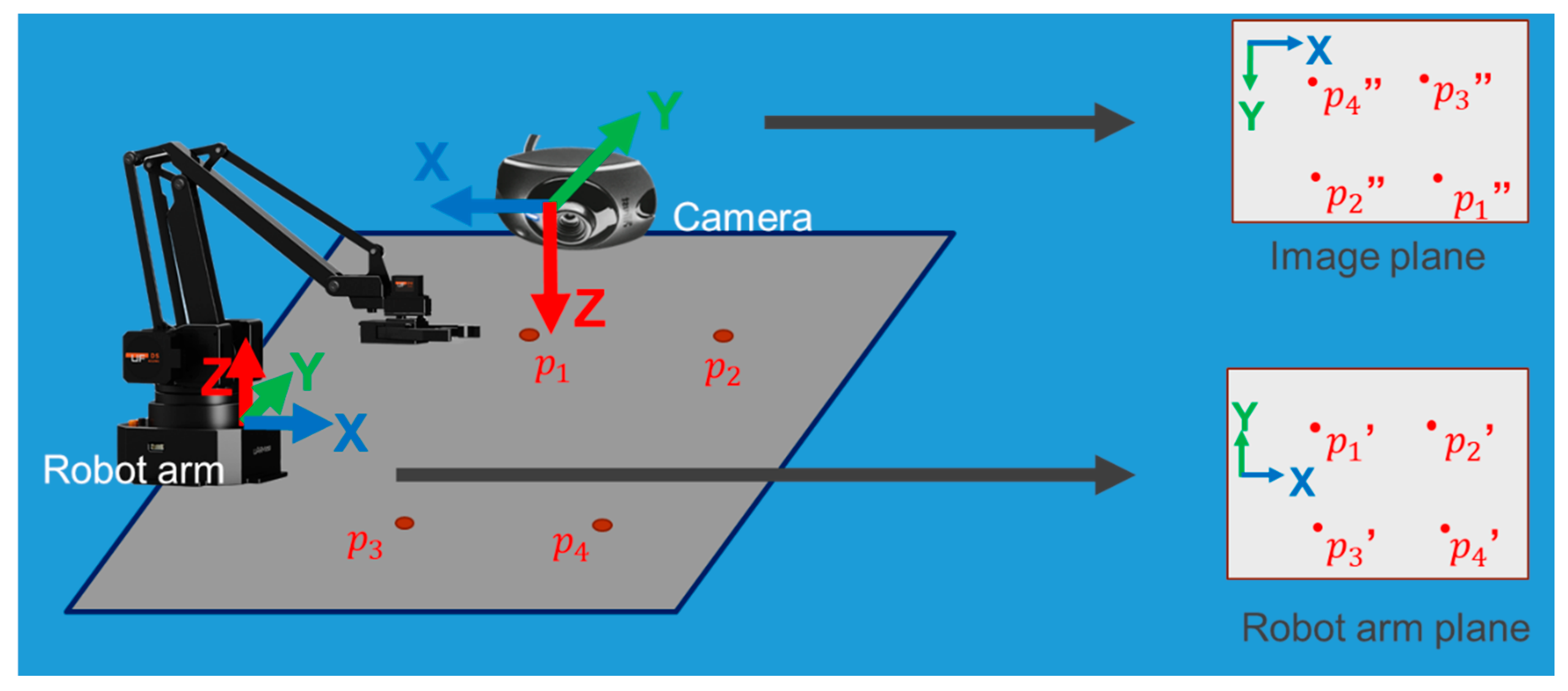
3.1. Hand-Eye Calibration
3.2. Transformation Matrix Calculation
4. Automated Detection of Deqi Event
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Statista, Smartphone user penetration as percentage of total global population from 2014 to 2021. Available online: https://www.statista.com/statistics/203734/global-smartphone-penetration-per-capita-since-2005 (accessed on 22 May 2019).
- Jiang, H.; Starkman, J.; Kuo, C.H.; Huang, M.C. Acu glass: Quantifying acupuncture therapy using google glass. In Proceedings of the 10th EAI International Conference on Body Area Networks, Sydney, Australia, 28–30 September 2015; pp. 7–10. [Google Scholar]
- Chang, M.; Zhu, Q. Automatic location of facial acupuncture-point based on facial feature points positioning. In Proceedings of the 5th International Conference on Frontiers of Manufacturing Science and Measuring Technology (FMSMT), Taiyuan, China, 24–25 June 2017. [Google Scholar]
- Kazemi, V.; Sullivan, J. One millisecond face alignment with an ensemble of regression trees. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Washington, WA, USA, 23–28 June 2014; pp. 1867–1874. [Google Scholar]
- Ren, S.; Cao, X.; Wei, Y.; Sun, Y. Face alignment at 3000 fps via regressing local binary features. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1685–1692. [Google Scholar]
- King, D.E. Dlib-ml: A machine learning toolkit. J. Mach. Learn. Res. 2009, 10, 1755–1758. [Google Scholar]
- Schaefer, S.; McPhail, T.; Warren, J. Image deformation using moving least squares. ACM Trans. Graph. 2006, 25, 533–540. [Google Scholar] [CrossRef]
- Kim, J.; Kang, D.I. Partially automated method for localizing standardized acupuncture points on the heads of digital human models. Evid. Based Complement. Altern. Med. 2015, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Qin, B.; Zhuang, T.; Tiede, U.; Höhne, K.H. Localization of acupoints on a head based on a 3d virtual body. Image Vis. Comput. 2005, 23, 1–9. [Google Scholar] [CrossRef]
- Kim, J.; Kang, D.I. Positioning standardized acupuncture points on the whole body based on x-ray computed tomography images. Med. Acupunct. 2014, 26, 40–49. [Google Scholar] [CrossRef]
- Blanz, V.; Vetter, T. A morphable model for the synthesis of 3d faces. In Proceedings of the 26th annual conference on Computer Graphics and Interactive Techniques (SIGGRAPH), Los Angeles, CA, USA, 8–13 August 1999; pp. 187–194. [Google Scholar]
- Huber, P.; Feng, Z.H.; Christmas, W.; Kittler, J.; Rätsch, M. Fitting 3d morphable models using local features. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 1195–1199. [Google Scholar]
- Paysan, P.; Knothe, R.; Amberg, B.; Romdhani, S.; Vetter, T. A 3d face model for pose and illumination invariant face recognition. In Proceedings of the 6th IEEE International Conference on Advanced Video and Signal based Surveillance (AVSS) for Security, Safety and Monitoring in Smart Environments, Genova, Italy, 2–4 September 2009. [Google Scholar]
- Huber, P.; Hu, G.; Tena, R.; Mortazavian, P.; Koppen, P.; Christmas, W.; Ratsch, M.J.; Kittler, J. A multiresolution 3d morphable face model and fitting framework. In Proceedings of the 11th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Rome, Italy, 27–29 February 2016. [Google Scholar]
- Viola, P.; Jones, M. Rapid object detection using a boosted cascade of simple features. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Kauai, HI, USA, 8–14 December 2001; pp. 511–518. [Google Scholar]
- Wilson, P.I.; Fernandez, J. Facial feature detection using haar classifiers. J. Comput. Sci. Coll. 2006, 21, 127–133. [Google Scholar]
- Chen, Q.; Georganas, N.D.; Petriu, E.M. Hand gesture recognition using haar-like features and a stochastic context-free grammar. IEEE Trans. Instrum. Meas. 2008, 57, 1562–1571. [Google Scholar] [CrossRef]
- Zondag, J.A.; Gritti, T.; Jeanne, V. Practical study on real-time hand detection. In Proceedings of the 3rd International Conference on Affective Computing and Intelligent Interaction and Workshops, Amsterdam, The Netherlands, 10–12 September 2009; pp. 1–8. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–25 June 2005; pp. 886–893. [Google Scholar]
- Bolme, D.; Beveridge, J.R.; Draper, B.A.; Lui, Y.M. Visual object tracking using adaptive correlation filters. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 2544–2550. [Google Scholar]
- Danelljan, M.; Häger, G.; Khan, F.; Felsberg, M. Accurate scale estimation for robust visual tracking. In Proceedings of the British Machine Vision Conference BMVC, Nottingham, UK, 1–5 September 2014. [Google Scholar]
- Felzenszwalb, P.F.; Girshick, R.B.; McAllester, D.; Ramanan, D. Object detection with discriminatively trained part-based models. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1627–1645. [Google Scholar] [CrossRef]
- Chen, J.; Gu, H.; Wang, H.; Su, W. Mathematical analysis of main-to-sidelobe ratio after pulse compression in pseudorandom code phase modulation CW radar. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–5. [Google Scholar]
- Jiang, J.; Jiang, J.; Cui, B.; Zhang, C. Tencent Boost: A Gradient Boosting Tree System with Parameter Server. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017; pp. 281–284. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Grest, D.; Petersen, T.; Krüger, V. A comparison of iterative 2d-3d pose estimation methods for real-time applications. In Proceedings of the 16th Scandinavian Conference on Image Analysis, Oslo, Norway, 15–18 June 2009; pp. 706–715. [Google Scholar]
- The Homography transformation. Available online: http://www.corrmap.com/features/homography_transformation.php (accessed on 23 May 2019).
- Liang, F.R.; Zhao, J.P. Acupuncture and Moxibustion; People’s Medical Publishing House: Beijing, China, 2012. [Google Scholar]
- Xu, S.; Huang, B.; Zhang, C.Y.; Du, P.; Yuan, Q.; Bi, G.J.; Zhang, G.B.; Xie, M.J.; Luo, X.; Huang, G.Y.; et al. Effectiveness of strengthened stimulation during acupuncture for the treatment of Bell palsy: A randomized controlled trial. CMAJ 2013, 185, 473–479. [Google Scholar] [CrossRef]
- Park, J.E.; Ryu, Y.H.; Liu, Y. A literature review of de qi in clinical studies. Acupunct. Med. 2013, 31, 132–142. [Google Scholar] [CrossRef]
- Chen, J.; Li, G.; Zhang, G.; Huang, Y.; Wang, S.; Lu, N. Brain areas involved in acupuncture needling sensation of de qi: A single-photon emission computed tomography (SPECT) study. Acupunct. Med. 2012, 30, 316–323. [Google Scholar] [CrossRef] [PubMed]
- Sandberg, M.; Lindberg, L.; Gerdle, B. Peripheral effects of needle stimulation (acupuncture) on skin and muscle blood flow in fibromyalgia. Eur. J. Pain 2004, 8, 163–171. [Google Scholar] [CrossRef]
- Park, J.; Lee, H.; Lim, S. Deqi sensation between the acupuncture-experienced and the naive: A Korean study II. Am. J. Chin. Med. 2005, 33, 329–337. [Google Scholar] [CrossRef] [PubMed]
- MacPherson, H.; Asghar, A. Acupuncture needle sensations associated with De Qi: A classification based on experts’ ratings. J. Altern. Complement. Med. 2006, 12, 633–637. [Google Scholar] [CrossRef] [PubMed]
- Kong, J.; Fufa, D.T.; Gerber, A.J. Psychophysical outcomes from a randomized pilot study of manual, electro, and sham, acupuncture treatment on experimentally induced thermal pain. J. Pain 2005, 6, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.L.; Guo, T.P.; Du, H.B.; Zheng, H.B.; Ma, T.T. A survey of the practice and perspectives of Chinese acupuncturists on deqi. Evid. Based Comple. Altern. Med. 2014. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, H.D.; Seo, H.D.; Sawada, K.; Ishida, M. The effect of acupuncture at the PC-6 on the electroencephalogram and electrocardiogram. Am. J. Chin. Med. 2008. [Google Scholar] [CrossRef]
- Kim, S.Y.; Kim, S.W.; Park, H.J. Different responses to acupuncture in electroencephalogram according to stress level: A randomized, placebo-controlled, cross-over trial. Korean J. Acupunct. 2014, 31, 136–145. [Google Scholar] [CrossRef]
- Kim, M.S.; Cho, Y.C.; Moon, J.H.; Pak, S.C. A characteristic estimation of bio-signals for electro-acupuncture stimulations in human subjects. Am. J. Chin. Med. 2009, 37, 505–517. [Google Scholar] [CrossRef]
- Yin, C.S.; Park, H.J.; Kim, S.Y.; Lee, J.M.; Hong, M.S.; Chung, J.H.; Lee, H.J. Electroencephalogram changes according to the subjective acupuncture sensation. Neurol. Res. 2010, 32, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Streitberger, K.; Steppan, J.; Maier, C.; Hill, H.; Backs, J.; Plaschke, K. Effects of verum acupuncture compared to placebo acupuncture on quantitative EEG and heart rate variability in healthy volunteers. J. Altern. Complement. Med. 2008, 14, 505–513. [Google Scholar] [CrossRef] [PubMed]
- Sakai, S.; Hori, K.; Umeno, K.; Kitabayashi, N.; Ono, T.; Nishijo, H. Specific acupuncture sensation correlates with EEGs and autonomic changes in human subjects. Auton. Neurosci. Basic Clin. 2007, 133, 158–169. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y.; Koyama, Y.; Jodo, E. Effects of acupuncture to the sacral segment on the bladder activity and electroencephalogram. Psychiatry Clin. Neurosci. 2002, 56, 249–250. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.; Fang, J.; Wang, X. Characterization of De Qi with electroacupuncture at acupoints with different properties. J. Altern. Complement. Med. 2011, 17, 1007–1013. [Google Scholar] [CrossRef] [PubMed]
- Litscher, G. From basic science to robot-assisted acupuncture. Guest editorial. Med. Acupunct. 2019, 31, 139–140. [Google Scholar] [CrossRef]
- Jones, C. Robotically-Assisted Acupuncture Brings Ancient Healing Technique into the 21th Century; Science-Based Satire; Science-Based Medicine: New Haven, CT, USA, 2016. [Google Scholar]
- Litscher, G.; Cho, Z.H. Computer-Controlled Acupuncture; Pabst Science Publishers: Lengerich, Germany, 2000. [Google Scholar]
- Litscher, G.; Schwarz, G.; Sandner-Kiesling, A. Computer-controlled acupuncture. AKU 1998, 26, 133–142. [Google Scholar]
- Litscher, G.; Schwarz, G.; Sandner-Kiesling, A.; Hadolt, I. Transcranial Doppler sonography robotic-controlled sensors for quantification of the effects of acupuncture. DZA 1998, 3, 3–70. [Google Scholar]
- Litscher, G. Robot-assisted acupuncture a technology for the 21st century? Acupunct. Auricular Med. 2017, 4, 9–10. [Google Scholar]








| Method | Angle-aware | Shape-aware | Reference Model | Estimation | Limitation |
|---|---|---|---|---|---|
| Chang et al. [2] | No | No | 2D | Using cun measurement system by first converting pixel into cun | 1) Assuming that the hairline is not covered with hair 2) Does not work for side face |
| Jiang et al. [3] | Partially | No | 2D | Scaling of the reference model | 1) The scaling factor is based on the bounding box ratio returned by the edge detector, which can be unreliable 2) Does not work for side face |
| Proposed system | Yes | Yes | 3D | 3DMM, weighted deformation, landmarks | Need landmark points |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, K.-C.; Litscher, G. Robot-Controlled Acupuncture—An Innovative Step towards Modernization of the Ancient Traditional Medical Treatment Method. Medicines 2019, 6, 87. https://doi.org/10.3390/medicines6030087
Lan K-C, Litscher G. Robot-Controlled Acupuncture—An Innovative Step towards Modernization of the Ancient Traditional Medical Treatment Method. Medicines. 2019; 6(3):87. https://doi.org/10.3390/medicines6030087
Chicago/Turabian StyleLan, Kun-Chan, and Gerhard Litscher. 2019. "Robot-Controlled Acupuncture—An Innovative Step towards Modernization of the Ancient Traditional Medical Treatment Method" Medicines 6, no. 3: 87. https://doi.org/10.3390/medicines6030087
APA StyleLan, K.-C., & Litscher, G. (2019). Robot-Controlled Acupuncture—An Innovative Step towards Modernization of the Ancient Traditional Medical Treatment Method. Medicines, 6(3), 87. https://doi.org/10.3390/medicines6030087







