The Nematic Chiral Liquid Crystal Structure of the Cardiac Myoarchitecture: Disclinations and Topological Singularities
Abstract
:1. Introduction
2. Material and Methods
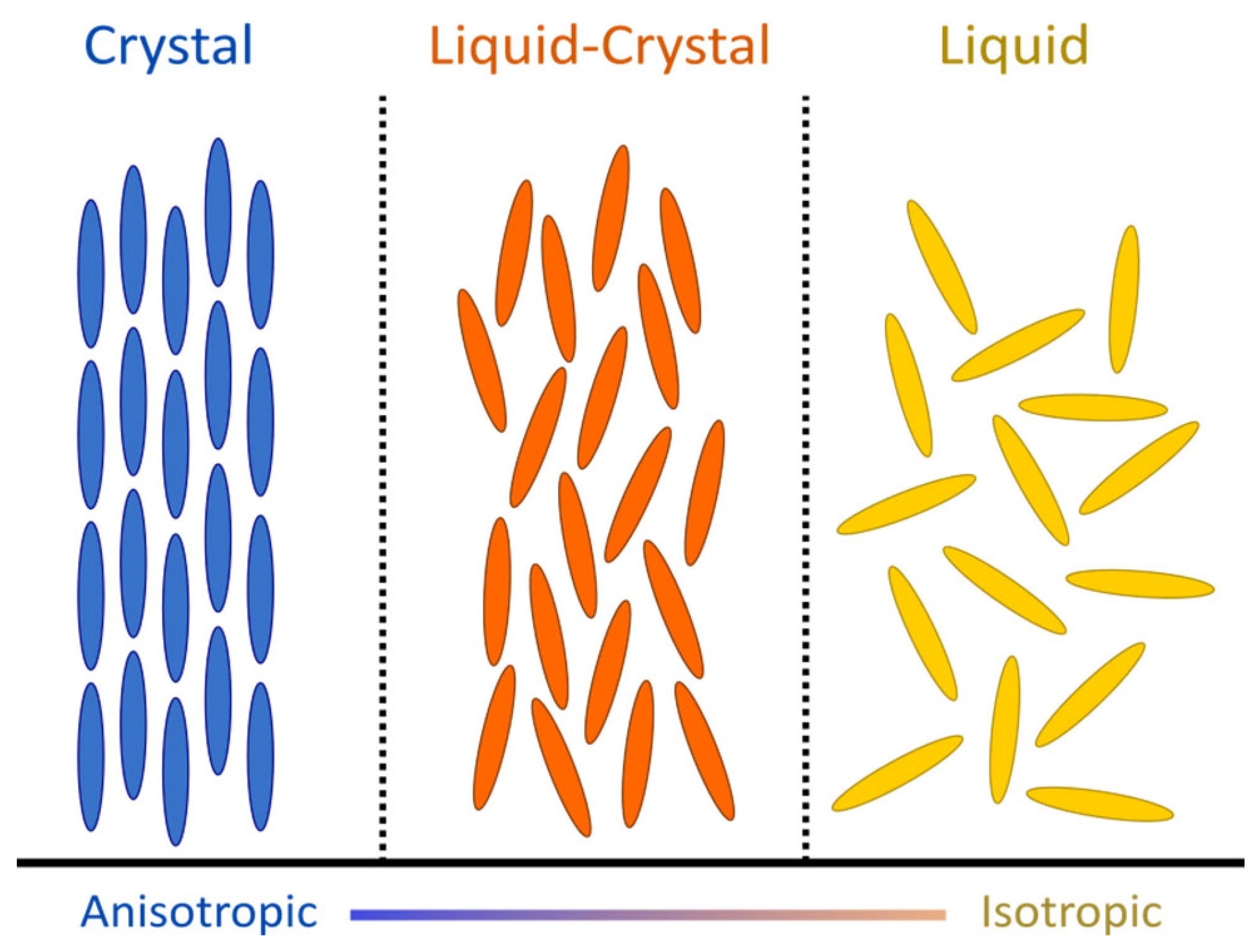
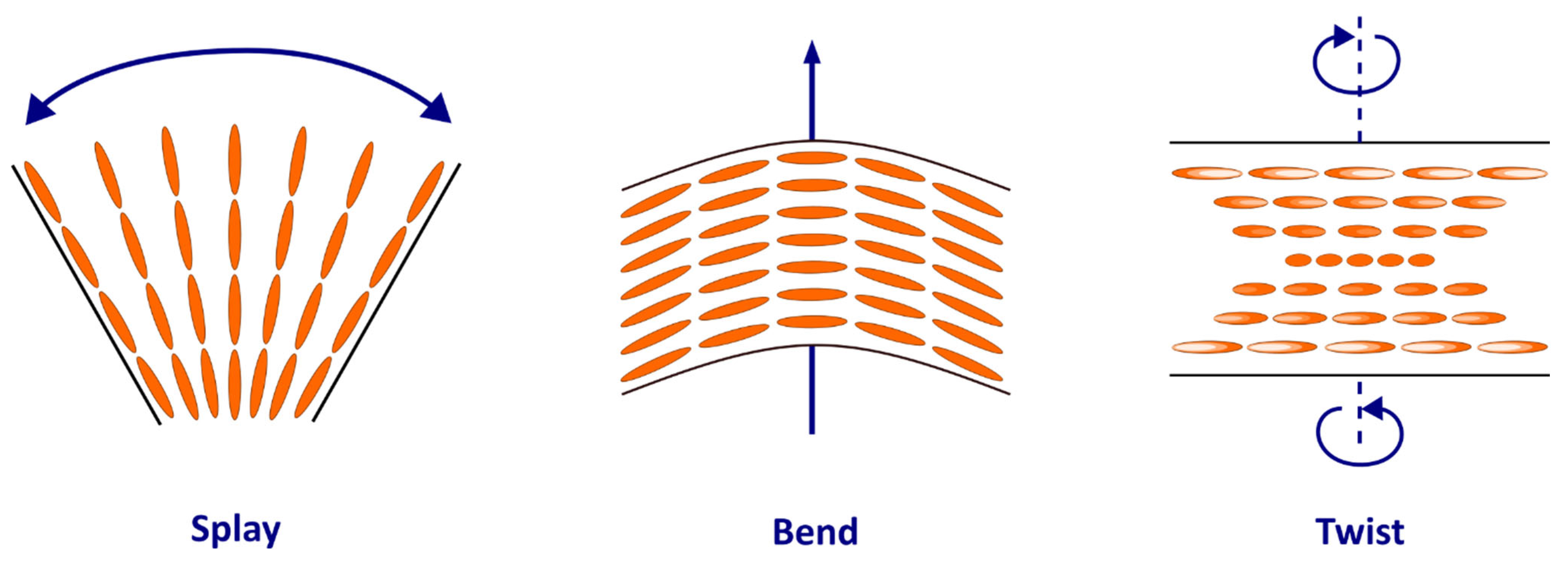
2.1. Physical Context: Liquid Crystals and Disclinations
2.2. Myocardial Material
2.3. Histology, Myocardial Maps, and Disclination Identification
2.4. Patient’s Characteristics
3. Results
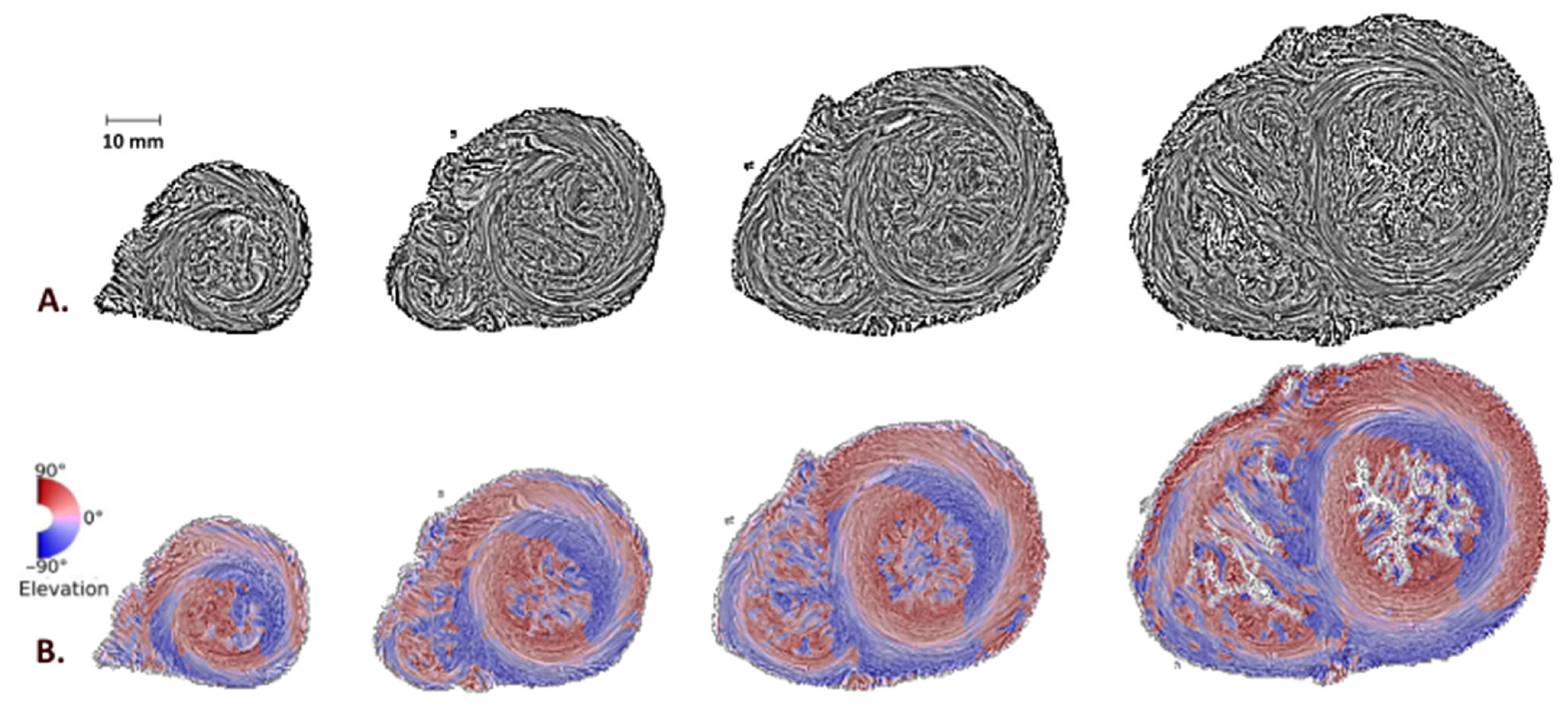
3.1. Disclination Identification
3.2. Left and Right Ventricular Connections to the IVS and “−1/2 Disclination”
3.3. Apex and “+1 Disclination”
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Hirst, L.S.; Charras, G. Liquid Crystals in Living Tissue. Nature 2017, 544, 164–165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tan, T.H.; Mietke, A.; Li, J.; Chen, Y.; Higinbotham, H.; Foster, P.J.; Gokhale, S.; Dunkel, J.; Fakhri, N. Odd Dynamics of Living Chiral Crystals. Nature 2022, 607, 287–293. [Google Scholar] [CrossRef] [PubMed]
- Saw, T.B.; Doostmohammadi, A.; Nier, V.; Kocgozlu, L.; Thampi, S.; Toyama, Y.; Marcq, P.; Lim, C.T.; Yeomans, J.M.; Ladoux, B. Topological Defects in Epithelia Govern Cell Death and Extrusion. Nature 2017, 544, 212–216. [Google Scholar] [CrossRef] [Green Version]
- Kawaguchi, K.; Kageyama, R.; Sano, M. Topological Defects Control Collective Dynamics in Neural Progenitor Cell Cultures. Nature 2017, 545, 327–331. [Google Scholar] [CrossRef] [PubMed]
- Jouk, P.-S.; Usson, Y. The Myosin Myocardial Mesh Interpreted as a Biological Analogous of Nematic Chiral Liquid Crystals. J. Cardiovasc. Dev. Dis. 2021, 8, 179. [Google Scholar] [CrossRef]
- Volterra, V. Sur l’équilibre des corps élastiques multiplement connexes. Ann. Sci. L’école Norm. Supérieure 1907, 24, 401–517. [Google Scholar] [CrossRef] [Green Version]
- de Gennes, P.-G.; Prost, J. The Physics of Liquid Crystals, 2nd ed.; International series of monographs on physics; Clarendon Press: Oxford, UK, 1993; ISBN 978-0-19-851785-6. [Google Scholar]
- Kleman, M. Défauts dans les cristaux liquides. Bull. Minéralogie 1972, 95, 215–230. [Google Scholar] [CrossRef]
- Kleman, M.; Friedel, J. Disclinations, Dislocations, and Continuous Defects: A Reappraisal. Rev. Mod. Phys. 2008, 80, 61. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Teran, M.A.; Hurle, J.M. Myocardial Fiber Architecture of the Human Heart Ventricles. Anat. Rec. 1982, 204, 137–147. [Google Scholar] [CrossRef]
- Sanchez-Quintana, D.; Garcia-Martinez, V.; Climent, V.; Hurle, J.M. Morphological Changes in the Normal Pattern of Ventricular Myoarchitecture in the Developing Human Heart. Anat. Rec. 1995, 243, 483–495. [Google Scholar] [CrossRef]
- Norvez, S. Les cristaux liquides. J. Phys. Théorique Appliquée 1909, 8, 713–735. [Google Scholar] [CrossRef]
- Mitov, M. Cholesteric Liquid Crystals in Living Matter. Soft Matter 2017, 13, 4176–4209. [Google Scholar] [CrossRef]
- Jouk, P.S.; Usson, Y.; Michalowicz, G.; Grossi, L. Three-Dimensional Cartography of the Pattern of the Myofibres in the Second Trimester Fetal Human Heart. Anat. Embryol. 2000, 202, 103–118. [Google Scholar] [CrossRef]
- Usson, Y.; Parazza, F.; Jouk, P.S.; Michalowicz, G. Method for the Study of the Three-Dimensional Orientation of the Nuclei of Myocardial Cells in Fetal Human Heart by Means of Confocal Scanning Laser Microscopy. J. Microsc. 1994, 174, 101–110. [Google Scholar] [CrossRef]
- Friedel, G. Les états mésomorphes de la matière. Ann. Phys. 1922, 9, 273–474. [Google Scholar] [CrossRef]
- Harris, W.F. Disclinations. Sci. Am. 1977, 237, 130–145. [Google Scholar] [CrossRef]
- Tang, X.; Selinger, J.V. Orientation of Topological Defects in 2D Nematic Liquid Crystals. Soft Matter 2017, 13, 5481–5490. [Google Scholar] [CrossRef] [Green Version]
- Aouini, A. Cristaux Liquides Nématiques de Type Twist-Bend-Mécanismes de Commutation et Applications. Ph.D. Thesis, Ecole nationale supérieure Mines-Télécom Atlantique, Brest, France, 2020. [Google Scholar]
- Jouk, P.-S.; Truong, B.L.; Michalowicz, G.; Usson, Y. Postnatal Myocardium Remodelling Generates Inhomogeneity in the Architecture of the Ventricular Mass. Surg. Radiol. Anat. 2018, 40, 75–83. [Google Scholar] [CrossRef] [Green Version]
- Jouk, P.-S.; Mourad, A.; Milisic, V.; Michalowicz, G.; Raoult, A.; Caillerie, D.; Usson, Y. Analysis of the Fiber Architecture of the Heart by Quantitative Polarized Light Microscopy. Accuracy, Limitations and Contribution to the Study of the Fiber Architecture of the Ventricles during Fetal and Neonatal Life. Eur. J. Cardio Thorac. Surg. 2007, 31, 915–921. [Google Scholar] [CrossRef]
- Morales-Navarrete, H.; Nonaka, H.; Scholich, A.; Segovia-Miranda, F.; de Back, W.; Meyer, K.; Bogorad, R.L.; Koteliansky, V.; Brusch, L.; Kalaidzidis, Y.; et al. Liquid-Crystal Organization of Liver Tissue. eLife 2019, 8, e44860. [Google Scholar] [CrossRef]
- Turiv, T.; Krieger, J.; Babakhanova, G.; Yu, H.; Shiyanovskii, S.V.; Wei, Q.-H.; Kim, M.-H.; Lavrentovich, O.D. Topology Control of Human Fibroblast Cells Monolayer by Liquid Crystal Elastomer. Sci. Adv. 2020, 6, eaaz6485. [Google Scholar] [CrossRef]
- Bouligand, Y. Sur L’existence de “Pseudomorphoses Cholestériques” Chez Divers Organismes Vivants. J. Phys. Colloq. 1969, 30, C4-90–C4-103. [Google Scholar] [CrossRef]
- Duvert, M.; Bouligand, Y.; Salat, C. The Liquid Crystalline Nature of the Cytoskeleton in Epidermal Cells of the Chaetognath Sagitta. Tissue Cell 1984, 16, 469–481. [Google Scholar] [CrossRef]
- Streeter, D.D., Jr. Gross Morphology and Fiber Geometry of the Heart. In Handbook of Physiology; Section 2: The Cardiovascular System; Williams and Wilkins: Bethesda, MD, USA, 1979; Volume 1, pp. 61–112. ISBN 0-683-00605-3. [Google Scholar]
- Hoffman, J.I.E. Will the Real Ventricular Architecture Please Stand Up? Physiol. Rep. 2017, 5, e13404. [Google Scholar] [CrossRef]
- Anderson, R.H.; Ho, S.Y.; Redmann, K.; Sanchez-Quintana, D.; Lunkenheimer, P.P. The Anatomical Arrangement of the Myocardial Cells Making up the Ventricular Mass. Eur. J. Cardio Thorac. Surg. 2005, 28, 517–525. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torrent-Guasp, F.; Buckberg, G.D.; Clemente, C.; Cox, J.L.; Coghlan, H.C.; Gharib, M. The Structure and Function of the Helical Heart and Its Buttress Wrapping. I. The Normal Macroscopic Structure of the Heart. Semin. Thorac. Cardiovasc. Surg. 2001, 13, 301–319. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, E.; Smerup, M.; Agger, P.; Frandsen, J.; Ringgard, S.; Pedersen, M.; Vestergaard, P.; Nyengaard, J.R.; Andersen, J.B.; Lunkenheimer, P.P.; et al. Normal Right Ventricular Three-Dimensional Architecture, as Assessed with Diffusion Tensor Magnetic Resonance Imaging, Is Preserved during Experimentally Induced Right Ventricular Hypertrophy. Anat. Rec. 2009, 292, 640–651. [Google Scholar] [CrossRef] [PubMed]




| Perinatal Hearts (>22 Weeks of Gestation or <1 Week of Life) | Early Infant Hearts (>1 Week of Life) | |
|---|---|---|
| Total, n | 11 | 7 |
| Sex, n Female Male Missing data | 4 5 2 | 2 4 1 |
| Gestational age, weeks Median (min–max) | 38 (29–41) | 39 (33–40) |
| In utero death, n | 5 | NA |
| Weeks of life when born alive Median (min–max) | 0.3 (0.1–0.4) | 30 (4–80) |
| Ventricular weight, g median (min–max) | 14.1 (7.6–19.2) | 34 (11.7–46.5) |
| Number of cardiac sections, n Median (min–max) | 32 (26–40) | 42 (31–51) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Auriau, J.; Usson, Y.; Jouk, P.-S. The Nematic Chiral Liquid Crystal Structure of the Cardiac Myoarchitecture: Disclinations and Topological Singularities. J. Cardiovasc. Dev. Dis. 2022, 9, 371. https://doi.org/10.3390/jcdd9110371
Auriau J, Usson Y, Jouk P-S. The Nematic Chiral Liquid Crystal Structure of the Cardiac Myoarchitecture: Disclinations and Topological Singularities. Journal of Cardiovascular Development and Disease. 2022; 9(11):371. https://doi.org/10.3390/jcdd9110371
Chicago/Turabian StyleAuriau, Johanne, Yves Usson, and Pierre-Simon Jouk. 2022. "The Nematic Chiral Liquid Crystal Structure of the Cardiac Myoarchitecture: Disclinations and Topological Singularities" Journal of Cardiovascular Development and Disease 9, no. 11: 371. https://doi.org/10.3390/jcdd9110371
APA StyleAuriau, J., Usson, Y., & Jouk, P.-S. (2022). The Nematic Chiral Liquid Crystal Structure of the Cardiac Myoarchitecture: Disclinations and Topological Singularities. Journal of Cardiovascular Development and Disease, 9(11), 371. https://doi.org/10.3390/jcdd9110371







