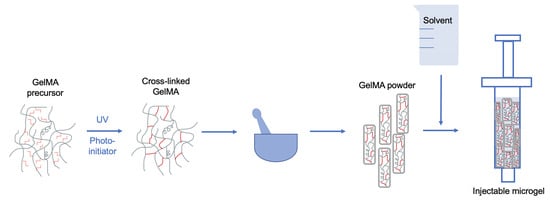
Powdered Cross-Linked Gelatin Methacryloyl as an Injectable Hydrogel for Adipose Tissue Engineering
Abstract
:1. Introduction
2. Results and Discussion
2.1. Development and Characterization of the GelMA Precursors
2.1.1. Degree of Substitution (DS)
2.1.2. Molar Mass (MM)
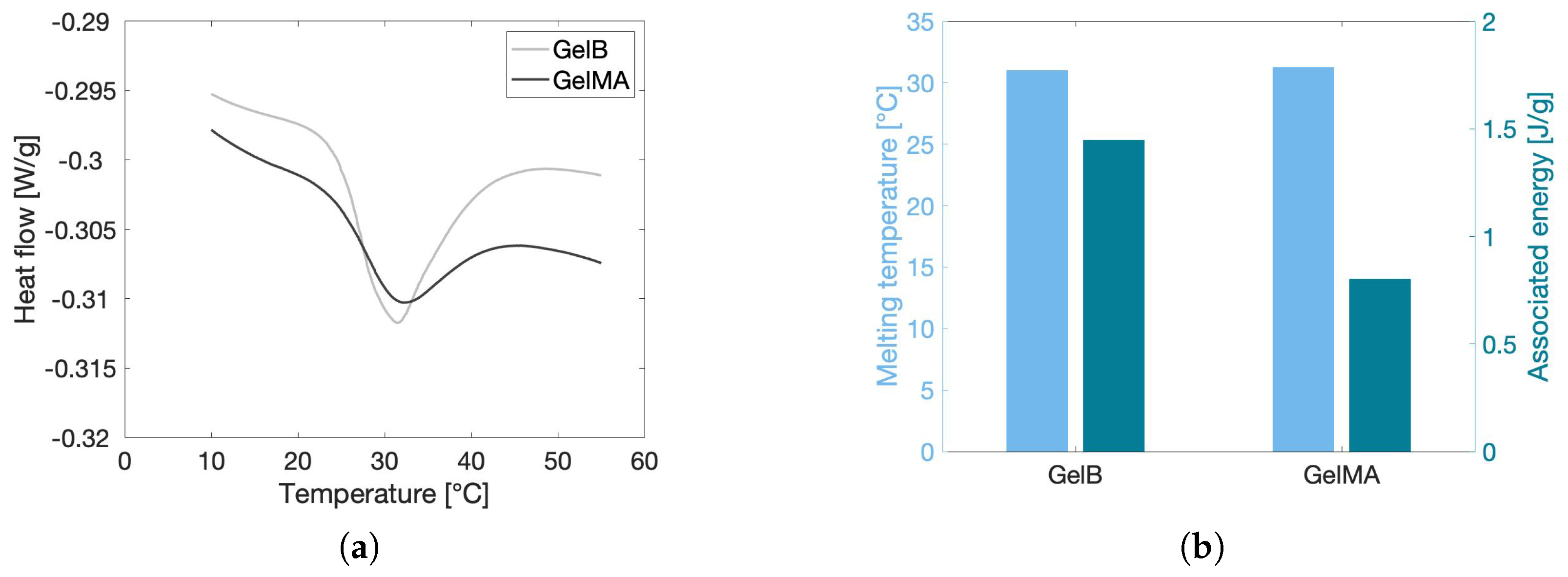
2.1.3. Melting Temperature and Enthalpy
2.2. Characterization of the GelMA Powder Particles and the Resulting Microgel
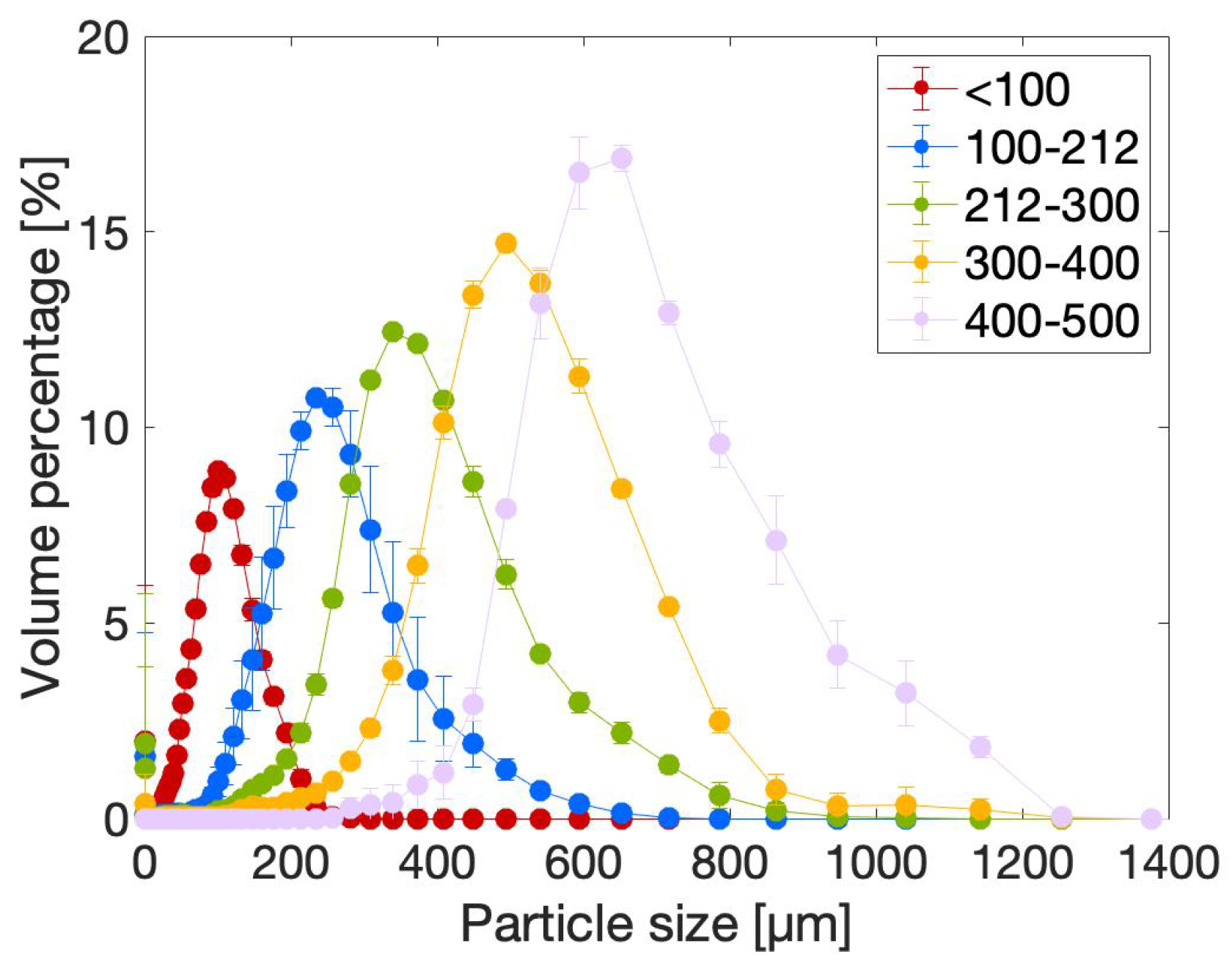
2.2.1. Particle Size Distribution (PSD)
2.2.2. Particle Aspect Ratio
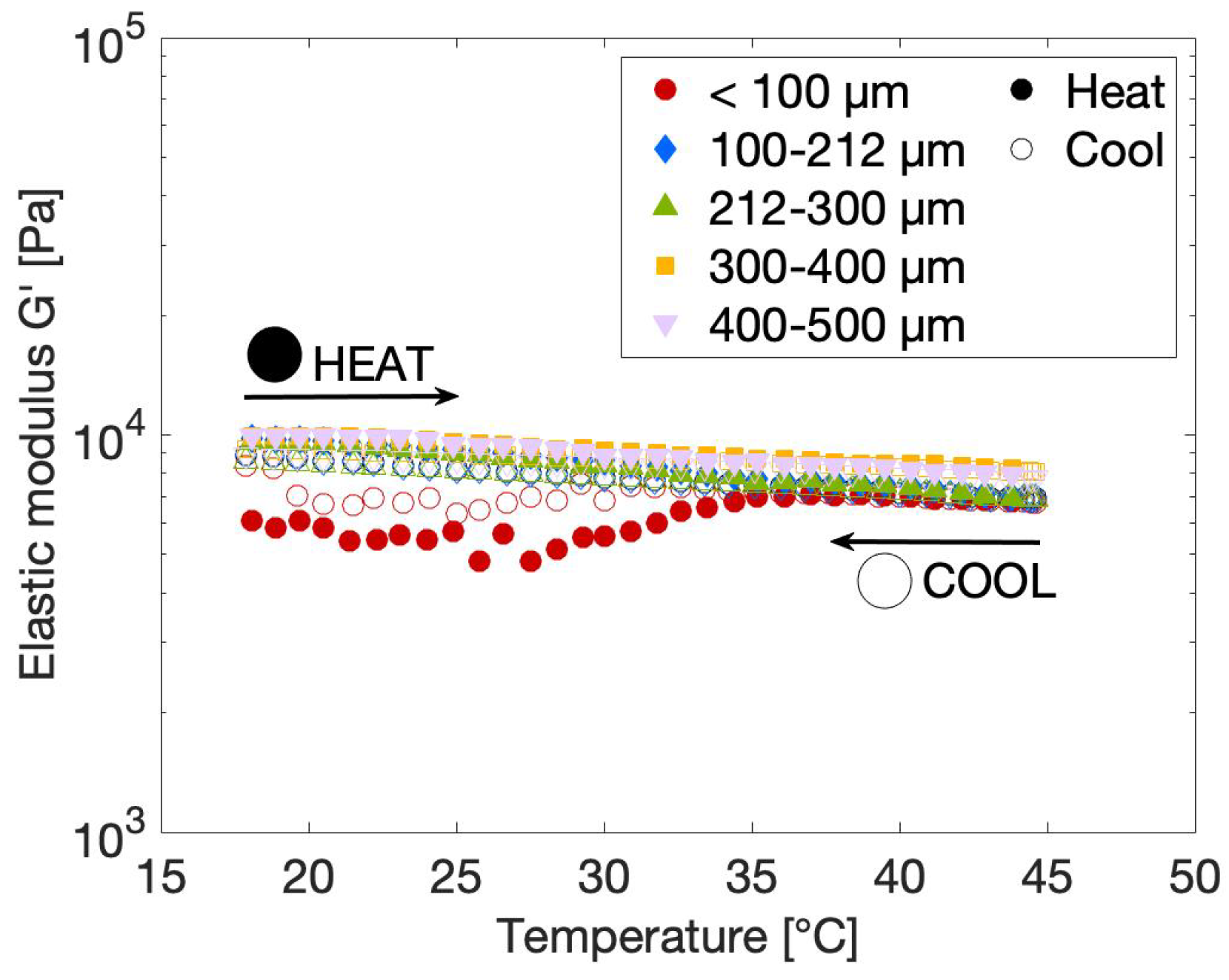
2.2.3. Effect of Particle Size on the Rheological Gel Properties
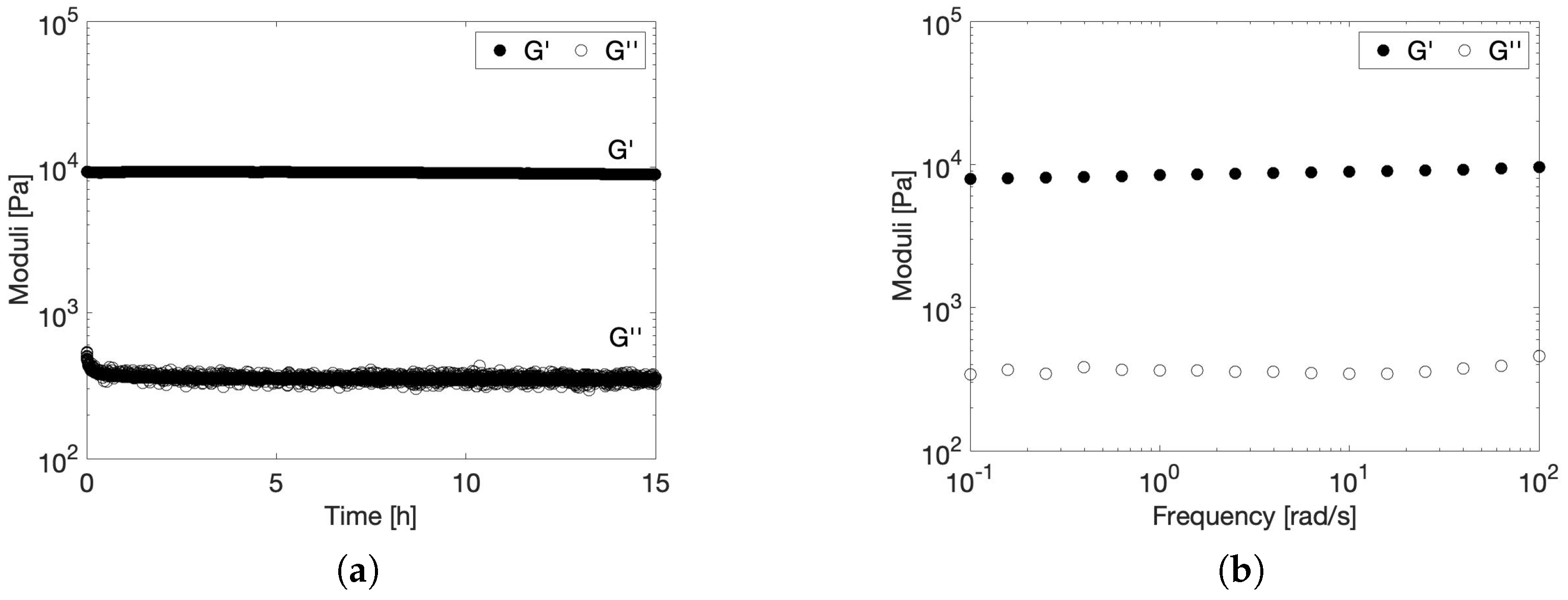
2.3. Stability of the Viscoelastic Gel at Physiological Conditions
2.3.1. Effect of Temperature on the Rheological Gel Properties
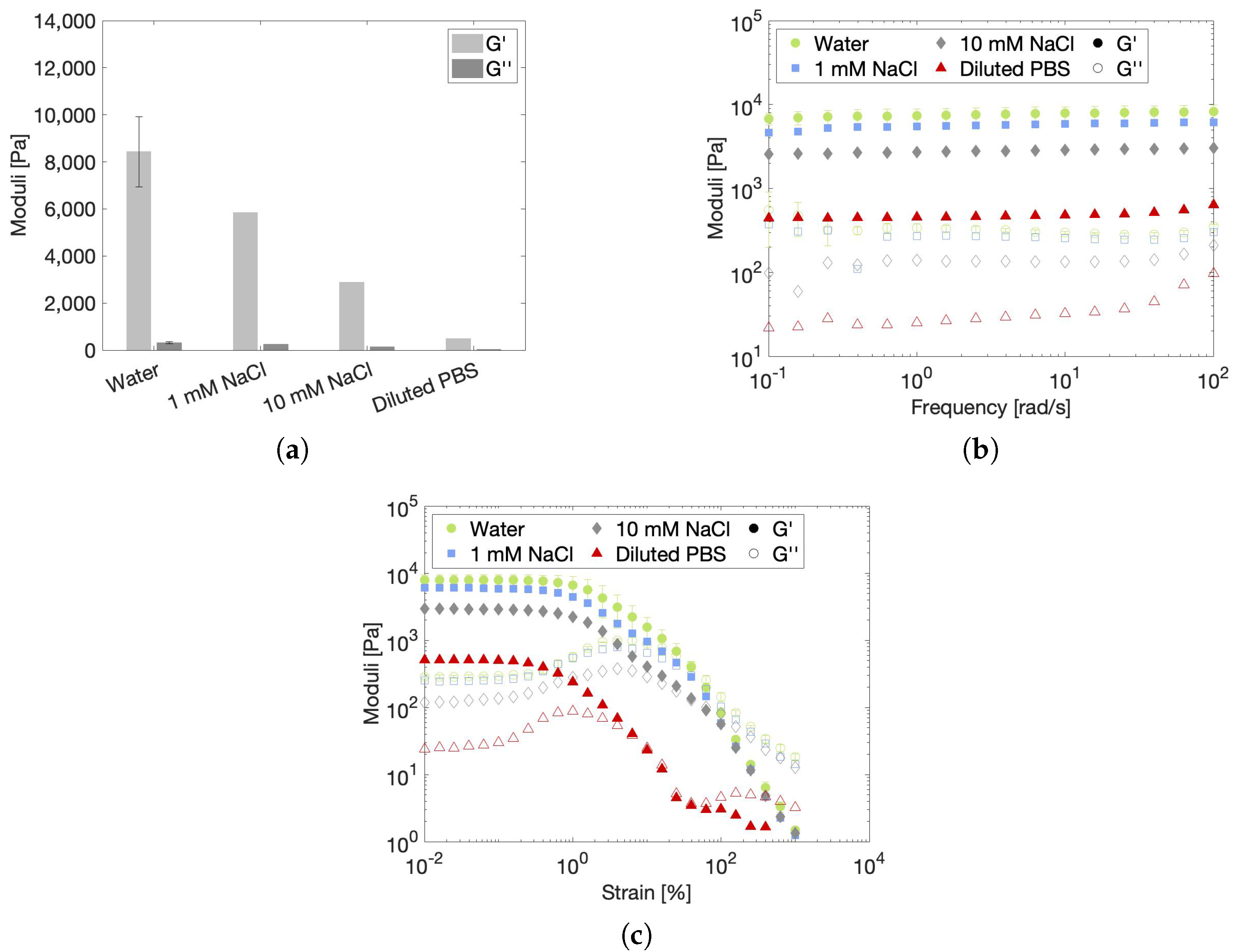
2.3.2. Effect of Ionic Strength on the Rheological Gel Properties
2.4. Characterization of the Microgel Structural Properties
2.4.1. Volume Fraction
2.4.2. Individual Particle Deformability
2.4.3. Helix Denaturation and Zeta Potential
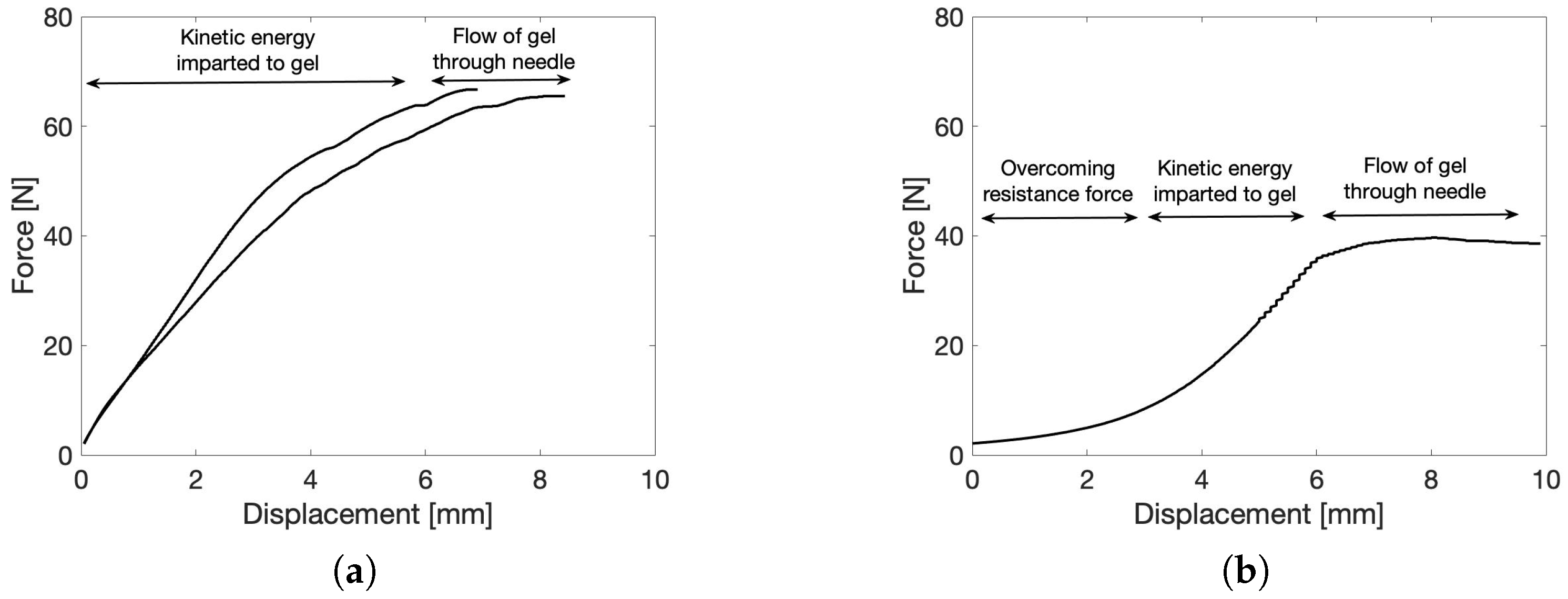
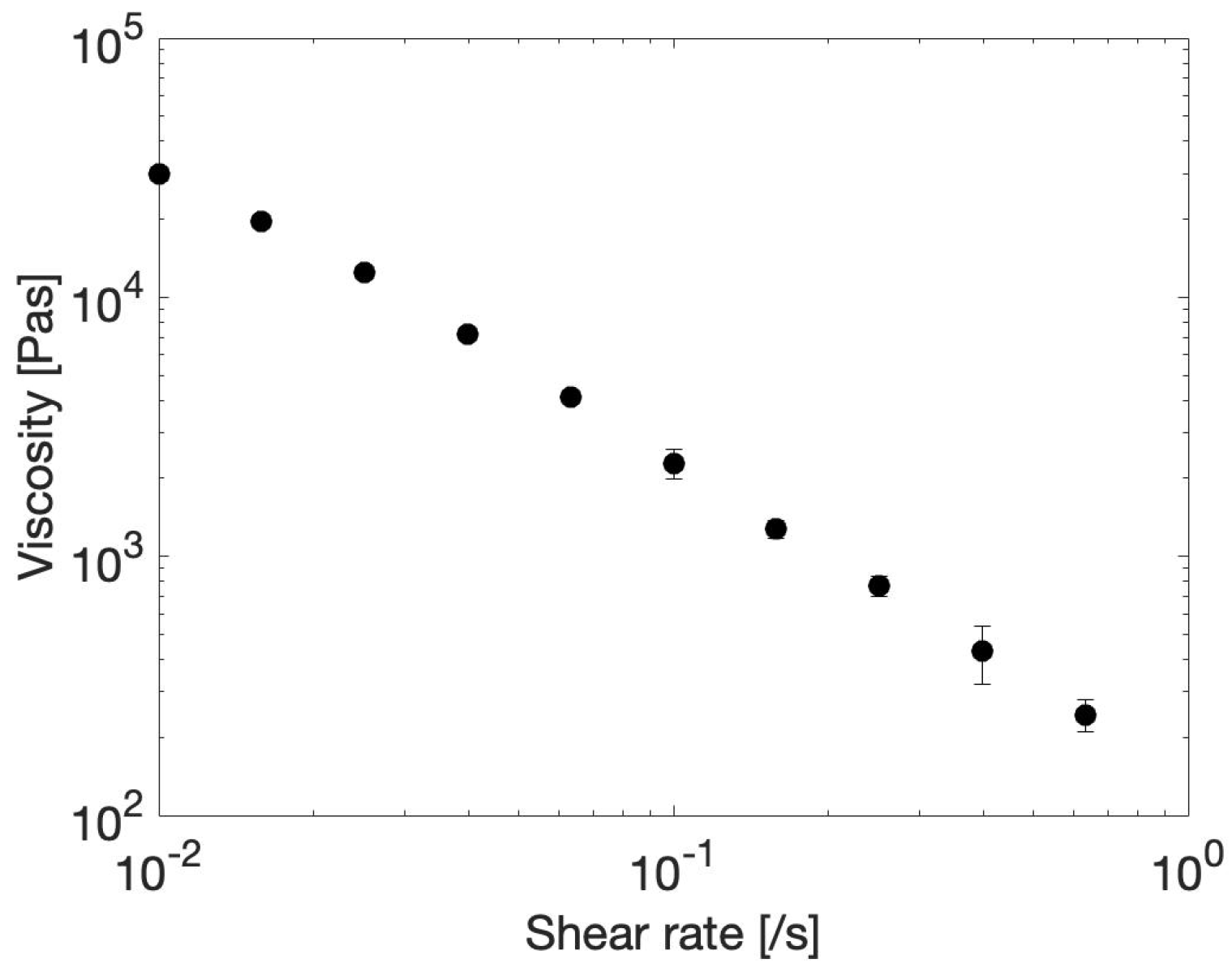
2.5. Injectability of the Gel
2.5.1. Force–Displacement Measurement
2.5.2. Flow Sweep
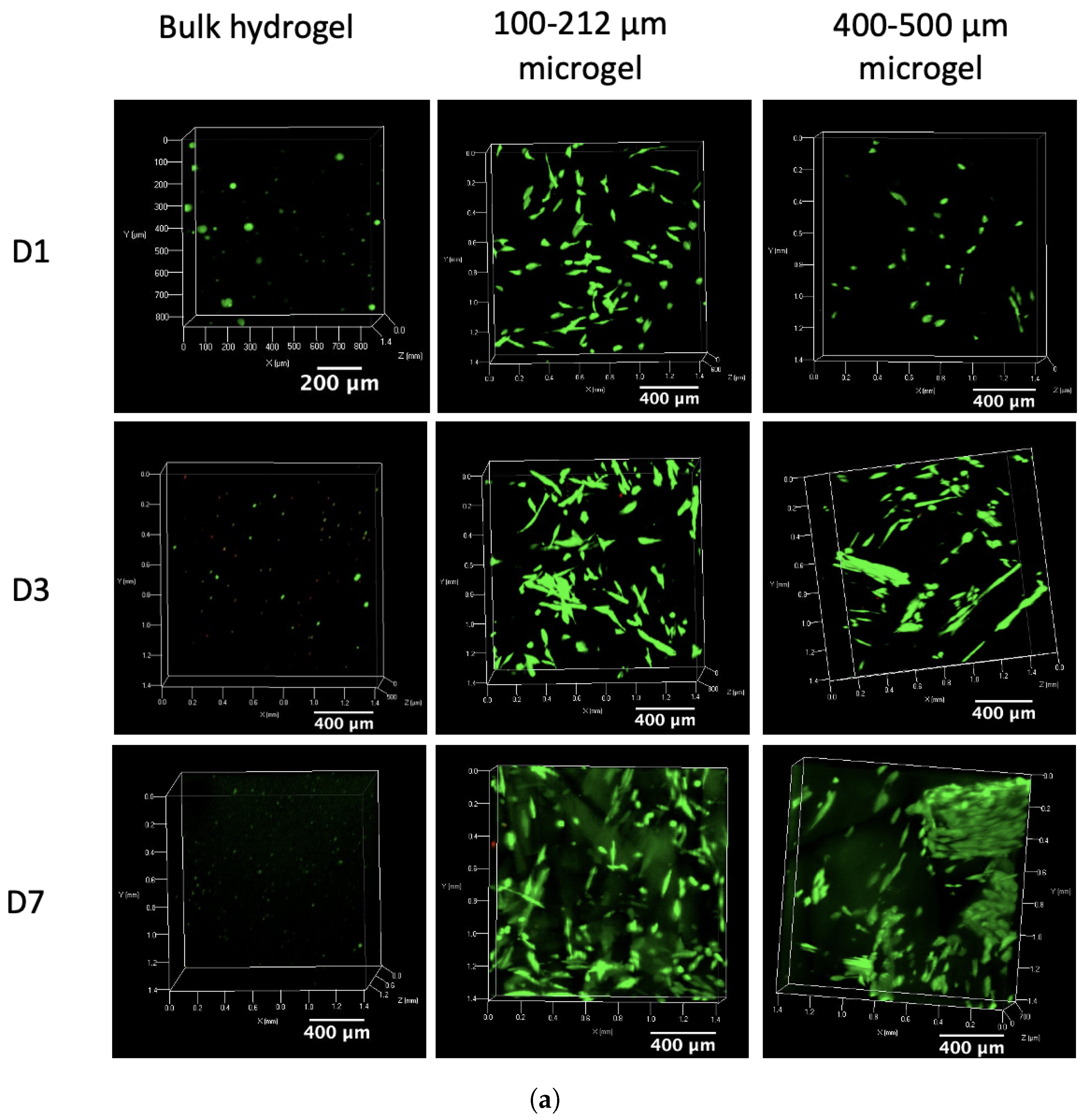
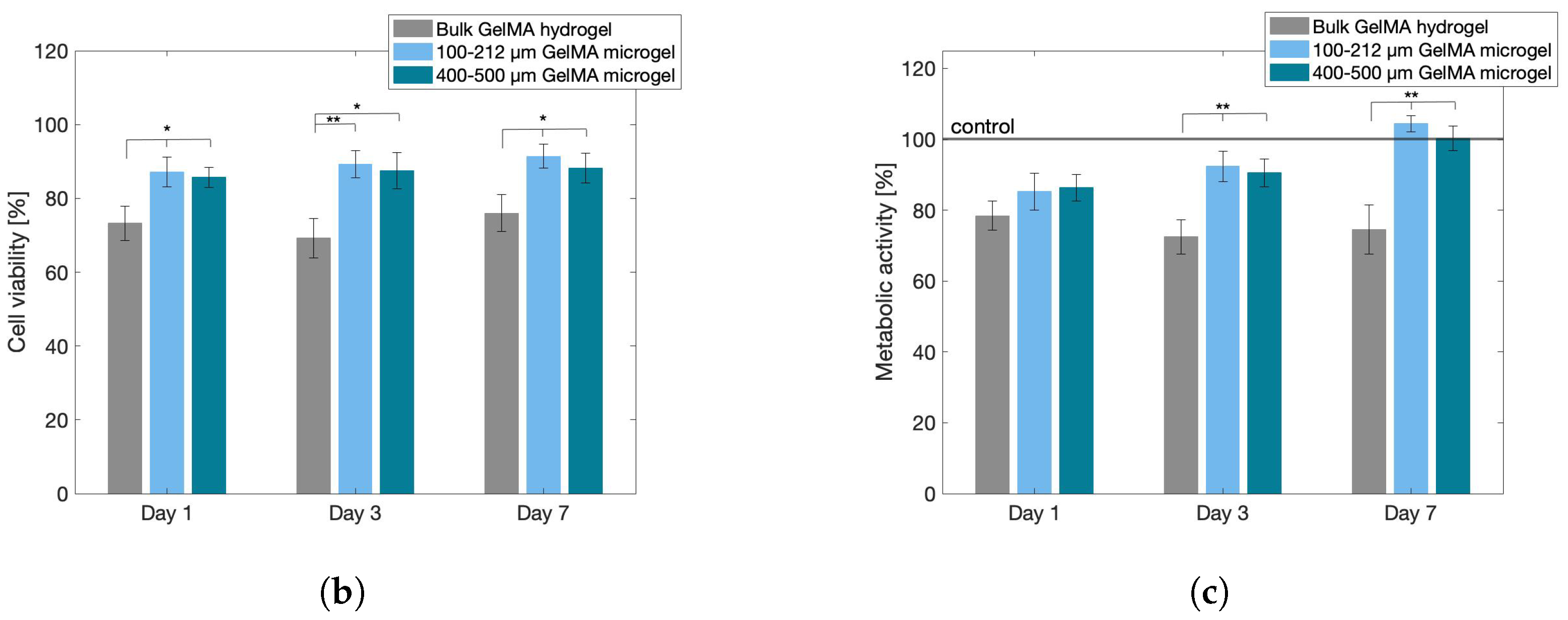
2.6. Cytocompatibility Assays
3. Conclusions
4. Materials and Methods
4.1. Materials
4.2. Synthesis of Gelatin Methacryloyl
4.3. Characterization of GelMA Precursors
4.3.1. Gel Permeation Chromatography (GPC)
4.3.2. Differential Scanning Calorimetry (DSC)
4.4. Processing into Swellable Powder
4.5. Rheological Characterization
4.6. Structural Characterization
4.6.1. Laser Diffraction
4.6.2. Micromechanics
4.6.3. Circular Dichroism (CD)
4.6.4. Zeta Potential
4.7. Injectability: Force–Displacement Measurement
4.8. Cytocompatibility
4.8.1. Live/Dead Assay
4.8.2. MTS Assay
4.9. Statistics
5. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASCs | Adipose tissue-derived stem cells |
| BSA | Bovine serum albumin |
| calcein-AM | calcein-acetoxymethyl |
| CD | Circular dichroism |
| DMEM | Dulbecco’s modified Eagle’s medium |
| DNA | Deoxyribonucleic acid |
| DS | Degree of substitution |
| DSC | Differential scanning calorimetry |
| ECM | Extracellular matrix |
| FBS | Fetal bovine serum |
| GelB | Gelatin type B |
| GelMA | Gelatin methacryloyl |
| GFP | Green fluorescent protein |
| GPC | Gel permeation chromatography |
| HUVECs | Human umbilical vein endothelial cells |
| LAP | Lithium phenyl-2,4,6-trimethylbenzoylphosphinate |
| LVE | Linear viscoelastic |
| MA | Methacryloyl |
| MM | Molar mass |
| MTS | 3-(4,5-dimethylthiazol-2-yl)-5-(3-carboxymethoxyphenyl)- |
| 2-(4-sulfophenyl)-2H-tetrazolium | |
| NMR | Nuclear magnetic spectroscopy |
| PBS | Phosphate buffered saline |
| PI | Propidium iodide |
| PSD | Particle size distribution |
| RGD | Arg-Gly-Asp amino acid triplet |
| ROS | Reactive oxygen species |
| TE | Tissue engineering |
| TxRed | Texas Red |
| UCST | Upper critical solution temperature |
| UV | Ultraviolet |
References
- Patrick, C.W.; Mikos, A.G.; McIntire, L.V. Frontiers in Tissue Engineering, 1st ed.; Pergamon: Oxford, UK, 1998. [Google Scholar]
- Simonacci, F.; Bertozzi, N.; Grieco, M.P.; Grignaffini, E.; Raposio, E. Procedure, applications, and outcomes of autologous fat grafting. Ann. Med. Surg. 2017, 20, 49–60. [Google Scholar] [CrossRef] [PubMed]
- Patrick, C.W. Tissue engineering strategies for adipose tissue repair. Anat. Rec. 2001, 263, 361–366. [Google Scholar] [CrossRef] [PubMed]
- Sterodimas, A.; de Faria, J.; Nicaretta, B.; Pitanguy, I. Tissue engineering with adipose-derived stem cells (ADSCs): Current and future applications. J. Plast. Reconstr. Aesthetic Surg. 2009, 63, 1886–1892. [Google Scholar] [CrossRef] [PubMed]
- Van Damme, L.; Blondeel, P.; Van Vlierberghe, S. Injectable biomaterials as minimal invasive strategy towards soft tissue regeneration—An overview. J. Phys.-Mater. 2021, 4, 22001. [Google Scholar] [CrossRef]
- Van Nieuwenhove, I.; Tytgat, L.; Ryx, M.; Blondeel, P.; Stillaert, F.; Thienpont, H.; Ottevaere, H.; Dubruel, P.; Van Vlierberghe, S. Soft tissue fillers for adipose tissue regeneration: From hydrogel development toward clinical applications. Acta Biomater. 2017, 63, 37–49. [Google Scholar] [CrossRef]
- Tanzi, M.C.; Farè, S. Adipose tissue engineering: State of the art, recent advances and innovative approaches. Expert Rev. Med. Devices 2009, 6, 533–551. [Google Scholar] [CrossRef]
- Sivashanmugam, A.; Arun Kumar, R.; Vishnu Priya, M.; Nair, S.V.; Jayakumar, R. An overview of injectable polymeric hydrogels for tissue engineering. Eur. Polym. J. 2015, 72, 543–565. [Google Scholar] [CrossRef]
- Mano, J.F.; Silva, G.A.; Azevedo, H.S.; Malafaya, P.B.; Sousa, R.A.; Silva, S.S.; Boesel, L.F.; Oliveira, J.M.; Santos, T.C.; Marques, A.P.; et al. Natural origin biodegradable systems in tissue engineering and regenerative medicine: Present status and some moving trends. J. R. Soc. Interface 2007, 4, 999–1030. [Google Scholar] [CrossRef]
- Gorgieva, S.; Kokol, V. Collagen- vs. Gelatine-Based Biomaterials and Their Biocompatibility: Review and Perspectives. In Biomaterials Applications for Nanomedicine; Pignatello, R., Ed.; InTech: London, UK, 2011; Chapter 2; pp. 17–52. [Google Scholar]
- Ruoslahti, E. RGD and Other Recognition Sequences for Integrins. Annu. Rev. Cell Dev. Biol. 1996, 12, 697–715. [Google Scholar] [CrossRef]
- Yang, G.; Xiao, Z.; Long, H.; Ma, K.; Zhang, J.; Ren, X.; Zhang, J. Assessment of the characteristics and biocompatibility of gelatin sponge scaffolds prepared by various crosslinking methods. Sci. Rep. 2018, 8, 1616. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Xiao, Z.; Ren, X.; Long, H.; Qian, H.; Ma, K.; Guo, Y. Enzymatically crosslinked gelatin hydrogel promotes the proliferation of adipose tissue-derived stromal cells. PeerJ 2016, 4, e2497. [Google Scholar] [CrossRef]
- Van Den Bulcke, A.I.; Bogdanov, B.; De Rooze, N.; Schacht, E.H.; Cornelissen, M.; Berghmans, H. Structural and Rheological Properties of Methacrylamide Modified Gelatin Hydrogels. Biomacromolecules 2000, 1, 31–38. [Google Scholar] [CrossRef]
- Colle, J.; Blondeel, P.; De Bruyne, A.; Bochar, S.; Tytgat, L.; Vercruysse, C.; Van Vlierberghe, S.; Dubruel, P.; Declercq, H. Bioprinting predifferentiated adipose-derived mesenchymal stem cell spheroids with methacrylated gelatin ink for adipose tissue engineering. J. Mater. Sci. Mater. Med. 2020, 31, 36. [Google Scholar] [CrossRef]
- De Moor, L.; Smet, J.; Plovyt, M.; Bekaert, B.; Vercruysse, C.; Asadian, M.; De Geyter, N.; Van Vlierberghe, S.; Dubruel, P.; Declercq, H. Engineering microvasculature by 3D bioprinting of prevascularized spheroids in photo-crosslinkable gelatin. Biofabrication 2021, 13, 45021. [Google Scholar] [CrossRef] [PubMed]
- Piao, Y.; You, H.; Xu, T.; Bei, H.P.; Piwko, I.Z.; Kwan, Y.Y.; Zhao, X. Biomedical applications of gelatin methacryloyl hydrogels. Eng. Regen. 2021, 2, 47–56. [Google Scholar] [CrossRef]
- Yue, K.; Trujillo-de Santiago, G.; Alvarez, M.M.; Tamayol, A.; Annabi, N.; Khademhosseini, A. Synthesis, properties, and biomedical applications of gelatin methacryloyl (GelMA) hydrogels. Biomaterials 2015, 73, 254–271. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Liu, S.; Yildirimer, L.; Zhao, H.; Ding, R.; Wang, H.; Cui, W.; Weitz, D. Injectable Stem Cell-Laden Photocrosslinkable Microspheres Fabricated Using Microfluidics for Rapid Generation of Osteogenic Tissue Constructs. Adv. Funct. Mater. 2016, 26, 2809–2819. [Google Scholar] [CrossRef]
- Zoratto, N.; Di Lisa, D.; Rutte, J.; Sakib, M.N.; Alves e Silva, A.R.; Tamayol, A.; Di Carlo, D.; Khademhosseini, A.; Sheikhi, A. In situ forming microporous gelatin methacryloyl hydrogel scaffolds from thermostable microgels for tissue engineering. Bioeng. Transl. Med. 2020, 5, e10180. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, H.; Li, J. Recent advances on gelatin methacrylate hydrogels with controlled microstructures for tissue engineering. Int. J. Biol. Macromol. 2022, 221, 91–107. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Zhang, Q.; Xie, L.; Zhang, R.; Qian, R.; Tian, Y.; Chen, G.; Tian, W. hDPSC-laden GelMA microspheres fabricated using electrostatic microdroplet method for endodontic regeneration. Mater. Sci. Eng. C- Biol. Appl. 2021, 121, 111850. [Google Scholar] [CrossRef] [PubMed]
- Shewan, H.M.; Stokes, J.R. Viscosity of soft spherical micro-hydrogel suspensions. J. Colloid Interface Sci. 2015, 442, 75–81. [Google Scholar] [CrossRef]
- Nikolov, S.V.; Fernandez-Nieves, A.; Alexeev, A. Behavior and mechanics of dense microgel suspensions. Proc. Natl. Acad. Sci. USA 2020, 117, 27096–27103. [Google Scholar] [CrossRef]
- Cloitre, M.; Borrega, R.; Monti, F.; Leibler, L. Structure and flow of polyelectrolyte microgels: From suspensions to glasses. Comptes Rendus. Phys. 2003, 4, 221–230. [Google Scholar] [CrossRef]
- Senff, H.; Richtering, W. Influence of cross-link density on rheological properties of temperature-sensitive microgel suspensions. Colloid Polym. Sci. 2000, 278, 830–840. [Google Scholar] [CrossRef]
- Adams, S.; Frith, W.J.; Stokes, J.R. Influence of particle modulus on the rheological properties of agar microgel suspensions. J. Rheol. 2004, 48, 1195–1213. [Google Scholar] [CrossRef]
- Hashmi, S.M.; Dufresne, E.R. Mechanical properties of individual microgel particles through the deswelling transition. Soft Matter 2009, 5, 3682–3688. [Google Scholar] [CrossRef]
- Seth, J.R.; Cloitre, M.; Bonnecaze, R.T. Elastic properties of soft particle pastes. J. Rheol. 2006, 50, 353–376. [Google Scholar] [CrossRef]
- Daly, A.C.; Riley, L.; Segura, T.; Burdick, J.A. Hydrogel microparticles for biomedical applications. Nat. Rev. Mater. 2020, 5, 20–43. [Google Scholar] [CrossRef]
- Thiele, J.; Ma, Y.; Bruekers, S.M.C.; Ma, S.; Huck, W.T.S. 25th Anniversary Article: Designer Hydrogels for Cell Cultures: A Materials Selection Guide. Adv. Mater. 2013, 26, 125–148. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Yuan, X.; Zhao, Y.; Cai, Q.; Wang, Y.; Luo, R.; Yu, S.; Wang, Y.; Han, J.; Ge, L.; et al. Injectable GelMA Cryogel Microspheres for Modularized Cell Delivery and Potential Vascularized Bone Regeneration. Small 2021, 17, e2006596. [Google Scholar] [CrossRef]
- Wu, J.; Li, G.; Ye, T.; Lu, G.; Li, R.; Deng, L.; Wang, L.; Cai, M.; Cui, W. Stem cell-laden injectable hydrogel microspheres for cancellous bone regeneration. Chem. Eng. J. 2020, 393, 124715. [Google Scholar] [CrossRef]
- Diba, M.; Koons, G.L.; Bedell, M.L.; Mikos, A.G. 3D printed colloidal biomaterials based on photo-reactive gelatin nanoparticles. Biomaterials 2021, 274, 120871. [Google Scholar] [CrossRef] [PubMed]
- Seymour, A.J.; Shin, S.; Heilshorn, S.C. 3D Printing of Microgel Scaffolds with Tunable Void Fraction to Promote Cell Infiltration. Adv. Healthc. Mater. 2021, 10, e2100644. [Google Scholar] [CrossRef] [PubMed]
- Alzanbaki, H.; Moretti, M.; Hauser, C.A.E. Engineered microgels—Their manufacturing and biomedical applications. Micromachines 2021, 12, 45. [Google Scholar] [CrossRef] [PubMed]
- Elzoghby, A.O.; Elgohary, M.M.; Kamel, N.M. Chapter Six—Implications of Protein- and Peptide-Based Nanoparticles as Potential Vehicles for Anticancer Drugs. In Protein and Peptide Nanoparticles for Drug Delivery; Donev, R., Ed.; Advances in Protein Chemistry and Structural Biology; Academic Press: Cambridge, MA, USA, 2015; Volume 98, pp. 169–221. [Google Scholar] [CrossRef]
- Farjami, T.; Madadlou, A. Fabrication methods of biopolymeric microgels and microgel-based hydrogels. Food Hydrocoll. 2017, 62, 262–272. [Google Scholar] [CrossRef]
- Van Damme, L.; Van Hoorick, J.; Blondeel, P.; Van Vlierberghe, S. Toward Adipose Tissue Engineering Using Thiol-Norbornene Photo-Crosslinkable Gelatin Hydrogels. Biomacromolecules 2021, 22, 2408–2418. [Google Scholar] [CrossRef] [PubMed]
- Van Hoorick, J.; Gruber, P.; Markovic, M.; Tromayer, M.; Van Erps, J.; Thienpont, H.; Liska, R.; Ovsianikov, A.; Dubruel, P.; Van Vlierberghe, S. Cross-Linkable Gelatins with Superior Mechanical Properties through Carboxylic Acid Modification: Increasing the Two-Photon Polymerization Potential. Biomacromolecules 2017, 18, 3260–3272. [Google Scholar] [CrossRef] [PubMed]
- Pelc, D.; Marion, S.; Po ek, M.; Basleti, M. Role of microscopic phase separation in gelation of aqueous gelatin solutions. Soft Matter 2014, 1, 348–356. [Google Scholar] [CrossRef]
- Rebers, L.; Reichsöllner, R.; Regett, S.; Tovar, G.E.M.; Borchers, K.; Baudis, S.; Southan, A. Differentiation of physical and chemical cross-linking in gelatin methacryloyl hydrogels. Sci. Rep. 2021, 11, 3256. [Google Scholar] [CrossRef]
- Van Vlierberghe, S.; Schacht, E.; Dubruel, P. Reversible gelatin-based hydrogels: Finetuning of material properties. Eur. Polym. J. 2011, 47, 1039–1047. [Google Scholar] [CrossRef]
- Lee, B. Isoenthalpic and isoentropic temperatures and the thermodynamics of protein denaturation. Proc. Natl. Acad. Sci. USA 1991, 88, 5154–5158. [Google Scholar] [CrossRef]
- Hahn, C.; Nöbel, S.; Maisch, R.; Rösingh, W.; Weiss, J.; Hinrichs, J. Adjusting rheological properties of concentrated microgel suspensions by particle size distribution. Food Hydrocoll. 2015, 49, 183–191. [Google Scholar] [CrossRef]
- Rao, M.A. Rheology of Fluid and Semisolid Foods: Principles and Applications, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Hyun, K.; Kim, S.H.; Ahn, K.H.; Lee, S.J. Large amplitude oscillatory shear as a way to classify the complex fluids. J. Non-Newton. Fluid Mech. 2002, 107, 51–65. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Wyss, H.M.; Miyazaki, K.; Mattsson, J.; Hu, Z.; Reichman, D.R.; Weitz, D.A. Strain-Rate Frequency Superposition: A rheological probe of structural relaxation in soft materials. Phys. Rev. Lett. 2007, 98, 238303. [Google Scholar] [CrossRef]
- Orlowski, J.; Grinstein, S.; Casey, J.R. Sensors and regulators of intracellular pH. Nat. Rev. Mol. Cell Biol. 2010, 11, 50–61. [Google Scholar] [CrossRef]
- Ninan, G.; Joseph, J.; Aliyamveettil, Z.A. A comparative study on the physical, chemical and functional properties of carp skin and mammalian gelatins. J. Food Sci. Technol. 2014, 51, 2085–2091. [Google Scholar] [CrossRef] [PubMed]
- Bianchetti, M.G.; Simonetti, G.D.; Bettinelli, A. Body fluids and salt metabolism—Part I. Ital. J. Pediatr. 2009, 35, 36. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.S.; Regenstein, J.M. Physicochemical and Sensory Characteristics of Fish Gelatin. J. Food Sci. 2000, 65, 194–199. [Google Scholar] [CrossRef]
- Haug, I.J.; Draget, K.I.; Smidsrød, O. Physical and rheological properties of fish gelatin compared to mammalian gelatin. Food Hydrocoll. 2004, 18, 203–213. [Google Scholar] [CrossRef]
- Sarabia, A.I.; Gómez-Guillén, M.C.; Montero, P. The effect of added salts on the viscoelastic properties of fish skin gelatin. Food Chem. 2000, 70, 71–76. [Google Scholar] [CrossRef]
- Sow, L.C.; Yang, H. Effects of salt and sugar addition on the physicochemical properties and nanostructure of fish gelatin. Food Hydrocoll. 2015, 45, 72–82. [Google Scholar] [CrossRef]
- Rebers, L.; Granse, T.; Tovar, G.E.M.; Southan, A.; Borchers, K. Physical interactions strengthen chemical gelatin methacryloyl gels. Gels 2019, 5, 4. [Google Scholar] [CrossRef] [PubMed]
- Lopes, J.L.S.; Miles, A.J.; Whitmore, L.; Wallace, B.A. Distinct circular dichroism spectroscopic signatures of polyproline II and unordered secondary structures: Applications in secondary structure analyses. Protein Sci. 2014, 23, 1765–1772. [Google Scholar] [CrossRef]
- Wüstneck, R.; Wetzel, R.; Buder, E.; Hermel, H. The modification of the triple helical structure of gelatin in aqueous solution I. The influence of anionic surfactants, pH-value, and temperature. Colloid Polym. Sci. 1988, 266, 1061–1067. [Google Scholar] [CrossRef]
- Fernández-Barbero, A.; Suárez, I.J.; Sierra-Martín, B.; Fernández-Nieves, A.; de las Nieves, F.J.; Marquez, M.; Rubio-Retama, J.; López-Cabarcos, E. Gels and microgels for nanotechnological applications. Adv. Colloid Interface Sci. 2009, 147, 88–108. [Google Scholar] [CrossRef]
- Lee, B.H.; Lum, N.; Seow, L.Y.; Lim, P.Q.; Tan, L.P. Synthesis and characterization of types A and B gelatin methacryloyl for bioink applications. Materials 2016, 9, 797. [Google Scholar] [CrossRef]
- Alexa, R.L.; Iovu, H.; Ghitman, J.; Serafim, A.; Stavarache, C.; Marin, M.M.; Ianchis, R. 3D-printed gelatin methacryloyl-based scaffolds with potential application in tissue engineering. Polymers 2021, 13, 727. [Google Scholar] [CrossRef] [PubMed]
- Luxbacher, T. The Zeta Potential for Solid Surface Analysis. A Practical Guide to Streaming Potential Measurement; Anton Paar Gmbh: Graz, Austria, 2014. [Google Scholar]
- Young, D.A.; Choi, Y.S.; Engler, A.J.; Christman, K.L. Stimulation of adipogenesis of adult adipose-derived stem cells using substrates that mimic the stiffness of adipose tissue. Biomaterials 2013, 34, 8581–8588. [Google Scholar] [CrossRef] [PubMed]
- Ramião, N.G.; Martins, P.S.; Rynkevic, R.; Fernandes, A.A.; Barroso, M.; Santos, D.C. Biomechanical properties of breast tissue, a state-of-the-art review. Biomech. Model. Mechanobiol. 2016, 15, 1307–1323. [Google Scholar] [CrossRef]
- Geerligs, M.M.; Peters, G.W.M.; Ackermans, P.A.J.; Oomens, C.W.; Baaijens, F.P.T. Linear viscoelastic behavior of subcutaneous adipose tissue. Biorheology 2008, 45, 677–688. [Google Scholar] [CrossRef]
- Patel, P.N.; Smith, C.K.; Patrick, C.W., Jr. Rheological and recovery properties of poly(ethylene glycol) diacrylate hydrogels and human adipose tissue. J. Biomed. Mater. Res. Part A 2005, 73A, 313–319. [Google Scholar] [CrossRef]
- Allahham, A.; Mainwaring, D.; Stewart, P.; Marriott, J. Development and application of a micro-capillary rheometer for in-vitro evaluation of parenteral injectability. J. Pharm. Pharmacol. 2004, 56, 709–716. [Google Scholar] [CrossRef]
- Astin, A.D. Finger Force Capability: Measurement and Prediction Using Anthropometric and Myoelectric Measures. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 1999. [Google Scholar]
- Haasters, F.; Prall, W.C.; Anz, D.; Bourquin, C.; Pautke, C.; Endres, S.; Mutschler, W.; Docheva, D.; Schieker, M. Morphological and immunocytochemical characteristics indicate the yield of early progenitors and represent a quality control for human mesenchymal stem cell culturing. J. Anat. 2009, 214, 759–767. [Google Scholar] [CrossRef] [PubMed]
- Eagle, H.; Levine, E.M. Growth Regulatory Effects of Cellular Interaction. Nature 1967, 213, 1102–1106. [Google Scholar] [CrossRef] [PubMed]
- Dahle, J.; Kvam, E. Induction of delayed mutations and chromosomal instability in fibroblasts after UVA-, UVB-, and X-radiation. Cancer Res. 2003, 63, 1464–1469. [Google Scholar]
- Dahle, J.; Kvam, E.; Stokke, T. Bystander effects in UV-induced genomic instability: Antioxidants inhibit delayed mutagenesis induced by ultraviolet A and B radiation. J. Carcinog. 2005, 4, 11. [Google Scholar] [CrossRef]
- Urushibara, A.; Kodama, S.; Yokoya, A. Induction of genetic instability by transfer of a UV-A-irradiated chromosome. Mutat. Research. Genet. Toxicol. Environ. Mutagen. 2014, 766, 29–34. [Google Scholar] [CrossRef]
- Lim, K.S.; Klotz, B.; Lindberg, G.C.J.; Melchels, F.P.W.; Hooper, G.J.; Malda, J.; Gawlitta, D.; Woodfield, T.B.F. Visible Light Cross-Linking of Gelatin Hydrogels Offers an Enhanced Cell Microenvironment with Improved Light Penetration Depth. Macromol. Biosci. 2019, 19, e1900098. [Google Scholar] [CrossRef] [PubMed]
- Farrell, R.E. Chapter 8—Stringency: Conditions that Influence Nucleic Acid Structure. In RNA Methodologies, 4th ed.; Farrell, R.E., Ed.; Academic Press: San Diego, CA, USA, 2010; pp. 173–178. [Google Scholar] [CrossRef]
- Potočar, U.; Hudoklin, S.; Kreft, M.E.; Završnik, J.; Božikov, K.; Fröhlich, M. Adipose-derived stem cells respond to increased osmolarities. PLoS ONE 2016, 11, e0163870. [Google Scholar] [CrossRef]
- Prado, J.R.; Vyazovkin, S. Melting of Gelatin Gels Containing Laponite, Montmorillonite, and Chitosan Particles. Macromol. Chem. Phys. 2014, 215, 867–872. [Google Scholar] [CrossRef]
- Van Vlierberghe, S.; Van Damme, L.; Depypere, B.; Blondeel, P. Swellable Gelatin Compositions. WO2021255295, 23 December 2021. [Google Scholar]
- Vleminckx, G.; Jofore, B.D.; Moldenaers, P.; Clasen, C. Effect of geometrical confinement on the flow of soft microgel particle pastes. Rheol. Acta 2020, 59, 435–453. [Google Scholar] [CrossRef]
- Guo, M.; Wyss, H.M. Micromechanics of Soft Particles. Macromol. Mater. Eng. 2011, 296, 223–229. [Google Scholar] [CrossRef]
- Wyss, H.M.; Franke, T.; Mele, E.; Weitz, D.A. Capillary micromechanics: Measuring the elasticity of microscopic soft objects. Soft Matter 2010, 6, 4550. [Google Scholar] [CrossRef]
- Kelly, S.M.; Jess, T.J.; Price, N.C. How to study proteins by circular dichroism. Biochim. Biophys. Acta-Proteins Proteom. 2005, 1751, 119–139. [Google Scholar] [CrossRef]




| Technique | Drawback | References |
|---|---|---|
| Microfluidics | Need for an oil phase, which might impart biocompatibility | [30] |
| Low throughput | [30] | |
| Need for deep cleaning of the device | [36] | |
| Emulsification | Need for an oil phase, which might impart biocompatibility | [30] |
| High polydispersity | [30] | |
| Electrostatic droplet generation | High polydispersity | [36] |
| Two-step desolvation | Use of toxic solvents | [37] |
| Complex coacervation | Agglomeration and stabilization issues | [38] |
| Lithography | Low throughput | [30] |
| Physical removal of molds leading to deformations | [36] | |
| Mechanical fragmentation | High polydispersity | [30] |
| (in the wet state) |
| Size Fraction | Aspect Ratio (-) |
|---|---|
| <100 µm | 4.51 ± 1.81 |
| 100–212 µm | 3.79 ± 0.69 |
| 212–300 µm | 1.73 ± 0.24 |
| 300–400 µm | 1.46 ± 0.31 |
| 400–500 µm | 1.36 ± 0.24 |
| Solvent | Ionic Strength (mM) | Conductivity (mS/cm) | Osmolality (mOsm/L) | pH |
|---|---|---|---|---|
| Water | ≈0 | ≈0 | 0 | 6.39 |
| 1 mM NaCl | 1 | 0.36 | 2 | 7.07 |
| 10 mM NaCl | 10 | 1.52 | 20 | 7.25 |
| Diluted PBS | 110 | 8.85 | 243 | 7.57 |
| Solvent | Volume Fraction (%) |
|---|---|
| Water | 104 |
| 1 mM NaCl | 59.8 |
| 10 mM NaCl | 48.0 |
| Diluted PBS | 31.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Maeseneer, T.; Van Damme, L.; Aktan, M.K.; Braem, A.; Moldenaers, P.; Van Vlierberghe, S.; Cardinaels, R. Powdered Cross-Linked Gelatin Methacryloyl as an Injectable Hydrogel for Adipose Tissue Engineering. Gels 2024, 10, 167. https://doi.org/10.3390/gels10030167
De Maeseneer T, Van Damme L, Aktan MK, Braem A, Moldenaers P, Van Vlierberghe S, Cardinaels R. Powdered Cross-Linked Gelatin Methacryloyl as an Injectable Hydrogel for Adipose Tissue Engineering. Gels. 2024; 10(3):167. https://doi.org/10.3390/gels10030167
Chicago/Turabian StyleDe Maeseneer, Tess, Lana Van Damme, Merve Kübra Aktan, Annabel Braem, Paula Moldenaers, Sandra Van Vlierberghe, and Ruth Cardinaels. 2024. "Powdered Cross-Linked Gelatin Methacryloyl as an Injectable Hydrogel for Adipose Tissue Engineering" Gels 10, no. 3: 167. https://doi.org/10.3390/gels10030167
APA StyleDe Maeseneer, T., Van Damme, L., Aktan, M. K., Braem, A., Moldenaers, P., Van Vlierberghe, S., & Cardinaels, R. (2024). Powdered Cross-Linked Gelatin Methacryloyl as an Injectable Hydrogel for Adipose Tissue Engineering. Gels, 10(3), 167. https://doi.org/10.3390/gels10030167