Comparison of Finite Difference and Finite Volume Simulations for a Sc-Drying Mass Transport Model
Abstract
1. Introduction
2. Mass Transport Model of Supercritical Drying
- and for the effective diffusion coefficient (assumption: Gel porosity , gel tortuosity ),
- and for the mixture concentration and the fluid density ,
- and for the diffusion coefficient in the bulk fluid,
- and for the viscosity of the bulk fluid and between
- and for the resulting Schmidt number.
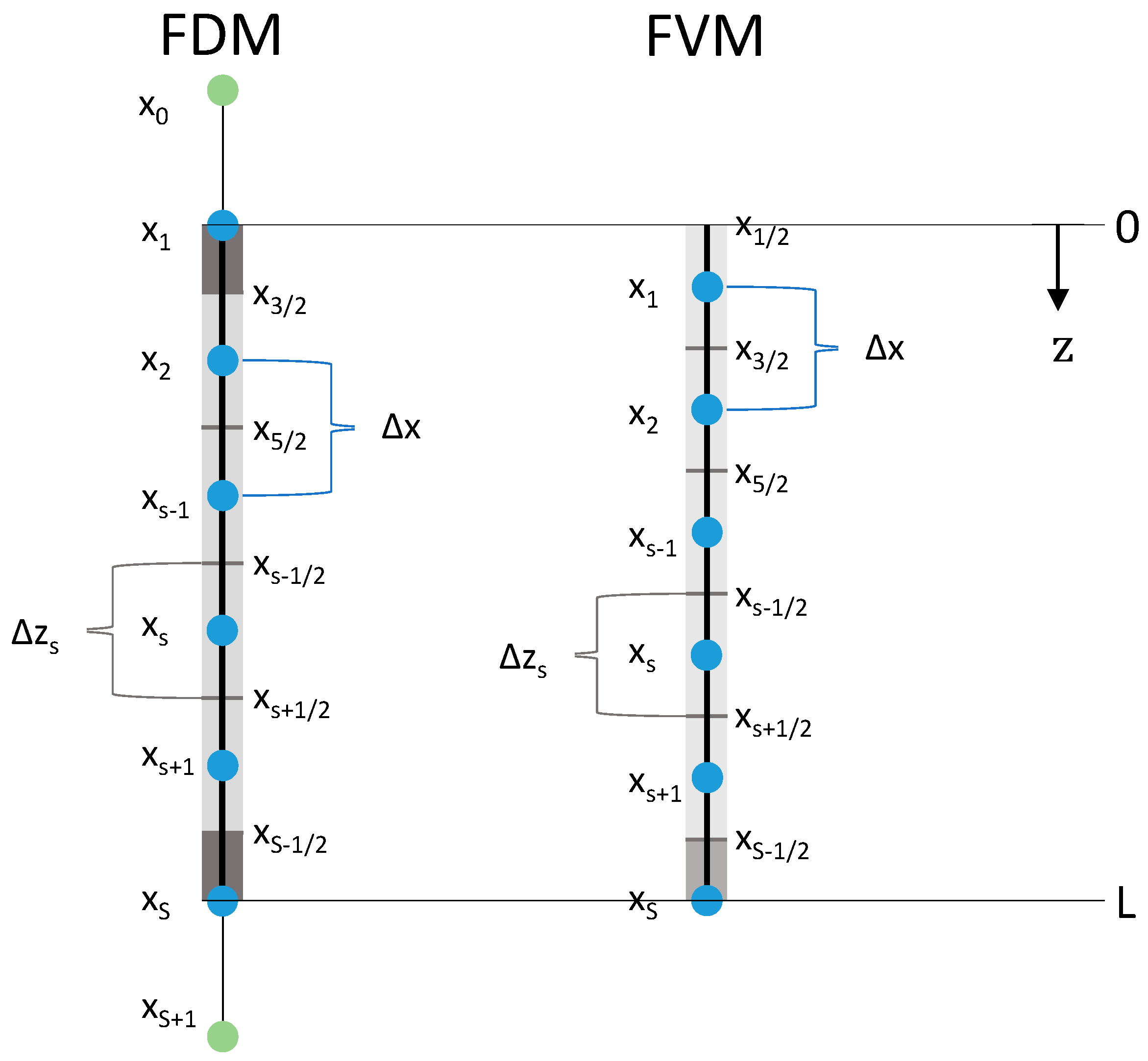
3. Numerical Solution of the Mass Transport Model
3.1. Solving the Diffusion-Advection Equation Using the Finite Difference Method
3.1.1. Discretization of Advection Term: Version A
3.1.2. Discretization of Advection Term: Version B
| Version A: | (31) | |
| Version B: |
| Where is nonzero only for the indices and given by | |||
| Version A: | Version B: | (32) | |
3.2. Solving the Diffusion-Advection Equation Using the Finite Volume Method
| Where is nonzero only for the indices and given by | (49) |
4. Results and Discussion
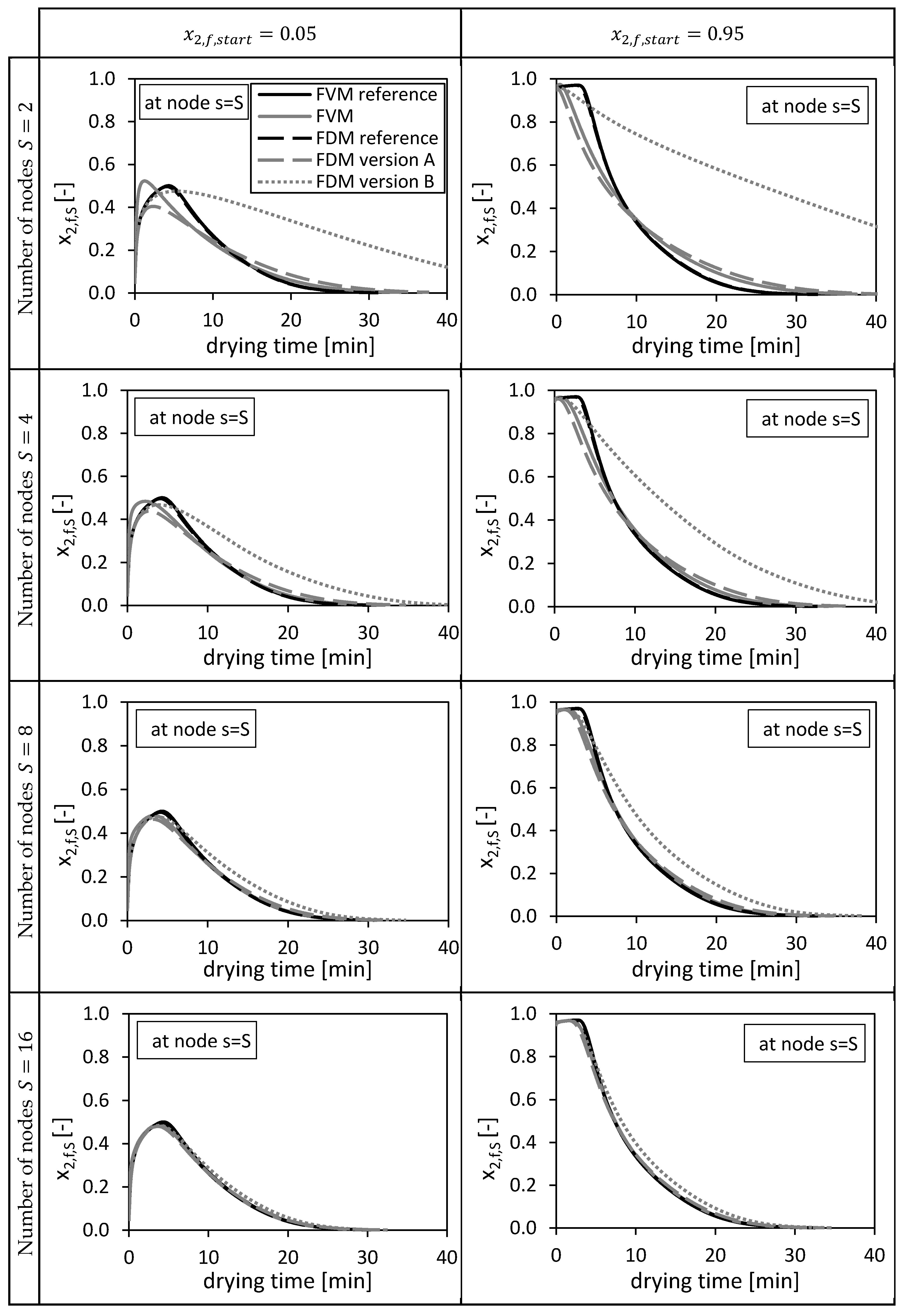
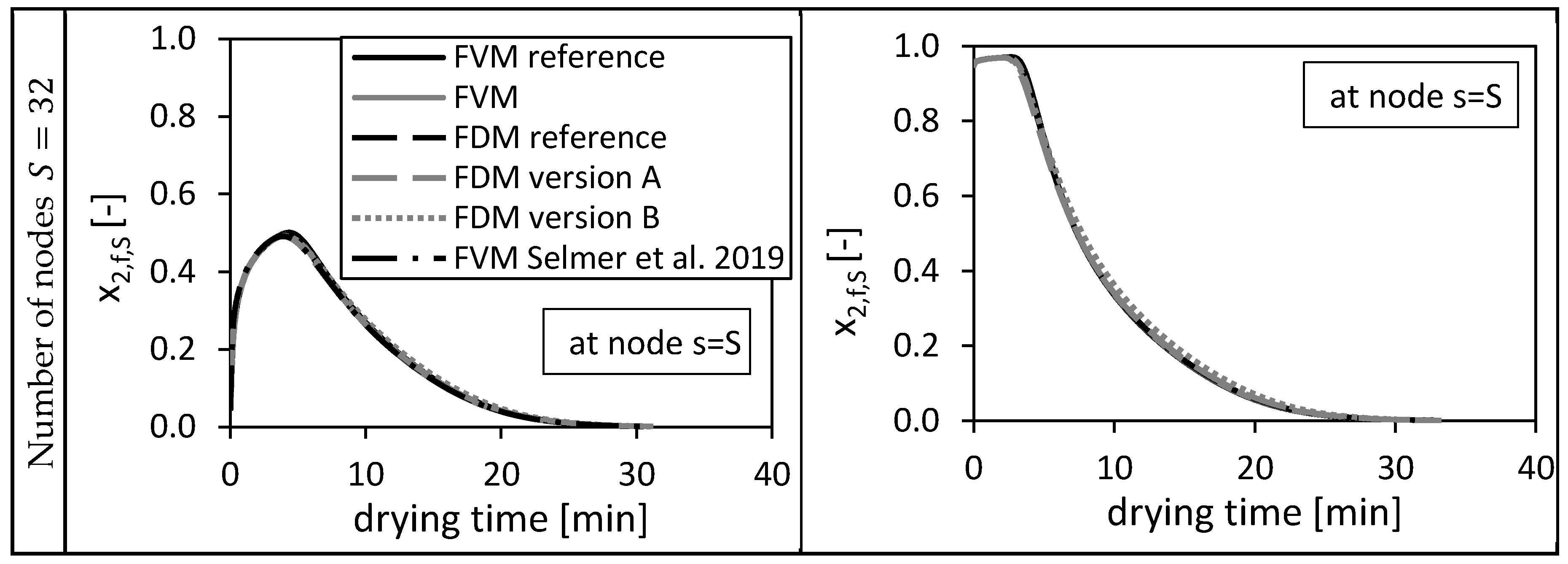
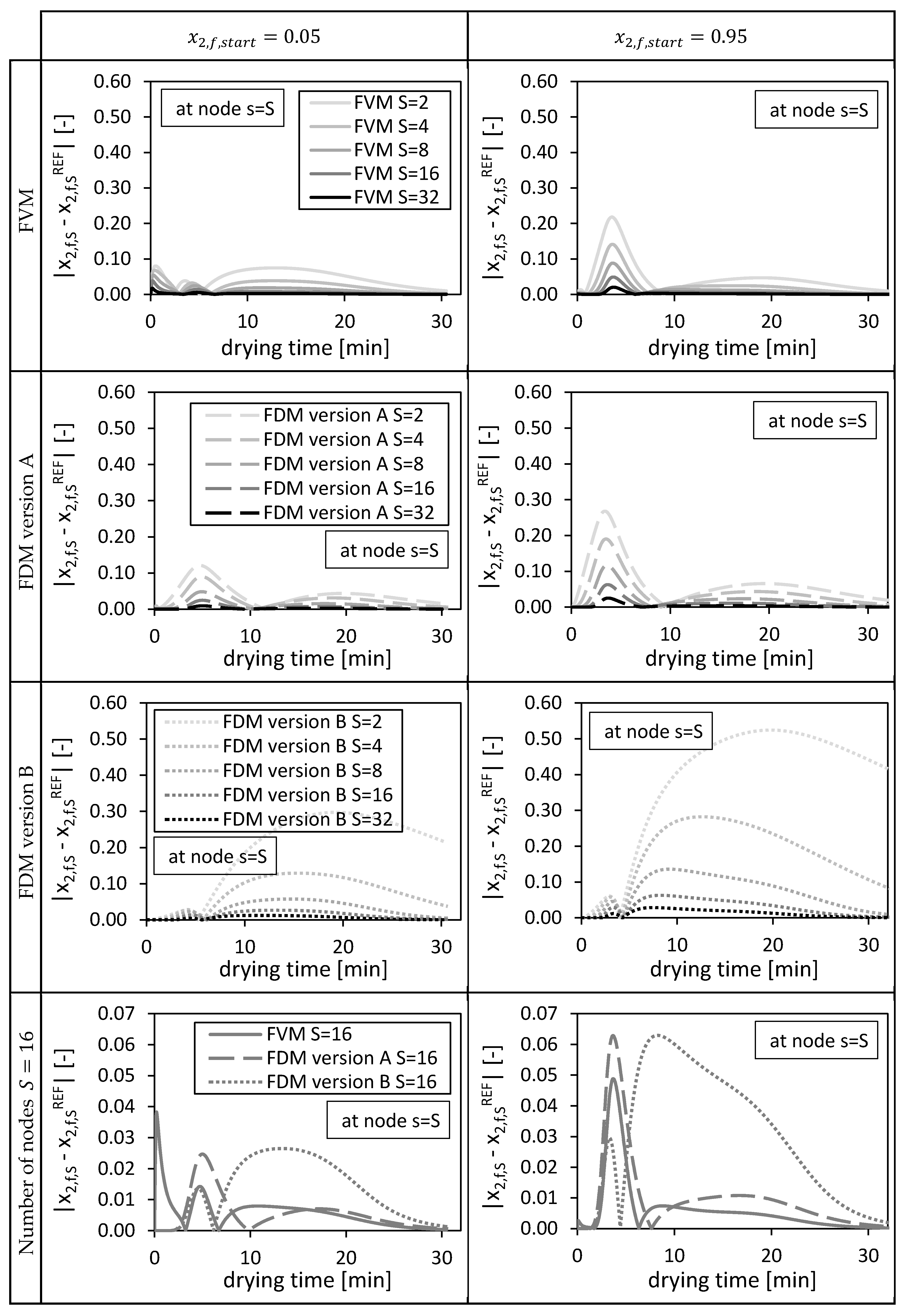
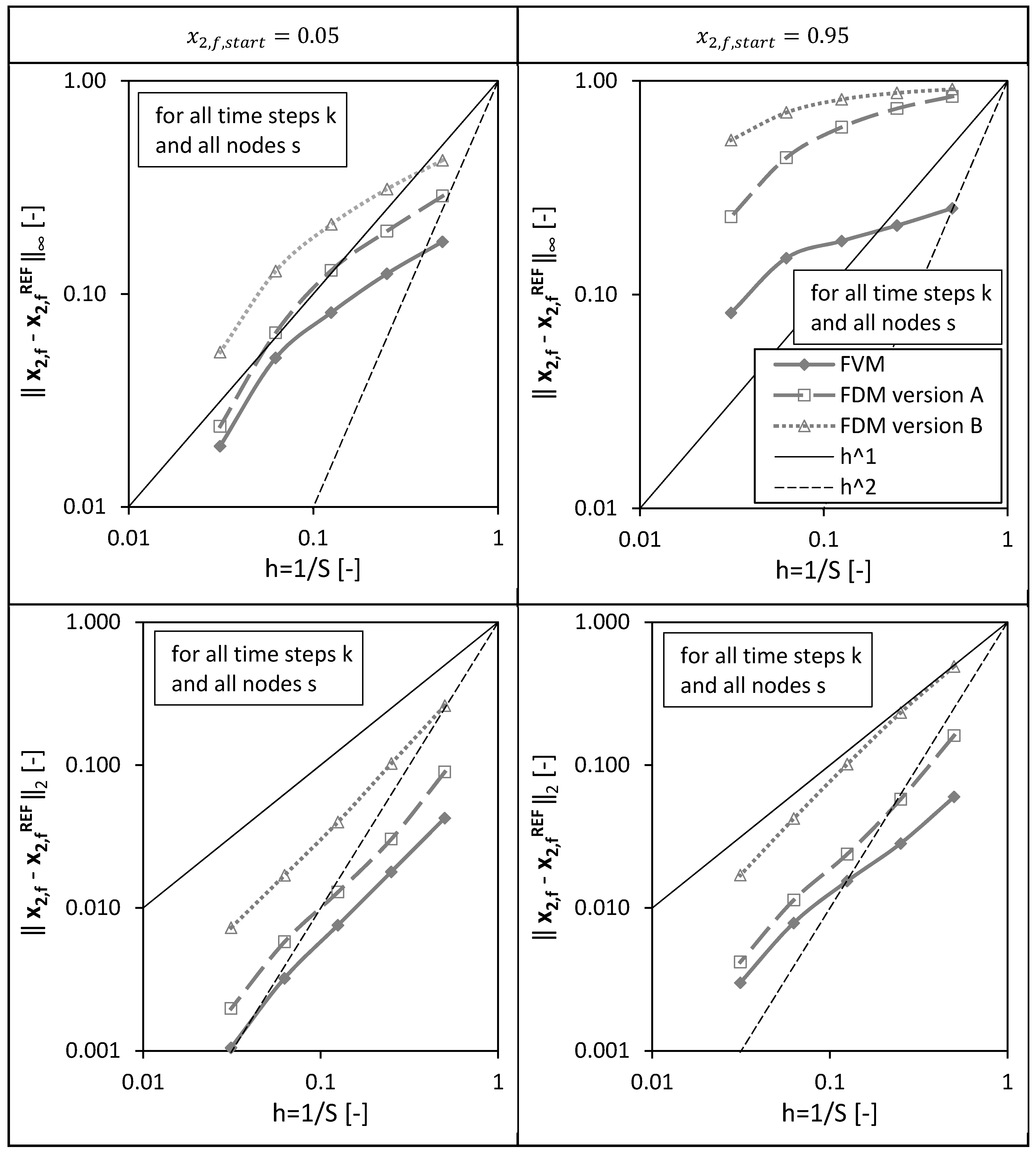
4.1. Accuracy
4.1.1. Convergence Behavior
- (a)
- With excess ethanol: corresponding to ;
- (b)
- Without excess ethanol: corresponding to .
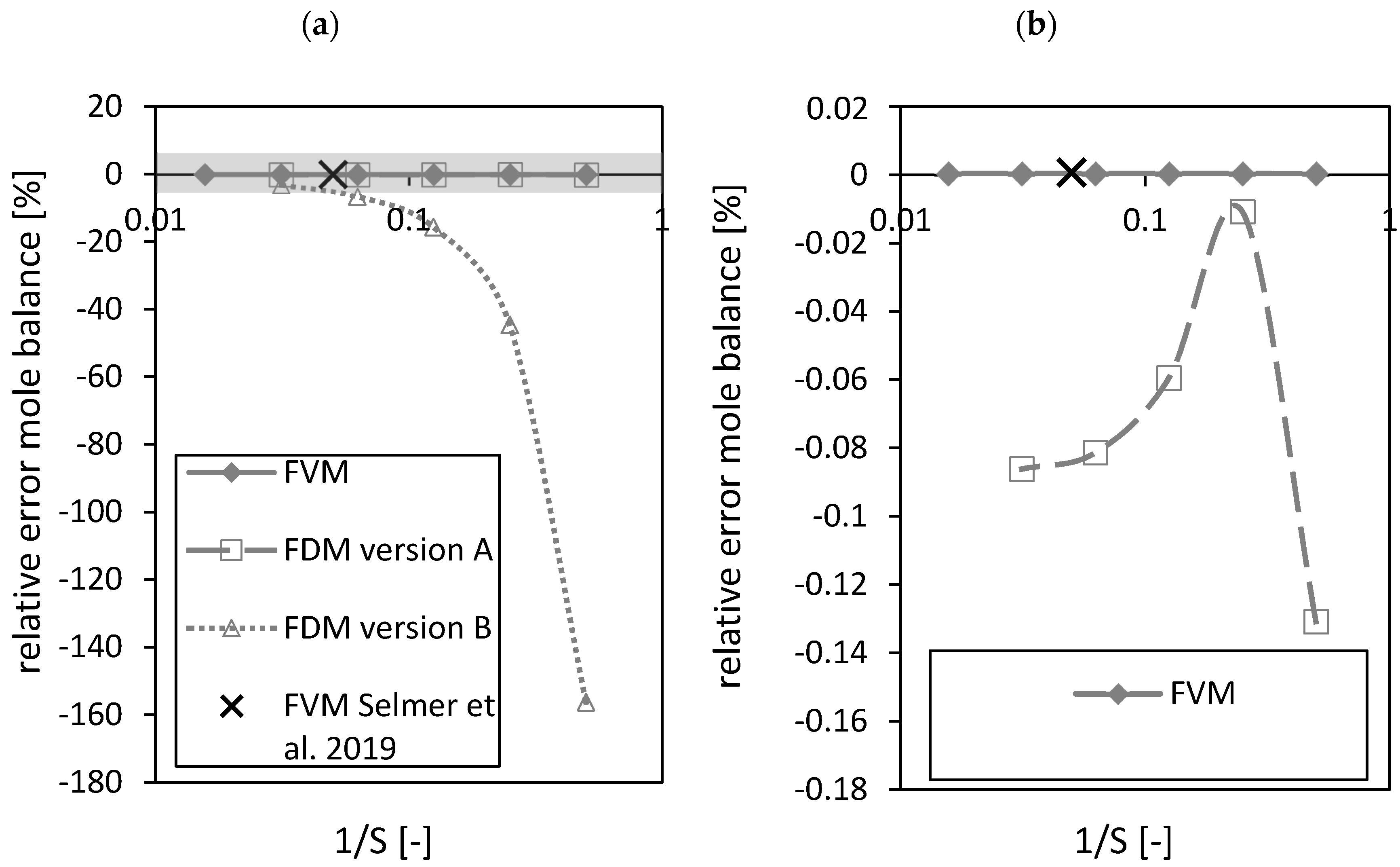
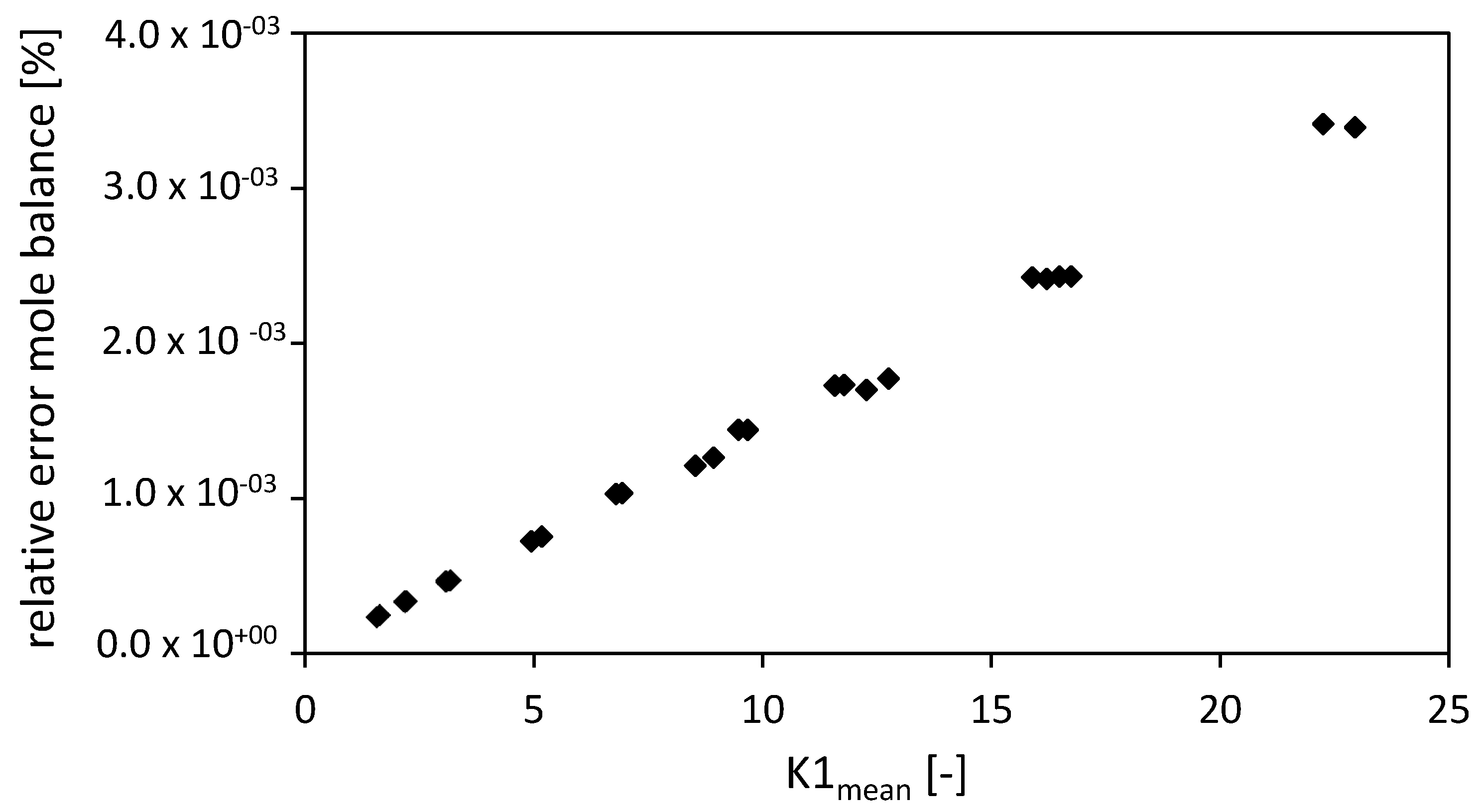
4.1.2. Mole Balances
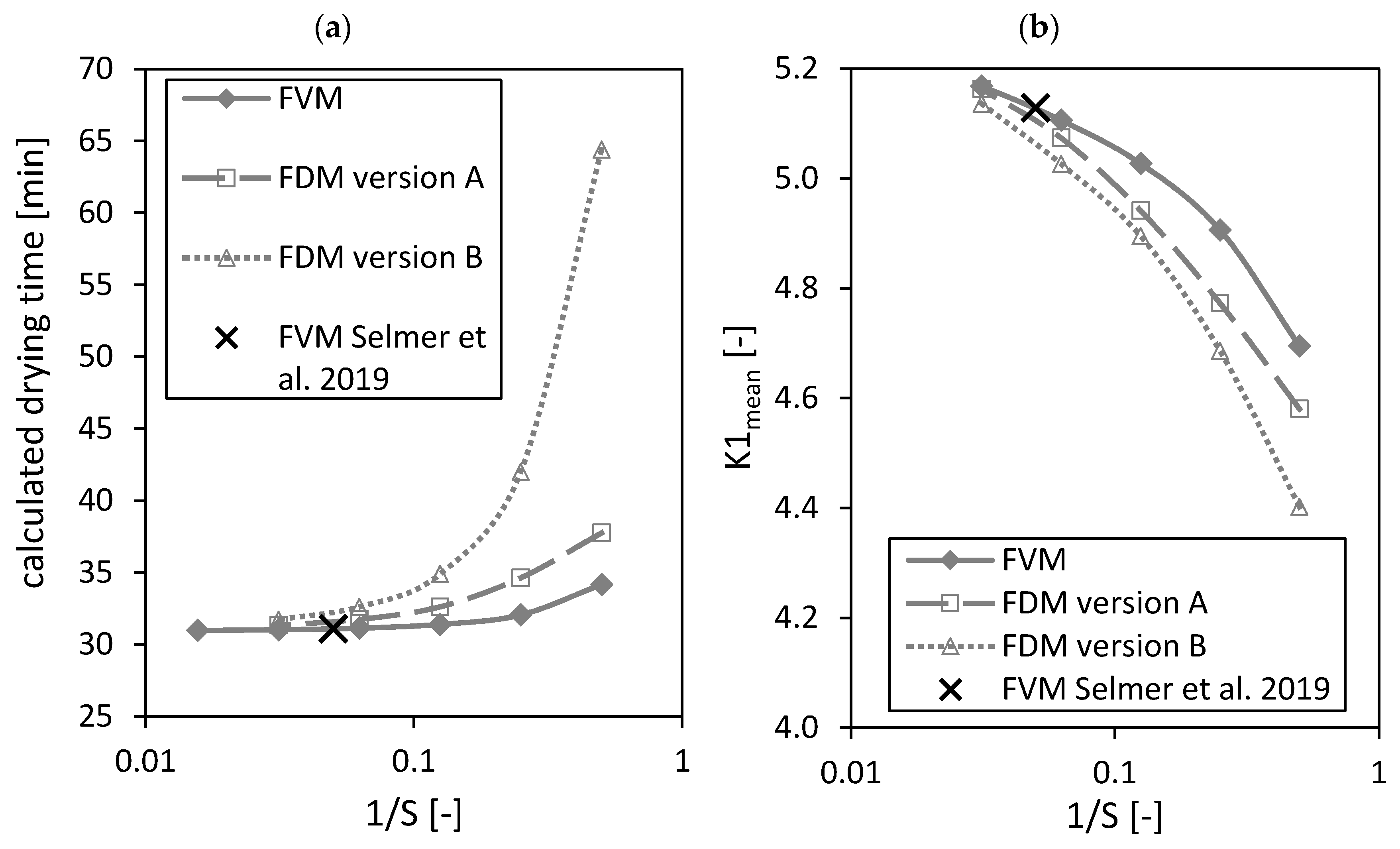
4.2. Efficiency
4.2.1. Condition Numbers
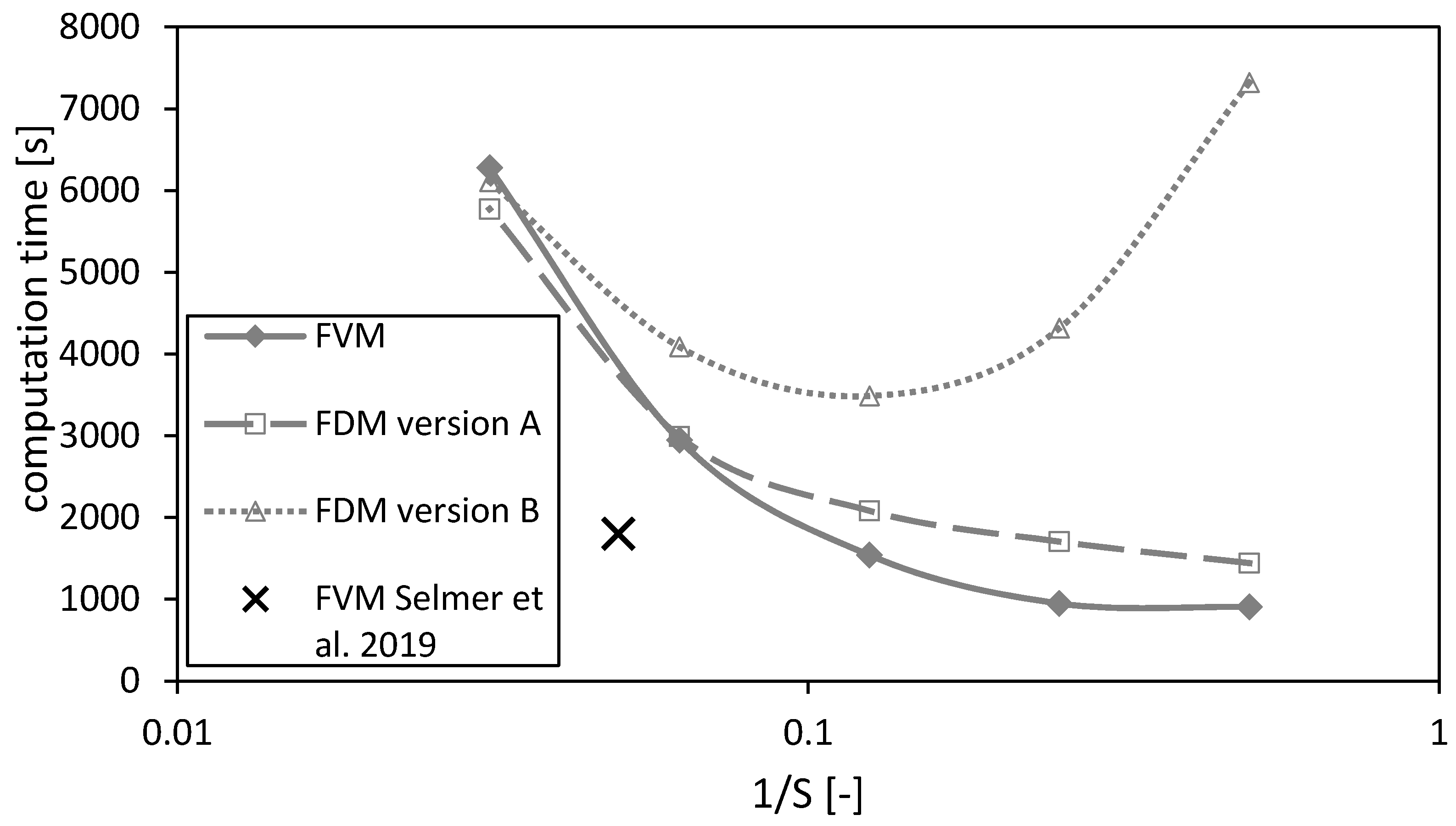
4.2.2. Computation Time
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Cross-sectional area of the cylindrical autoclave | ||
| Row vector in finite volume matrix | ||
| Row vector in finite difference matrix | ||
| Finite volume method matrix | ||
| Finite difference method matrix | ||
| Surface area of the spherical particle | ||
| Bernoulli function | ||
| Right-hand side vector for finite volume method | ||
| Right-hand side vector for finite difference method | ||
| Concentration | ||
| Ethanol concentration in the bulk fluid | ||
| Vector ethanol concentration of the axial bulk fluid elements | ||
| Ethanol concentration within the porous gel particle | ||
| Mixture concentration in the bulk fluid | ||
| Mixture concentration within the porous gel particle | ||
| Diffusion coefficient | ||
| Axial dispersion coefficient in the packed bed | ||
| Effective diffusion coefficient within the porous gel particle | ||
| Function | ||
| Flux of ethanol | ||
| Dimensionless grid size | ||
| Time index | ||
| Number of time steps | ||
| Dimensionless number | ||
| Length of the packed bed | ||
| Euclidean norm | ||
| Maximum norm | ||
| Mass flowrate of the ethanol–CO2 mixture | ||
| Maximum | ||
| Radial index in gel particle domain | ||
| Number of nodes in gel particle domain | ||
| End mole number of ethanol | ||
| Start mole number of ethanol | ||
| Number of particles | ||
| Pressure | ||
| Numerical Péclet number | ||
| Radial coordinate of the spherical particle | ||
| Particle radius | ||
| Axial index in autoclave/bulk fluid domain | ||
| Number of nodes in autoclave/bulk fluid domain | ||
| Ethanol source term within the bulk fluid | ||
| Time | ||
| Temperature | ||
| Interstitial fluid velocity | ||
| Superficial fluid velocity | ||
| Volume flow | ||
| Function | ||
| Volume bulk fluid | ||
| Volume element of spherical gel particle | ||
| Ethanol molar fraction in the bulk fluid | ||
| Vector ethanol molar fraction of the axial bulk fluid elements and time indices | ||
| Reference vector ethanol molar fraction of the axial bulk fluid elements and time indices | ||
| Vector ethanol molar fraction of the time indices | ||
| Ethanol molar fraction within the porous particle | ||
| Molar fraction of component i | ||
| Node | ||
| Cell interface | ||
| Axial coordinate of the autoclave/packed bed | ||
| Greek letters | ||
| Mass transfer coefficient | ||
| Distance between neighboring nodes in gel particles | ||
| Time step | ||
| Distance between neighboring nodes in autoclave/bulk fluid domain | ||
| Length of volume element | ||
| Vector lengths of volume elements | ||
| (Aero)gel particle porosity | ||
| Porosity of the packed bed (spherical porous particles are here assumed to be nonporous) | ||
| Density of ethanol-CO2 mixture in the bulk fluid | ||
| Tortuosity within the porous gel particle | ||
| Super and subscripts | ||
| Start | ||
| Component carbon dioxide | ||
| Component ethanol | ||
| Autoclave | ||
| Complete flux scheme | ||
| Carbon dioxide | ||
| End | ||
| Ethanol | ||
| Bulk fluid | ||
| Finite difference method | ||
| Finite volume method | ||
| Gel | ||
| Homogenous | ||
| Substance component i | ||
| , | Inhomogeneous | |
| Time index | ||
| Number of time steps | ||
| Radial index in gel particle domain | ||
| Particle | ||
| Reference | ||
| Axial index in autoclave/bulk fluid domain | ||
| Number of nodes in autoclave/bulk fluid domain | ||
| Transposed |
References
- Şahin, İ.; Özbakır, Y.; İnönü, Z.; Ulker, Z.; Erkey, C. Kinetics of Supercritical Drying of Gels. Gels 2018, 4, 3. [Google Scholar] [CrossRef] [PubMed]
- Selmer, I.; Behnecke, A.-S.; Quiño, J.; Braeuer, A.S.; Gurikov, P.; Smirnova, I. Model development for sc-drying kinetics of aerogels: Part 1. J. Supercrit. Fluids 2018, 140, 415–430. [Google Scholar] [CrossRef]
- Selmer, I.; Behnecke, A.-S.; Farrell, P.; Morales, A.B.; Gurikov, P.; Smirnova, I. Model development for sc-drying kinetics of aerogels: Part 2. J. Supercrit. Fluids 2019, 147, 149–161. [Google Scholar] [CrossRef]
- Şahin, İ.; Uzunlar, E.; Erkey, C. Investigation of kinetics of supercritical drying of alginate alcogel particles. J. Supercrit. Fluids 2019, 146, 78–88. [Google Scholar] [CrossRef]
- Şahin, İ.; Uzunlar, E.; Erkey, C. Investigation of the effect of gel properties on supercritical drying kinetics of ionotropic alginate gel particles. J. Supercrit. Fluids 2019, 152, 104571. [Google Scholar] [CrossRef]
- Hatami, T.; Viganó, J.; Innocentini Mei, L.H.; Martínez, J. Production of alginate-based aerogel particles using supercritical drying: Experiment, comprehensive mathematical model, and optimization. J. Supercrit. Fluids 2020, 160, 104791. [Google Scholar] [CrossRef]
- Santos, P.d.; Viganó, J.; Furtado, G.d.F.; Cunha, R.L.; Hubinger, M.D.; Rezende, C.A.; Martínez, J. Production of resveratrol loaded alginate aerogel: Characterization, mathematical modeling, and study of impregnation. J. Supercrit. Fluids 2020, 163, 104882. [Google Scholar] [CrossRef]
- Forsythe, G.E.; Wasow, W.R. Finite Difference Methods for Partial Differential Equations; Wiley: New York, NY, USA, 1960. [Google Scholar]
- Morton, K.W.; Mayers, D.F. Numerical Solution of Partial Differential Equations; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. In Solution of Equations in R^n (Part 3), Techniques of Scientific Computing (Part 3); Ciarlet, P.G., Lions, J.L., Eds.; Elsevier: Amsterdam, The Netherlands, 2000; Volume 7, pp. 713–1018. [Google Scholar] [CrossRef]
- Farrell, P.; Linke, A. Uniform Second Order Convergence of a Complete Flux Scheme on Unstructured 1D Grids for a Singularly Perturbed Advection–Diffusion Equation and Some Multidimensional Extensions. J. Sci. Comput. 2017, 72, 373–395. [Google Scholar] [CrossRef]
- Danckwerts, P.V. Continuous flow systems. Chem. Eng. Sci. 1953, 2, 1–13. [Google Scholar] [CrossRef]
- Si, H.; Gärtner, K.; Fuhrmann, J. Boundary conforming Delaunay mesh generation. Comput. Math. Math. Phys. 2010, 50, 38–53. [Google Scholar] [CrossRef]
- Thiart, G.D. Improved Finite-Difference Scheme for the Solution of Convection-Diffusion Problems with Simplen Algorithm. Numer. Heat Transfer Part B Fundamentals 1990, 18, 81–95. [Google Scholar] [CrossRef]
- Ten Thije Boonkkamp, J.H.M.; Anthonissen, M.J.H. The Finite Volume-Complete Flux Scheme for Advection-Diffusion-Reaction Equations. J. Sci. Comput. 2011, 46, 47–70. [Google Scholar] [CrossRef]
- Ten Thije Boonkkamp, J.H.M.; Schilders, W.H.A. An exponential fitting scheme for the electrothermal device equations, specially for the simulation of avalanche generation. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 1993, 12, 95–111. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selmer, I.; Farrell, P.; Smirnova, I.; Gurikov, P. Comparison of Finite Difference and Finite Volume Simulations for a Sc-Drying Mass Transport Model. Gels 2020, 6, 45. https://doi.org/10.3390/gels6040045
Selmer I, Farrell P, Smirnova I, Gurikov P. Comparison of Finite Difference and Finite Volume Simulations for a Sc-Drying Mass Transport Model. Gels. 2020; 6(4):45. https://doi.org/10.3390/gels6040045
Chicago/Turabian StyleSelmer, Ilka, Patricio Farrell, Irina Smirnova, and Pavel Gurikov. 2020. "Comparison of Finite Difference and Finite Volume Simulations for a Sc-Drying Mass Transport Model" Gels 6, no. 4: 45. https://doi.org/10.3390/gels6040045
APA StyleSelmer, I., Farrell, P., Smirnova, I., & Gurikov, P. (2020). Comparison of Finite Difference and Finite Volume Simulations for a Sc-Drying Mass Transport Model. Gels, 6(4), 45. https://doi.org/10.3390/gels6040045






