Numerical Study of the Influence of Coupling Interface Emissivity on Aerogel Metal Thermal Protection Performance
Abstract
:1. Introduction
2. Results and Discussion
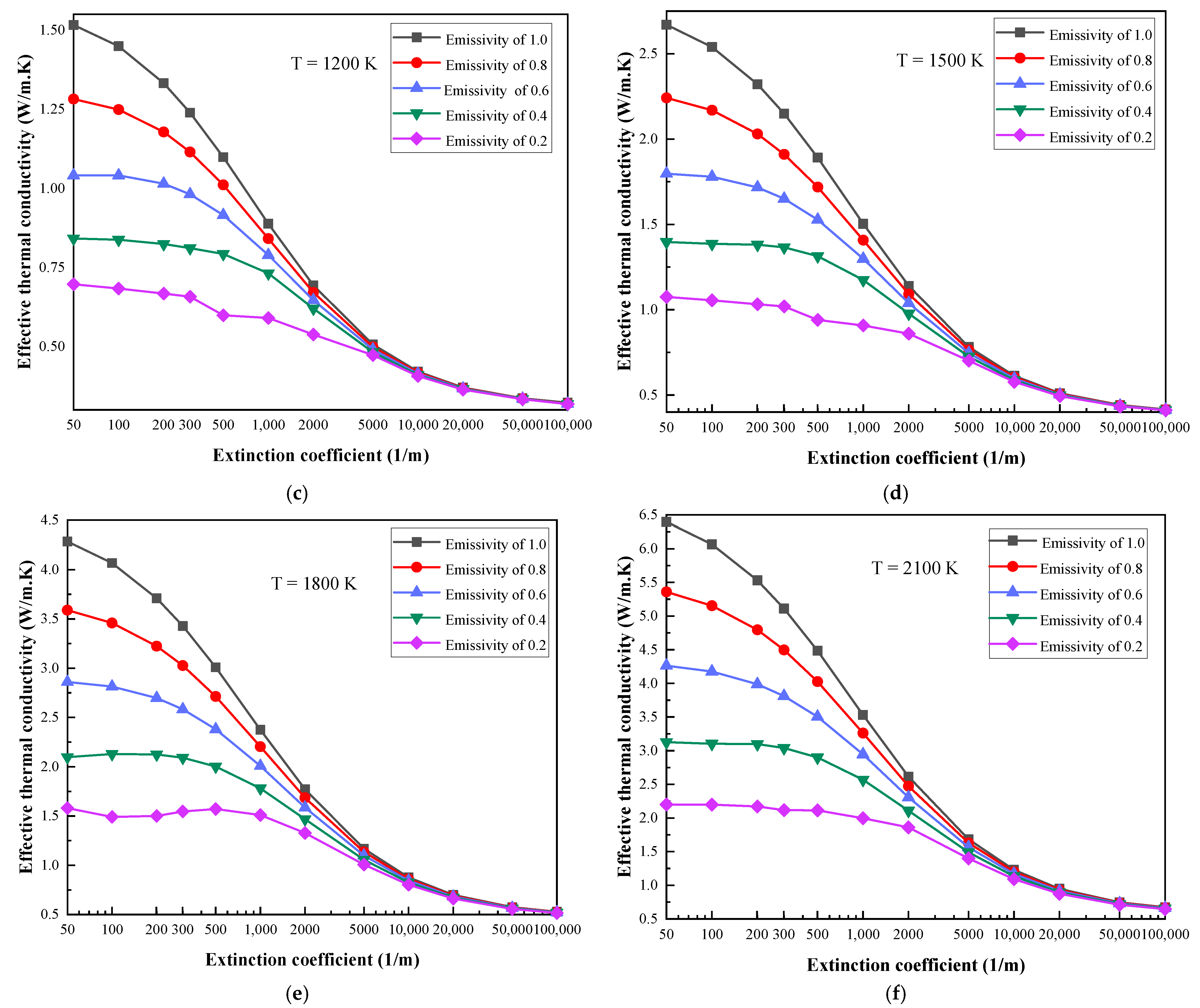
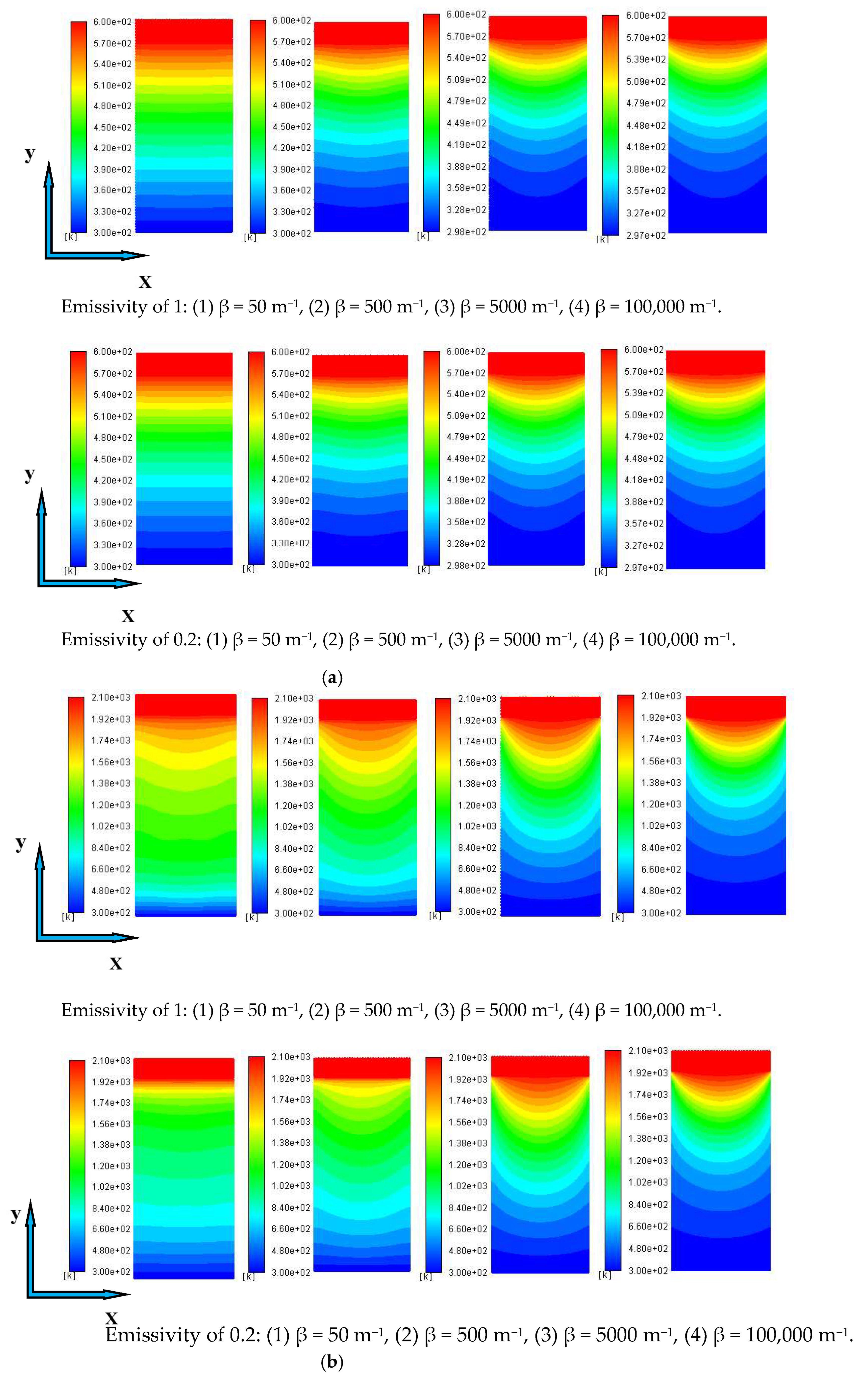
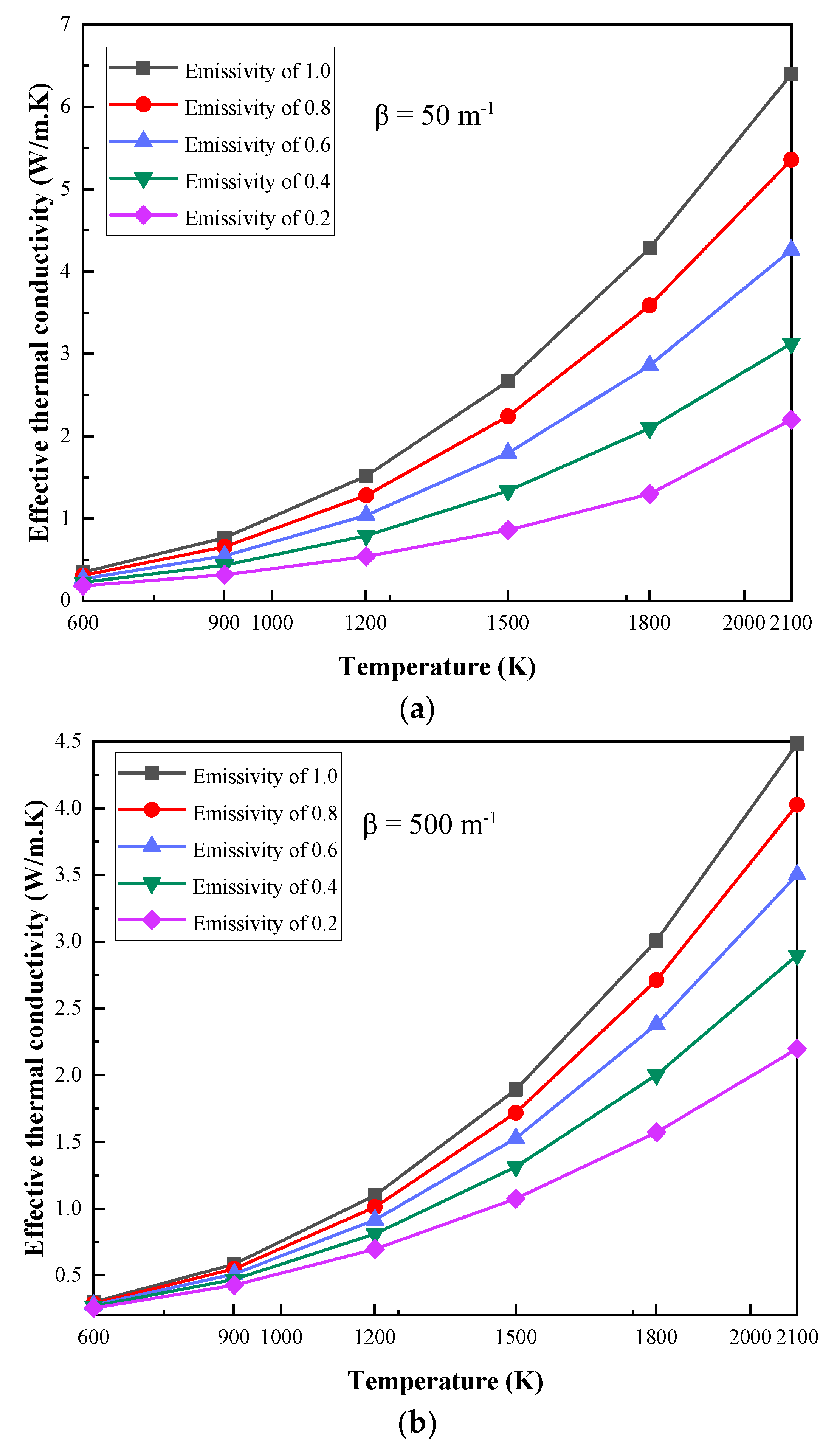
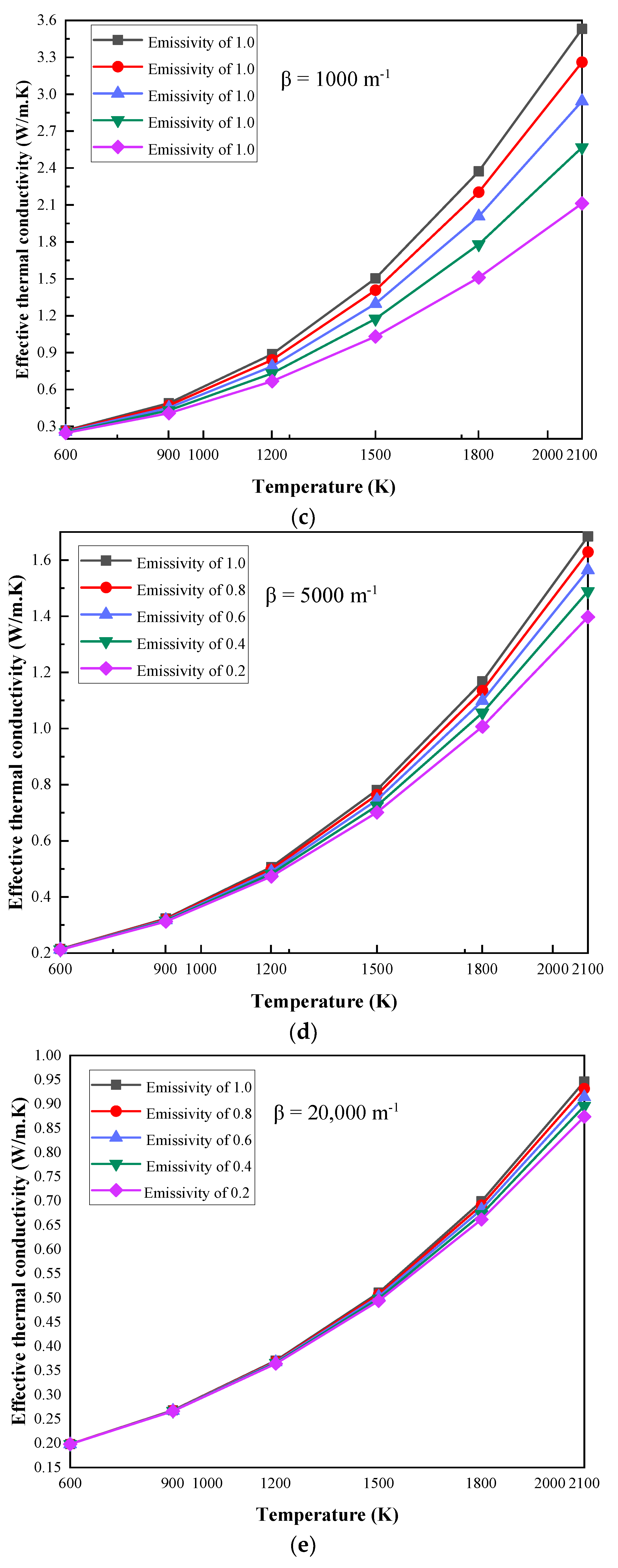
2.1. The Influence of Emissivity Variation with Different Extinction Coefficients
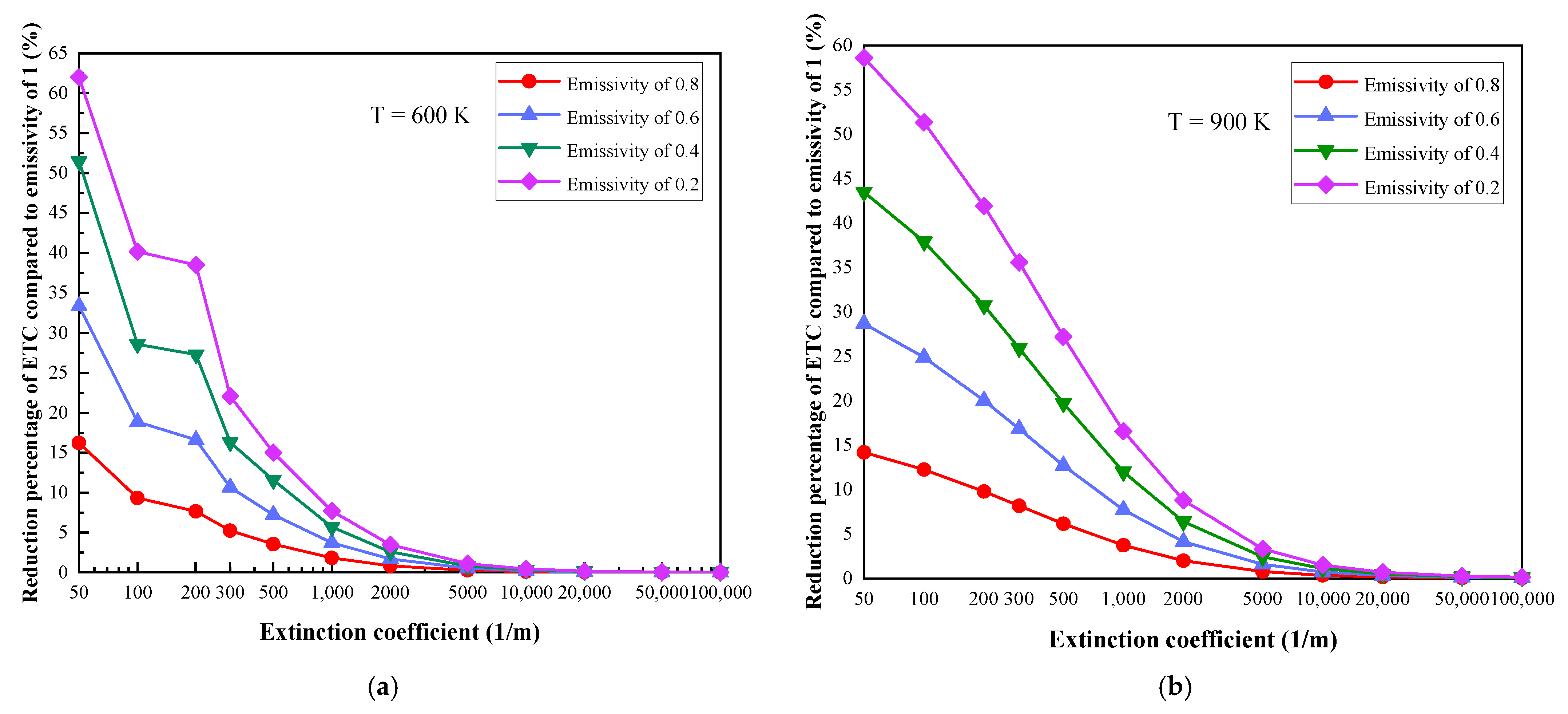
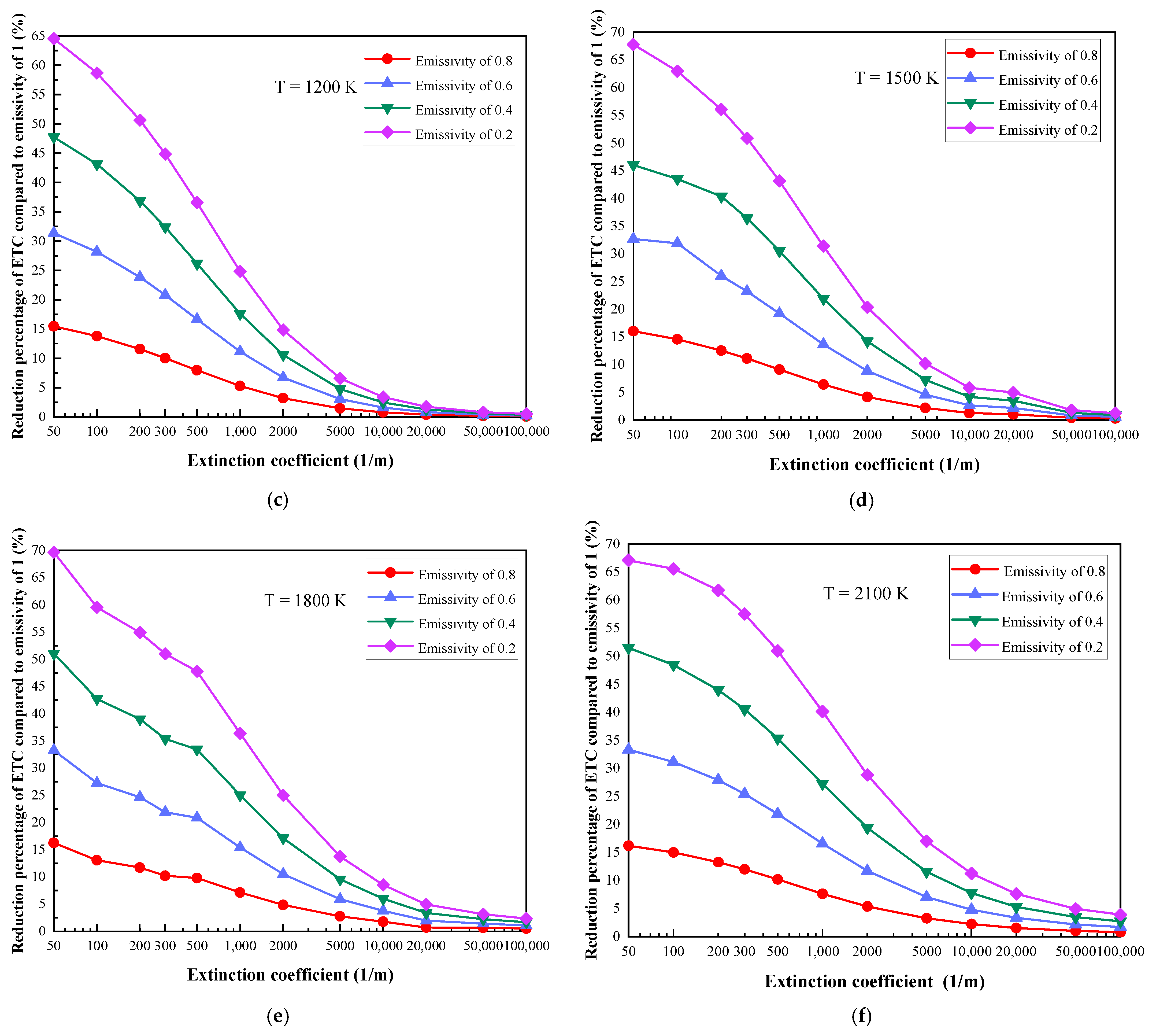
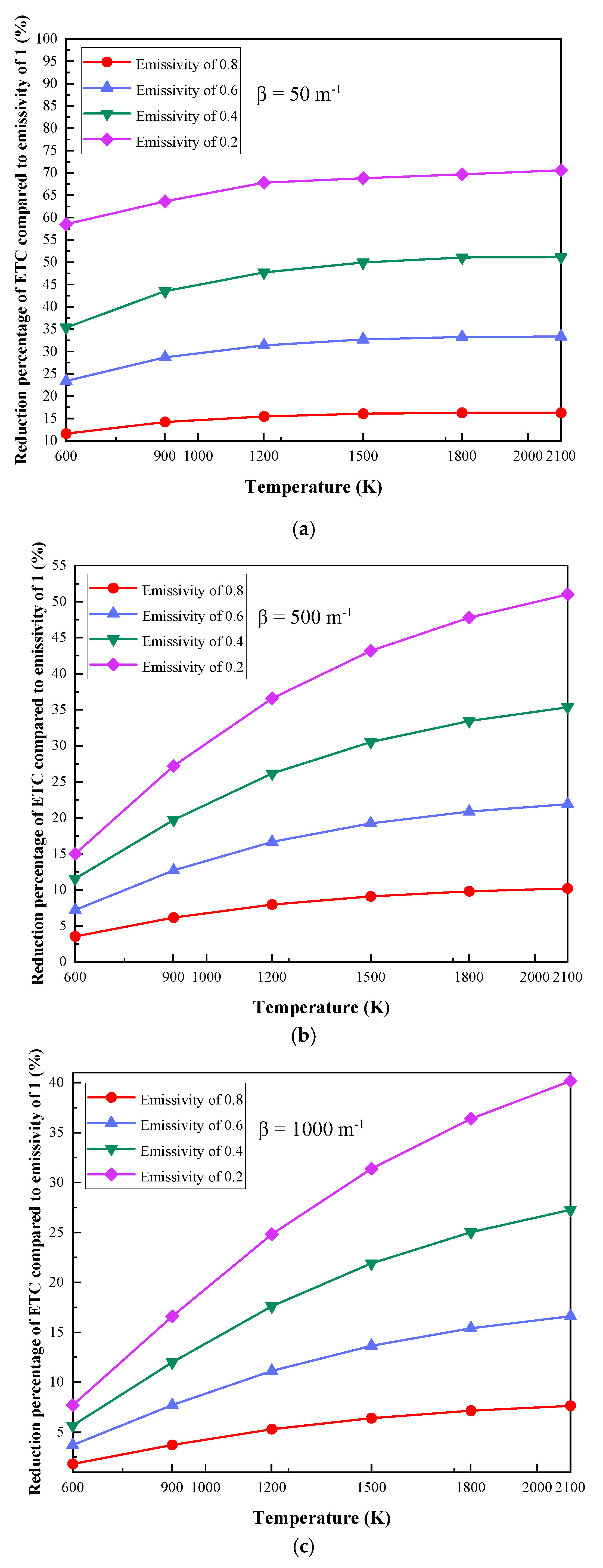
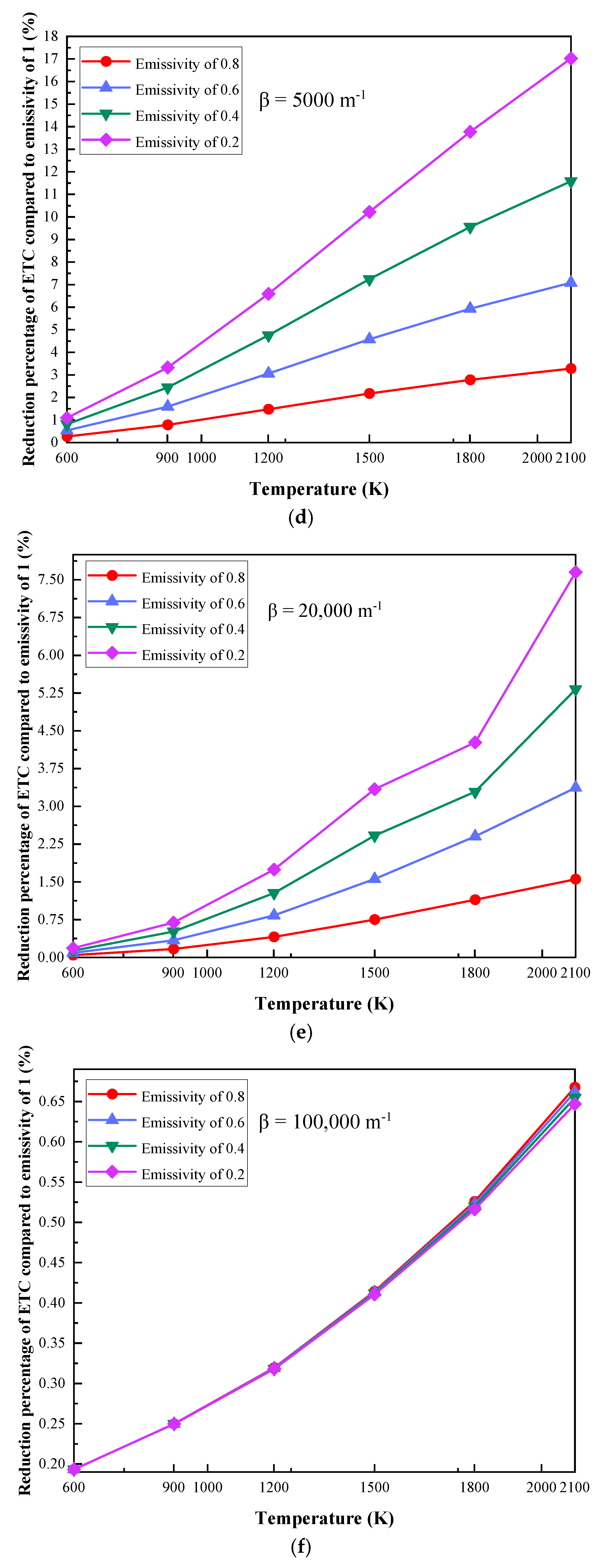
2.2. The Influence of Emissivity Variation with Different Boundary Temperatures
3. Conclusions
- (1)
- At specific boundary temperatures, the ETC decreases with the increase in the extinction coefficient. When the extinction coefficient increases from 50 m−1 to 100,000 m−1, ETC with an emissivity of 1 can be reduced by 44.76% and 89.47% at boundary temperatures of 600 K and 2100 K, respectively.
- (2)
- Compared to the system with an emissivity of 1, the reduction percentage of the ETC decreases with the increase in the extinction coefficient and increases with the decrease in emissivity at specific boundary temperatures. When the boundary temperature is 2100 K, the extinction coefficients are 50 m−1 and 100,000 m−1, and the ETC with emissivity values of 0.8 and 0.2 are reduced by 16.22% and 69.8%, and 0.82% and 3.94%, respectively.
- (3)
- For materials with small extinction coefficients, the decrease in emissivity has a great effect on the thermal insulation performance, and the reduction percentage of ETC can be up to 69.8%. However, when the extinction coefficient is large, the influence of emissivity variation can be ignored in this situation.
- (4)
- The ETC increases with the increase in the boundary temperature at specific extinction coefficients. When the boundary temperatures are 600 K and 2100 K, the ETC values are 0.3496 W/m. K and 6.3958 W/m. K at the extinction coefficient of 50 m−1 and emissivity of 1, respectively. This shows that the ETC increases greatly.
- (5)
- The reduction percentage of the ETC increases with the increase in the boundary temperature. When the extinction coefficient is 50 m−1, the boundary temperatures are 600 K and 1500 K, and the ETC with emissivity values of 0.8 and 0.2 are reduced by 11.61% and 47.5%, and 16.05% and 67.8%, respectively.
- (6)
- Higher boundary temperatures have a greater influence on the radiative heat transfer, and the reduction in emissivity has a good effect on the thermal insulation performance of the MTPS in this situation.
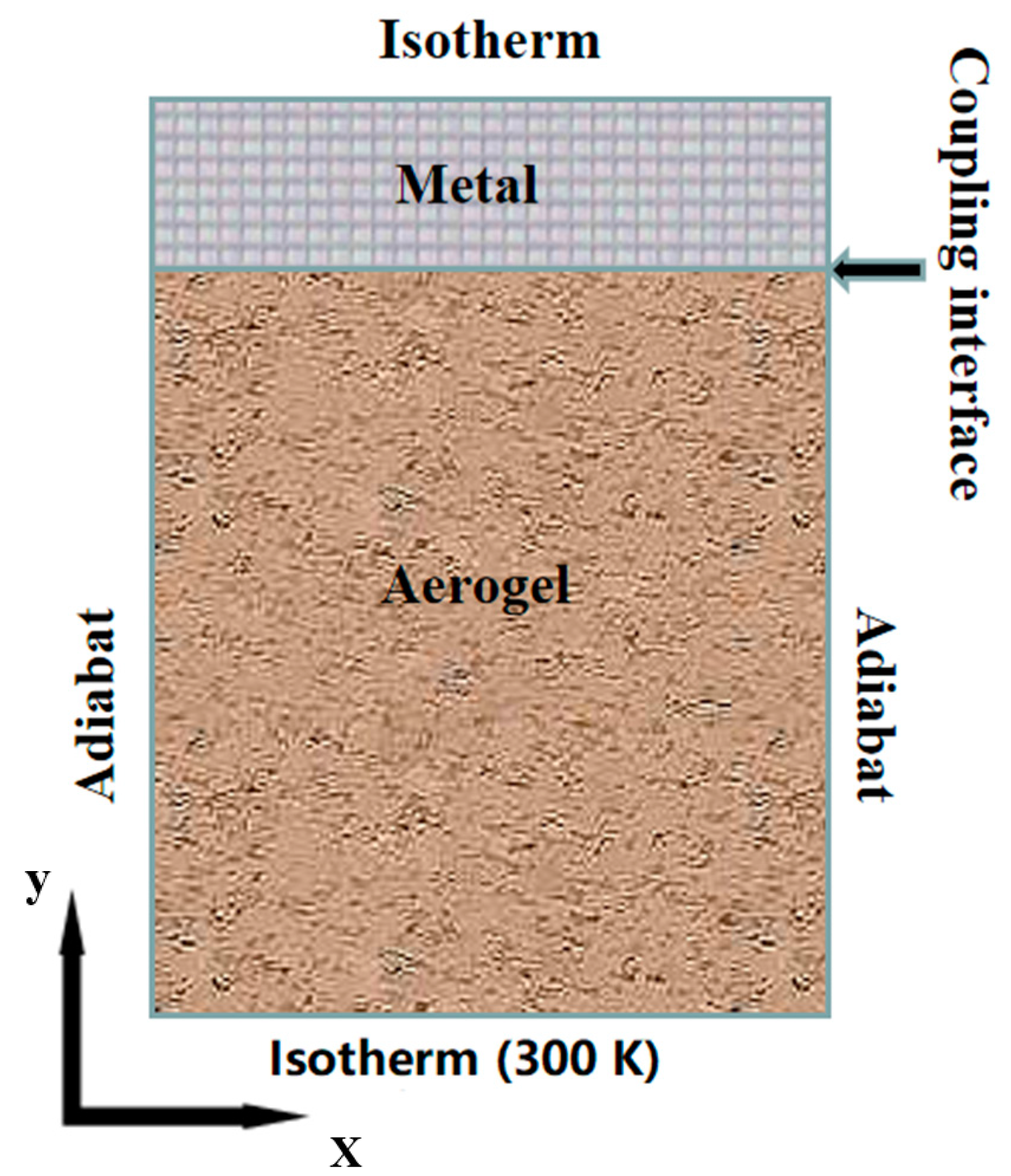
4. Methodology and Preparation Work
4.1. Methodology
4.2. Preparation Work
4.2.1. Verification of the Simulation
4.2.2. Computational Domain and Boundary Conditions
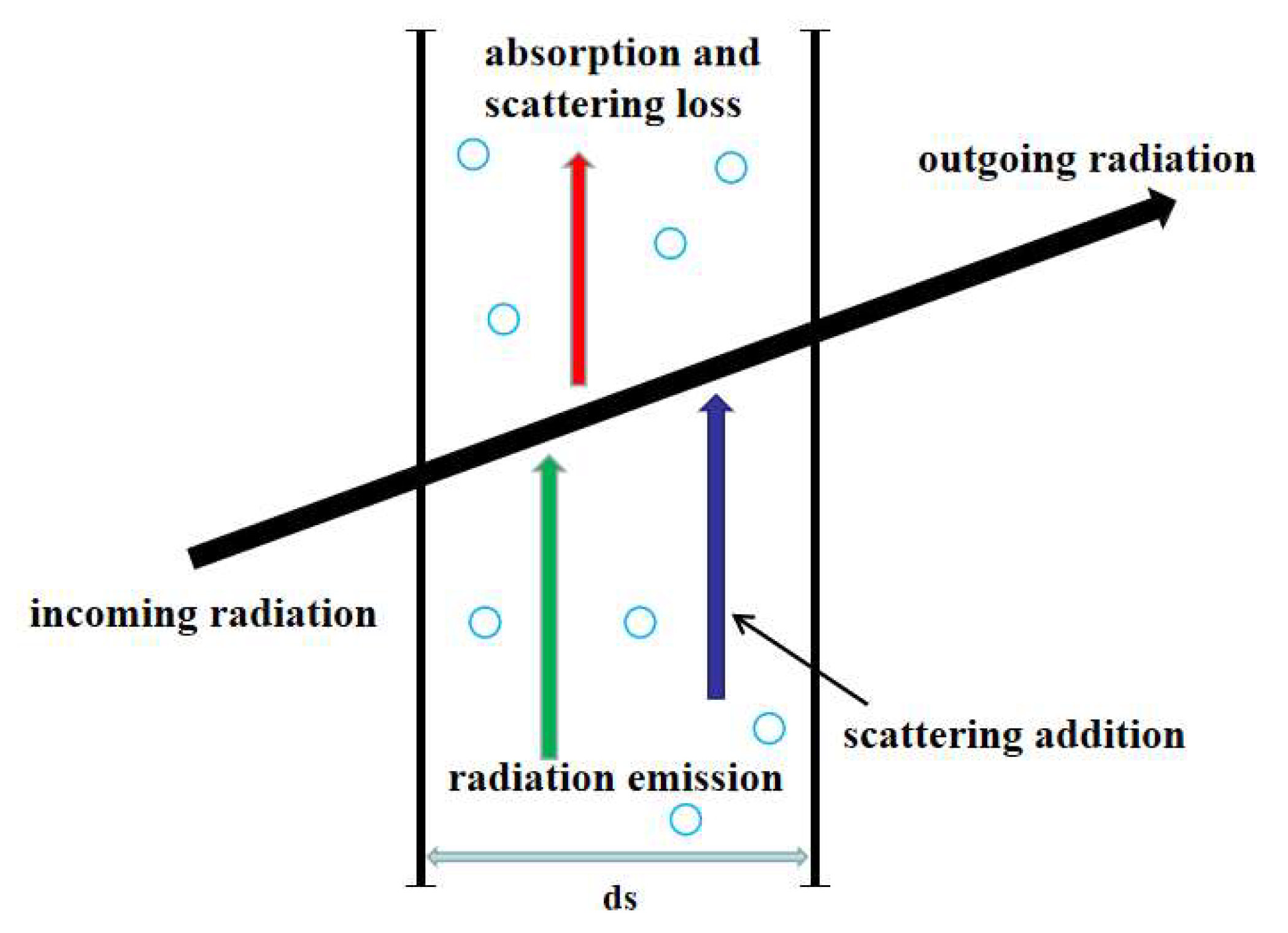
5. Numerical Method
5.1. Govern Equations
5.2. Numerical Methods
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Nomenclature | |
| the optical thickness | |
| the radiation emission from the coupling interface, | |
| the coupling interface temperature, | |
| the cold surface temperature, | |
| the boundary temperature, | |
| the temperature difference across the MTPS, | |
| specific heat capacity, | |
| the refractive index | |
| ,, | total heat flux, conductive heat flux and radiative heat flux, |
| radiative intensity emitted by a black body, | |
| the radiative intensity of space position r and transmission direction s, | |
| , | the components of radiative heat flux in and coordinates, |
| , | the th and th solid angle of the space direction |
| the total number of solid angles with a space direction of 4π | |
| the integral weight coefficient | |
| the radiation intensity of the wall, | |
| the temperature of the wall, | |
| the normal vector of the wall | |
| Greek symbols | |
| thickness of the aerogel, | |
| thickness of the MTPS, | |
| ,, | extinction, absorption and scattering coefficients, |
| λ | thermal conductivity of conduction, |
| density, | |
| the Stefan–Boltzmann constant | |
| inner emissivity of the aerogel | |
| emissivity of the coupling interface | |
| emissivity of the wall | |
| solid angle, | |
| scattering phase function | |
| , | direction cosine along the coordinate and coordinate, respectively |
| , | zenith angle and circumference angle, respectively |
| the scattering phase function after discretization |
References
- Xie, W.; Peng, Z.; Meng, S.; Xu, C.; Yi, F.; Jin, H.; Du, S. Thermal stress analysis of the FGLCS in hypersonic vehicles: Their application to fuel injection struts in scramjets. Compos. Part A 2017, 99, 157–165. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, X.; Huang, W.; Li, S.; Yan, L. Experimental investigation on drag and heat flux reduction in supersonic/hypersonic flows: A survey. Acta Astronaut. 2016, 129, 95–110. [Google Scholar] [CrossRef]
- Liu, H.; Liu, W. Thermal-structural analysis of the platelet heat-pipe-cooled leading edge of hypersonic vehicle. Acta Astronaut. 2016, 127, 13–19. [Google Scholar]
- Liu, G.; Zhou, B.; Du, A.; Shen, J.; Yu, Q. Effect of the thermal treatment on microstructure and physical properties of low-density and high transparency silica aerogels via acetonitrile supercritical drying. J. Porous Mater. 2013, 20, 1163–1170. [Google Scholar] [CrossRef]
- Zhang, H.; Gu, W.; Li, M.; Fang, W.; Li, Z.; Tao, W. Influence of environmental factors on the adsorption capacity and thermal conductivity of silica nano-porous materials. J. Nanosci. Nanotechnol. 2015, 15, 3048–3054. [Google Scholar] [CrossRef]
- Qiu, L.; Zou, H.; Tang, D.; Wen, D.; Feng, Y.; Zhang, X. Inhomogeneity in pore size appreciably lowering thermal conductivity for porous thermal insulators. Appl. Therm. Eng. 2018, 130, 1004–1011. [Google Scholar] [CrossRef]
- Kim, D.; Oh, S. Measurement and comparison of thermal conductivity of porous materials using box, dual-needle, and single-needle probe methods-a case study. Int. J. Heat Mass Transf. 2020, 118, 104815. [Google Scholar] [CrossRef]
- Coquard, R.; Randrianalisoa, J.; Lallich, S.; Baillis, D. Extension of the flash method to semitransparent polymer foams. ASME J. Heat Transf. 2011, 133, 112604. [Google Scholar] [CrossRef]
- Coquard, R.; Baillis, D.; Quenard, D. Experimental and theoretical study of the hot-wire method applied to low-density thermal insulators. Int. J. Heat Mass Transf. 2008, 47, 324–338. [Google Scholar] [CrossRef]
- Coquard, R.; Coment, E.; Flasquin, G.; Baillis, D. Analysis of the hot-disk technique applied to low-density insulating materials. Int. J. Therm. Sci. 2013, 65, 242–253. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Tao, W. Effect of radiative heat transfer on determining thermal conductivity of semi-transparent materials using transient plane source method. Appl. Therm. Eng. 2017, 114, 337–345. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, Y.; Wang, X.; Tang, G. Numerical study of the influence of thermal radiation on measuring semi-transparent thermal insulation material with hot wire method. Int. Commun. Heat Mass Transf. 2021, 121, 105120. [Google Scholar] [CrossRef]
- Jabbari, F.; S Aed Odin, S. Calculation of combined conduction-radiation heat transfer reduction using thick concentric spheres with temperature-dependent emissivity as radiation shields. Thermophys. Aeromech. 2016, 23, 567–574. [Google Scholar] [CrossRef]
- Zu, H.; Dai, W.; Li, Y.; Li, K.; Li, J. Analysis of enhanced heat transfer on a passive heat sink with high-emissivity coating. Int. J. Therm. Sci. 2021, 166, 106971. [Google Scholar] [CrossRef]
- Saravanan, S.; Raja, N. Coupled radiative and convective heat transfer in enclosures: Effect of inner heater-enclosure wall emissivity contrast. Phys. Fluids 2020, 32, 1–13. [Google Scholar] [CrossRef]
- Tan, W.; Petorak, C.A.; Trice, R.W. Rare-Earth Modified Zirconium Diboride High Emissivity Coatings for Hypersonic Applications. J. Eur. Ceram. Soc. 2014, 34, 1–11. [Google Scholar] [CrossRef]
- Chen, M.J.; Zhang, P.; Li, Q. Design and heat transfer analysis of a compound multi-layer insulations for use in high temperature cylinder thermal protection systems. Sci. China Technol. Sci. 2018, 61, 994–1002. [Google Scholar] [CrossRef]
- Ji, T.; Zhang, R.; Sunden, B.; Xie, G. Investigation on thermal performance of high temperature multilayer insulations for hypersonic vehicles under aerodynamic heating condition. Appl. Therm. Eng. 2014, 70, 957–965. [Google Scholar] [CrossRef]
- Paul, H.; Greenberger, D.M.; Stenholm, S.T.; Schleich, W.P. The Stefan–Boltzmann law: Two classical laws give a quantum one. Phys. Scr. 2015, 2015, 014027. [Google Scholar] [CrossRef]
- Zeng, S.Q.; Hunt, A.; Greif, R. Theoretical modeling of carbon content to minimize heat transfer in silica aerogel. J. Non-Cryst. Solids 1995, 186, 271–277. [Google Scholar] [CrossRef]
- Lu, X.; Arduini-Schuster, M.C.; Kuhn, J.; Nilsson, O.; Fricke, J.; Pekala, R.W. Thermal conductivity of monolithic organic aerogels. Science 1992, 221, 971–972. [Google Scholar] [CrossRef]
- Lu, X.; Caps, R.; Fricke, J.; Alviso, C.; Pekala, R. Correlation between structure and thermal conductivity of organic aerogels. J. Non-Cryst. Solids 1995, 188, 226–234. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, X.; Mei, X. High-Resolution Plasmonic Refractive-Index Sensor Based on a Metal-Insulator-Metal Structure. Chin. Phys. Lett. 2011, 28, 054205. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.; Bi, C.; Zhao, Y.; Tao, W. Thermal transport in nano-porous insulation of aerogel: Factors, models and outlook. Energy 2015, 90, 701–721. [Google Scholar] [CrossRef]
- Fu, T.; Peng, T.; Zhong, M. Experimental research on the influence of surface conditions on the total hemispherical emissivity of iron-based alloys. Exp. Therm. Fluid Sci. 2012, 40, 159–167. [Google Scholar] [CrossRef]
- Huang, Z.; Zhou, W.; Tang, X.; Luo, F.; Zhu, D. High-temperature application of the low-emissivity Au/Ni films on alloys. Appl. Surf. Sci. 2010, 256, 6893–6898. [Google Scholar] [CrossRef]
- Michael, F. Modest. Radiative Heat Transfer; American Academic Press: New York, NY, USA, 2003. [Google Scholar]
- Tao, W. Progress in Numerical Heat Transfer; Science & Technology Publishing Press: Beijing, China, 2000. [Google Scholar]




| TC (K) | 300 K | ||||||||||||||||||
| ε | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | ||||||||||||||
| TH (K) | 600 | 900 | 1200 | 1500 | 1800 | 2100 | |||||||||||||
| β (m−1) | 5 × 101 | 1 × 102 | 2 × 102 | 3 × 102 | 5 × 102 | 1 × 103 | 2 × 103 | 5 × 103 | 1 × 104 | 2 × 104 | 5 × 104 | 1 × 105 | |||||||
| Parameter | (kg/m3) | (J/kg·K) | (W/m·K) | |||
|---|---|---|---|---|---|---|
| Material | ||||||
| Metal | 8470 | 812 | 28 | 1.6 | 28 | |
| Aerogel | 300 | 1000 | 0.05 | 1.05 | 0.05 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, F.; Dong, S.; Ma, Y.; Qi, B.; Zhu, K. Numerical Study of the Influence of Coupling Interface Emissivity on Aerogel Metal Thermal Protection Performance. Gels 2021, 7, 250. https://doi.org/10.3390/gels7040250
Lou F, Dong S, Ma Y, Qi B, Zhu K. Numerical Study of the Influence of Coupling Interface Emissivity on Aerogel Metal Thermal Protection Performance. Gels. 2021; 7(4):250. https://doi.org/10.3390/gels7040250
Chicago/Turabian StyleLou, Fengfei, Sujun Dong, Yinwei Ma, Bin Qi, and Keyong Zhu. 2021. "Numerical Study of the Influence of Coupling Interface Emissivity on Aerogel Metal Thermal Protection Performance" Gels 7, no. 4: 250. https://doi.org/10.3390/gels7040250
APA StyleLou, F., Dong, S., Ma, Y., Qi, B., & Zhu, K. (2021). Numerical Study of the Influence of Coupling Interface Emissivity on Aerogel Metal Thermal Protection Performance. Gels, 7(4), 250. https://doi.org/10.3390/gels7040250





