Colloidal and Sedimentation Behavior of Kaolinite Suspension in Presence of Non-Ionic Polyacrylamide (PAM)
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
2.2. Transmission and Scanning Electron Microscopies
2.3. Particle Size Analysis Using Dynamic Light Scattering
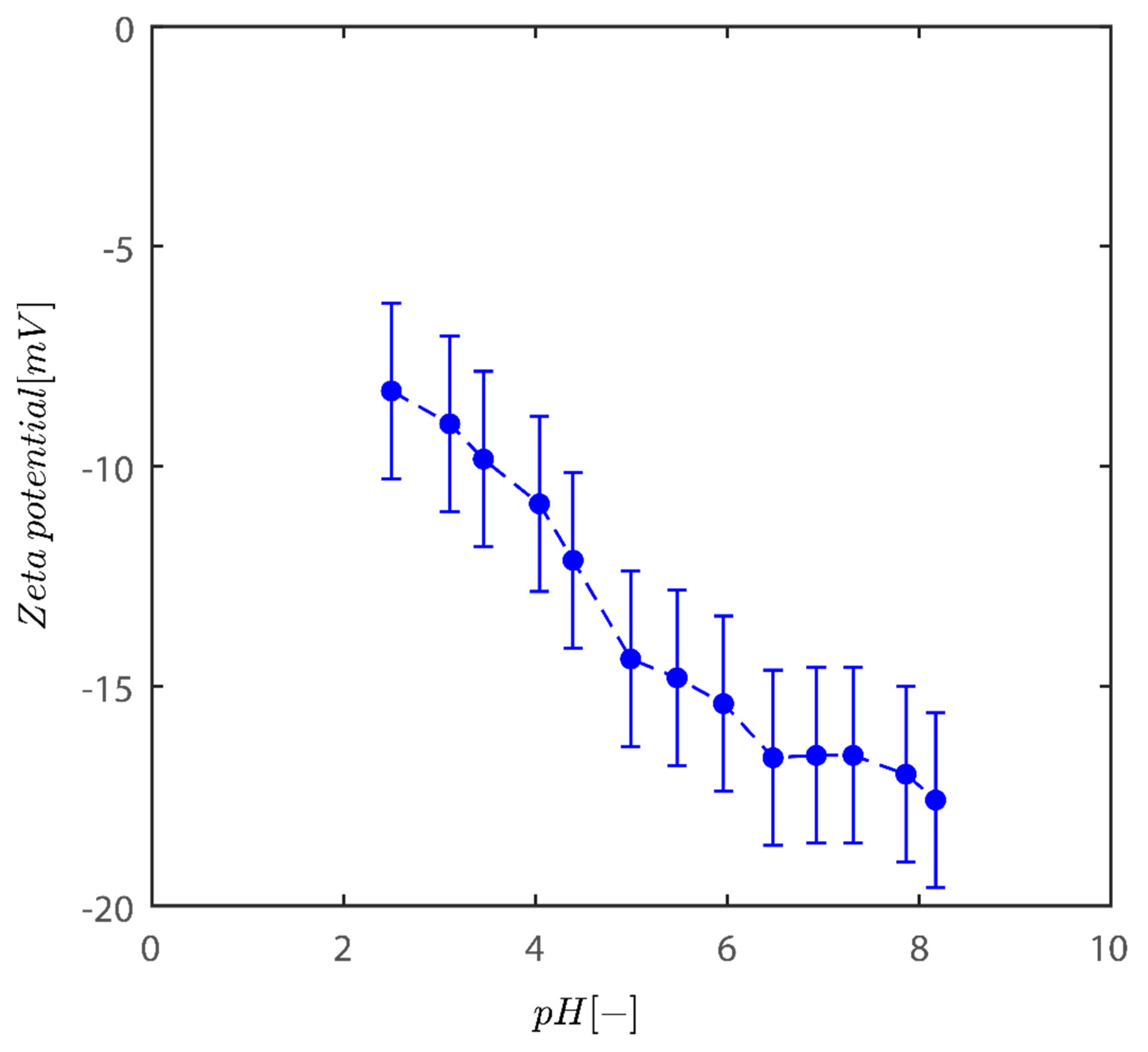
2.4. Zeta Potential Analysis
2.5. LUMisizer
2.5.1. Sedimentation Velocity Analysis
Description of Sedimentation Analysis Test
Centrifugal Force
Earth Gravity Conversion
Determining the Effective Maximum Volume Fraction
3. Results and Discussion
3.1. Dynamic Light Scattering
3.2. Transmission Electron Microscopy
3.3. Scanning Electron Microscopy of Freeze-Dried Flocs
3.4. Settling Behavior Analysis
3.5. Sedimentation Behavior in Presence of PAM
3.6. Simulation: Lubachevsky-Stillinger (LS)
3.7. Connection between DLS and Simulation Results
3.8. Compressive Yield Stress Estimation
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Edraki, M.; Berry, L. Investigating the settling behaviour of saline tailing suspensions using kaolinite, bentonite, and illite clay minerals. Powder Technol. 2018, 326, 228–236. [Google Scholar] [CrossRef] [Green Version]
- Abbasi Moud, A.; Poisson, J.; Hudson, Z.M.; Hatzikiriakos, S.G. Yield stress and wall slip of kaolinite networks. Phys. Fluid 2021, 33, 053105. [Google Scholar] [CrossRef]
- Piette, J.; Moud, A.A.; Poisson, J.; Derakhshandeh, B.; Hudson, Z.M.; Hatzikiriakos, S.G. Rheology of mature fine tailings. Phys. Fluid 2022, 34, 063104. [Google Scholar] [CrossRef]
- Johnston, C.T. Surface chemistry of oil-sands clay minerals. In Introduction to Oil Sands Clays; Clay Minerals Society: Chantilly, VA, USA, 2018; pp. 33–60. [Google Scholar]
- Li, Z.; Schulz, L.; Ackley, C.; Fenske, N. Adsorption of tetracycline on kaolinite with pH-dependent surface charges. J. Colloid Interface Sci. 2010, 351, 254–260. [Google Scholar] [CrossRef] [PubMed]
- Quezada, G.R.; Jeldres, M.; Toro, N.; Robles, P.; Toledo, P.G.; Jeldres, R.I. Understanding the flocculation mechanism of quartz and kaolinite with polyacrylamide in seawater: A molecular dynamics approach. Colloids Surf. Physicochem. Eng. Asp. 2021, 608, 125576. [Google Scholar] [CrossRef]
- Nakazawa, Y.; Abe, T.; Matsui, Y.; Shinno, K.; Kobayashi, S.; Shirasaki, N.; Matsushita, T. Differences in removal rates of virgin/decayed microplastics, viruses, activated carbon, and kaolin/montmorillonite clay particles by coagulation, flocculation, sedimentation, and rapid sand filtration during water treatment. Water Res. 2021, 203, 117550. [Google Scholar] [CrossRef] [PubMed]
- Moud, A.A. Polymer based flocculants: Review of water purification applications. J. Water Process Eng. 2022, 48, 102938. [Google Scholar] [CrossRef]
- Mpofu, P.; Addai-Mensah, J.; Ralston, J.J.I.J.o.M.P. Investigation of the effect of polymer structure type on flocculation, rheology and dewatering behaviour of kaolinite dispersions. Int. J. Miner. Process. 2003, 71, 247–268. [Google Scholar] [CrossRef]
- Lee, K.E.; Teng, T.T.; Morad, N.; Poh, B.T.; Hong, Y.F. Flocculation of kaolin in water using novel calcium chloride-polyacrylamide (CaCl2-PAM) hybrid polymer. Sep. Purif. Technol. 2010, 75, 346–351. [Google Scholar] [CrossRef]
- Zhang, L.; Min, F.; Wang, L.; Shu, Q. Polymeric flocculants based on the interfacial characteristics of fine clay minerals: A review. Physicochem. Probl. Miner. Process. 2022, 58, 149652. [Google Scholar] [CrossRef]
- Li, S.; Zhao, J.; Lu, P.; Xie, Y. Maximum packing densities of basic 3D objects. Chin. Sci. Bull. 2010, 55, 114–119. [Google Scholar] [CrossRef]
- Song, C.; Wang, P.; Makse, H.A. A phase diagram for jammed matter. Nature 2008, 453, 629–632. [Google Scholar] [CrossRef] [PubMed]
- Khirevich, S.; Höltzel, A.; Tallarek, U. Validation of pore-scale simulations of hydrodynamic dispersion in random sphere packings. Commun. Comput. Phys. 2013, 13, 801–822. [Google Scholar] [CrossRef]
- Zinchenko, A.Z. Algorithm for random close packing of spheres with periodic boundary conditions. J. Comput. Phys. 1994, 114, 298–307. [Google Scholar] [CrossRef]
- Scott, G.D.; Kilgour, D.M. The density of random close packing of spheres. J. Phys. D Appl. Phys. 1969, 2, 863. [Google Scholar] [CrossRef]
- CS, O.H.; Silbert, L.A.; Liu, A.J.; Nagel, S.R. Jamming at zero temperature and zero applied stress: The epitome of disorder. Phys. Rev. E 2003, 68, 011306. [Google Scholar]
- Jin, Y.; Makse, H.A. A first-order phase transition defines the random close packing of hard spheres. Phys. A Stat. Mech. Its Appl. 2010, 389, 5362–5379. [Google Scholar] [CrossRef] [Green Version]
- Bernal, J.; Mason, J. Packing of spheres: Co-ordination of randomly packed spheres. Nature 1960, 188, 910–911. [Google Scholar] [CrossRef]
- Berryman, J.G. Random close packing of hard spheres and disks. Phys. Rev. A 1983, 27, 1053. [Google Scholar] [CrossRef]
- Anikeenko, A.; Medvedev, N.; Aste, T. Structural and entropic insights into the nature of the random-close-packing limit. Phys. Rev. E 2008, 77, 031101. [Google Scholar] [CrossRef] [Green Version]
- Kapfer, S.C.; Mickel, W.; Mecke, K.; Schröder-Turk, G.E. Jammed spheres: Minkowski tensors reveal onset of local crystallinity. Phys. Rev. E 2012, 85, 030301. [Google Scholar] [CrossRef] [PubMed]
- Khrapak, S.; Klumov, B.; Morfill, G. Electric potential around an absorbing body in plasmas: Effect of ion-neutral collisions. Phys. Rev. Lett. 2008, 100, 225003. [Google Scholar] [CrossRef]
- Bargiel, M.; Tory, E.M. Packing fraction and measures of disorder of ultradense irregular packings of equal spheres. II. Transition from dense random packing. Adv. Powder Technol. 2001, 12, 533–557. [Google Scholar] [CrossRef]
- Aste, T.; Di Matteo, T. Structural transitions in granular packs: Statistical mechanics and statistical geometry investigations. Eur. Phys. J. B 2008, 64, 511–517. [Google Scholar] [CrossRef] [Green Version]
- Aste, T.; Coniglio, A. Cell theory for liquid solids and glasses: From local packing configurations to global complex behaviors. EPL Europhys. Lett. 2004, 67, 165. [Google Scholar] [CrossRef] [Green Version]
- Lochmann, K.; Anikeenko, A.; Elsner, A.; Medvedev, N.; Stoyan, D. Statistical verification of crystallization in hard sphere packings under densification. Eur. Phys. J. B-Condens. Matter Complex Syst. 2006, 53, 67–76. [Google Scholar] [CrossRef]
- Baranau, V.; Hlushkou, D.; Khirevich, S.; Tallarek, U. Pore-size entropy of random hard-sphere packings. Soft Matter 2013, 9, 3361–3372. [Google Scholar] [CrossRef]
- Parisi, G.; Zamponi, F. Mean-field theory of hard sphere glasses and jamming. Rev. Mod. Phys. 2010, 82, 789. [Google Scholar] [CrossRef]
- Abbasi Moud, A.; Hatzikiriakos, S.G. Kaolinite colloidal suspensions under the influence of sodium dodecyl sulfate. Phys. Fluid 2022, 34, 013107. [Google Scholar] [CrossRef]
- Li, W.; Zhao, C.; Zheng, H.; Ding, J.; Hao, S.; Zhou, Y.; Li, X. Review of the Template Copolymerization of Cationic Polyacrylamide. Mini-Rev. Org. Chem. 2018, 15, 141–147. [Google Scholar] [CrossRef]
- Antonopoulou, E.; Rohmann-Shaw, C.F.; Sykes, T.C.; Cayre, O.J.; Hunter, T.N.; Jimack, P.K. Numerical and experimental analysis of the sedimentation of spherical colloidal suspensions under centrifugal force. Phys. Fluid 2018, 30, 030702. [Google Scholar] [CrossRef]
- Derakhshandeh, B. Kaolinite suspension as a model fluid for fluid dynamics studies of fluid fine tailings. Rheol. Acta 2016, 55, 749–758. [Google Scholar] [CrossRef]
- Au, P.-I.; Leong, Y.-K. Rheological and zeta potential behaviour of kaolin and bentonite composite slurries. Colloids Surf. Physicochem. Eng. Asp. 2013, 436, 530–541. [Google Scholar] [CrossRef]
- Goh, R.; Leong, Y.-K.; Lehane, B. Bentonite slurries—zeta potential, yield stress, adsorbed additive and time-dependent behaviour. Rheol. Acta 2011, 50, 29–38. [Google Scholar] [CrossRef]
- Shankar, P.; Teo, J.; Leong, Y.-K.; Fourie, A.; Fahey, M. Adsorbed phosphate additives for interrogating the nature of interparticles forces in kaolin clay slurries via rheological yield stress. Adv. Powder Technol. 2010, 21, 380–385. [Google Scholar] [CrossRef]
- Leong, Y.-K.; Teo, J.; Teh, E.; Smith, J.; Widjaja, J.; Lee, J.-X.; Fourie, A.; Fahey, M.; Chen, R. Controlling attractive interparticle forces via small anionic and cationic additives in kaolin clay slurries. Chem. Eng. Res. Des. 2012, 90, 658–666. [Google Scholar] [CrossRef]
- Tombácz, E.; Szekeres, M. Surface charge heterogeneity of kaolinite in aqueous suspension in comparison with montmorillonite. Appl. Clay Sci. 2006, 34, 105–124. [Google Scholar] [CrossRef]
- Kelessidis, V.C.; Tsamantaki, C.; Dalamarinis, P. Effect of pH and electrolyte on the rheology of aqueous Wyoming bentonite dispersions. Appl. Clay Sci. 2007, 38, 86–96. [Google Scholar] [CrossRef]
- Chang, C.-W.; Liao, Y.-C. Accelerated sedimentation velocity assessment for nanowires stabilized in a non-Newtonian fluid. Langmuir 2016, 32, 13620–13626. [Google Scholar] [CrossRef] [PubMed]
- Licea-Claverie, A.; Schwarz, S.; Steinbach, C.; Montserrat Ponce-Vargas, S.; Genest, S. Combination of natural and thermosensitive polymers in flocculation of fine silica dispersions. Int. J. Carbohydr. Chem. 2013, 2013. [Google Scholar] [CrossRef]
- Sobisch, T.; Lerche, D. Experimental evaluation of effect of continuous phase rheology on sedimentation behaviour. In Proceedings of the Filtech Köln, Cologne, Germany, 11–13 October 2016; pp. 11–13. [Google Scholar]
- Lerche, D.; Sobisch, T. Direct and accelerated characterization of formulation stability. Journal Dispers. Sci. Technol. 2011, 32, 1799–1811. [Google Scholar] [CrossRef]
- Tehrani-Bagha, A. Cationic gemini surfactant with cleavable spacer: Emulsion stability. Colloids Surf. A Physicochem. Eng. Asp. 2016, 508, 79–84. [Google Scholar] [CrossRef]
- Hayes, M.; Smith, M. Slip in adhesion tests of a Kaolin clay. Eur. Phys. J. E 2021, 44, 102. [Google Scholar] [CrossRef]
- Metin, C. Characterization of Nanoparticle Transport in Flow through Permeable Media; The University of Texas at Austin: Austin, TX, USA, 2012. [Google Scholar]
- Qi, F.; Tanner, R.I. Random close packing and relative viscosity of multimodal suspensions. Rheol. Acta 2012, 51, 289–302. [Google Scholar] [CrossRef]
- Overbeek, J.T.G. Recent developments in the understanding of colloid stability. In Plenary and Invited Lectures; Elsevier: Amsterdam, The Netherlands, 1977; pp. 431–445. [Google Scholar]
- Alagha, L.; Wang, S.; Xu, Z.; Masliyah, J. Adsorption kinetics of a novel organic–inorganic hybrid polymer on silica and alumina studied by quartz crystal microbalance. J. Phys. Chem. C 2011, 115, 15390–15402. [Google Scholar] [CrossRef]
- Alagha, L.; Wang, S.; Yan, L.; Xu, Z.; Masliyah, J. Probing adsorption of polyacrylamide-based polymers on anisotropic basal planes of kaolinite using quartz crystal microbalance. Langmuir 2013, 29, 3989–3998. [Google Scholar] [CrossRef]
- Lerche, D. Dispersion stability and particle characterization by sedimentation kinetics in a centrifugal field. Journal Dispers. Sci. Technol. 2002, 23, 699–709. [Google Scholar] [CrossRef]
- He, W.; Zhang, Y.; Fatehi, P. Sulfomethylated kraft lignin as a flocculant for cationic dye. Colloids Surf. Physicochem. Eng. Asp. 2016, 503, 19–27. [Google Scholar] [CrossRef]
- Rao, J.; Fernández-Ronco, M.P.; Vong, M.; Gaan, S. Enhanced flame-retardancy and controlled physical properties of flexible polyurethane foams based on a shear-responsive internal network. RSC Adv. 2017, 7, 44013–44020. [Google Scholar] [CrossRef] [Green Version]
- Richardson, J. WN Zaki Sedimentation and fluidization: Part I. Chem. Ical Eng. Res. Des. 1997, 75, S82. [Google Scholar] [CrossRef]
- Rao, R.; Mondy, L.; Sun, A.; Altobelli, S. A numerical and experimental study of batch sedimentation and viscous resuspension. Int. J. Numer. Methods Fluids 2002, 39, 465–483. [Google Scholar] [CrossRef]
- Hasan, A.; Fatehi, P. Flocculation of kaolin particles with cationic lignin polymers. Sci. Rep. 2019, 9, 2672. [Google Scholar] [CrossRef] [PubMed]
- Solomon, M.J.; Spicer, P.T. Microstructural regimes of colloidal rod suspensions, gels, and glasses. Soft Matter 2010, 6, 1391–1400. [Google Scholar] [CrossRef]
- Growney, D.J.; Fowler, P.W.; Mykhaylyk, O.O.; Fielding, L.A.; Derry, M.J.; Aragrag, N.; Lamb, G.D.; Armes, S.P. Determination of effective particle density for sterically stabilized carbon black particles: Effect of diblock copolymer stabilizer composition. Langmuir 2015, 31, 8764–8773. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Lubachevsky, B.D. Crystalline—Amorphous interface packings for disks and spheres. J. Stat. Phys. 1993, 73, 497–514. [Google Scholar] [CrossRef]
- Lubachevsky, B.D.; Stillinger, F.H. Geometric properties of random disk packings. J. Stat. Phys. 1990, 60, 561–583. [Google Scholar] [CrossRef]
- Lubachevsky, B.D. How to simulate billiards and similar systems. J. Comput. Phys. 1991, 94, 255–283. [Google Scholar] [CrossRef] [Green Version]
- Lubachevsky, B.D.; Stillinger, F.H. Epitaxial frustration in deposited packings of rigid disks and spheres. Phys. Rev. E 2004, 70, 041604. [Google Scholar] [CrossRef] [Green Version]
- Lubachevsky, B.D.; Graham, R.L.; Stillinger, F.H. Spontaneous Patterns in Disk Packings. In Bridges: Mathematical Connections in Art, Music, and Science; Sarhangi, R., Ed.; Gilliland Printing: Arkansas City, KS, USA, 1998; pp. 181–193. [Google Scholar]
- Kansal, A.R.; Torquato, S.; Stillinger, F.H. Computer generation of dense polydisperse sphere packings. J. Chem. Phys. 2002, 117, 8212–8218. [Google Scholar] [CrossRef] [Green Version]
- Monti, J.M.; Clemmer, J.T.; Srivastava, I.; Silbert, L.E.; Grest, G.S.; Lechman, J.B. Large-scale frictionless jamming with power-law particle size distributions. Phys. Rev. E 2022, 106, 034901. [Google Scholar] [CrossRef] [PubMed]
- Petit, J.C.; Kumar, N.; Luding, S.; Sperl, M. Bulk modulus along jamming transition lines of bidisperse granular packings. Phys. Rev. E 2022, 106, 054903. [Google Scholar] [CrossRef]
- Gnidovec, A.; Božič, A.; Čopar, S. Dense packings of geodesic hard ellipses on a sphere. Soft Matter 2022, 18, 7670–7678. [Google Scholar] [CrossRef] [PubMed]
- Mościński, J.; Bargieł, M.; Rycerz, Z.; Jacobs, P. The force-biased algorithm for the irregular close packing of equal hard spheres. Mol. Simul. 1989, 3, 201–212. [Google Scholar] [CrossRef]
- Zhang, W.; He, L.; Wang, F.; Zhang, G. A Stochastic Filling and Modeling Algorithm of Non-Equal Diameter Particles with Specified Probability Density for Porous Permeable Materials. Materials 2022, 15, 4733. [Google Scholar] [CrossRef] [PubMed]
- Blétry, M.; Russier, V.; Barbé, E.; Blétry, J. Structure of sticky-hard-sphere random aggregates: The viewpoint of contact coordination and tetrahedra. Phys. Rev. E 2018, 98, 012101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Woodcock, L.V. Glass transition in the hard-sphere model and Kauzmann’s paradox. Ann. N. Y. Acad. Sci 1981, 371, 274–298. [Google Scholar] [CrossRef]
- Baranau, V.; Tallarek, U. Random-close packing limits for monodisperse and polydisperse hard spheres. Soft Matter 2014, 10, 3826–3841. [Google Scholar] [CrossRef] [Green Version]
- Donev, A.; Stillinger, F.H.; Chaikin, P.; Torquato, S. Unusually dense crystal packings of ellipsoids. Phys. Rev. Lett. 2004, 92, 255506. [Google Scholar] [CrossRef] [Green Version]
- Skoge, M.; Donev, A.; Stillinger, F.H.; Torquato, S. Packing hyperspheres in high-dimensional Euclidean spaces. Phys. Rev. E 2006, 74, 041127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dickinson, E. Polydisperse suspensions of spherical colloidal particles: Analogies with multicomponent molecular liquid mixtures. Ind. Eng. Chem. Prod. Res. Dev. 1986, 25, 82–87. [Google Scholar] [CrossRef]
- Adamczyk, Z.; Siwek, B.; Zembala, M.; Weroński, P. Influence of polydispersity on random sequential adsorption of spherical particles. J. Colloid Interface Sci. 1997, 185, 236–244. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Molecular size distribution in linear condensation polymers1. J. Am. Chem. Soc. 1936, 58, 1877–1885. [Google Scholar] [CrossRef]
- Zhang, C.; O’Donovan, C.B.; Corwin, E.I.; Cardinaux, F.; Mason, T.G.; Möbius, M.E.; Scheffold, F. Structure of marginally jammed polydisperse packings of frictionless spheres. Phys. Rev. E 2015, 91, 032302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farr, R.S. Random close packing fractions of lognormal distributions of hard spheres. Powder Technol. 2013, 245, 28–34. [Google Scholar] [CrossRef] [Green Version]
- Sohn, H.Y.; Moreland, C. The effect of particle size distribution on packing density. Can. J. Chem. Eng. 1968, 46, 162–167. [Google Scholar] [CrossRef]
- Brouwers, H. Packing fraction of particles with lognormal size distribution. Phys. Rev. E 2014, 89, 052211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, A.; Miller, C.; Turcoliver, L. Simulation of correlated and uncorrelated packing of random size spheres. Phys. Rev. E 1996, 53, 1516. [Google Scholar] [CrossRef] [PubMed]
- Cárdenas-Barrantes, M.; Cantor, D.; Barés, J.; Renouf, M.; Azéma, E. Three-dimensional compaction of soft granular packings. Soft Matter 2022, 18, 312–321. [Google Scholar] [CrossRef] [PubMed]
- Buscall, R.; White, L.R. The consolidation of concentrated suspensions. Part 1.—The theory of sedimentation. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1987, 83, 873–891. [Google Scholar] [CrossRef]
- De Kretser, R.G.; Boger, D.V.; Scales, P.J. Compressive rheology: An overview. Rheol. Rev. 2003, 1, 125–166. [Google Scholar]
- Abbasi Moud, A. Chiral Liquid Crystalline Properties of Cellulose Nanocrystals: Fundamentals and Applications. ACS Omega 2022, 7, 30673–30699. [Google Scholar] [CrossRef] [PubMed]
- Aboutalebi, S.H.; Gudarzi, M.M.; Zheng, Q.B.; Kim, J.K. Spontaneous formation of liquid crystals in ultralarge graphene oxide dispersions. Adv. Funct. Mater. 2011, 21, 2978–2988. [Google Scholar] [CrossRef]
- Yu, A.B.; Standish, N.; McLean, A. Porosity calculation of binary mixtures of nonspherical particles. J. Am. Ceram. Soc. 1993, 76, 2813–2816. [Google Scholar] [CrossRef]
- Westman, A.E.R. The packing of particles: Empirical equations for intermediate diameter ratios. J. Am. Ceram. Soc. 1936, 19, 127–129. [Google Scholar] [CrossRef]












| Sample | Concentration [vol%] | Sediment Bed Length [mm] | Maximum Length [mm] | Length Difference [mm] | Volume of Particle Added [mm3] | Maximum Packing [-] |
|---|---|---|---|---|---|---|
| Sigma I | 2.7 | 126.7 ± 0.5 | 130 | 3.3 ± 0.5 | 29.6 | 0.4 (0.35,0.46) |
| Sigma I | 5.4 | 123.7 ± 0.5 | 130 | 6.3 ± 0.5 | 59.2 | 0.42 (0.41,0.48) |
| Sigma II | 2.7 | 125.1 ± 0.5 | 130 | 4.9 ± 0.5 | 29.6 | 0.27 (0.25,0.31) |
| Sigma II | 5.4 | 121.9 ± 0.3 | 130 | 8.1 ± 0.3 | 59.2 | 0.33 (0.32,0.34) |
| Riedel | 2.7 | 126.1 ± 1.1 | 130 | 3.9 ± 0.3 | 29.6 | 0.34 (0.32,0.37) |
| Riedel | 5.4 | 122.9 ± 0.5 | 130 | 7.1 ± 0.5 | 59.2 | 0.38 (0.35,0.41) |
| Sample | Applied Centrifugation [RPM] | Mean Speed of Sedimentation [%/s] |
|---|---|---|
| Sigma I | 4000 | 0.25 |
| Sigma II | 4000 | 0.27 |
| Riedel | 4000 | 0.28 |
| Sigma I | 200 | 0.16 |
| Sigma I | 500 | 0.29 |
| Sigma I | 1000 | 0.33 |
| Sigma I | 4000 | 0.25 |
| Sigma I + 7.5 ppm PAM | 200 | 0.04 |
| Sigma I + 15 ppm PAM | 200 | 0.04 |
| Sigma I + 7.5 ppm PAM | 4000 | 0.03 |
| Sigma I + 15 ppm PAM | 4000 | 0.04 |
| Condition [rpm] | Median, [nm] | Harmonic Mean, [nm] | Kaolinite Concentration [wt%] | PAM Concentration [ppm] |
|---|---|---|---|---|
| 200 | 10100 | 10557 | 0.1 | 0 |
| 500 | 3957 | 2630 | 0.1 | 0 |
| 1000 | 2112 | 1300 | 0.1 | 0 |
| 4000 | 1302 | 893 | 0.1 | 0 |
| 200 | 1695 | 2135 | 0.1 | 7.5 |
| 4000 | 278.7 | 254 | 0.1 | 7.5 |
| 200 | 2719 | 2497 | 0.1 | 15 |
| 4000 | 262 | 241 | 0.1 | 15 |
| Compression Rate | Polydispersity [-] | Force-Biased (FB) | LS | LSGD | Visual Depiction |
|---|---|---|---|---|---|
| 1.00 × 10−1 | 2.89 × 10−1 | 6.18 × 10−1 | 6.42 × 10−1 |  | |
| 1.00 × 10−2 | 5.07 × 10−1 | 6.41 × 10−1 | 6.41 × 10−1 |  | |
| 1.00 × 10−3 | 5.85 × 10−1 | 6.45 × 10−1 | 6.45 × 10−1 |  | |
| 1.00 × 10−4 | 6.29 × 10−1 | 6.34 × 10−1 | 6.34 × 10−1 |  | |
| 1.00 × 10−5 | 6.47 × 10−1 | 6.48 × 10−1 | 6.48 × 10−1 |  | |
| 1.00 × 10−1 | 3.13 × 10−1 | 6.01 × 10−1 | 6.29 × 10−1 |  | |
| 1.00 × 10−2 | 5.10 × 10−1 | 6.29 × 10−1 | 6.37 × 10−1 |  | |
| 1.00 × 10−3 | 5.99 × 10−1 | 6.43 × 10−1 | 6.43 × 10−1 |  | |
| 1.00 × 10−4 | 6.32 × 10−1 | 6.34 × 10−1 | 6.34 × 10−1 |  | |
| 1.00 × 10−5 | 6.38 × 10−1 | 6.39 × 10−1 | 6.39 × 10−1 |  | |
| 1.00 × 10−1 | 2.99 × 10−1 | 6.29 × 10−1 | 6.37 × 10−1 |  | |
| 1.00 × 10−2 | 4.70 × 10−1 | 6.48 × 10−1 | 6.50 × 10−1 |  | |
| 1.00 × 10−3 | 6.12 × 10−1 | 6.46 × 10−1 | 6.46 × 10−1 |  | |
| 1.00 × 10−4 | 6.44 × 10−1 | 6.53 × 10−1 | 6.53 × 10−1 |  | |
| 1.00 × 10−5 | 6.47 × 10−1 | 6.47 × 10−1 | 6.47 × 10−1 |  | |
| 1.00 × 10−1 | 3.12 × 10−1 | 6.19 × 10−1 | 6.65 × 10−1 |  | |
| 1.00 × 10−2 | 5.24 × 10−1 | 6.45 × 10−1 | 6.50 × 10−1 |  | |
| 1.00 × 10−3 | 6.08 × 10−1 | 6.61 × 10−1 | 6.61 × 10−1 |  | |
| 1.00 × 10−4 | 6.54 × 10−1 | 6.68 × 10−1 | 6.68 × 10−1 |  | |
| 1.00 × 10−5 | 6.54 × 10−1 | 6.55 × 10−1 | 6.55 × 10−1 |  | |
| 1.00 × 10−1 | 3.17 × 10−1 | 6.19 × 10−1 | 6.72 × 10−1 |  | |
| 1.00 × 10−2 | 5.11 × 10−1 | 6.67 × 10−1 | 6.71 × 10−1 |  | |
| 1.00 × 10−3 | 6.19 × 10−1 | 6.78 × 10−1 | 6.78 × 10−1 |  | |
| 1.00 × 10−4 | 6.59 × 10−1 | 6.86 × 10−1 | 6.86 × 10−1 |  | |
| 1.00 × 10−5 | 6.69 × 10−1 | 6.70 × 10−1 | 6.70 × 10−1 |  |
| Sample | Concentration [vol%] | Sediment Bed Length [mm] | Maximum Length [mm] | Length Difference [mm] | Compressive Yield Stress [kPa] |
|---|---|---|---|---|---|
| Sigma I | 2.7 | 126.7 ± 0.5 | 130 | 3.3 ± 0.5 | 49 |
| Sigma I | 5.4 | 123.7 ± 0.5 | 130 | 6.3 ± 0.5 | 94 |
| Sigma II | 2.7 | 125.1 ± 0.5 | 130 | 4.9 ± 0.5 | 48 |
| Sigma II | 5.4 | 121.9 ± 0.3 | 130 | 8.1 ± 0.3 | 92 |
| Riedel | 2.7 | 126.1 ± 1.1 | 130 | 3.9 ± 0.3 | 48 |
| Riedel | 5.4 | 122.9 ± 0.5 | 130 | 7.1 ± 0.5 | 93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbasi Moud, A. Colloidal and Sedimentation Behavior of Kaolinite Suspension in Presence of Non-Ionic Polyacrylamide (PAM). Gels 2022, 8, 807. https://doi.org/10.3390/gels8120807
Abbasi Moud A. Colloidal and Sedimentation Behavior of Kaolinite Suspension in Presence of Non-Ionic Polyacrylamide (PAM). Gels. 2022; 8(12):807. https://doi.org/10.3390/gels8120807
Chicago/Turabian StyleAbbasi Moud, Aref. 2022. "Colloidal and Sedimentation Behavior of Kaolinite Suspension in Presence of Non-Ionic Polyacrylamide (PAM)" Gels 8, no. 12: 807. https://doi.org/10.3390/gels8120807
APA StyleAbbasi Moud, A. (2022). Colloidal and Sedimentation Behavior of Kaolinite Suspension in Presence of Non-Ionic Polyacrylamide (PAM). Gels, 8(12), 807. https://doi.org/10.3390/gels8120807






