Modeling Tunable Fracture in Hydrogel Shell Structures for Biomedical Applications
Abstract
:1. Introduction
2. Material Models for Fracture
2.1. Phase Field Discretization
2.2. A Material Model for Heart Tissue
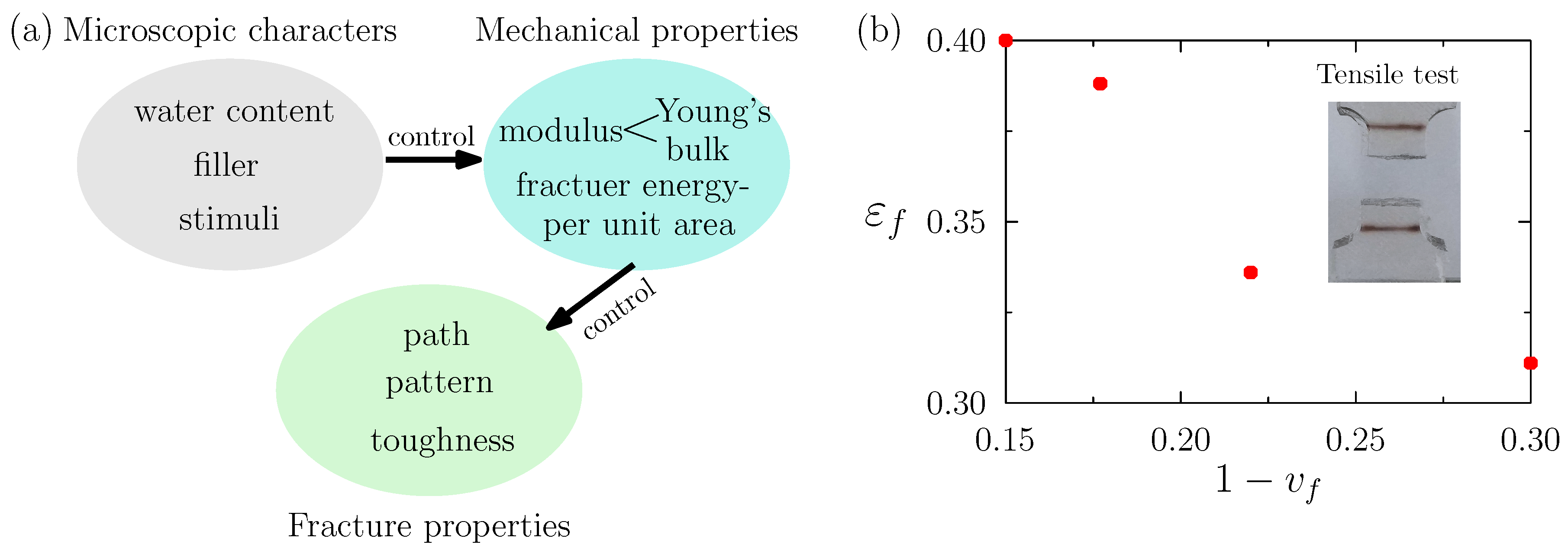
2.3. Toward Tuned Fracture Properties of Devices
3. Numerical Results
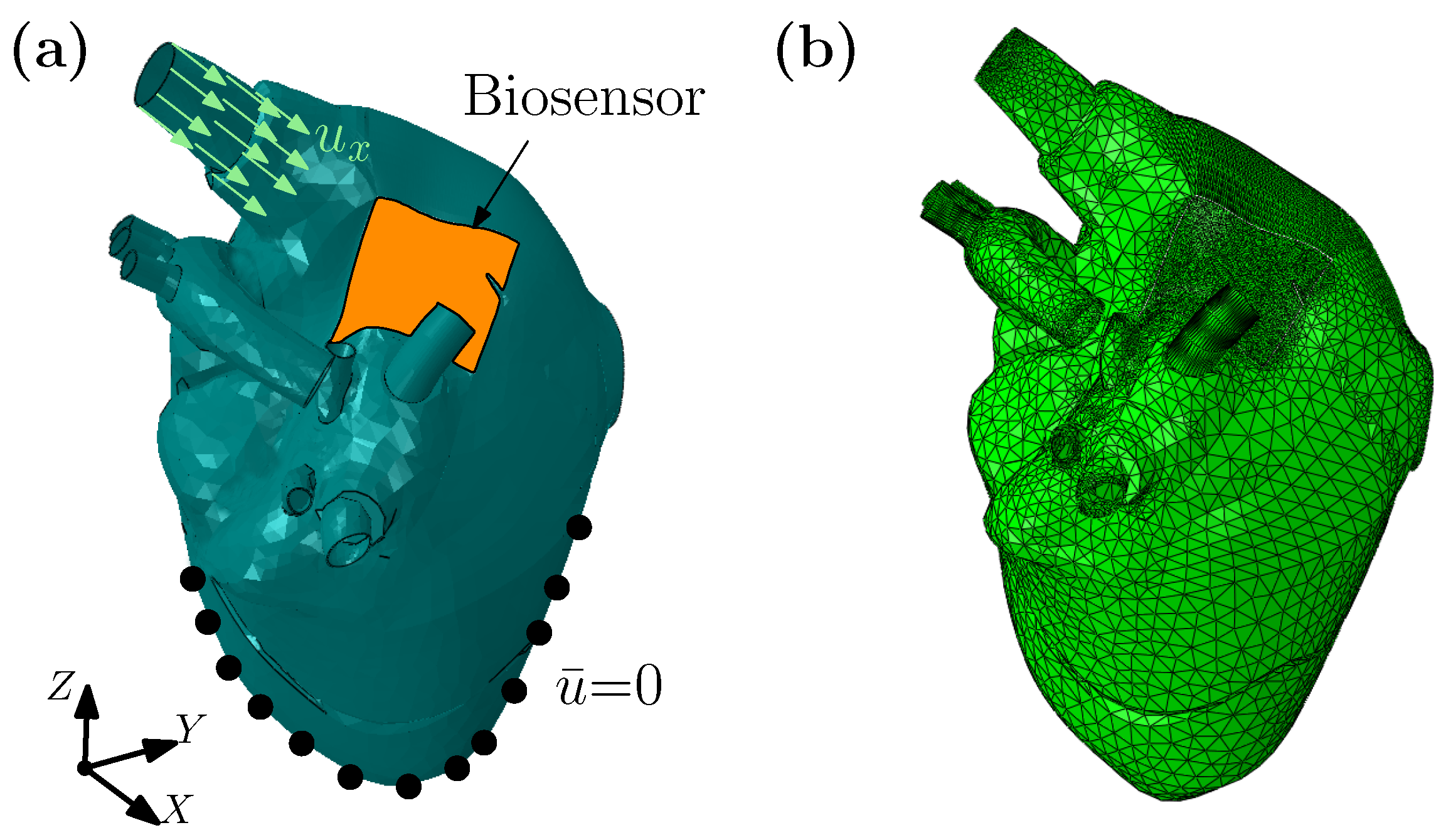
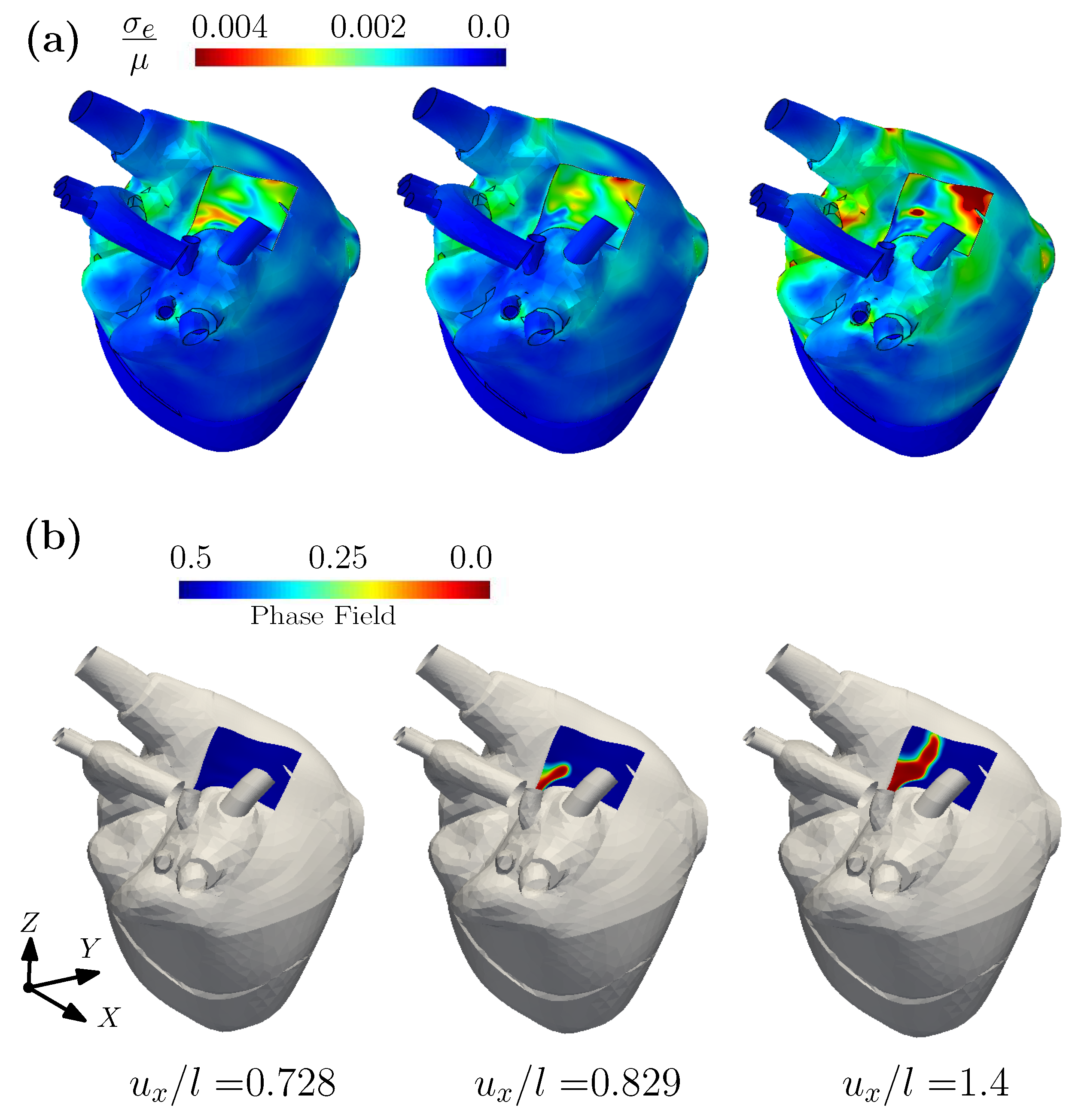
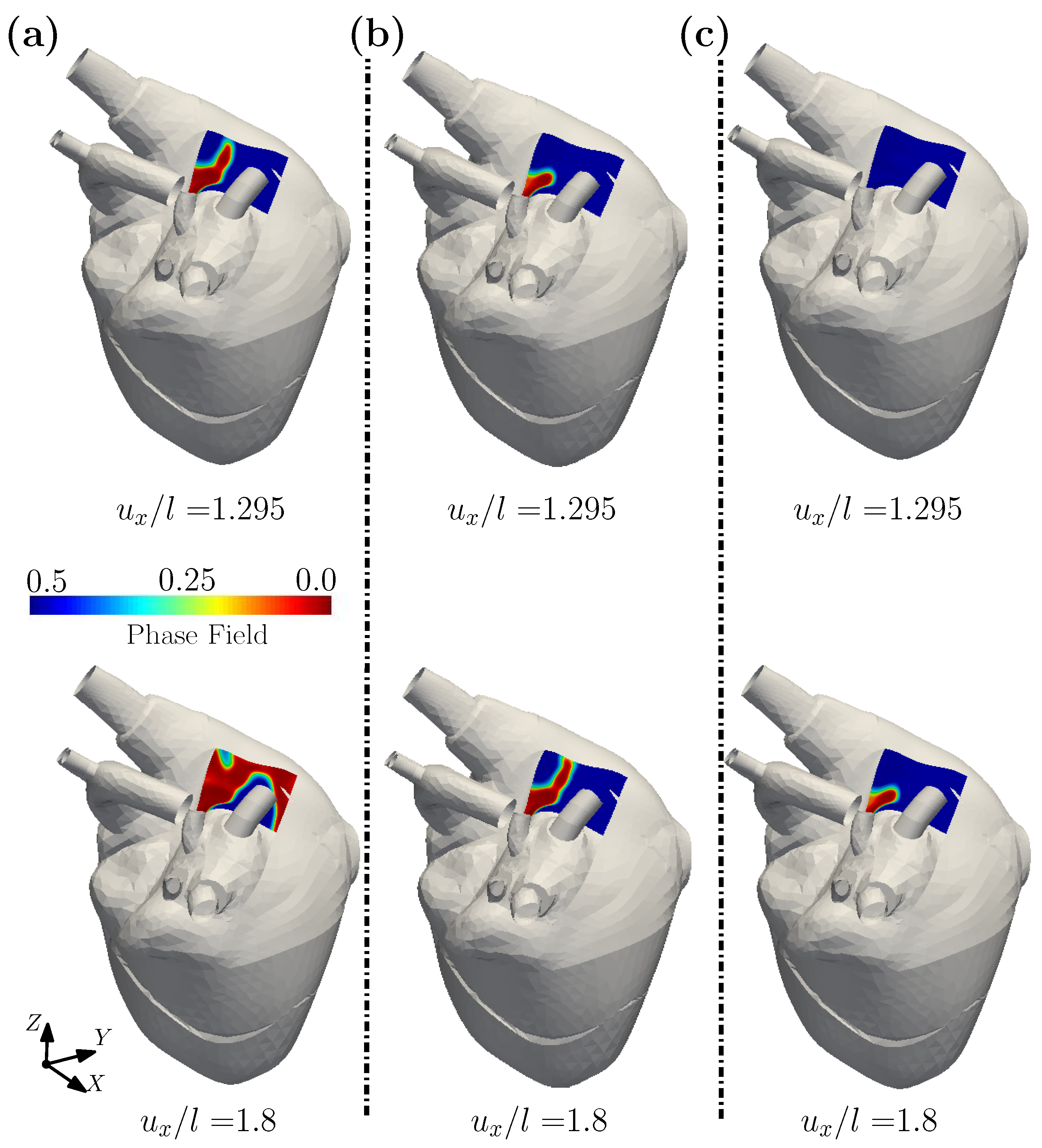
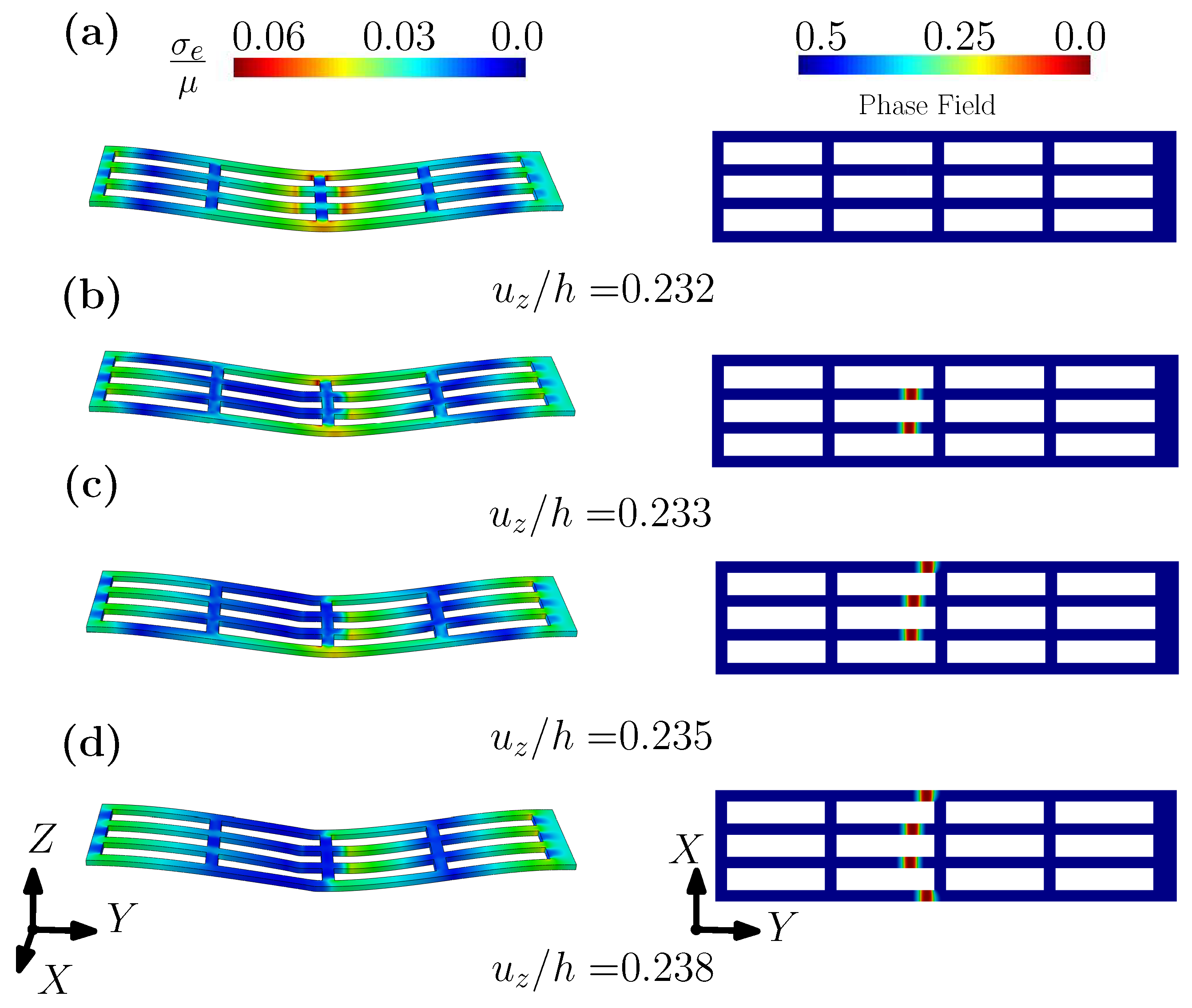
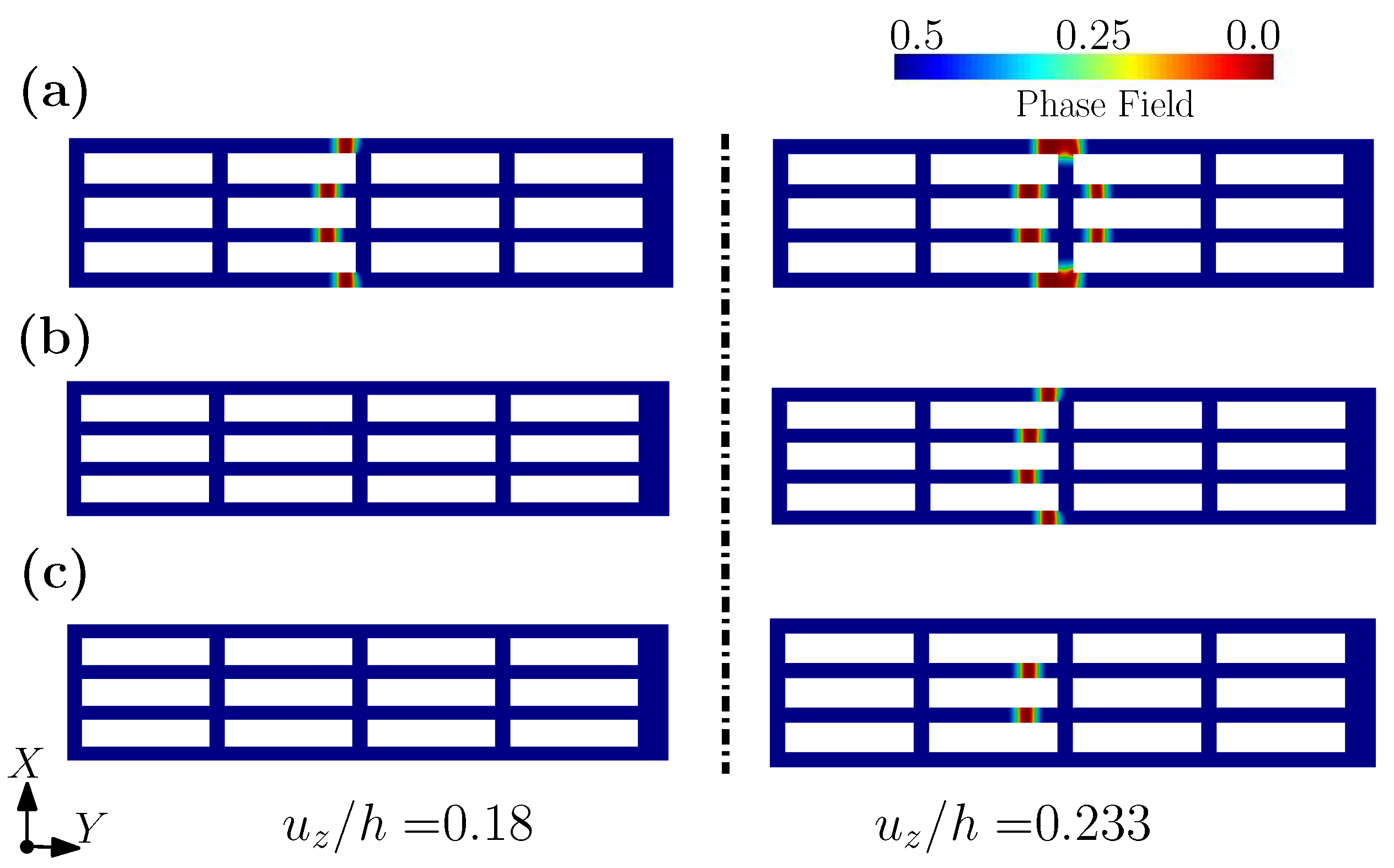
3.1. A Wearable Biosensor
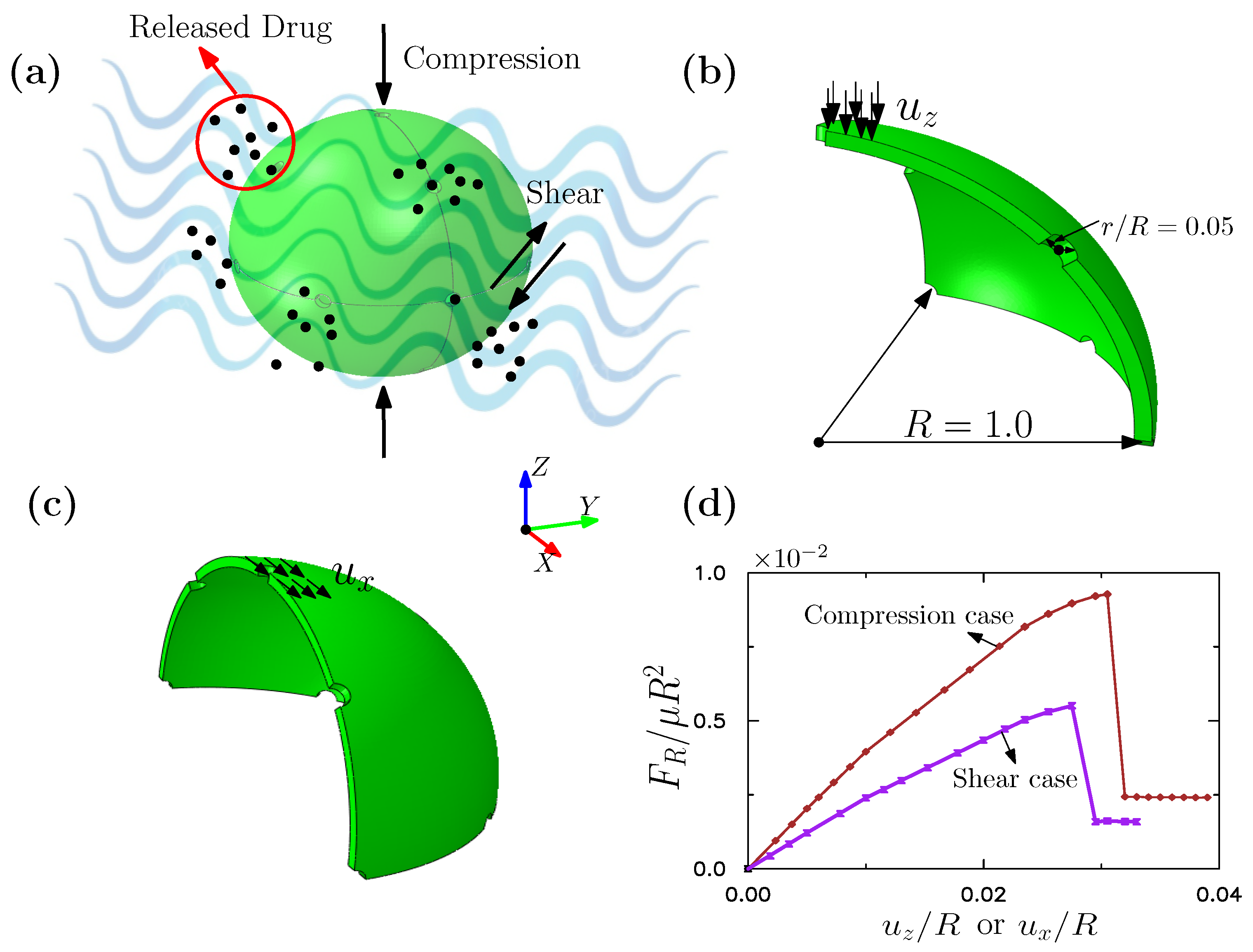
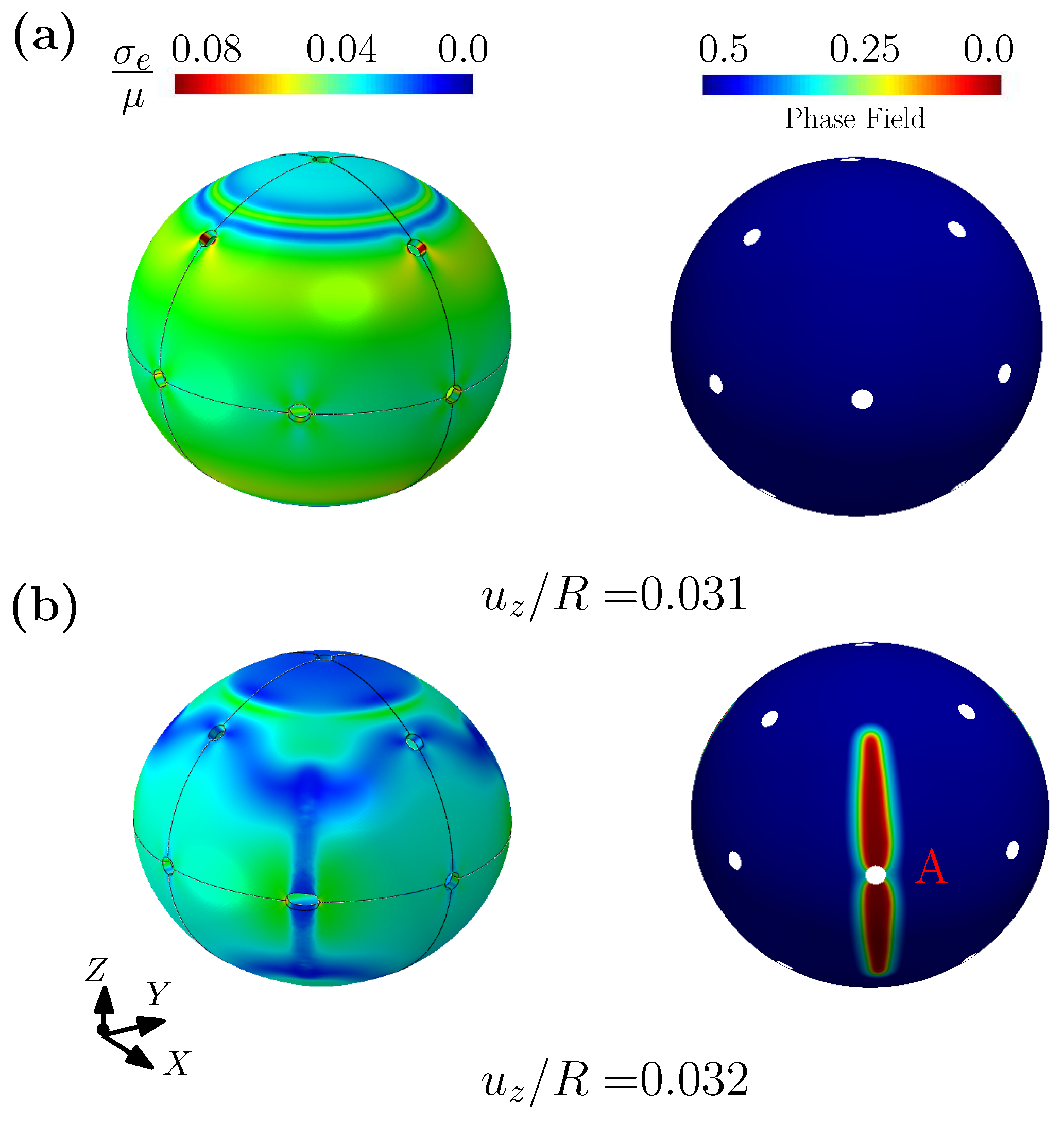
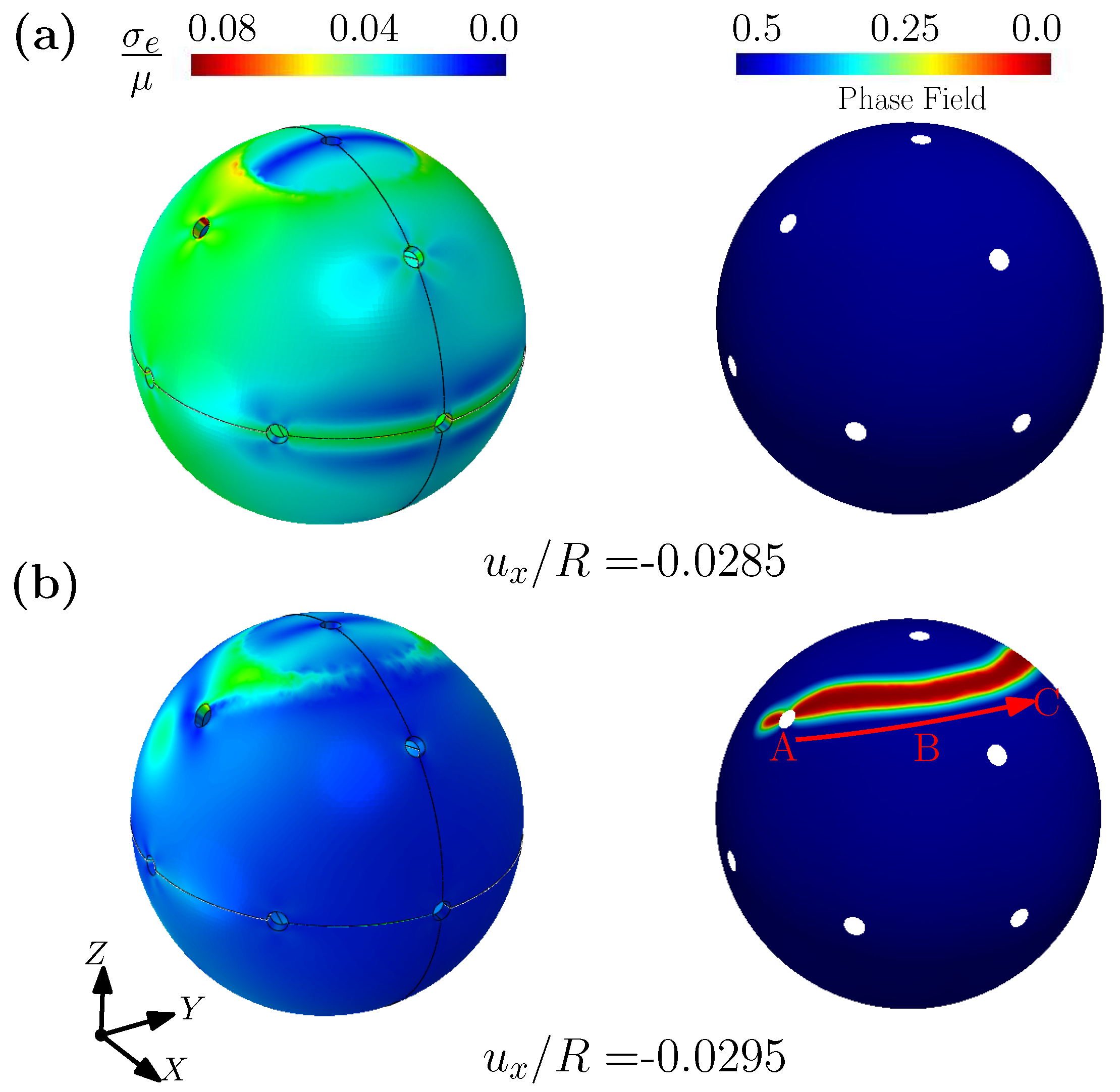
3.2. Outer Membrane of Drug-Delivery Capsule
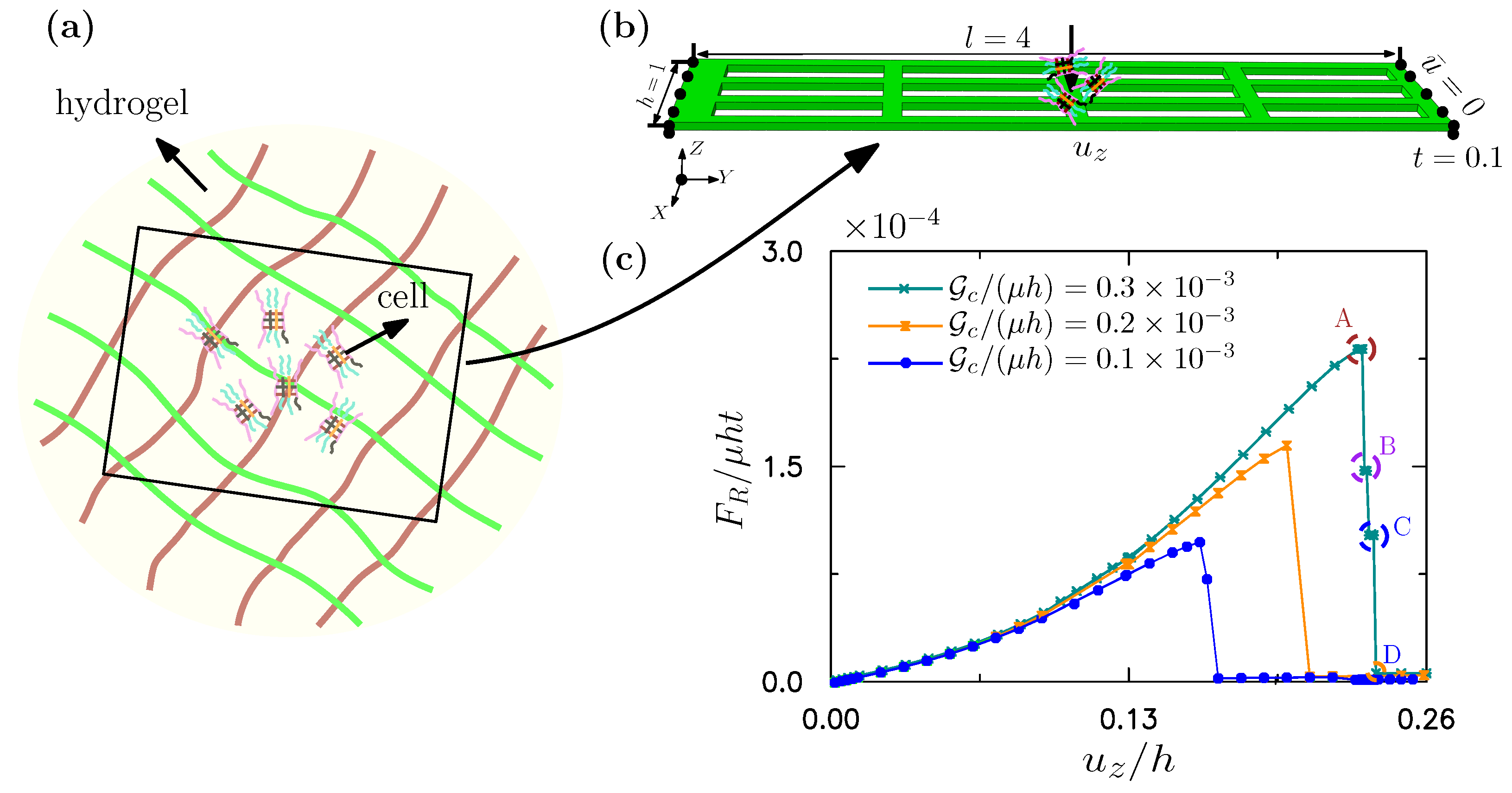
3.3. A Fibered Matrix for a Cell Culture
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Awasthi, S. A Review on Hydrogels and Ferrogels for Biomedical Applications. JOM 2021, 73, 2440–2451. [Google Scholar] [CrossRef]
- Tavakoli, J.; Tang, Y. Hydrogel Based Sensors for Biomedical Applications: An Updated Review. Polymers 2017, 9, 364. [Google Scholar] [CrossRef] [PubMed]
- Gibbs, D.M.R.; Black, C.R.M.; Dawson, J.I.; Oreffo, R.O.C. A review of hydrogel use in fracture healing and bone regeneration. J. Tissue Eng. Regen. Med. 2016, 10, 187–198. [Google Scholar] [CrossRef] [PubMed]
- Calo, E.; Khutoryanskiy, V.V. Biomedical applications of hydrogels: A review of patents and commercial products. Eur. Polym. J. 2015, 65, 252–267. [Google Scholar] [CrossRef]
- Chai, Q.; Jiao, Y.; Yu, X. Hydrogels for Biomedical Applications: Their Characteristics and the Mechanisms behind Them. Gels 2017, 3, 6. [Google Scholar] [CrossRef]
- Ghorbanizamani, F.; Moulahoum, H.; Guler Celik, E.; Timur, S. Ionic liquids enhancement of hydrogels and impact on biosensing applications. J. Mol. Liq. 2022, 357, 119075. [Google Scholar] [CrossRef]
- Tenje, M.; Cantoni, F.; Hernández, A.M.P.; Searle, S.S.; Johansson, S.; Barbe, L.; Antfolk, M.; Pohlit, H. A practical guide to microfabrication and patterning of hydrogels for biomimetic cell culture scaffolds. Organs-on-a-Chip 2020, 2, 100003. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, G.; Yang, R.; Lu, X.; Cheng, M.; He, C.; Xie, G.; Meng, J.; Shi, D.X.; Zhang, G. Tunable Piezoresistivity of Nanographene Films for Strain Sensing. ACS Nano 2015, 9, 1622–1629. [Google Scholar] [CrossRef]
- Zhou, J.; Yu, H.; Xu, X.; Han, F.; Lubineau, G. Ultrasensitive, Stretchable Strain Sensors Based on Fragmented Carbon Nanotube Papers. ACS Appl. Mater. Interfaces 2017, 9, 4835–4842. [Google Scholar] [CrossRef]
- Lim, G.H.; Lee, N.E.; Lim, B. Highly sensitive, tunable, and durable gold nanosheet strain sensors for human motion detection. J. Mater. Chem. C 2017, 4, 5642–5647. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, D.Y.; Pang, Y.; Li, Y.X.; Wang, Q.; Zhang, T.Y.; Wang, J.B.; Liu, X.; Yang, Y.Y.; Jian, J.M.; et al. Simultaneously Detecting Subtle and Intensive Human Motions Based on a Silver Nanoparticles Bridged Graphene Strain Sensor. Acs Appl. Mater. Interfaces 2018, 10, 3948–3954. [Google Scholar] [CrossRef] [PubMed]
- Sorber, J.; Steiner, G.; Schulz, V.; Guenther, M.; Gerlach, G.; Salzer, R.; Arndt, K.F. Hydrogel-based piezoresistive pH sensors: Investigations using FT-IR attenuated total reflection spectroscopic imaging. Anal. Chem. 2008, 80, 2957–2962. [Google Scholar] [CrossRef] [PubMed]
- Richter, A.; Bund, A.; Keller, M.; Arndt, K.F. Characterization of a microgravimetric sensor based on pH sensitive hydrogels. Sens. Actuators B Chem. 2004, 99, 579–585. [Google Scholar] [CrossRef]
- Milo, S.; Thet, N.T.; Liu, D.; Nzakizwanayo, J.; Jones, B.V.; Jenkins, A.T.A. An in-situ infection detection sensor coating for urinary catheters. Biosens. Bioelectron. 2016, 81, 166–172. [Google Scholar] [CrossRef] [PubMed]
- Wischerhoff, E.; Zacher, T.; Laschewsky, A.; Rekaï, E.D. Direct Observation of the Lower Critical Solution Temperature of Surface-Attached Thermo-Responsive Hydrogels by Surface Plasmon Resonance. Angew. Chem. Int. Ed. 2000, 39, 4602–4604. [Google Scholar] [CrossRef]
- Lagus, T.P.; Edd, J.F. A review of the theory, methods and recent applications of high-throughput single-cell droplet microfluidics. J. Phys. D Appl. Phys. 2013, 46, 114005. [Google Scholar] [CrossRef]
- Zeng, S.; Zhang, D.; Sun, L. Bio-inspired sensitive and reversible mechanochromisms via strain-dependent cracks and folds. Nat. Commun. 2016, 7, 11802. [Google Scholar] [CrossRef]
- Johner. Wing. Available online: https://m.quanjing.com/imgbuy/qj9103024971.html (accessed on 8 June 2022).
- Wu, X. T3 Terminal of Capital Airport. Available online: https://m.quanjing.com/imgbuy/QJ6325712014.html (accessed on 15 June 2022).
- Reichenspurner, H.; Schaefer, D.; Linke, A.; Spence, M.; Sondergaard, L.; LeBreton, H.; Schymik, G.; Abdel-Wahab, M.; Leipsic, J.; Walters, D.; et al. Self-Expanding Transcatheter Aortic Valve System for Symptomatic High-Risk Patients With Severe Aortic Stenosis. J. Am. Coll. Cardiol. 2017, 70, 3127–3136. [Google Scholar] [CrossRef]
- Han, M.; Chen, L.; Aras, K.; Liang, C.; Chen, X.; Zhao, H.; Li, K.; Ndeye Rokhaya, F.; Sun, B.; Kim, J.H.; et al. Catheter-integrated soft multilayer electronic arrays for multiplexed sensing and actuation during cardiac surgery. Nat. Biomed. Eng. 2020, 4, 1–13. [Google Scholar] [CrossRef]
- Mao, Y.; Lin, S.; Zhao, X.; Anand, L. A large deformation viscoelastic model for double-network hydrogels. J. Mech. Phys. Solids 2017, 100, 103–130. [Google Scholar] [CrossRef]
- Long, R.; Mayumi, K.; Creton, C.; Narita, T.; Hui, C.Y. Time Dependent Behavior of a Dual Cross-Link Self-Healing Gel: Theory and Experiments. Macromolecules 2014, 47, 7243–7250. [Google Scholar] [CrossRef]
- Long, R.; Hui, C.Y. Fracture toughness of hydrogels: Measurement and interpretation. Soft Matter 2016, 12, 8069–8086. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Liu, M.; Zehnder, A.T.; Zhao, J.; Narita, T.; Creton, C.; Hui, C.Y. Fracture mechanics of a self-healing hydrogel with covalent and physical crosslinks: A numerical study. J. Mech. Phys. Solids 2018, 120, 79–95. [Google Scholar] [CrossRef]
- Liu, M.; Guo, J.; Hui, C.Y.; Creton, C.; Narita, T.; Zehnder, A. Time-temperature equivalence in a PVA dual cross-link self-healing hydrogel. J. Rheol. 2018, 62, 991–1000. [Google Scholar] [CrossRef]
- Liu, M.; Guo, J.; Hui, C.Y.; Zehnder, A. Crack tip stress based kinetic fracture model of a PVA dual-crosslink hydrogel. Extrem. Mech. Lett. 2019, 29, 100457. [Google Scholar] [CrossRef]
- Shen, T.; Vernerey, F.J. Rate-dependent fracture of transient networks. J. Mech. Phys. Solids 2020, 143, 104028. [Google Scholar] [CrossRef]
- Liu, D.; Ma, S.; Yuan, H.; Markert, B. Modelling and simulation of coupled fluid transport and time-dependent fracture in fibre-reinforced hydrogel composites. Comput. Methods Appl. Mech. Eng. 2022, 390, 114470. [Google Scholar] [CrossRef]
- Liu, D.; Ma, S.; Yuan, H.; Markert, B. Computational modelling of poro-visco-hyperelastic effects on time-dependent fatigue crack growth of hydrogels. Int. J. Plast. 2022, 155, 103307. [Google Scholar] [CrossRef]
- Wang, X.; Hong, W. Delayed fracture in gels. Soft Matter 2012, 8, 8171–8178. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Dolbow, J.; Moës, N.; Belytschko, T. Modeling fracture in Mindlin-Reissner plates with the eXtended finite element method. Int. J. Solids Struct. 2000, 37, 7161–7183. [Google Scholar] [CrossRef]
- Areias, P.; Belytschko, T. Non-linear analysis of shells with arbitrary evolving cracks using XFEM. J. Mech. Phys. Solids 2005, 62, 384–415. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Grinspun, E. A discrete model of thin shells. In Proceedings of the ACM SIGGRAPH 2005 Courses, Los Angeles, CA, USA, 31 July–4 August 2005; pp. 14–19. [Google Scholar]
- Desbrun, M.; Kanso, E.; Tong, Y. Discrete differential forms for computational modeling. In Discrete Differential Geometry; Springer: Berlin/Heidelberg, Germany, 2008; pp. 287–324. [Google Scholar]
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric deep learning: Going beyond euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef]
- Yang, H.; Guo, X.; Tang, S.; Liu, W. Derivation of heterogeneous material laws via data-driven principal component expansions. Comput. Mech. 2019, 64, 365–379. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, G.; Yang, H.; Li, Y.; Liu, W.K.; Guo, X. MAP123: A data-driven approach to use 1D data for 3D nonlinear elastic materials modeling. Comput. Methods Appl. Mech. Eng. 2019, 357, 112587. [Google Scholar] [CrossRef]
- Kirchdoerfer, T.; Ortiz, M. Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 2016, 304, 81–101. [Google Scholar] [CrossRef]
- Kirchdoerfer, T.; Ortiz, M. Data Driven Computing with Noisy Material Data Sets. Comput. Methods Appl. Mech. Eng. 2017, 326, 622–641. [Google Scholar] [CrossRef]
- Eggersmann, R.; Kirchdoerfer, T.; Reese, S.; Stainier, L.; Ortiz, M. Model-Free Data-Driven Inelasticity. Comput. Methods Appl. Mech. Eng. 2018, 350, 81–99. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Sobh, N.A.; Sehitoglu, H. Deep learning for plasticity and thermo-viscoplasticity. Int. J. Plast. 2021, 136, 102852. [Google Scholar] [CrossRef]
- Logarzo, H.J.; Capuano, G.; Rimoli, J.J. Smart constitutive laws: Inelastic homogenization through machine learning. Comput. Methods Appl. Mech. Eng. 2021, 373, 113482. [Google Scholar] [CrossRef]
- Liu, Z.; Bessa, M.A.; Liu, W.K. Self-consistent clustering analysis: An efficient multi-scale scheme for inelastic heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2016, 306, 319–341. [Google Scholar] [CrossRef]
- Liu, Z.; Moore, J.A.; Liu, W.K. An extended micromechanics method for probing interphase properties in polymer nanocomposites. J. Mech. Phys. Solids 2016, 95, 663–680. [Google Scholar] [CrossRef]
- Zhang, G.; Guo, T.F.; Zhou, Z.; Tang, S.; Guo, X. A phase-field model for fracture in water-containing soft solids. Eng. Fract. Mech. 2019, 212, 180–196. [Google Scholar] [CrossRef]
- Tvergaard, V.; Hutchinson, J.W. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids. J. Mech. Phys. Solids 1992, 40, 1377–1397. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Amor, H.; Marigo, J.J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217, 77–95. [Google Scholar] [CrossRef]
- Zhang, G.; Guo, T.F.; Elkhodary, K.I.; Tang, S.; Guo, X. Mixed Graph-FEM phase field modeling of fracture in plates and shells with nonlinearly elastic solids. Comput. Methods Appl. Mech. Eng. 2022, 389, 114282. [Google Scholar] [CrossRef]
- Lin, J.; Zheng, S.Y.; Xiao, R.; Yin, J.; Wu, Z.L.; Zheng, Q.; Qian, J. Constitutive behaviors of tough physical hydrogels with dynamic metal-coordinated bonds. J. Mech. Phys. Solids 2020, 139, 103935. [Google Scholar] [CrossRef]
- Krishnan, V.; Hui, C.Y.; Long, R. Finite Strain Crack Tip Fields in Soft Incompressible Elastic Solids. Langmuir ACS J. Surfaces Colloids 2008, 24, 14245–14253. [Google Scholar] [CrossRef] [PubMed]
- Faghihi, S.; Karimi, A.; Jamadi, M.; Imani, R.; Salarian, R. Graphene oxide/poly(acrylic acid)/gelatin nanocomposite hydrogel: Experimental and numerical validation of hyperelastic model. Mater. Sci. Eng. C 2014, 38, 299–305. [Google Scholar] [CrossRef]
- Pillai, U.; Triantafyllou, S.P.; Ashcroft, I.; Essa, Y.; de la Escalera, F.M. Phase-field modelling of brittle fracture in thin shell elements based on the MITC4+ approach. Comput. Mech. 2020, 65, 1413–1432. [Google Scholar] [CrossRef]
- Needleman, A. A Continuum Model for Void Nucleation by Inclusion Debonding. J. Appl. Mech. 1987, 54, 525. [Google Scholar] [CrossRef]
- Francfort, G.A.; Marigo, J.J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. The variational approach to fracture. J. Elast. 2008, 91, 5–148. [Google Scholar] [CrossRef]
- Wardetzky, M. Convergence of the cotangent formula: An overview. Discret. Differ. Geom. 2008, 38, 275–286. [Google Scholar]
- Trabelsi, K. Nonlinear thin plate models for a family of Ogden materials. Comptes Rendus Math. 2003, 337, 819–824. [Google Scholar] [CrossRef]
- Moerman, K.M.; Simms, C.K.; Nagel, T. Control of Tension-Compression Asymmetry in Ogden Hyperelasticity with Application to Soft Tissue Modelling. J. Mech. Behav. Biomed. Mater. 2016, 56, 218–228. [Google Scholar] [CrossRef]
- Yu, D.; Du, D.; Yang, H.; Tu, Y. Parallel computing simulation of electrical excitation and conduction in the 3D human heart. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBC 2014, Chicago, IL, USA, 26–30 August 2014; pp. 4315–4324. [Google Scholar]
- Thuy, P.; Fatiesa, S.; Erica, S.; Di, W.; Wei, S. Quantification andcomparison of the mechanical properties of four human cardiac valves. Acta Mater. 2017, 54, 345–355. [Google Scholar]
- Tang, S.; Zhang, G.; Guo, T.F.; Guo, X.; Liu, W.K. Phase field modeling of fracture in nonlinearly elastic solids via energy decomposition. Comput. Methods Appl. Mech. Eng. 2019, 347, 477–494. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, Y.; Weihin, W.; Guo, T.; Tang, S.; Luo, J. Transition of Surface-Interface Creasing in Bilayer Hydrogels. Soft Matter 2017, 13, 6011–6020. [Google Scholar] [CrossRef]
- Jordan, B.; Gorji, M.B.; Mohr, D. Neural network model describing the temperature- and rate-dependent stress-strain response of polypropylene. Int. J. Plast. 2020, 135, 102811. [Google Scholar] [CrossRef]
- Najjar, Y.M.; Huang, C. Simulating the stress-strain behavior of Georgia kaolin via recurrent neuronet approach. Comput. Geotech. 2007, 34, 346–361. [Google Scholar] [CrossRef]
- Mahdi, E.S.; El Kadi, H. Crushing behavior of laterally compressed composite elliptical tubes: Experiments and predictions using artificial neural networks. Compos. Struct. 2008, 83, 399–412. [Google Scholar] [CrossRef]
- Bratskaya, S.; Skatova, A.; Privar, Y.; Boroda, A.; Kantemirova, E.; Maiorova, M.; Pestov, A. Stimuli-Responsive Dual Cross-Linked N-Carboxyethylchitosan Hydrogels with Tunable Dissolution Rate. Gels 2021, 7, 188. [Google Scholar] [CrossRef]
- Danko, M.; Kronekova, Z.; Krupa, I.; Tkac, P.; Kasak, P. Exchange Counterion in Polycationic Hydrogels: Tunability of Hydrophobicity, Water State, and Floating Capability for a Floating pH Device. Gels 2021, 7, 109. [Google Scholar] [CrossRef]
- Jafari, H.; Dadashzadeh, A.; Moghassemi, S.; Zahedi, P.; Amorim, C.A.; Shavandi, A. Ovarian Cell Encapsulation in an Enzymatically Crosslinked Silk-Based Hydrogel with Tunable Mechanical Properties. Gels 2021, 7, 138. [Google Scholar] [CrossRef]
- Kuntawong, P.; Kongintr, U.; Promptmas, C. M021 3D printed-lactate amperometric biosensor for real-time noninvasive health monitoring in human sweat. Clinica Chimica Acta 2022, 530, S11. [Google Scholar] [CrossRef]
- Zhu, P.; Peng, H.; Rwei, A.Y. Flexible, wearable biosensors for digital health. Med. Nov. Technol. Devices 2022, 14, 100118. [Google Scholar] [CrossRef]
- Laliberte, K.E.; Scott, P.; Khan, N.I.; Mahmud, M.S.; Song, E. A wearable graphene transistor-based biosensor for monitoring IL-6 biomarker. Microelectron. Eng. 2022, 262, 111835. [Google Scholar] [CrossRef]
- Komkova, M.A.; Eliseev, A.A.; Poyarkov, A.A.; Daboss, E.V.; Evdokimov, P.V.; Eliseev, A.A.; Karyakin, A.A. Simultaneous monitoring of sweat lactate content and sweat secretion rate by wearable remote biosensors. Biosens. Bioelectron. 2022, 202, 113970. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Zhang, N.; Ma, M. Electroconductive hydrogels for biomedical applications. WIREs Nanomed. Nanobiotechnol. 2019, 11, 1568–1583. [Google Scholar] [CrossRef]
- Tpgimages. Pulse Sign. Available online: https://m.quanjing.com/imgbuy/qj7118890985.html (accessed on 7 June 2022).
- Del Corso, G.; Verzicco, R.; Viola, F. A fast computational model for the electrophysiology of the whole human heart. J. Comput. Phys. 2022, 457, 111084. [Google Scholar] [CrossRef]
- Budday, S.; Ovaert, T.C.; Holzapfel, G.A.; Steinmann, P.; Kuhl, E. Fifty shades of brain: A review on the mechanical testing and modeling of brain tissue. Arch. Comput. Methods Eng. 2020, 27, 1187–1230. [Google Scholar] [CrossRef]
- Deng, Y.; Hussain, I.; Kang, M.; Li, K.; Yao, F.; Liu, S.; Fu, G. Self-recoverable and mechanical-reinforced hydrogel based on hydrophobic interaction with self-healable and conductive properties. Chem. Eng. J. 2018, 353, 900–910. [Google Scholar] [CrossRef]
- Huang, S.; Shuyi, S.; Gan, H.; Linjun, W.; Lin, C.; Danyuan, X.; Zhou, H.; Lin, X.; Qin, Y. Facile fabrication and characterization of highly stretchable lignin-based hydroxyethyl cellulose self-healing hydrogel. Carbohydr. Polym. 2019, 223, 115080. [Google Scholar] [CrossRef]
- Jia, Z.; Zeng, Y.; Pengfei, T.; Gan, D.; Xing, W.; Hou, Y.; Wang, K.; Xie, C.; Lu, X. Conductive, Tough, Transparent, and Self-Healing Hydrogels Based on Catechol-Metal Ion Dual Self-Catalysis. Chem. Mater. 2019, 31, 5625–5632. [Google Scholar] [CrossRef]
- Chen, W.; Bu, Y.; Li, D.; Liu, Y.; Chen, G.; Wan, X.; Li, N. Development of High-Strength, Tough, and Self-Healing Carboxymethyl Guar Gum-Based Hydrogels for Human Motion Detection. J. Mater. Chem. C 2020, 8, 900–908. [Google Scholar] [CrossRef]
- Liu, Y.J.; Cao, W.; Ma, M.G.; Wan, P. Ultrasensitive Wearable Soft Strain Sensors of Conductive, Self-healing, and Elastic Hydrogels with Synergistic "Soft and Hard" Hybrid Networks. ACS Appl. Mater. Interfaces 2017, 9, 25559–25570. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Lu, S.; Li, Q.; Ren, Y.; Ding, Y.; Wu, H.; He, X.; Shang, Y. High strength zwitterionic nano-micelle hydrogels with superior self-healing, adhesive and ion conductive properties. Eur. Polym. J. 2020, 133, 109761. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhiliang, G.; Wang, Y.; Guo, L.; Yin, C.; Zhang, X.; Hao, J.; Zhang, G.; Chen, L. Eco-Friendly, Self-Healing Hydrogels for Adhesive and Elastic Strain Sensors, Circuit Repairing, and Flexible Electronic Devices. Macromolecules 2019, 52, 2531–2541. [Google Scholar] [CrossRef]
- Zhao, M.; Tang, Z.; Zhang, X.; Li, Z.; Xiao, H.; Zhang, M.; Liu, K.; Ni, Y.; Huang, L.; Chen, L.; et al. A self-healing, stretchable, and conductive Poly(N-vinylpyrrolidone)/gallic acid composite hydrogel formed via hydrogen bonding for wearable electronic sensors. Compos. Sci. Technol. 2020, 198, 108294. [Google Scholar] [CrossRef]
- An, R.; Zhang, X.; Han, L.; Wang, X.; Zhang, Y.; Shi, L.; Ran, R. Healing, flexible, high thermal sensitive dual-network ionic conductive hydrogels for 3D linear temperature sensor. Mater. Sci. Eng. C 2019, 107, 110310. [Google Scholar] [CrossRef] [PubMed]
- Pang, J.; Wang, L.; Xu, Y.; Wu, M.; Wang, M.; Liu, Y.; Yu, S.; Li, L. Skin-inspired cellulose conductive hydrogels with integrated self-healing, strain, and thermal sensitive performance. Carbohydr. Polym. 2020, 240, 116360. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zheng, S.; Qu, C.; Wang, D.; Liu, C.; Wang, Y.; Fan, X.; Xiao, W.; Li, H.; Zhao, D.; et al. Simple and environmentally friendly approach for preparing high-performance polyimide precursor hydrogel with fully aromatic structures for strain sensor. Eur. Polym. J. 2019, 114, 346–352. [Google Scholar] [CrossRef]
- Wu, J.; Wu, Z.; Xu, H.; Wu, Q.; Liu, C.; Yang, B.R.; Gui, X.; Xie, X.; Tao, K.; Shen, Y.; et al. An intrinsically stretchable humidity sensor based on anti-drying, self-healing and transparent organohydrogels. Mater. Horizons 2019, 6, 595–603. [Google Scholar] [CrossRef]
- Liu, S.; Qiu, Y.; Yu, W.; Zhang, H. Highly Stretchable and Self-Healing Strain Sensor Based on Gellan Gum Hybrid Hydrogel for Human Motion Monitoring. ACS Appl. Polym. Mater. 2020, 2, 1325–1334. [Google Scholar] [CrossRef]
- Tong, R.; Chen, G.; Pan, D.; Qi, H.; Li, R.; Tian, J.; Lu, F.; He, M. Highly Stretchable and Compressible Cellulose Ionic Hydrogels for Flexible Strain Sensors. Biomacromolecules 2019, 20, 2096–2104. [Google Scholar] [CrossRef]
- Zou, P.; Yao, J.; Cui, Y.N.; Zhao, T.; Che, J.; Yang, M.; Li, Z.; Gao, C. Advances in Cellulose-Based Hydrogels for Biomedical Engineering: A Review Summary. Gels 2022, 8, 364. [Google Scholar] [CrossRef] [PubMed]
- Ansari, M.J.; Rajendran, R.R.; Mohanto, S.; Agarwal, U.; Panda, K.; Dhotre, K.; Manne, R.; Deepak, A.; Zafar, A.; Yasir, M.; et al. Poly(N-isopropylacrylamide)-Based Hydrogels for Biomedical Applications: A Review of the State-of-the-Art. Gels 2022, 8, 454. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wang, X.; Yang, F.; Wang, L.; Wu, D. Highly elastic and ultratough hybrid ionic–covalent hydrogels with tunable structures and mechanics. Adv. Mater. 2018, 30, 1707071. [Google Scholar] [CrossRef] [PubMed]
- Peppas, N.A.; Van Blarcom, D.S. Hydrogel-based biosensors and sensing devices for drug delivery. J. Control. Release 2016, 240, 142–150. [Google Scholar] [CrossRef] [PubMed]
- Culver, H.R.; Clegg, J.R.; Peppas, N.A. Analyte-Responsive Hydrogels: Intelligent Materials for Biosensing and Drug Delivery. Accounts Chem. Res. 2017, 50, 170–178. [Google Scholar] [CrossRef]
- PantherMedia. Blood Corpuscle. Available online: https://m.quanjing.com/imgbuy/qj6714931654.html (accessed on 20 June 2022).
- Dimatteo, R.; Darling, N.; Segura, T. In Situ forming injectable hydrogels for drug delivery and wound repair. Adv. Drug Deliv. Rev. 2018, 127, 167–184. [Google Scholar] [CrossRef]
- Li, Y.; Yang, H.; Lee, D. Advances in biodegradable and injectable hydrogels for biomedical applications. J. Control. Release 2021, 330, 151–160. [Google Scholar] [CrossRef]
- Wang, Q.; Qu, Y.; Zhang, Z.; Huang, H.; Xu, Y.; Shen, F.; Wang, L.; Sun, L. Injectable DNA Hydrogel-Based Local Drug Delivery and Immunotherapy. Gels 2022, 8, 400. [Google Scholar] [CrossRef]
- Xie, Y.; Guan, Q.; Guo, J.; Chen, Y.; Yin, Y.; Han, X. Hydrogels for Exosome Delivery in Biomedical Applications. Gels 2022, 8, 328. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, H.; Du, Z.; Hong, W.; Lu, T.; Wang, T. Rate-dependent fracture of hydrogels due to water migration. J. Mech. Phys. Solids 2022, 167, 105007. [Google Scholar] [CrossRef]
- Li, C.; Wang, Z.; Wang, Y.; He, Q.; Long, R.; Cai, S. Effects of network structures on the fracture of hydrogel. Extrem. Mech. Lett. 2021, 49, 101495. [Google Scholar] [CrossRef]
- Desai, R.M.; Koshy, S.T.; Hilderbrand, S.A.; Mooney, D.J.; Joshi, N.S. Versatile click alginate hydrogels crosslinked via tetrazine-norbornene chemistry. Biomaterials 2015, 50, 30–37. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Luo, Y.N.; Zhang, P.; Yang, W.F.; Zhang, C.Y.; Yin, Y.L. The Preparation of Novel P(OEGMA-co-MEO2MA) Microgels-Based Thermosensitive Hydrogel and Its Application in Three-Dimensional Cell Scaffold. Gels 2022, 8, 313. [Google Scholar] [CrossRef]
- Jiao, W.; Li, X.; Shan, J.; Wang, X. Study of Several Alginate-Based Hydrogels for In Vitro 3D Cell Cultures. Gels 2022, 8, 147. [Google Scholar] [CrossRef]
- Nguyen, H.Q.D.; Kao, C.Y.; Chiang, C.P.; Hung, Y.H.; Lo, C.M. Investigating the Immunomodulatory Potential of Dental Pulp Stem Cell Cultured on Decellularized Bladder Hydrogel towards Macrophage Response In Vitro. Gels 2022, 8, 187. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Wei, Q.; Wang, Y.; Lei, M.; Li, M.; Li, D.; Zhang, L.; Wu, Y. Self-Healing Mechanism and Conductivity of the Hydrogel Flexible Sensors: A Review. Gels 2021, 7, 216. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, M.; Peng, J.; Wang, X.; Liu, Y.; Wang, W.; Wu, D. Robust, anti-freezing and conductive bonding of chitosan-based double-network hydrogels for stable-performance flexible electronic. Carbohydr. Polym. 2022, 276, 118753. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Wang, L.; Feng, X.; Bu, Y.; Wu, D.; Jin, Z. Supramolecular Hydrogel Formation Based on Tannic Acid. Macromolecules 2017, 50, 666–676. [Google Scholar] [CrossRef]
- Chen, S.; Dong, Y.; Ma, S.; Ren, J.; Yang, X.; Wang, Y.; Lu, S. Superstretching MXene Composite Hydrogel as a Bidirectional Stress Response Thixotropic Sensor. ACS Appl. Mater. Interfaces 2021, 13, 13629–13636. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Qiu, H.; Elkhodary, K.I.; Tang, S.; Peng, D. Modeling Tunable Fracture in Hydrogel Shell Structures for Biomedical Applications. Gels 2022, 8, 515. https://doi.org/10.3390/gels8080515
Zhang G, Qiu H, Elkhodary KI, Tang S, Peng D. Modeling Tunable Fracture in Hydrogel Shell Structures for Biomedical Applications. Gels. 2022; 8(8):515. https://doi.org/10.3390/gels8080515
Chicago/Turabian StyleZhang, Gang, Hai Qiu, Khalil I. Elkhodary, Shan Tang, and Dan Peng. 2022. "Modeling Tunable Fracture in Hydrogel Shell Structures for Biomedical Applications" Gels 8, no. 8: 515. https://doi.org/10.3390/gels8080515





