How the Addition of Chitosan Affects the Transport and Rheological Properties of Agarose Hydrogels
Abstract
:1. Introduction
2. Results and Discussion
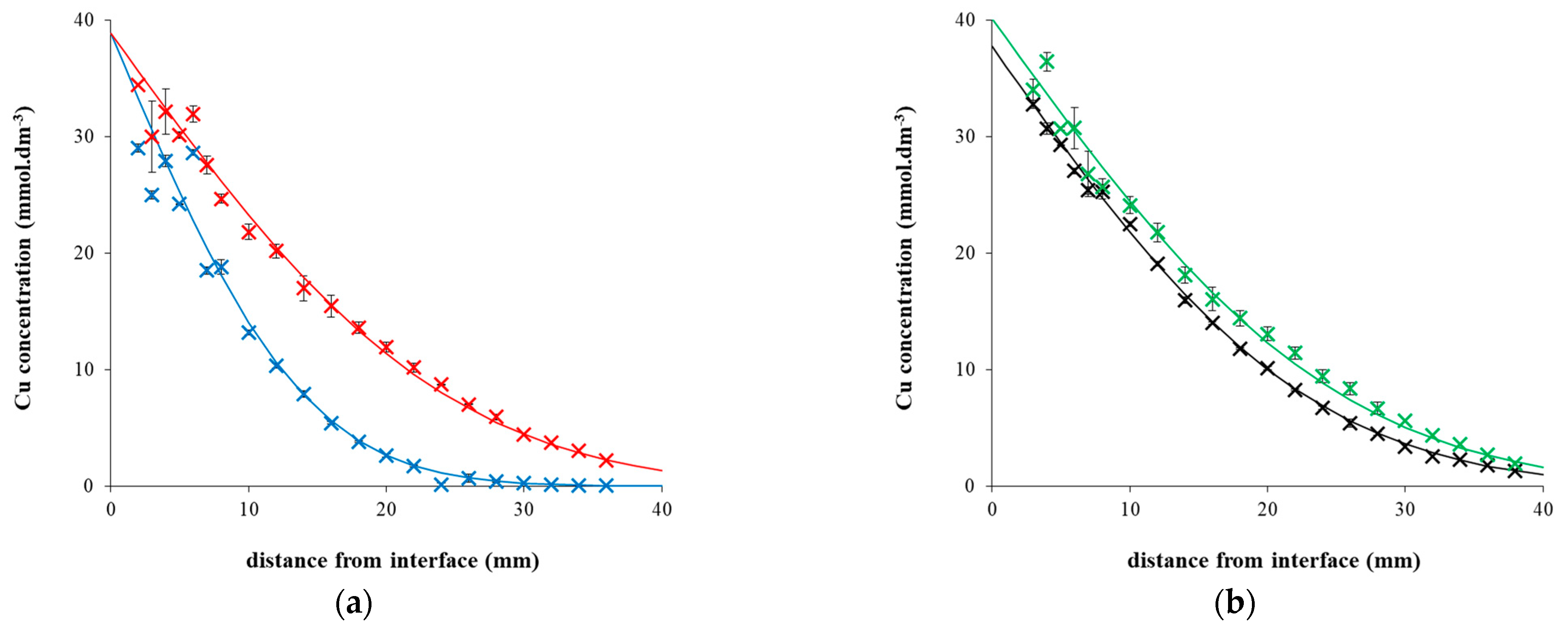
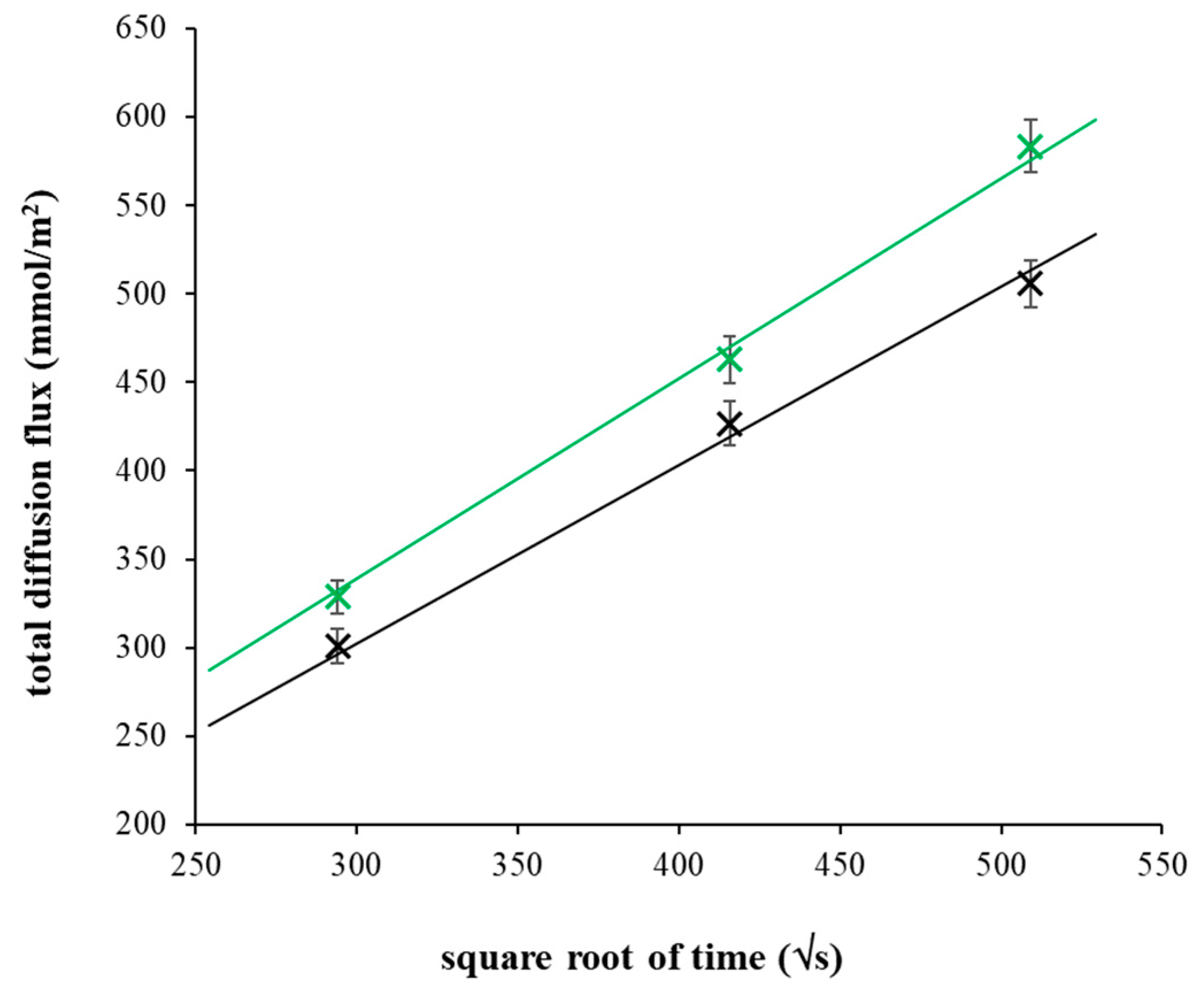
2.1. Diffusion Experiments
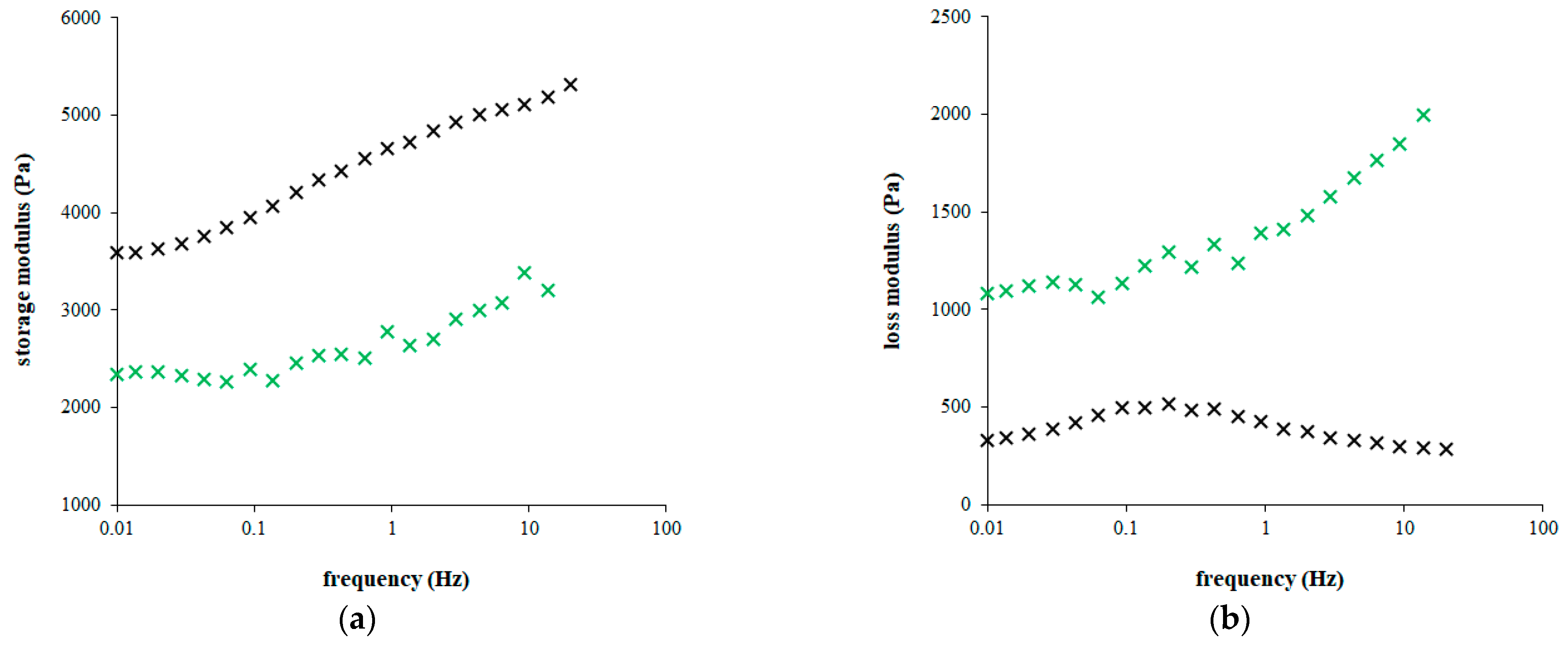
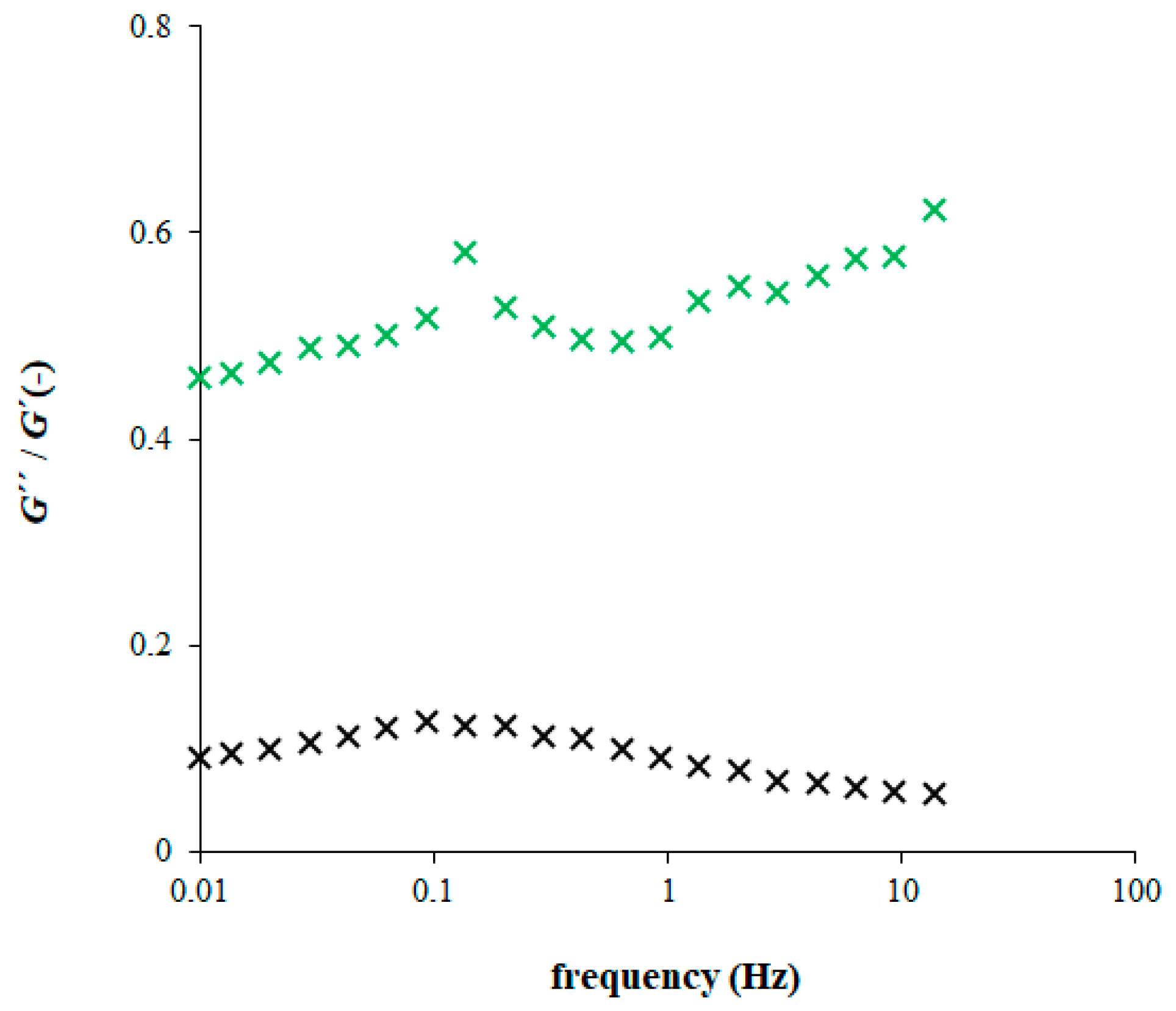
2.2. Rheological Experiments
3. Conclusions
4. Materials and Methods
4.1. Chemicals
4.2. Preparation of Hydrogels
4.3. Diffusion Experiments
4.4. Rheological Experiments
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Duarte, M.L.; Ferreira, M.C.; Marvao, M.R.; Rocha, J. An Optimised Method to Determine the Degree of Acetylation of Chitin and Chitosan by FTIR Spectroscopy. Int. J. Biol. Macromol. 2002, 31, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Paulino, A.T.; Simionato, J.-I.; Garcia, J.C.; Nozaki, J. Characterization of Chitosan and Chitin Produced from Silkworm Crysalides. Carbohydr. Polym. 2006, 64, 98–103. [Google Scholar] [CrossRef]
- Martinez-Ruvalcaba, A.; Chornet, E.; Rodrigue, D. Viscoelastic Properties of Dispersed Chitosan/Xanthan Hydrogels. Carbohydr. Polym. 2007, 67, 586–595. [Google Scholar] [CrossRef]
- Wan Ngah, W.S.; Fatinathan, S. Adsorption of Cu(II) Ions in Aqueous Solution Using Chitosan Beads, Chitosan-GLA Beads and Chitosan-Alginate Beads. Chem. Eng. J. 2008, 143, 62–72. [Google Scholar] [CrossRef]
- Mourza, V.K.; Inamdar, N.N. Chitosan-Modifications and Applications: Opportunities Galore. React. Funct. Polym. 2008, 68, 1013–1051. [Google Scholar] [CrossRef]
- Jayakumar, R.; Menon, D.; Manzoor, K.; Nair, S.V.; Tamura, H. Biomedical Applications of Chitin and Chitosan Based Nanomaterials. Carbohydr. Polym. 2010, 82, 227–232. [Google Scholar] [CrossRef]
- Kamari, A.; Pulford, I.D.; Hargreaves, J.S.J. Chitosan as a Potential Amendment to Remediate Metal Contaminated Soil—A Characterisation Study. Colloid. Surface. B 2011, 82, 71–80. [Google Scholar] [CrossRef]
- Bensaha, S.; Slimane, S.K. A Comparative Study on the Chitosan Membranes Prepared from Acetic Acid and Glycine Hydrochloride for Removal of Copper. Russ. J. Appl. Chem. 2016, 89, 1991–2000. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Q.; Wang, A. Synthesis and Characterization of Chitosan-g-poly(acrylic acid)/Attapulgite Superabsorbent Composites. Carbohydr. Polym. 2007, 68, 367–374. [Google Scholar] [CrossRef]
- Narayanan, A.; Kartik, R.; Sangeetha, E.; Dhamodharan, R. Super Water Absorbing Polymeric Gel from Chitosan, Citric Acid and Urea: Synthesis and Mechanism of Water Absorption. Carbohydr. Polym. 2018, 191, 152–160. [Google Scholar] [CrossRef]
- Funakoshi, T.; Majima, T.; Iwasaki, N.; Yamane, S.; Masuko, T.; Minami, A.; Harada, K.; Tamura, H.; Tokura, S.; Nishimura, S.-I. Novel Chitosan-Based Hyaluronan Hybrid Polymer Fibers as a Scaffold in Ligament Tissue Engineering. J. Biomed. Mater. Res. A 2005, 74, 338–346. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.; Ho, J.; McCandlish, E.; Buckley, B.; Patel, R.; Li, Z.; Shapley, N.C. Copper Ion Adsorption by Chitosan Nanoparticles and Alginate Microparticles for Water Purification Applications. Colloid. Surface. A 2013, 425, 31–41. [Google Scholar] [CrossRef]
- Yasmeen, S.; Lo, M.K.; Bajracharya, S.; Roldo, M. Injectable Scaffolds for Bone Regeneration. Langmuir 2014, 30, 12977–12985. [Google Scholar] [CrossRef] [Green Version]
- Kyzas, G.Z.; Bikiaris, D.N.; Lambropoulou, D. Effect of Humic Acid on Pharmaceuticals Adsorption using Sulfonic Acid Grafted Chitosan. J. Mol. Liq. 2017, 230, 1–5. [Google Scholar] [CrossRef]
- Jakubec, M.; Klimša, V.; Hanuš, J.; Biegaj, K.; Heng, J.Y.Y.; Štěpánek, F. Formation of Multi-Compartmental Drug Carriers by Hetero-Aggregation of Polyelectrolyte Microgels. Colloid. Surface. A 2017, 522, 250–259. [Google Scholar] [CrossRef]
- Zhao, F.; Binyu, Y.; Zhengrong, Y.; Wang, T.; Wen, X.; Liu, Z.; Zhao, C. Preparation of Porous Chitosan Gel Beads for Copper(II) Ion Adsorption. J. Hazard. Mater. 2007, 147, 67–73. [Google Scholar] [CrossRef]
- Babel, S.; Kurniawan, T.A. Low-Cost Adsorbents for Heavy Metals Uptake from Contaminated Water: A Review. J. Hazard. Mater. 2003, 97, 219–243. [Google Scholar] [CrossRef]
- Li, N.; Bai, R. Copper Adsorption on Chitosan-Cellulose Hydrogel Beads: Behaviors and Mechanisms. Sep. Purif. Technol. 2005, 42, 237–247. [Google Scholar] [CrossRef]
- Schmuhl, R.; Krieg, H.M.; Keizer, K. Adsorption of Cu(II) and Cr(VI) Ions by Chitosan: Kinetics and Equilibrium Studies. Water SA 2001, 27, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Elshaarawy, R.F.M.; El-Azim, H.A.; Hegazy, W.H.; Mustafa, F.H.A.; Talkhan, T.A. Poly(Ammonium/ Pyridinium)-Chitosan Schiff Base as a Smart Biosorbent for Scavenging of Cu2+ Ions from Aqueous Effluents. Polym. Test. 2020, 83, 106244. [Google Scholar] [CrossRef]
- Kara, A.; Demirbel, E. Physicochemical Parameters of Cu2+ Ions Adsorption from Aqueous Solution by Magnetic-Poly(Divinylbenzene-N-vinylimidazole) Microbeads. Sep. Sci. Technol. 2012, 47, 709–722. [Google Scholar] [CrossRef]
- Bassi, R.; Prasher, S.O.; Simpson, B.K. Removal of Selected Metal Ions from Aqueous Solutions Using Chitosan Flakes. Sep. Sci. Technol. 2000, 35, 547–560. [Google Scholar] [CrossRef]
- Ahmad, M.; Manzoor, K.; Ikram, S. Versatile Nature of Hetero-Chitosan Based Derivatives as Biodegradable Adsorbent for Heavy Metal Ions; A Review. Int. J. Biol. Macromol. 2017, 105, 190–203. [Google Scholar] [CrossRef]
- Yang, X.; Wan, Y.; Zheng, Y.; He, F.; Yu, Z.; Huang, J.; Wang, H.; Ok, Y.S.; Jiang, Y.; Gao, B. Surface Functional Groups of Carbon-Based Adsorbents and Their Roles in the Removal of Heavy Metals from Aqueous Solutions: A Critical Review. Chem. Eng. J. 2019, 366, 608–621. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, M.; Cheng, Q.; Wan, C.; Han, X.; Fan, Z.; Su, G.; Pan, D.; Li, Z. Research Progress of Adsorption and Removal of Heavy Metals by Chitosan and Its Derivatives: A Review. Chemosphere 2021, 279, 130927. [Google Scholar] [CrossRef]
- Lee, S.T.; Mi, F.L.; Shen, Z.J.; Shyu, S.S. Equilibrium and Kinetic Studies of Copper(II) Ion Uptake by Chitosan-Tripolyphosphate Chelating Resin. Polymer 2021, 42, 1879–1892. [Google Scholar] [CrossRef]
- Guibal, E. Interactions of Metal Ions with Chitosan-Based Sorbents: A Review. Sep. Purif. Technol. 2004, 38, 43–74. [Google Scholar] [CrossRef]
- Guibal, E.; Jansson-Charrier, M.; Saucedo, I.; Le Cloirec, P. Enhancement of Metal Ion Sorption Performances of Chitosan: Effect of the Structure on the Diffusion Properties. Langmuir 1995, 11, 591–598. [Google Scholar] [CrossRef]
- Jansson-Charrier, M.; Guibal, E.; Roussy, J.; Delanghe, B.; Le Cloirec, P. Vanadium (IV) Sorption by Chitosan: Kinetics and Equilibrium. Wat. Res. 1996, 30, 465–475. [Google Scholar] [CrossRef]
- Karthikeyan, G.; Anbalagan, K.; Muthulakshmi Andal, N. Adsorption Dynamics and Equilibrium Studies of Zn (II) onto Chitosan. J. Chem. Sci. 2004, 116, 119–127. [Google Scholar] [CrossRef]
- Milosavljevic, N.B.; Ristic, M.D.; Peric-Grujic, A.A.; Filipovic, J.M.; Strbac, S.B.; Rakocevic, Z.L.; Kalagasidis Krusic, M.T. Removal of Cu2+ Ions Using Hydrogels of Chitosan, Itaconic and Methacrylic Acid: FTIR, SEM/EDX, AFM, Kinetic and Equilibrium Study. Colloid. Surface. A 2011, 388, 59–69. [Google Scholar] [CrossRef]
- de Vasconcelos, C.L.; Rocha, A.N.L.; Pereira, M.R.; Foncesa, J.L.C. Electrolyte Diffusion in a Chitosan Membrane. Polym. Int. 2001, 50, 309–312. [Google Scholar] [CrossRef]
- Krajewska, B. Diffusion of Metal Ions through Gel Chitosan Membranes. React. Funct. Polym. 2001, 47, 37–47. [Google Scholar] [CrossRef]
- Yoshida, C.M.P.; Bastos, C.E.N.; Franco, T.T. Modeling of Potassium Sorbate Diffusion through Chitosan Films. LWT—Food Sci. Technol. 2010, 43, 584–589. [Google Scholar] [CrossRef]
- Modrzejewska, Z.; Rogacki, G.; Sujka, W.; Zarzycky, R. Sorption of Copper by Chitosan Hydrogel: Kinetics and Equilibrium. Chem. Eng. Process. 2016, 109, 104–113. [Google Scholar] [CrossRef]
- Mankidy, B.D.; Coutinho, C.A.; Gupta, V.K. Probing the Interplay of Size, Shape, and Solution Environment in Macromolecular Diffusion Using a Simple Refraction Experiment. J. Chem. Educ. 2010, 87, 515–518. [Google Scholar] [CrossRef]
- Klučáková, M.; Smilek, J.; Sedláček, P. How Humic Acids Affect the Rheological and Transport Properties of Hydrogels. Molecules 2019, 24, 1545. [Google Scholar] [CrossRef] [Green Version]
- Klučáková, M. Agarose Hydrogels Enriched by Humic Acids as Complexation Agent. Polymers 2020, 12, 687. [Google Scholar] [CrossRef] [Green Version]
- Sedláček, P.; Smilek, J.; Klučáková, M. How the Interactions with Humic Acids Affect the Mobility of Ionic Dyes in Hydrogels—2. Non-Stationary Diffusion Experiments. React. Funct. Polym. 2014, 75, 41–50. [Google Scholar] [CrossRef]
- Klučáková, M.; Pekař, M. Study of Structure and Properties of Humic and Fulvic Acids. IV. Study of Interactions of Cu2+ Ions with Humic Gels and Final Comparison. J. Polym. Mater. 2003, 20, 155–162. [Google Scholar]
- Klučáková, M.; Kalina, M.; Sedláček, P.; Grasset, L. Reactivity and Transport Mapping of Cu(II) Ions in Humic Hydrogels. J. Soil. Sediment. 2014, 14, 368–376. [Google Scholar] [CrossRef]
- Klučáková, M.; Kalina, M.; Smilek, J.; Laštůvková, M. The Transport of Metal Ions in Hydrogels Containing Humic Acids as Active Complexation Agent. Colloid. Surface. A 2018, 557, 116–122. [Google Scholar] [CrossRef]
- Chiessi, E.; Paradossi, G.; Venanzi, M.; Pispisa, B. Copper Complexes Immobilized to Chitosan. J. Inorg. Biochem. 1992, 46, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Monteiro Jr, O.A.C.; Airoldi, C. Some Thermodynamic Data on Copper–Chitin and Copper–Chitosan Biopolymer Interactions. J. Colloid Interface Sci. 1999, 212, 212–219. [Google Scholar] [CrossRef]
- Onsoyen, E.; Skaugrud, O. Metal Recovery Using Chitosan. J. Chem. Technol. Biotechnol. 1990, 49, 395–404. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 1st ed.; Clarendon Press: Oxford, UK, 1956; pp. 26–41. [Google Scholar]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 1984; pp. 13–49. [Google Scholar]
- Kyzas, G.Z.; Kostoglou, M.; Layaridis, N.K. Copper and Chromium(VI) Removal by Chitosan Derivatives—Equilibrium and Kinetic Studies. Chem. Eng. J. 2009, 152, 440–448. [Google Scholar] [CrossRef]
- Lobo, V.M.M.; Quaresma, J.L. Handbook of Electrolyte Solutions; Physical Science Data Series 41; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Zhang, H.; Davison, W. Diffusional Characteristics of Hydrogels Used in DGT and DET Techniques. Anal. Chim. Acta 1999, 398, 329–340. [Google Scholar] [CrossRef]
- Chu, H.H. Removal of Copper from Aqueous Solution by Chitosan in Prawn Shell: Adsorption Equilibrium and Kinetics. J. Hazard. Mater. 2002, 90, 77–95. [Google Scholar] [CrossRef]
- Modrzejewska, Z. Sorption Mechanism of Copper in Chitosan Hydrogel. React. Funct. Polym. 2013, 73, 719–729. [Google Scholar] [CrossRef]
- Guzman, J.; Saucedo, I.; Revilla, J.; Navarro, R.; Guibal, E. Copper Sorption by Chitosan in the Presence of Citrate Ions: Influence of Metal Speciation on Sorption Mechanism and Uptake Capacities. Int. J. Biol. Macromol. 2003, 33, 57–65. [Google Scholar] [CrossRef]
- Lagzi, I. Controlling and Engineering Precipitation Patterns. Langmuir 2012, 28, 3350–3354. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Mi, Y.; Jia, D.; Guo, N.; An, Y.; Miao, Y. Polymorphs Co Hydroxides Formed between Hydrazine and Co2+ as Liesegang Bands in Semisolid Agar Gel. J. Mol. Liq. 2019, 285, 416–423. [Google Scholar] [CrossRef]
- Izsák, F.; Lagzi, I. A New Universal Law for the Liesegang Pattern Formation. J. Chem. Phys. 2005, 122, 184707. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Gao, Y.; Feng, Y.; Ma, B.; Zhu, R.; Zhou, Y. Formation of Concentric Multilayers in a Chitosan Hydrogel Inspired by Liesegang Ring Phenomen. J. Biomater. Sci. 2011, 22, 2295–2304. [Google Scholar] [CrossRef]
- Gegel, N.; Babicheva, T.; Shipovskaya, A. Morphology of Chitosan-Based Hollow Cylindrical Materials with a Layered Structure. BioNanoScience 2018, 8, 661–667. [Google Scholar] [CrossRef]
- Babicheva, T.S.; Konduktorova, A.A.; Shmakov, S.L.; Shipovskaya, A.B. Formation of Liesegang Structures under the Conditions of the Spatiotemporal Reaction of Polymer-Analogous Transformation (Salt Base) of Chitosan. J. Phys. Chem. B 2020, 124, 9255–9266. [Google Scholar] [CrossRef]
- Kumar, P.; Sebok, D.; Kukovecs, A.; Horvath, D.; Toth, A. Hierarchical Self-Assembly of Metal-Ion-Modulated Chitosan Tubules. Langmuir 2021, 37, 12690–12696. [Google Scholar] [CrossRef] [PubMed]
- Nabika, H.; Itatani, M.; Lagzi, I. Pattern Formation in Precipitation Reactions: The Liesegang Phenomenon. Langmuir 2020, 36, 481–497. [Google Scholar] [CrossRef]
- Shimizu, Y.; Matsui, J.; Unoura, K.; Nabika, H. Liesegang Mechanism with a Gradual Phase Transition. J. Phys. Chem. B 2017, 121, 2495–2501. [Google Scholar] [CrossRef]
- Monk, P. Physical Chemistry. Understanding Our Chemical World, 1st ed.; John Wiley & Sons Ltd.: Chichester, UK, 2004; pp. 177–229. [Google Scholar]
- Saad, M.; Safieddine, A.; Sultan, R. Revisited Chaos in a Diffusion-Precipitation-Redissolution Liesegang System. J. Phys. Chem. B 2018, 122, 6043–6047. [Google Scholar] [CrossRef]
- Nakouzi, E.; Steinbock, O. Self-Organization in Precipitation Reactions Far from the Equilibrium. Sci. Adv. 2016, 2, e1601144. [Google Scholar] [CrossRef] [PubMed]
- Sedláček, P.; Smilek, J.; Klučáková, M. How Interactions with Polyelectrolytes Affect Mobility of Low Molecular Ions—Results from Diffusion Cells. React. Funct. Polym. 2013, 73, 1500–1509. [Google Scholar] [CrossRef]
- Garcia, L.G.S.; de Melo Guedes, G.M.; da Silva, M.L.Q.; Castelo-Branco, D.S.C.M.; Sidrim, J.J.C.; de Aguiar Cordeiro, R.; Rocha, M.F.G.; Vieira, R.S.; Brilhante, R.S.N. Effect of the Molecular Weight of Chitosan on its Antifungal Activity against Candida spp. in Planktonic Cells and Biofilm. Carbohydr. Polym. 2018, 195, 662–669. [Google Scholar] [CrossRef] [PubMed]



| Time t | Distance x | Concentration c |
|---|---|---|
| t = 0 | x > 0 | c = 0 |
| t > 0 | x = 0 | c = cs |
| t > 0 | x → ∞ | c = 0 |
| Chitosan Content (mg g−1) | Concentration at Interface (mmol dm−3) | Diffusion Coefficient (m2 s−1) |
|---|---|---|
| 0 | 37.73 ± 0.62 | (6.25 ± 0.06) × 10−10 |
| 0.2 | 38.48 ± 0.86 | (6.03 ± 0.13) × 10−10 |
| 0.5 | 38.86 ± 1.15 | (6.98 ± 0.24) × 10−10 |
| 1 | 40.15 ± 1.12 | (7.41 ± 0.22) × 10−10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klučáková, M. How the Addition of Chitosan Affects the Transport and Rheological Properties of Agarose Hydrogels. Gels 2023, 9, 99. https://doi.org/10.3390/gels9020099
Klučáková M. How the Addition of Chitosan Affects the Transport and Rheological Properties of Agarose Hydrogels. Gels. 2023; 9(2):99. https://doi.org/10.3390/gels9020099
Chicago/Turabian StyleKlučáková, Martina. 2023. "How the Addition of Chitosan Affects the Transport and Rheological Properties of Agarose Hydrogels" Gels 9, no. 2: 99. https://doi.org/10.3390/gels9020099
APA StyleKlučáková, M. (2023). How the Addition of Chitosan Affects the Transport and Rheological Properties of Agarose Hydrogels. Gels, 9(2), 99. https://doi.org/10.3390/gels9020099








