Impact of Solid Particle Concentration and Liquid Circulation on Gas Holdup in Counter-Current Slurry Bubble Columns
Abstract
1. Introduction
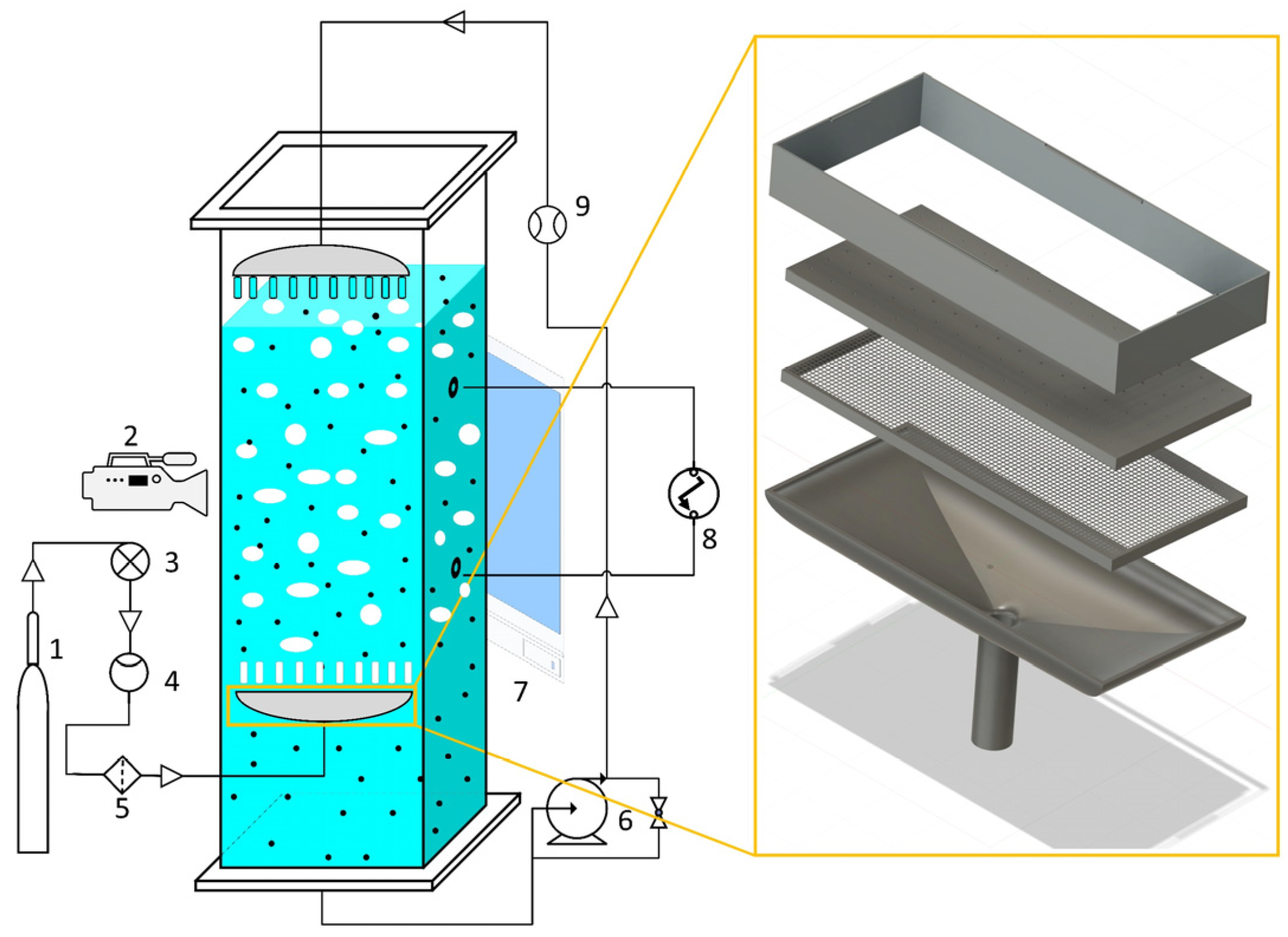
2. Experimental Setup and Method
2.1. Experimental Setup
2.2. Experimental Method
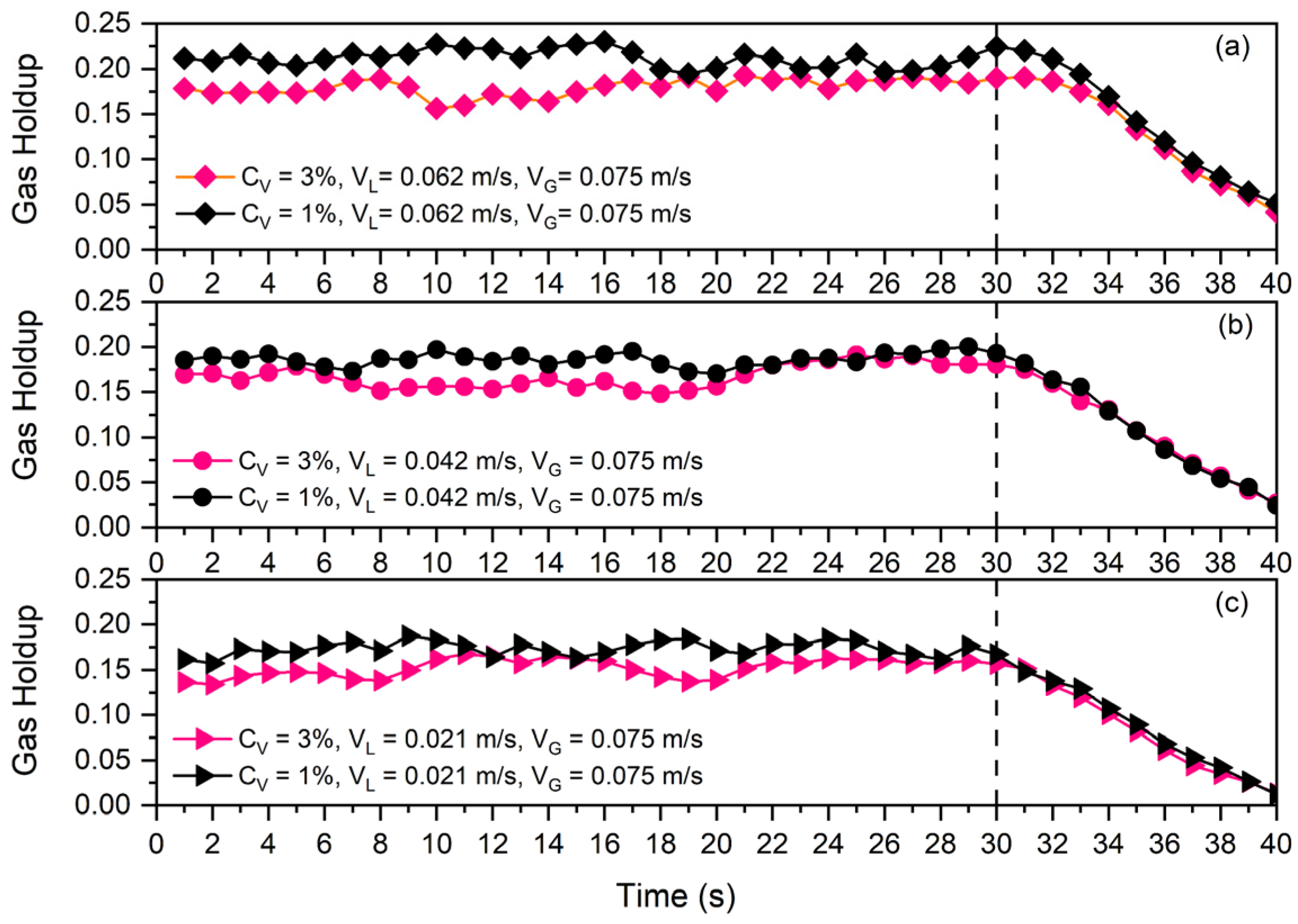
2.2.1. Gas Holdup
2.2.2. Differential Gas Disengagement
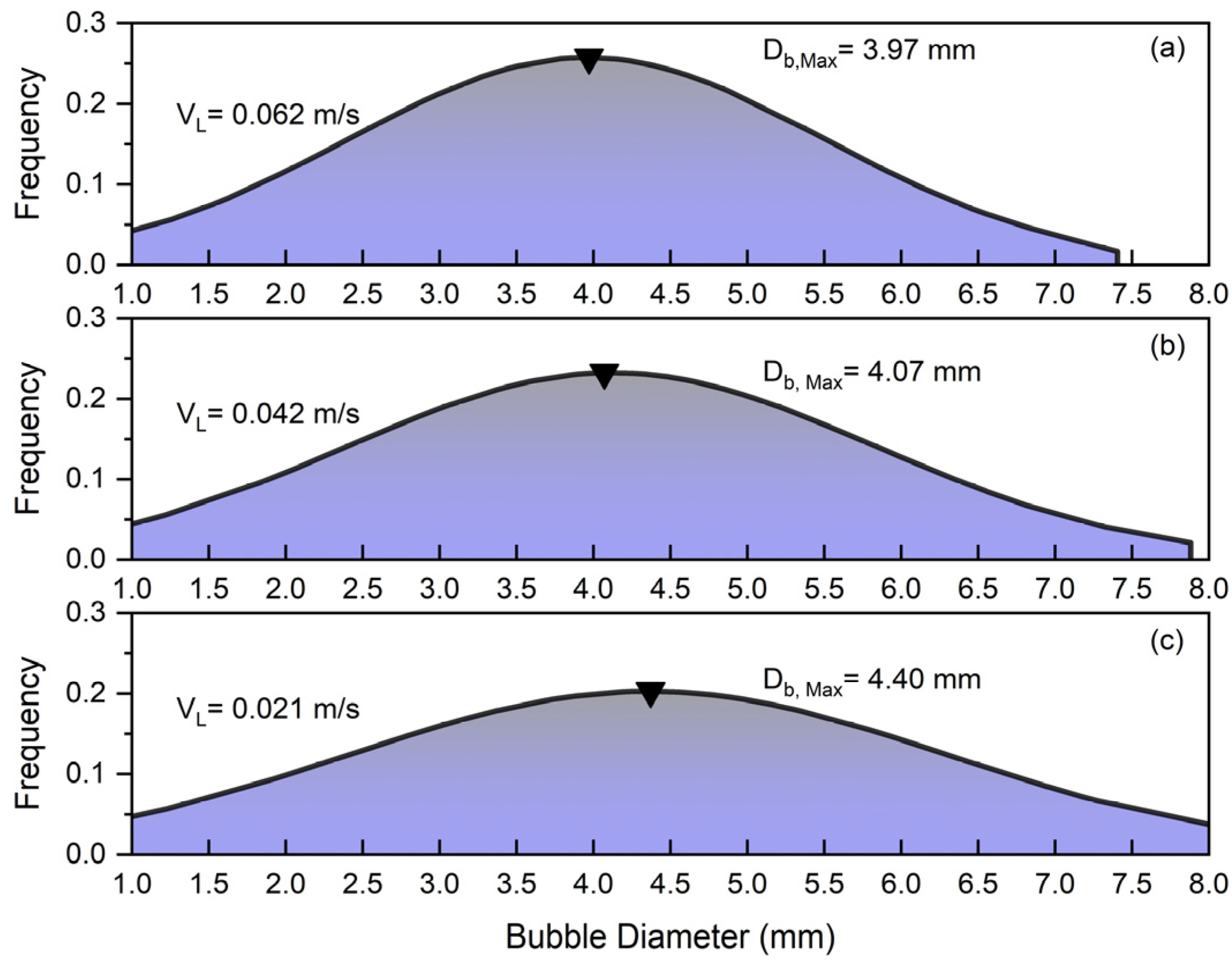
2.2.3. Bubble Diameter
3. Modeling
4. Results and Discussion
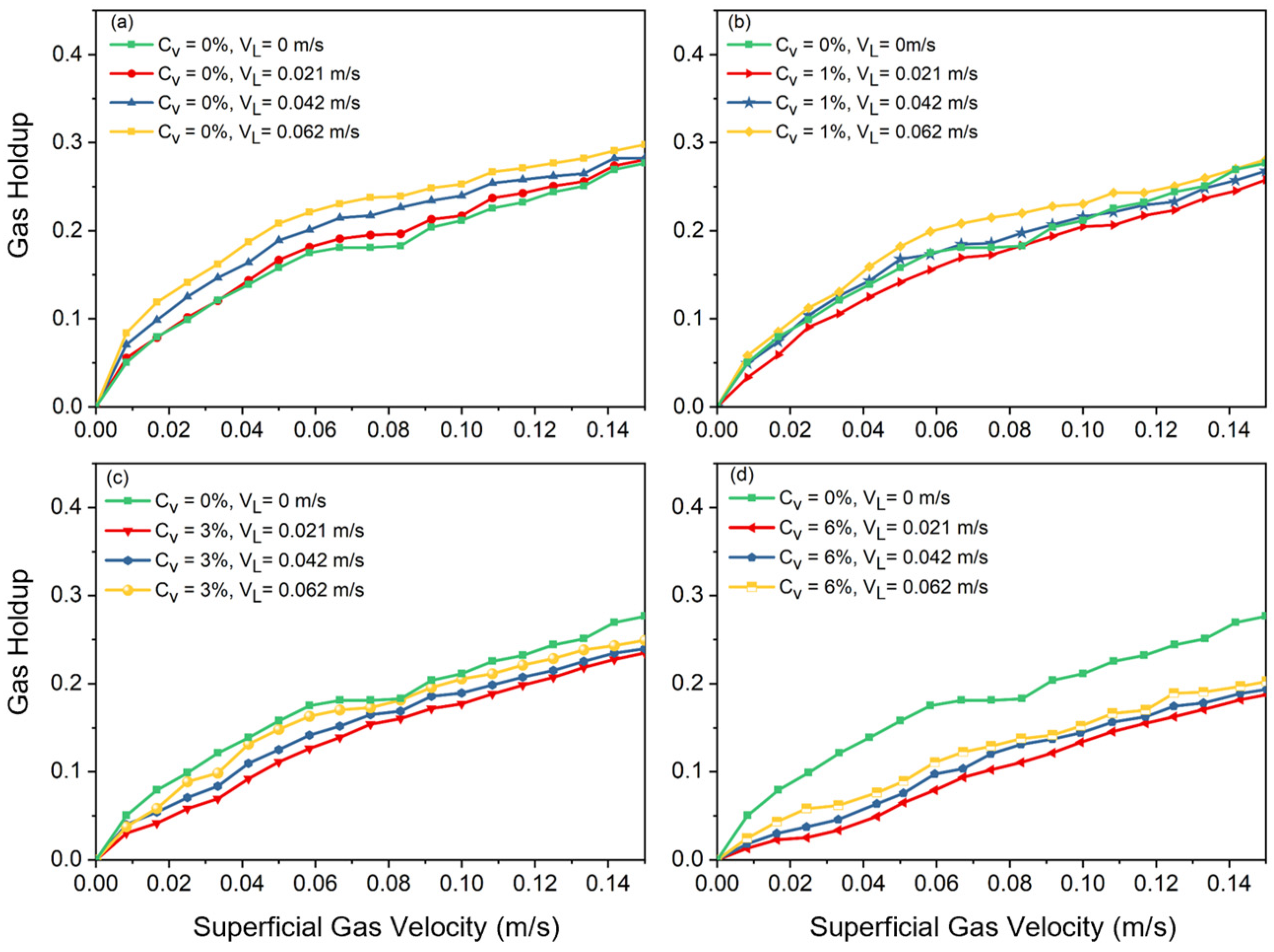
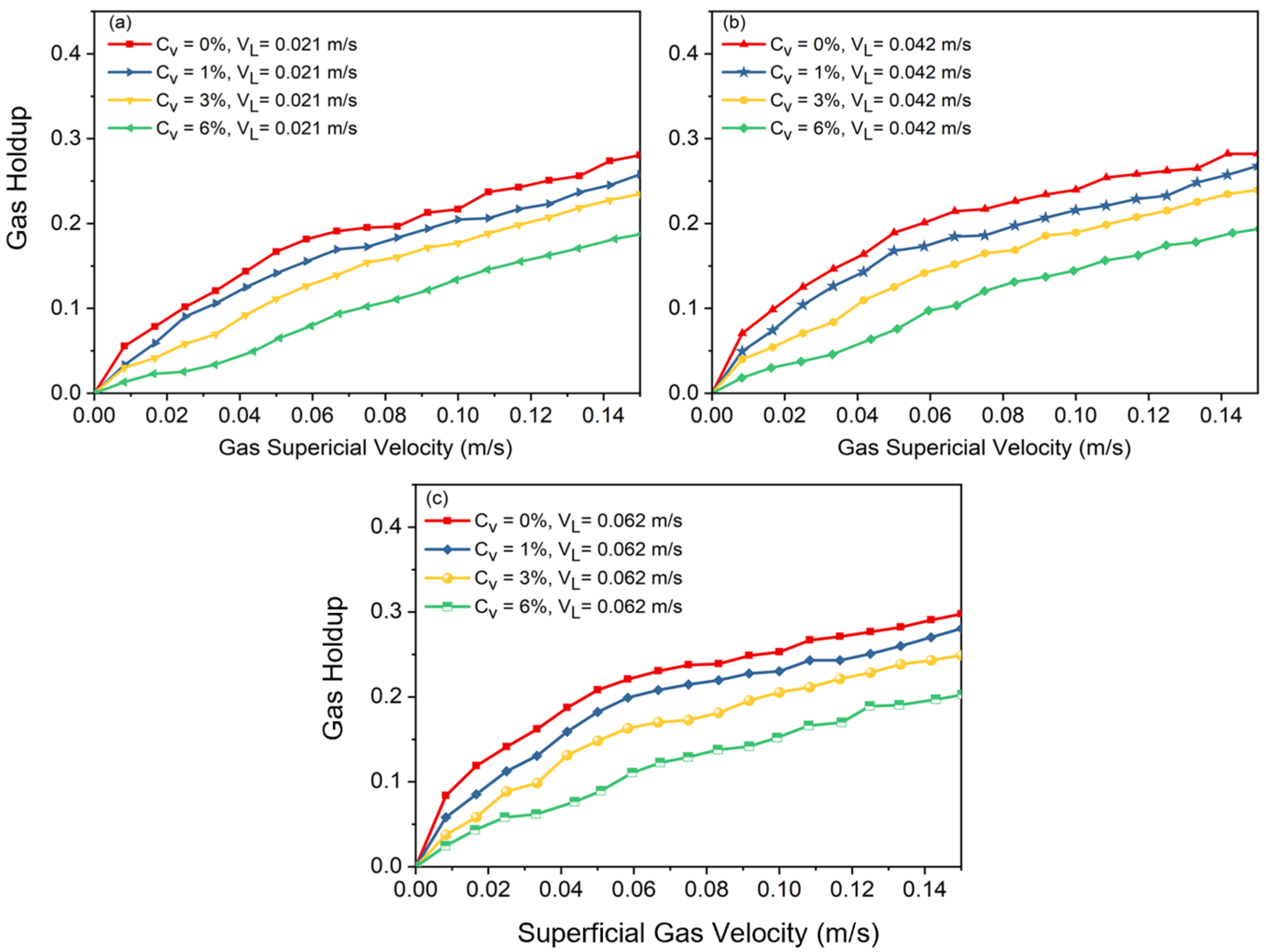
4.1. Gas Holdup in Two- and Three-Phase Systems
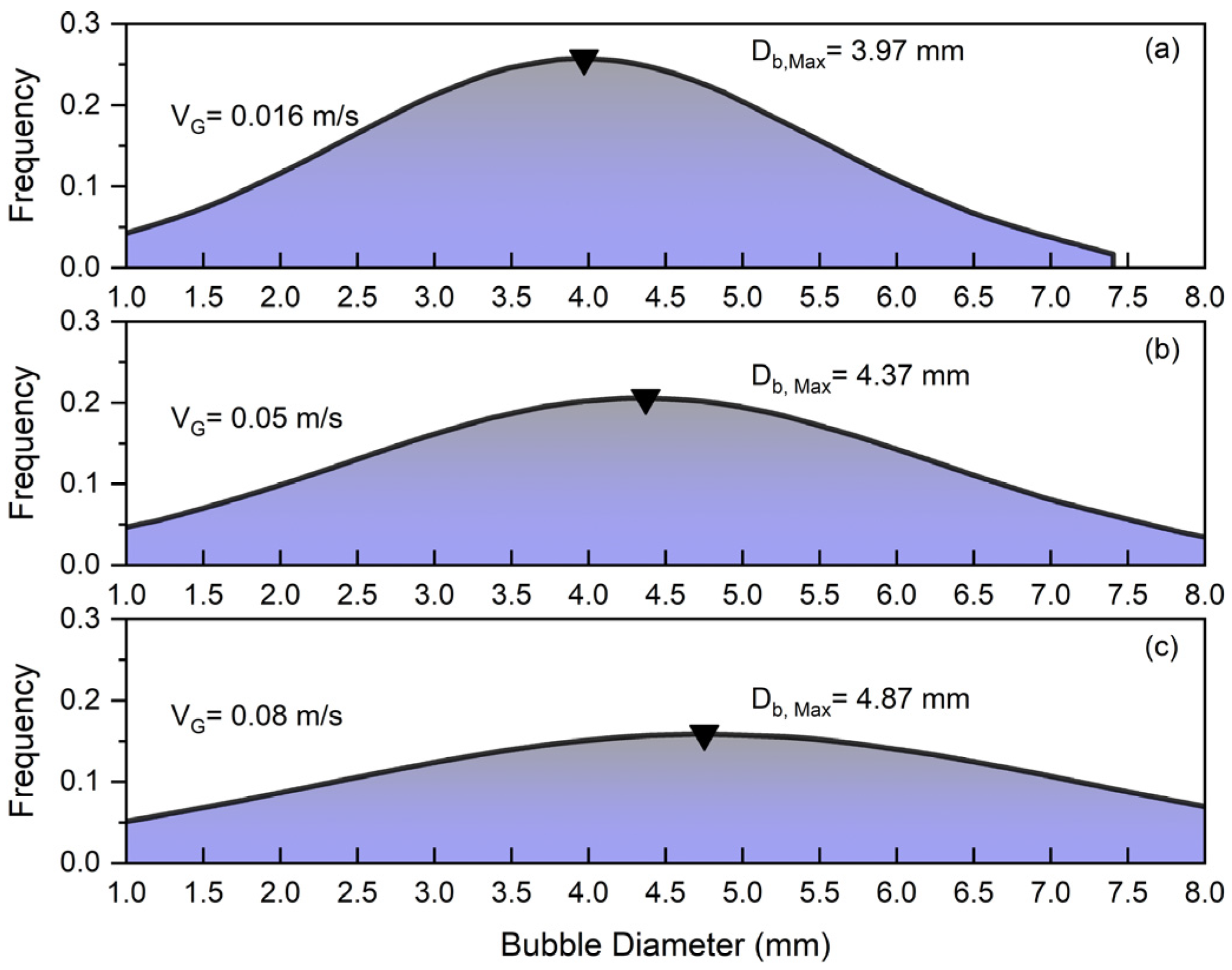
4.2. Bubble Size Distribution
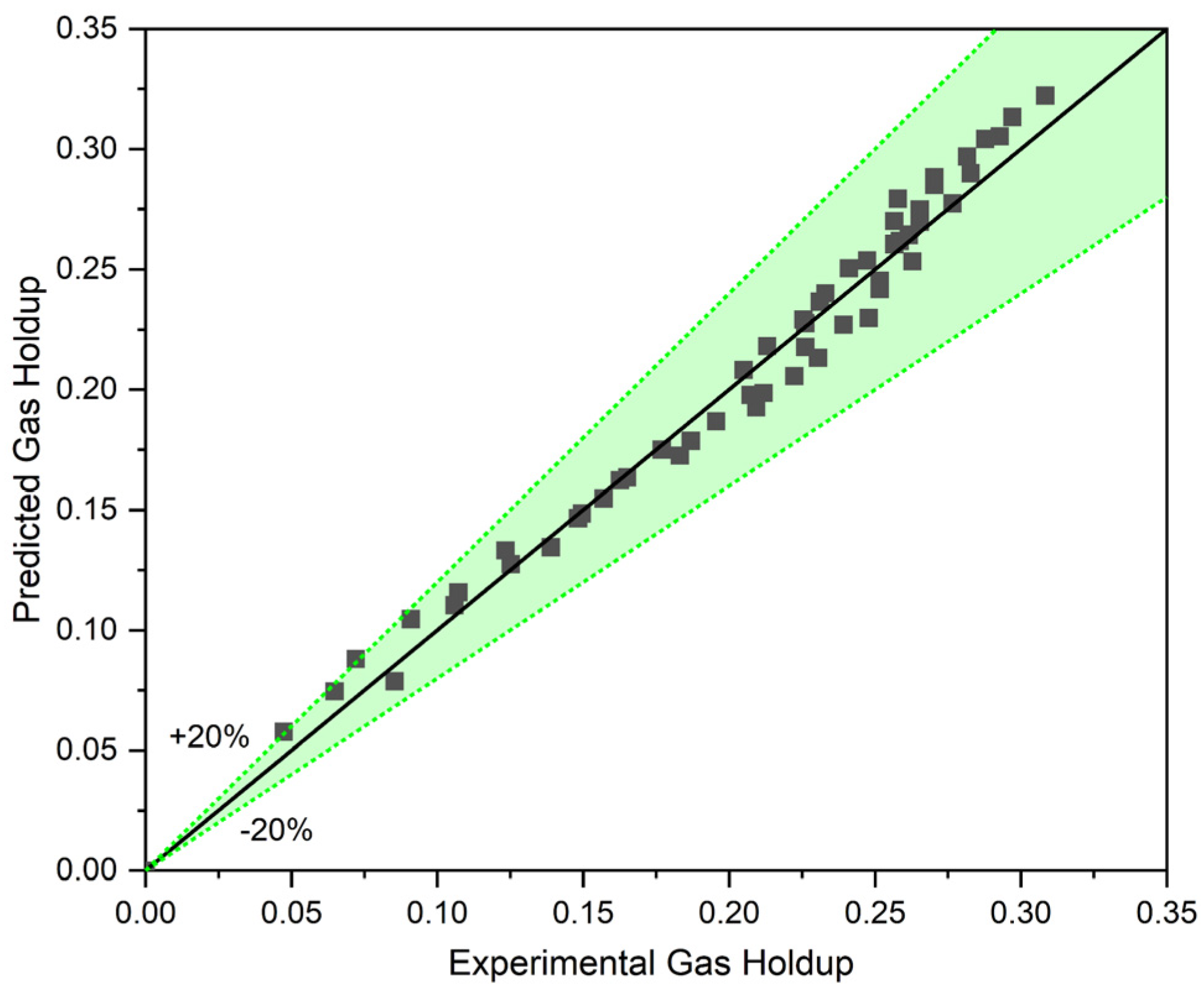
4.3. Gas Holdup Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| Bond number, | |
| Concentration, | |
| Column equivalent diameter, | |
| Bubble equivalent diameter, | |
| Solid particle diameter, | |
| Largest bubble diameter, | |
| Smallest bubble diameter, | |
| Collision efficiency | |
| Froude number, | |
| Galilei number, | |
| Gravitational acceleration, | |
| Pressure, | |
| Reynolds number, | |
| Stokes number, | |
| Superficial liquid velocity, | |
| Superficial slurry velocity, , | |
| Superficial gas velocity, | |
| Bubble rising velocity, | |
| Weber number, | |
| Subscripts | |
| b | Bubble |
| c-GSE | Generalized Sutherland equation |
| c-SU | Sutherland model |
| G | Gas |
| L | Liquid |
| P | Particle |
| S | Solid |
| SL | Slurry |
| Two-phase | |
| Three-phase | |
| Greek symbols | |
| Viscosity, | |
| Density, | |
| Holdup | |
| Surface tension, | |
| Height difference, | |
| Pressure difference, |
References
- Bahrami, M.; Mahmoudi, S.; Hamoule, T.; Aghajani, M. Hydroconversion of n-Heptane over bifunctional Pt–Ti–MSU/Al–Ti–MSU catalysts in a micro reactor. Pet. Chem. 2021, 61, 455–464. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; Ziegenhein, T. Two-phase bubble columns: A comprehensive review. ChemEngineering 2018, 2, 13. [Google Scholar] [CrossRef]
- Trivedi, R.; Renganathan, T.; Krishnaiah, K. Hydrodynamics of countercurrent bubble column: Experiments and predictions. Chem. Eng. J. 2018, 338, 636–650. [Google Scholar] [CrossRef]
- An, M.; Gao, J.; Wang, T.; Li, X. Particle effects on the hydrodynamics in slurry bubble column reactors: A review from multiscale mechanisms. Particuology 2024, 91, 176–189. [Google Scholar] [CrossRef]
- Mahmoudi, S.; Hlawitschka, M.W. Effect of solid particles on the slurry bubble columns behavior—A review. ChemBioEng Rev. 2022, 9, 63–92. [Google Scholar] [CrossRef]
- Abdulrahman, M.W. Effect of solid particles on gas holdup in a slurry bubble column. In Proceedings of the 6th World Congress on Mechanical, Chemical, and Material Engineering (MCM 2020), Prague, Czech Republic, 16–18 August 2020; Avestia Publishing: Orléans, ON, Canada, 2020. [Google Scholar]
- Besagni, G.; Di Pasquali, A.; Gallazzini, L.; Gottardi, E.; Colombo, L.P.M.; Inzoli, F. The effect of aspect ratio in counter-current gas-liquid bubble columns: Experimental results and gas holdup correlations. Int. J. Multiph. Flow 2017, 94, 53–78. [Google Scholar] [CrossRef]
- Mahmoudi, S.; Saeedipour, M.; Hlawitschka, M.W. Bubble dynamics under the influence of the Marangoni force induced by a stratified field of contamination. Exp. Comput. Multiph. Flow 2024, 6, 353–364. [Google Scholar] [CrossRef]
- Prakash, R.; Bhattacharyya, A.; Majumder, S.K. Experimental investigation and its analysis of gas holdup in a three-phase counter-current microstructured bubble column. J. Dispers. Sci. Technol. 2022, 43, 243–258. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.A.; Munshi, P.; Khanna, A. Gas hold-up in three phase co-current bubble columns. Procedia Eng. 2012, 42, 782–794. [Google Scholar] [CrossRef]
- Li, W.; Zhou, G.; Sun, J.; Guo, Y.; Wang, R. Impacts of particle properties on gas holdup under four flow regimes in three-phase bubble columns. Chem. Eng. Technol. 2021, 44, 2347–2354. [Google Scholar] [CrossRef]
- Sommerfeld, M. Bubbly Flows: Analysis, Modelling and Calculation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wu, Y.; Liu, Z.; Wang, F.; Li, B.; Gan, Y. Experimental investigation of trajectories, velocities and size distributions of bubbles in a continuous-casting mold. Powder Technol. 2021, 387, 325–335. [Google Scholar] [CrossRef]
- Krishna, R.; Urseanu, M.I.; De Swart, J.W.A.; Ellenberger, J. Gas hold-up in bubble columns: Operation with concentrated slurries versus high viscosity liquid. Can. J. Chem. Eng. 2000, 78, 442–448. [Google Scholar] [CrossRef]
- Rabha, S.; Schubert, M.; Hampel, U. Regime transition in viscous and pseudo viscous systems: A comparative study. AIChE J. 2014, 60, 3079–3090. [Google Scholar] [CrossRef]
- Li, H.; Prakash, A. Influence of slurry concentrations on bubble population and their rise velocities in a three-phase slurry bubble column. Powder Technol. 2000, 113, 158–167. [Google Scholar] [CrossRef]
- Mokhtari, M.; Chaouki, J. Effect of solid loading and particle size on the phase holdup distribution and bubble behaviour in a pilot-scale slurry bubble column. Chem. Eng. Sci. 2021, 243, 116732. [Google Scholar] [CrossRef]
- Rabha, S.; Schubert, M.; Hampel, U. Intrinsic flow behavior in a slurry bubble column: A study on the effect of particle size. Chem. Eng. Sci. 2013, 93, 401–411. [Google Scholar] [CrossRef]
- Dai, Z.; Fornasiero, D.; Ralston, J. Particle-bubble collision models-a review. Adv. Colloid Interface Sci. 2000, 85, 231–256. [Google Scholar] [CrossRef]
- Kantarci, N.; Borak, F.; Ulgen, K.O. Bubble column reactors. Process Biochem. 2005, 40, 2263–2283. [Google Scholar] [CrossRef]
- Behkish, A.; Lemoine, R.; Sehabiague, L.; Oukaci, R.; Morsi, B.I. Gas holdup and bubble size behavior in a large-scale slurry bubble column reactor operating with an organic liquid under elevated pressures and temperatures. Chem. Eng. J. 2007, 128, 69–84. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Saxena, S.C.; Chen, Z.D. Hydrodynamics and heat transfer of baffled and unbaffled slurry bubble columns. Rev. Chem. Eng. 1994, 10, 193–400. [Google Scholar]
- Lakhdissi, E.M.; Soleimani, I.; Guy, C.; Chaouki, J. Simultaneous effect of particle size and solid concentration on the hydrodynamics of slurry bubble column reactors. AIChE J. 2020, 66, e16813. [Google Scholar] [CrossRef]
- Jin, H.; Yang, S.; He, G.; Wang, M.; Williams, R.A. The effect of gas-liquid counter-current operation on gas hold-up in bubble columns using electrical resistance tomography. J. Chem. Technol. Biotechnol. 2010, 85, 1278–1283. [Google Scholar] [CrossRef]
- Prakash, R.; Majumder, S.K. Effect of particle size and concentration on bubble size distribution and aspect ratio in a counter-current microstructured bubble column. J. Ind. Eng. Chem. 2020, 90, 105–116. [Google Scholar] [CrossRef]
- Prakash, R.; Majumder, S.K.; Singh, A. Dispersion characteristics in a counter-current microstructured slurry bubble column and its analysis based on the turbulence and circulation. Ind. Eng. Chem. Res. 2020, 59, 8093–8111. [Google Scholar] [CrossRef]
- Shah, M.; Kiss, A.A.; Zondervan, E.; van der Schaaf, J.; de Haan, A.B. Gas Holdup, axial dispersion, and mass transfer studies in bubble columns. Ind. Eng. Chem. Res. 2012, 51, 14268–14278. [Google Scholar] [CrossRef]




| Parameter | Description |
|---|---|
| Input | |
| Accuracy (Percentage of Full Scale) | |
| Output | |
| Response Time |
| Parameter | Value |
|---|---|
| A | 0.99 |
| B | −0.113 |
| C | −0.022 |
| D | −0.147 |
| E | 0.139 |
| F | 0.112 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoudi, S.; Hlawitschka, M.W. Impact of Solid Particle Concentration and Liquid Circulation on Gas Holdup in Counter-Current Slurry Bubble Columns. Fluids 2025, 10, 14. https://doi.org/10.3390/fluids10010014
Mahmoudi S, Hlawitschka MW. Impact of Solid Particle Concentration and Liquid Circulation on Gas Holdup in Counter-Current Slurry Bubble Columns. Fluids. 2025; 10(1):14. https://doi.org/10.3390/fluids10010014
Chicago/Turabian StyleMahmoudi, Sadra, and Mark W. Hlawitschka. 2025. "Impact of Solid Particle Concentration and Liquid Circulation on Gas Holdup in Counter-Current Slurry Bubble Columns" Fluids 10, no. 1: 14. https://doi.org/10.3390/fluids10010014
APA StyleMahmoudi, S., & Hlawitschka, M. W. (2025). Impact of Solid Particle Concentration and Liquid Circulation on Gas Holdup in Counter-Current Slurry Bubble Columns. Fluids, 10(1), 14. https://doi.org/10.3390/fluids10010014







