Vaporization Dynamics of a Volatile Liquid Jet on a Heated Bubbling Fluidized Bed ^†

Abstract

In this paper, droplet vaporization dynamics in a heated bubbling fluidized bed was studied. A volatile hydrocarbon liquid jet comprising acetone was injected into a hot bubbling fluidized bed of Geldart A-type glass ballotini particles heated at 150 °C, well above the saturation temperature of acetone (56 °C). Intense interactions were observed among the evaporating droplets and hot particles during contact with the re-suspension of particles due to a release of vapour. A non-intrusive schlieren imaging method was used to track the hot air and vapour mixture plume in the freeboard region of the bed and the acetone vapour fraction therein was mapped. The jet vaporization dynamics in the bubbling fluidized bed was modelled in a Eulerian–Lagrangian CFD (computational fluid dynamics) modelling framework involving heat and mass transfer sub models. The CFD model indicated a dispersion of the vapour plume from the evaporating droplets which was qualitatively compared with the schlieren images. Further, the CFD simulation predicted a significant reduction (~60 °C) in the local bed temperature at the point of the jet injection, which was indirectly confirmed in an experiment by the presence of particle agglomerates.

1. Introduction

The simultaneous injection and vaporization of a liquid stream in gas–solid fluidized bed reactors have a number of significant process engineering applications due to excellent transport characteristics which include, but are not limited to, fluid catalytic cracking (FCC) for producing lighter hydrocarbons from heavy petroleum feedstocks [1,2,3], bitumen upgrading by fluid coking [4], particle coating [5,6], granulation [7], and combustion of liquid waste [8]. Depending on the void fraction of the system, the complex hydrodynamic interactions of the injected droplets and particles occur coupled with heat transfer, which includes boiling at the solid–liquid interface and evaporation from the gas–liquid interface, thereby controlling the process efficiency and product distribution and quality [8,9,10].

In this overarching category of multiphase systems involving phase change, a liquid jet interaction with a dense gas–solid system (gas volume fraction < 0.7) leads to heterogeneous vaporization. Specific to FCC systems, dense bed interactions occur at the bottom of the riser where atomized fuel droplets interact with the regenerated catalyst stream. Mirgain et al. (2000) [9] suggested that in the dense bed operating regime of FCC, due to the closely packed nature of the catalyst particles, feed droplets cannot penetrate the catalyst jet which acts like a rough cylindrical surface. Feed droplets repeatedly impinge on this jet surface, wetting the particles through a liquid film formation and gradually vaporizing, resulting in the cooling of the catalyst particles.

In the heterogeneous vaporization process, both heat and mass transfer phenomena are largely governed by the droplet–particle collision process [2,3,4,11]. In the increasing order of the temperature difference between droplets and solid particles, both evaporation at the gas–liquid interface and nucleate or film boiling occurs at the solid–liquid interface. In the nucleate boiling regime, when the particle surface temperature is higher than the saturation temperature of the droplet, heat flux from the particle surface increases dramatically and numerous vapour bubbles are produced at the contact surface. When the particle surface temperature increases further, a non-continuous insulating vapour film develops at the contact surface which reduces the heat transfer rate drastically and increases droplet evaporation time. At a much higher temperature, a stable vapour film forms at the contact surface which separates the particle and droplet, allowing the heat transfer to occur purely by conduction mode through this vapour film. This temperature is known as the Leidenfrost temperature.

Although many theories exist to define the Leidenfrost phenomena, Segev and Bankoff (1980) [12] provided a plausible explanation based on the surface wetting characteristics. According to them, when the droplet spreads over a solid surface, a microscopic liquid precursor film advances over the solid surface. The presence of this microscopic film essentially depends on the temperature-dependent surface Langmuir-type adsorption characteristics. The film thickness reduces to zero when the Leidenfrost temperature is approached, indicating no further adsorption of liquid molecules beyond a monolayer and cessation of the surface wetting. The film boiling phenomenon in the context of single droplet–particle interactions shows interesting outcomes which involve droplet rebound and disintegration depending on the competition between inertia, surface tension, and viscous force. These phenomena have been demonstrated comprehensively through both experiments and computational fluid dynamics modelling [3,13,14,15].

Droplet impact in a packed bed heated above the Leidenfrost temperature also leads to many interesting phenomena, e.g., explosive boiling of droplets, re-suspension of particles, and finally agglomerate formation [16]. This behaviour is explained by the high conductive heat flux at the particle–droplet interface due to the temperature difference between the particle and droplet. Heat transfer during such interactions is, however, inefficient, leading to the partial vaporization of droplets which produces particle agglomerates in the bed due to the adhesive nature of the unvaporized trapped liquid.

Liquid injection behaviour in the particulate systems has been extensively studied, focused on quantifying particle agglomeration conditions in a heated packed bed [17,18] as well as a fluidized bed [1,5,19,20]. It is noted that agglomerate formation depends on spray droplet size and liquid (binder) injection rate per unit bed area above the bed saturation limit which controls the droplet evaporation time. The internal porosity of the particles and injection time also control liquid distribution in the bed [5]. For numerical modelling purposes, both the Eulerian–Eulerian [4,11] and the Eulerian–Lagrangian [6,20,21,22] approaches have been adopted, where the choice remains to treat the droplet phase as continuum or discrete. Droplet evaporation in these cases has been considered through interfacial heat transfer [6,21,22] as well as direct contact between droplets and particles [4,11,20].

It is noted that although some advances have been made in the numerical modelling of this complex process, the heterogeneous vaporization of droplets in fluidized beds at high temperature is still not explored in depth. Recognizing a dearth of knowledge in this area, this study aimed to (1) understand the collision interactions within a volatile hydrocarbon (acetone) liquid jet with a dense fluidized bed at the minimum bubbling state heated at a temperature well above the saturation temperature of the impinging jet; and (2) quantify the vapour concentration profile resulting from the liquid jet impinging on a heated fluidized bed, both experimentally and computationally. Based on the refractive index of the medium, a schlieren imaging technique was used to visualize the vapour flow field. A two-way coupled Eulerian–Lagrangian CFD model was also developed, incorporating a suitable heat transfer model to simulate the heterogeneous vaporization dynamics.

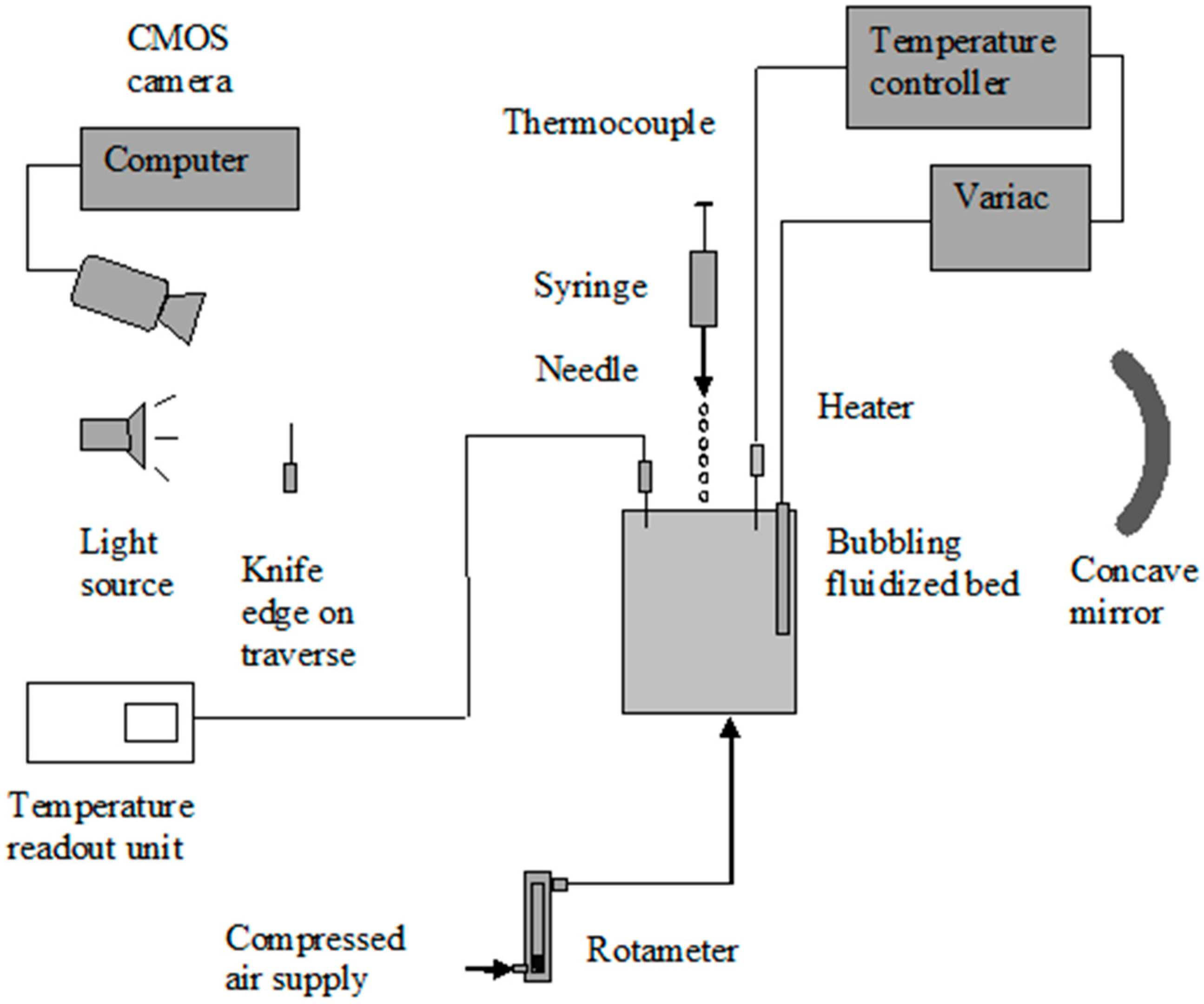
2. Experimental

2.1. Apparatus

A schematic of the experimental setup is presented in Figure 1 [23]. A circular (ID: 45 mm) cross-section borosilicate glass column (height: 45 mm) fitted with a sintered ceramic gas distributor at the base was filled with Geldart B category glass ballotini particles (Burwell Technologies, Whitebridge, Australia) (D₃₂ = 114 μm) up to 40 mm height. Particle size distribution was determined using a MALVERN (Malvern, UK) particle size analyser.

A temperature controller (Pyrosales, Sydney, Australia) connected to a 200 W cartridge heater (Watlow, Tullamarine, Australia) and a 1 mm diameter T-type thermocouple (OMEGA Engineering, Sydney, Australia) was used to control the bed temperature. Due to the small heating load, the heater was connected to a variac to regulate the power suitably for better temperature control of the bed.

At start-up, the air flow was set between 2.5 and 3.0 L/min to maintain a bubbling state, ensuring the bed was well fluidized and uniformly heated. The thermocouple tip was dipped ~5 mm under the bed surface, ensuring that the measured temperature was close to the surface temperature. The bed was operated for about 45 min. At this point, the bed temperature was 150 °C, which was well above the saturation temperature of acetone (56 °C). Any higher temperature was not set to avoid the fusing of glass particles on the cartridge heater due to intense localized heating.

After reaching the set point temperature, a second thermocouple was used to check the bed temperature at various surface locations to ensure that steady surface temperature was reached. The flow rate of air was then reduced to 1.5 L/min to maintain a minimum bubbling condition. The eruption of a few air bubbles occurred at the bed surface, while most of the bed remained almost stationary. After a steady state temperature was reached, 0.2 mL AR grade acetone was injected manually using a 1 mL syringe fitted with a 20 G needle onto the top of the fluidized bed and images were captured at the same time. Acetone droplet size was separately measured using high-speed imaging by generating a single droplet at the needle tip which was ~2 mm. The concentration of acetone vapour in the air was quantified from a separate calibration experiment by vaporizing pure acetone into air and then mapping the grayscale values from high-speed imaging (Figure 2).

To visualize the hot gas plume and map the concentration profile of acetone vapour in air in the freeboard region over the fluidized bed, a non-intrusive high-speed schlieren imaging (400 fps) technique [24,25] was used. The fact that light rays travel at different speeds through the optically transparent medium of different refractive indexes, which leads to the refraction of light rays and a corresponding deflection in the light’s path, forms the physical basis (Snell’s law) of schlieren imaging. These deflection angles are represented in terms of refractive index gradients of the medium. Following the empirical law of Gladstone–Dale [24], the refractive index of the medium can again be expressed as a linear function of the medium density. Using this relationship, the density variations in the system can be profiled and the corresponding light intensity variations can be directly visualized.

The schlieren imaging system comprised a large focal length (f = 6D), a 200 mm diameter (D) concave mirror, a light source, a knife edge, and a high-speed camera. The mirror was mounted on a vibration-resistant aluminium frame. A microscope arc lamp (12 V DC) mounted on an optical table was used as the light source and placed at the focal length of the mirror. The focal point was ascertained by carefully positioning the light source until a clear view of the bulb filament was obtained on a white background. A knife-edge device was positioned on a precision optical traverse at this focal point. After the focal point was fixed, a CMOS camera (Dantec Dynamics, XS-3, IDT Vision, Tallahassee, FL, USA) (5) was placed at this position fitted with a 100 mm focal length lens (Tokina, Tokyo, Japan), ensuring the proper alignment of the centre-point of the camera with the incident light ray. The brightness and contrast of the image was controlled by adjusting the knife-edge device position and cutting the incident light ray on camera. The fluidized bed set-up was placed closed to the mirror and covered from all sides to prevent any unwanted air draft.

2.2. Image Processing Methodology

The order of magnitude difference in the refractive index between the acetone (1.001090) and air (1.000292) makes it possible to capture the distinct acetone vapour plume amidst the hot air medium directly above the heated fluidized bed. The vapour generated during the liquid jet impact on hot solid particles was quantified using an in-house MATLAB (ver: 2012) image processing code. In this process, the pure vapour mass fraction obtained from a separate acetone jet experiment was used for the calibration purpose. Then, a time averaged image of the vapour jet (Figure 2b) was generated from the 1019 instantaneous image sequences (Figure 2a) captured over a time span of ~2 s.

An acetone mass fraction of 1.0 was assigned at the nozzle tip (Figure 2b) with the brightest pixel intensity (255), and a mass fraction value of 0.0 was assigned to the background outside the jet envelope. A linear calibration curve was therefore obtained with background intensity corresponding to 100% air or 0% acetone and maximum pixel intensity corresponding to 100% acetone or 0% air.

Away from the nozzle tip, the velocity of the jet decreases and molecular diffusion governs over the convection. The surrounding air is entrained into the core of the jet which eventually blurs the interface at a sufficient distance from the issuing nozzle tip. Consequently, the concentration of acetone in the jet gradually decreases axially as the jet diffuses and spreads more into the radial direction. For denoising purposes, the background intensity contribution from the hot air was eliminated by subtracting the time averaged background value from the image sequence prior to acetone injection. The pixel intensity distribution provides a mass fraction contour of acetone vapour within the left half of the jet envelope along the symmetry axis (Figure 2c). Only half of the jet envelope was considered due to the presence of an unavoidable dark half corresponding to regions where the light was blocked by the knife-edge device.

3. Computational Model

3.1. Governing Equations

A three dimensional Eulerian–Lagrangian CFD model [23] involving a gas and a liquid phase was developed comprising continuity, momentum, energy, species transport, and turbulence equations in commercial finite volume code ANSYS FLUENT, version 14.0 [26]. The gas phase continuity equation with density ρ_g and velocity u with a mass source term (${\dot{m}}_d$) for the evaporation of a liquid jet can be written as follows:

$${\displaystyle \frac{\partial {\rho }_g}{\partial t}}+\nabla ·({\rho }_g\overrightarrow{u})={\dot{m}}_d$$

(1)

The momentum equation for gas phase, including the effect of buoyancy force due to large temperature gradient as per Boussinesque approximation and an external source term (S_mom), is given as follows:

$${\displaystyle \frac{\partial ({\rho }_g\overrightarrow{u})}{\partial t}}+\nabla ·({\rho }_g\overrightarrow{u}\overrightarrow{u})=-\nabla P+\nabla ·\left[{\mu }_g(\nabla \overrightarrow{u}+\nabla {\overrightarrow{u}}^T)\right]-{\rho }_g(T_{\infty }){\beta }_{exp}(T-T_{\infty })\overrightarrow{g}+S_{mom}$$

(2)

where P is pressure, μ_g is gas viscosity, ρ_g(T_∞) is gas density at a reference temperature (T_∞) of the surrounding atmosphere, and β_exp is the thermal expansion coefficient 1/ρ_g(dρ_g/dT).

The solid phase was not exclusively modelled due to the fact that the system was kept at the minimum bubbling fluidized state with low gas holdup, and the dynamics at the bed surface was the focus here rather than the entire solid bed. A computationally inexpensive porous media approach was therefore applied, accounting for the viscous and inertial resistances due to the solid phase which appears as a negative source term in the momentum equation and can be written as follows:

$$S_{mom}=-\left({\alpha }_{1}u+{\displaystyle \frac{{\beta }_1}{2}}{\rho }_g\left|\overrightarrow{u}\right|\overrightarrow{u}\right)$$

(3)

where α₁ and β₁ are the viscous and inertial resistance, respectively, and calculated comparing Equation (3) with Ergun equation [27] as follows:

$${\displaystyle \frac{dP}{dx}}=A{\displaystyle \frac{{\mu }_g{\left(1-{\alpha }_b\right)}^2}{{\phi }^2{d}_p^2{\alpha }_b^3}}u+B{\displaystyle \frac{{\rho }_g\left(1-{\alpha }_b\right)}{\phi d_p{\alpha }_b^3}}{u}^2$$

(4)

where α_b is bed void fraction, φ is particle sphericity, d_p is particle diameter and A and B are system constants.

In the present work, values of 150 and 1.75 were considered for system constants A and B, respectively. The porous media was further considered to be isotropic, implying that these momentum source terms equal in all three directions. A void fraction (α_b) value of 0.5 was considered in the model which was slightly higher than the value (0.45) reported by Leclere et al. (2001) [17] in their experiments with a non-bubbling fluidized bed.

The energy equation for gas phase was written as in the following equation:

$${\displaystyle \frac{\partial ({\rho }_g{c}_{p,g}T)}{\partial t}}+\nabla ·(\overrightarrow{u}({\rho }_g{c}_{p,g}T+P))=\nabla ·\left[\left(k_{th}+k_{th,t}\right)\nabla T\right]+S_e$$

(5)

where c_p,g is gas heat capacity, and k_th and k_th,t are laminar and turbulent thermal conductivity, respectively, S_e is an energy source term due to vaporization of injected liquid jet given as $S_e=-{\dot{m}}_d\Delta H_{lv}$ where ${\dot{m}}_d$ the is liquid jet vaporization rate and ΔH_lv is the latent heat of vaporization.

The species transport equation was used to model the concentration of acetone vapour in the gas mixture, as follows:

$${\displaystyle \frac{\partial (\rho y_i)}{\partial t}}+\nabla ·(\overrightarrow{u}\rho y_i)=-\nabla ·J_i+S_i$$

(6)

where flux J of ith component in the mixture having mole fraction y is given by the following equation:

$$J_i=-\left(\rho D_i+{\displaystyle \frac{{\mu }_t}{S{c}_t}}{\displaystyle \frac{\partial (\rho y_i)}{\partial t}}\right)\nabla y_i$$

(7)

where D_i is the diffusivity of the ith component in the mixture, µ_t is turbulent diffusivity, Sc_t is turbulent Schmidt number, y_i is the mole fraction and S_i is the source term for ith component in the mixture, respectively.

A two-equation RNG k-ε turbulence model was used which is suitable for low Reynolds number system with swirling flow.

$${\displaystyle \frac{\partial ({\rho }_{g}k)}{\partial x_i}}+\nabla ·({\rho }_{g}k{\overrightarrow{u}}_i)=\nabla ·\left[\left({\mu }_g+{\displaystyle \frac{{\mu }_{g,t}}{{\sigma }_k}}\right)\nabla k\right]+G_k+G_b-{\rho }_g\epsilon$$

(8)

$${\displaystyle \frac{\partial ({\rho }_g\epsilon )}{\partial x_i}}+\nabla ·({\rho }_g\epsilon {\overrightarrow{u}}_i)=\nabla ·\left[\left({\mu }_g+{\displaystyle \frac{{\mu }_{g,t}}{{\sigma }_{\epsilon }}}\right)\nabla \epsilon \right]+C_{1\epsilon }{\displaystyle \frac{\epsilon }{k}}\left(G_k+C_{3\epsilon }{G}_b\right)-C_{2\epsilon }{\rho }_g{\displaystyle \frac{{\epsilon }^2}{k}}+{\rho }_g{S}_{\epsilon }$$

(9)

where G_k and G_b represent turbulent kinetic energy generation due to mean velocity gradient and buoyancy, C_1ε, C_2ε, C_3ε are constants, σ_k and σ_ε are the turbulent Prandtl numbers for k and ε, respectively. Turbulent viscosity µ_g,t was modelled using the following:

$${\mu }_{g,t}={\rho }_g{C}_{\mu }\left({\displaystyle \frac{k^2}{\epsilon }}\right)$$

(10)

Turbulence boundary conditions were specified using turbulence intensity (I) and hydraulic radius, where turbulence intensity was obtained by the following equation:

$$I=0.16{\mathit{Re}}^{-1/8}$$

(11)

The liquid jet was modelled using a Lagrangian approach with the Discrete Particle Model (DPM) where the liquid jet was considered to consist of several mono-sized droplets. Coalescence and break-up of the droplets were not considered in the present work. In the force balance model for the individual liquid droplet, three forces were considered—drag force, gravity force, and buoyancy force. The force balance per unit mass of the individual liquid droplet was expressed as follows:

$${\displaystyle \frac{d{\overrightarrow{u}}_d}{dt}}={\displaystyle \frac{18}{{\rho }_p{d}_p^2}}\left({\displaystyle \frac{C_d\mathit{Re}}{24}}\right)\left({\overrightarrow{u}}_g-{\overrightarrow{u}}_d\right)+\overrightarrow{g}{\displaystyle \frac{\left({\rho }_d-{\rho }_g\right)}{{\rho }_d}}$$

(12)

where ρ_d and u_d are droplet density and velocity, ρ_g, μ_g, and u_g are surround gas density, viscosity and velocity respectively, C_d is drag coefficient, and Re_d is droplet Reynolds number expressed as follows:

$${\mathit{Re}}_d={\displaystyle \frac{{\rho }_g{d}_d}{{\mu }_g}}\left({\overrightarrow{u}}_g-{\overrightarrow{u}}_d\right)$$

(13)

Drag coefficient C_d was obtained from the following spherical drag law equations:

$$C_d=0.424$$

(14)

For Re > 1000, the following equation was used:

$$C_d={\displaystyle \frac{24}{R{e}_d}}\left(1+{\displaystyle \frac{1}{6}}{\mathit{Re}}_d^{2/3}\right)when{\mathit{Re}}_d<1000.$$

(15)

The individual droplet path was tracked by integrating the droplet velocity over time as follows:

$${\displaystyle \frac{d\overrightarrow{z}}{dt}}={\overrightarrow{u}}_d$$

(16)

where z is the path travelled by the droplet.

Due to high vapour pressure of acetone, vaporization of the liquid jet was assumed to occur involving both mass and heat transfer effects. The rate of mass transfer was modelled by relating the flux of the droplet vapour into gas phase to the gradient of vapour concentration between the droplet surface and bulk gas. The following equation was used to model the mass transfer flux:

$$N_i=k_c\left(C_{i,sat}-C_{\infty }\right)$$

(17)

where N_i is the mass transfer flux, k_c is mass transfer coefficient, and C_sat and C_∞ are the saturation and bulk concentration of droplet vapour, respectively, and obtained from the ideal gas law as follows:

$$C_{i,sat}={\displaystyle \frac{P_{sat}(T_d)}{R{T}_d}},\mathrm{and}$$

(18)

$$C_{\infty }={\displaystyle \frac{y_{i,\infty }{P}_{\infty }}{R{T}_{\infty }}}.$$

(19)

In the above equations, P_sat is the saturation vapour pressure at gas-liquid interface at the droplet temperature T_d given by the Antoine equation, and y_i,∞ and P_∞ are the vapour concentration and pressure away from the interface in bulk, respectively.

In Equation (17), mass transfer coefficient k_c was calculated from the Ranz–Marshall correlation [28] as follows:

$$Sh={\displaystyle \frac{k_c{d}_d}{D_i}}=2.0+0.6{\mathit{Re}}_d^{0.5}S{c}^{0.33}.$$

(20)

Changes in the mass of droplets (m_d) due to mass transfer at interfacial area (a_d) with time (t) was computed using the following mass balance expression:

$$m_d(t+\Delta t)=m_d(t)-N_i{a}_d{M}_{w,i}\Delta t.$$

(21)

Finally, the temperature of the droplet (T_d) was obtained by performing a heat balance over a droplet as follows:

$$m_d{c}_{p,d}{\displaystyle \frac{d{T}_d}{dt}}=h{a}_d\left(T_g-T_d\right)+{\displaystyle \frac{d{m}_d}{dt}}\Delta H_{lv}$$

(22)

where c_p,d is the droplet heat capacity, h is the heat transfer coefficient calculated in a similar way using Equation (20) but replacing Sh with Nu.

When the liquid jet impacts on the bed surface, droplet motion ceases. This “no slip” condition on the particle bed surface was implemented by a user-defined function (UDF). Since droplets come to rest after impacting on the surface, convection no longer governs the heat transfer, and it is reasonable to assume that conduction dominates this phase of heat transfer process. The droplets, upon impact on the hot solid particles with a temperature much higher than the saturation temperature of the droplets, form a thin layer of vapour film [3,9] at the contact surface. Considering all the heat transferred to droplet through this vapour layer is used for vaporization, the following heat balance equation can be written [16]:

$$-k_v{a}_d\left({\displaystyle \frac{T_b-T_d}{e_v}}\right)={\dot{m}}_d\Delta H_{lv}$$

(23)

where T_b is the bed temperature, k_v is vapour phase thermal conductivity, e_v is the vapour layer thickness, ${\dot{m}}_d$ is the evaporation rate, and ΔH_lv is the latent heat of vaporization.

Generally, the vapour layer thickness is much smaller than the droplet radius. Ge and Fan (2007) [3] reported this vapour layer thickness in the range of 5–20 μm. An average value of 10 μm was therefore assumed for modelling purposes. The heat transfer sub-model (Equation (23)) was incorporated using a user-defined function (UDF).

A second-order upwind scheme was used for all variables except pressure, which was discretized using the standard scheme. The pressure–velocity coupling was achieved using the SIMPLE algorithm. Gas phase density was calculated using incompressible ideal gas law, and the temperature-dependent physical properties of fluids were used in the simulations. To achieve close interactions between the phases through the mass, momentum, and energy source terms, a two-way coupling scheme was used. All thermophysical properties of acetone used in the CFD model were computed using the UNIQUAC thermodynamic package of the process modelling software Aspen Hysys (version: 7) and presented in

Table 1. Physical properties of acetone at different temperatures determined by UNIQUAC thermodynamic model of Aspen Hysys (v7).

Physical Properties	Acetone (l) (20 °C)	Acetone (l) (56 °C)	Acetone (v) (56 °C)	Acetone (v) (150 °C)
Density (kg/m3)	785.3	744.5	2.15	1.673
Viscosity (Pa·s)	0.318 × 10−3	0.225 × 10−3	7.01 × 10−6	9.385 × 10−6
Surface tension (N/m)	0.02491	0.02039	-	-
Heat capacity (kJ/kg/K)	2.105	2.236	1.365	1.648
Thermal conductivity (w/m/K)	0.1596	0.145	0.0143	0.02194
Latent heat of evaporation (kJ/kg)		501.9

.

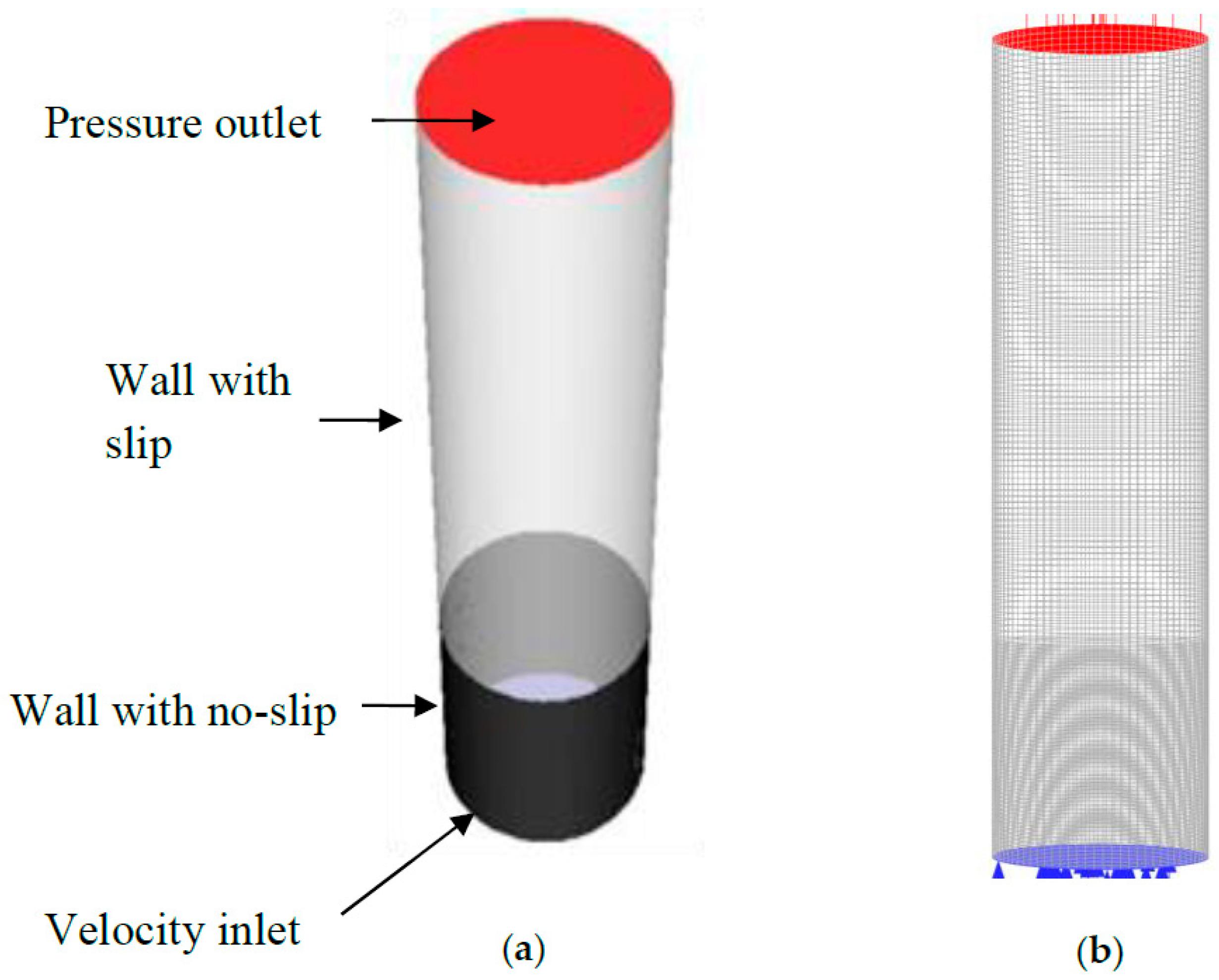
3.2. Mesh and Boundary Conditions

A computational domain diameter of 45 mm (diameter of fluidized bed) and height of 170 mm (bed height = 50 mm and freeboard height over bed surface = 120 mm) were selected for the simulations.

Figure 3 shows the computational domains along with the boundary conditions used. Three different meshes were prepared to check the grid dependency of the numerical solutions of the bubbling fluidized bed. In these three mesh configurations, cell sizes of 1.5 mm, 1.25 mm, and 1.0 mm were used, resulting in total cell numbers of 91,350, 159,392, and 300,220 cells, respectively, in the computational domain. Less than 1% variations were obtained in the final configuration for calculating the volume-averaged temperature, turbulence intensity, and velocity magnitude over the bed surface. Trading off with the computational time and accuracy in the results, no further refinement in the mesh density was considered, and the third mesh configuration was used for all successive calculations. The operating and boundary conditions used in the simulations are listed below in

Table 2. Operating and boundary conditions used in the CFD model.

Variables	Values
Bed void fraction	0.5
Sauter Mean Diameter of solid particles (D32)	114 µm
Inlet velocity	0.0157 m/s
Inlet temperature	423 K
Outlet pressure	101,325 Pa
Bed wall temperature	423 K
Ambient temperature	293 K
Injection position	(x, y): (0, 0.17 m)
Acetone droplet size	0.002 m
Acetone mass flow rate	2.145 × 10−4 kg/s
Inlet temperature	293 K

.

4. Results and Discussion

4.1. Minimum Bubbling Fluidization

Figure 4 shows the time series dynamics of the bed at the minimum bubbling state captured in the shadowgraphy mode.

In this state, single bubbles or “gas voids” form at the porous distributor region and rise up. Due to the wall insulation, these bubbles are not visible in the bed. The bubbles rising from the bed of solids are displaced with an inflow of solids from their perimeter, forming a thin solid layer around them. Due to the shallow angles of repose, the solid particles slide down the bubbles’ interface into their south pole where the tangential fluid streams interact and form wakes. Once the bubbles arrive at the gas–solid interface, they erupt at multiple locations, followed by the dispersion of solid particles which fall back due to gravity.

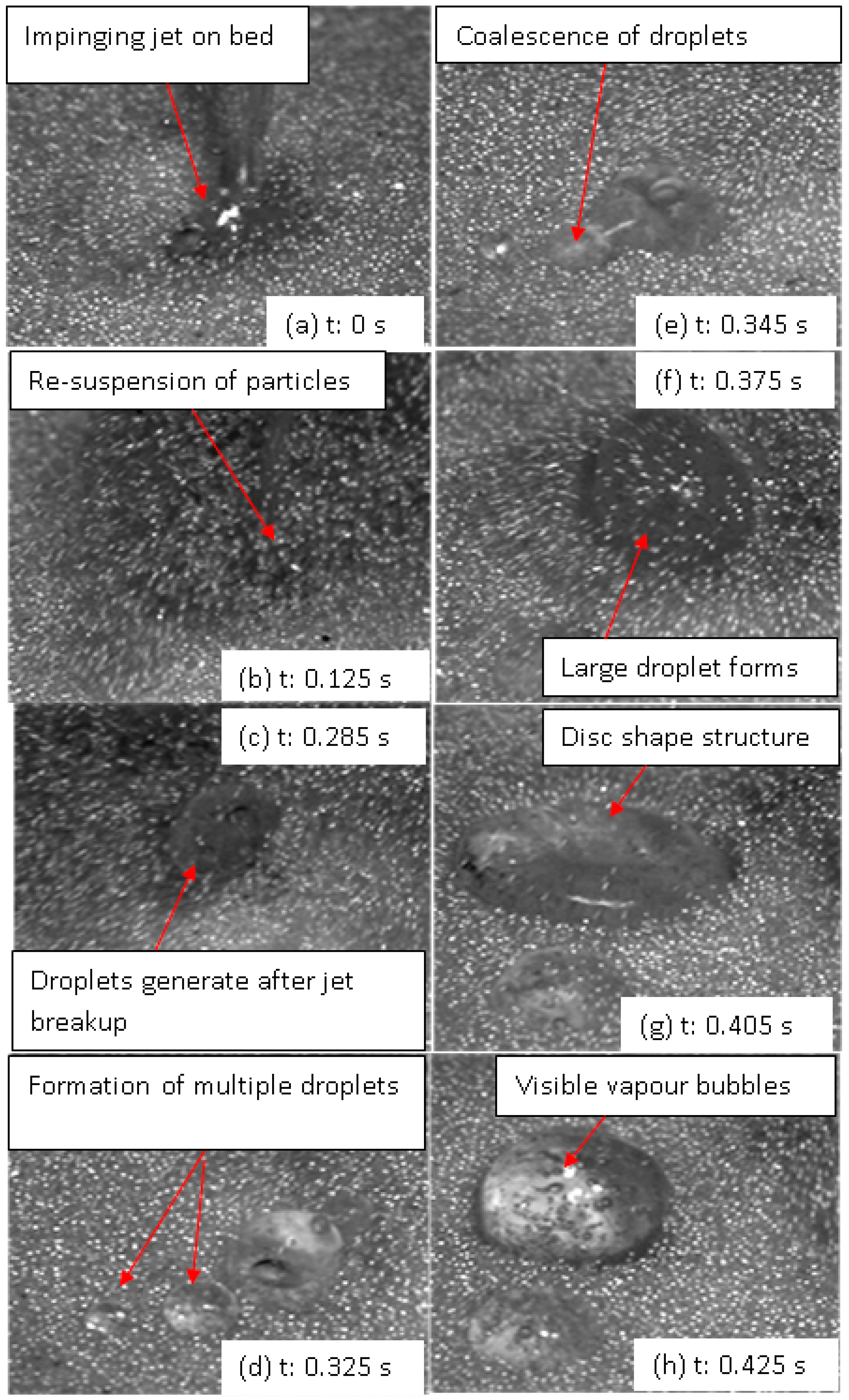
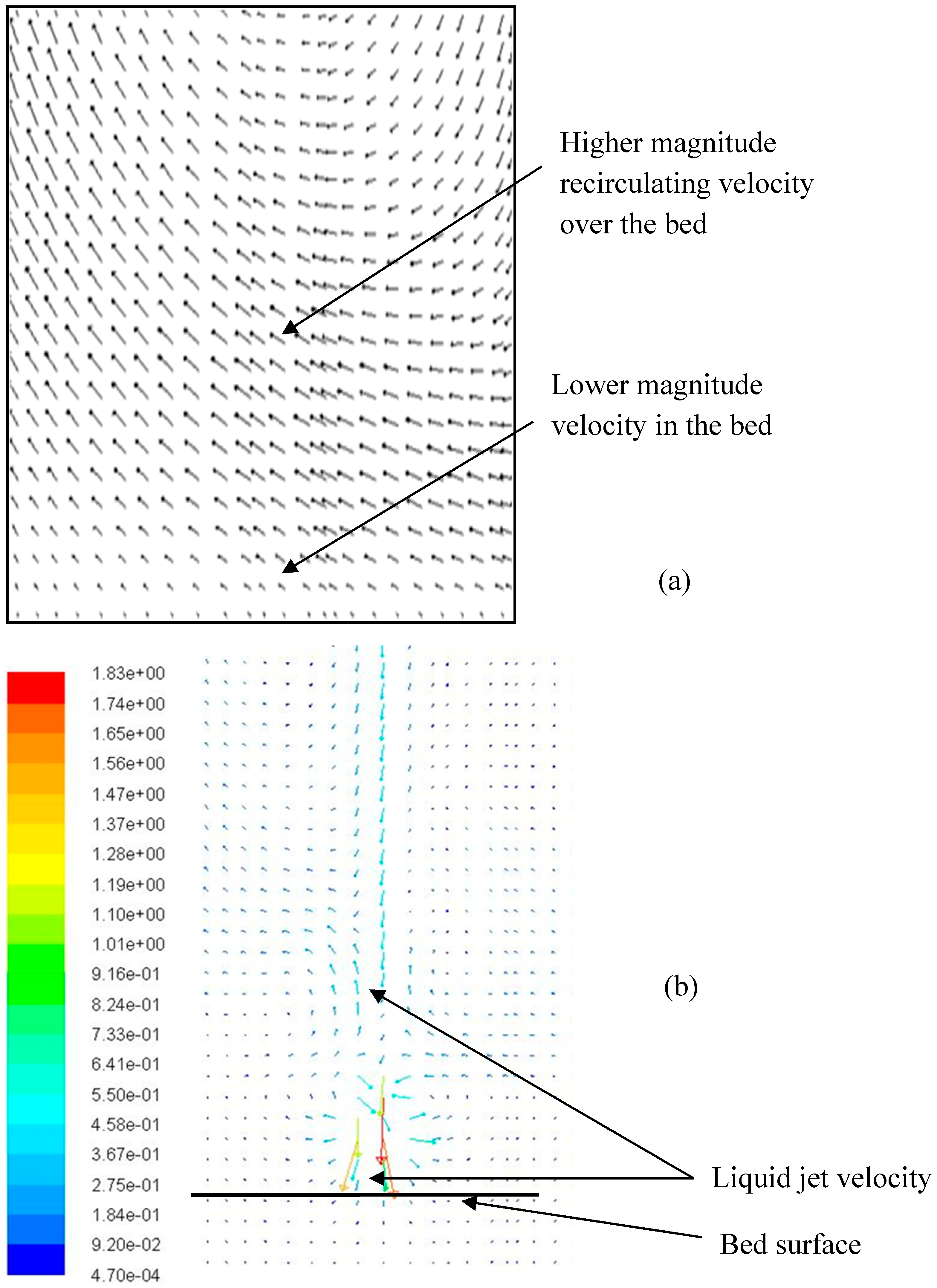
4.2. Droplet–Bed Interaction Mechanisms

Impingement of the acetone jet on the hot bubbling fluidized bed involving vaporization was captured with high-speed imaging. Figure 5a indicates the impact of a jet on the solid particles carried out at We ~ 13. While colliding with the solid particles, the liquid jet dissipates kinetic energy and undergoes vaporization. Eventually, the jet breaks up into multiple smaller droplets. Smaller droplets evaporate instantaneously with the fast release of vapour which resuspends the solid particles around the jet (Figure 5b). Figure 5c,d show multiple droplets generated due to the breakup of the jet. Some of these droplets coalesce (Figure 5e) and form larger droplets (Figure 5f). These large droplets levitate due to the generation of a thin vapour film at the contact region with hot particles, which was also reported by Gehrke and Wirth (2009) [16] in their droplet–particle interaction experiments involving water, ethanol, and FCC particles.

In the film boiling regime, fast vapour generation at the solid–liquid interface causes a large pressure-drop in the thin vapour layer which eventually balances the weight of the droplet, leading to levitation. Interestingly, the impact of the droplet has no significant effect on this phenomenon. After rebounding, such droplets settle down and their kinetic energy dissipates by spreading to form a disc-shaped structure (Figure 5g).

These droplets, after repetitive spreading and recoiling, finally come to a sessile state. They stay on the bed and gradually dip below the particle bed surface while evaporating. Due to effusing vapour around the periphery, the particles in the vicinity are observed to undergo a continuous motion. Leclere et al. (2001) [17] noted in their experiments with FCC catalysts and water that large droplets reduce bed surface temperature significantly (~25 °C) and form agglomerates by forming a liquid bridge between the particles. This granulation behaviour was also observed in the present study.

In the similar temperature difference used in the present work, the film boiling phenomenon was reported for n-heptane on a stainless-steel surface [29] and acetone on a brass surface [13,14], which was ascertained by droplets rebounding off the solid surface. However, in the present experiment, at the same temperature difference, the presence of vapour bubbles inside the droplet confirms nucleate boiling (Figure 5h) instead of film boiling.

In reality, an accurate prediction of film boiling/Leidenfrost temperature is rather challenging since it depends on many system parameters which include the physical properties of the fluid and solid, the temperature difference between the solid and fluid, and the solid surface characteristics. Although few models have been reported to predict the Leidenfrost temperature based on theoretical analysis and experiments [30,31,32], not much is known about the Leidenfrost temperature on a bed of solid particles.

Theoretically, the Leidenfrost temperature should exist at the thermodynamic limit of superheat which, in simpler terms, could be explained as the maximum temperature sustained by a liquid without phase change. Berenson (1961) [33] suggested a more physical interpretation of the vapour film formation at Leidenfrost temperature involving the formation of numerous micro-vapour bubbles at the solid–liquid interface, where the spacing between the bubbles are hydrodynamically controlled by Taylor-type instability. The wavelength of such gravity induced interface instability can be scaled as ~ $\sqrt{{\sigma }_{lg}/g({\rho }_l-{\rho }_v)}$ and the following expression can be used to determine the minimum film boiling temperature:

$$T_{Leidenfrost}=T_{sat}+0.127{\displaystyle \frac{\Delta H_{lv}{\rho }_v}{k_v}}{\left[{\displaystyle \frac{g\left({\rho }_l-{\rho }_v\right)}{\left({\rho }_l+{\rho }_v\right)}}\right]}^{2/3}{\left[{\displaystyle \frac{{\sigma }_{\lg }}{g\left({\rho }_l-{\rho }_v\right)}}\right]}^{1/2}{\left[{\displaystyle \frac{{\mu }_v}{g\left({\rho }_l-{\rho }_v\right)}}\right]}^{1/3}$$

(24)

Equation (24) yields a minimum film boiling temperature of 401 K, using physical property values at the saturation temperature. The bed temperature in the current study was maintained above this predicted limit, thus the Leidenfrost effect was expected to occur.

Another expression suggested by Baumeister and Simon (1973) [34], taking into consideration the effect of the heated surface properties, estimates Leidenfrost temperature as follows:

$$T_{Leidenfrost}=T_l+{\displaystyle \frac{\left(\frac{27}{32}{T}_c-T_l\right)}{\left[\exp \left(\frac{0.00175}{k_s{\rho }_s{c}_s}\right)erfc\left(0.042\sqrt{\frac{1}{k_s{\rho }_s{c}_s}}\right)\right]}}$$

(25)

where T_l is the droplet temperature, and k_s, ρ_s, and c_s are the thermal conductivity, density, and heat capacity of the solid particle.

The term 1/k_sρ_sc_s in Equation (25) is a variation of the heat penetration coefficient [16]. The Leidenfrost temperature obtained using Equation (25) was 469 K when the droplet was assumed to be at saturation state; however, the prediction increased to 500 K when the subcooled droplet temperature was used.

Apparently, determining the Leidenfrost temperature is rather fuzzy, especially for the particles in a dense fluidized bed where reported data are inadequate. It could be concluded, however, that the operating temperature in the present study was possibly in the transition regime from nucleate to film boiling. This is substantiated by the presence of visible vapour bubbles inside the droplets, ascertaining the occurrence of heterogeneous nucleate boiling (Figure 5h) where the void spaces in the interstitial locations of particles at the bed surface acted as active sites for vapour bubble nucleation. For CFD modelling purposes, it was assumed that under the prevailing operating conditions, the film boiling regime persists, where the conduction mechanism dominates the heat transfer process through a thin vapour film formed at the droplet–particle interface.

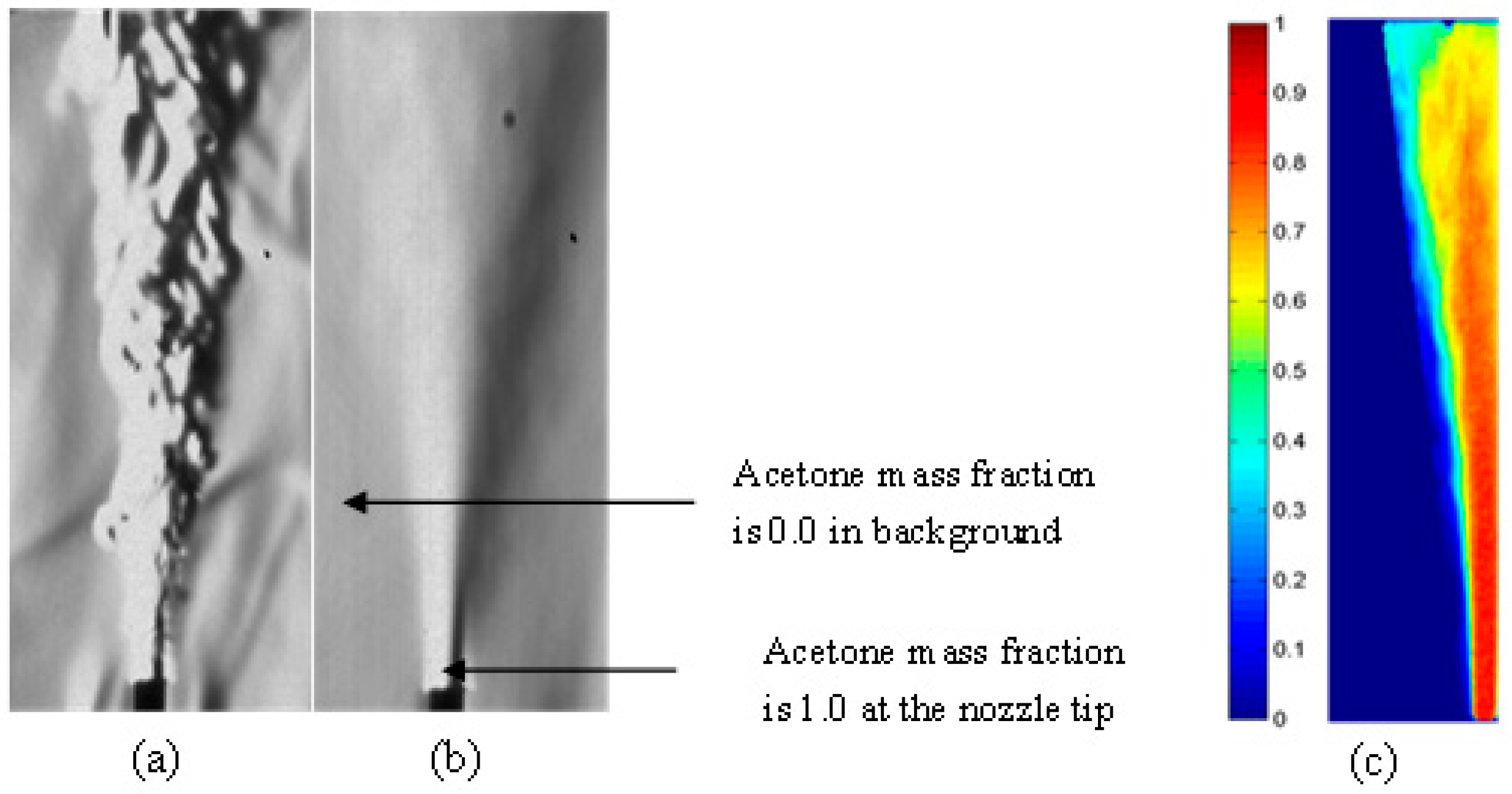
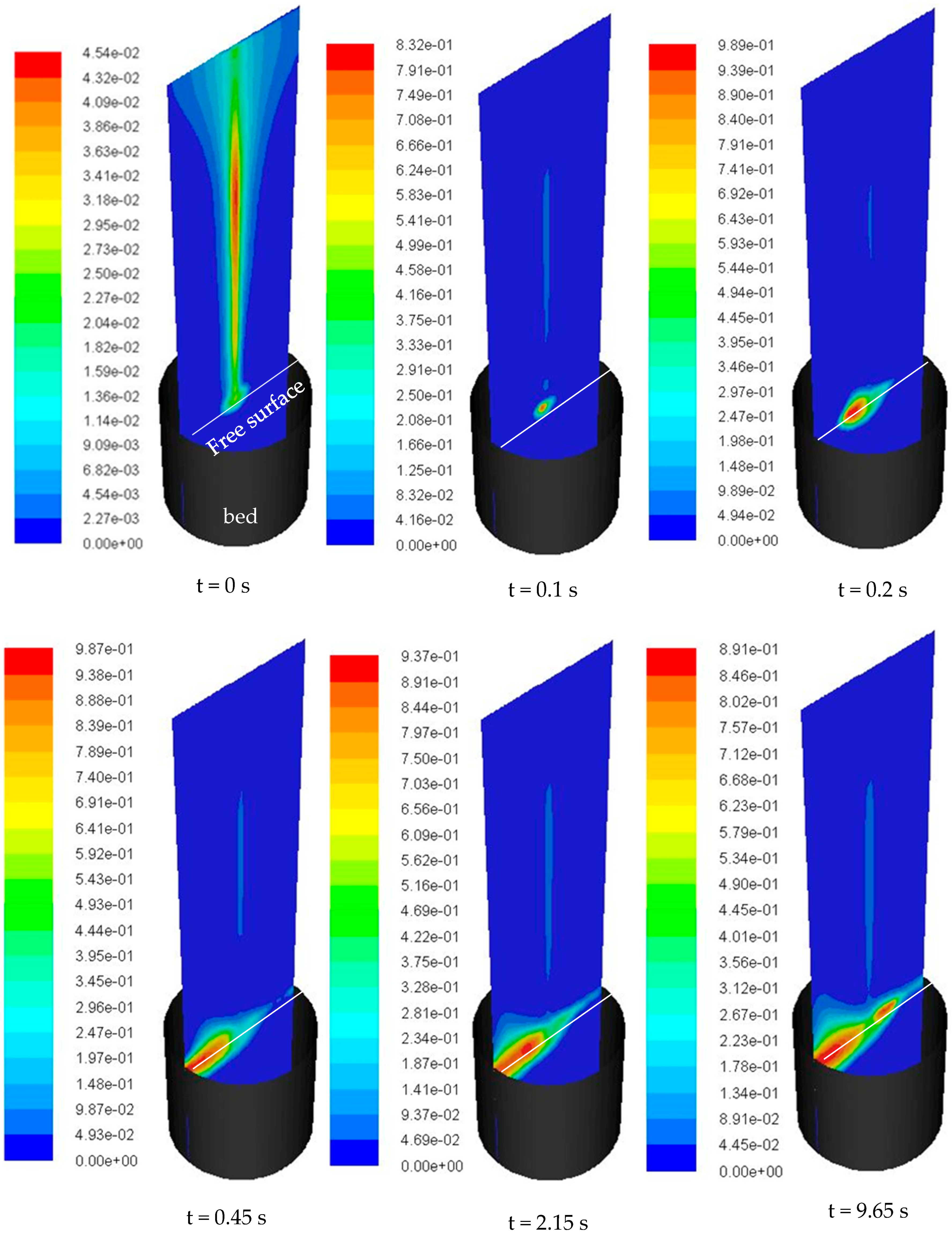
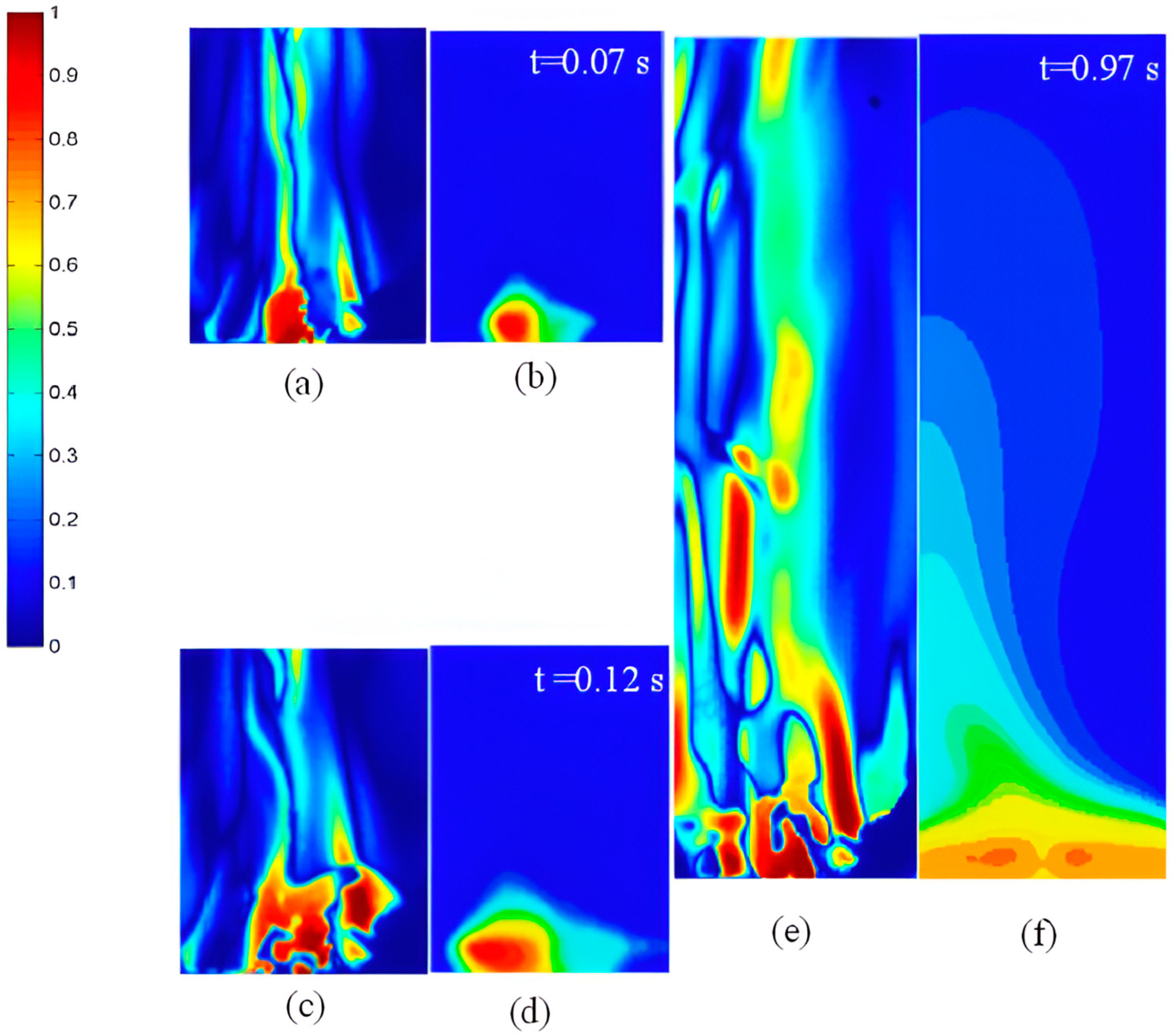
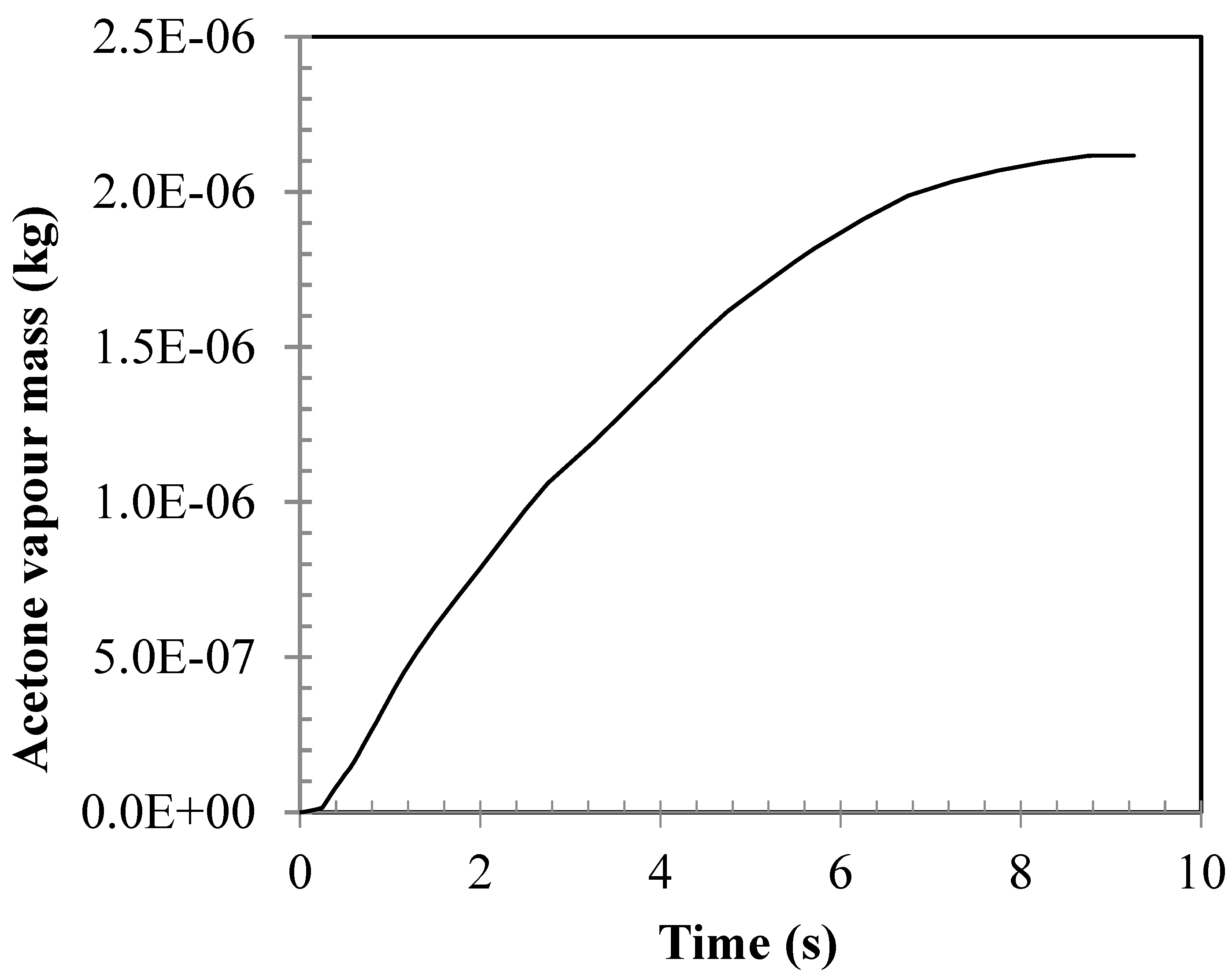
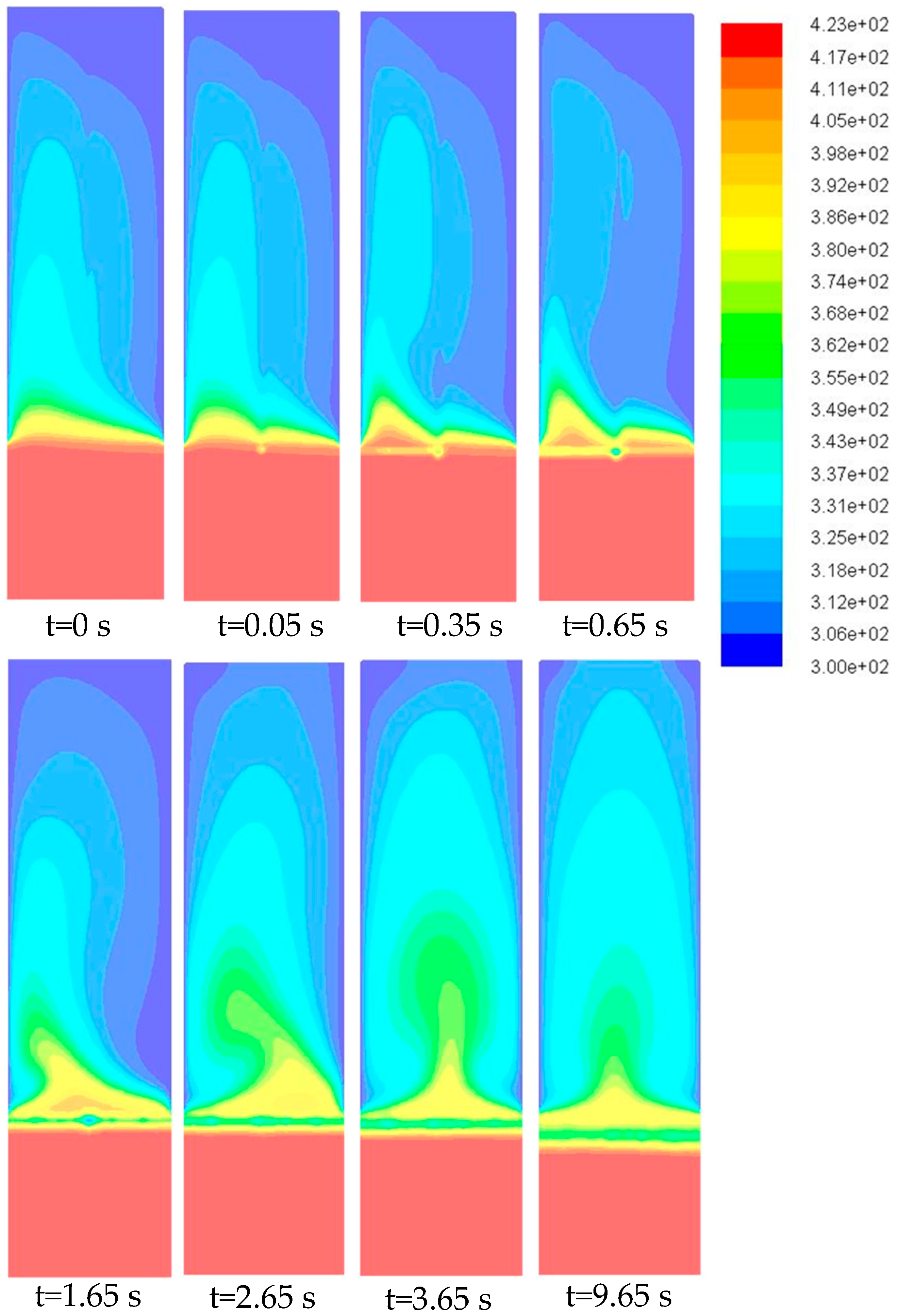
4.3. Vaporization of Acetone Jet in the Fluidized Bed

Figure 6 presents the hot gas plume captured with schlieren imaging before and after the injection of acetone jet into the bubbling fluidized bed.

Prior to jet injection (Figure 6a), the hot air plume noted in the freeboard region occurred due to the hot fluidizing gas as well as the natural convection of the surrounding air. Due to the large temperature difference, convection currents were established in the freeboard region. The plume was apparently turbulent in nature and had visible eddies in it (Figure 6a). The larger turbulent structures contained more energy and were therefore more prominent near the bed surface due to a higher temperature difference and higher velocity of hot air. However, away from the bed surface, these structures became relatively weak due to the decreasing driving force, i.e., temperature gradients.

When the liquid jet was injected onto the bed surface, it instantly disintegrated into many smaller droplets which underwent intense vaporization upon contact with the heated solid particles. These bed surface dynamics are shown in Figure 5. The instant vaporization resulted in intense interactions of the evolving vapour plume with the surrounding solid particles, leading to the re-suspension of a few particles and the generation of significant local turbulence in the freeboard region (Figure 6b). It can be noticed that due to a higher refractive index, the acetone vapour was distinctly visible from the surrounding air which also showed the turbulent nature of the vapour plume containing several multi-scale eddies in the schlieren images.

Figure 7 presents the transient evolution of the vapour plume predicted by the CFD model in the vertical direction of the freeboard region following the liquid jet injection. The colour scales indicate the gradual rise in concentration of acetone (volatile species) in the vapour plume. It could be noted that the amount of vapour generated during the homogeneous vaporization (jet in flight) is an order of magnitude lower than the heterogeneous vaporization counterpart when the jet impinges onto the particle surface. This is because only a smaller part of the jet was evaporated during its travel in contact with the rising hot air plume.

However, after liquid injection, an intense vaporization occurred due to the accumulation of droplets on the bed (Figure 5) and the corresponding boiling of droplets which contributed to much higher vaporization compared to the homogeneous vaporization of the impinging jet.

Figure 8 presents the gradual spread of the vaporization zone on the bed surface at the point of jet impingement. In the CFD framework, the impinging jet was modelled as numerous discrete droplets which were added at each time-step to match the liquid mass flow rate defined in Table 2. With time, more and more vaporization occur (t = 0 to 0.45 s) on the bed surface which eventually leads to the formation of a near uniform concentration field on the bed surface (t = 2.15 s to 9.65 s).

Figure 9 presents a qualitative comparison of the experimentally mapped vapour mass fraction with the CFD model predictions.

Figure 9a,c,e exhibit the propagation of the plume in the freeboard region, depicted by the contour of the acetone vapour mass fraction obtained from image processing at different time instances after the injection of the liquid acetone jet, while Figure 9b,d,f show the corresponding CFD model predictions. The comparison mainly shows the transient dispersion of acetone vapour (coloured by the acetone vapour mass fraction) from the point of impingement of the jet on the bed surface (high conc. denoted by red colour) to the surrounding bulk (zero conc. denoted by blue colour). The CFD model indicates a gradual evolution of the acetone vapour plume along with the convection currents, having maximum vapour concentration on the bed surface (t = 0.07 s) and then gradually diminishing concentration away from the bed surface (t = 0.97 s) in the freeboard region which qualitatively agree with the experimental observations. Although adequate measures were taken to remove the background contributions during image processing, some consistent streaks can still be seen in these figures. These disturbances around the impinging jet are attributed to the continuous changing density of the background medium due to the turbulent natural convection motions comprising the upward movement of hot air coming from the bed surface and the downward movement of ambient air.

The correct modelling of the dispersion of a vapour plume in the freeboard region depends on the successful capture of turbulence at all possible length scales which contribute to turbulent diffusion. The schlieren imaging in Figure 6 indeed shows the presence of different scales of eddies in the vapour plume which are difficult to compute by any RANS-based turbulence modelling approach in a time averaging sense.

The effect of various RANS-type turbulence models on the overall flow characteristics, however, remains rather speculative. A few of the previous studies [35,36] have indicated almost similar results, predicted by using all three members of the k-ε turbulence model family for the simulation of indoor air flow. For brevity, it could be concluded that for large-scale flow fluctuations, any member of the k-ε family RANS model would possibly provide a reasonable estimation of the effect of a flow field on coupled scalar fields like concentration and temperature. Due to the highly unstable nature of the plume and the presence of multi-scale eddies, a large eddy simulation (LES) is inevitable. However, due to the very high computational cost involved, this approach was not used in the present study.

Figure 10 presents the mass of acetone vapour generated with time which reaches a steady value at 9.25 s. A deviation of ~22% was found in the CFD simulation while comparing the mass of the liquid acetone injected in the bed and the total mass of the vapour produced.

The circulating flow pattern of the surrounding ambient air due to the natural convection process arising from the density difference at the particle bed surface can be seen in the simulated velocity vector plot (Figure 11a). Although the bed was kept at a minimum bubbling state, the dominance of natural convection over forced convection can be explained by the relative magnitudes of Grashof number (Gr = gβ∆TL³/ν²) and Reynolds number (Re = Lu/ν) where g is the gravitational constant, β is the coefficient of volume expansion expressed as 1/T_avg, ∆T is the temperature difference between the bed surface and the surroundings, L is the characteristic length of the system, u is the gas velocity, and ν is the kinematic viscosity of the gas. Considering L = bed diameter, u = superficial gas velocity, T_avg = average temperature of bed and the ambient, Gr = as 6.33 × 10⁵ and Re = 71 were obtained. The ratio Gr/Re² >> 1 in this case clearly indicates the dominance of natural convection over forced convection.

Circulations due to natural convection currents change the refractive index of the medium, which causes fluctuations in the background illumination intensity and introduces some noise in the images. The patches in the schlieren images presented in Figure 9 result from these fluctuations and imply the positive and negative density gradients of the fluid. These artefacts make it difficult to completely match the CFD results with the experiment.

Figure 11b presents the velocity vectors of the system during jet impingement. The relatively larger vectors indicate the higher velocity magnitude of the droplets compared to the surrounding gas. It can be noticed that due to implementation of a no-slip boundary condition on the bed surface, the droplets cannot penetrate the bed further and remain on the bed surface whilst their kinetic energy dissipates. During the interactions between the impinging jet and the heated solid particles, the bed temperature is reduced due to a direct contact conduction heat transfer process.

This causes a reduction in the evaporation rate, thereby increasing the droplet lifetime on the bed surface.

Consequently, the possibility of the coalescence of droplets and granulation is also increased (Leclere et al., 2001) [17], which is also noted in the present study. Figure 12 presents the simulated temperature profile of the system before and after liquid jet impingement on the particle bed. Time t = 0 instance indicates a pseudo-steady state condition of temperature field in the freeboard region prior to jet impingement, exhibiting a gradually decreasing temperature gradient. Following the jet impingement at t = 0.05 s, a sharp reduction in the bed temperature in a small region on the bed surface can be noted. Rapid evaporation of the accumulated droplets on the bed surface causes a significant temperature reduction in the radial direction which can be seen to prevail up to t = 0.65 s. After completion of the jet impingement process, a dispersion of the vapour plume occurs in the freeboard region with the gradually diminishing temperature gradient (t = 1.65 s to 9.65 s).

During jet impingement on the bed surface, instant vaporization occurs due to close interactions between the jet and the heated particles, which leads to a reduction in the local bed temperature. This temperature drop profile (area averaged temperature) starting from bed surface (axial distance = 0 mm) to up to 5 mm, at 1 mm spatial intervals, is presented at different time instances in Figure 13. It can be seen that the largest temperature drop occurs on the bed surface at the point of jet injection and this temperature drop gradually increases as time progresses (t = 0 to 11.65 s). A steep temperature drop of ~60 °C in the bed within the first 5 mm depth is quite evident for all time instances. This sudden reduction in bed temperature results in significant liquid entrapment within the particles and causes granulation to occur which was verified in the experiment. This observed temperature reduction can be explained by the vaporization of the acetone droplets, which consumes the latent heat of vaporization from the hot solid particles and, in effect, reduces the bed temperature. Away from the bed surface, this temperature reduction effect gradually reduces, and the gradients almost diminish at 5 mm below the bed surface at all time instances.

It was noted earlier in Figure 5, when the liquid jet impinged on the fluidized bed surface, intense vaporization occurred with significant particle re-suspension. This could be explained by the turbulence caused by the fast effusion of vapour. Figure 14 indicates both the area-averaged (averaged over the different radial planes from bed surface (0 mm) to 5 mm in the axial direction) and volume-averaged (averaged over the entire freeboard volume) turbulence energy dissipation rate profiles at different time instances. Both profiles show a peak during the jet injection duration due to intense evaporation, but it quickly decays once the jet injection is completed. It can be noted that the area-averaged turbulence energy dissipation rate shows a much greater peak compared to the volume-averaged profile.

This is because the turbulence due to vapour effusion is generated in the vicinity of the bed surface and decays further away, similar to grid-generated turbulence.

5. Conclusions

In this study, the vaporization dynamics of a volatile hydrocarbon liquid jet interaction with hot Geldart A-type solid particles in a minimum bubbling fluidized bed involving both homogeneous and heterogeneous evaporation were studied. A summary of the findings is presented as follows:

• The heterogeneous vaporization phenomenon involves complex droplet–particle interactions comprising liquid jet breakup to multiple droplets, the coalescence of droplets, intense vaporization followed by the re-suspension of solid particles, the levitation of droplets, the shape deformation of droplets, and the nucleate boiling of droplets.
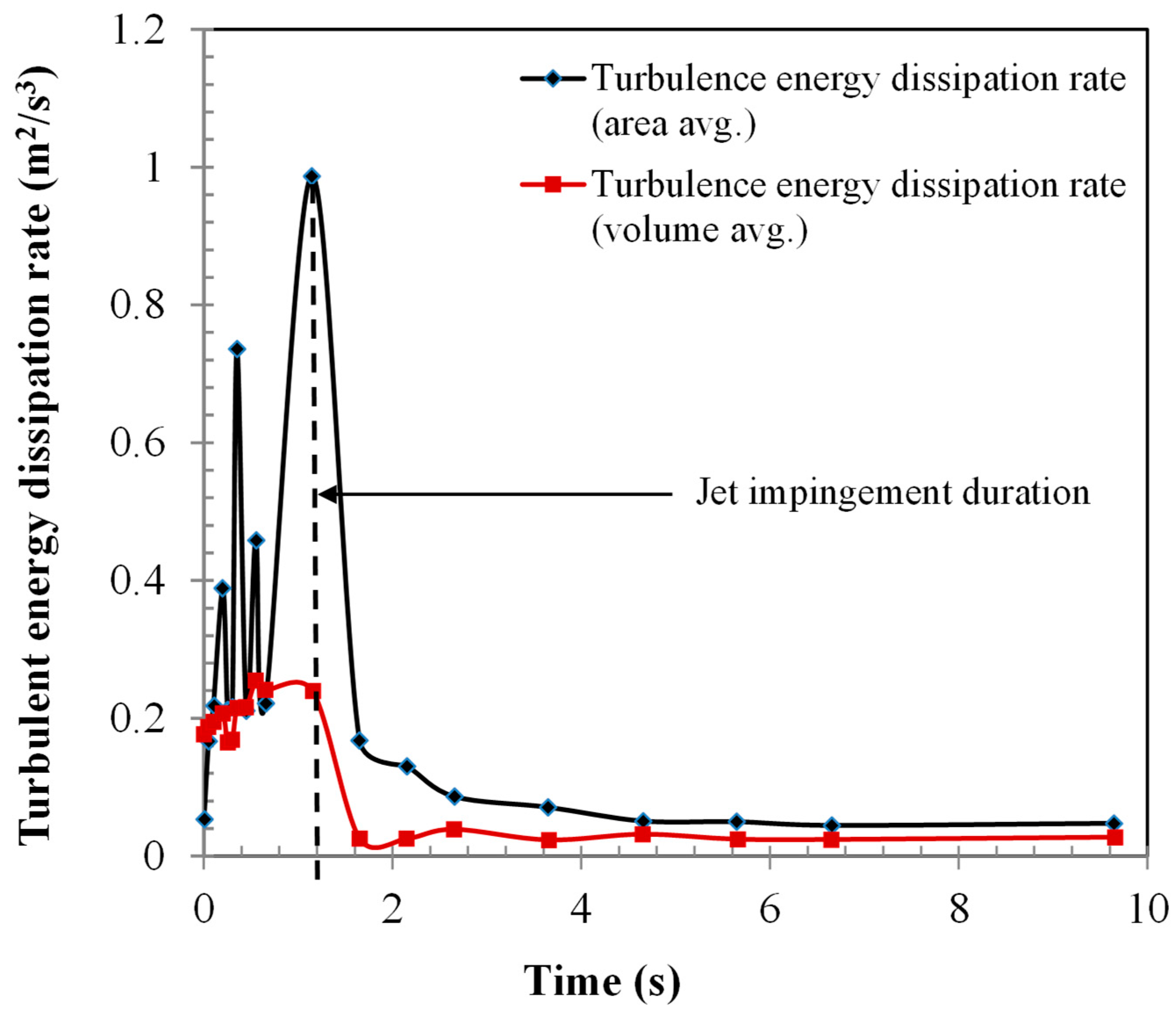
• The jet evaporation behaviour predicted by the CFD model qualitatively agreed with the schlieren imaging which captured the key feature of the emerging vapour plume, showing higher vapour concentration on the bed surface and diminishing concentration in the freeboard region. The same profile was also noted for the turbulence energy dissipation rate.
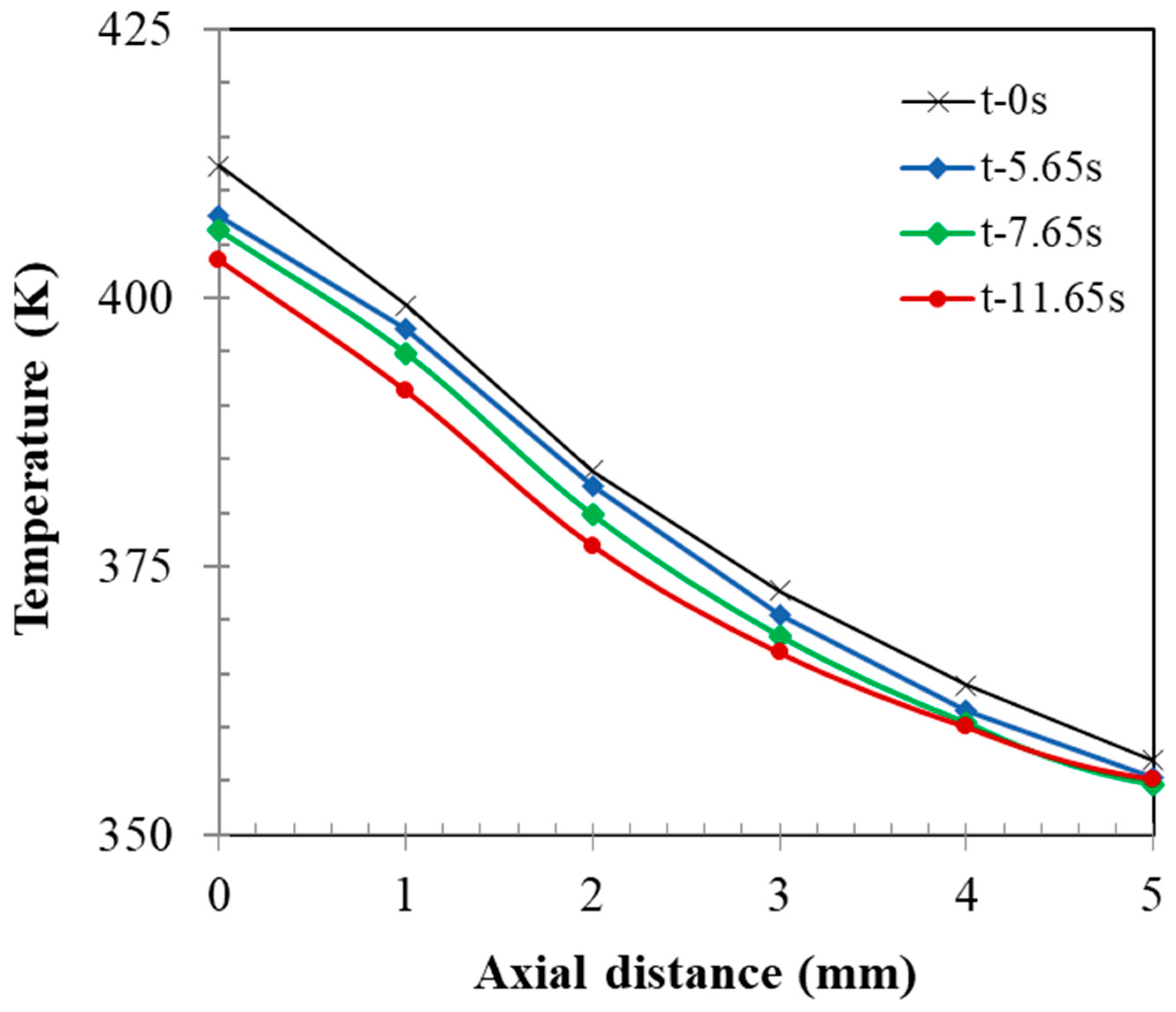
• Although the initial temperature difference between the heated particles and the liquid jet was well above 100 °C, jet impingement caused a significant reduction in the bed temperature locally. This was verified by the CFD model prediction which showed ~60 °C temperature reduction within the first 5 mm of bed depth and explained the formation of granules at the bed surface.
• While the present model does not explicitly capture the intense interactions between the droplets, particles, and vapour plume, which ideally would require a fully coupled CFD-DEM (discrete element method) with an LES sub-model for resolving the eddies, it should be considered in any future study in this area.