Hybridization of a Micro-Scale Savonius Rotor Using a Helical Darrieus Rotor
Abstract
1. Introduction
2. Proposed Hybrid Savonius and Helical Darrieus Rotors
2.1. Problem Statement
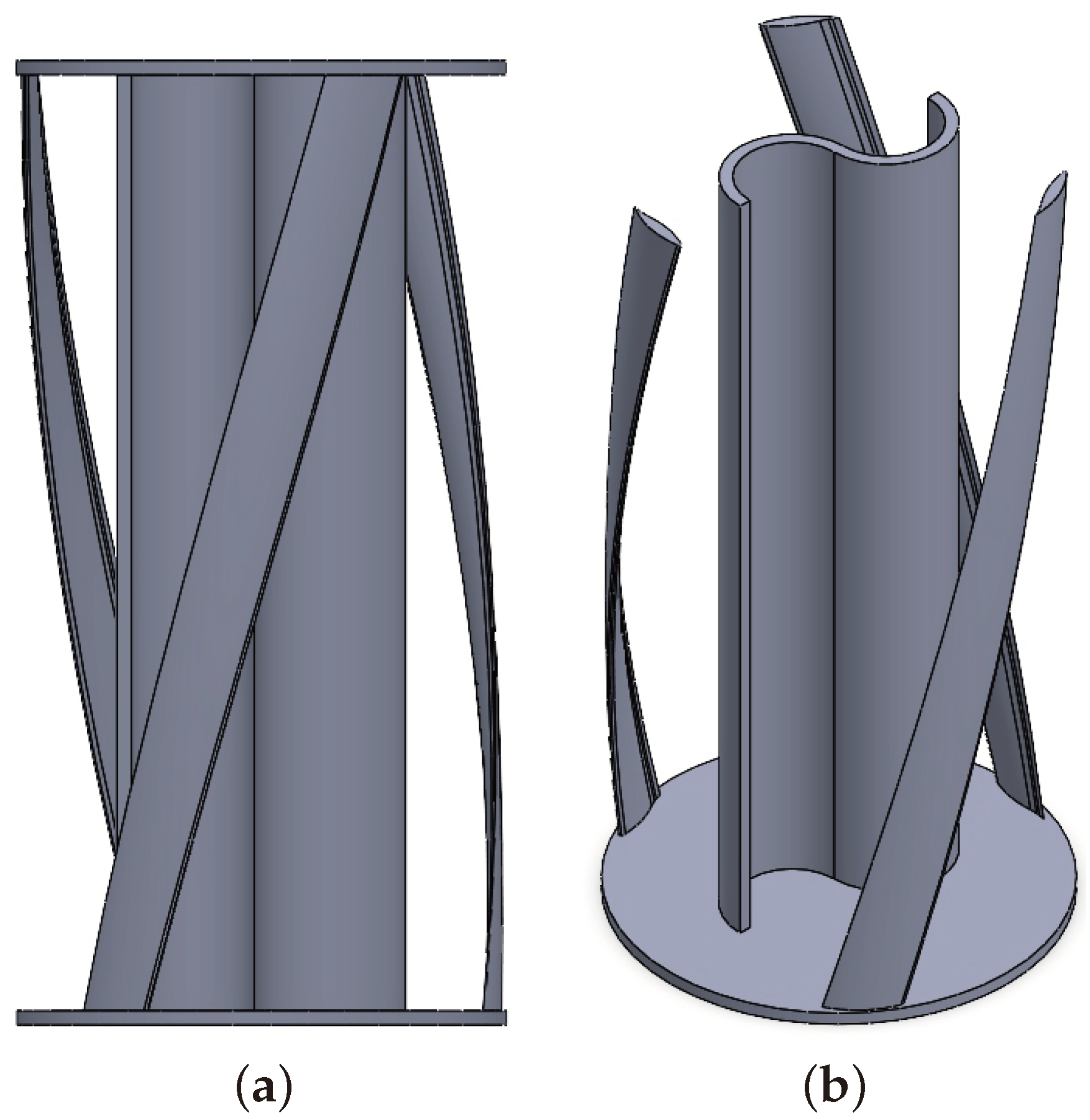
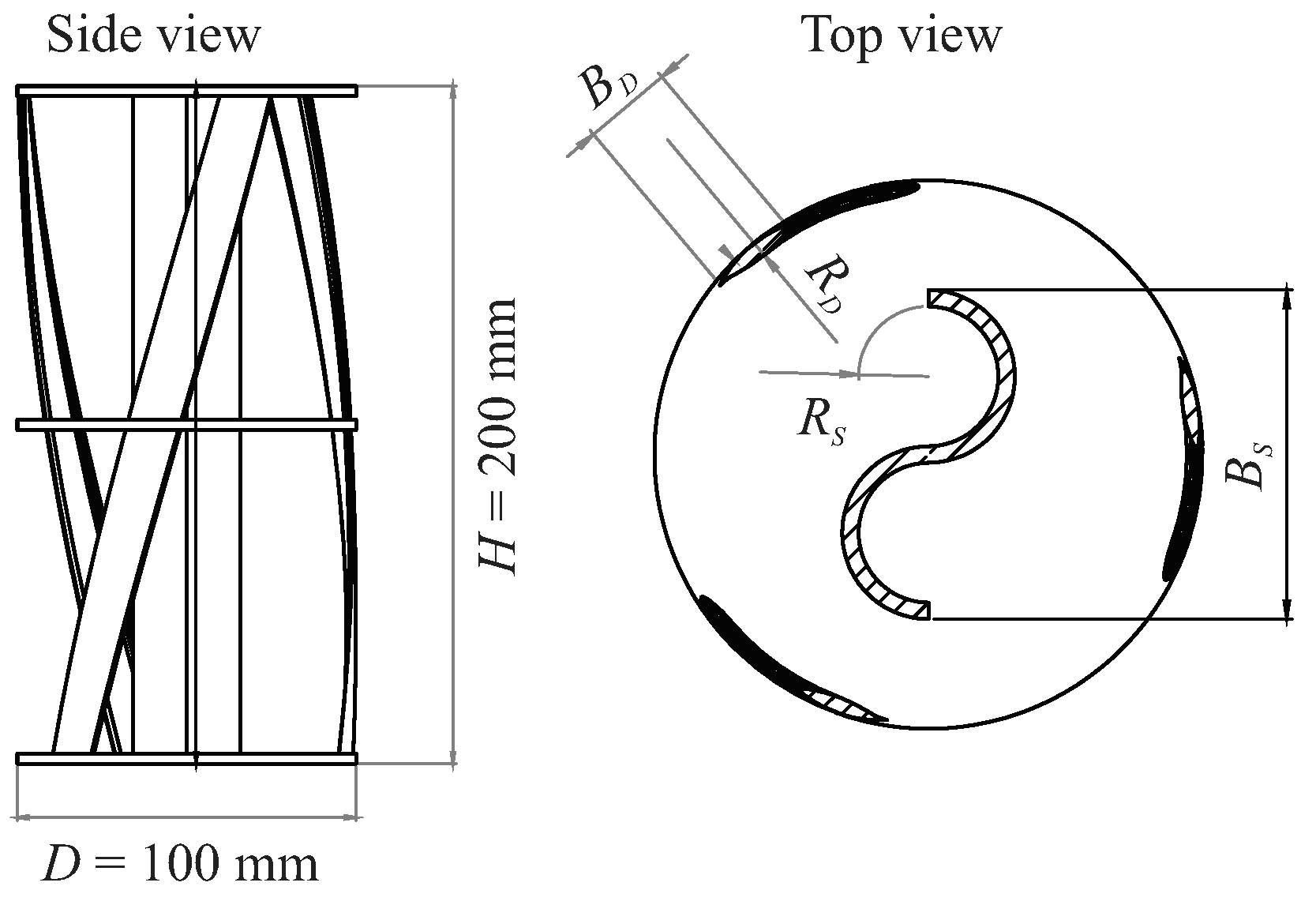
2.2. HSHDR Design
2.3. Governing Equations
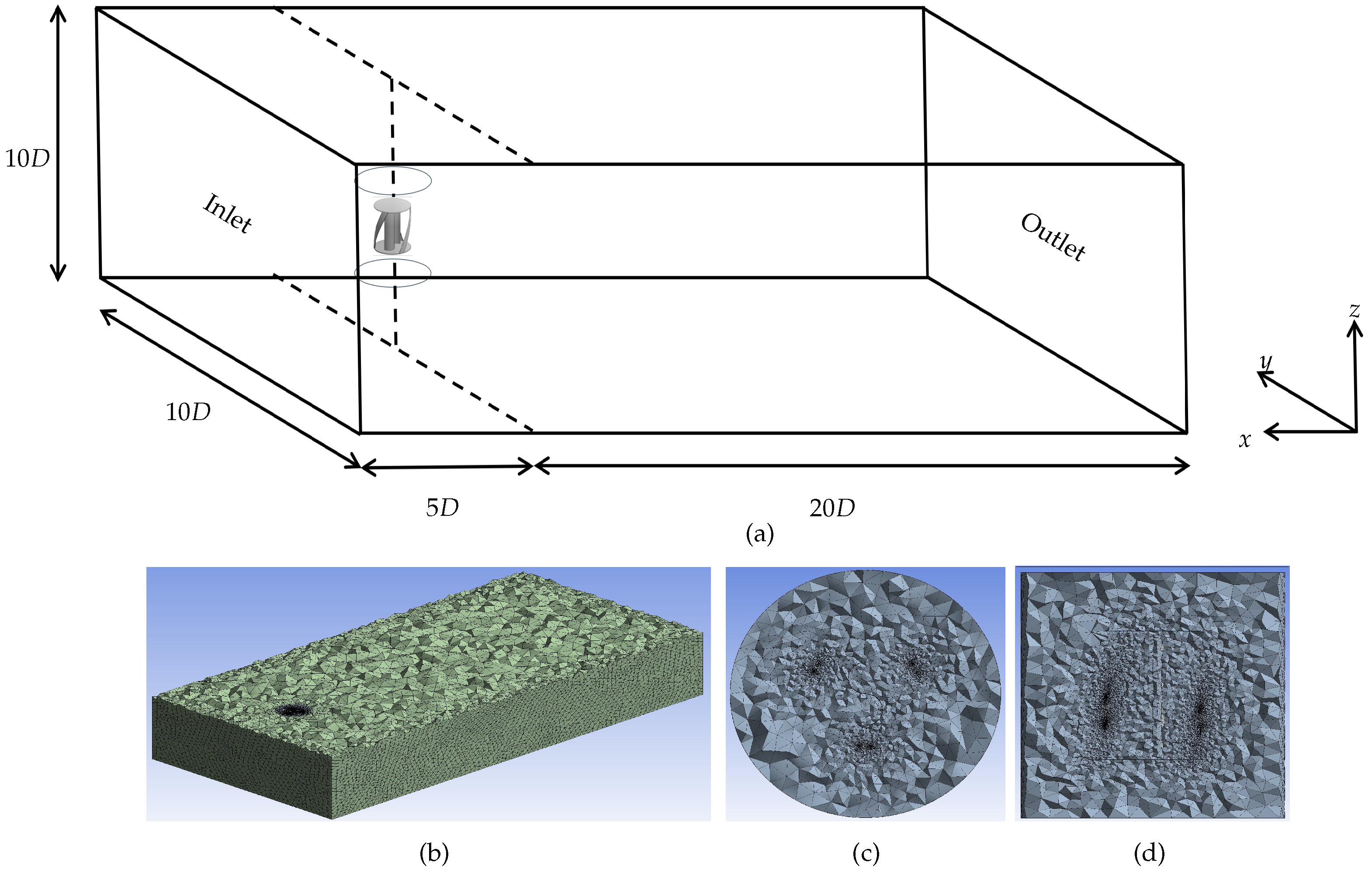
2.4. Numerical Methods and Domain Details
3. Results
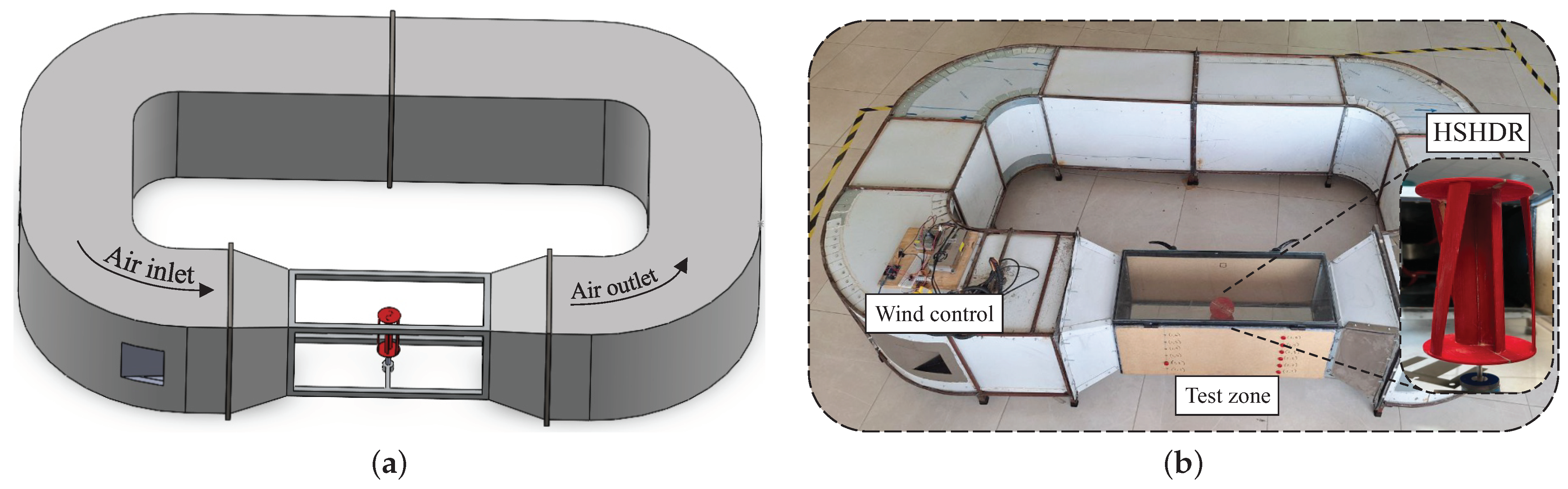
3.1. Experimental Setup
3.2. Experimental Validation
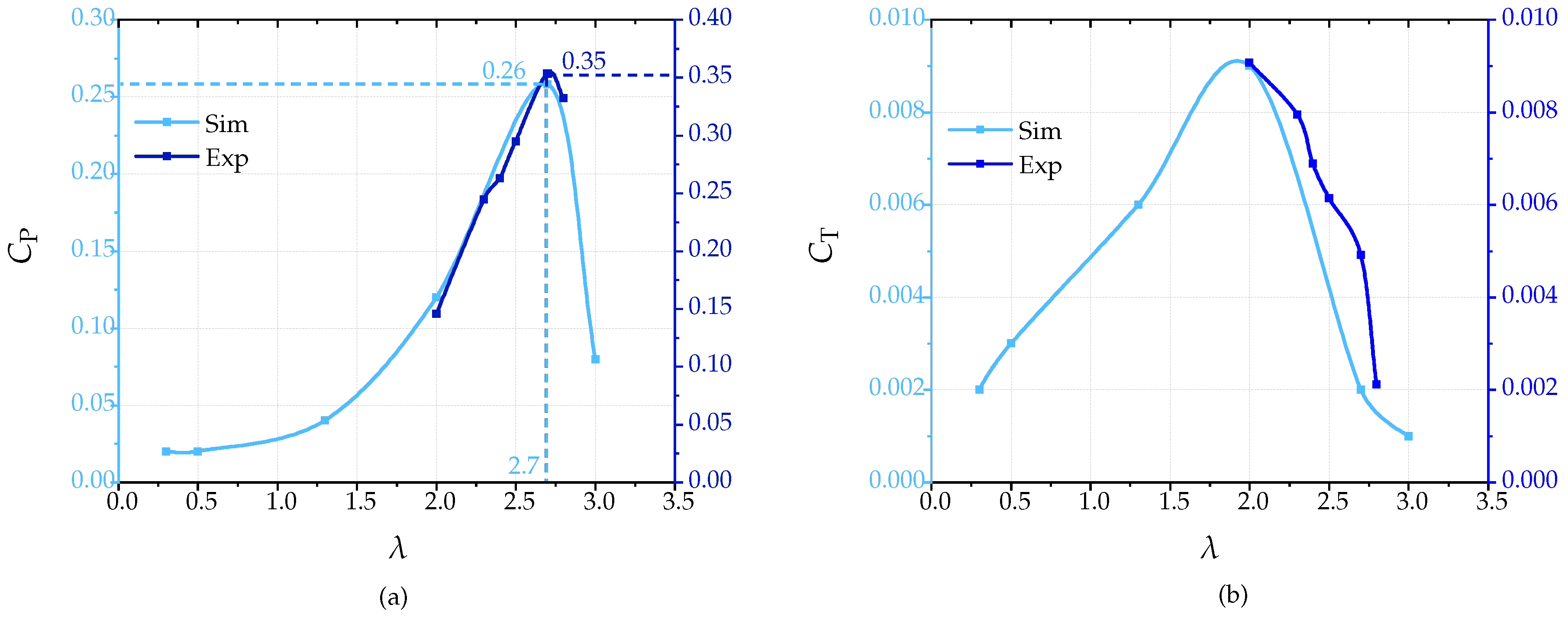
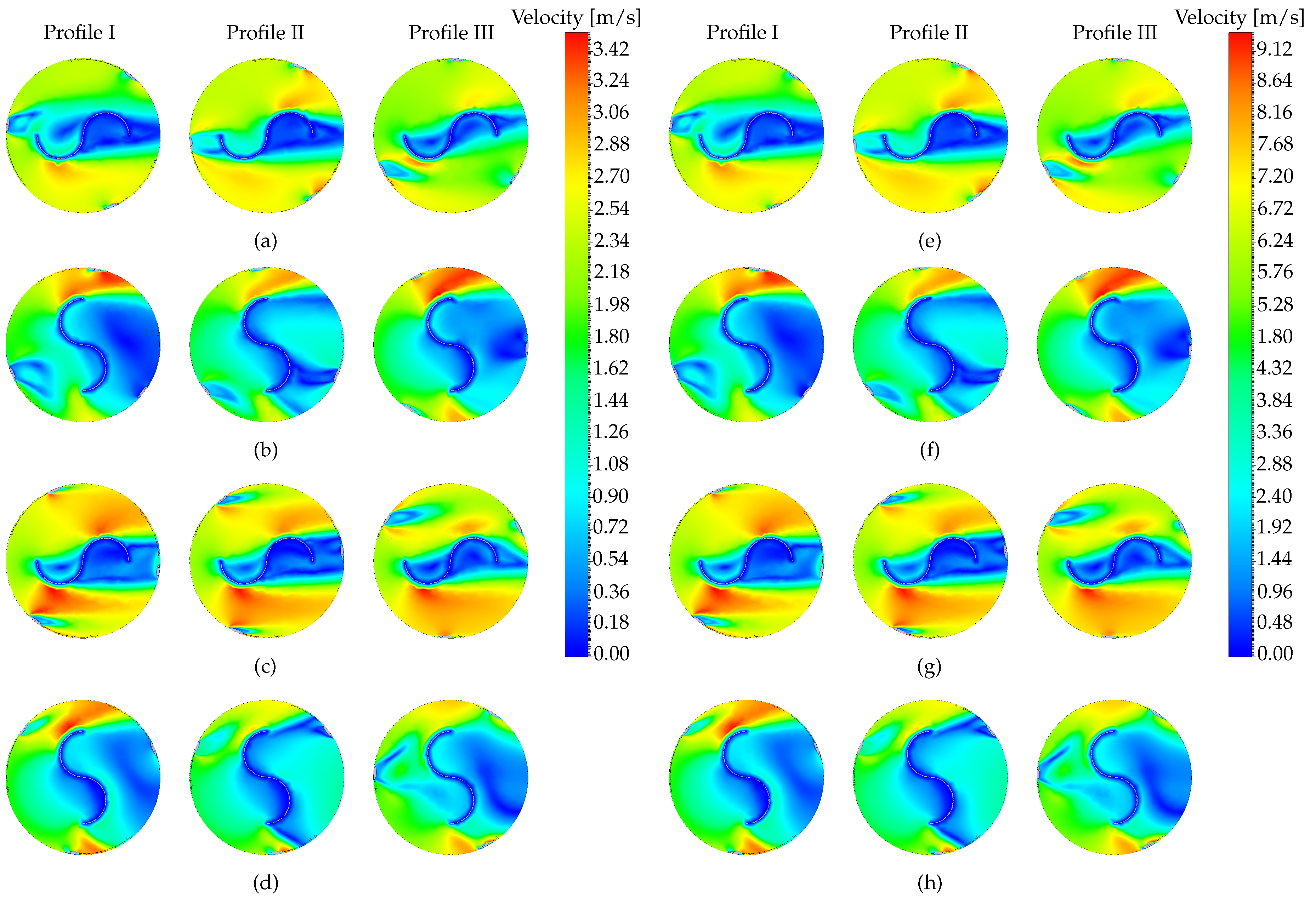
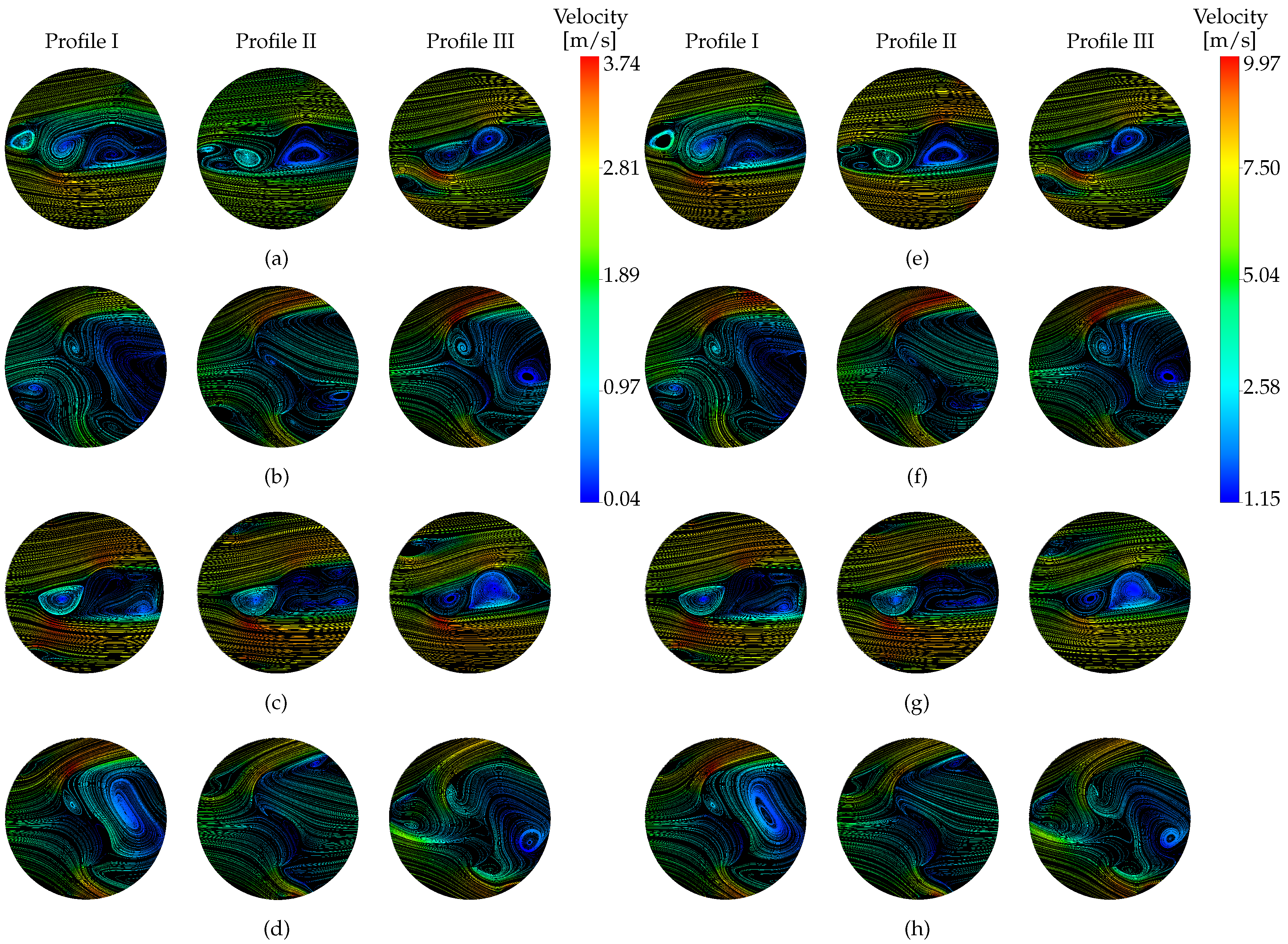
3.3. Performance Assessment
4. Discussion
| Ref. | H/D SR [mm] | H/D DR [mm] | Blade SR | Airfoil DR | Material | Type | V [m/s] | |||
|---|---|---|---|---|---|---|---|---|---|---|
| [22] | NR | NR | 0.60 | 0.89 | NR | SC | NR | NR | Sim | NR |
| [24] | 600/300 | 1000/600 | 0.45 | 0.22 | 2.50 | SCH | NACA0021 | NR | Sim | 7 |
| [11] | NR | NR/300 | 0.42 | NR | 3.50 | SC | NREL S809 | NR | Sim | 3–7 |
| [25] | NR/1000 | NR | 0.41 | NR | 0.80 | SC | NACA0018 | NR | Sim | 5–10 |
| [26] | NR | NR | 0.39 | NR | 1.50 | B | NACA0018 | NR | Sim | 5–10 |
| [10] | 220/220 | 750/750 | 0.36 | NR | 2.80 | SC | NACA0012 | NR | Sim | 1–3 |
| [27] | 370/200 | 1030/500 | 0.33 | NR | 1.40 | SC | NACA0021 | NR | Sim | 2–10 |
| [23] | 1000/952.4 | 1450/1030 | 0.19 | 0.08 | 3.00 | SC | NACA0021 | NR | Sim | 7–9 |
| [28] | NR | NR | 0.15 | NR | NR | SC | NR | CF+Al | Sim | 3.2–13 |
| [9] | 200/57.5 | NR/200 | NR | NR | 0.30 | SC | NACA0012 | NR | Sim | 3–7 |
| [12] | 250/80 | 300/300 | 0.34 | NR | 2.29 | SC | NREL S818 | Wood | Exp | 7.5–12 |
| [14] | 1000/500 | 1450/1030 | 0.36 | 0.68 | 0.45 | SCH | NACA0021 | NR | Both | 2–3 |
| [29] | 800/456 | 1000/1100 | 0.33 | NR | NR | SCH | NACA0010 | NR | Both | 0.65–10 |
| [13] | 1000/500 | 1000/750 | 0.32 | NR | 2.24 | SC | NREL S818 | Al | Both | 3–10 |
| HSHDR | 200/60 | 200/100 | 0.26 | 0.009 | 2.70 | SC | NACA 4412 | PLA | Both | 3-8 |
| [15] | 160/46 | 330/100 | 0.20 | NR | 4.00 | SC | NACA4418 | PVC+Al | Both | 5–20 |
| [30] | 710/NR | NR | 0.03 | NR | 0.60 | SC | NACA0018 | PVC+Wood | Both | 4 |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Güney, T.; Üstündağ, E. Wind energy and CO2 emissions: AMG estimations for selected countries. Environ. Sci. Pollut. Res. 2021, 29, 21303–21313. [Google Scholar] [CrossRef] [PubMed]
- Barthelmie, R.J.; Pryor, S.C. Climate Change Mitigation Potential of Wind Energy. Climate 2021, 9, 136. [Google Scholar] [CrossRef]
- Im, H.; Kim, B. Power Performance Analysis Based on Savonius Wind Turbine Blade Design and Layout Optimization through Rotor Wake Flow Analysis. Energies 2022, 15, 9500. [Google Scholar] [CrossRef]
- Mohamed, M.H.; Alqurashi, F.; Thévenin, D. Automatic Blade Shape Optimization of a Three-Bladed Modified Savonius Turbine. Front. Energy Res. 2022, 9, 796860. [Google Scholar] [CrossRef]
- Mahesa Prabowoputra, D.; Hadi, S.; Sohn, J.M.; Prabowo, A.R. The effect of multi-stage modification on the performance of Savonius water turbines under the horizontal axis condition. Open Eng. 2020, 10, 793–803. [Google Scholar] [CrossRef]
- Saad, A.S.; Elwardany, A.; El-Sharkawy, I.I.; Ookawara, S.; Ahmed, M. Performance evaluation of a novel vertical axis wind turbine using twisted blades in multi-stage Savonius rotors. Energy Convers. Manag. 2021, 235, 114013. [Google Scholar] [CrossRef]
- Pérez-Terrazo, A.; Moreno, M.; Trejo-Zúñiga, I.; López, J.A. A Two-Stage Twisted Blade μ-Vertical Axis Wind Turbine: An Enhanced Savonius Rotor Design. Energies 2024, 17, 2835. [Google Scholar] [CrossRef]
- Sarma, J.; Jain, S.; Mukherjee, P.; Saha, U.K. Hybrid/Combined Darrieus–Savonius Wind Turbines: Erstwhile Development and Future Prognosis. J. Sol. Energy Eng. 2021, 143, 050801. [Google Scholar] [CrossRef]
- Chawla, S.; Chauhan, A.; Bala, S. Parametric study of hybrid Savonius-Darrieus turbine. In Proceedings of the 2015 2nd International Conference on Recent Advances in Engineering & Computational Sciences (RAECS), Chandigarh, India, 21–22 December 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Liang, X.; Fu, S.; Ou, B.; Wu, C.; Chao, C.Y.; Pi, K. A computational study of the effects of the radius ratio and attachment angle on the performance of a Darrieus-Savonius combined wind turbine. Renew. Energy 2017, 113, 329–334. [Google Scholar] [CrossRef]
- Irawan, E.N.; Sitompul, S.; Yamashita, K.I.; Fujita, G. Computational Fluid Dynamics Analysis on the Improvement of Hybrid Savonius-Darrieus NREL S809 at Various Fluid Flows. In Proceedings of the 2023 4th International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Denpasar, Indonesia, 6–10 August 2023; pp. 389–394. [Google Scholar] [CrossRef]
- Bhuyan, S.; Biswas, A. Investigations on self-starting and performance characteristics of simple H and hybrid H-Savonius vertical axis wind rotors. Energy Convers. Manag. 2014, 87, 859–867. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.; Sayed, E.T.; Alalmi, A.H.; Abdelkareem, M.A. Wind turbine concepts for domestic wind power generation at low wind quality sites. J. Clean. Prod. 2023, 394, 136137. [Google Scholar] [CrossRef]
- Eftekhari, H.; Al-Obaidi, A.S.M.; Srirangam, S. Numerical Investigation of Hybrid Savonius-Darrieus Vertical Axis Wind Turbine at Low Wind Speeds. J. Phys. Conf. Ser. 2023, 2523, 012032. [Google Scholar] [CrossRef]
- Pallotta, A.; Pietrogiacomi, D.; Romano, G. HYBRI—A combined Savonius-Darrieus wind turbine: Performances and flow fields. Energy 2020, 191, 116433. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transf. 2003, 1, 625–632. [Google Scholar]
- ANSYS, Inc. ANSYS Fluent User’s Guide, Version 2022; ANSYS, Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- Song, K.; Wang, W.Q.; Yan, Y. Numerical and experimental analysis of a diffuser-augmented micro-hydro turbine. Ocean Eng. 2019, 171, 590–602. [Google Scholar] [CrossRef]
- Le Fouest, S.; Mulleners, K. The dynamic stall dilemma for vertical-axis wind turbines. Renew. Energy 2022, 198, 505–520. [Google Scholar] [CrossRef]
- Araya, D.B.; Colonius, T.; Dabiri, J.O. Transition to bluff-body dynamics in the wake of vertical-axis wind turbines. J. Fluid Mech. 2017, 813, 346–381. [Google Scholar] [CrossRef]
- Pan, J.; Ferreira, C.; van Zuijlen, A. Performance analysis of an idealized Darrieus–Savonius combined vertical axis wind turbine. Wind Energy 2024, 27, 612–627. [Google Scholar] [CrossRef]
- Roshan, A.; Sagharichi, A.; Maghrebi, M.J. Nondimensional Parameters’ Effects on Hybrid Darrieus–Savonius Wind Turbine Performance. J. Energy Resour. Technol. 2019, 142, 011202. [Google Scholar] [CrossRef]
- Abdelsalam, A.M.; Kotb, M.; Yousef, K.; Sakr, I. Performance study on a modified hybrid wind turbine with twisted Savonius blades. Energy Convers. Manag. 2021, 241, 114317. [Google Scholar] [CrossRef]
- Asadi, M.; Hassanzadeh, R. Effects of internal rotor parameters on the performance of a two bladed Darrieus-two bladed Savonius hybrid wind turbine. Energy Convers. Manag. 2021, 238, 114109. [Google Scholar] [CrossRef]
- Asadi, M.; Hassanzadeh, R. On the application of semicircular and Bach-type blades in the internal Savonius rotor of a hybrid wind turbine system. J. Wind Eng. Ind. Aerodyn. 2022, 221, 104903. [Google Scholar] [CrossRef]
- Ghafoorian, F.; Mirmotahari, S.R.; Eydizadeh, M.; Mehrpooya, M. A systematic investigation on the hybrid Darrieus-Savonius vertical axis wind turbine aerodynamic performance and self-starting capability improvement by installing a curtain. Next Energy 2025, 6, 100203. [Google Scholar] [CrossRef]
- Nuñez-Quispe, J.J.; Nuñez-Quispe, A.A.; Cedamanos-Cuenca, R.O. Performance analysis of a hybrid vertical axis wind turbine through CFD for distributed generation in rural areas of Peru. J. Phys. Conf. Ser. 2020, 1618, 042013. [Google Scholar] [CrossRef]
- Budea, S.; Simionescu, S.M. Performances of a Savonius-Darrieus Hybrid Wind Turbine. In Proceedings of the 2023 11th International Conference on ENERGY and ENVIRONMENT (CIEM), Bucharest, Romania, 26–27 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Kumar, Y.; Roga, S.; Wanmali, N.K. Experimental analysis of hybrid VAWT and the effect of semi-cylindrical attachment to the trailing edge. Energy Sustain. Dev. 2023, 74, 115–126. [Google Scholar] [CrossRef]



| Mesh Density | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 |
|---|---|---|---|---|---|---|
| Total number of cells | 2,517,379 | 2,613,656 | 2,744,195 | 2,840,472 | 3,209,911 | 3,306,188 |
| Number of cells in rotating zone | 1,796,074 | 1,861,454 | 1,796,074 | 1,861,454 | 1,796,074 | 1,861,454 |
| Number of cells in stationary zone | 419,733 | 419,733 | 646,549 | 646,549 | 1,112,265 | 1,112,265 |
| 0.788 | 0.776 | 0.788 | 0.776 | 0.785 | 0.777 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno, M.; Trejo-Zúñiga, I.; Terrazas, J.; Díaz-Ponce, A.; Pérez-Terrazo, A. Hybridization of a Micro-Scale Savonius Rotor Using a Helical Darrieus Rotor. Fluids 2025, 10, 63. https://doi.org/10.3390/fluids10030063
Moreno M, Trejo-Zúñiga I, Terrazas J, Díaz-Ponce A, Pérez-Terrazo A. Hybridization of a Micro-Scale Savonius Rotor Using a Helical Darrieus Rotor. Fluids. 2025; 10(3):63. https://doi.org/10.3390/fluids10030063
Chicago/Turabian StyleMoreno, Martin, Iván Trejo-Zúñiga, Jesús Terrazas, Arturo Díaz-Ponce, and Andrés Pérez-Terrazo. 2025. "Hybridization of a Micro-Scale Savonius Rotor Using a Helical Darrieus Rotor" Fluids 10, no. 3: 63. https://doi.org/10.3390/fluids10030063
APA StyleMoreno, M., Trejo-Zúñiga, I., Terrazas, J., Díaz-Ponce, A., & Pérez-Terrazo, A. (2025). Hybridization of a Micro-Scale Savonius Rotor Using a Helical Darrieus Rotor. Fluids, 10(3), 63. https://doi.org/10.3390/fluids10030063








