Next Article in Journal
Leaky Flow through Simplified Physical Models of Bristled Wings of Tiny Insects during Clap and Fling
Next Article in Special Issue
Rheology of an Inverted Cholesteric Droplet under Shear Flow
Previous Article in Journal
Extension of the Dupuit–Forchheimer Model for Non-Hydrostatic Flows in Unconfined Aquifers
Previous Article in Special Issue
Flow and Nematic Director Profiles in a Microfluidic Channel: The Interplay of Nematic Material Constants and Backflow
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Fluids
Volume 3
Issue 2
10.3390/fluids3020043
fluids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Exploring “Dormant” Opto-Mechanical Properties of the Isotropic Phase of Liquid Crystals and Revealing Hidden Elasticity of (Ordinary) Liquids

by
Laurence Noirez
* and
Philipp Kahl
Laboratoire Léon Brillouin (CEA-CNRS), University Paris-Saclay, CEA-Saclay, 91191 Gif-sur-Yvette CEDEX, France
*
Author to whom correspondence should be addressed.
Fluids 2018, 3(2), 43; https://doi.org/10.3390/fluids3020043
Submission received: 15 April 2018 / Revised: 28 May 2018 / Accepted: 6 June 2018 / Published: 13 June 2018
(This article belongs to the Special Issue Liquid Crystal Rheology)
Browse Figures
Versions Notes

Abstract

:
There is little literature on the flow properties of the isotropic phase of liquid crystalline fluids. However, this phase is an ideal tool to bridge the physics of liquid crystals with those of (ordinary) fluids. Optical and mechanical studies are presented, demonstrating that away from any phase transition, the isotropic phase of liquid crystalline molecules (LCs) and liquid crystalline polymers (LCPs) can work as an optical oscillator in response to low-frequency mechanical excitation, establishing the elastic origin of the flow birefringence and “visualizing” the very existence of the elastic nature of the liquid state. Additionally, mimicking the excellent anchoring ability of liquid crystals, an alternative rheological protocol optimizing the fluid/substrate interfaces is presented to access the low-frequency shear elasticity in various one-component liquids and salt-free aqueous solutions.

1. Introduction

Liquid crystalline molecules (LCs) are typically made of one or several flexible alkyl chains linked to rigid and polar cores (~5.0 D). The repetition of this antagonistic coupling along or within a polymer chain forms the so-called liquid crystalline polymers (LCPs). The symmetry and the characteristics of the liquid crystalline phases of LCPs and low molecular weight LCs are similar, being strongly related to short-range intermolecular liquid crystal interactions. While the flexible nature of the alkyl part favors amorphous glasses at low temperature, the rigid part self-assemblies to form a crystal. These antagonistic properties are the key parameter to produce intermediate states between liquid and crystalline solid materials; the liquid crystallinity results from frustrated states. The frustration releases away from the phase transitions, in the isotropic phase, where the liquid crystal is thermodynamically, crystallographically, and hydrodynamically similar to an ordinary liquid.
The present contribution investigates newly elastic properties firstly identified in the non-mesomorphic phase of liquid crystals; i.e., in the isotropic phases of thermotropic LCs (including LCPs) or of lyotropic LCs, and then transposed to ordinary liquids or melts. While the elastic properties of the nematic phase of LCs and LCPs are largely documented via the dimensional Frank elastic constants [1], there is little literature on the mechanical behavior of the isotropic phase of liquid crystalline fluids. The main reason is that in the isotropic phase, the fluid is free from long-range liquid crystalline correlations, and therefore is undifferentiated from ordinary viscous liquids or from ordinary viscoelastic melts [2]. The investigation of the isotropic phase is however extremely rich: elastically-induced mechanical and optical properties are experimentally revealed.
The search for hidden elastic properties in the isotropic phase of liquid crystals was primary motivated by non-elucidated observations in steady-state flow conditions of non-linear stress behaviors, and of the emergence of flow birefringence above a critical shear rate. Systems as varied as wormlike micellar solutions [3,4,5], rigid-rod suspensions [6,7], and isotropic phases of thermotropic liquid crystal polymers (shear-induced isotropic to nematic [8,9,10] or isotropic to smectic phase transitions [11]) exhibit abrupt shear-induced transitions. These spectacular non-linear effects cannot be explained on the basis of flow coupling to a molecular relaxation time or a pretransitional lifetime [12,13,14,15] since, for example, the flow birefringence of LCPs is observed before reaching shear rates corresponding to the pretransitional lifetimes and the viscoelastic relaxation times [8,9,10,16,17,18]. Theoretical predictions based on a coupling with molecular dynamics can neither account for non-extensive parameters like the dimensionality (shear-induced phase transitions have been found to be thickness-dependent) nor for external conditions (boundary conditions such as surface wetting, surface curvature) [19]. These spectacular flow effects hide a different mechanism. Since the time scales are much larger than individual relaxation times, long-range collective processes are involved. The present work gathers some experimental results and theoretical developments, indicating that intermolecular interactions might play an important role in the dynamic response of the liquid to a flow field or a mechanical strain field. As a result, upon low-frequency excitation, the intermolecular forces act as a weak elastic network in which liquid molecules do behave not dynamically freely, but elastically (at the submillimeter scale).
The identification of elastic properties of the isotropic phase is of prime importance. Static shear elasticity tells that the molecules remain strongly elastically correlated even when the orientational (liquid crystal) interactions are lost in the (isotropic) liquid state. This article focuses on the fact that this property is not specific to liquid crystalline materials but concern fluids in general. Indeed, the isotropic phase bridges the physics of LCs with those of fluids, highlighting the route to access generic shear elasticity in the liquid state. Shear elasticity is extremely important to understand fluidics: it reveals that the liquid state is a low-threshold elastic medium; molecules are not free in the liquid state but dynamically elastically correlated. Shear elasticity sheds a new light on a comprehensive approach toward flow properties, involving flow birefringence, optical banded textures, flow instabilities, shear-induced stratification in liquid crystals, complex fluids (lyotropic solutions, colloids, vesicle membrane), and simple liquids (hydrodynamics…). Additionally, the liquid phase of usual liquid crystals can work as a low-frequency (low-energy) opto-active material, and this is as such a property immediately available for macroscopic applications.
The first part of this contribution is devoted to the new identified strain optical properties induced at low frequency in the isotropic phase of LCPs and LCs, while the second part describes the origin of the low-frequency birefringence on the basis of the identification of shear elasticity in LCPs and LCs and in various fluids away from any phase transition. Both optical and stress behaviors challenge the Maxwell (molecular) definition of liquids (that are supposed to exhibit shear elasticity at high frequency only (typically at MHz or GHz)) and show that low-frequency (around Hz) shear elasticity exists. This long wavelength excitation reveals collective effects largely ignored in fluidics and points out a new no man’s land to explore.

2. Isotropic Phase under a Low-Frequency Mechanical Field: Spectacular Optical Effects

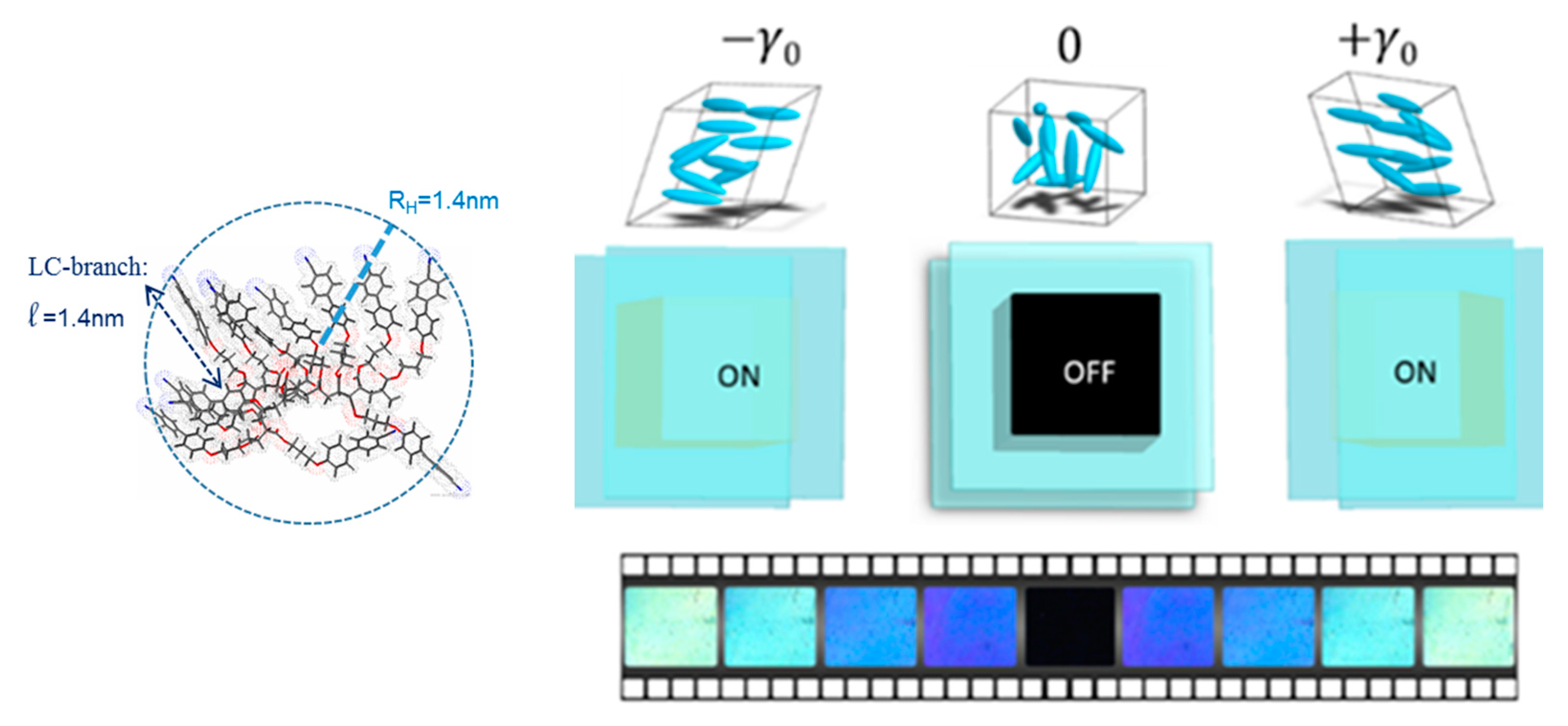
Low-Frequency Optical Response in the Isotropic Phase

We describe recent developments indicating that it is possible to produce a strong strain-induced optical signal of the isotropic phase of low molecular weight LCPs upon applying low-frequency (Hertz-range) mechanical excitation. This spectacular property was unknown to liquid crystal physics since dynamic correlations are assumed to be lost in the liquid phase.
The isotropic phase of liquid crystals is an ideal tool to explore liquid properties. From conventional rheological, thermodynamic, and crystallographic perspectives, it is an ordinary liquid. The liquid crystal/liquid transition is a first-order transition (the phase transition occurs at less than 0.1 °C). This implies that the pretransitional fluctuations, which are the phase precursors, do not mix with the liquid and coexist within the isotropic phase. The latter form clusters of randomly dispersed birefringent molecules. The strategy is to use them as optical tracers of the deformation field during the oscillating stress, similarly to bioluminescent phytoplankton organisms that emit light under oscillatory beach waves (Figure 1).
Figure 2 illustrates that a strain-induced optical transmittance can be observed in the isotropic liquid phase of a 12-units LC upon applying an oscillatory strain wave at low frequency (0.5 Hz; true colors were obtained between crossed polarizers with a polychromatic incident light). This molecule is made of 12 liquid crystal moieties attached to an acrylate backbone. It is a commercially available product used in LC displays under the name LCP95 [20]. With a cyanobiphenyl side-chain moiety of 14 Å in length, a propyl spacer, the liquid crystal part is nearly as long as the repetitive 12-unit acrylate backbone. Its short length and the strong lateral hindrance do not enable several backbone conformations (no entropic conformation) and the smectic phase at lower temperature indicates that side-chain moieties are interdigitated in the bulk state [4,20,21].
The low strain amplitude stress field stretches the isotropic phase that transits reversibly from a non-birefringent state (at rest) to a birefringent state (stretched state) [22]. The induced signal is reversible and synchronous with the strain wave, indicating that the involved mechanism is conservative and not dissipative. The remarkable point is that pretransitional fluctuations reorient under deformation at low frequencies (0.5 Hz) at timescales that do not enable a dynamic coupling with their lifetime (10−9 s in usual LCs [23] and about 10−4 s for LCPs [24]). The analysis of the strain dependence provides information on the underlying mechanism that gives rise to the low-frequency birefringence.
Figure 3 quantitatively details the low-frequency optical response of the isotropic phase [22]. The signal is observed at ω = 0.5 Hz as a function of the strain amplitude:
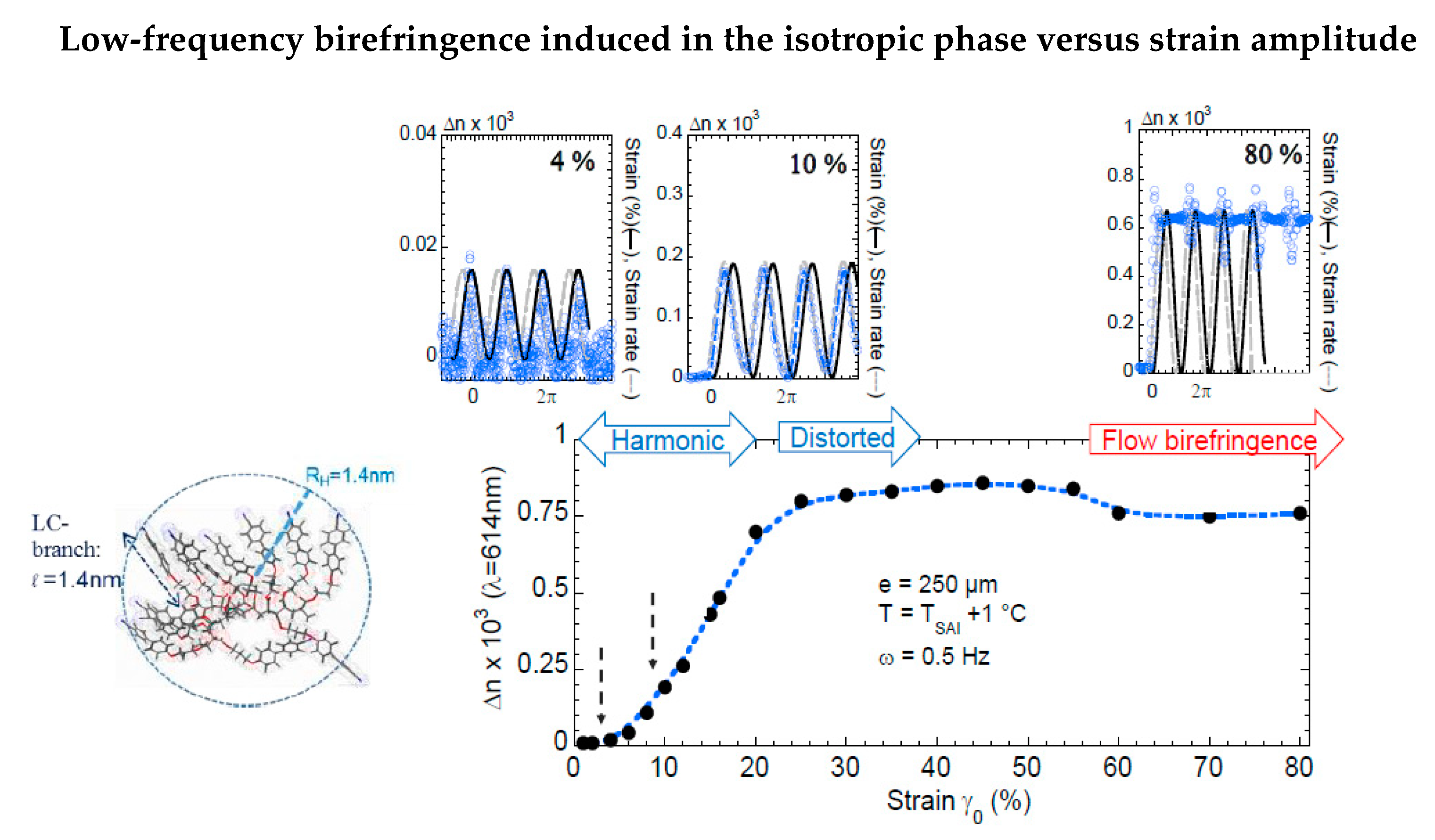
  • At the smallest strains (γ0 < 5%), the birefringence is harmonic and in phase with the applied strain.
  • In the intermediate regime (5% < γ0 < 25%) the signals are also harmonic but are phase-shifted by π/2 (in phase with the strain rate).
  • At larger strains (γ0 > 25%), the signals become distorted, exhibiting higher harmonics. The waves no longer relax between two periods and saturated. The observed, almost continuous signal, as shown for γ0 > 80%, indicates a nearly strain-independent value. The asymptotic behavior at high strain amplitude of the birefringence corresponds to the flow birefringence.
The oscillatory signals at γ0 = 4%, 10%, and 80% strain amplitude displayed at the top (the applied strain is represented by the continuous black sine wave) indicate that:
-
At a very low strain regime (γ0 < 4%), the birefringent signal is in phase with the applied strain wave (upper left inset).
-
For 4% < γ0 < 30%, the optical signal is π/2 phase-shifted in respect to the strain and increases linearly up to 25% strain amplitude (upper medium inset).
-
Above 25% strain amplitude, the optical signal does not relax, reaching an asymptotic value corresponding to the flow birefringence.
The three regimes pointed out in Figure 3 can be interpreted as follows:
-
The birefringence at very small strain amplitudes (γ0 < γcrit) is in phase with the excitation, indicating an elastic mechanism alternating stretching state and relaxation under oscillatory strain.
-
The second regime (γ0 > γcrit), characterized by a π/2 phase-shifted birefringence that increases linearly with the strain, is also harmonic with the excitation. The conservation of the shape of the strain wave (harmonicity) indicates that the strain-induced birefringence is associated to a conservative mechanism (as opposed to a dissipative process). The linearity with the increasing strain amplitude characterizes an elastic process. Finally, the π/2 shift of the phase of the signal indicates a two-step process wherein the first step is achieved in the first elastic regime identified at very low strain rates (γ0 < 4%) close to the transition.
-
At higher strain amplitudes, the optical wave is not more harmonic, does not relax between two successive oscillations, and saturates to an asymptotic birefringence value, indicating a dissipative regime. The asymptotical limit of large strains is the steady state shear flow. In this regime, the nearly constant asymptotic value of the birefringence corresponds to the so-called flow birefringence.
Similar strain-induced optical behavior is observed with high molecular weight side-chain LCPs but without necessarily exhibiting higher optical signals. Figure 4 compares the signals of the strain-induced oscillatory birefringence of the 12-units LC to an 80-units LCP [25].
The identification of strain-induced optical birefringence in the isotropic phase at low frequency is new. The effect has been easily observed for side-chain liquid crystalline polymers of various chemical formulae [22,24,25] and is much less accessible on low molecular liquid crystals, likely because the pretransitional fluctuations are much less extended in space and in temperature range compared to larger molecular liquid crystals (Figure 5).
However, the higher molecular weights do not provide the highest strain-induced optical signal (Figure 4). While the elastic nature is reinforced by the increase of the degree of polymerization, the anchoring is weakened and generates instabilities (interfacial slippage) and therefore optical anharmonicity. A good compromise seems to be a highly viscous isotropic phase while avoiding the typical sliding ability of long polymer chains. The 12-units LC (Figure 3) allows effective interdigitation without being a polymer. Interdigitation is a key word; i.e., strong intermolecular interactions play a key role in such collective optical responses that imply long range correlations.
The low-frequency optical response of the isotropic phase is incompatible with the lifetime of pretransitional fluctuations (of the order of τ ≈ 10−9 s for the usual liquid crystals or τ ≈ 10−4 s for the liquid crystal polymers). Similarly, surface or capillary effects cannot explain the low-frequency birefringence; Thicknesses probed far exceed the coherence lengths that are of the order of several molecular lengths.
Since the strain-induced optical birefringence cannot be explained on the basis of conventional timescales, it contains important fundamental information. The succession of events from in-phase birefringence to this asymptotic (flow) birefringence is instructive with respect to the mechanism. It indicates that the strain-induced birefringence exhibits the characteristics of an elastic process (at low frequency) and thus is not necessary coupled to any particular time.
Indeed, the long-range order evidenced by the optical birefringence and the harmonicity of the response are in opposition to a dissipative state (the birefringence signal immediately relaxes back once the stress is released). Although the material gains energy under deformation, the induced order indicates that there is a loss of entropy compared to the isotropic state (and not an entropy gain). This result can be explained by considering that the molecules are elastically correlated. The energy transferred under deformation is accumulated to produce an ordered phase (orientation of pretransitional fluctuations) and not to reinforce a disordered liquid. The stretching process decreases the entropy, which is why the material relaxes immediately once the deformation is removed (entropy gain). The isotropic phase behaves like an elastic material alternating entropic loss and elastic relaxation during the round-trip motion. The free energy of the isotropic phase can be expressed according to the formalism of the liquid crystal elastomers by adding a term coupling the orientational fluctuations to the deformation (at small amplitudes):
F = F0 + ½·G0·γ2 − σ·γ − k·S(γ)·γ
where S is the order parameter assumed to be proportional to the birefringence (S ≅ 0 without constraint), G0 the elastic shear modulus identified in the isotropic phase, σ is the applied stress, and k is the coupling constant binding the parameter from order to deformation γ. This expression indicates that the energy is lowered under deformation by an increase of the order parameter (birefringence) and thus a decrease of the entropy.
Beside the study of the isotropic phase under oscillatory shear strain demonstrates that pretransitional fluctuations are efficient probes to visualize, via the optical birefringence, the strain field during the mechanical excitation. The strain-induced optical signal is detectable far above the clearing point (at least above TSAI +15 °C) and at frequencies as low as 0.01 Hz in viscous isotropic phases [5]. The usage of the pretransitional swarms as an optical probe is however limited by their temperature dependence. Since the optical response of the isotropic phase reveals an elastically-induced process, viscous (LC) or viscoelastic (LCP) spectra should contain an elastic response to an applied mechanical stress. This point is developed in the second part.

3. Introduction to the Viscoelastic Approach: From the Macroscopic to Sub-Millimeter Scale

A Young Discipline

The spectral analysis versus frequency of fluid dynamic properties is a recent discipline resulting from the need to characterize a plethora of materials for which flow behaviors are intermediate between Newtonian liquids and Hookean solids following the time of observation; i.e., versus frequency. While the general framework has existed since the 19th century to describe the linear behavior of these intermediate materials in particular via mechanical models of springs (Poynting, Thomson [26]), Boltzmann [27]), the principle of a time-dependent measurement relating the strain to the stress and associated with the design of specific apparatus, first called rheogoniometers, is due to Weissenberg and coworkers [28]. The rheology with the emergence of the rheometers, rapidly became the technique for characterizing the dynamic properties of fluids, in particular for viscoelastic materials. Its principle consists in the analysis of the response transmitted by the material subjected to dynamic mechanical stress. With the stress being transferred to the sample by the molecular contact to the substrate, this technique is entirely dependent on conditions of the quality of interaction between the material and the substrate.
Rheological measurements are generally carried out applying a small amplitude oscillatory motion to keep the sample as close as possible to equilibrium conditions (in agreement with the causality-linearity principles). The fluid is placed in contact with and between two surfaces (generally metallic substrate); one oscillating, the other one fixed measuring the stress transmitted by the sample via a sensor (Figure 6). In conventional measurements (generally using aluminum, stainless steel, or glass substrates), the dynamic relaxation spectrum is measured on millimeter-thick samples. From the difference between the input and the output signals and supposing the sine wave is (harmonically) conserved, two parameters are extracted: the component in phase with the strain determines the shear elastic (or storage) modulus (G’), whereas the out-of-phase component defines the viscous (or loss) modulus (G”) following the relationship: σ(ω) = γ0· (G’(ω)·cos(ω·t) + G”(ω) ·sin(ω·t)). The representation of G’(ω) and G”(ω) versus frequency provides the dynamic signature of the material with its eigenmodes.
The analysis of the viscoelastic spectrum serves as the basis of the elegant theoretical approaches for polymer physics such as the tube model (Doi-Edwards 1978 [29]; de Gennes 1971 [30]) and earlier the Rouse theory (Rouse 1953 [31]) that was elaborated for dilute solutions, linking conformational polymer dynamics and viscoelasticity (Figure 7). Since relaxation spectra of dilute solutions, concentrated solutions, and polymer melts present similar features; i.e., the character of the frequency dependence seen was essentially similar, Ferry’s works extended the Rouse theory to try to explain bulk polymer behavior, developing the concept of a direct link between the rheological viscoelastic properties and the molecular structure (Ferry 1970 [32]).
Polymers in diluted, concentrated solutions or in the molten state exhibit versus frequency the typical viscoelastic curve [33]. The low-frequency range characterizes the terminal behavior and is called flow behavior. It is depicted by a ω-scaling decrease of the viscous modulus (G”) and a ω2-scaling of the elastic modulus (G’). The flow behavior thus describes the frequency part where the viscous component becomes major. The interception of the two curves defines the terminal time; i.e., the largest time before the material enters in a flow regime. This characteristic time is interpreted as a single molecular relaxation time on the basis of the Rouse theory or the reptation concept. The viscoelasticity is thus a molecular theory interpreting macroscopic mechanical responses in terms of molecular-scale properties.
These elegant theoretical works are essentially based on a single chain picture where the relaxation modes (generating viscous and elastic contributions) originate mainly from the intrachain properties. The intermolecular interactions are neglected in agreement with the early Rouse model of diluted polymer solutions (Rouse 1953 [31]).
The primary assumption of the Rouse theory is that the viscoelastic spectrum reflects the single chain dynamics. The chains are supposed sufficiently away from each other to not interact in a diluted solution; i.e., the theory assumes that the solvent has a negligible contribution, while it is however the vector of transfer of the stress from the substrate. The chain is seen as a succession of independent elastic springs (“bead-spring” model). Each spring representing a group of monomers (subchain) is sufficiently long to be decoupled from others (Gaussian statistics).
The elastic modulus takes the form of the Maxwell expression:
G ′ ( ω ) = n k T ∑ p = 1 Z ω 2 τ p 2 1 + ω 2 . τ p 2
where τp is the relaxation time of the group p, Z the number of springs, n the number of chains per volume unit, and T the temperature.
At low frequency, G’ exhibits a ω2-scale behavior (Figure 1) and the zero-frequency limit predicts a collapse of the elastic component.
The viscous part is expressed as:
G ″ ( ω ) = ω . η s + n k T ∑ p = 1 Z ω τ p 1 + ω 2 . τ p 2
where ηs is the solvent viscosity.
One can note that the G” zero-frequency limit gives also rise to a collapse of the viscous part. To distinguish viscoelastic liquids from viscoelastic solids, a term Ge is added to the viscoelastic function (Ferry 1980):
G ′ ( ω ) = n k T ∑ p = 1 Z ω 2 τ p 2 1 + ω 2 . τ p 2 + G e ( T )
Ge is the equilibrium modulus. It expresses the existence of infinite relaxation times (i.e., of infinite correlation ranges), that defines the elastic character of solid-like materials (typically cross-linked polymers). It is taken as Ge ≡ 0 for liquids and viscoelastic liquids at low frequency.

4. The Optical Response of LCs and LCPs in the Isotropic Phase Challenges the Single Molecular Approach

The optical response of LCs and LCPs in the isotropic phase (2) challenges this theoretical frame since it suggests an elastic behavior that is not compatible with the single molecular picture (elementary timescales in low molecular weight liquid crystal are extremely short of the order of τ ≈ 10–9 s for the usual liquid crystals or τ ≈ 10–4 s for the liquid crystal polymers compared to the low-frequency range).
In the following, it is demonstrated that LCs and LCPs challenge the expected viscous or viscoelastic responses described above and that there is a multiscale behavior in which the conventional viscoelastic behavior represents only a part of the dynamic response; i.e., the asymptotic stress response at large thickness.

5. Mechanical Response of LC and LCPs in the Isotropic Phase

Gallani et al. reported as early as 1994 on “abnormal” viscoelastic behavior in the isotropic phase of liquid crystalline polymer [34]. The gel-like response (106 Pa) was measured on thin films of 13–20 µm thicknesses on different LCPs and firstly interpreted as a reminiscence of a liquid crystalline network structure [35]. A couple of years later, using a conventional rheometer, solid-like responses were reported up to the millimeter-length scale in the isotropic phase of a liquid crystalline polymer (L. Noirez 2005 [17,36]) while the molecular dimensions are less than 100 Å. The shear elasticity was measurable from the nematic phase, in the isotropic phase, and away from any liquid crystalline transitions. Figure 8 illustrates the mechanical response of an LCP isotropic phase at +14 °C above the isotropic–nematic transition and at more than +100 °C above the glass transition. The shear (elastic) modulus G’ is higher than the viscous modulus G’’ and independent of the frequency (within the frequency range). The solid-like response is detected far away from any phase transition and at large thickness, ruling out an interpretation in terms of reminiscent glass transition or mesomorphic effects but highlighting that long-range elastic intermolecular interactions govern the isotropic melt.
Low-frequency shear elastic behaviors have been reported actually on several occasions but restricted to very low scales and are thus interpreted as surface-induced effects. In this sense, LCs or LCPs are fascinating since they enable to access the elasticity at much larger scales. The strong anchoring ability of the liquid crystal molecules reinforces the boundary contacts between the fluid and the substrate whereby the stress is transmitted and facilitates the measurement. This might explain why the elastic response is easily measurable in mesormorphic fluids. For polymer melts, beginning in 1991 Granick and coworkers [37,38,39] measured a solid-like component at nanoscales using a surface force apparatus (SFA) and mica surfaces. These results were generally interpreted as resulting from surface-induced effects. The disappearance of the solid-like response at larger thicknesses was interpreted by a transition from surface to bulk properties. Other authors reported on an elastic behavior at a 3–4 µm thickness by micro-rheology, but these observations were mostly interpreted as artefacts attributed to trapped dust particles [40]. The very first analysis in terms of physical property was performed by Derjaguin [41,42] revealing in different fluids, including polymers and liquid water, an elastic response at the micron scale which was for the first time interpreted as an intrinsic property due to the force of intermolecular interactions. At larger scales and lower frequency, Collin et al. reported, using treated glass surfaces and small strains delivered by a piezorheometer, a gel-like response of up to 50-µm thicknesses in a low molecular weight polystyrene melt that was interpreted as reminiscent of the glass transition, i.e., clusters of finite size [43]. Since 2006, with the consideration of the wetting conditions to the substrate (paragraph 6), decisive steps have been taken for easy access to shear elasticity, generalizing its identification to a wide panel of liquids and elucidating its intermolecular interaction origin as a condensed matter property [44,45,46,47,48,49,50,51,52,53,54].
In this framework, the study of liquid crystalline fluids is very instructive, since low-frequency shear elasticity was identified both in the isotropic phases of low molecular weight liquid crystals [49] and of high molecular weight liquid crystals of side-chain architecture [17,22,25,34,35,36,46,49,51], ruling out a reminiscence of glass transition effects. Figure 9 illustrates and compares the elastic response displayed by 4-octyl-4-cyano-biphenyl (8CB) [49] to the one of a side-chain liquid crystal polymer (methoxy-phenyl benzoate substituted polyacrylate of 85 repetitive units [36]). In both cases, the low-frequency regime exhibits an elastic behavior (G’ is higher than G” and is weakly frequency dependent). The elastic response is the signature of a collective response; that is, intermolecular interactions dominate the mechanical response. They act as connectors creating a three-dimensional physical network in the isotropic state. The comparison of the low-frequency shear moduli indicates that the branched architecture of the side chain polymer intensifies the elastic signal (≅ 900 Pa) which is about three decades over the signal of the small molecule modulus (8CB; 2–3 Pa). The shear elasticity therefore strongly depends on the molecular architecture and the interdigitation ability.
Both measurements were carried out at about 0.050 mm. At larger thicknesses, the shear elasticity weakens, leaving room for the viscous behavior conventionally observed. The conventional viscous (or viscoelastic) behavior is thus the asymptotic behavior of the large-scale elastic regime. At small scales (several tens of microns), shear elasticity dominates and indicates that the liquid reacts like a solid at the length scale, far from several molecular lengths; that is, it is a macroscopic property. During mechanical excitation, the resistance of the cohesive forces diminishes as the thickness increases (Figure 5), becoming hidden at the millimeter scale. The following paragraph illustrates that the strain amplitude produces an effect similar as the thickness weakening the cohesive forces as the strain stress increases.
Figure 10 shows the evolution of the shear elasticity of the isotropic phase of 8CB as a function of the amplitude of deformation (from reference [34]). The mechanical signal analysis informs on the strain-induced transition of a solid-type behavior to a viscous-like behavior. At large stress amplitude, the viscous modulus dominates the elastic modulus, the latter becoming negligible (less than 1%). The conventional viscous behavior of the isotropic phase is recovered by applying high deformation amplitudes, thus far away from mechanical equilibrium conditions. As a result, a linear solid-type regime precedes the conventional flow regime. The solid type response collapses by increasing the strain amplitude. The deformation and the thickness produce a similar effect on G’. The two parameters are linked by the relation: γ = δl/e indicating that δl, the displacement is the relevant parameter, and suggesting a transition to a dissipative process (slippage effects, shear banding, band structuration) above a critical strain γcrit or a critical thickness ecrit that defines the limit of the linear regime of shear elasticity.
The second example is the low-frequency behavior reported in the isotropic phase of the 12-units LCs (Figure 11). With a cyanobiphenyl side-chain moiety of 14 Å length, a propyl spacer, the liquid crystal part is nearly as long as the backbone. This molecule in solution has a spherical shape with a 1.4-nm hydrodynamic radius. Its short length and the strong lateral hindrance do not enable conformational entropy, but the smectic phase at lower temperature indicates that side-chain moieties are strongly interdigitated in the bulk state [20,21] in agreement with its relatively large viscosity in the isotropic melt (η ≈ 160 Pa·s at +25 °C up to 800 Pa·s at +1 °C above the isotropic–smectic transition).
Similarly, as for 8CB, the isotropic phase of the 12 units-LC exhibits an elastomeric behavior at low strain amplitude (Figure 11). By increasing the strain amplitude, the signals become slightly distorted (signals for γ0 = 50%) and phase-shifted with respect to the applied strain. The shear elasticity is lost above a critical strain amplitude γcrit, and by further increasing the strain amplitude, the strain/stress signals become phase shifted by π/2, in agreement with a viscous behavior. The viscous modulus dominates while the elastic modulus becomes negligible, recovering a viscous behavior (flow regime). The modulus of elasticity in shear of this liquid crystal of 12 units is about 150 Pa [22], which is an intermediate value between those reported for the isotropic phase of the side-chain polymers reaching thousands of Pa [17,31,34,35,36] and 8CB of around 1 Pascal [49]. In conclusion, 8CB and 12-units LCs, two examples of untangled non-crosslinked isotropic fluids, show that elastomer-like behavior can be obtained in the low-frequency regime provided that the isotropic liquid is excited at the scale of tens or hundreds of microns by a low strain stress. In addition, the elastomeric character of the isotropic phase is reinforced by a moderate branching of the liquid crystal moieties.
This overview of shear elasticity in liquid crystalline fluids would not be complete without mentioning lyotropic liquid crystal polymers. The low concentration (isotropic) phase of the lyotropic phase is the counterpart of the thermotropic isotropic phase. We show here that low-frequency shear elasticity has been identified in worm-like micellar solutions (Figure 12) bringing possible new input in the long debate on the origin of shear-induced phase transitions in lyotropic solutions. Figure 12 displays the low-frequency behavior in the isotropic phase of CTAB–water (Cetyl TrimethylAmmonium Bromide solution). Similarly, as for the isotropic phase of the thermotropic systems, the elastic modulus (G’) is higher than the viscous modulus (G’’), with G’ and G’’ relatively independent of the frequency, indicating a dominant elastic response [51].
The identification of shear elasticity in both thermotropic and lyotropic systems indicates that the molecules are not dynamically free but long-range correlated via the intermolecular interactions. These electrostatic interactions between molecules provide the liquid cohesion. The dynamic behavior of surfactant solution (Figure 7b) is in agreement with what was found on various liquids, including ionic liquids, alkanes, and liquid water [47,50]. This was obtained by strongly interacting surfaces to optimize the stress transmission (see Section 6.).

6. Optimizing the Stress Transmission and Accessing Shear Elasticity in Ordinary Fluids

Up-to-date advances in instrumentation in mechanical rheometry have considerably widened the frequency window and the modulus range, and therefore enable the detection of subtle properties that would not been considered at the time of the first concepts of the viscoelasticity. However, the validity of a dynamic relaxation experiment is also primary depending on the efficiency of the stress transmission which is ensured by molecular contact between the sample and the surfaces. For symmetry reasons, surface properties differ from the bulk properties. Therefore, looking for ideal boundary conditions is a challenge. To lower the energy barrier at the solid/liquid interface when molecules do not anchor on substrate as liquid crystalline molecules usually do, reaching total wetting can supply by reinforcing the liquid/substrate interaction, and thus prevents the slippage.
In the framework of this, the wetting protocol has provided easier access to the solid-like response hidden in conventional mechanical measurements. The viscoelastic moduli using the total wetting boundary conditions (alumina surfaces) are higher and reveal the low-frequency shear elasticity in fluids and liquids. The low-frequency shear elasticity (regime of invariance of the dynamic response versus frequency) is observed far away from any phase transition, thus in the liquid state at typically submillimeter (0.025–0.5 mm) thicknesses. It has been reported both in unentangled [36] and in high molecular weight polymers [51,52], in glass formers [53,54], ordinary alkanes [47], and liquid water, highlighting its generic character related to the liquid cohesion energy.
Figure 13 illustrates the response obtained using full wetting conditions for H-bond oligomer polypropyleneglycol (PPG4000). The superposition of the stress wave to strain stress wave confirms directly the instant transmission of the stress to the sensor, which characterizes a solid-like behavior. This result is coherent with the conclusions in terms of elastic contribution carried on the same liquid on the analysis of the dynamic of the capillary waves by synchrotron radiation [54].
If the shear elasticity of the fluid is observable by improving the wettability of the substrate, it is progressively lost by increasing the thickness or by increasing the strain amplitude, giving rise asymptotically to the viscous or in the case of polymer melts to the conventional flow behavior in agreement with what was observed in the mechanical behavior of liquid crystals. The shear strain acts as a selector with respect to the boundary contacts between the fluid and the substrate. Fast relaxation time contacts are easily restored and give rise to the conventional flow behavior, whereas long relaxation (solid-like) contacts bear only small strains and exhibit the elastic response. Finally, the analysis of the stress wave instructively shows that the transition from elastic to viscous regime by increasing strain rate generates non-harmonics, as for example in the case of the heptadecane (Figure 14).

7. Conclusions

Because flow is eminently an interface problem, the consideration of the boundary conditions between the surface and the sample is an important challenge. The optical response of the isotropic phase under mechanical oscillatory excitation at macroscopic scale is a splendid illustration of the physics revealed by strong anchoring effects. The isotropic phase of liquid crystals submitted to low-frequency excitation exhibits an optical birefringence synchronized at low applied strains [22,25]. Because this effect is visible at low frequency and at length scales much larger than molecular lengths (at a scale of several hundreds of microns), it rules out the pertinence of a coupling to pretransitional timescales (the latter of τ ≈ 10−9 s for (low molecular weight) rod-like liquid crystals corresponding to GHz or MHz excitation [23] and about τ ≈ 10−4 s for side-chain liquid crystalline polymers [24]) or surface-induced effects. Because the optical signal reproduces the shape of the applied strain wave, a conservative mechanism is suggested (as opposed to a dissipative process). This optical property is the visual demonstration of the very existence of an elastic process. This process gives rise at very high strain rate to the flow birefringence, which is the asymptotic elastic regime. A similar mechanism is reproduced by the stress behavior of the shear elasticity in the isotropic phases of LCs and LCPs which exhibit at low-strain-value elastic behavior, and viscous (low molecular weight) or viscoelastic (high molecular weight) behavior at large strain values, corresponding to asymptotic stress regimes.
Mimicking the excellent anchoring properties of liquid crystals by using total wetting substrates, a similar strain dependence is observed in various one-component liquids and salt-free aqueous solutions; a dominant shear elasticity is identified in the low-frequency regime, suggesting that the conventional viscous or viscoelastic regimes identified at large strain values correspond to the asymptotic part of a wider rheological scheme [36,41,42,47,49,50,51,52,53]. The experimental evidence that liquids do possess low-frequency shear elasticity and thus that the flow is obtained at the price of an overpassing an elastic threshold was already provided a couple of years ago by the pioneering group Derjaguin [41,42]. These works seem to have been ignored. This resistance of the fluid can be revealed when the molecules have a strong interaction with the surfaces. The boundary conditions play thus a key role that is rarely taken into consideration and is integrated in very few hydrodynamic models only [55]. Because shear elasticity is intrinsically linked to the compressibility, it enables the identification of shear-induced cooling in liquid water [56] and of thermal shear bands in polymer melts (Figure 15) [57] and is likely at the origin of stronger well-known effects [58,59], as well as shear-induced stratification or transverse phonon modes in the isotropic phase of liquid crystals using inelastic scattering [60]. These effects introduce the possibility of a stretched liquid state, in agreement with the excitation of long-range elastic interactions.
In this context, it is urgent to consider not only single molecular dynamics but also collective effects in liquids and thus reintroduce intermolecular interactions since they are responsible for long-range correlations. In polymer physics, this implies taking into account also interchain non-covalent interactions [61] and not only intrachain interactions despite the dominant single (non-interacting) chain concept. Simulation models [62] foresee that the dominant viscoelastic contribution should be due to excluded volume interactions, i.e., interchain forces. The simulation is in agreement with NMR results [63] and fluorescence polarization measurements [64], showing that free or dangling chains become locally oriented in an anisotropic chain network.
In (generic) liquids, long-range elastic correlations were predicted at equilibrium [65] much prior the recent experimental identification at the sub-millimeter scale of low-frequency elasticity [17,34,35,36,44,45,46,47,48,49,50,51,52,53,54]. In this frame the density fluctuations are not simply linked to thermal fluctuations but are also correlated, introducing dynamic and dimensional scaling. New experimental approaches have already emerged describing at the molecular scale possible elastic-like mechanisms in liquids [66,67]. New modelling inspired from liquid crystal elastomers, revisiting solid melting [68] or current molecular models to elaborate an alternative solid-like gap-based approach [69,70], have already converged to integrate the dynamic role of the intermolecular interactions to understand liquid properties. Experimentally, the continuous emergence of new liquid crystalline molecules and the correlative discovery of unsuspected properties around the isotropic phase [71,72] highlight day after day the need for understanding the key role of intermolecular interactions.

Author Contributions

L.N. develops researches highlighting elastic correlations in liquids. She wrote this chapter on the basis of the last advances, in particular the results concerning the low-frequency birefringence identified and analyzed by P.K. in the frame of his PhD training.

Acknowledgments

This work has benefited from CNRS funding. The authors would like to thank P. Baroni for innovative technical and instrumental developments. One of the authors (L.N.) is particularly grateful to F. Volino for the multiple discussions on the shear elasticity in liquids. A special thought also to the late P.G. de Gennes who accepted to chair the first PhD thesis (H. Mendil) on the identification of low-frequency shear elasticity.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Denniston, C.; Marenduzzo, D.; Orlandini, E.; Yeomans, J.M. Lattice Boltzmann algorithm for three-dimensional liquid-crystal hydrodynamics. Phil. Trans. R. Soc. Lond. A 2004, 362, 1745–1754. [Google Scholar] [CrossRef]
  2. Marrucci, G. Theoretical aspects of the flow of liquid crystal polymers. In Rheology and Processing of Liquid Crystal Polymers, 1st ed.; Acierno, D., Collyer, A.A., Eds.; Chapman & Hall: London, UK, 1996; pp. 30–48. [Google Scholar]
  3. Decruppe, J.-P.; Cressely, R.; Makhloufi, R.; Cappelaere, E. Flow birefringence experiments showing a shear-banding structure in a CTAB solution. Colloid Polym. Sci. 1995, 273, 346–351. [Google Scholar] [CrossRef]
  4. Schmitt, V.; Lequeux, F.; Pousse, A.; Roux, D. Flow behavior and shear induced transition near an isotropic/nematic transition in equilibrium polymers. Langmuir 1994, 10, 955–961. [Google Scholar] [CrossRef]
  5. Berret, J.F.; Roux, D.C.; Porte, G.; Lindner, P. Shear-Induced Isotropic-to-Nematic Phase Transition in Equilibrium Polymers. Europhys. Lett. 1994, 25, 521. [Google Scholar] [CrossRef]
  6. See, H.; Doi, M.; Larson, R. The effect of steady flow fields on the isotropic to nematic phase transition in equilibrium polymers. J. Chem. Phys. 1990, 92, 792–800. [Google Scholar] [CrossRef]
  7. Olmsted, P.D.; Lu, C.-Y.D. Coexistence and phase separation in sheared complex fluids. Phys. Rev. E 1997, 56, 55. [Google Scholar] [CrossRef]
  8. Pujolle-Robic, C.; Noirez, L. Observation of shear-induced nematic-isotropic transition in side-chain liquid crystal polymers. Nature 2001, 409, 167. [Google Scholar] [CrossRef] [PubMed]
  9. Pujolle-Robic, C.; Olmsted, P.D.; Noirez, L. Transient and stationary flow behaviour of side chain liquid-crystalline polymers: Evidence of a shear-induced isotropic-to-nematic phase transition. Europhys. Lett. 2002, 59, 364–369. [Google Scholar] [CrossRef] [Green Version]
  10. Kahl, P.; Noirez, L. From flow birefringence in the isotropic phase to the identification of shear elasticity in liquids. Liquid Cryst. Rev. 2017, 4, 135. [Google Scholar] [CrossRef]
  11. Bailey, C.; Fodor-Csorba, K.; Verduzco, R.; Gleeson, J.T.; Sprunt, S.; Jakli, A. Large Flow Birefringence of Nematogenic Bent-Core Liquid Crystals. Phys. Rev. Lett. 2009, 103, 237803. [Google Scholar] [CrossRef] [PubMed]
  12. Hess, S. Flow Alignment and Flow-Induced Phase Transition in Liquid Crystals. Z. Naturforsch. A 1976, 31, 1507–1513. [Google Scholar] [CrossRef]
  13. Olmsted, P.D.; Goldbart, P.M. Theory of the nonequilibrium phase transition for nematic liquid crystals under shear flow. Phys. Rev. A 1990, 41, 4578. [Google Scholar] [CrossRef] [PubMed]
  14. Olmsted, P.D.; Goldbart, P.M. Isotropic-nematic transition in shear flow: State selection, coexistence, phase transitions, and critical behavior. Phys. Rev. A 1992, 46, 4966. [Google Scholar] [CrossRef] [PubMed]
  15. Cates, M.E.; Fielding, S.M. Rheology of giant micelles. Adv. Phys. 2006, 55, 799–879. [Google Scholar] [CrossRef] [Green Version]
  16. Jimenez, M.L.; Mantegazza, F.; Gallazzi, L.; Zanchetta, G.; Bellini, T. Optical and electro-optical derivation of the pretransitional behavior of orientational and shear viscosities in the isotropic phase of liquid crystals. Phys. Rev. E 2006, 74, 011707. [Google Scholar] [CrossRef] [PubMed]
  17. Noirez, L. Origin of shear-induced phase transitions in melts of liquid-crystal polymers. Phys. Rev. E 2005, 72, 051701. [Google Scholar] [CrossRef] [PubMed]
  18. Mendil, H.; Baroni, P.; Noirez, L. Unexpected giant elasticity in side-chain liquid crystal polymer melts: A new approach for the understanding of shear induced phase transitions. Europhys. Lett. 2005, 72, 983. [Google Scholar] [CrossRef]
  19. Mendil-Jakani, H.; Baroni, P.; Noirez, L. Shear-Induced Isotropic to Nematic Transition of Liquid-Crystal Polymers: Identification of Gap Thickness and Slipping Effects. Langmuir 2009, 25, 5248–5252. [Google Scholar] [CrossRef] [PubMed]
  20. Farrand, L.D.; Patrick, J.; Marden, S.A. Merck Patent GmbH. EP1690917 B1, 8 October 2008. [Google Scholar]
  21. Jadzyn, J.; Dabrwoski, R.; Lech, T.; Czechowski, C. Viscosity of the Homologous Series of n-Alkylcyanobiphenyls. J. Chem. Eng. Data 2001, 46, 110–112. [Google Scholar] [CrossRef]
  22. Kahl, P.; Baroni, P.; Noirez, L. Bringing to Light Hidden Elasticity in the Liquid State Using In-Situ Pretransitional Liquid Crystal Swarms. PLoS ONE 2016, 11, e0147914. [Google Scholar] [CrossRef] [PubMed]
  23. Rzoska, S.J.; Drozd-Rzoska, A.; Mukherjee, P.K.; Lopez, D.-O.; Martinez-Garcia, J.-C. Distortion-sensitive insight into the pretransitional behavior of 4-n-octyloxy-4’-cyanobiphenyl (8OCB). J. Phys. Condens. Matter 2013, 25, 245105. [Google Scholar] [CrossRef] [PubMed]
  24. Reys, V.; Dormoy, Y.; Gallani, J.L.; Martinoty, P.; le Barny, P.; Dubois, J.C. Short-Range-Order Effects in the Isotropic Phase of a Side-Chain Polymeric Liquid Crystal. Phys. Rev. Lett. 1988, 61, 2340. [Google Scholar] [CrossRef] [PubMed]
  25. Kahl, P.; Baroni, P.; Noirez, L. Harmonic strain-optical response revealed in the isotropic (liquid) phase of liquid crystals. Appl. Phys. Lett. 2015, 107, 084101. [Google Scholar] [CrossRef] [Green Version]
  26. Poynting, J.H.; Thomson, J.J. Properties of Matter; C. Griffin and Co.: London, UK, 1902. [Google Scholar]
  27. Boltzmann, L. Sitzler Kgl Akad; Wiss: Wien, Austria, 1878; pp. 815–842. [Google Scholar]
  28. Freeman, S.M.; Weissenberg, K. Some new anisotropic time effects in rheology. Nature 1948, 161, 324. [Google Scholar] [CrossRef] [PubMed]
  29. Doi, M.; Edwards, S.F. Dynamics of Concentrated Polymer Systems. J. Chem. Soc. Faraday Trans. II 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
  30. De Gennes, P.G. Reptation of a Polymer Chain in the Presence of Fixed Obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
  31. Rouse, P.E. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
  32. Ferry, J.D. Viscoelastic Properties of Polymers; Wiley & Sons: New York, NY, USA, 1970. [Google Scholar]
  33. Ferry, J.D. Probing Macromolecular Motions through Viscoelasticity. Rubber Chem. Tech. 1981, 54, 72–82. [Google Scholar] [CrossRef]
  34. Gallani, J.L.; Hilliou, L.; Martinoty, P.; Keller, P. Abnormal Viscoelastic Behavior of Side-Chain Liquid-Crystal Polymers. Phys. Rev. Lett. 1994, 72, 2109–2112. [Google Scholar] [CrossRef] [PubMed]
  35. Martinoty, P.; Hilliou, L.; Mauzac, M.; Benguigui, L.; Collin, D. Side-Chain Liquid-Crystal Polymers: Gel-like Behavior below Their Gelation Points. Macromolecules 1999, 32, 1746–1752. [Google Scholar] [CrossRef]
  36. Mendil, H.; Baroni, P.; Noirez, L. Solid-like rheological response of non-entangled polymers in the molten state. Eur. Phys. J. E 2006, 19, 77–85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  37. Hu, H.W.; Carson, G.A.; Granick, S. Relaxation time of confined liquids under shear. Phys. Rev. Lett. 1991, 66, 2758–2761. [Google Scholar] [CrossRef] [PubMed]
  38. Levent Demirel, A.; Granick, S. Origins of solidification when a simple molecular fluid is confined between two plates. J. Am. Chem. Phys. 2001, 115, 1498–1512. [Google Scholar] [CrossRef]
  39. Zhu, Y.; Granick, S. Superlubricity: A paradox about confined fluids resolved. Phys. Rev. Lett. 2004, 93, 096101. [Google Scholar] [CrossRef] [PubMed]
  40. Kavehpour, H.P.; McKinley, G.H. Tribo-rheometry: From gap-dependent rheology to tribology. Tribol. Lett. 2004, 17, 327–335. [Google Scholar] [CrossRef]
  41. Badmaev, B.B.; Bazaron, U.B.; Derjaguin, B.V.; Budaev, O.R. Measurement of the shear elasticity of polymethylsiloxane liquids. Phys. B 1983, 122, 241–245. [Google Scholar] [CrossRef]
  42. Derjaguin, B.V.; Bazaron, U.B.; Zandanova, K.T.; Budaev, O.R. The complex shear modulus of polymeric and small-molecule liquids. Polymer 1989, 30, 97–103. [Google Scholar] [CrossRef]
  43. Collin, D.; Martinoty, P. Dynamic macroscopic heterogeneities in a flexible linear polymer melt. Physica A 2002, 320, 235–248. [Google Scholar] [CrossRef]
  44. Baroni, P.; Mendil, H.; Noirez, L. Méthode de détermination des propriétés dynamiques d’un matériau fluide ou solide déformable. France Patent n° 0510988, 27 November 2005. [Google Scholar]
  45. Baroni, P.; Mendil-Jakani, H.; Noirez, L. Innovations pour une mesure complète des propriétés viscoélastiques des fluides. In Techniques de l’Ingénieur, TI Editions ed; Techniques de l’Ingénieur: Paris, France, 2010. [Google Scholar]
  46. Mendil, H.; Grillo, I.; Baroni, P.; Noirez, L. The frozen state in the liquid phase of side-chain liquid-crystal polymers. Phys. Rev. Lett. 2006, 96, 077801. [Google Scholar] [CrossRef] [PubMed]
  47. Noirez, L.; Baroni, P.; Cao, H. Identification of Low Frequency Shear elasticity in Liquids n-Heptadecane, Liquid Water and RT-Ionic Liquids [emim][Tf2N]. J. Mol. Liq. 2012, 176, 71–75. [Google Scholar] [CrossRef]
  48. Wang, S.-Q.; Ravindranath, S.; Wang, Y.; Boukany, P. New theoretical considerations in polymer rheology: Elastic breakdown of chain entanglement network. J. Chem. Phys. 2007, 127, 064903. [Google Scholar] [CrossRef] [PubMed]
  49. Kahl, P.; Baroni, P.; Noirez, L. Hidden solidlike properties in the isotropic phase of the 8CB liquid crystal. Phys. Rev. E 2013, 88, 050501. [Google Scholar] [CrossRef] [PubMed]
  50. Noirez, L.; Baroni, P. Identification of a low-frequency elastic behaviour in liquid water. J. Phys. Condens. Matter 2012, 24, 372101. [Google Scholar] [CrossRef] [PubMed]
  51. Noirez, L. Importance of Interfacial Interactions to Access Shear Elasticity of Liquids and Understand Flow Induced Birefringence from Liquid Crystals to Worm-Like Micellar Solutions. Oil Gas Sci. Technol. Rev. IFP Energ. Nouv. 2017, 72, 10–17. [Google Scholar] [CrossRef]
  52. Noirez, L.; Mendil-Jakani, H.; Baroni, P. Identification of finite shear-elasticity in the liquid state of molecular (OTP) and polymeric glass formers (PBuA). Philos. Mag. 2011, 91, 1977–1986. [Google Scholar] [CrossRef] [Green Version]
  53. Noirez, L.; Baroni, P. Revealing the solid-like nature of Glycerol at ambient temperature. J. Mol. Struct. 2010, 972, 16–21. [Google Scholar] [CrossRef]
  54. Chushkin, Y.; Caronna, C. Madsen A Low-frequency elastic behavior of a supercooled liquid. EPL 2008, 83, 36001. [Google Scholar] [CrossRef]
  55. Heidenreich, S.; Ilg, P.; Hess, S. Boundary conditions for fluids with internal orientational degrees of freedom: Apparent velocity slip associated with the molecular alignment. Phys. Rev. E 2007, 75, 066302. [Google Scholar] [CrossRef] [PubMed]
  56. Baroni, P.; Bouchet, P.; Noirez, L. Highlighting a Cooling Regime in Liquids under Submillimeter Flows. J. Phys. Chem. Lett. 2013, 4, 2026–2029. [Google Scholar] [CrossRef] [PubMed]
  57. Noirez, L.; Baroni, P. Identification of thermal shear bands in a low molecular weight polymer melt under oscillatory strain field. Colloid Polym. Sci. 2018, 296, 713–720. [Google Scholar] [CrossRef]
  58. Adams, J.M.; Fielding, S.M.; Olmsted, P.D. Transient shear banding in entangled polymers: A study using the Rolie-Poly model. J. Rheol. 2011, 55. [Google Scholar] [CrossRef] [Green Version]
  59. Adams, J.M.; Olmsted, P.D. Nonmonotonic Models are not Necessary to Obtain Shear Banding Phenomena in Entangled Polymer Solutions. Phys. Rev. Lett. 2009, 102, 067801. [Google Scholar] [CrossRef] [PubMed]
  60. Bolmatov, D.; Zhernenkov, M.; Sharpnack, L.; Agra-Kooijman, D.M.; Kumar, S.; Suvorov, A.; Pindak, R.; Cai, Y.Q.; Cunsolo, A. Emergent Optical Phononic Modes upon Nanoscale Mesogenic Phase Transitions. Nano Lett. 2017, 17, 3870–3876. [Google Scholar] [CrossRef] [PubMed]
  61. Guenza, M. Cooperative Dynamics in Unentangled Polymer Fluids. Phys. Rev. Lett. 2002, 88, 0259011–0259014. [Google Scholar] [CrossRef] [PubMed]
  62. Fixman, M. Stress Relaxation in Polymer Melts and Concentrated Solutions. J. Chem. Phys. 1991, 95, 1410–1413. [Google Scholar] [CrossRef]
  63. Sotta, P.; Deloche, B.; Herz, J.; Lapp, A.; Durand, D.; Rabadeux, J.C. Evidence for short-range orientational couplings between chain segments in strained rubbers: A deuterium magnetic resonance investigation. Macromolecules 1987, 20, 2769–2774. [Google Scholar] [CrossRef]
  64. Erman, B.; Queslelt, J.-P.; Monnerie, L. Orientation and anisotropy of dangling chains in a deformed network. Polymer 1988, 29, 1823–1826. [Google Scholar] [CrossRef]
  65. Volino, F. Théorie viscoélastique non-extensive. Annales de Physique 1997, 22, 181–231. [Google Scholar] [CrossRef]
  66. Pronin, A.A.; Trachenko, K.; Kondrin, M.V.; Lyapin, A.G.; Brazhkin, V.V. Non local dielectric relmaxation in glycerol. Phys. Rev. B 2011, 84, 012201. [Google Scholar] [CrossRef]
  67. Bolmatov, D.; Zhernenkov, M.; Zav’yalov, D.; Stoupin, S.; Cunsolo, A.; Cai, Y.Q. Thermally triggered phononic gaps in liquids at THz scale. Sci. Rep. 2016, 6, 19469. [Google Scholar] [CrossRef] [PubMed]
  68. Zaccone, A.; Blundell, J.R.; Terentjev, E.M. Network disorder and nonaffine deformations in marginal solids. Phys. Rev. B 2011, 84, 174119. [Google Scholar] [CrossRef]
  69. Trachenko, K.; Brazhkin, V.V. Collective modes and thermodynamics of the liquid state. Rep. Prog. Phys. 2016, 79, 016502–016538. [Google Scholar] [CrossRef] [PubMed]
  70. Trachenko, K.; Brazhkin, V.V. Understanding the problem of glass transition on the basis of elastic waves in a liquid. J. Phys. Condens. Matter 2009, 21, 425104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  71. Salili, S.M.; Tamba, M.G.; Sprunt, S.N.; Welch, C.; Mehl, G.H.; Jákli, A.; Gleeson, J.T. Anomalous Increase in Nematic-Isotropic Transition Temperature in Dimer Molecules Induced by a Magnetic Field. Phys. Rev. Lett. 2016, 116, 217801. [Google Scholar] [CrossRef] [PubMed]
  72. Wiant, D.; Stojadinovic, S.; Neupane, K.; Sharma, S.; Fodor-Csorba, K.; Jákli, A.; Gleeson, J.T.; Sprunt, S. Critical behavior at the isotropic-to-nematic phase transition in a bent-core liquid crystal. Phys. Rev. E 2006, 73, 30703. [Google Scholar] [CrossRef] [PubMed]
Fluids 03 00043 g001 550
Figure 1. Like bioluminescent phytoplankton organisms that emit light under stress (see beach waves), pretransitional fluctuations produce birefringence by reorientation under shear strain stress (image from https://furthermore.equinox.com/articles/2014/10/seven-incredible-bodies-of-water).
Figure 1. Like bioluminescent phytoplankton organisms that emit light under stress (see beach waves), pretransitional fluctuations produce birefringence by reorientation under shear strain stress (image from https://furthermore.equinox.com/articles/2014/10/seven-incredible-bodies-of-water).
Fluids 03 00043 g001
Fluids 03 00043 g002 550
Figure 2. The isotropic phase exhibits a “mechano-stimuli responsive” behavior upon applying an oscillatory strain wave γ = γ0·sin(ω·t), where γ0 is the rate of the displacement δl to the slab thickness e (γ0 = 10%, ω = 0.5 Hz, e = 0.250 mm, quartz substrate). Photos recorded between crossed polarizers using a polychromatic light, sample: 12 monomer units of cyanobiphenyl acrylate displaying the following phase sequence: Tg–54 °C–SA–80 °C–I (from [22]). Link for the video: https://www.youtube.com/watch?v=0NPjNG6FkTE. LC: liquid crystalline molecule.
Figure 2. The isotropic phase exhibits a “mechano-stimuli responsive” behavior upon applying an oscillatory strain wave γ = γ0·sin(ω·t), where γ0 is the rate of the displacement δl to the slab thickness e (γ0 = 10%, ω = 0.5 Hz, e = 0.250 mm, quartz substrate). Photos recorded between crossed polarizers using a polychromatic light, sample: 12 monomer units of cyanobiphenyl acrylate displaying the following phase sequence: Tg–54 °C–SA–80 °C–I (from [22]). Link for the video: https://www.youtube.com/watch?v=0NPjNG6FkTE. LC: liquid crystalline molecule.
Fluids 03 00043 g002
Fluids 03 00043 g003 550
Figure 3. Strain dependence of the birefringent signal (peak value of the signal) in the isotropic phase of the 12-units liquid crystal (T-TSAI = +1 °C, quartz substrate) at 0.5 Hz. The strain amplitude is the maximum displacement length δl divided by the sample thickness (γ0 = δl/e).
Figure 3. Strain dependence of the birefringent signal (peak value of the signal) in the isotropic phase of the 12-units liquid crystal (T-TSAI = +1 °C, quartz substrate) at 0.5 Hz. The strain amplitude is the maximum displacement length δl divided by the sample thickness (γ0 = δl/e).
Fluids 03 00043 g003
Fluids 03 00043 g004 550
Figure 4. Low-frequency birefringence is larger for the small molecular weight LC under the same stress conditions (ω = 0.5 Hz, 250 µm, γ0 = 10%), +1 °C above the isotropic transition. (a) A 12-unit cyanobiphenyl side-chain acrylate molecule. (b) An 80-units cyanobiphenyl side-chain polyacrylate molecule (polydispersity: 1.1). In the insert: the optical signals of (a) and (b) of the isotropic phase of the 12-units and 80-units LCs are reported (double scale—the birefringence is normalized to the strain amplitude).
Figure 4. Low-frequency birefringence is larger for the small molecular weight LC under the same stress conditions (ω = 0.5 Hz, 250 µm, γ0 = 10%), +1 °C above the isotropic transition. (a) A 12-unit cyanobiphenyl side-chain acrylate molecule. (b) An 80-units cyanobiphenyl side-chain polyacrylate molecule (polydispersity: 1.1). In the insert: the optical signals of (a) and (b) of the isotropic phase of the 12-units and 80-units LCs are reported (double scale—the birefringence is normalized to the strain amplitude).
Fluids 03 00043 g004
Fluids 03 00043 g005 550
Figure 5. Optical response (transmittance intensity) measured upon applying a low-frequency mechanical strain in the isotropic phase of 4-octyl-4′-cyanobiphenyl (8CB) (T − TNI = +0.1 °C, quartz substrate, strain rate γ0 = 100%). The transmittance displayed at ω = 0.3 Hz, 0.6 Hz and 0.9 Hz is weak. Device limitations do not enable a conclusive analysis (top figure).
Figure 5. Optical response (transmittance intensity) measured upon applying a low-frequency mechanical strain in the isotropic phase of 4-octyl-4′-cyanobiphenyl (8CB) (T − TNI = +0.1 °C, quartz substrate, strain rate γ0 = 100%). The transmittance displayed at ω = 0.3 Hz, 0.6 Hz and 0.9 Hz is weak. Device limitations do not enable a conclusive analysis (top figure).
Fluids 03 00043 g005
Fluids 03 00043 g006 550
Figure 6. (a) The rheology measurement results from a transmission chain of the information: the stress is transmitted via the first surface from the motor (here a sine oscillation) to the sample via molecular contacts, is communicated along the sample thickness, and is transferred via molecular contacts to the second surface coupled to a force (torque) sensor. (b) When input and output waves are close in phase, the fluid exhibits a solid-like behavior (G’ > G” and G’ and G” weakly dependent on the frequency). (c) When input and output waves are out of phase with a phase shift > π/4 (here π/2), the fluid exhibits a viscous behavior (G’ negligible and G’ and G” vanishing with the frequency).
Figure 6. (a) The rheology measurement results from a transmission chain of the information: the stress is transmitted via the first surface from the motor (here a sine oscillation) to the sample via molecular contacts, is communicated along the sample thickness, and is transferred via molecular contacts to the second surface coupled to a force (torque) sensor. (b) When input and output waves are close in phase, the fluid exhibits a solid-like behavior (G’ > G” and G’ and G” weakly dependent on the frequency). (c) When input and output waves are out of phase with a phase shift > π/4 (here π/2), the fluid exhibits a viscous behavior (G’ negligible and G’ and G” vanishing with the frequency).
Fluids 03 00043 g006
Fluids 03 00043 g007 550
Figure 7. The Rouse model has been explicitly developed in the frame of non-interacting polymer chains in dilute solutions. Reproduced from [31], with the permission of AIP Publishing.
Figure 7. The Rouse model has been explicitly developed in the frame of non-interacting polymer chains in dilute solutions. Reproduced from [31], with the permission of AIP Publishing.
Fluids 03 00043 g007
Fluids 03 00043 g008 550
Figure 8. A strong solid-like response is measured above the isotropic–nematic transition by a liquid crystal polymer (viscoelastic moduli G’ (♦), G” (◊) recorded at 14 °C above the transition and 0.150 mm gap thickness). The lower inset displays for comparison the conventional polymer melt behavior fulfilling the Maxwell model [32]). From Mendil, Noirez, Baroni 2006 [36]). With kind permission from The European Physical Journal (EPJ).
Figure 8. A strong solid-like response is measured above the isotropic–nematic transition by a liquid crystal polymer (viscoelastic moduli G’ (♦), G” (◊) recorded at 14 °C above the transition and 0.150 mm gap thickness). The lower inset displays for comparison the conventional polymer melt behavior fulfilling the Maxwell model [32]). From Mendil, Noirez, Baroni 2006 [36]). With kind permission from The European Physical Journal (EPJ).
Fluids 03 00043 g008
Fluids 03 00043 g009 550
Figure 9. The solid-like dynamic response was highlighted in the isotropic phase of various liquid crystals including low molecular weight liquid crystals. The right figure shows superposed strain/stress waves measured on 8CB at T = TNI + 2 °C (phase sequence: K–21 °C–SA−33 °C–N–40 °C–I) and 0.050-mm gap thickness (reproduced with permission from reference [34]). The left figure compares the elastic responses identified in LCPs with 85 repetitive units (phase sequence: Tg–22 °C–SA–89 °C–N−116 °C) and 8CB, illustrating that the branched architecture reinforces the elastic response (reproduced with permission from [36,49]). The solid-like responses are measured at comparable thicknesses (0.050 mm and 0.060 mm).
Figure 9. The solid-like dynamic response was highlighted in the isotropic phase of various liquid crystals including low molecular weight liquid crystals. The right figure shows superposed strain/stress waves measured on 8CB at T = TNI + 2 °C (phase sequence: K–21 °C–SA−33 °C–N–40 °C–I) and 0.050-mm gap thickness (reproduced with permission from reference [34]). The left figure compares the elastic responses identified in LCPs with 85 repetitive units (phase sequence: Tg–22 °C–SA–89 °C–N−116 °C) and 8CB, illustrating that the branched architecture reinforces the elastic response (reproduced with permission from [36,49]). The solid-like responses are measured at comparable thicknesses (0.050 mm and 0.060 mm).
Fluids 03 00043 g009
Fluids 03 00043 g010 550
Figure 10. Mechanical response of 4-octyl-4′-cyanobiphenyl (8CB) in the isotropic phase at a 0.050-mm gap thickness (reproduced with permission from reference [50]). Upper figure: The elastic response is evidenced by in-phase behavior of strain and stress waves. At larger strain amplitudes, the strain (black line) and stress (red line) waves become progressively π/2 phase-shifted, indicating a liquid-like behavior characterized by the tabulated viscosity of 14 mPa.s. Bottom figure: Strain dependence (logarithmic scales) of the viscoelastic moduli (G’(•), G”(■)): (a) At low strain amplitude (typically γ0 = 6%), the isotropic liquid exhibits an elastic response with G’ > G’’ and G’, G’’ nearly constant. The grey dotted line indicates the reference value of the stress modulus in nearly equilibrium conditions and the grey vertical bar indicates the modulus loss with respect to the elastic regime.
Figure 10. Mechanical response of 4-octyl-4′-cyanobiphenyl (8CB) in the isotropic phase at a 0.050-mm gap thickness (reproduced with permission from reference [50]). Upper figure: The elastic response is evidenced by in-phase behavior of strain and stress waves. At larger strain amplitudes, the strain (black line) and stress (red line) waves become progressively π/2 phase-shifted, indicating a liquid-like behavior characterized by the tabulated viscosity of 14 mPa.s. Bottom figure: Strain dependence (logarithmic scales) of the viscoelastic moduli (G’(•), G”(■)): (a) At low strain amplitude (typically γ0 = 6%), the isotropic liquid exhibits an elastic response with G’ > G’’ and G’, G’’ nearly constant. The grey dotted line indicates the reference value of the stress modulus in nearly equilibrium conditions and the grey vertical bar indicates the modulus loss with respect to the elastic regime.
Fluids 03 00043 g010
Fluids 03 00043 g011 550
Figure 11. Strain dependence (logarithmic scales) of the viscoelastic moduli (G’ (•), G” (■)) of the 12-unit LC in the isotropic phase (T = TSAI + 25 °C) at a 0.170-mm gap thickness and ω = 0.1 Hz (from reference [22]). The solid-like response at small strain amplitudes is progressively replaced by a liquid-like behavior with increasing strains. This behavior is highlighted by the strain (black line) and stress (red line) waves that are in phase in the elastic regime and π/2 phase shifted in the viscous regime (top figure). The grey dotted line indicates the reference value of the stress modulus in nearly equilibrium conditions.
Figure 11. Strain dependence (logarithmic scales) of the viscoelastic moduli (G’ (•), G” (■)) of the 12-unit LC in the isotropic phase (T = TSAI + 25 °C) at a 0.170-mm gap thickness and ω = 0.1 Hz (from reference [22]). The solid-like response at small strain amplitudes is progressively replaced by a liquid-like behavior with increasing strains. This behavior is highlighted by the strain (black line) and stress (red line) waves that are in phase in the elastic regime and π/2 phase shifted in the viscous regime (top figure). The grey dotted line indicates the reference value of the stress modulus in nearly equilibrium conditions.
Fluids 03 00043 g011
Fluids 03 00043 g012 550
Figure 12. Using total wetting conditions, the liquid phase (dilution 18%) of salt-free CTAB-water (Cetyl TrimethylAmmonium Bromide solution) measured at 33 °C (isotropic phase) and the 0.300-mm gap thickness exhibit solid-like behavior with G’ independent of the frequency and exceeding G’’ [51].
Figure 12. Using total wetting conditions, the liquid phase (dilution 18%) of salt-free CTAB-water (Cetyl TrimethylAmmonium Bromide solution) measured at 33 °C (isotropic phase) and the 0.300-mm gap thickness exhibit solid-like behavior with G’ independent of the frequency and exceeding G’’ [51].
Fluids 03 00043 g012
Fluids 03 00043 g013 550
Figure 13. Frequency dependence of the elastic G’(ω):● and viscous moduli G”(□): □, measured for a glass former liquid (polypropyleneglycol (PPG4000), MW = 4000, Tg = −75 °C) at T = +5 °C (0.075 mm gap thickness–alumina plate-plate fixtures). The insert shows the superposition of the strain (green points) and the stress (red points) waves highlighting the instant response of the liquid.
Figure 13. Frequency dependence of the elastic G’(ω):● and viscous moduli G”(□): □, measured for a glass former liquid (polypropyleneglycol (PPG4000), MW = 4000, Tg = −75 °C) at T = +5 °C (0.075 mm gap thickness–alumina plate-plate fixtures). The insert shows the superposition of the strain (green points) and the stress (red points) waves highlighting the instant response of the liquid.
Fluids 03 00043 g013
Fluids 03 00043 g014 550
Figure 14. (a) Transition from solid-like to viscous behavior-induced response in liquid n-heptadecane at 24 °C by increasing the strain amplitude (γ0). The data points display the shear (G’(•)) and the viscous (G”(□)) moduli at ω = 1 rad/s. At low strain amplitude, a solid-like behavior is observed. The moduli in the intermediate non-linear regime are not presented since the signal is not a sinusoidal wave. At very large strain amplitudes, an apparent viscous behavior is displayed. (b) From left to right: input sin wave (■: strain amplitude γ(%)) and output shear stress wave (•: shear stress: σ(a.u.)) corresponding to the liquid at different imposed strain amplitudes (γ0 = 1, 10, 1000 and 5000%, e = 0.058 mm), reproduced with permission from [47]. Similar behaviors are observed in polypropylenglycol, water, ionic liquids...
Figure 14. (a) Transition from solid-like to viscous behavior-induced response in liquid n-heptadecane at 24 °C by increasing the strain amplitude (γ0). The data points display the shear (G’(•)) and the viscous (G”(□)) moduli at ω = 1 rad/s. At low strain amplitude, a solid-like behavior is observed. The moduli in the intermediate non-linear regime are not presented since the signal is not a sinusoidal wave. At very large strain amplitudes, an apparent viscous behavior is displayed. (b) From left to right: input sin wave (■: strain amplitude γ(%)) and output shear stress wave (•: shear stress: σ(a.u.)) corresponding to the liquid at different imposed strain amplitudes (γ0 = 1, 10, 1000 and 5000%, e = 0.058 mm), reproduced with permission from [47]. Similar behaviors are observed in polypropylenglycol, water, ionic liquids...
Fluids 03 00043 g014
Fluids 03 00043 g015 550
Figure 15. Polymer slab of 0.185-mm-thickness under oscillatory strain: the melt exhibits non-uniform temperatures with the emergence of cold thermal bands (dark blue) coexisting upon applying an oscillatory shear stress of (γ = 1200%, ω = 2 rad/s). The bottom curves illustrate the strain and the velocity over a period. Complementary information is available in references [58,59].
Figure 15. Polymer slab of 0.185-mm-thickness under oscillatory strain: the melt exhibits non-uniform temperatures with the emergence of cold thermal bands (dark blue) coexisting upon applying an oscillatory shear stress of (γ = 1200%, ω = 2 rad/s). The bottom curves illustrate the strain and the velocity over a period. Complementary information is available in references [58,59].
Fluids 03 00043 g015

Share and Cite

MDPI and ACS Style

Noirez, L.; Kahl, P. Exploring “Dormant” Opto-Mechanical Properties of the Isotropic Phase of Liquid Crystals and Revealing Hidden Elasticity of (Ordinary) Liquids. Fluids 2018, 3, 43. https://doi.org/10.3390/fluids3020043

AMA Style

Noirez L, Kahl P. Exploring “Dormant” Opto-Mechanical Properties of the Isotropic Phase of Liquid Crystals and Revealing Hidden Elasticity of (Ordinary) Liquids. Fluids. 2018; 3(2):43. https://doi.org/10.3390/fluids3020043

Chicago/Turabian Style

Noirez, Laurence, and Philipp Kahl. 2018. "Exploring “Dormant” Opto-Mechanical Properties of the Isotropic Phase of Liquid Crystals and Revealing Hidden Elasticity of (Ordinary) Liquids" Fluids 3, no. 2: 43. https://doi.org/10.3390/fluids3020043

APA Style

Noirez, L., & Kahl, P. (2018). Exploring “Dormant” Opto-Mechanical Properties of the Isotropic Phase of Liquid Crystals and Revealing Hidden Elasticity of (Ordinary) Liquids. Fluids, 3(2), 43. https://doi.org/10.3390/fluids3020043

Article Metrics

Back to TopTop