Instability of a Diffusive Boundary Layer beneath a Capillary Transition Zone
Abstract
:1. Introduction
2. Methodology
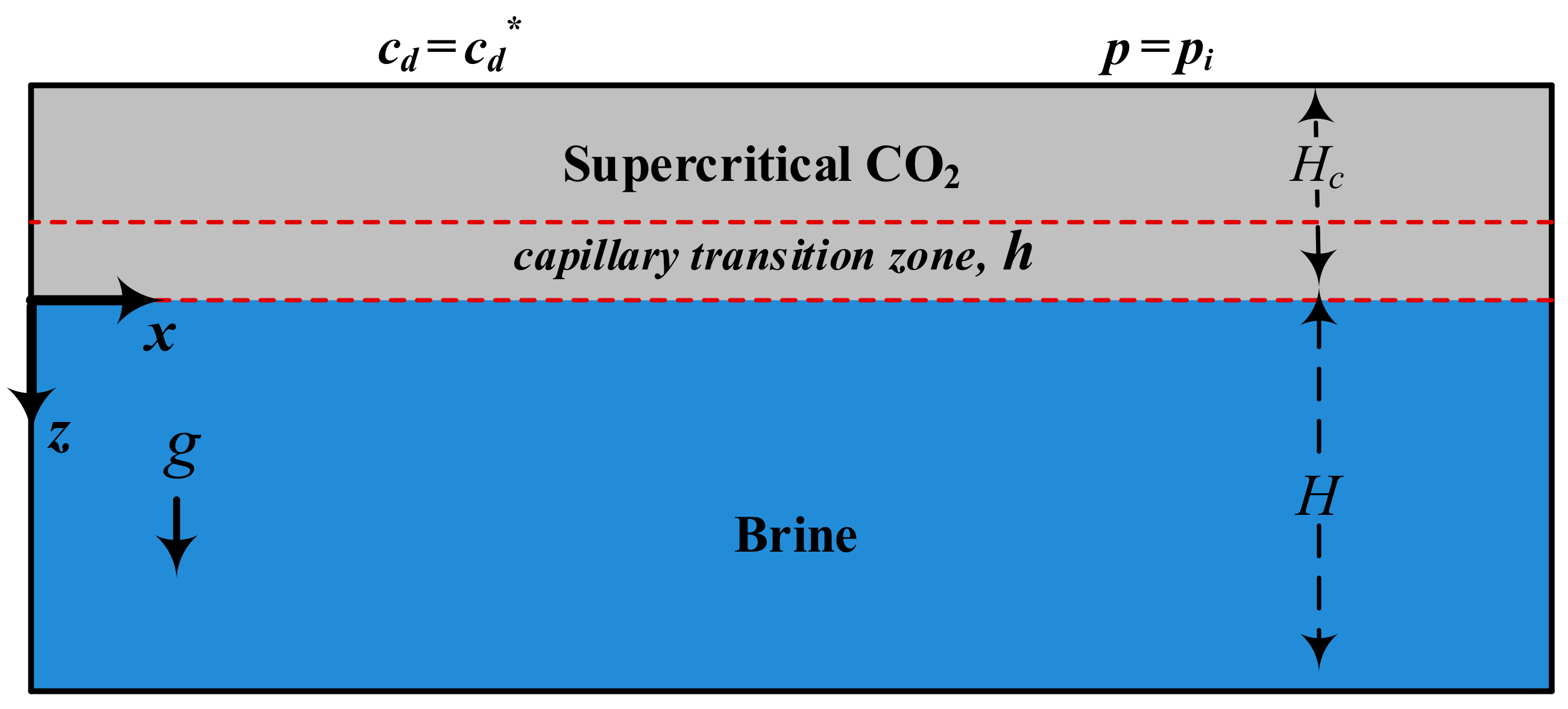
2.1. Conceptual Model
2.2. Governing Equations
2.3. Linear Stability Analysis
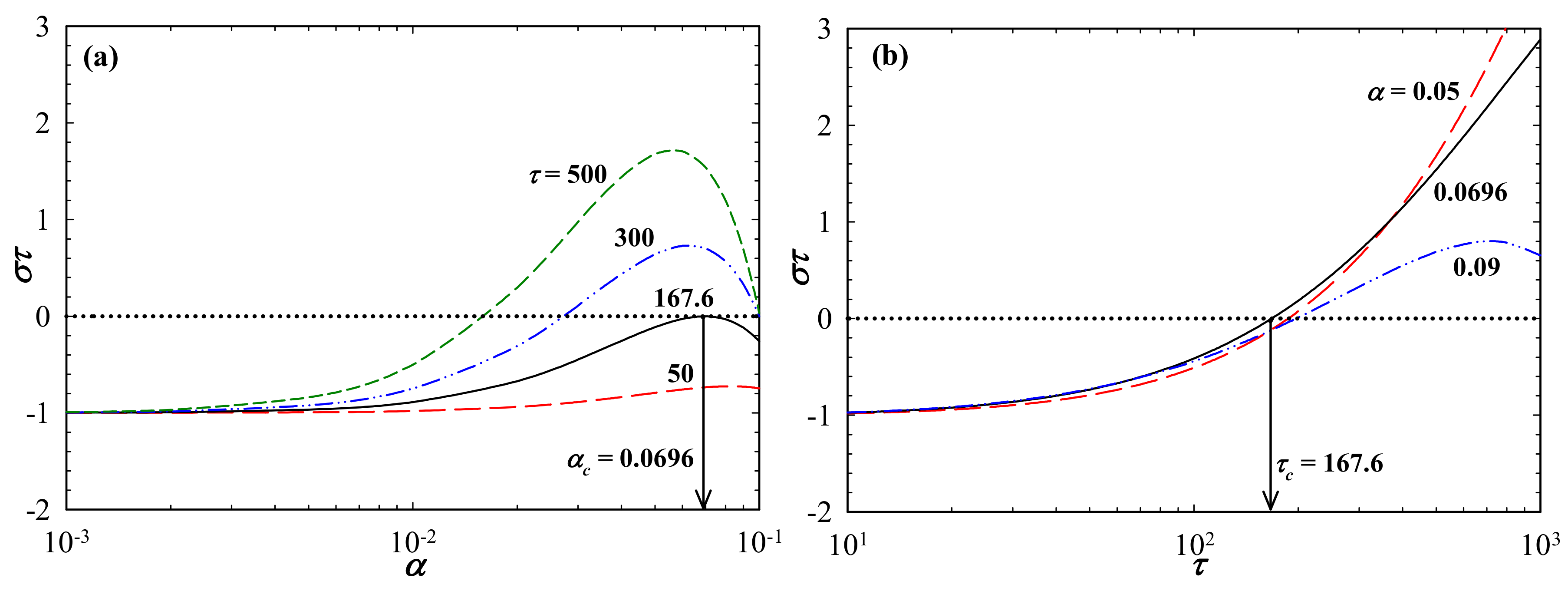
3. Results and Discussions
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Emami-Meybodi, H.; Hassanzadeh, H.; Ennis-King, J. CO2 dissolution in the presence of background flow of deep saline aquifers. Water Resour. Res. 2015, 51, 2595–2615. [Google Scholar] [CrossRef]
- Slim, A.C.; Ramakrishnan, T. Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 2010, 22, 124103. [Google Scholar] [CrossRef]
- Elenius, M.T.; Nordbotten, J.M.; Kalisch, H. Convective mixing influenced by the capillary transition zone. Comput. Geosci. 2014, 18, 417–431. [Google Scholar] [CrossRef]
- Elenius, M.T.; Nordbotten, J.M.; Kalisch, H. Effects of a capillary transition zone on the stability of a diffusive boundary layer. IMA J. Appl. Math. 2012, 77, 771–787. [Google Scholar] [CrossRef]
- Kim, M.C. The effect of boundary conditions on the onset of buoyancy-driven convection in a brine-saturated porous medium. Transp. Porous Med. 2015, 107, 469–487. [Google Scholar] [CrossRef]
- Emami-Meybodi, H.; Hassanzadeh, H. Stability analysis of two-phase buoyancy-driven flow in the presence of a capillary transition zone. Phys. Rev. E 2013, 87, 033009. [Google Scholar] [CrossRef]
- Emami-Meybodi, H.; Hassanzadeh, H. Two-phase convective mixing under a buoyant plume of co2 in deep saline aquifers. Adv. Water Resour. 2015, 76, 55–71. [Google Scholar] [CrossRef]
- Emami-Meybodi, H. Stability analysis of dissolution-driven convection in porous media. Phys. Fluids 2017, 29, 014102. [Google Scholar] [CrossRef]
- Voorhees, P.W. The theory of ostwald ripening. J. Stat. Phys. 1985, 38, 231–252. [Google Scholar] [CrossRef]
- Xu, K.; Bonnecaze, R.; Balhoff, M. Egalitarianism among bubbles in porous media: An ostwald ripening derived anticoarsening phenomenon. Phys. Rev. Lett. 2017, 119, 264502. [Google Scholar] [CrossRef] [PubMed]
- De Chalendar, J.A.; Garing, C.; Benson, S.M. Pore-scale modelling of ostwald ripening. J. Fluid Mech. 2018, 835, 363–392. [Google Scholar] [CrossRef]
- Buchgraber, M.; Kovscek, A.R.; Castanier, L.M. A study of microscale gas trapping using etched silicon micromodels. Transp. Porous Med. 2012, 95, 647–668. [Google Scholar] [CrossRef]
- Loodts, V.; Thomas, C.; Rongy, L.; De Wit, A. Control of convective dissolution by chemical reactions: General classification and application to CO2 dissolution in reactive aqueous solutions. Phys. Rev. Lett. 2014, 113, 114501. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Garcia, J.E. Density of Aqueous Solutions of CO2; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2001. [Google Scholar]
- Chen, Z.; Huan, G.; Ma, Y. Computational Methods for Multiphase Flows in Porous Media; SIAM: Philadelphia, PA, USA, 2006; Volume 2. [Google Scholar]
- Aziz, K.; Settari, A. Petroleum Reservoir Simulation; Applied Science Publication Ltd.: London, UK, 1979. [Google Scholar]
- Yang, C.; Gu, Y. Accelerated mass transfer of CO2 in reservoir brine due to density-driven natural convection at high pressures and elevated temperatures. Ind. Eng. Chem. Res. 2006, 45, 2430–2436. [Google Scholar] [CrossRef]
- Leverett, M. Capillary behavior in porous solids. Trans. AIME 1941, 142, 152–169. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, T. Hydraulic properties of porous media. Hydrol. Pap. Colo. State Univ. 1964, 24, 37. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Li, B.; Tchelepi, H.A.; Benson, S.M. Influence of capillary-pressure models on CO2 solubility trapping. Adv. Water Resour. 2013, 62, 488–498. [Google Scholar] [CrossRef]
- Mualem, Y. Hysteretical models for prediction of the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 1248–1254. [Google Scholar] [CrossRef]
- Ippisch, O.; Vogel, H.-J.; Bastian, P. Validity limits for the van genuchten–mualem model and implications for parameter estimation and numerical simulation. Adv. Water Resour. 2006, 29, 1780–1789. [Google Scholar] [CrossRef]
- McBride-Wright, M.; Maitland, G.C.; Trusler, J.M. Viscosity and density of aqueous solutions of carbon dioxide at temperatures from (274 to 449) K and at pressures up to 100 MPa. J. Chem. Eng. Data 2014, 60, 171–180. [Google Scholar] [CrossRef]
- Hassanzadeh, H.; Pooladi-Darvish, M.; Elsharkawy, A.M.; Keith, D.W.; Leonenko, Y. Predicting pvt data for CO2–brine mixtures for black-oil simulation of CO2 geological storage. Int. J. Greenh. Gas Control 2008, 2, 65–77. [Google Scholar] [CrossRef]
- Lick, W. The instability of a fluid layer with time-dependent heating. J. Fluid Mech. 1965, 21, 565–576. [Google Scholar] [CrossRef]
- Singh, A.K.; Bhadauria, B. Finite difference formulae for unequal sub-intervals using Lagrange’s interpolation formula. Int. J. Math. Anal 2009, 3, 815. [Google Scholar]
- Lin, C.-C.; Segel, L.A. Mathematics Applied to Deterministic Problems in the Natural Sciences; SIAM: Philadelphia, PA, USA, 1988; Volume 1. [Google Scholar]
- Emami-Meybodi, H. Dispersion-driven instability of mixed convective flow in porous media. Phys. Fluids 2017, 29, 094102. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Emami-Meybodi, H. Instability of a Diffusive Boundary Layer beneath a Capillary Transition Zone. Fluids 2018, 3, 85. https://doi.org/10.3390/fluids3040085
Zhang F, Emami-Meybodi H. Instability of a Diffusive Boundary Layer beneath a Capillary Transition Zone. Fluids. 2018; 3(4):85. https://doi.org/10.3390/fluids3040085
Chicago/Turabian StyleZhang, Fengyuan, and Hamid Emami-Meybodi. 2018. "Instability of a Diffusive Boundary Layer beneath a Capillary Transition Zone" Fluids 3, no. 4: 85. https://doi.org/10.3390/fluids3040085
APA StyleZhang, F., & Emami-Meybodi, H. (2018). Instability of a Diffusive Boundary Layer beneath a Capillary Transition Zone. Fluids, 3(4), 85. https://doi.org/10.3390/fluids3040085



