A Correction and Discussion on Log-Normal Intermittency B-Model
Abstract
:1. Introduction
2. Breakage Models
2.1. The Gurvich–Yaglom Model
2.2. B-Model
2.3. B-Model Corrections
2.4. Model Extension
3. Flume Experiment
4. Discussion
4.1. Breakage Coefficient:
4.2. Correction Factor:
4.3. Power Law Coefficient:
4.4. Range of and
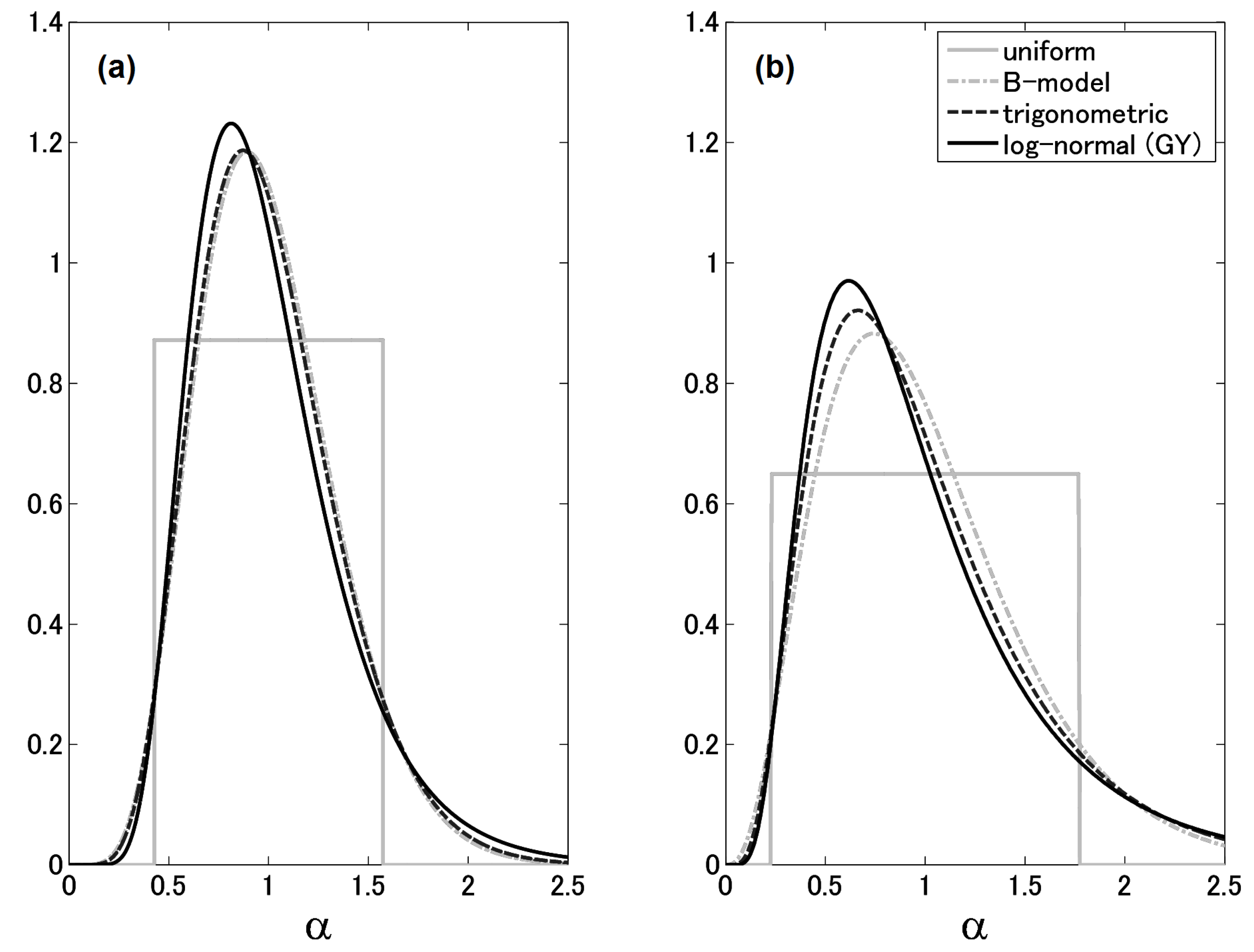
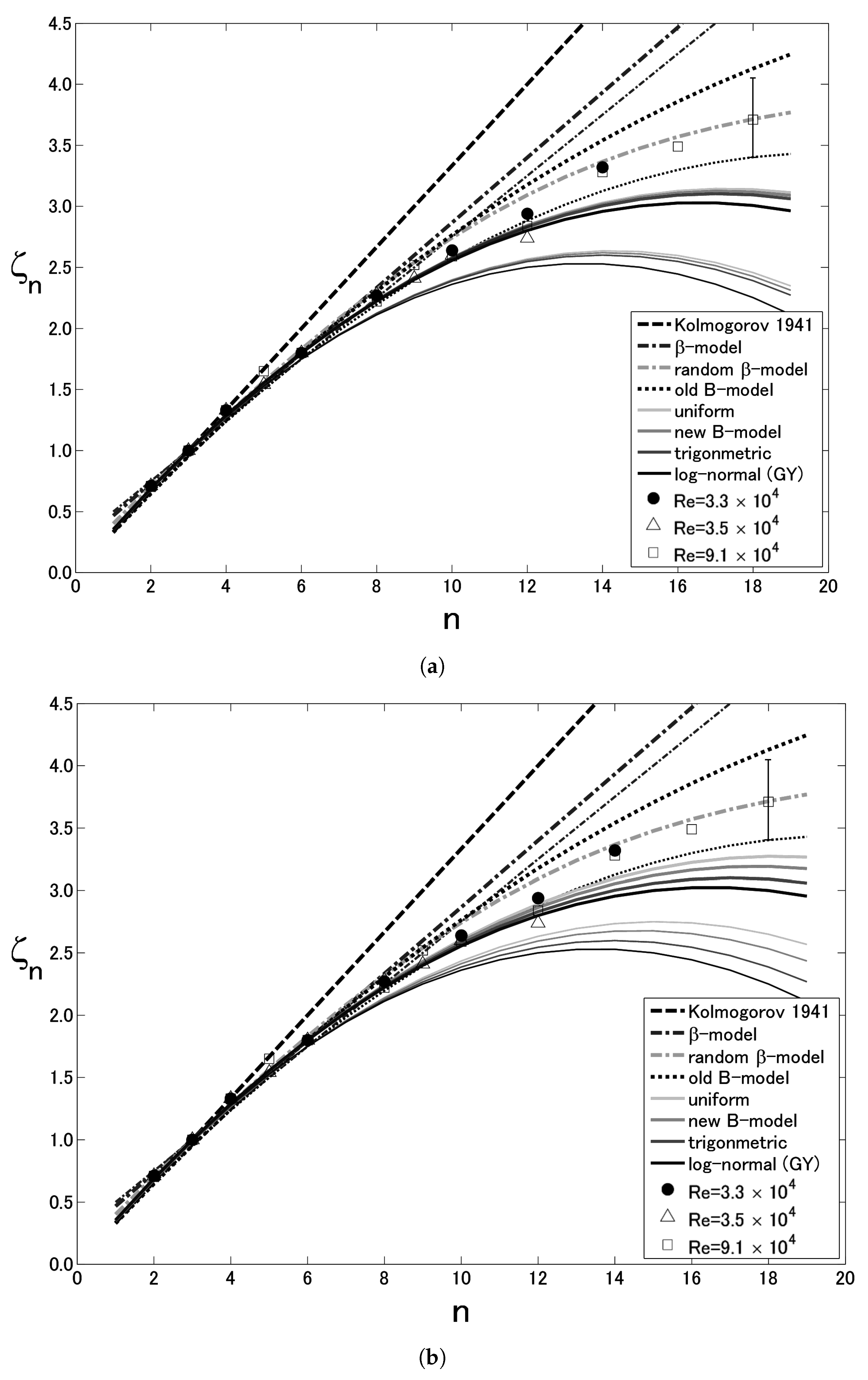
4.5. Model Comparisons
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Speziale, C.G.; Sarkar, S.; Gatski, T.B. Modelling the pressure—Strain correlation of turbulence: An invariant dynamical systems approach. J. Fluid Mech. 1991, 227, 245–272. [Google Scholar] [CrossRef]
- Mishra, A.A.; Girimaji, S.S. Toward approximating non-local dynamics in single-point pressure–strain correlation closures. J. Fluid Mech. 2017, 811, 168–188. [Google Scholar] [CrossRef]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Yamazaki, H. Breakage models: Lognormality and intermittency. J. Fluid Mech. 1990, 219, 181–193. [Google Scholar]
- Frisch, U. The Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Doklady Akad. Nauk SSSR 1941, 30, 299–303. [Google Scholar] [CrossRef]
- Frisch, U. Fully developed turbulence and intermittency. Ann. N. Y. Acad. Sci. 1995, 357, 359–367. [Google Scholar] [CrossRef]
- Gurvich, A.S.; Yaglom, A.M. Breakdown of eddies and probability distributions for small scale turbulence. Phys. Fluids 1967, 10, 59–65. [Google Scholar] [CrossRef]
- Monin, A.S.; Ozmidov, R.V. Turbulence in the Ocean; Springer: Dordrecht, The Netherlands, 1985; p. 247. [Google Scholar]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Batchelor, G.K. The Theory of Homogeneous Turbulence; Cambridge University Press: Cambridge, UK, 1953. [Google Scholar]
- Anselmet, F.; Gagne, Y.; Hopfinger, E.J.; Antonia, R.A. High-order velocity structure functions in turbulent shear flows. J. Fluid Mech. 1984, 140, 63–89. [Google Scholar] [CrossRef]
- Seuront, L.; Yamazaki, H.; Schmitt, F. Intermittency (Chapter 7). In Marine Turbulence: Theories, Observations and Models; Cambridge University Press: Cambridge, UK, 2005; pp. 66–78. [Google Scholar]
- Tennekes, H.; Lumley, J.L. A First Course In Turbulence; MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Saito, Y. Log-gamma distribution model of intermittency in turbulence. J. Phys. Soc. Jpn. 1992, 61, 403–406. [Google Scholar]
- She, Z.-S.; Leveque, E. Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 1994, 72, 336–339. [Google Scholar]
- Frisch, U.; Sulem, P.-L.; Nelkin, M. A simple dynamical model of intermittent fully developed turbulence. J. Fluid Mech. 1978, 87, 719–736. [Google Scholar] [CrossRef]
- Benzi, R.; Paladin, G.; Parisi, G.; Vulpiani, A. On the multifractal nature of fully developed turbulence and chaotic systems. J. Phys. A 1984, 17, 3521–3531. [Google Scholar] [CrossRef] [Green Version]
- Schertzer, D.; Lovejoy, S. On the dimension of atmospheric motions. In Turbulence and Chaotic Phenomena in Fluids; Tatsumi, T., Ed.; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1984; pp. 505–512. [Google Scholar]
- Schertzer, D.; Lovejoy, S. The Dimension and Intermittency of Atmosphereic Dynamics; Springer: Berlin/Heidelberg, Germany, 1985; pp. 7–33. [Google Scholar]
- Meneveau, C.; Sreenivasan, K.R. Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 1987, 59, 1424–1427. [Google Scholar]
- Schertzer, D.; Lovejoy, S. Physical modeling and analysis of rain and clouds by anisotropic scaling multiplicative processes. J. Geophys. Res. 1987, 92, 9693–9714. [Google Scholar] [CrossRef]
- Dubrulle, B. Intermittency in fully developed turbulence: Log-Poisson statistics and generalized scale covariance. Phys. Rev. Lett. 1994, 73, 959–962. [Google Scholar] [CrossRef]
- She, Z.-S.; Waymire, E.C. Quantized energy cascade and log-Poisson statistics in fully developed turbulence. Phys. Rev. Lett. 1995, 74, 262–265. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications; Wiley: New York, NY, USA, 1968; Volume 1. [Google Scholar]
- Benzi, R.; Ciliberto, S.; Baudet, C.; Ruiz Chavarria, G.; Tripiccione, R. Extended self-similarity in the dissipation range of fully developed turbulence. Europhys. Lett. 1993, 24, 275–279. [Google Scholar] [CrossRef]
- Yamazaki, H.; Mitchell, J.G.; Seuront, L.; Wolk, F.; Li, H. Phytoplankton microstructure in fully developed oceanic turbulence. Geophys. Res. Lett. 2006, 33, L01603. [Google Scholar] [CrossRef]
- Benzi, R.; Ciliberto, S.; Baudet, C.; Chavarria, G.R. On the scaling of three-dimensional homogeneous and isotropic turbulence. Phys. D Nonlinear Phenom. 1995, 80, 385–398. [Google Scholar] [CrossRef]
- Ruiz-Chavarria, G.; Baudet, C.; Ciliberto, S. Scaling laws and dissipation scale of a passive scalar in fully developed turbulence. Phys. D Nonlinear Phenom. 1996, 99, 369–380. [Google Scholar] [CrossRef]
- Schmitt, F.; Schertzer, D.; Lovejoy, S.; Brunet, Y. Multifractal temperature and flux of temperature variance in fully developed turbulence. Eur. Phys. Lett. 1996, 34, 195–200. [Google Scholar] [CrossRef]





| Model | |||||
|---|---|---|---|---|---|
| B-model | −0.06250 | −0.07643 | −0.1352 | −0.1634 | |
| 0.1318 | 0.1631 | 0.2961 | 0.3645 | ||
| 0.0049 | 0.0074 | 0.0080 | 0.012 | ||
| Uniform pdf | −0.06124 | −0.07446 | −0.1243 | −0.1475 | |
| 0.1306 | 0.1611 | 0.2853 | 0.3488 | ||
| 0.0059 | 0.0088 | 0.011 | 0.017 | ||
| Trigonometric pdf | −0.06389 | −0.07848 | −0.1485 | −0.1824 | |
| 0.1332 | 0.1651 | 0.3094 | 0.3836 | ||
| 0.0039 | 0.0059 | 0.0039 | 0.0058 | ||
| Log-normal (GY) | −0.06930 | −0.08663 | −0.1609 | −0.2012 | |
| 0.1386 | 0.1733 | 0.3219 | 0.4024 | ||
| 0.000007 | 0.000007 | 0.000003 | 0.000002 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Locke, C.; Seuront, L.; Yamazaki, H. A Correction and Discussion on Log-Normal Intermittency B-Model. Fluids 2019, 4, 35. https://doi.org/10.3390/fluids4010035
Locke C, Seuront L, Yamazaki H. A Correction and Discussion on Log-Normal Intermittency B-Model. Fluids. 2019; 4(1):35. https://doi.org/10.3390/fluids4010035
Chicago/Turabian StyleLocke, Christopher, Laurent Seuront, and Hidekatsu Yamazaki. 2019. "A Correction and Discussion on Log-Normal Intermittency B-Model" Fluids 4, no. 1: 35. https://doi.org/10.3390/fluids4010035
APA StyleLocke, C., Seuront, L., & Yamazaki, H. (2019). A Correction and Discussion on Log-Normal Intermittency B-Model. Fluids, 4(1), 35. https://doi.org/10.3390/fluids4010035







