Efficiently Generating Mixing by Combining Differing Small Amplitude Helical Geometries
Abstract
:1. Introduction
2. Rationale for Combined Helical Geometries
3. Methods
3.1. Geometry and Parameters
3.2. Numerical Methods
3.2.1. Velocity Field Calculation
3.2.2. Particle Tracking
3.3. Methods for Studying Mixing
Entropic Measure
3.4. Poincaré Sections and Residence Time Distributions
4. Results and Discussion
4.1. Idealised Prediction of Mixing
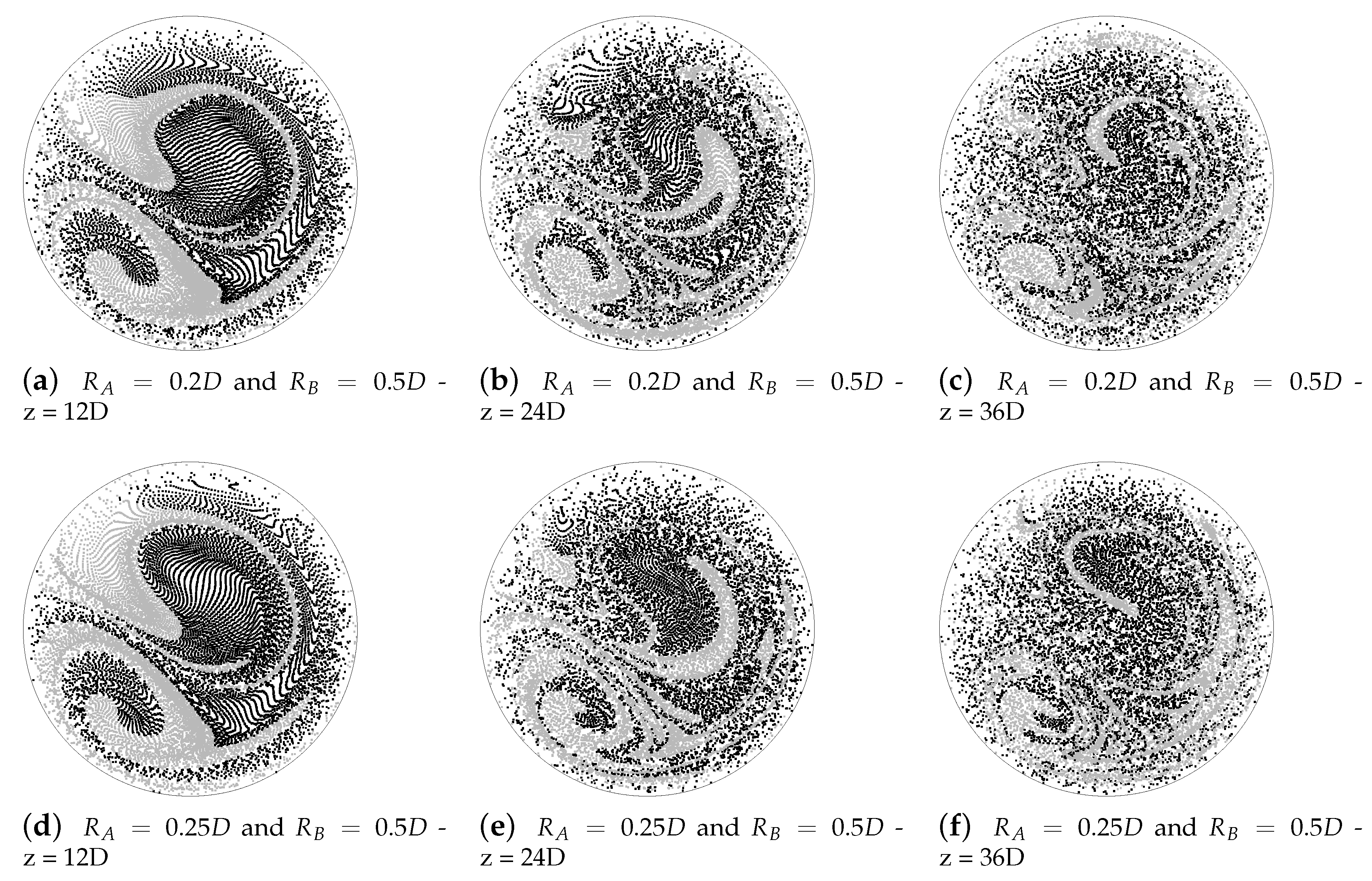
4.1.1. Visual Representation of Mixing Structures
4.1.2. Entropic Measure of Mixing Performance
4.1.3. Poincaré Sections and Residence Times
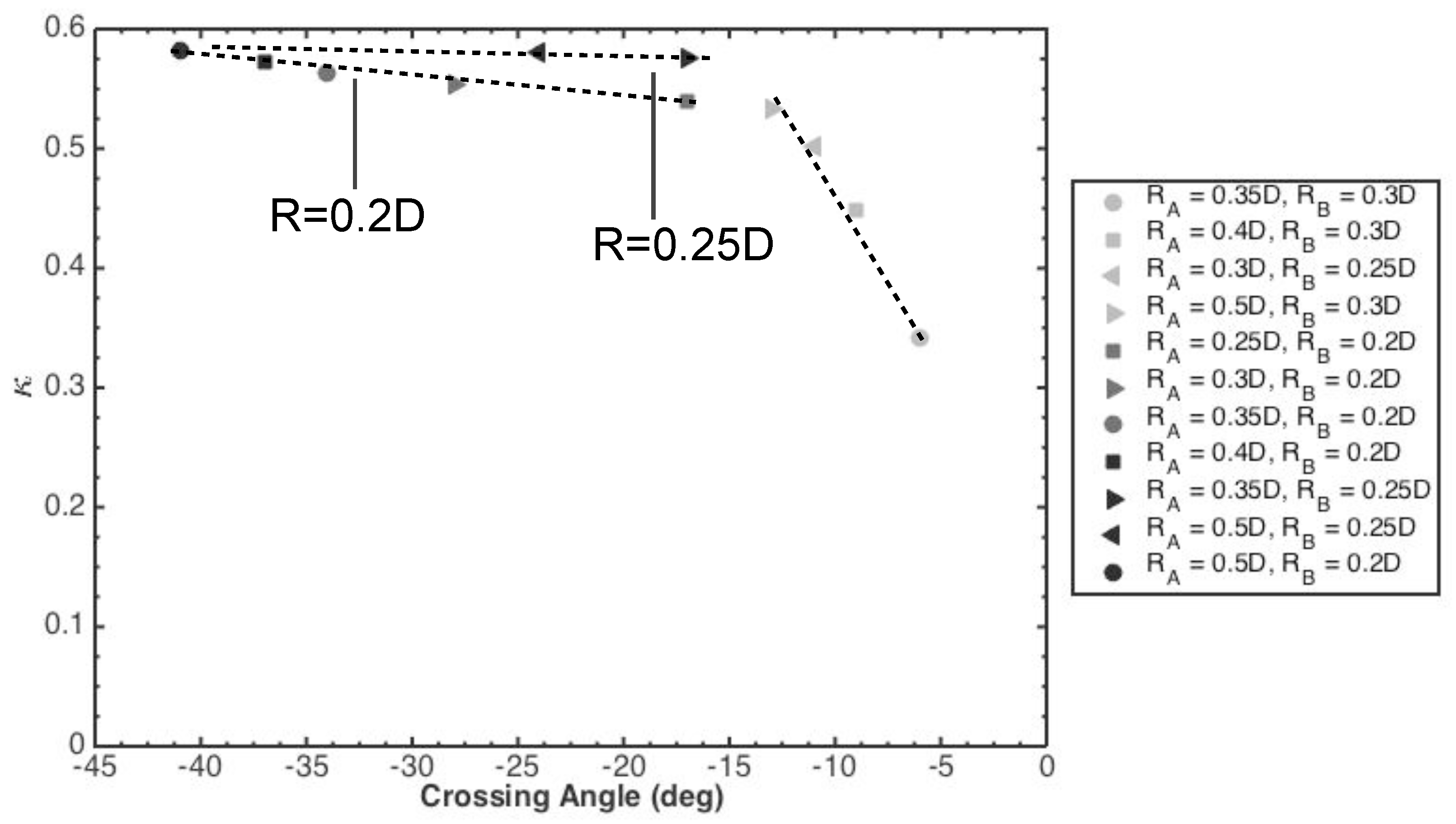
4.1.4. Significance of Crossing Angle
4.2. Comparison of Predicted and Actual Mixing Behaviour of Combined Helical Geometries
4.2.1. Entropic Measure
4.2.2. Axial Pressure Loss
4.3. Poincaré Sections and Residence Times
4.4. Limitations
4.5. Significance for Future Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cookson, A.N.; Doorly, D.J.; Sherwin, S.J. Mixing Through Stirring of Steady Flow in Small Amplitude Helical Tubes. Ann. Biomed. Eng. 2009, 37, 710–721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caro, C.G.; Cheshire, N.J.; Watkins, N. Preliminary comparative study of small amplitude helical and conventional ePTFE arteriovenous shunts in pigs. J. R. Soc. Interface 2005, 2, 261–266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taggart, D.P. Current status of arterial grafts for coronary artery bypass grafting. Ann. Cardiothorac. Surg. 2013, 2, 427–430. [Google Scholar] [PubMed]
- Desai, M.; Seifalian, A.M.; Hamilton, G. Role of prosthetic conduits in coronary artery bypass grafting. Eur. J. Cardio-Thorac. Surg. 2011, 40, 394–398. [Google Scholar] [CrossRef] [PubMed]
- Akoh, J.A. Prosthetic arteriovenous grafts for hemodialysis. J. Vasc. Access 2009, 10, 137–147. [Google Scholar] [CrossRef] [PubMed]
- Murphy, E.A.; Boyle, F.J. Reducing In-Stent Restenosis Through Novel Stent Flow Field Augmentation. Cardiovasc. Eng. Technol. 2012, 3, 353–373. [Google Scholar] [CrossRef] [Green Version]
- Garg, S.; Serruys, P.W. Coronary stents: Current status. J. Am. Coll. Cardiol. 2010, 56, S1–S42. [Google Scholar] [CrossRef] [PubMed]
- Caro, C.G.; Doorly, D.J.; Tarnawski, M.; Scott, K.T.; Long, Q.; Dumoulin, C.L. Non-Planar Curvature and Branching of Arteries and Non-Planar-Type Flow. Proc. Math. Phys. Eng. Sci. 1996, 452, 185–197. [Google Scholar]
- Huijbregts, H.J.T.A.M.; Blankestijn, P.J.; Caro, C.G.; Cheshire, N.J.W.; Hoedt, M.T.C.; Tutein Nolthenius, R.P.; Moll, F.L. A Helical PTFE Arteriovenous Access Graft to Swirl Flow Across the Distal Anastomosis: Results of a Preliminary Clinical Study. Eur. J. Vasc. Endovasc. Surg. 2007, 33, 472–475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Doormaal, M.A.; Ethier, C.R. Design optimization of a helical endothelial cell culture device. Biomech. Model. Mechanobiol. 2010, 9, 523–531. [Google Scholar] [CrossRef] [PubMed]
- Coppola, G.; Caro, C. Arterial geometry, flow pattern, wall shear and mass transport: Potential physiological significance. J. R. Soc. Interface 2009, 6, 519–528. [Google Scholar] [CrossRef]
- Coppola, G.; Caro, C. Oxygen mass transfer in a model three-dimensional artery. J. R. Soc. Interface 2008, 5, 1067–1075. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, K.E.; Lee, J.S.; Yoo, J.Y. A numerical study on steady flow in helically sinuous vascular prostheses. Med. Eng. Phys. 2011, 33, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Ha, H.; Hwang, D.; Choi, W.R.; Baek, J.; Lee, S.J. Fluid-Dynamic Optimal Design of Helical Vascular Graft for Stenotic Disturbed Flow. PLoS ONE 2014, 9, e11104. [Google Scholar] [CrossRef] [PubMed]
- Zheng, T.; Fan, Y.; Xiong, Y.; Jiang, W.; Deng, X. Hemodynamic performance study on small diameter helical grafts. ASAIO J. 2009, 55, 192–199. [Google Scholar] [CrossRef]
- Zheng, T.; Wang, W.; Jiang, W.; Deng, X.; Fan, Y. Assessing hemodynamic performances of small diameter helical grafts: Transient simulation. J. Mech. Med. Biol. 2012, 12, 1250008. [Google Scholar] [CrossRef]
- Van Canneyt, K.; Morbiducci, U.; Eloot, S.; De Santis, G.; Segers, P.; Verdonck, P. A computational exploration of helical arterio-venous graft designs. J. Biomech. 2013, 46, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Stonebridge, P.A.; Vermassen, F.; Dick, J.; Belch, J.J.F.; Houston, G. Spiral Laminar Flow Prosthetic Bypass Graft: Medium-Term Results From a First-In-Man Structured Registry Study. Ann. Vasc. Surg. 2012, 26, 1093–1099. [Google Scholar] [CrossRef]
- El Sayed, H.F.; Davies, M. Early Results of Using the Spiral Flow AV Graft: Is It a Breakthrough Solution to a Difficult Problem? J. Vasc. Surg. 2015, 62, 811. [Google Scholar] [CrossRef]
- Ruiz-Soler, A.; Kabinejadian, F.; Slevin, M.A.; Bartolo, P.J.; Keshmiri, A. Optimisation of a Novel Spiral-Inducing Bypass Graft Using Computational Fluid Dynamics. Sci. Rep. 2017, 7, 1865. [Google Scholar] [CrossRef]
- Kabinejadian, F.; McElroy, M.; Ruiz-Soler, A.; Leo, H.L.; Slevin, M.A.; Badimon, L.; Keshmiri, A. Numerical Assessment of Novel Helical/Spiral Grafts with Improved Hemodynamics for Distal Graft Anastomoses. PLoS ONE 2016, 11, e0165892. [Google Scholar] [CrossRef]
- Caro, C.G.; Seneviratne, A.; Heraty, K.B.; Monaco, C.; Burke, M.G.; Krams, R.; Chang, C.C.; Gilson, P.; Coppola, G. Intimal hyperplasia following implantation of helical-centreline and straight-centreline stents in common carotid arteries in healthy pigs: Influence of intraluminal flow. J. R. Soc. Interface 2013, 10, 20130578. [Google Scholar] [CrossRef]
- Shinke, T.; Mullins, L.P.; O’Brien, N.; Heraty, K.B.; McMahon, T.; Burke, M.G.; Taylor, C.; Gilson, P.; Robinson, K.; Caro, C.G. Abstract 6059: Novel helical stent design elicits swirling blood flow pattern and inhibits neointima formation in porcine carotid arteries. Circulation 2008, 118, S1054. [Google Scholar]
- Zeller, T.; Gaines, P.A.; Ansel, G.M.; Caro, C.G. Helical Centerline Stent Improves Patency: Two-Year Results From the Randomized Mimics Trial. Circ. Cardiovasc. Interv. 2016, 9, e00293. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, T.M.; Zeller, T.; Nakamura, M.; Caro, C.G.; Lichtenberg, M. Swirling Flow and Wall Shear: Evaluating the BioMimics 3D Helical Centerline Stent for the Femoropopliteal Segment. Int. J. Vasc. Med. 2018, 2018, 9795174. [Google Scholar] [CrossRef] [PubMed]
- Rajbanshi, P.; Ghatak, A. Flow through triple helical microchannel. Phys. Rev. Fluids 2018, 3, 024201. [Google Scholar] [CrossRef]
- Ramstack, J.M.; Zuckerman, L.; Mockros, L.F. Shear-induced activation of platelets. J. Biomech. 1979, 12, 113–125. [Google Scholar] [CrossRef]
- Jones, S.W.; Thomas, O.M.; Aref, H. Chaotic advection by laminar flow in a twisted pipe. J. Fluid Mech. 1989, 209, 335–357. [Google Scholar] [CrossRef]
- Aref, H. Stirring by chaotic advection. J. Fluid Mech. 1984, 143, 1–21. [Google Scholar] [CrossRef]
- Sturman, R.; Ottino, J.M.; Wiggins, S. The Mathematical Foundations of Mixing: The Linked Twist Map as a Paradigm in Applications: Micro to Macro, Fluids to Solids; Cambridge University Press: Cambridg, UK, 2006. [Google Scholar]
- Sturman, R.; Wiggins, S. Eulerian indicators for predicting and optimizing mixing quality. New J. Phys. 2009, 11, 075031. [Google Scholar] [CrossRef] [Green Version]
- McIlhany, K.L.; Wiggins, S. Eulerian indicators under continuously varying conditions. Phys. Fluids 2012, 24, 073601. [Google Scholar] [CrossRef]
- Galaktionov, O.; Anderson, P.; Peters, G.; Meijer, H. Analysis and optimization of Kenics static mixers. Int. Polym. Process. 2003, 18, 138–150. [Google Scholar] [CrossRef]
- Qian, S.; Bau, H.H. A Chaotic Electroosmotic Stirrer. Anal. Chem. 2002, 74, 3616–3625. [Google Scholar] [CrossRef]
- Moore, J.A.; Steinman, D.A.; Prakash, S.; Johnston, K.W.; Ethier, C.R. A Numerical Study of Blood Flow Patterns in Anatomically Realistic and Simplified End-to-Side Anastomoses. J. Biomech. Eng. 1999, 121, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Sherwin, S.J.; Shah, O.; Doorly, D.J.; Peiro, J.; Papaharilaou, Y.; Watkins, N.; Caro, C.G.; Dumoulin, C.L. The Influence of Out-of-Plane Geometry on the Flow Within a Distal End-to-Side Anastomsis. ASME J. Biomech. 2000, 122, 86–95. [Google Scholar] [CrossRef]
- Cookson, A.N.; Doorly, D.J.; Sherwin, S.J. Using coordinate transformation of Navier-Stokes equations to solve flow in multiple helical geometries. J. Comput. Appl. Math. 2009, 234, 2069–2079. [Google Scholar] [CrossRef]
- Koberg, W.H. Turbulence Control for Drag Reduction with Active Wall Deformation. Ph.D. Thesis, Imperial College London, London, UK, 2008. [Google Scholar]
- Darekar, R.M.; Sherwin, S.J. Flow Past a Bluff Body With A Wavy Stagnation Face. J. Fluids Struct. 2001, 15, 587–596. [Google Scholar] [CrossRef]
- Darekar, R.M.; Sherwin, S.J. Flow past a square-section cylinder with a wavy stagnation face. J. Fluid Mech. 2001, 426, 263–295. [Google Scholar] [CrossRef] [Green Version]
- Newman, D. A Computational Study of Fluid/Structure Interactions: Flow-Induced Vibrations of a Flexible Cable. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1996. [Google Scholar]
- Evangelinos, C. Parallel Spectral/hp Methods and Simulations of Flow/Structure Interactions. Ph.D. Thesis, Brown University, Providence, RI, USA, 1999. [Google Scholar]
- Sherwin, S.J.; Karniadakis, G.E. Spectral/hp Element Methods for Computational Fluid Dynamics; Oxford Science Publications: Oxford, UK, 2005. [Google Scholar]
- Doorly, D.J.; Sherwin, S.J.; Franke, P.T.; Peiro, J. Vortical flow structure identification and flow transport in arteries. Comput. Methods Biomech. Biomech. Eng. 2002, 5, 261–275. [Google Scholar] [CrossRef] [PubMed]
- Coppola, G.; Sherwin, S.J.; Peiro, J. Non-linear particle tracking for high-order elements. J. Comput. Phys. 2001, 172, 356–386. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wang, W.; Manas-Zloczower, I.; Kaufman, M. Entropic characterization of distributive mixing in polymer processing equipment. AIChE J. 2003, 49, 1637–1644. [Google Scholar] [CrossRef]
- Kang, T.G.; Kwon, T.H. Colored particle tracking method for mixing analysis of chaotic micromixers. J. Micromech. Microeng. 2004, 14, 891. [Google Scholar] [CrossRef]
- Nielsen, L.B. Transfer of low density lipoprotein into the arterial wall and risk of atherosclerosis. Atherosclerosis 1996, 123, 1–15. [Google Scholar] [CrossRef]
- Danckwerts, P.V. The Definition and Measurement of Some Characteristic Mixtures. Appl. Sci. Res. 1952, A3, 279. [Google Scholar] [CrossRef]
- Khakhar, D.V.; Franjione, J.G.; Ottino, J.M. A case study chaotic mixing in deterministic flows: The partitioned pipe mixer. Chem. Eng. Sci. 1987, 42, 2909–2926. [Google Scholar] [CrossRef]
- Mezic, I.; Wiggins, S.; Betz, D. Residence-time distributions for chaotic flows in pipes. Chaos 1999, 9, 173–182. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedman, M.H. Arteriosclerosis research using vascular flow models: From 2-D branches to compliant replicas. J. Biomech. Eng. 1993, 115, 595–601. [Google Scholar] [CrossRef]
- Doorly, D.J. Flow Transport In Arteries. In Cardiovascular Flow Modelling and Measurement with Application to Clinical Medicine; Sajjadi, S.G., Nash, G.B., Rampling, M.W., Eds.; Oxford University Press: Oxford, UK, 1999; pp. 67–81. [Google Scholar]














| (D) | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 | |
|---|---|---|---|---|---|---|---|---|
| (D) | ||||||||
| 0.2 | 0 | 17 | 28 | 34 | 37 | 40 | 41 | |
| 0.25 | −17 | 0 | 11 | 17 | 20 | 23 | 24 | |
| 0.3 | −28 | −11 | 0 | 6 | 9 | 12 | 13 | |
| 0.35 | −34 | −17 | −6 | 0 | 3 | 6 | 7 | |
| 0.4 | −37 | −20 | −9 | −3 | 0 | 3 | 4 | |
| 0.45 | −40 | −23 | −12 | −6 | −3 | 0 | 1 | |
| 0.5 | −41 | −24 | −13 | −7 | −4 | −1 | 0 | |
| Helix A (D) | 0.25 | 0.3 | 0.3 | 0.35 | 0.35 | 0.35 | 0.4 | 0.4 | 0.5 | 0.5 | 0.5 |
| Helix B (D) | 0.2 | 0.2 | 0.25 | 0.2 | 0.25 | 0.3 | 0.2 | 0.3 | 0.2 | 0.25 | 0.3 |
| — Predicted | — Actual | — Increase | ||
|---|---|---|---|---|
| 0.2D | 0.5D | 2.08 | 2.21 | 5.86% |
| 0.25D | 0.5D | 2.22 | 2.26 | 1.76% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cookson, A.N.; Doorly, D.J.; Sherwin, S.J. Efficiently Generating Mixing by Combining Differing Small Amplitude Helical Geometries. Fluids 2019, 4, 59. https://doi.org/10.3390/fluids4020059
Cookson AN, Doorly DJ, Sherwin SJ. Efficiently Generating Mixing by Combining Differing Small Amplitude Helical Geometries. Fluids. 2019; 4(2):59. https://doi.org/10.3390/fluids4020059
Chicago/Turabian StyleCookson, Andrew N., Denis J. Doorly, and Spencer J. Sherwin. 2019. "Efficiently Generating Mixing by Combining Differing Small Amplitude Helical Geometries" Fluids 4, no. 2: 59. https://doi.org/10.3390/fluids4020059






