Geophysical Equatorial Edge Wave with Underlying Currents in the f-Plane Approximation
Abstract
:1. Introduction
2. Governing Equations
3. An Exact Solution in the Lagrangian Description
4. Discussion
4.1. Wave Phase Celerity
4.2. Vorticity
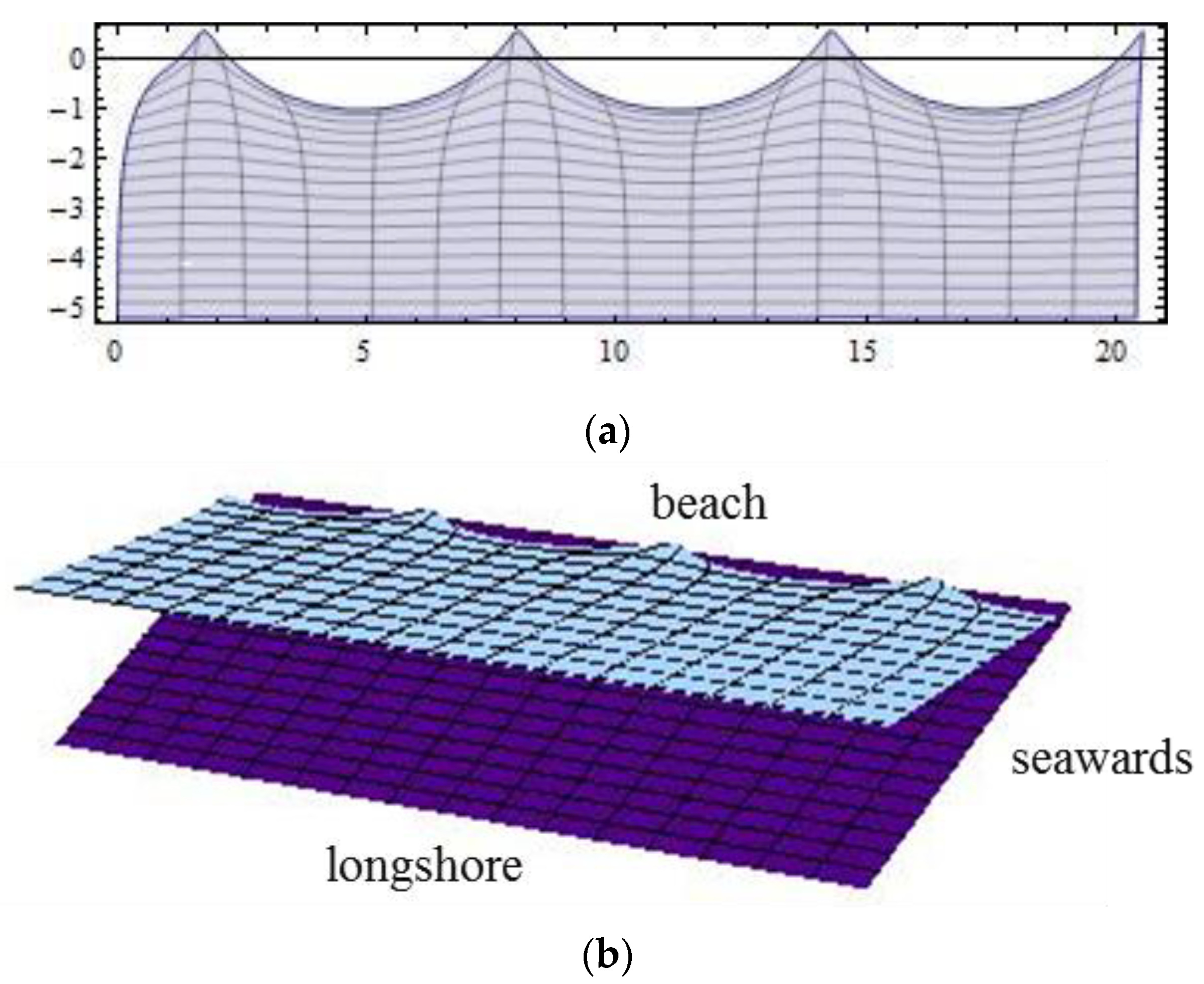
4.3. Run-Up Pattern
4.4. Amplitude of the Equatorial Edge Wave with Longshore Currents
4.5. Mass Transport Velocity
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Leblond, P.H.; Mysak, L.A. Waves in the Ocean; Elsevier: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Komar, P. Beach Processes and Sedimentation; Prentice-Hall: Englewood Cliffs, NJ, USA, 1998. [Google Scholar]
- Stokes, G.G. Report on recent researches in hydrodynamics. In Report of the British Association for the Advancement of Science; John Murray: London, UK, 1846; pp. 1–20. [Google Scholar]
- Lamb, H. Hydrodynamics; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Ursell, F. Edge waves on a sloping beach. Proc. R. Soc. Lond. Ser. A 1952, 214, 79–97. [Google Scholar]
- Ehrenmark, U. Oblique wave incidence on a plane beach: The classical problem revisited. J. Fluid Mech. 1998, 368, 291–319. [Google Scholar] [CrossRef]
- Whitham, G.B. Nonlinear effects in edge waves. J. Fluid Mech. 1976, 74, 353–368. [Google Scholar] [CrossRef] [Green Version]
- Yeh, H. Nonlinear progressive edge waves: Their instability and evolution. J. Fluid Mech. 1985, 152, 479–499. [Google Scholar] [CrossRef]
- Ehrnstrom, M.; Escher, J.; Matioc, B.-V. Two-dimensional stead edge waves. Wave Motion 2009, 46, 363–371. [Google Scholar] [CrossRef]
- Johnson, R.S. Edge waves: Theories past and present. Philos. Trans. R. Soc. Lond. A 2007, 365, 2359–2376. [Google Scholar] [CrossRef]
- Yih, C. Note on edge waves in a stratified fluid. J. Fluid Mech. 1966, 24, 765–767. [Google Scholar] [CrossRef]
- Mollo-Christensen, E. Allowable discontinuities in a Gerstner wave field. Phys. Fluids 1982, 25, 586–587. [Google Scholar] [CrossRef]
- Gerstner, F. Theorie der Wellen samt einer daraus abgeleiteten Theorie der Deichprofile (in German). Ann. Phys. 1809, 2, 412–445. [Google Scholar] [CrossRef]
- Constantin, A. An exact solution for equatorially trapped waves. J. Geophys. Res. Ocean. 2012, 117, C05029. [Google Scholar] [CrossRef]
- Constantin, A. Some three-dimensional nonlinear equatorial flows. J. Phys. Oceanogr. 2013, 43, 165–175. [Google Scholar] [CrossRef]
- Constantin, A. Some nonlinear, equatorially trapped, nonhydrostatic internal geophysical waves. J. Phys. Oceanogr. 2014, 44, 781–789. [Google Scholar] [CrossRef]
- Henry, D. An exact solution for equatorial geophysical water waves with an underlying current. Eur. J. Mech. B Fluids 2013, 38, 18–21. [Google Scholar] [CrossRef]
- Henry, D. Equatorially trapped nonlinear water waves in a β-plane approximation with centripetal forces. J. Fluid Mech. 2016, 804, R1. [Google Scholar] [CrossRef]
- Henry, D. A modified equatorial β-plane approximation modelling nonlinear wave-current interactions. J. Differ. Equ. 2017, 263, 2554–2566. [Google Scholar] [CrossRef]
- Kluczek, M. Exact and explicit internal equatorial water waves with underlying currents. J. Math. Fluid Mech. 2017, 19, 305–314. [Google Scholar] [CrossRef]
- Rodríguez-Sanjurjo, A. Internal equatorial water waves and wave-current interactions in the f-plane. Mon. Math. 2018, 186, 685–701. [Google Scholar] [CrossRef]
- Constantin, A. Edge waves along a sloping beach. J. Phys. A 2001, 34, 9723–9731. [Google Scholar] [CrossRef]
- Matioc, A.V. An exact solution for geophysical equatorial edge waves over a sloping beach. J. Phys. A 2012, 45, 365501. [Google Scholar] [CrossRef] [Green Version]
- Ionescu-Kruse, D. An exact solution for geophysical edge waves in the f-plane approximation. Nonlinear Anal. Real World Appl. 2015, 24, 190–195. [Google Scholar] [CrossRef]
- Fan, L.; Gao, H. Instability of equatorial edge waves in the background flow. Proc. Am. Math. Soc. 2017, 145, 765–778. [Google Scholar] [CrossRef]
- Howd, P.A.; Bowen, A.J.; Holman, R.A. Edge waves in the presence of strong longshore currents. J. Geophys. Res. 1992, 97, 11357–11371. [Google Scholar] [CrossRef]
- Constantin, A. On the deep water wave motion. J. Phys. A 2001, 34, 1405–1417. [Google Scholar] [CrossRef]
- Henry, D. On Gerstner’s water wave. J. Nonlinear Math. Phys. 2008, 15, 87–95. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Beckers, J.-M. Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects; Academic Press: Waltham, MA, USA, 2011. [Google Scholar]
- Constantin, A. On the modelling of equatorial waves. Geophys. Res. Lett. 2012, 39, L05602. [Google Scholar] [CrossRef]
- Constantin, A. The trajectories of particles in Stokes waves. Invent. Math. 2006, 166, 523–535. [Google Scholar] [CrossRef]
- Henry, D. On the deep-water Stokes flow. Int. Math. Res. Not. 2008, 2008. [Google Scholar] [CrossRef]
- Constantin, A.; Strauss, W. Pressure beneath a Stokes wave. Commun. Pure Appl. Math. 2010, 53, 533–557. [Google Scholar] [CrossRef]
- Inman, D.L.; Guza, R.T. The origin of swash cusps on beaches. Mar. Geol. 1982, 49, 133–148. [Google Scholar] [CrossRef]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, H.-C. Geophysical Equatorial Edge Wave with Underlying Currents in the f-Plane Approximation. Fluids 2019, 4, 118. https://doi.org/10.3390/fluids4030118
Hsu H-C. Geophysical Equatorial Edge Wave with Underlying Currents in the f-Plane Approximation. Fluids. 2019; 4(3):118. https://doi.org/10.3390/fluids4030118
Chicago/Turabian StyleHsu, Hung-Chu. 2019. "Geophysical Equatorial Edge Wave with Underlying Currents in the f-Plane Approximation" Fluids 4, no. 3: 118. https://doi.org/10.3390/fluids4030118



