Meshless Modeling of Flow Dispersion and Progressive Piping in Poroelastic Levees †
Abstract
:1. Introduction
1.1. Background
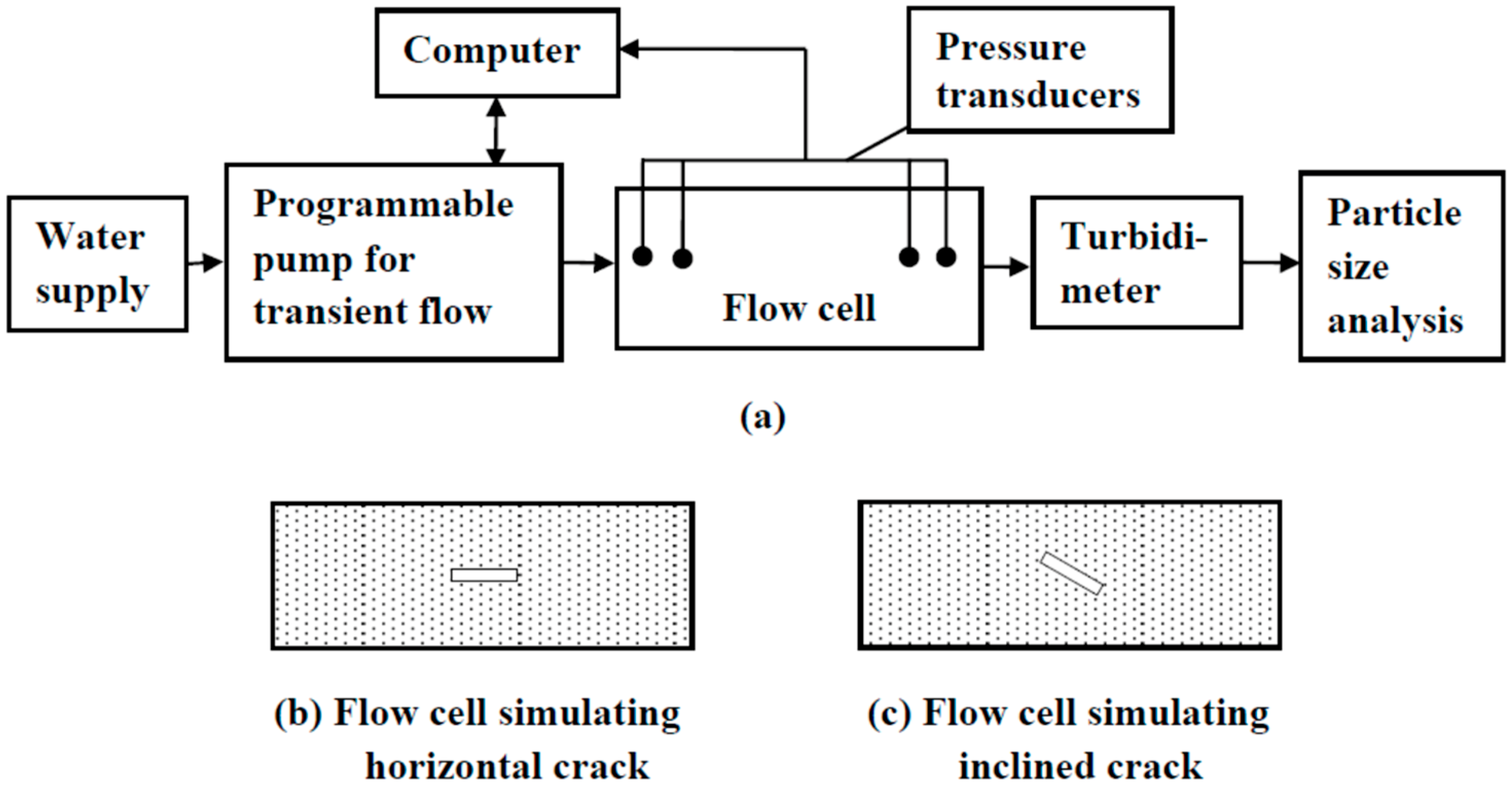
1.2. Experimental Investigations of Progressive Piping
1.3. Numerical Modeling
2. Materials and Methods
2.1. Mathematical Model and Governing Equations
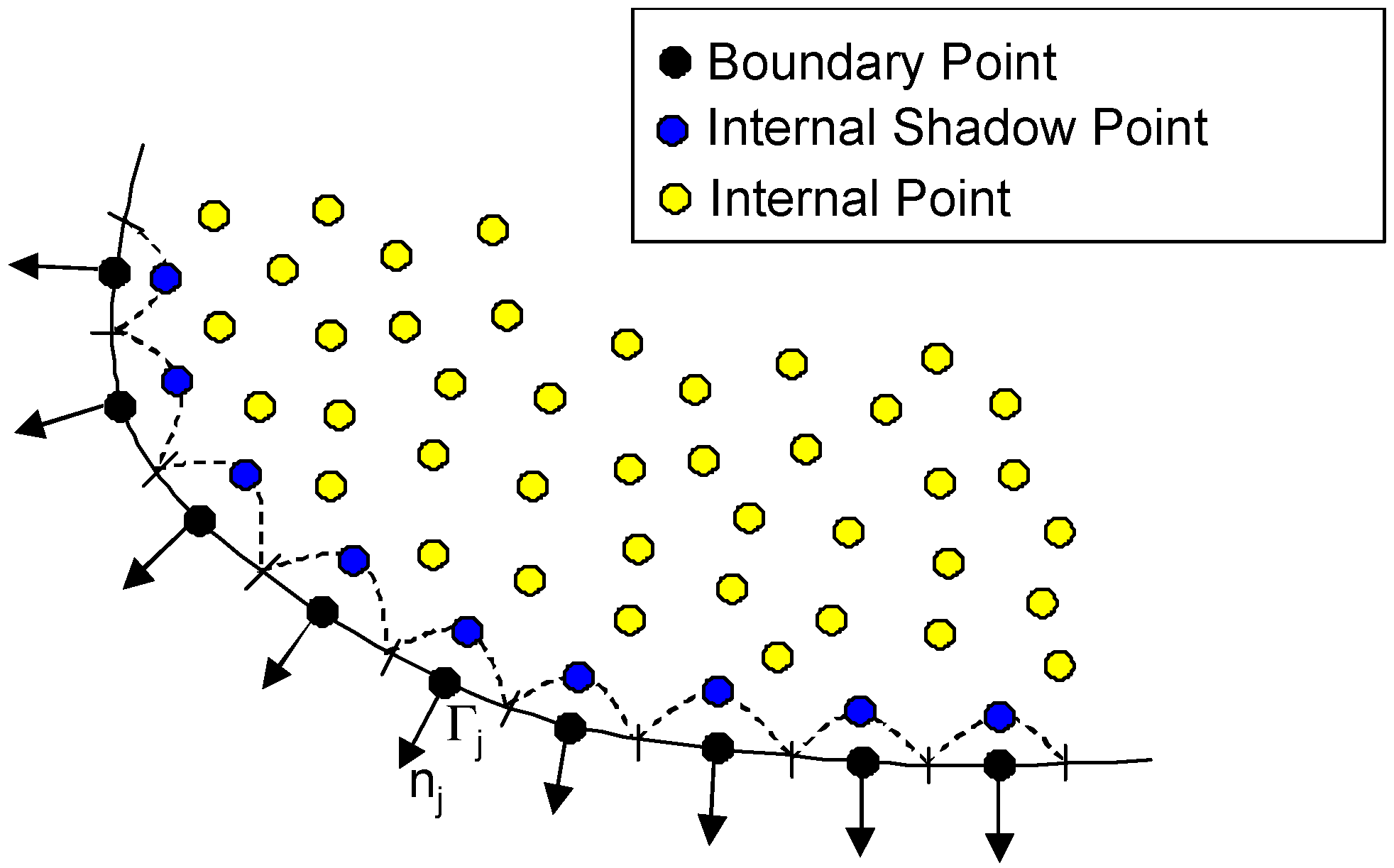
2.2. Localized Collocation Meshless Method Formulation
2.3. Up-Winding Schemes
3. Results
3.1. Dam-Breaking Problem
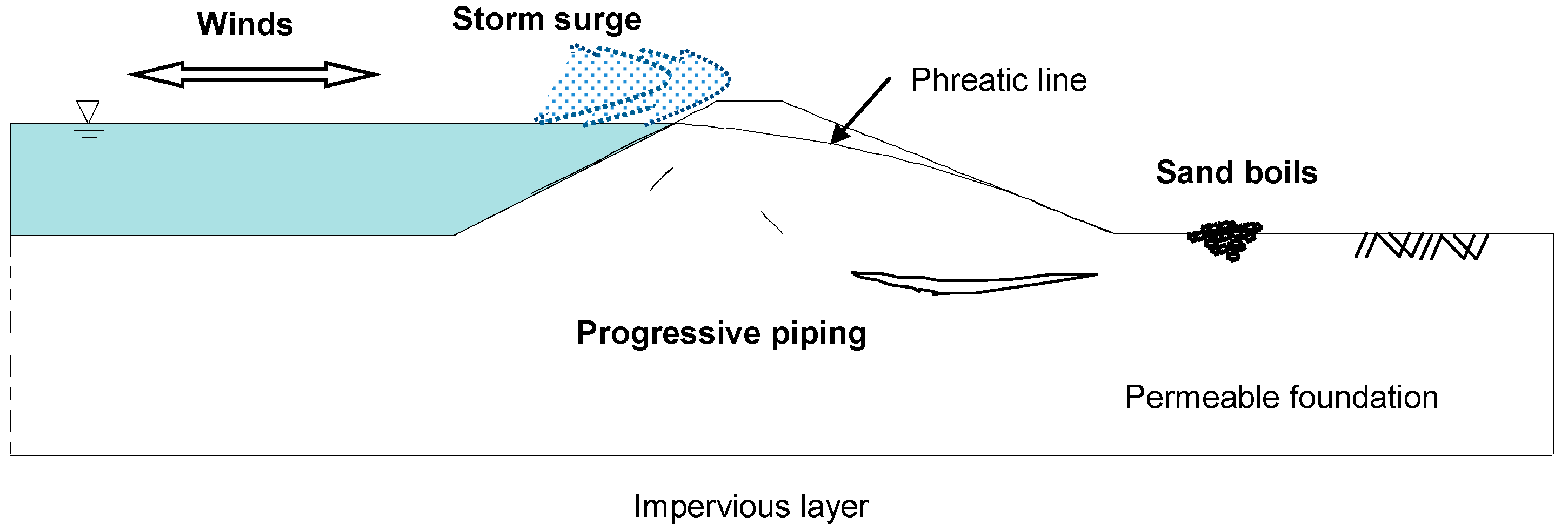
3.2. The Levee Problem
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- (i)
- First-order:
- (ii)
- Second-order:
- (iii)
- Third-order:
References
- ICOLD. Dam Failures—Statistical Analysis; Bulletin 99; International Commission on Large Dams: Paris, France, 1995; pp. 30–31. [Google Scholar]
- Foster, M.; Fell, R.; Spannagle, M. The statistics of embankment dam failures and accidents. Candian Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
- Zaslavsky, D.; Kassiff, G. Formulation of piping mechanism in cohesive soils. Geotechnique 1965, 15, 305–316. [Google Scholar] [CrossRef]
- Vallejo, L.E. Shear stress and the hydraulic fracturing of earth dam soils. Soils Found. 1993, 33, 14–27. [Google Scholar] [CrossRef]
- Kakuturu, S.; Reddi, L.N. Mechanistic Model for Self-Healing of Core Cracks in Earth Dams. ASCE J. Geotech. Geoenviron. Eng. 2006, 132, 890–901. [Google Scholar] [CrossRef]
- Zhang, L.M.; Chen, Q. Seepage failure mechanism of the Gouhou rockfill dam during reservoir water infiltration. Soils Found. 2006, 46, 557–568. [Google Scholar] [CrossRef]
- Lakshmikantha, M.R.; Prat, P.C.; Ledesma, A. An experimental study of cracking mechanisms in drying soils. In Proceedings of the 5th ICEG Environmental Geotechnics: Opportunities, Challenges and Responsibilities, Wales, UK, 26–30 June 2006; Volume 1, pp. 533–540. [Google Scholar]
- Watts, R.; Burk, K.; McLaren, M.; Wolfe, J.; Zender, K. Failure of the Teton dam: Geotechnical aspects. Int. Water Power Dam Constr. 2002, 54, 30–31. [Google Scholar]
- Evans, J.E.; Scuddkr, D.M.; Gottgens, J.F.; Gill, W.M. Lessons from a Dam Failure. Ohio J. Sci. 2000, 100, 121–131. [Google Scholar]
- Mansur, C.I.; Postol, G.; Salley, J.R. Performance of relief well systems along Mississippi River levees. J. Geotech. Geoenviron. Eng. 2000, 126, 727–738. [Google Scholar] [CrossRef]
- Sills, G.L.; Vroman, N.D.; Wahl, R.E.; Schwanz, N.T. Overview of New Orleans levee failures: Lessons learned and their impact on national levee design and assessment. J. Geotech. Geoenviron. Eng. 2008, 134, 556–565. [Google Scholar] [CrossRef]
- Hagerty, D.J. Piping/sapping erosion. I: Basic considerations. J. Hydraul. Eng. 1991, 117, 991–1008. [Google Scholar]
- Hagerty, D.J. Piping/sapping erosion. II: Identification-diagnosis. J. Hydraul. Eng. 1991, 117, 1009–1025. [Google Scholar] [CrossRef]
- Gattinoni, P.; Francani, V. A Tool for Modeling Slope Instability Triggered by Piping. World Acad. Sci. Eng. Technol. 2009, 56, 471–477. [Google Scholar]
- Johansen, P.M.; Eikevik, J.H. Internal erosion and rehabilitation of Jukla rockfill dams. Int. Congr. Large Dams 1997, 19, 245–253. [Google Scholar]
- Chen, C.; Liu, J.; Xia, J.; Li, Z. Integrated geophysical techniques in detecting hidden dangers in river embankments. J. Environ. Eng. Geophys. 2006, 11, 83–94. [Google Scholar] [CrossRef]
- Sjödahl, P. Resistivity Investigation and Monitoring for Detection of Internal Erosion and Anomalous Seepage in Embankment Dams. Ph.D. Thesis, Engineering Geology, Lund University, Sweden, 2006. [Google Scholar]
- Inazaki, T. Integrated geophysical investigation for the vulnerability assessment of earthen levee. In Proceedings of the Symposium on the Application of Geophysics to Environmental and Engineering Problems (SAGEEP), Denver, CO, USA, 1–5 April 2007. [Google Scholar]
- Rucker, M.L.; Greenslade, M.D.; Weeks, R.E.; Fergason, K.C.; Panda, B. Geophysical and remote sensing characterization to mitigate McMicken Dam. In Proceedings of the GeoCongress 2008: Geosustainability and Geohazard Mitigation, GSP, New Orleans, LA, USA, 9–12 March 2008; Volume 178, pp. 207–214. [Google Scholar]
- Hung, M.-H.; Lauchle, G.C.; Wang, M.C. Seepage-Induced Acoustic Emission in Granular Soils. J. Geotech. Geoenviron. Eng. 2009, 135, 566–572. [Google Scholar] [CrossRef]
- Williams, G.W. Seepage studies using tracers and the self potential test. In Use of In Situ Tests in Geotechnical Engineering; ASCE Geotechnical Special Publication: Reston, VA, USA, 1986; Volume 6, pp. 1134–1149. [Google Scholar]
- Holden, J. Hydrological connectivity of soil pipes determined by Ground Penetrating Radar tracer detection. Earth Surf. Process. Landf. 2004, 29, 437–442. [Google Scholar] [CrossRef]
- Wang, X.-J.; Chen, J.-S. Research of temperature tracer method to detect tubular leakage passage in earth-dam. J. China Univ. Min. Technol. 2006, 16, 353–358. [Google Scholar]
- Lee, J.-Y.; Kim, H.-S.; Choi, Y.-K.; Kim, J.-W.; Cheon, J.-Y.; Yi, M.-J. Sequential tracer tests for determining water seepage paths in a large rockfill dam, Nakdong River basin, Korea. Eng. Geol. 2007, 89, 300–315. [Google Scholar] [CrossRef]
- Sellmeijer, J.B.; Koenders, M.A. A mathematical model for piping. Appl. Math. Model. 1991, 15, 646–651. [Google Scholar] [CrossRef]
- Ojha, C.S.P.; Singh, V.P.; Adrian, D.D. Influence of porosity on piping models of levee failure. J. Geotech. Geoenviron. Eng. 2001, 127, 1071–1074. [Google Scholar] [CrossRef]
- Ojha, C.S.P.; Singh, V.P.; Adrian, D.D. Determination of critical head in soil piping. J. Hydraul. Eng. 2003, 129, 511–518. [Google Scholar] [CrossRef]
- Bonelli, S.; Brivois, O.; Borghi, R.; Benahmed, N. Observation, analysis and modeling in complex fluid media—On the modeling of piping erosion. C. R. Mec. 2006, 334, 555–559. [Google Scholar] [CrossRef]
- El Shamy, U.; Aydin, F. Multi-scale modeling of flood-induced piping in river levees. J. Geotech. Geoenviron. Eng. 2008, 134, 1385–1389. [Google Scholar] [CrossRef]
- Bonelli, S.; Brivois, O. The scaling law in the hole erosion test with a constant pressure drop. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1573–1595. [Google Scholar] [CrossRef]
- Fell, R.; Wan, C.F.; Cyganiewicz, J.; Foster, M. Time for Development of Internal Erosion and Piping in Embankment Dams. ASCE J. Geotech. Geoenviron. Eng. 2003, 129, 307–314. [Google Scholar] [CrossRef]
- Ozkan, S.; Adrian, D.D.; Sills, G.L.; Singh, V.P. Transient Head Development due to Flood Induced Seepage under Levees. ASCE J. Geotech. Geoenviron. Eng. 2008, 134, 781–789. [Google Scholar] [CrossRef]
- Yi, C.; Wang, B.; Jin, M.; Guo, Z. Two-dimensional simulation of underground seepage in a dangerous piping zone of the Jingjiang Great Levee, the middle reach of the Yangtze River. Q. J. Eng. Geol. Hydrogeol. 2007, 40, 85–92. [Google Scholar] [CrossRef]
- Kakuturu, S.; Reddi, L.N. Evaluation of the Parameters Influencing Self-Healing in Earth Dams. ASCE J. Geotech. Geoenviron. Eng. 2006, 132, 879–889. [Google Scholar] [CrossRef]
- Belytscho, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Atluri, S.N.; Shen, S. The Meshless Method; Tech. Science Press: Henderson, NV, USA, 2002. [Google Scholar]
- Atluri, S.N.; Zhu, T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics. Comput. Mech. 1998, 22, 117–127. [Google Scholar] [CrossRef]
- Onate, E.; Idehlson, S.; Zienkiewicz, O.C.; Taylor, R.L.; Sacco, C. A stabilized finite point method for analysis of fluid mechanics problems. Comput. Methods Appl. Mech. Eng. 1996, 139, 315–346. [Google Scholar] [CrossRef]
- Liu, G.R. Mesh Free Methods: Moving Beyond the Finite Element Method; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Melenk, J.M.; Babuska, I. The partition of unity finite element method: Basic theory and application. Comput. Meth. Appl. Mech. Eng. 1996, 139, 289–316. [Google Scholar] [CrossRef]
- Gu, Y.T.; Liu, G.R. Meshless techniques for convection dominated problems. Comput. Mech. 2006, 38, 171–182. [Google Scholar] [CrossRef]
- Gottlieb, D.; Orzag, S.A. Numerical Analysis of Spectral Methods: Theory and Applications; Society for Industrial and Applied Mathematics: Bristol, UK, 1977. [Google Scholar]
- Maday, Y.; Quateroni, A. Spectral and Pseudo-Spectral Approximations of the Navier-Stokes Equations. SIAM J. Numer. Anal. 1982, 19, 761–780. [Google Scholar] [CrossRef]
- Patera, A. A Spectral Element Method of Fluid Dynamics: Laminar flow in a channel expansion. J. Comput. Phys. 1984, 54, 468–488. [Google Scholar] [CrossRef]
- Macaraeg, M.; Street, C.L. Improvement in Spectral Collocation Discretization through a Multiple Domain Technique. Appl. Numer. Math. 1986, 2, 95–108. [Google Scholar] [CrossRef]
- Hwar, C.K.; Hirsch, R.; Taylor, T.; Rosenberg, A.P. A Pseudo-Spectral Matrix Element Method for Solution of Three Dimensional Incompressible Flows and its Parallel Implementation. J. Comput. Phys. 1989, 83, 260–291. [Google Scholar]
- Fasshauer, G. RBF Collocation Methods as Pseudo-Spectral Methods. Boundary Elements XVII; Kassab, A., Brebbia, C.A., Divo, E., Eds.; WIT Press: Billerica, MA, USA, 2005; pp. 47–57. [Google Scholar]
- Powell, M.J.D. The Theory of Radial Basis Function Approximation. In Advances in Numerical Analysis; Light, W., Ed.; Oxford Science Pub.: Oxford, UK, 1992; Volume 2, pp. 143–167. [Google Scholar]
- Buhmann, M.D. Cambridge Radial Basis Functions: Theory and Implementation; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Dyn, N.; Levin, D.; Rippa, S. Numerical Procedures for Surface Fitting of Scattered Data by Radial Basis Functions. SIAM J. Sci. Stat. Comput. 1986, 7, 639–659. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric Equations of Topography and Other Irregular Surfaces. J. Geophys. Res. 1971, 176, 1905–1915. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid dynamics I-surface approximations and partial derivative estimates. Comput. Math. Appl. 1990, 19, 127–145. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics- a scattered data approximation scheme with applications to computational fluid dynamics II-solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput. Math. Appl. 1990, 19, 147–161. [Google Scholar] [CrossRef]
- Kansa, E.J.; Hon, Y.C. Circumventing the Ill-Conditioning Problem with Multiquadric Radial Basis Functions: Applications to Elliptic Partial Differential Equations. Comput. Math. Appl. 2000, 39, 123–137. [Google Scholar] [CrossRef]
- Franke, R. Scattered data interpolation: Test of some methods. Math. Comput. 1982, 38, 181–200. [Google Scholar]
- Mai-Duy, N.; Tran-Cong, T. Mesh-Free Radial Basis Function Network Methods with Domain Decomposition for Approximation of Functions and Numerical Solution of Poisson’s Equation. Eng. Anal. Bound. Elem. 2002, 26, 133–156. [Google Scholar] [CrossRef]
- Cheng, A.H.-D.; Golberg, M.A.; Kansa, E.J.; Zammito, G. Exponential Convergence and H-c Multiquadric Collocation Method for Partial Differential Equations. Numer. Methods Part Differ. Equ. 2003, 19, 571–594. [Google Scholar] [CrossRef]
- Sarler, B.; Vertnik, R. Local Explicit Radial Basis Function Collocation Method for Diffusion Problems. Comput. Math. Appl. 2006, 51, 1269–1282. [Google Scholar] [CrossRef]
- Vertnik, R.; Sarler, B. Meshless local radial basis function collocation method for convective-diffusive solid-liquid phase change problems. Int. J. Numer. Methods Heat Fluid Flow 2006, 16, 617–640. [Google Scholar] [CrossRef]
- Vertnik, R.; Zaloznik, M.; Sarler, B. Solution of transient direct-chill aluminium billet casting problem with simultaneous material and interphase moving boundaries by a meshless method. Eng. Anal. Bound. Elem. 2006, 30, 847–855. [Google Scholar] [CrossRef]
- Divo, E.; Kassab, A.J. A Meshless Method for Conjugate Heat Transfer Problems. Eng. Anal. 2005, 29, 136–149. [Google Scholar] [CrossRef]
- Gerace, S.A.; Divo, E.; Kassab, A.J. A Localized Radial-Basis-Function Meshless Method Approach to Axisymmetric Thermo-Elasticity. In Proceedings of the 9th AIAA/ASME Joint Thermophysics and Heat Transfer Conference 2006, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Divo, E.; Kassab, A.J. Iterative Domain Decomposition Meshless Method Modeling of Incompressible Flows and Conjugate Heat Transfer. Eng. Anal. 2006, 30, 465–478. [Google Scholar] [CrossRef]
- Divo, E.; Kassab, A.J. An Efficient Localized RBF Meshless Method for Fluid Flow and Conjugate Heat Transfer. ASME J. Heat Transf. 2007, 129, 124–136. [Google Scholar] [CrossRef]
- Divo, E.; Kassab, A.J. Localized Meshless Modeling of Natural Convective Viscous Flows. Numer. Heat Transf. Part A Fundam. 2008, 53, 487–509. [Google Scholar] [CrossRef]
- Erhart, K.; Kassab, A.J.; Divo, E. An Inverse Localized Meshless Technique for the Determination of Non-Linear Heat Generation Rates in Living Tissues. Int. J. Numer. Methods Heat Fluid Flow 2008, 18, 401–414. [Google Scholar] [CrossRef]
- El Zahab, Z.; Divo, E.; Kassab, A.J. A Localized Collocation Meshless Method (LCMM) for Incompressible Flows CFD Modeling with Applications to Transient Hemodynamics. Eng. Anal. Bound. Elem. 2009, 33, 1045–1061. [Google Scholar] [CrossRef]
- El Zahab, Z.; Divo, E.; Kassab, A. Minimization of the Wall Shear Stress Gradients in Bypass Grafts Anastomoses using Meshless CFD and Genetic Algorithms Optimization. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Divo, E.; Kassab, A.J.; Reddi, L.; Kakuturu, S.; Hagen, S. RBF-FVM Numerical Solution of the Poro-Elasticity Levee Problem with Time-Varying Boundary Conditions. In Proceedings of the ECCOMAS Couple Problems 2009, Ischia Island, Italy, 8–10 June 2009. [Google Scholar]
- Gerace, S.; Erhart, K.; Divo, E.; Kassab, A.J. Adaptively Refined Hybrid Meshless Scheme with Applications to High-Speed Turbulent Flow. Comput. Model. Eng. Sci. 2011, 1927, 1–33. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Publications, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Wang, H.F.; Anderson, M.P. Introduction to Groundwater Modeling: Finite and Finite Element Methods; W.H. Freeman and Company: San Francisco, CA, USA, 1982. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Fluids 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic interpolation. Comput. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Borris, J.P.; Book, D.L. Flux-corrected transport II: Generalizations of the method. J. Comput. Phys. 1983, 18, 248. [Google Scholar]
- Harten, A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 1983, 49, 357–393. [Google Scholar] [CrossRef] [Green Version]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Osher, S. High resolution applications of the OSHER upwind scheme for the Euler equations. In Proceedings of the 6th Computational Fluid Dynamics Conference Danvers, Danvers, MA, USA, 13–15 July 1983. [Google Scholar]
- Roe, P.L. Some contributions to the modelling of discontinuous flows. Lect. Appl. Math. 1985, 22, 163–193. [Google Scholar]
- Gaskell, P.H.; Lau, A.K.C. Curvature compensated convective transport: SMART, a new boundedness preserving transport algorithm. Int. J. Numer. Methods Fluids 1988, 8, 617–641. [Google Scholar] [CrossRef]
- Leonard, B.P. The ULTIMATE conservative difference scheme applied to unsteady one-dimensional advection. Comput. Methods Appl. Mech. Eng. 1991, 88, 17–74. [Google Scholar] [CrossRef]
- Jasak, H.; Weller, H.G.; Gosman, A.D. High resolution NVD differencing scheme for arbitrary unstructured meshes. Int. J. Numer. Methods Fluids 1999, 31, 431–449. [Google Scholar] [CrossRef]
- Chandhini, G.; Sanyasiraju, Y.V.S. Local RBF-FD solutions for steady convection–diffusion problems. Int. J. Numer. Methods Eng. 2007, 72, 352–378. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical Calculation of time dependent viscous incompressible flow of fluids with a free surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere Press: Coral Gables, FL, USA, 1980. [Google Scholar]
- Kim, D.; Choi, H. A Second-order time-accurate finite volume method for unsteady incompressible flow on hybrid unstructured grids. J. Comput. Phys. 2000, 162, 411–428. [Google Scholar] [CrossRef]
- Zhang, Y.; Street, R.L.; Koseff, J.R. A Non-staggered grid, fractional step method for time-dependent incompressible Navier-Stokes equations in curvilinear coordinates. J. Comput. Phys. 1994, 114, 18–33. [Google Scholar] [CrossRef]











© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoury, A.; Divo, E.; Kassab, A.; Kakuturu, S.; Reddi, L. Meshless Modeling of Flow Dispersion and Progressive Piping in Poroelastic Levees. Fluids 2019, 4, 120. https://doi.org/10.3390/fluids4030120
Khoury A, Divo E, Kassab A, Kakuturu S, Reddi L. Meshless Modeling of Flow Dispersion and Progressive Piping in Poroelastic Levees. Fluids. 2019; 4(3):120. https://doi.org/10.3390/fluids4030120
Chicago/Turabian StyleKhoury, Anthony, Eduardo Divo, Alain Kassab, Sai Kakuturu, and Lakshmi Reddi. 2019. "Meshless Modeling of Flow Dispersion and Progressive Piping in Poroelastic Levees" Fluids 4, no. 3: 120. https://doi.org/10.3390/fluids4030120
APA StyleKhoury, A., Divo, E., Kassab, A., Kakuturu, S., & Reddi, L. (2019). Meshless Modeling of Flow Dispersion and Progressive Piping in Poroelastic Levees. Fluids, 4(3), 120. https://doi.org/10.3390/fluids4030120




