Abstract
Drop impacts (onto dry or wet surfaces or into deep pools) are important in a wide range of applications, and, consequently, many studies, both experimental and numerical, are available in the literature. However, such works are focused either on statistical analyses of drop populations or on single drops. The literature is heavily lacking in information about the mutual interactions between a few drops during the impact. This work describes a computational fluid dynamics (CFD) study on the impact of two, three, and four synchronized drops into a deep pool. The two-phase finite-volume solver interFoam of the open source CFD package OpenFOAM® was used. After validation with respect to high speed videos, to confirm the performance of the solver in this field, impact conditions and aspects that would have been difficult to obtain and to study in experiments were investigated: namely, the energy conversion during the crater evolution, the effect of varying drop interspace and surface tension, and multiple drop impacts. The results show the very significant effect of these aspects. This implies that an extension of the results of single-drop, distilled-water laboratory experiments to real applications may not be reliable.
1. Introduction
A large number of phenomena, both of natural and technological interest, involve the interaction between one or—much more commonly—many liquid drops and a solid surface or a gas-liquid interface. This interaction may be mechanical, thermal, or chemical, and it usually starts with an impact of the drop onto the surface or interface. The impact velocity may be low or high, normal or oblique, and in most cases, a series of drops impact the surface at the same time or nearly simultaneously. For example, this happens in internal combustion engines, firefighting systems, surface cooling, or painting by sprays, pesticide deposition in agriculture, pollution and microbial transport in air and water, forensic analysis of blood stains, and rain effects on planes, wind turbines, and buildings. This, therefore, demonstrates the importance of a deep understanding of this phenomenon, which is still not fully understood despite its apparent simplicity and more than a century of investigation. In particular, many studies can be found in the literature about:
- The impact of a single drop onto dry solid surfaces, onto surfaces wetted by a liquid film, and onto gas-liquid interfaces alone in deep pools;
- The behavior of sprays, where the multitude of drops in the spray are considered in statistical terms, mainly with empirical models.
Detailed introductory information and reviews can be found in [1,2,3,4,5]. On impacts into deep pools, the work by Cole [6] is a specifically valuable reference. On the contrary, studies are quite scarce about the intermediate step, i.e., the outcomes of the combined impact of more than one drop in parallel (with simultaneous or delayed impacts) [7,8,9,10] or in a series [11,12,13].
As it may involve solid, one, or more liquids, and a surrounding gas, drop impact is a multiphase fluid mechanics problem, where inertial, viscous, and capillary forces merge their effects. It may also become a multi-physics problem in the case of heat or mass transfer, or chemical reactions may play a significant role (e.g., for hot or cold drops or surfaces or for drops impacting onto a chemically different liquid, for reactive wetting). Therefore, a rigorous model of the phenomenon can theoretically be created, but its analytical solution is not viable. Consequently, very simplified models and experiments have been the primary method of investigation for a long time. In recent years, the increase in the power of calculus has also made computational fluid dynamics (CFD) simulations feasible. Many remarkable studies were developed (e.g., [14,15,16,17,18]) using different approaches, ranging from the most used Eulerian models in finite volume or finite element frameworks, to Lattice Boltzmann and molecular dynamic simulations. Commercial, open-source, and in-house software packages were used. Specifically, the Volume-of-Fluid [19] approach is one of the most used algorithms, even though other techniques were also developed, e.g., Level-Set [20], markers [21], combined models [22,23,24,25,26], and (as already noted) Lattice Boltzmann [27,28] and molecular dynamics simulations (for nanodrops) [29].
In this study, CFD was used to investigate the outcomes of double and multiple synchronized drop impacts into a deep pool with the same temperature as the drops. The numerical campaign consisted of two steps: the first for validation, with simulations carried out to replicate experimental conditions that had been previously investigated by means of high-speed video acquisitions, and the second, to simulate conditions that would have been difficult to obtain in experiments. Energy conversion during the crater evolution and the effects of varying drop interspace and surface tension and multiple drop impacts were investigated. For the first phase, the agreement between simulations and experiments was satisfactory, particularly for some impact conditions. The results of the second phase evidenced the very significant effect of the investigated aspects. This outcome implies that an extension of the results from single-drop, distilled-water laboratory experiments to real applications may not be reliable.
2. Materials and Methods
2.1. Experimental Setup
The experimental set-up and procedures, including uncertainty analysis of the main parameters, were described in detail in a previous paper [10], so they will be only briefly summarized here. A thorough analysis of the experimental data against which the simulation results will be validated is available in the same paper. Drop impact experiments were performed by high-speed visualization with continuous back-light illumination. Millimeter-size deionized water droplets were produced with an on-demand droplet generator [7], which allows the synchronous detaching of two drops of equal size. Falling drops are accelerated by gravity, and during their free fall, they are detected by a light sensor, triggering the high-speed (1000 fps) charge-coupled device (CCD) camera acquisitions. Then, the drops impact the pool, which is contained in a cubic box with a side length of 40 mm. The pool depth is one order of magnitude larger than the drop diameter, to avoid any influence on the studied relevant part of the crater evolution. The drops are pigmented by a solution with well-known rheological behavior [30] and with a concentration of 1% in weight, so that the drop water can be distinguished from the pool water in the high-speed video frames, without significantly affecting the water’s density and viscosity. For each recorded sequence, the images before drop impact are post-processed by an algorithm that comprises background subtraction, contrast enhancement, image cleaning, edge detection using the Laplacian of Gaussian (LoG) method, and feature detection to determine the drop section and center of each drop [31]. Using consecutive images coupled with the camera acquisition rate and the pixel-to-meter conversion factor, the diameter and velocity of the impinging droplets can be evaluated with an accuracy of ±0.03 mm and ±0.02 m/s, respectively. The drop sphericity S is also calculated for each falling drop, defined here as the aspect ratio of the vertical to horizontal axis (thus, S > 1 represents a prolate-shaped and S < 1 represents an oblate-shaped drop) before the instant of impact, and assuming a rotational symmetry around the vertical axis. The sphericity of the falling drops before impact is crucial for obtaining accurate and repeatable experimental results, as sphericity heavily affects crater dimensions and impact-generated vorticity [32,33,34,35]. Another critical aspect is the oscillation mode of the drop at the instant of impact [36,37]. The experiments were performed at ambient pressure, with the temperature of the pool equal to 30 ± 1 °C and the temperature of the drops equal to 27 ± 1 °C. The investigated experimental conditions in terms of drop diameter D, inter-drop distance L0, and impact velocity w are summarized in Table 1, along with the values of the dimensionless groups typically used for drop impact characterization.

Table 1.
Investigated conditions.
2.2. Numerical Simulations
Concerning the numerical setup, simulations were performed using the interFoam solver of the OpenFOAM® open source CFD toolbox [38]. interFoam is an isothermal finite volume (FV) solver based on the volume-of-fluid (VOF) method and implementing a model to include surface tension at the interface [39]. OpenFOAM® was selected due to its free and open source nature and because of its many favorable reviews [40,41,42,43] and successful cases of use, which are described in the literature [42,43,44,45,46,47,48]. The model implemented in interFoam includes the continuity and momentum equations for a Newtonian and incompressible fluid, whose density and viscosity are calculated on the basis of an indicator function named volume fraction γ. The latter assumes a value of 0 for one phase, 1 for the other, and between 0 and 1 in the interfacial regions, and it is transported by the fluid velocity field w. Volume tracking and interface reconstruction (typically as the isosurface at γ = 0.5), with no explicit interface tracking, is, therefore, performed. The advantage of the VOF method with respect to the two-fluid models is that a single set of equations must be solved. The expressions of all the used equations, a discussion of the meaning of the included terms, and further details about the interFoam solver and models can be found in [47,49,50]. Very promising modified versions of interFoam were also presented in the literature [48,51], but the source code was not made publicly available, so the version included in the official OpenFOAM® distribution was used.
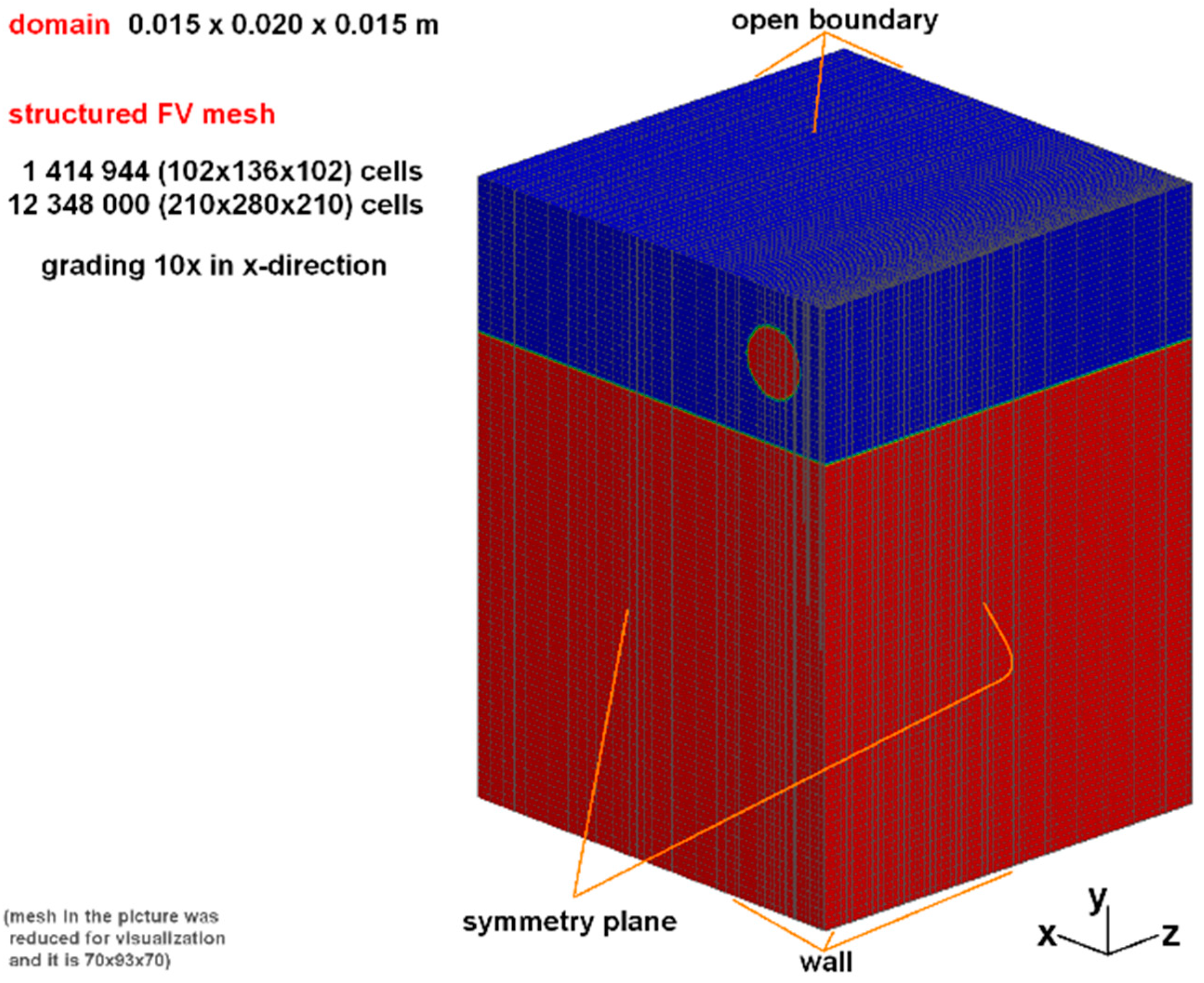
As the investigation is at a constant temperature and the impact velocities are low, both phases were assumed to be incompressible and in laminar motion, in agreement with all the previously cited papers in this field. For each phase, the values of all the relevant thermophysical properties were taken at the respective temperatures measured during the experiments. The initial conditions of the two phases and their positions within the domain were fixed using the setFields OpenFOAM® utility. The implicit Euler scheme (first-order accurate) was used for the time derivative, as it proved to offer better results in comparison with the second-order Crank-Nicholson discretization schemes that were tested during preliminary simulations, selecting different blending factors between 0.5 and 1. The conventional advection term was discretized using Gauss schemes: limited Van Leer for the volume fraction and limited linear for the velocity. For the latter, variations of the limiter parameter were tested, but the best results were obtained by keeping it equal to 1. Finally, the OpenFOAM® specific “interface compression” scheme [52] proved to be the best choice for the discretization of the compression term. The maximum allowed Courant–Friedrichs–Lewy (CFL) number was 0.3. In fact, the solver is allowed to adapt the time step to keep the CFL number under the desired limit, and the requirement for the interface compression scheme used in interFoam for 3D cases is to limit it under 0.3 for 3D cases [40,52]. Some volume fraction sub-cycles are also performed to further improve the accuracy. Three-dimensional simulations were performed within a domain that is a rectangular cuboid having dimensions 0.015 m × 0.015 m × 0.020 m. This domain represents 1/4 of the real pool system, as the computational effort was reduced by exploiting two symmetry planes: the longitudinal plane passing through the two impact points and the transversal plane orthogonal to the previous one, passing through the midpoint between the impact points [10]. To reduce the domain height, drops’ detachment from the drop generator and their fall towards the pool surface were not simulated. The drops were directly initialized as spheres near the free surface of the pool, with an initial velocity corresponding to the experimental one. This approach has a weakness in the fact that drop oscillations after the detachment from the needle are not considered. As already mentioned, drop shape and oscillatory behavior have an important influence on the impact outcomes (as it was confirmed also by the preliminary simulations described in the following section), but in the experiments, the drops’ shapes were also nearly spherical, so this approximation seemed to be acceptable for these cases. The used mesh was a purely structured one, with hexahedral cells and grading along the axis connecting the drop centers (with a size ratio of 10 between the last and the first cell) to better capture the thin neck that separates the craters created by neighboring impact drops. In the other directions, the aspect ratio was fixed to 1 for all the cells. For the simulations involving three drops with one centered in the origin of the axes, no grading was used, and the mesh resolution was doubled along both the horizontal axes (x,z).
Domain characteristics, together with the imposed boundary conditions, the initial position of the interfaces, and the mesh details are summarized in Figure 1.
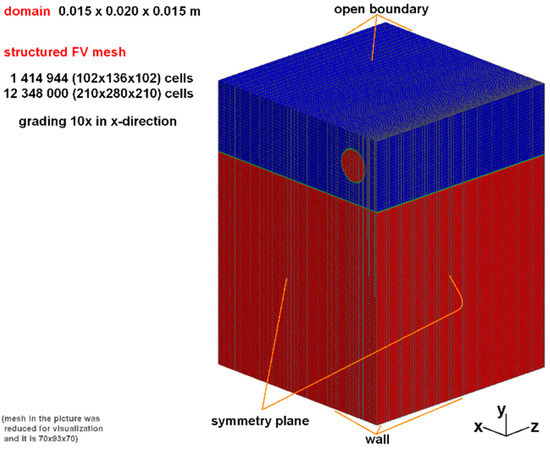
Figure 1.
Domain dimensions, boundary conditions, and mesh details.
Single drop impacts were also performed for comparison, leaving everything equal to the double impact cases apart from the initial drop position, which was centered on the y-axis.
3. Results and Discussion
3.1. Validation against Experimental Data
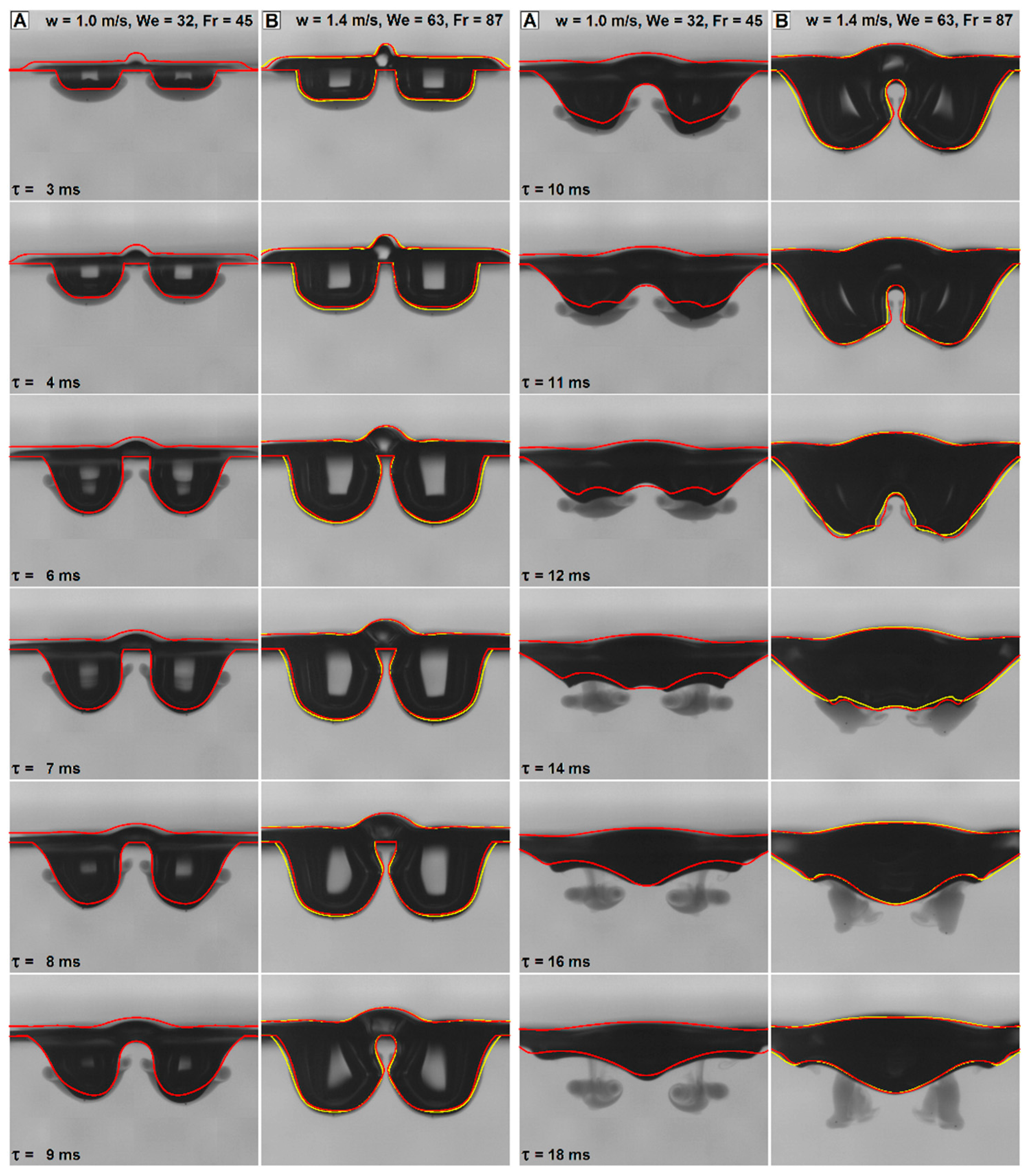
To validate the numerical simulations, crater evolution and drop-formed vortex structures were compared with those observed by means of high-speed video acquisitions. Details about the latter can be found in [10]. All these simulations were performed using the properties of distilled water for the liquid phase. Simulation results were sliced along the longitudinal plane and saved as images with the same pixel-to-meter ratio of the experimental images, then, the time steps corresponding to the experimental frames were selected and superposed to the latter. Figure 2 and Figure 3 show the results, up to time τ = 8 ms for all three investigated cases and for the entire simulated time for cases A (w = 1.0 m/s) and B (w = 1.4 m/s). This comparison is the most severe in evaluating the agreement, as it allows a direct visualization of the correspondence between the experimental features of the craters and the numerical ones. The agreement is very good for all the investigated cases during the inertial phase of the impact (Figure 2) and for case B during the crater recession (Figure 3, column b). On the contrary, some significant discrepancies appear during this second phase for case A (Figure 3, column a). This will be commented on in the following section, when discussing the crater depth profiles. The results after τ = 8 ms are not shown for case C because, with all the used meshes, the two craters merge, such that the crater depth is still reproduced well, but the crater shape is substantially altered, and the agreement is completely lost. With the VOF approach, air regions coming into contact merge instantaneously because the underlying model is not able to represent retarded coalescence (modified models would be needed, e.g., see [53]). On the other hand, real-world interfaces may resist even with direct contact—at least for a certain time—if the pressure of the contacting regions is not too different (e.g., bouncing bubbles or drops). Thus, in the experiments, the very thin neck between the two crates in case C is conserved, while in the simulations, a much finer mesh than that used for the simulations would have been needed to avoid crater contact and merging (OpenFOAM® is very slow in adaptive remeshing, so this feature could not be exploited).

Figure 2.
Superposition of the numerical crater contours to the experimental high-speed photos, for the three investigate cases A (w = 1.0 m/s), B (w = 1.4 m/s), C (w = 2.0 m/s), time up to 8 ms. In case B, the red line shows the results of the 12.35 Mcell simulation, while the yellow line shows the results of the 1.4 Mcell simulation.
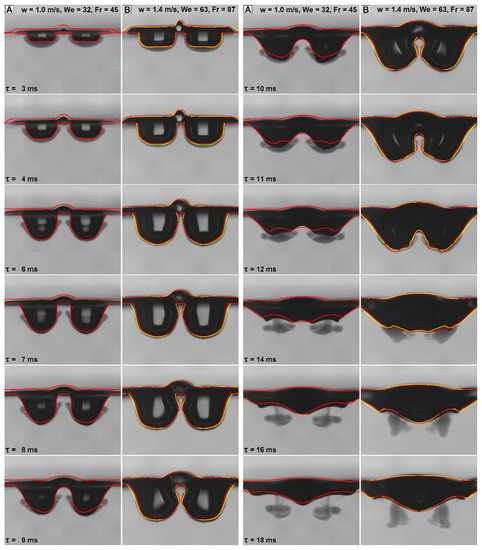
Figure 3.
Superposition of the numerical crater contours to the experimental high-speed photos, for case A and case B (for the latter: red line, results from the 12.35 Mcell simulation; yellow line, results for the 1.4 Mcell simulation); time up to 18 ms.
Different mesh sizes were evaluated to analyze the mesh independence of the solution, which, for fine details, is always an issue when using the VOF technique. Mesh sizes were varied between 176 kcell and 12.35 Mcell, but meshes under 1 Mcell proved unsuitable because the already mentioned neck between the craters also disappeared (resulting in a coalescence of the cavities not observed in the experiments) for cases A and B. Thus, only the finest two meshes (1.4 Mcell and 12.35 Mcell) were used for the final simulations. For the latter, a good overall mesh independence was found, even if some details are still captured differently. No mesh is always the most accurate (as can be seen in Figure 2 and Figure 3 for case B).
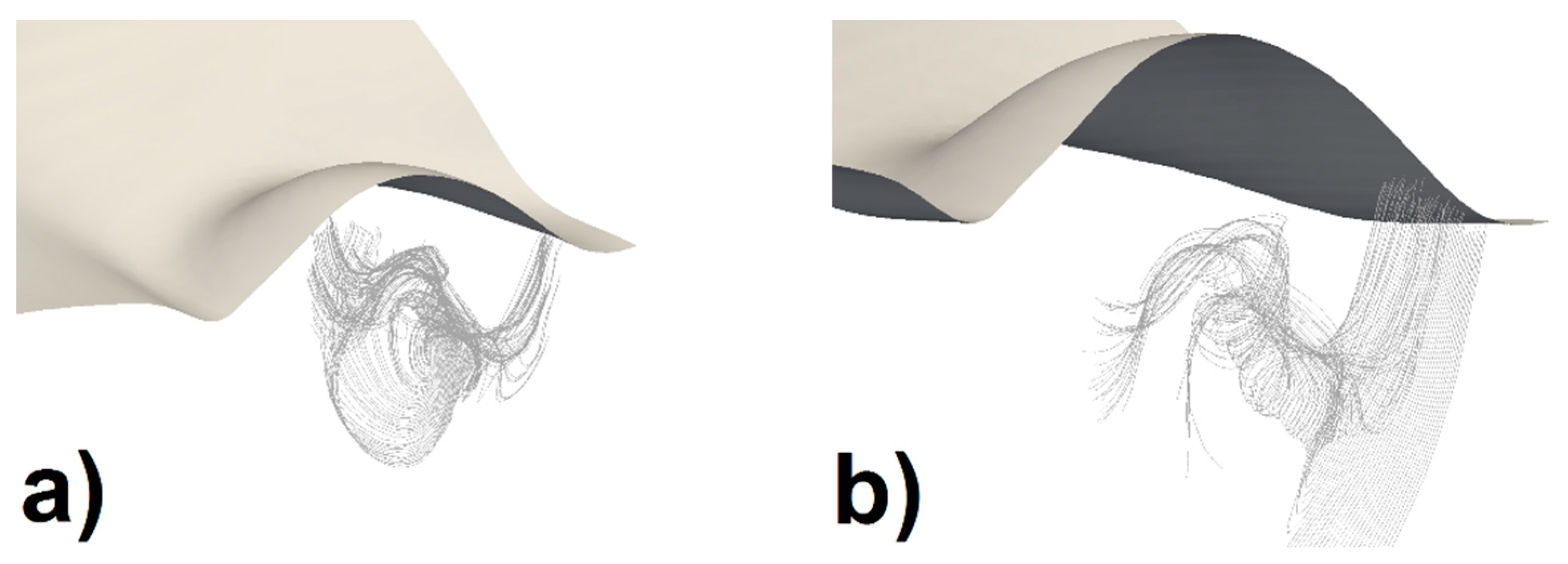
The vortices generated by drop impacts—peculiar and different from the single-drop impact case [10]— were visualized in the experiments by dying the drop water. In this way, the dye highlights the drop water, distinguishing it from the pool water, and allowing to follow its motion. In the simulations, this could be accomplished by numerically “dying” the drop water with a passive tracer, by using a multiphase solver (e.g., multiphaseInterFoam) or simply by tracing the flow streamlines [18]. An example of the latter approach is shown in Figure 4, which includes two pictures referring to case A at τ = 18 ms. These two images were obtained by tracing streamlines with different origins, thereby evidencing how the streamline aspect heavily depends on the latter. The complex structure of the simulated flow streamlines is consistent with the experimental observation of vortex structures in the same region [10]. This behaviour is also in agreement with the experimental findings by other authors [54], who showed that after a certain time from the drop impact (for the investigated case, this time should be around 14 ms) the original azimuthal vorticity is progressively tilted and becomes a stream-wise vorticity. Despite the validity of this approach, using it to cover all the domain regions with good resolution would require a very large number of streamlines, such that they would be difficult to follow. Therefore, another visualization technique was preferred. Pictures showing the calculated vorticity (the curl of the velocity vector field) on the longitudinal plane were compared with the experimental images. Even if the vortex and vorticity are not related in a biunique way (due to irrotational vortices or vortex parts), vorticity offers a picture of the regions where vortices are most likely to occur, with a resolution equal to the number of mesh cells. Figure 5 shows the results for cases A and B. As can be seen, the agreement between simulations and experiments is also good for regions of high vorticity. The discrepancies are due to the differences in the crater evolution between the simulations and experiments. These differences influence the motion of the drop water under the crater itself. In any case, they are not significant enough to undermine the correct identification of the regions reached by the drop water and its swirling motion.
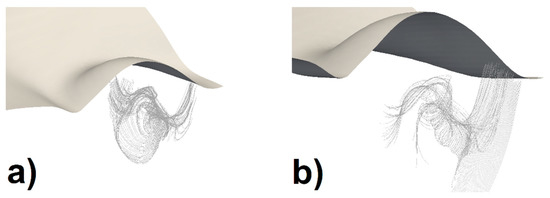
Figure 4.
Simulated flow streamlines in a region where vortices are experimentally observed (case A, w = 1.0 m/s, τ = 18 ms).
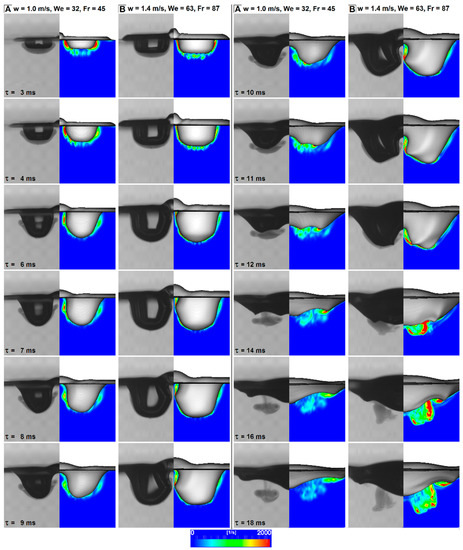
Figure 5.
Comparison between the experimentally detected vortex structures and the vorticity calculated by numerical simulations, for cases A and B, time up to 18 ms.
For case A in Figure 5, the drop fluid is symmetrically distributed below the liquid–air interface (τ = 4 ms). Later (τ = 6 ms), the drop fluid begins to roll up. The continuous deformation of the liquid–air interface generates an outer vortex structure in the form of a vortex filament, which is also visible in the numerically calculated vorticity in the same region. The roll-up is continuous while the expanding crater causes downward convection of the dyed drop fluid. Asymmetries of the outer vortex rings, having their origins in different convection velocities, are also found in the numerical results. When the crater recedes (τ = 9 ms), a central vortex structures is formed. Both vortex structures, the central vortex and the outer vortex, separate from the receding crater and form a unique complex vortex blob that continuous to move downward. This complex structure could not be captured in the simulation, but the region of vorticity is represented very well.
For case B in Figure 5, the generation of the outer vortex structure is superposed, and the dyed liquid spreads around the cavity. The interaction between the two evolving craters causes a local enlargement of the spreading dyed drop liquid, showing a vortical structure in both investigations (the experiment and simulation (τ = 8 ms)). When the cavities recede, apparently disorganized structures separate and move downward. The numerical results clearly show these downward moving structures.
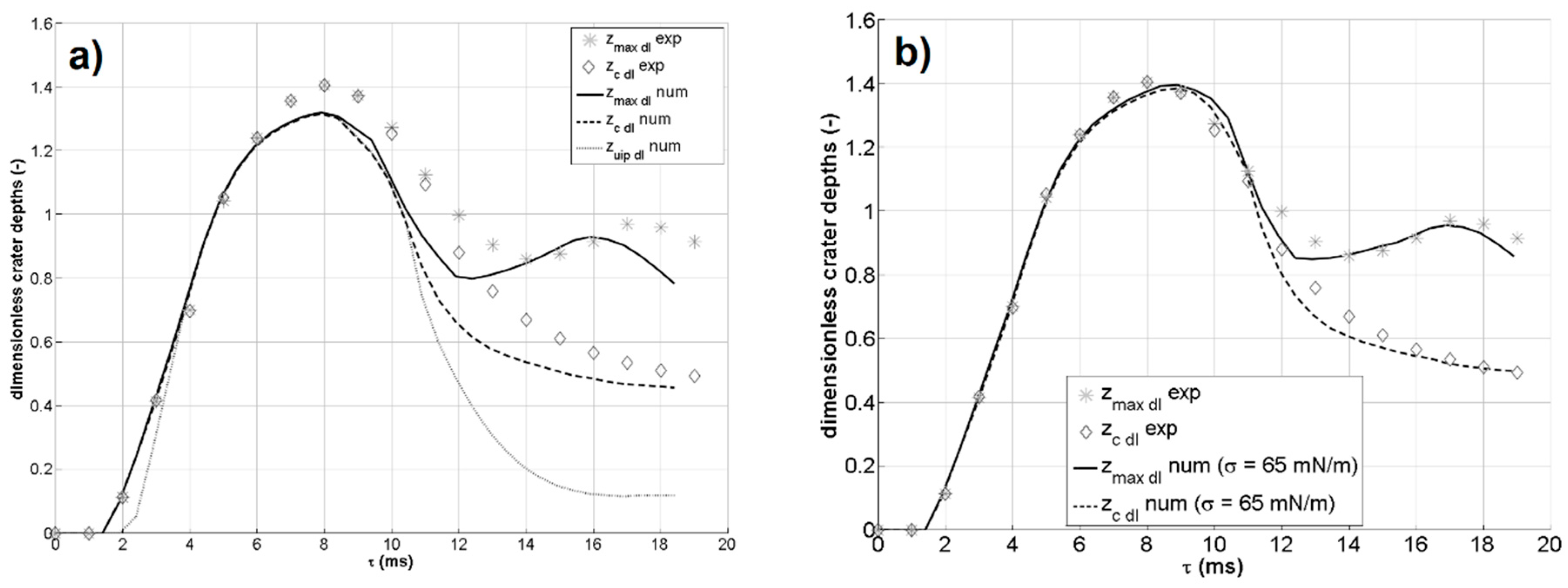
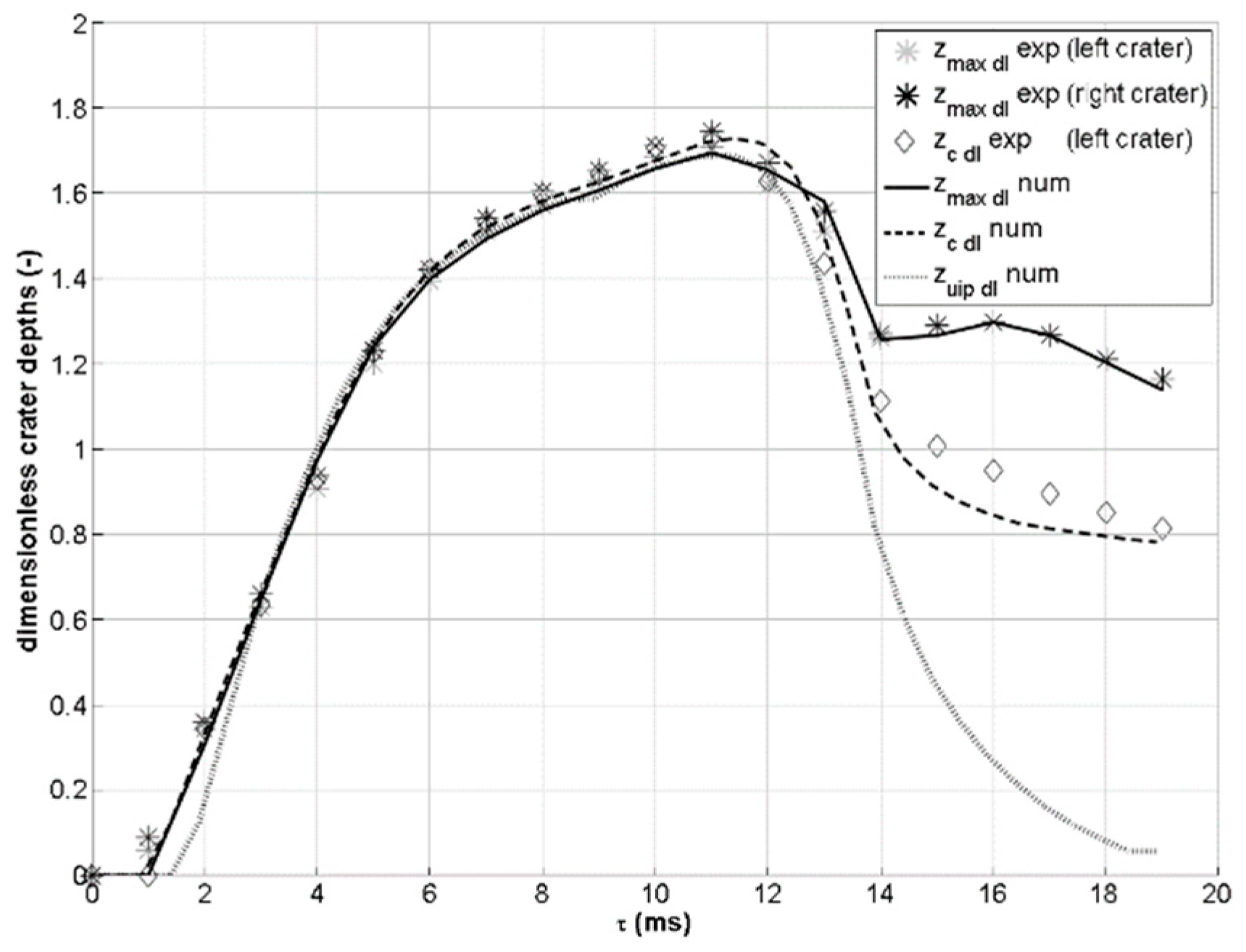
In terms of the characteristic dimensions of the drop craters, the crater’s maximum penetration depth zmax, the maximum crater penetration depth in the transverse plane including the impact point zc (i.e., parallel to the yz-plane and at a x-coordinate equal to half of the drop interspace [10]), and the crater penetration depth along the vertical line including the impact point zuip, were measured from both the experiments and the simulations. In this work, these quantities are always presented in a dimensionless form, by dividing them by the drop diameter before impact. Therefore, their symbols are completed by a “dl” subscript in all the following charts. For double drop impacts, these quantities do not always coincide during the crater evolution (differently from what happens for single drop impacts). This can be clearly seen, e.g., in Figure 2 and Figure 3. zmax and zc are accessible both to experiments and simulations, while zuip can be evaluated only by simulation because its measurement requires a cross-section of the craters (along the xy plane) and not just a side view. Figure 6 and Figure 7 show the values of these quantities for case A (w = 1.0 m/s) and case B (w = 1.4 m/s) as a function of time. As for all the charts in this paper, the initial time τ = 0 was fixed at the instant of impact. In the experimental results, the two craters are not perfectly equal, but their difference is very slight (as can be seen for zmax for case B in Figure 7). Therefore, only the values for the left crater are shown in Figure 6. More specifically, Figure 6 reports the results for case A (w = 1.0 m/s), comparing simulations and experiments for the two values of the water–air surface tension set in the simulations.
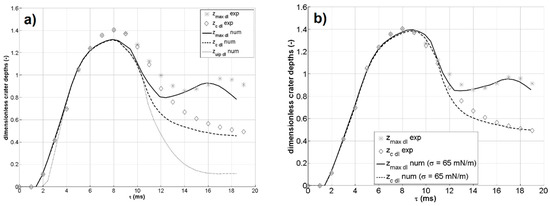
Figure 6.
Dimensionless zmax, zc and zuip extracted from the experiments and from the numerical simulations for case A (w = 1.0 m/s): (a) the results using σ = 71 mN/m; (b) the results using σ = 65 mN/m.
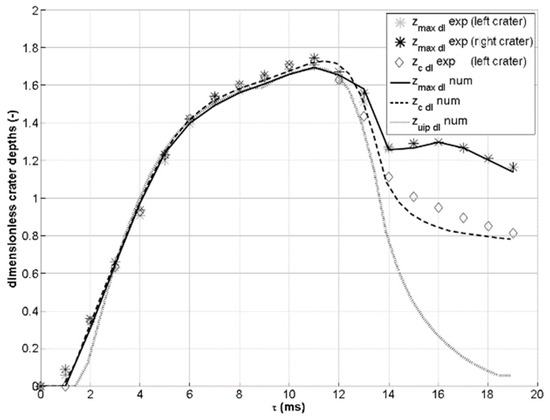
Figure 7.
Dimensionless zmax, zc and zuip extracted from the experiments and from the numerical simulations for case B (w = 1.4 m/s). volume-of-fluid (VOF) results using σ = 71 mN/m.
As can be seen in Figure 6, the experimental values are better reproduced when σ = 65 mN/m (Figure 6a) instead of σ = 71 mN/m (distilled water value, Figure 6b). This seems reasonable as the dye used for the droplet in the experiments [10] contains surfactants, which may cause—despite the very dilute solution—a reduction in the drop surface tension. For case B, reported in Figure 7, the agreement is already good for simulations with σ = 71 mN/m. This can be explained by the fact that in case B, the impact velocity is higher, so the importance of the capillary actions and surface tension is reduced with respect to case A.
In any case, the overall maximum depth reached by the crater during its evolution—which is one of the most important quantities because it limits the water layer directly reached by the crater—is always reproduced very well by the simulations. The deviation when using σ = 71 mN/m is −6.1% for case A, −1.7% for case B, and −0.14% for case C. The deviation for case A is reduced to −0.68% when using σ = 65 mN/m. In all cases, the numerical simulation underestimates the experimental value, with a discrepancy that decreases with an increasing impact velocity. This is again consistent with the fact that the set surface tension is probably larger than the correct experimental value (thus, the free surface more strongly opposes pulling).
3.2. Energy Conversion During Impact
After validation, the numerical simulations were used to extract information about some aspects that would be difficult or very time-consuming to study experimentally. Post-processing of the numerical results was first carried out to extract the kinetic and surface energies within the domain for all the simulated time steps. Given the small involved heights, the changes in the potential energy (of the drop liquid and of the pool liquid displaced by the drop) are minor, so the latter will not be described. Kinetic energy was calculated for each cell as:
where wcell is the velocity magnitude in the cell, ρwater and ρair are the water and air densities, and γ is the volume fraction. Summation over all cells was then performed to calculate the total Ek over the whole domain, which, before impact, is obviously equal to the kinetic energy of the drop alone. Surface energy Es was calculated as the product of the air–water interfacial energy σ (taken at its reference value for distilled water at the drop temperature, 71 N/m) by the total area of the air–water interface obtained as the isosurface of the color function γ = 0.5. This value was then decremented by the value of the total interfacial energy of the undisturbed pool surface, so that a direct comparison between the interfacial energy of the drop before the impact and the interfacial energy during crater evolution can be evaluated.
Ek = 1/2 wcell2 [(γ ρwater + (1 − γ) ρair]
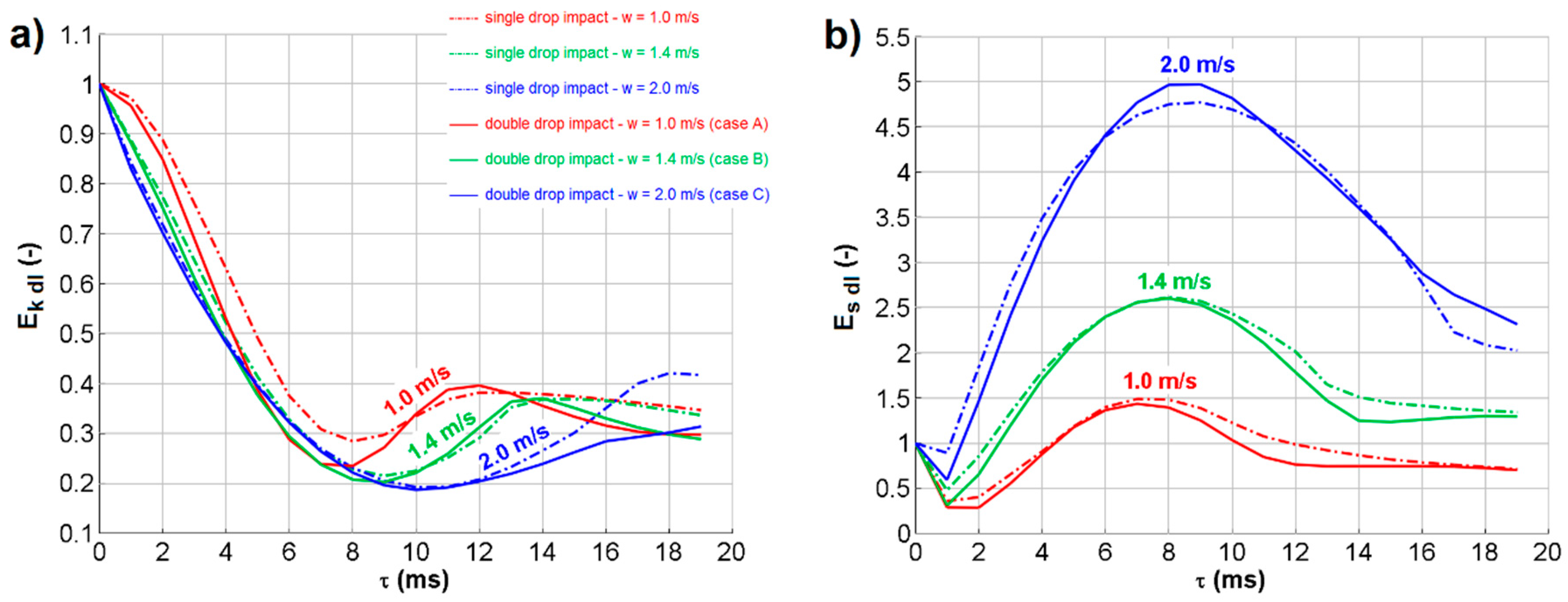
For both kinetic and surface energy, the values extracted from the numerical results at the time step immediately before impact were compared with the theoretical predictions for drops of known diameters and velocities to check their correctness and reliability. The average deviation was 0.78% for kinetic energy and 1.31% for surface energy, which was considered satisfactory. Figure 8 shows the results for both the double drop impacts and the corresponding (i.e., with same impact velocity) single drop impact, after normalization of the values with respect to the kinetic energy and the surface energy immediately before the impact. The time evolution of the two energy contributions appears consistent with the experimentally observed behavior and with each other. When kinetic energy increases, surface energy decreases, and vice versa. Surface energy decreases during the first instants after impact because the drop coalesces with the pool (so a part of the drop and the pool’s external surfaces are merged, with a consequent reduction in the total interface area), but the crater is not formed yet. The profiles also show a very regular evolution for impact velocity. The most interesting outcome is that the evolutions for single and double impacts are extremely similar, even if minor differences are obviously present due to the more complex evolution of the crater shape in double drop cases (e.g., causing the mutual intersections between the curves). This suggests that the latter has only a minor influence on energy conversion during the crater’s expansion and recession.
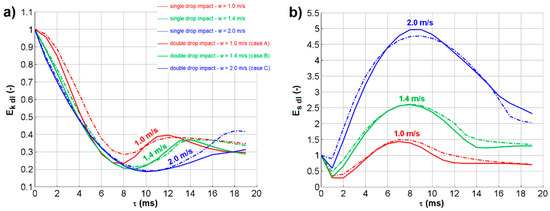
Figure 8.
Time evolution of the normalized kinetic energy (a) and normalized surface energy (b) in the domain after double drop impact, as a function of time for single (dash-dot lines) and double (continuous lines) drop impacts.
3.3. Sensitivity Analysis on Surface Tension
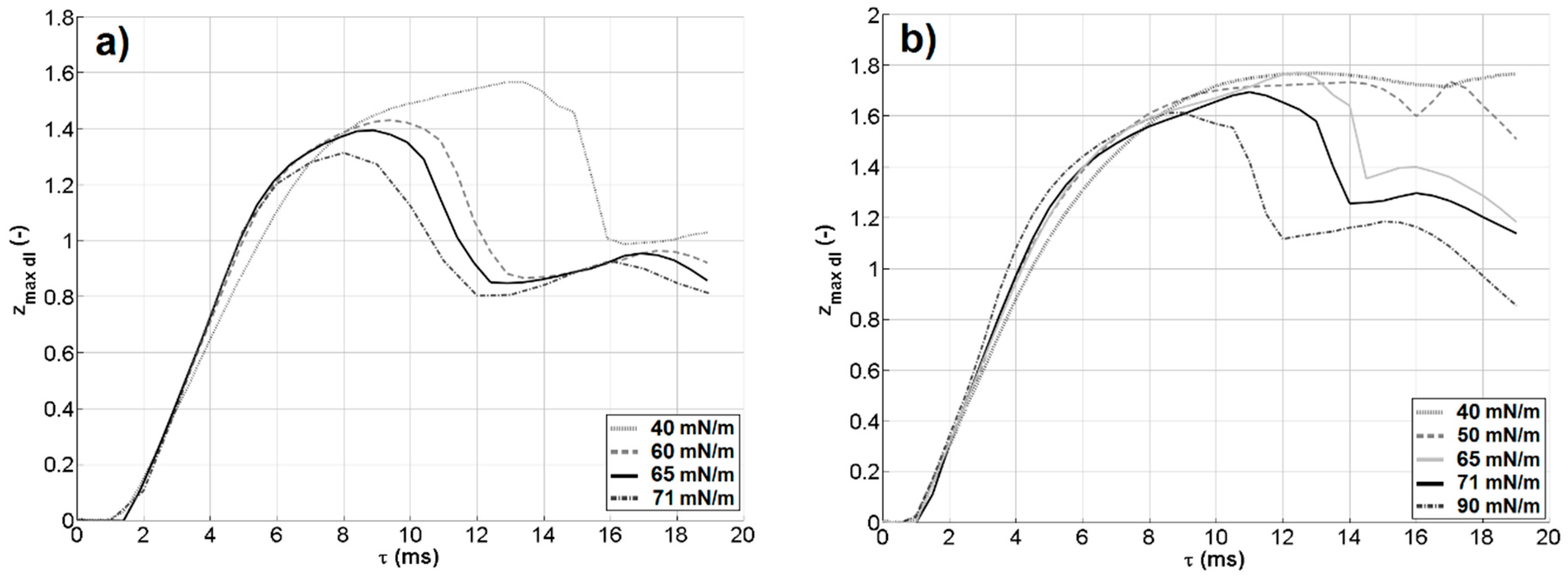
As water is easily contaminated, particularly in real applications, its surface energy may be quite different from the distilled water case. Given the observed influence of σ on the results, a sensitivity analysis was carried out on its value. Case B (w = 1.4 m/s) was selected as a reference case, changing only the surface tension value. It can be expected that larger surface tension values cause a more significant influence of the capillary action and thus a higher internal pressure within the original drop and a “tenser” pool interface. As can be observed from Figure 9, the trend of the inertial phase, in which the crater is expanding, is influenced only slightly by the water surface tension. The maximum expansion of the crater is reduced when the surface tension is larger (meaning that the tensing effect dominates with respect to the larger capillary pressure in the drop). The receding phase is heavily changed, and for larger surface tension values, the crater closes much faster. A few sudden changes in the path can be observed. These changes correspond to instants when the capillary waves caused very fast modification in the crater evolution. In fact, once the crater reaches its maximum depth and width, its starts receding, and the surface tension reduces the interface area. This causes the closure of the crater and perturbations of the interface that propagate as waves along the crater interface, resulting in peculiar shapes (e.g., see the time instants between τ = 10 ms and τ = 16 ms in Figure 3) and seemingly irregular trends in the charts. In particular, the changes in the maximum crater depth evidence the instants when different crater regions become deepest.
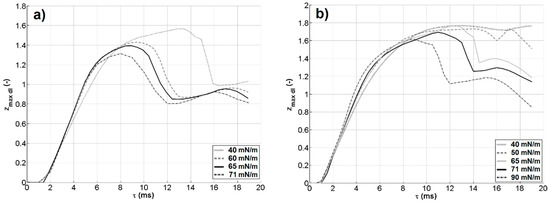
Figure 9.
Time evolution of zmax dl as a function of the water surface tension for case A (w = 1.0 m/s, (a)) and for case B (w = 1.4 m/s, (b)).
3.4. Sensitivity Analysis on Drop Spacing
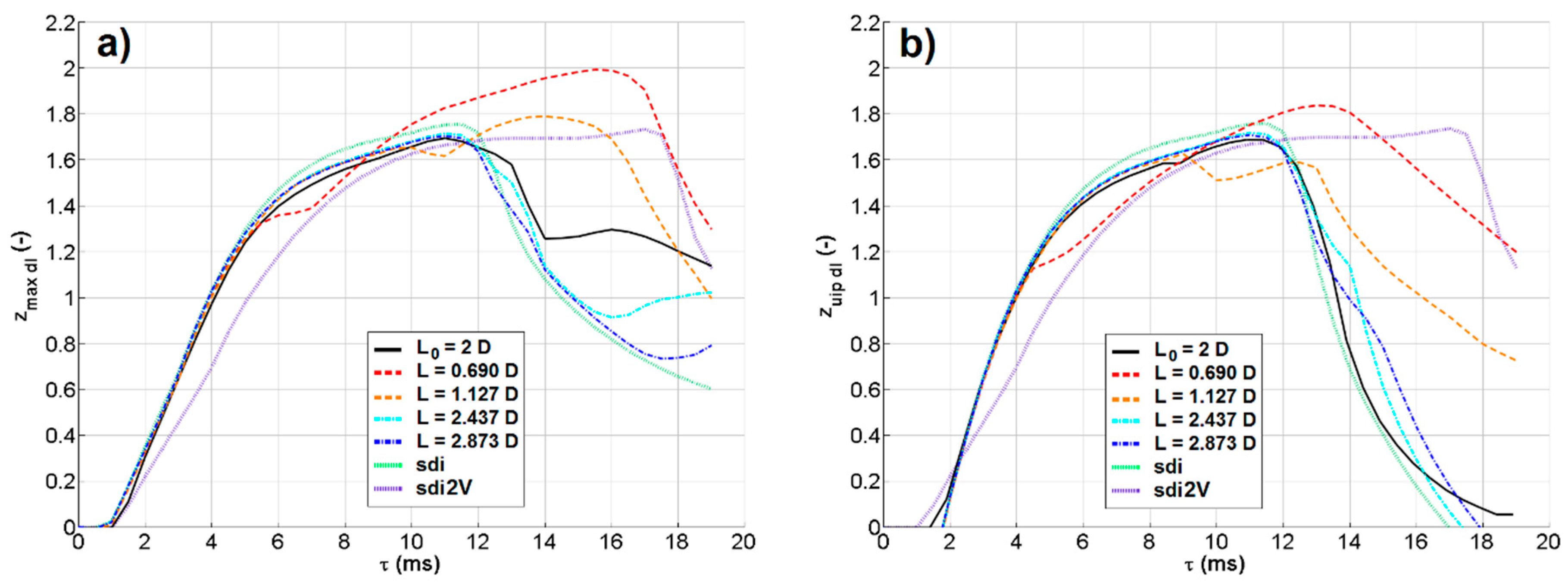
The second parameter that was varied is the distance between the drop centers. This distance was changed in the range of 2.58 to 6.58 mm by modifying the reference drop distance (L0 = 4.58 mm) of ±1 and ±2 mm. This resulted in a series of dimensionless drop distances equal to L/D = 1.127 ÷ 2.873, L/L0 =0.345 ÷ 1.437. Figure 10 shows the results in terms of zmax (a) and zuip (b), including also single drop impacts for comparison. Here, too, the sudden changes in the paths are evident. Paths are consistent between the different cases, with a progressive shift of the instants at which the crater’s main parameters change their trends due to the combined actions of inertia and capillarity. As expected, when the drop distance is large, the crater tends to behave as in a single drop impact. On the other hand, reduction of the interspace causes the deformation of the craters, which interact with each other first indirectly and then directly merge, affecting more and more the crater dimensions. A peculiar result is that for drops nearly touching each other, the time at which the maximum value of zmax is reached tends to the value for a single drop with double the volume and mass (as the density is not changed), but the maximum value of zmax dl is much larger than that in the corresponding single drop case. Thus, it can be concluded that direct interaction (merging) between the craters enhances crater penetration even more than a simple summation of inertial contributions would predict.
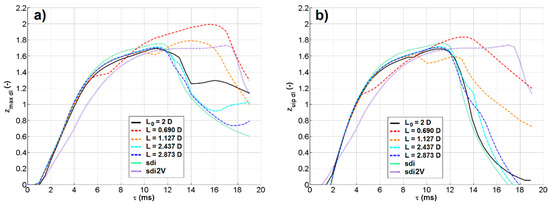
Figure 10.
Time evolution of zmax dl (a) and zuip dl (b) as a function of the distance L between the drops. Reference case (L0/D = 2) is case B; the other cases are with the drop interspace decreased and increased by 1 mm and 2 mm. Single drop impact (sdi) includes the same drop diameter and impact velocity; the single drop impact for a drop with the same impact velocity but a volume and mass double of the original one (sdi2V) is also added.
3.5. Three-Dimensional Visualization
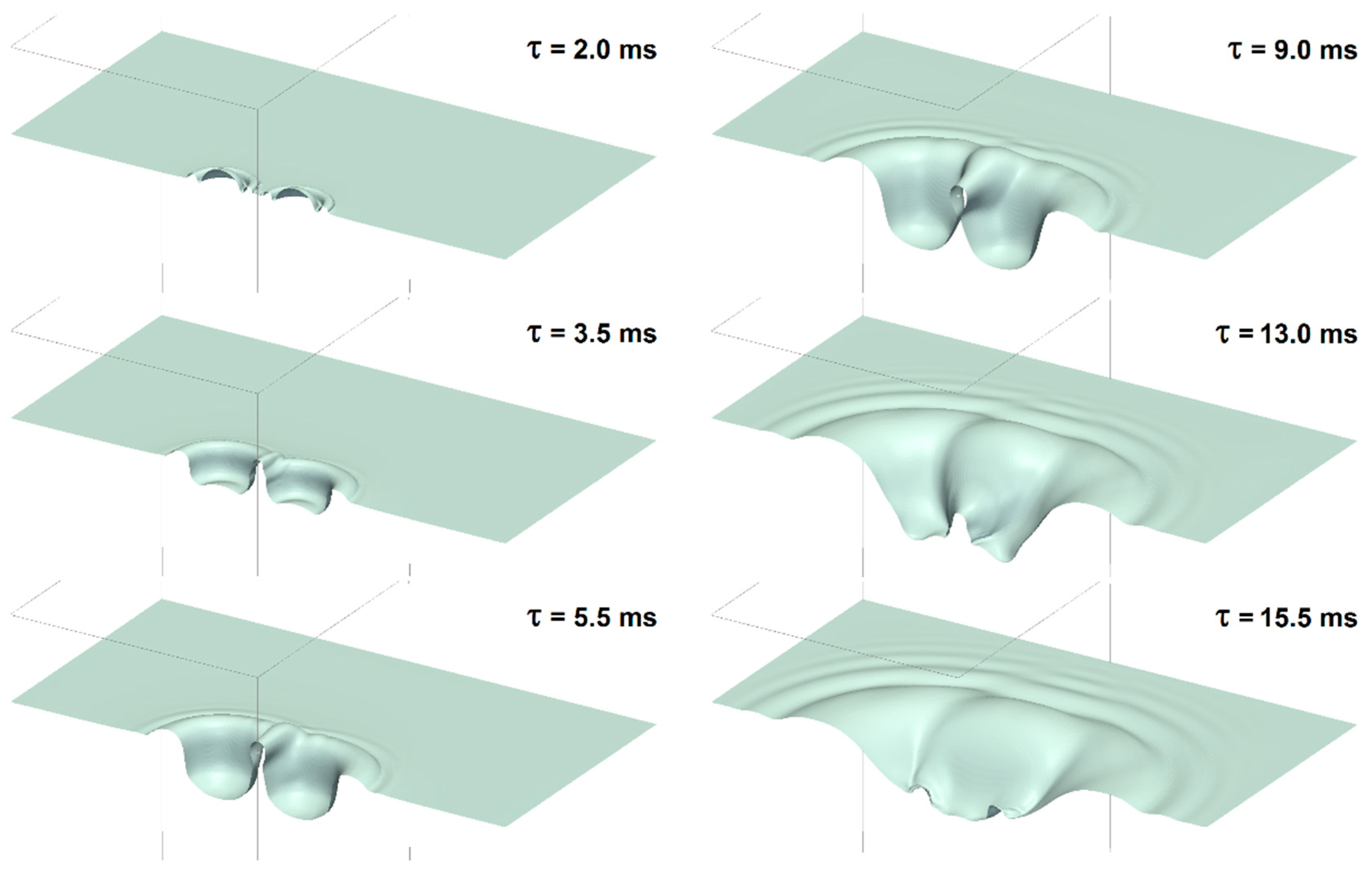
Unlike the experiments, where a single side or top view of the drop impacts can be observed, from the numerical simulations, a fully 3D description of the phenomenon can be obtained. First, the air–water interface can be extracted and visualized. Figure 11 shows a rendering of the crater evolution at different time instants—for case B (w = 1.4 m/s), simulated with 12.35 Mcell. For a more intuitive visualization, the simulated domain was mirrored once to reconstruct half of the real domain. It can be noticed how not only the major features, but also the details (including the neck and the surface and capillary waves) are very well captured.
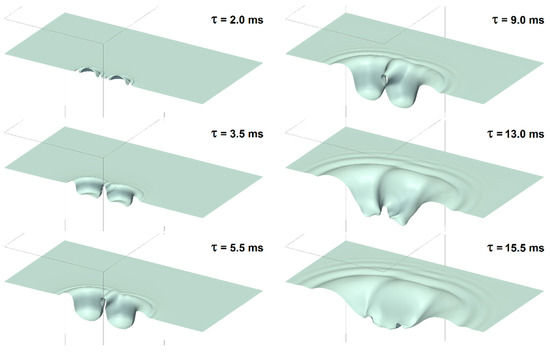
Figure 11.
Rendering of some frames showing the crater evolution from the simulation of case B (w = 1.4 m/s), simulated with 12.35 Mcells.
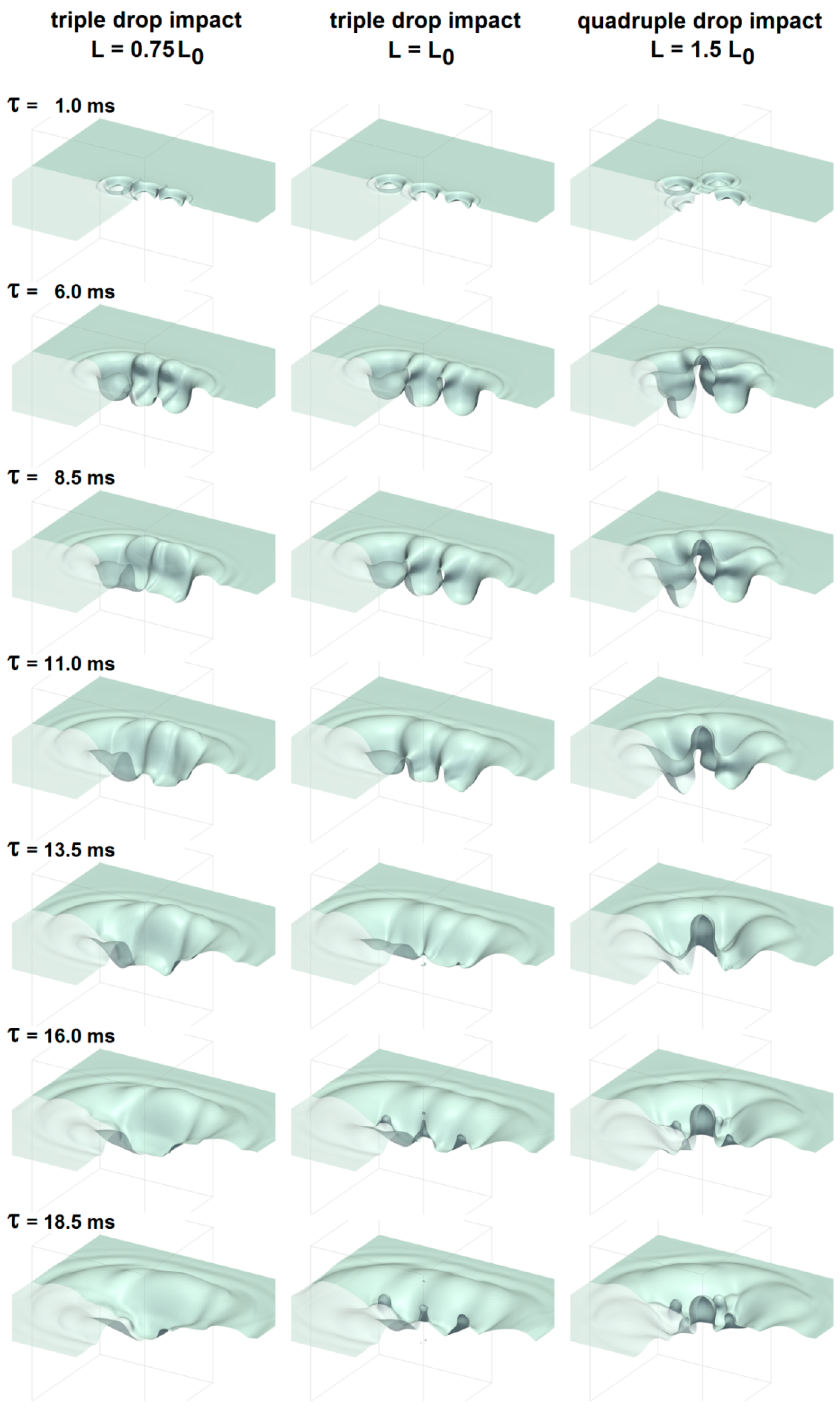
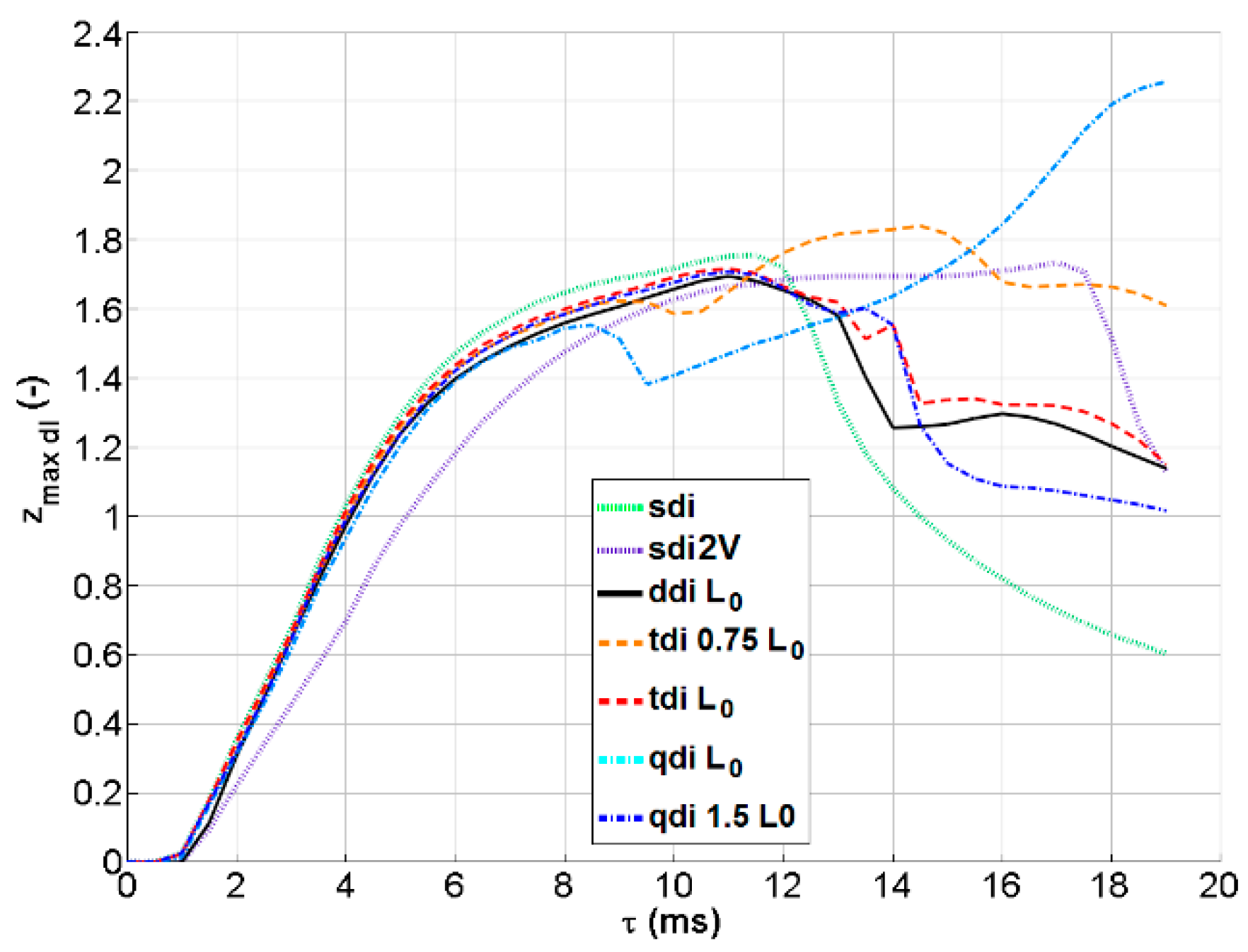
3.6. Impact of Three and Four Synchronized Drops.
Finally, simulations of multiple drop impacts were tested in all cases for impact velocity w = 1.4 m/s. For these cases, no corresponding experimental tests were performed. Three drops in a single row, aligned along the x-axis, and four drops, two aligned along x and two along z, were tested. Four cases were simulated—one with a drop interspace L equal to L0 for both three- and four-drop cases, a three-drop case with a drop interspace equal to 0.75 L0, and a four-drop case with a drop interspace of 1.5 L0. Figure 12 shows some rendered frames of the crater’s evolution for three of these simulated cases. It can be observed how for the three-drop case with L = L0 the craters do not merge, while for the other cases they do, resulting in a different evolution and a maximum crater depth that becomes much larger, as reported in Figure 13. In these cases, too, the interaction between the craters appears to have a significant effect on the maximum depth. Further studies will be needed to verify how multiple drop interactions would affect the crater depth when there is no “free space” left for expansion. On the other hand, each crater finds its way blocked by other interfaces in all directions. In this case, the crater depths might be reduced. Further studies will also be needed to investigate the effect of non-synchronous impacts.
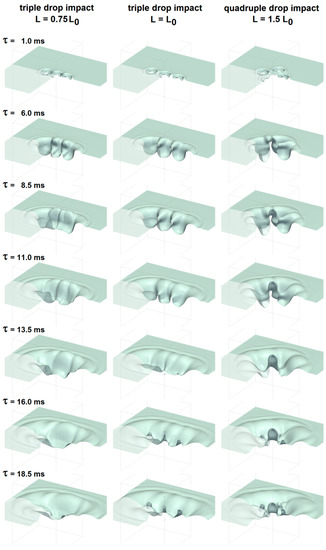
Figure 12.
Rendering of some frames showing the crater evolution from the simulations of three-drop and four-drop cases (w = 1.4 m/s).
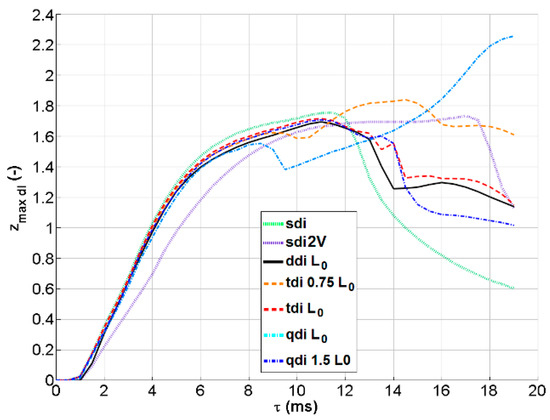
Figure 13.
Dimensionless zmax as a function of time from the numerical simulations for multiple drop impact cases (three drops, tdi, and four-drops, qdi) having w = 1.4 m/s and different inter-drop spacing. Results for single drop impacts for drops having the same volume (sdi) and two times the volume (sdi2V) are also added for comparison.
4. Conclusions
Numerical simulations of double and multiple synchronised drop impacts were performed using the interFoam solver of the OpenFOAM® open-source CFD package. Results for double drop impacts were validated against experimental data acquired by high-speed imaging. Crater shape and depth and vortex generation were compared between the simulation and experiments for double drop impacts, and a good agreement was found, particularly in the inertial phase (leading to the maximum crater penetration depth). Simulations were then performed to investigate energy conversion during the crater evolution, the effect of varying surface tension, and drop interspace and multiple drop impacts. The main findings are:
- Energy conversion between the kinetic and surface energies during double drop impacts shows a consistent behaviour very similar to that of single drop impacts, thus evidencing that it is not significantly influenced by the crater shape;
- Both the surface tension and the interspace have a very significant influence on the crater shape and depth. Concerning the surface tension, in real applications water is easily contaminated. This aspect must be kept in mind when using laboratory results obtained with distilled water. Concerning the drop interspace, obviously the more the drops are spaced, the more similar the crater evolution is to a single-drop impact case. More interestingly, when the drop interspace is large enough to avoid crater merging, the maximum depth reached by the crater is only slightly affected by the presence of other drops (even if the crater shape is heavily affected by the indirect (mediated by the liquid) interaction. Contrarily, when the craters merge, the maximum depth is heavily affected, with an increase that may reach more than the value corresponding to the impact of a single drop, with double the volume and mass.
In summary, direct extension of results from the study of single drop impacts to the case of multiple impacts with many unevenly spaced drops and non-simultaneous contact times (much more common in applications), appears not to be straightforward; on the contrary, neglecting mutual interactions can be quite misleading. It seems, therefore, mandatory to perform further studies including both more drops and different drop interactions (delayed impacts, different drop interspaces, etc.) to cast further light on these aspects. This would lead to the possibility of developing new models and correlations for multiple drop impacts, which are more reliable for use in all the applications fields where the phenomenon is of importance.
For such studies, improvements in the VOF approach may also be needed:
- Retarded coalescence or other related models should be added, to be able to manage situations in which interfaces are very near without need of extremely fine meshes. Otherwise, a much faster self-adaptive remeshing should be implemented;
- Hybrid methods, e.g., a combined VOF-Level Set, could be used to better manage the interface curvature and, consequently, reduce spurious velocities.
In addition, comparison with other methods (e.g., diffuse interface methods) could be interesting.
Author Contributions
Conceptualization, M.G., M.S., and S.F.-S.; Formal analysis, M.G., M.S., and S.F.-S.; Funding acquisition, S.F.-S.; Investigation, M.G., M.S., and S.F.-S.; Methodology, M.G.; Software, M.G.; Validation, M.G., M.S., and S.F.-S.; Visualization, M.G.; Writing—original draft, M.G., M.S., and S.F.-S.; Writing—review and editing, M.G., M.S., and S.F.-S.
Funding
This research received no external funding. The Research Grant of Stephanie Fest-Santini was financed within “Progetto ITALY® —Azione Giovani in Ricerca” of the University of Bergamo (Italy).
Acknowledgments
The contribution of Viola Knisel in performing the numerical simulations is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Worthington, A.M. On impact with a liquid surface. Proc. R. Soc. Lond. 1882, 34, 217–230. [Google Scholar] [CrossRef]
- Worthington, A.M. A Study of Splashes; Longmans Green and Co.: London, UK, 1908. [Google Scholar]
- Rein, M. Phenomena of liquid drop impact on solid and liquid surfaces. Fluid Dyn. Res. 1993, 12, 61–93. [Google Scholar] [CrossRef]
- Yarin, A.L. Drop impact dynamics: Splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Ashgriz, N. (Ed.) Handbook of Atomization and Sprays: Theory and Applications; Springer Science & Business Media: Berlin, Germany, 2011; ISBN 9781441972644. [Google Scholar] [CrossRef]
- Cole, D. The Splashing Morphology of Liquid-Liquid Impacts. Ph.D. Thesis, James Cook University, Townsville, Australia, 2007. [Google Scholar]
- Santini, M.; Cossali, G.E.; Marengo, M. Splashing characteristics of multiple and single drop impacts onto a thin liquid film. In Proceedings of the International Conference on Multiphase Flows, Leipzig, Germany, 9–13 July 2007. [Google Scholar]
- Bisighini, A.; Cossali, G.E. High-speed visualization of interface phenomena: Single and double drop impacts onto a deep liquid. J. Vis. 2011, 14, 103–110. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, G.; Shen, S.; Zhang, J. Double droplets simultaneous impact on liquid film. IOP Conf. Ser. Mater. Sci. Eng. 2015, 88, 012016. [Google Scholar] [CrossRef]
- Santini, M.; Fest-Santini, S.; Cossali, G.E. Experimental study of vortices and cavities from single and double drop impacts onto deep pools. Eur. J. Mech. B/Fluids 2017, 62, 21–31. [Google Scholar] [CrossRef]
- Roisman, I.V.; Prunet-Foch, B.; Tropea, C.; Vignes-Adler, M. Multiple Drop Impact onto a Dry Solid Substrate. J. Colloid Interface Sci. 2002, 256, 396–410. [Google Scholar] [CrossRef]
- Ray, B.; Biswas, G.; Sharma, A.; Welch, S.W.J. CLSVOF method to study consecutive drop impact on liquid pool. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 143–158. [Google Scholar] [CrossRef]
- Bouwhuis, W.; Huang, X.; Chan, C.U.; Frommhold, P.E.; Ohl, C.-D.; Lohse, D.; Snoeijer, J.H.; van der Meer, D. Impact of a high-speed train of microdrops on a liquid pool. J. Fluid Mech. 2016, 792, 850–868. [Google Scholar] [CrossRef]
- Oguz, H.N.; Prosperetti, A. Bubble entrainment by impact of a liquid drop on liquid surfaces. J. Fluid. Mech. 1990, 219, 143–179. [Google Scholar] [CrossRef]
- Rieber, M.; Frohn, A. A numerical study on the mechanism of splashing. Int. J. Heat Fluid Flow 1999, 20, 455–461. [Google Scholar] [CrossRef]
- Bussmann, M.; Mostaghimi, J.; Chandra, S. On a three-dimensional volume tracking model of droplet impact. Phys. Fluids 1999, 11, 1406. [Google Scholar] [CrossRef]
- Morton, D.; Rudman, M.; Liow, J.M. An investigation of the flow regimes resulting from splashing drops. Phys Fluids 2000, 12, 747. [Google Scholar] [CrossRef]
- Thoraval, M.-J.; Takehara, K.; Etoh, T.G.; Popinet, S.; Ray, P.; Josserand, C.; Zaleski, S.; Thoroddsen, S.T. von Karman Vortex Street within an Impacting Drop. Phys. Rev. Lett. 2012, 108, 264506. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comp. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S.J. A level set approach for computing solutions to incompressible two-phase flow. J. Comp. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Popinet, S.; Zaleski, S. A front tracking algorithm for accurate representation of surface tension. Int. J. Numer. Meth. Fluid. 1999, 30, 775–793. [Google Scholar] [CrossRef]
- Bonometti, T.; Magnaudet, J. An interface-capturing method for incompressible two-phase flows. Validation and application to bubble dynamics. Int. J. Multiph. Flow 2007, 33, 109–133. [Google Scholar] [CrossRef]
- Fuster, D.; Agbaglah, G.; Josserand, C.; Popinet, S.; Zaleski, S. Numerical simulation of droplets, bubbles and waves: State of the art. Fluid Dyn. Res. 2009, 41, 065001. [Google Scholar] [CrossRef]
- Albadawi, A.; Donoghue, D.B.; Robinson, A.J.; Murray, D.B.; Delauré, Y.M.C. Influence of surface tension implementation in Volume of Fluid and coupled Volume of Fluid with Level Set methods for bubble growth and detachment. Int. J. Multiph. Flow 2013, 53, 11–28. [Google Scholar] [CrossRef]
- Menard, T.; Tanguy, S.; Berlemont, A. Coupling level set/VOF/ghost fluid methods: Validation and application to 3D simulation of the primary break-up of a liquid jet. Int. J. Multiph. Flow 2007, 33, 510–524. [Google Scholar] [CrossRef]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, D.; Al-Rawahi, N.; Tauber, W.; Han, J.; Nas, S.; Jan, Y.-J. A Front-Tracking Method for the Computations of Multiphase Flow. J. Comp. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef]
- Zheng, H.W.; Shu, C.; Chew, Y.T.; Sun, J.H. Three-dimensional lattice Boltzmann interface capturing method for incompressible flows. Int. J. Numer. Meth. Fluids 2008, 56, 1653–1671. [Google Scholar] [CrossRef]
- Huang, J.J.; Shu, C.; Chew, Y.T. Lattice Boltzmann study of bubble entrapment during droplet impact. Int. J. Numer. Meth. Fluids 2011, 65, 655–682. [Google Scholar] [CrossRef]
- Gentner, F.; Rioboo, R.; Baland, J.P.; De Coninck, J. Low Inertia Impact Dynamics for Nanodrops. Langmuir 2004, 20, 4748–4755. [Google Scholar] [CrossRef] [PubMed]
- Telis-Romero, J.; Cabral, R.; Gabas, A.L.; Telis, V. Rheological properties and fluid dynamics of coffee extract. J. Food Process Eng. 2001, 24, 217–230. [Google Scholar] [CrossRef]
- Nixon, M.S.; Aguado, A.S. Feature Extraction and Image Processing, 2nd ed.; Academic Press: Cambridge, MA, USA, 2008; ISBN 9780080556727. [Google Scholar]
- Rodriguez, F.; Mesler, R. The penetration of drop-formed vortex rings into pools of liquid. J. Colloid Interface Sci. 1988, 121, 121–129. [Google Scholar] [CrossRef]
- Chapman, D.; Critchlow, P. Formation of vortex rings from falling drops. J. Fluid Mech. 1967, 29, 177–185. [Google Scholar] [CrossRef]
- Thoraval, M.-J.; Li, Y.; Thoroddsen, S. Vortex-ring induced large bubble entrainment during drop impact. Phys. Rev. E 2016, 93, 033128. [Google Scholar] [CrossRef]
- Saylor, J.; Grizzard, N. The optimal drop shape for vortices generated by drop impacts: The effect of surfactants on the drop surface. Exp. Fluids 2004, 36, 783–790. [Google Scholar] [CrossRef]
- Zou, J.; Ji, C.; Yuan, B.G.; Ren, Y.L.; Ruan, X.D.; Fua, X. Large bubble entrapment during drop impacts on a restricted liquid surface. Phys. Fluids 2012, 24, 057101. [Google Scholar] [CrossRef]
- Wang, A.-B.; Kuan, C.-C.; Tsai, P.-H. Do we understand the bubble formation by a single drop impacting upon liquid surface? Phys. Fluids 2013, 25, 101702. [Google Scholar] [CrossRef]
- OpenFOAM®. The Open Source CFD Toolbox. Available online: http://www.openfoam.org (accessed on 1 February 2019).
- Brackbill, J.U.; Khote, D.B.; Zemach, C. A Continuum Method for Modeling Surface Tension. J. Comp. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Gopala, V.R.; van Wachem, B.G.M. Volume of fluid methods for immiscible-fluid and free-surface flows. Chem. Eng. J. 1998, 141, 204–211. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comp. Sci. Discov. 2012, 5, 014016. [Google Scholar] [CrossRef]
- Trujillo, M.F.; Lewis, S.R. Thermal boundary layer analysis corresponding to droplet train impingement. Phys. Fluids 2012, 24, 112102. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Trujillo, M.F. Distinguishing features of shallow angle plunging jets. Phys. Fluids 2013, 25, 082103. [Google Scholar] [CrossRef]
- Costa, A.B.; Graham Cooks, R. Simulated splashes: Elucidating the mechanism of desorption electrospray ionization mass spectrometry. Chem. Phys. Lett. 2008, 464, 1–8. [Google Scholar] [CrossRef]
- Berberovic, E.; van Hinsberg, N.P.; Jakirlic, S.; Roisman, I.V.; Tropea, C. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Phys. Rev. E 2009, 79, 036306. [Google Scholar] [CrossRef]
- Roisman, I.V.; Weickgenannt, C.M.; Lembach, A.N.; Tropea, C. Drop impact close to a pore: Experimental and numerical investigations. In Proceedings of the ILASS—Europe 2010, 23rd Annual Conference on Liquid Atomization and Spray Systems, Brno, Czech, 6–9 September 2010. [Google Scholar]
- Trujillo, M.F.; Alvarado, J.; Gehring, E.; Soriano, G.S. Numerical simulations and experimental characterization of heat transfer from a periodic impingement of droplets. J. Heat Transf. 2011, 133, 122201. [Google Scholar] [CrossRef]
- Brambilla, P.; Guardone, A. Automatic tracking of corona propagation in three-dimensional simulations of non-normal drop impact on a liquid film. Computing 2013, 95, 415–424. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Trujillo, M.F.; Wu, X.; Chahine, G. Computational and experimental characterization of a liquid jet plunging into a quiescent pool at shallow inclination. Int. J. Heat Fluid Flow 2012, 34, 1–14. [Google Scholar] [CrossRef]
- Márquez Damián, S. Description and Utilization of InterFoam Multiphase Solver. Universidad Nacional del Litoral, Argentina. Available online: http://infofich.unl.edu.ar/upload/5e6dfd7ff282e2deabe7447979a16d49b0b1b675.pdf (accessed on 1 February 2019).
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comp. Phys. 2012, 231, 5653–5668. [Google Scholar] [CrossRef]
- Jasak, H.; Weller, H.G. Interface-Tracking Capabilities of the InterGamma Differencing Scheme; Technical Report; Imperial College of Science, Technology and Medicine, University of London: London, UK, 1995. [Google Scholar]
- Krause, F.; Li, X.; Fritsching, U. Simulation of droplet-formation and -interaction in emulsification processes. Eng. Appl. Comput. Fluid Mech. 2011, 5, 406–415. [Google Scholar] [CrossRef]
- Peck, B.; Sigurdson, L. The vortex ring velocity resulting from an impacting water drop. Exp. Fluids 1995, 18, 351–357. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).