Multi-Scale Modeling of the Dynamics of a Fibrous Reactor: Use of an Analytical Solution at the Micro-Scale to Avoid the Spatial Discretization of the Intra-Fiber Space
Abstract
:1. Introduction
2. Model Development
2.1. Problem Description
- Mass accumulation in the bulk liquid.
- Mass diffusion from the bulk liquid, across the boundary layer, and into the fibers.
- Mass diffusion, accumulation and consumption (via a first-order chemical reaction) in the intra-fiber space.
- Axial dispersion in the bulk liquid.
- The fiber locations are fixed.
- The system is isothermal.
- The first order reaction constant and the intra-fiber diffusion coefficient are constant.
- The bulk liquid concentration gradients in the perpendicular plane (along the fiber length), fiber aging and the pressure drop in the reactor are negligible. This implies that the bulk flow is strictly transverse to the fiber axes.
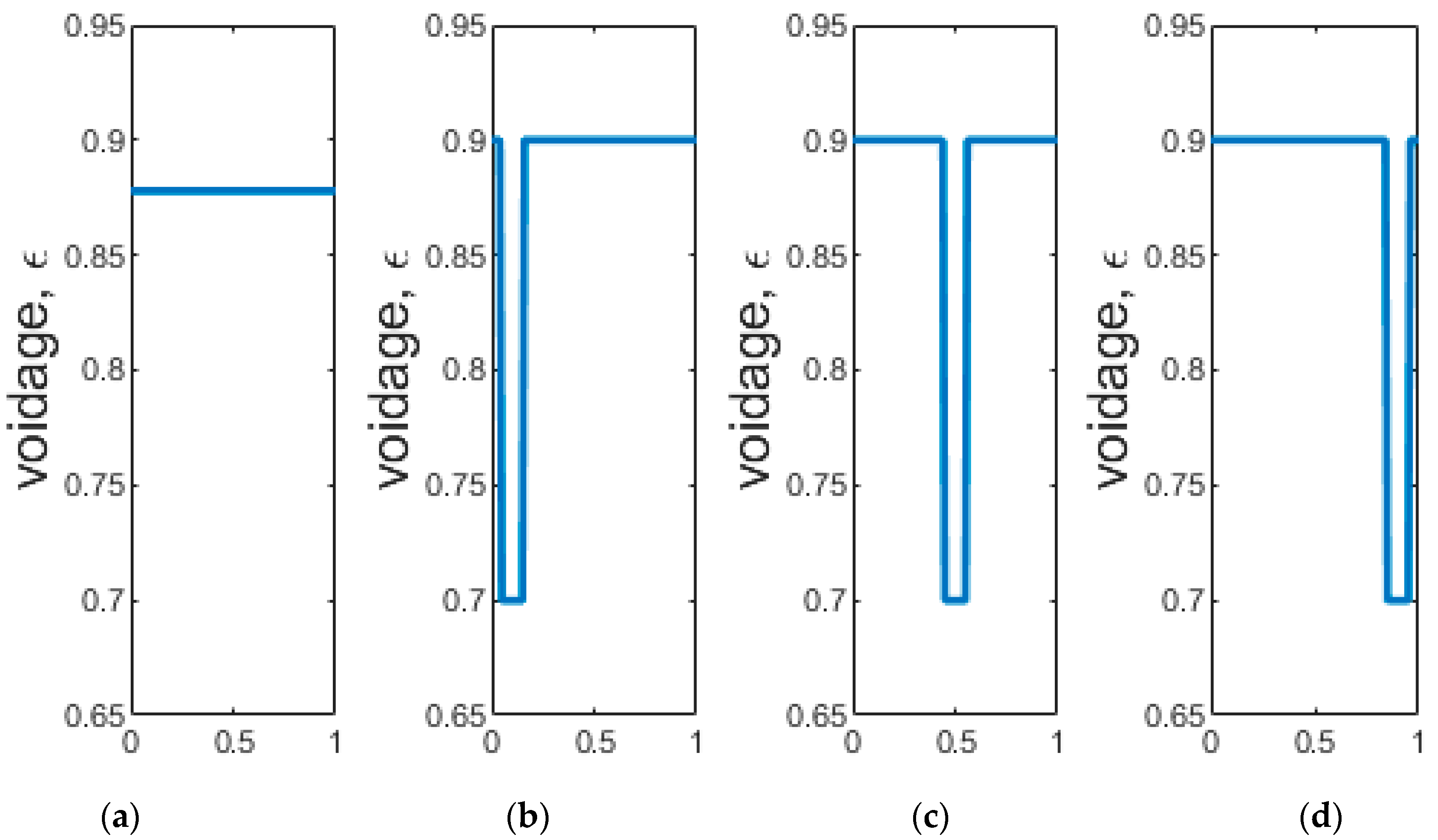
- The fibers are of uniform size and uniformly dispersed along the reactor.
2.2. Model Development
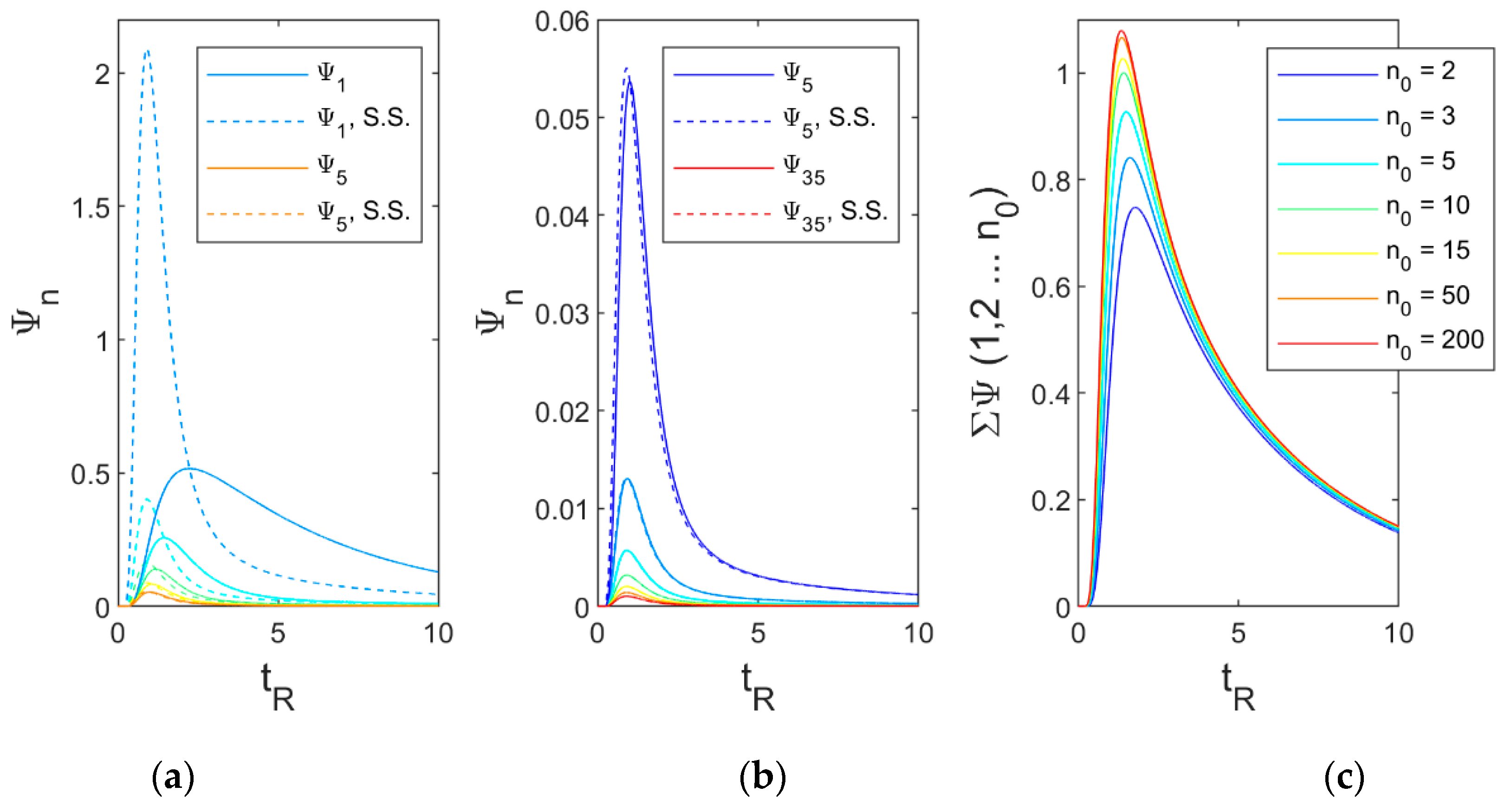
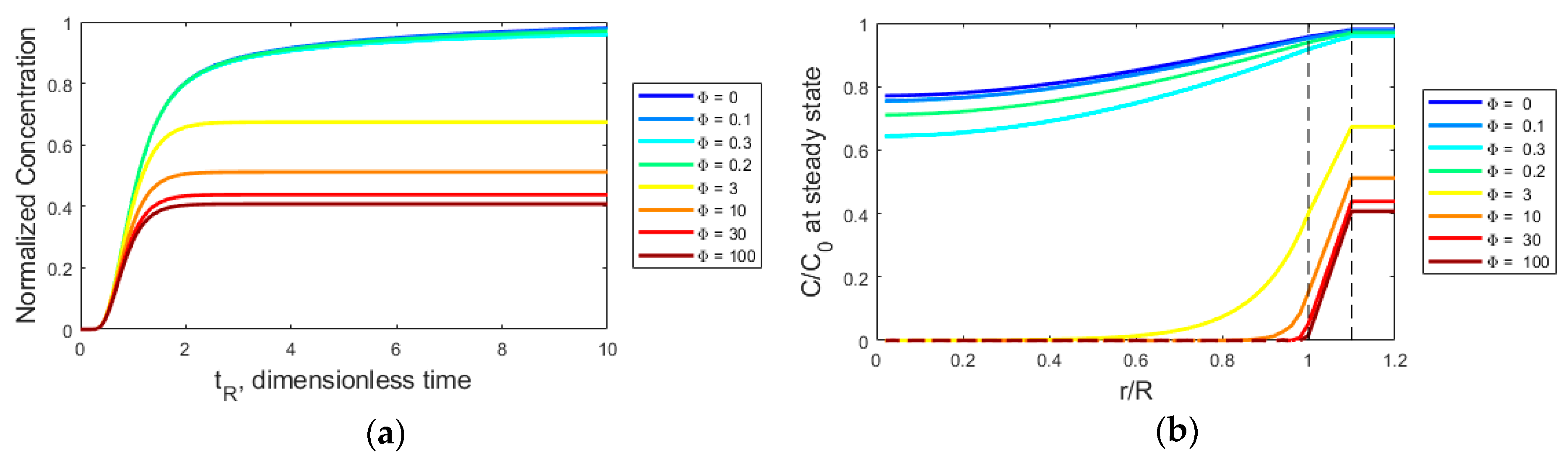
3. Results
4. Case Study
Author Contributions
Funding
Conflicts of Interest
Notation of Parameters
| positive roots of , where is a Bessel function of order | |
| reactor void fraction | |
| intra-fiber void fraction | |
| partition coefficient, | |
| functions defined by Equations (6) and (7) | |
| integration variable used in application of Duhamel’s Theorem | |
| Thiele modulus, | |
| Biot number (dimensionless), | |
| concentration in the bulk liquid at the inlet, mol/L | |
| concentration in the intra-fiber pore volume, mol/L | |
| concentration in the bulk liquid, mol/L | |
| concentration at the fiber surface, mol/L | |
| concentration at the innter side of the boundary layer, mol/L | |
| effective intrafiber diffusivity, m²/s | |
| axial dispersion coefficient, m²/s | |
| dimensionless diffusivity, | |
| reactor flow rate, L/s | |
| the parameter in parentheses evaluated at node | |
| first order reaction rate constant, s−1 | |
| external mass transfer coefficient, m/s | |
| parameter defined in Appendix A as | |
| reactor length, m | |
| number of terms to be solved | |
| number of nodes in the spatial discretization | |
| Péclet number, | |
| r | radial position within the fiber, m |
| fiber radius, m | |
| summation defined by Equation (A13) | |
| time, s | |
| dimensionless time, | |
| axial fluid velocity in the reactor, m/s | |
| total reactor volume, L | |
| dimensionless axial distance, | |
| axial distance from inlet, m |
Appendix A
Intra-Fiber Concentration Profile in the Presence of Diffusion and 1st Order Reaction under a Time-Varying Surface Concentration

References
- Cardellini, A.; Fasano, M.; Bigdeli, M.B.; Chiavazzo, E.; Asinari, P. Thermal transport phenomena in nanoparticle suspensions. J. Phys. Condens. Matter 2016, 28. [Google Scholar] [CrossRef] [PubMed]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A review of multiscale computational methods in polymeric materials. Polymers 2017, 9. [Google Scholar] [CrossRef] [PubMed]
- Sengar, A.; Kuipers, J.A.M.; van Santen, R.A.; Padding, J.T. Towards a particle based approach for multiscale modeling of heterogeneous catalytic reactors. Chem. Eng. Sci. 2019, 198, 184–197. [Google Scholar] [CrossRef]
- Boyle-Gotla, A.; Jensen, P.D.; Yap, S.D.; Pidou, M.; Wang, Y.; Batstone, D.J. Dynamic multidimensional modelling of submerged membrane bioreactor fouling. J. Membr. Sci. 2014, 467, 153–161. [Google Scholar] [CrossRef] [Green Version]
- Fusheng, O.; Yongqian, W.; Qiao, L. A lumped kinetic model for heavy oil catalytic cracking FDFCC process. Pet. Sci. Technol. 2016, 34, 335–342. [Google Scholar] [CrossRef]
- da Silva, W.P.; Precker, J.W.; Silva, C.M.D.P.S.E.; Gomes, J.P. Determination of effective diffusivity and convective mass transfer coefficient for cylindrical solids via analytical solution and inverse method: Application to the drying of rough rice. J. Food Eng. 2010, 98, 302–308. [Google Scholar] [CrossRef]
- Graiver, N.; Pinotti, A.; Califano, A.; Zaritzky, N. Mathematical modeling of the uptake of curing salts in pork meat. J. Food Eng. 2009, 95, 533–540. [Google Scholar] [CrossRef]
- Olafadehan, O.A.; Aribike, D.S.; Adeyemo, A.M. Mathematical modeling and simulation of steady state plug flow for lactose-lactase hydrolysis in fixed bed. Theor. Found. Chem. Eng. 2009, 43, 58–69. [Google Scholar] [CrossRef]
- Kerkhof, P.J.A.M. Countercurrent plug flow mass exchange with internal particle diffusion. Chem. Eng. Sci. 2007, 62, 2040–2067. [Google Scholar] [CrossRef]
- Andrievsky, A.; Brandenburg, A.; Noullez, A.; Zheligovsky, V. Negative magnetic eddy diffusivities from the test-field method and multiscale stability theory. Astrophys. J. 2015, 811. [Google Scholar] [CrossRef] [Green Version]
- Bec, J.; Biferale, L.; Cencini, M.; Lanotte, A.; Musachio, S.; Toschi, F. Heavy particle concentration in turbulence at dissipative and inertial scales. Phys. Rev. Lett. 2007, 98. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sulaiman, M.; Hammouti, A.; Climent, E.; Wachs, A. Coupling the fictitious domain and sharp interface methods for the simulation of convective mass transfer around reactive particles: Towards a reactive Sherwood number correlation for dilute systems. Chem. Eng. Sci. 2019, 198, 334–351. [Google Scholar] [CrossRef] [Green Version]
- Papathanasiou, T.D.; Kalogerakis, N.; Behie, L.A. Dynamic modelling of mass transfer phenomena with chemical reaction in immobilized-enzyme bioreactors. Chem. Eng. Sci. 1988, 43, 1489–1498. [Google Scholar] [CrossRef]
- Papadakis, E.; Pedersen, S.; Tula, A.K.; Fedorova, M.; Woodley, J.M.; Gani, R. Model-based design and analysis of glucose isomerization process operation. Comput. Chem. Eng. 2017, 98, 128–142. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxforn University Press: London, UK, 1975. [Google Scholar]
- Papathanasiou, T.D.; Bijeljic, B. Intraparticle diffusion alters the dynamic response of immobilized cell/enzyme columns. Bioprocess Eng. 1998, 18, 419–426. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobri, A.; Papathanasiou, T.D. Multi-Scale Modeling of the Dynamics of a Fibrous Reactor: Use of an Analytical Solution at the Micro-Scale to Avoid the Spatial Discretization of the Intra-Fiber Space. Fluids 2020, 5, 3. https://doi.org/10.3390/fluids5010003
Dobri A, Papathanasiou TD. Multi-Scale Modeling of the Dynamics of a Fibrous Reactor: Use of an Analytical Solution at the Micro-Scale to Avoid the Spatial Discretization of the Intra-Fiber Space. Fluids. 2020; 5(1):3. https://doi.org/10.3390/fluids5010003
Chicago/Turabian StyleDobri, Adam, and Thanasis D. Papathanasiou. 2020. "Multi-Scale Modeling of the Dynamics of a Fibrous Reactor: Use of an Analytical Solution at the Micro-Scale to Avoid the Spatial Discretization of the Intra-Fiber Space" Fluids 5, no. 1: 3. https://doi.org/10.3390/fluids5010003



