Flow in Fractured Porous Media Modeled in Closed-Form: Augmentation of Prior Solution and Side-Stepping Inconvenient Branch Cut Locations
Abstract
:1. Introduction
2. Complex Potential Solutions
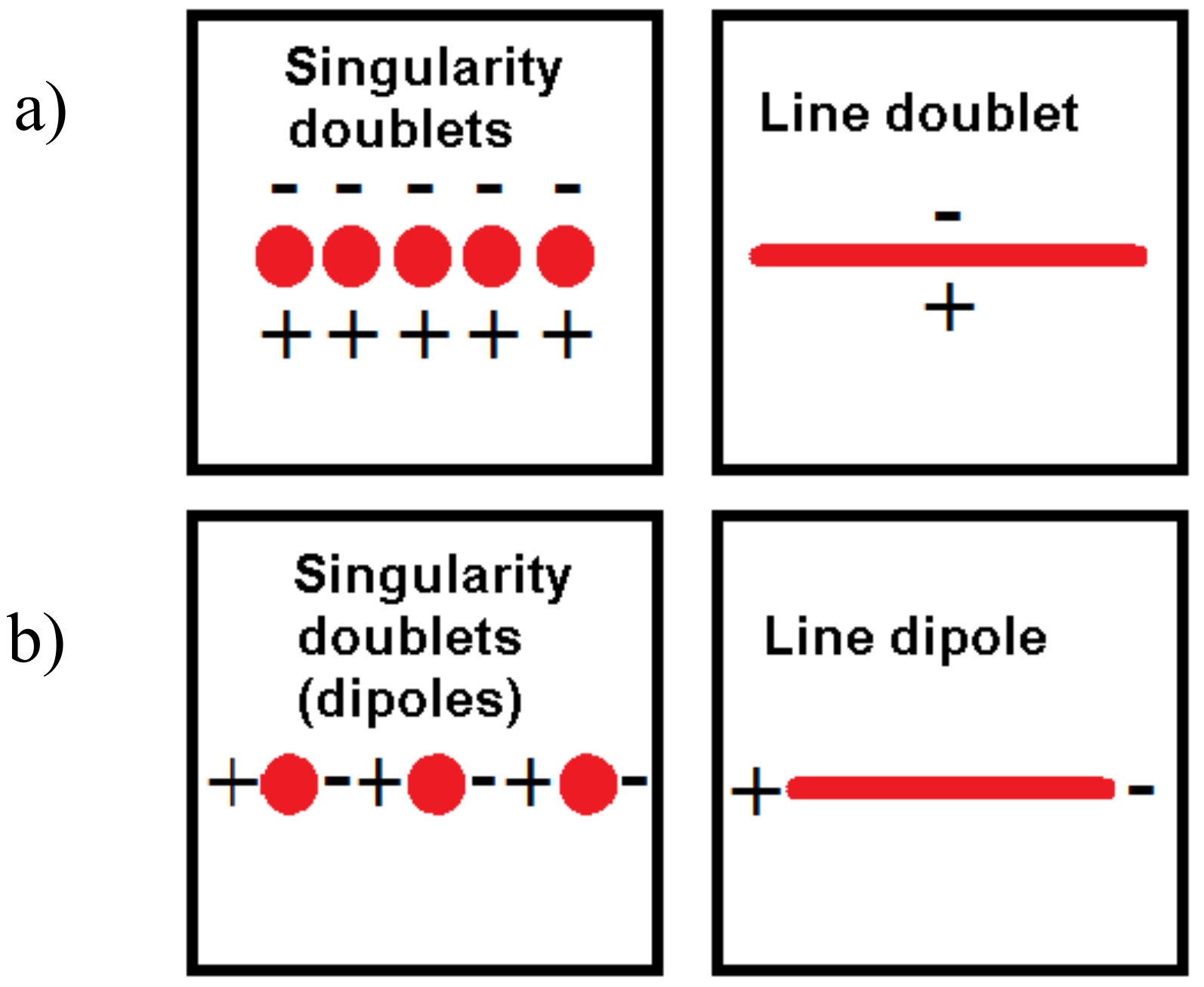
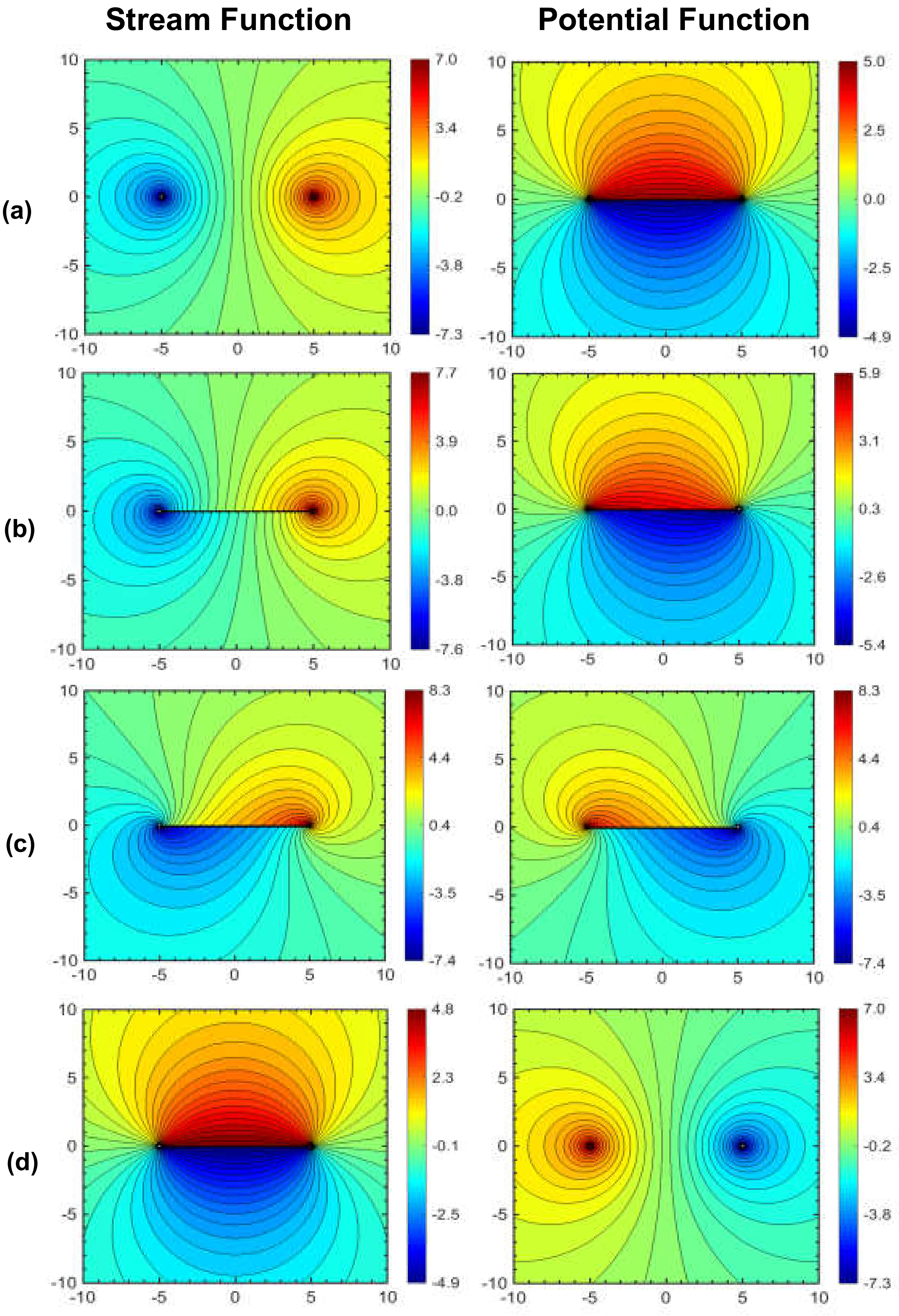
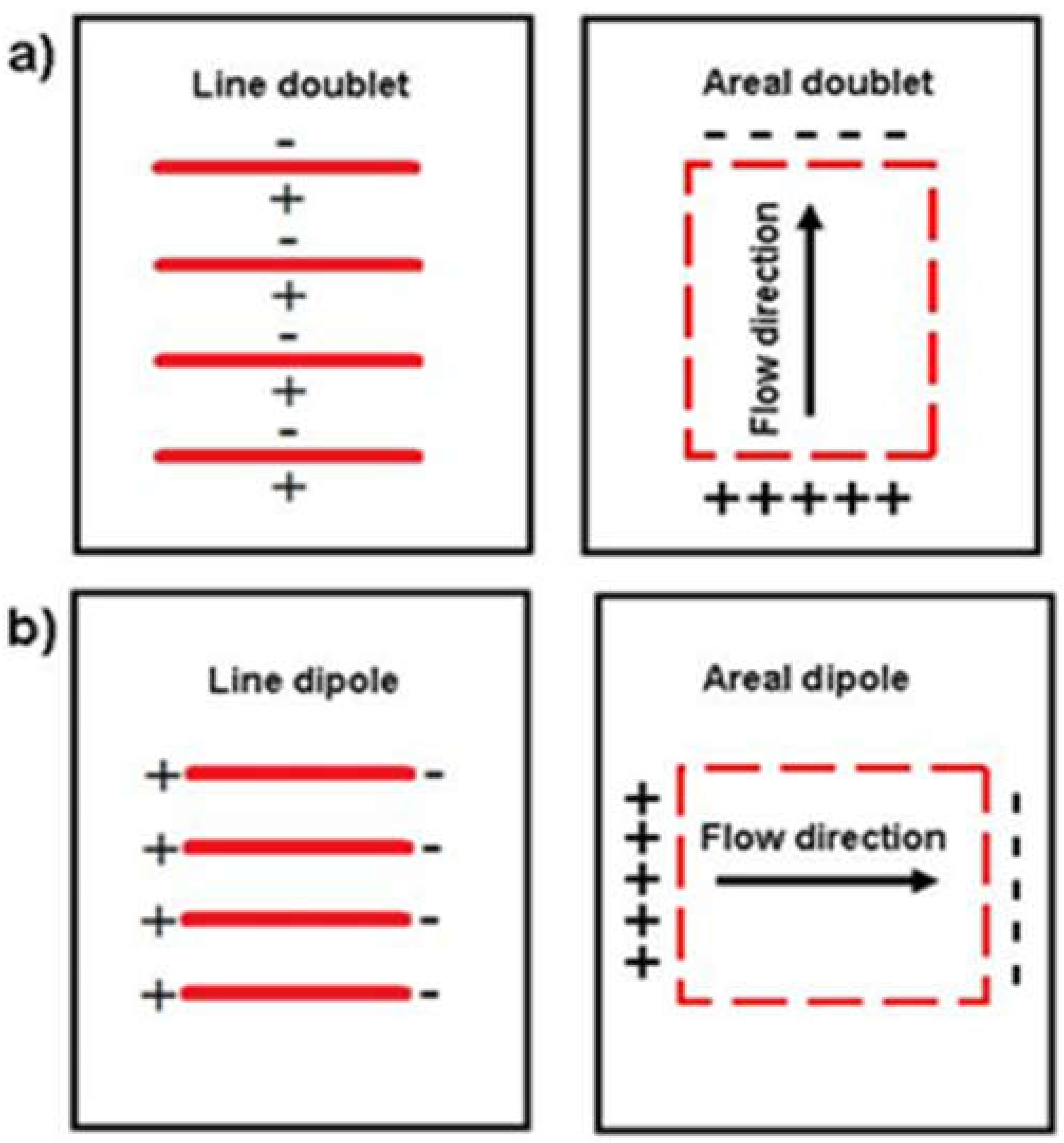
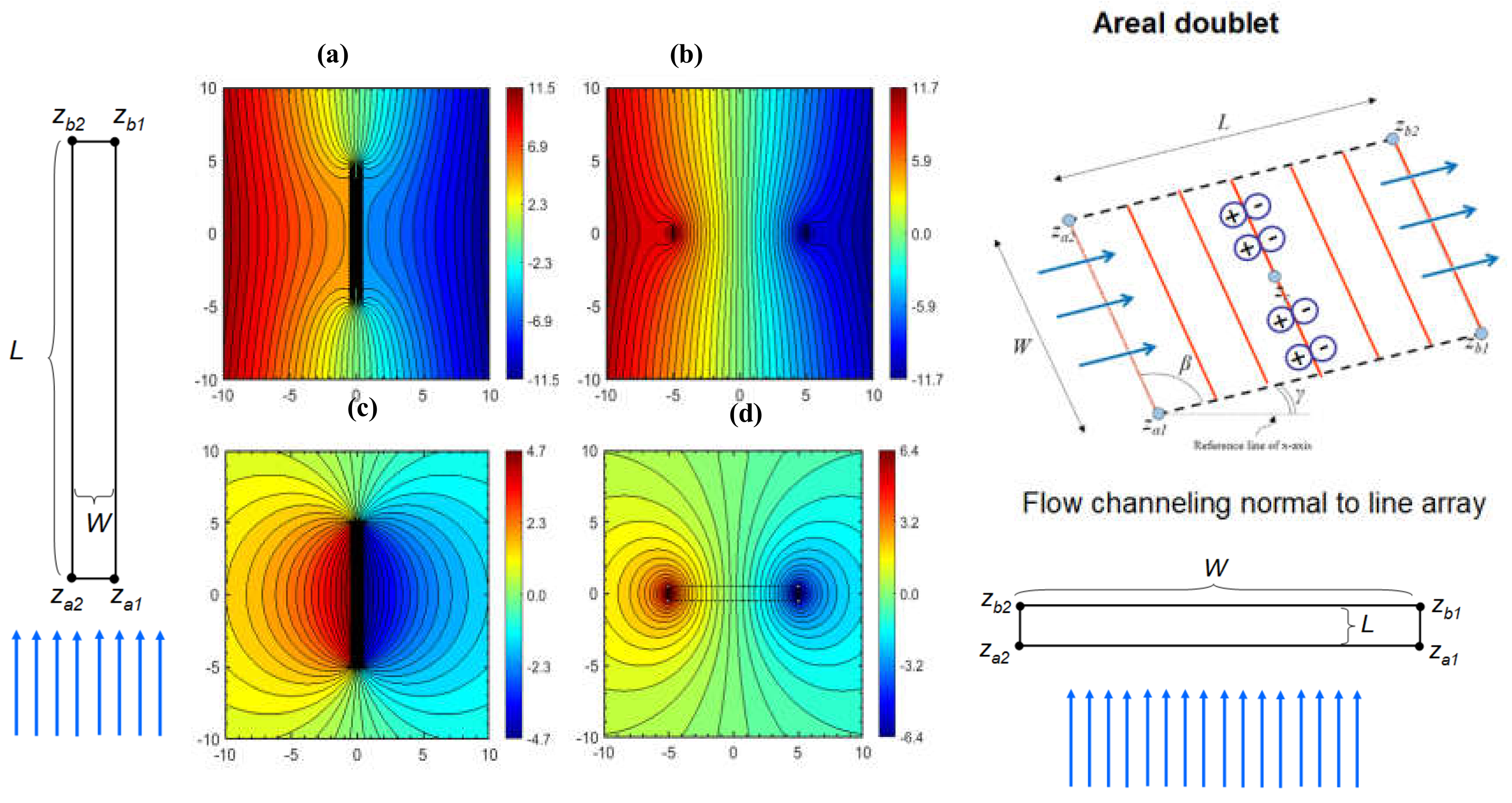
2.1. Line Doublets and Line Dipoles
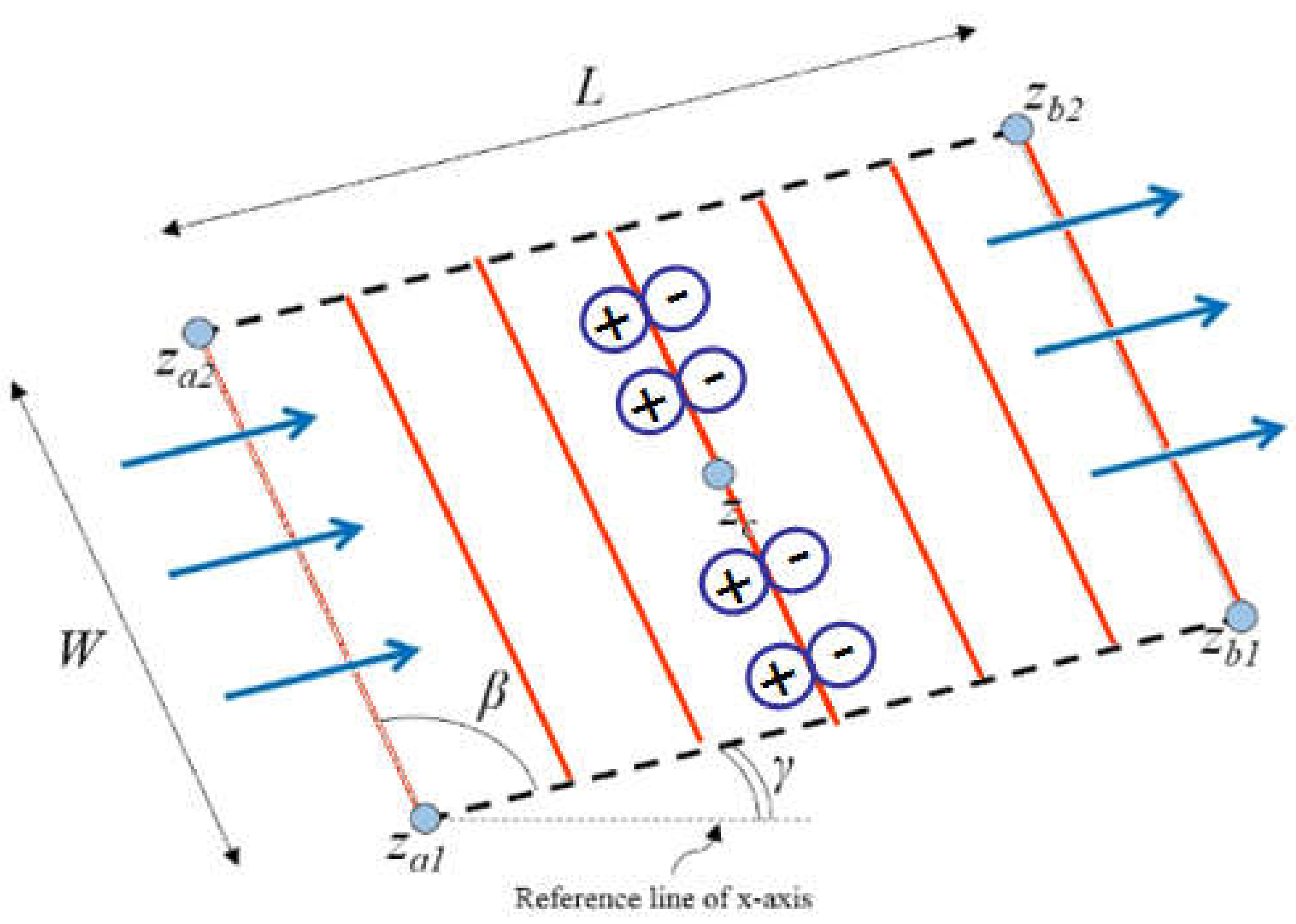
2.2. Areal Doublets and Areal Dipoles
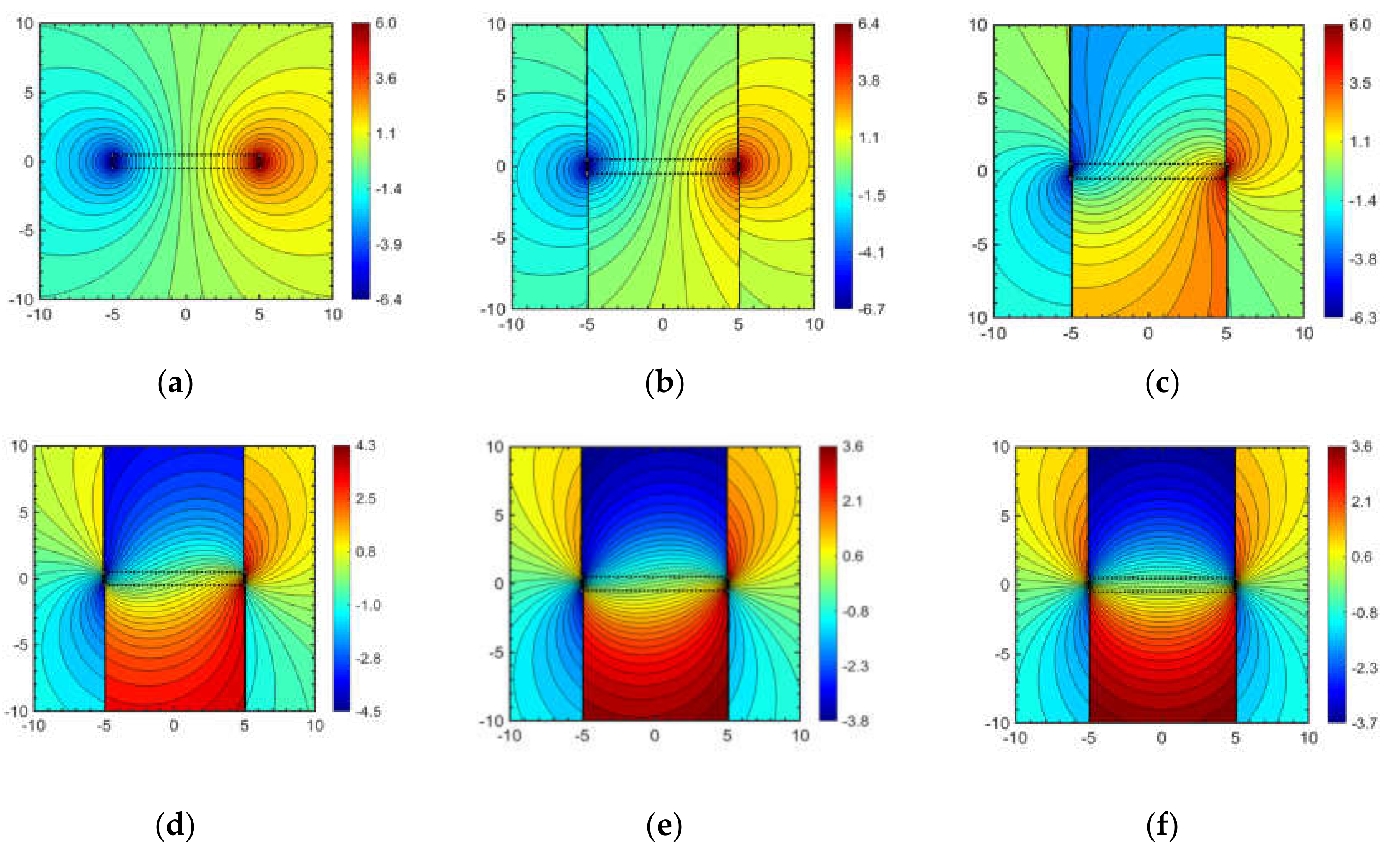
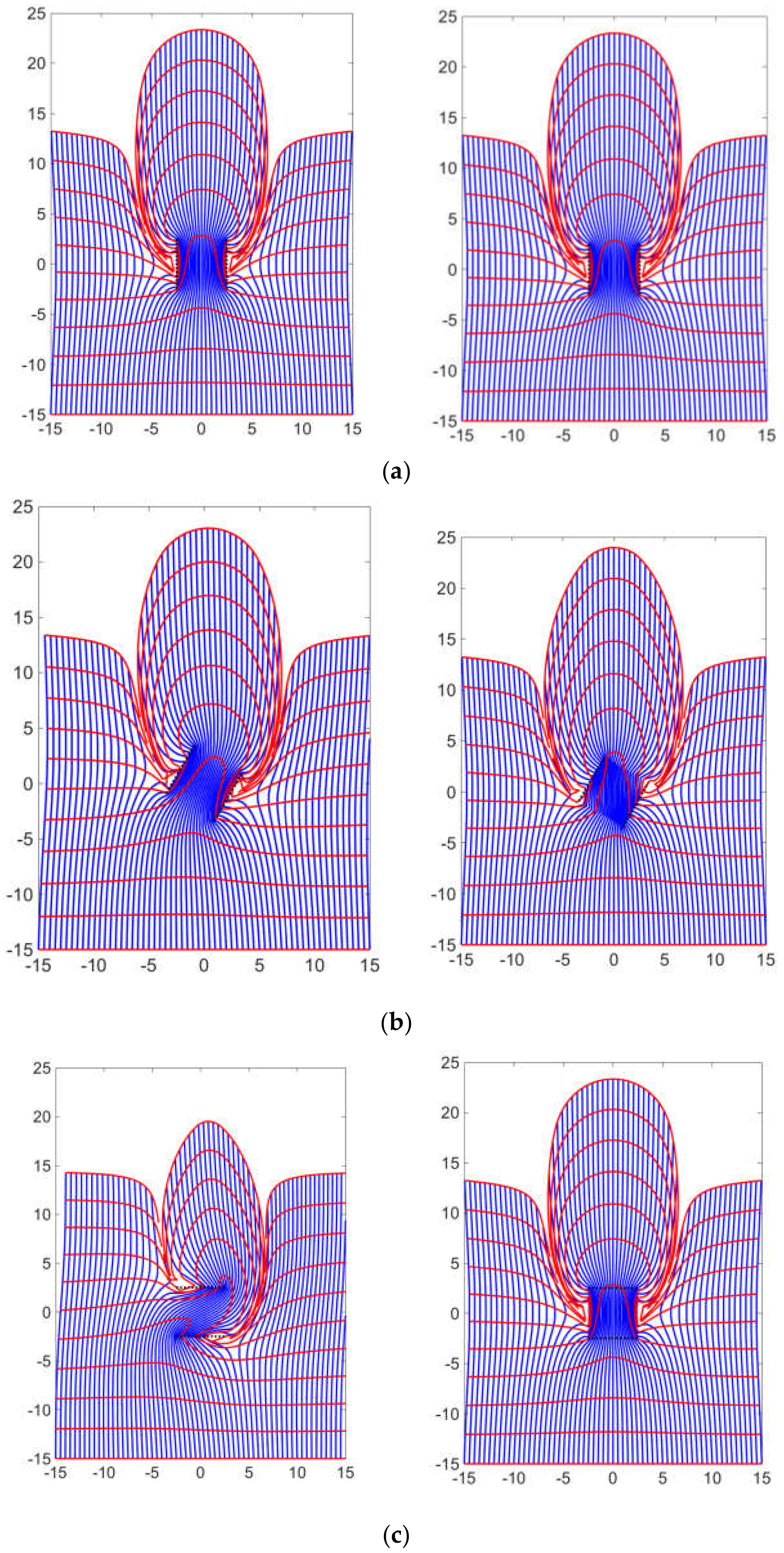
2.3. Branch Cut Effects
3. Augmented Solution
3.1. Shortcomings of the Prior Solution
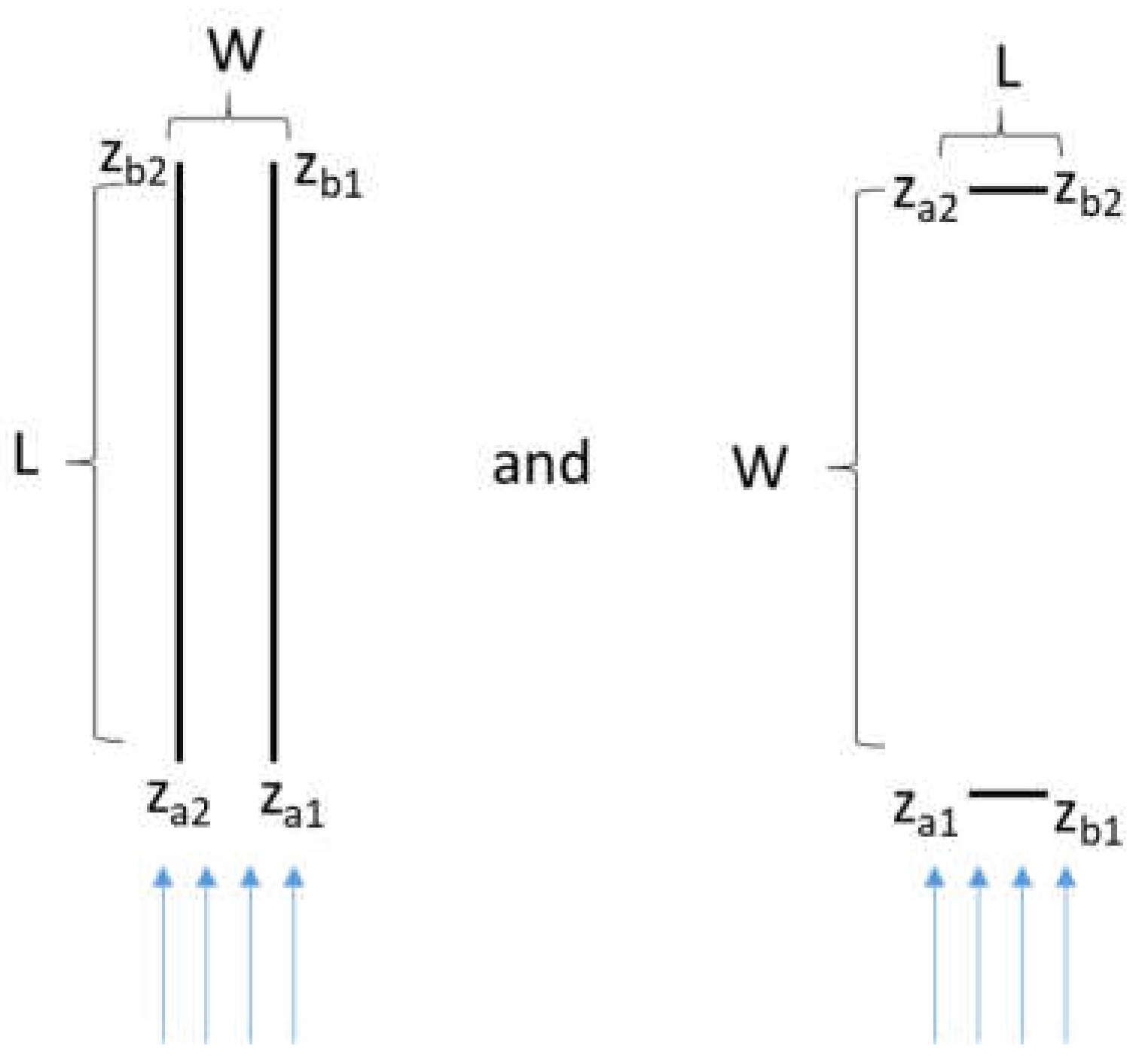
3.2. Areal Doublet Solution
3.3. Areal Dipole Solution
3.4. Superpositions
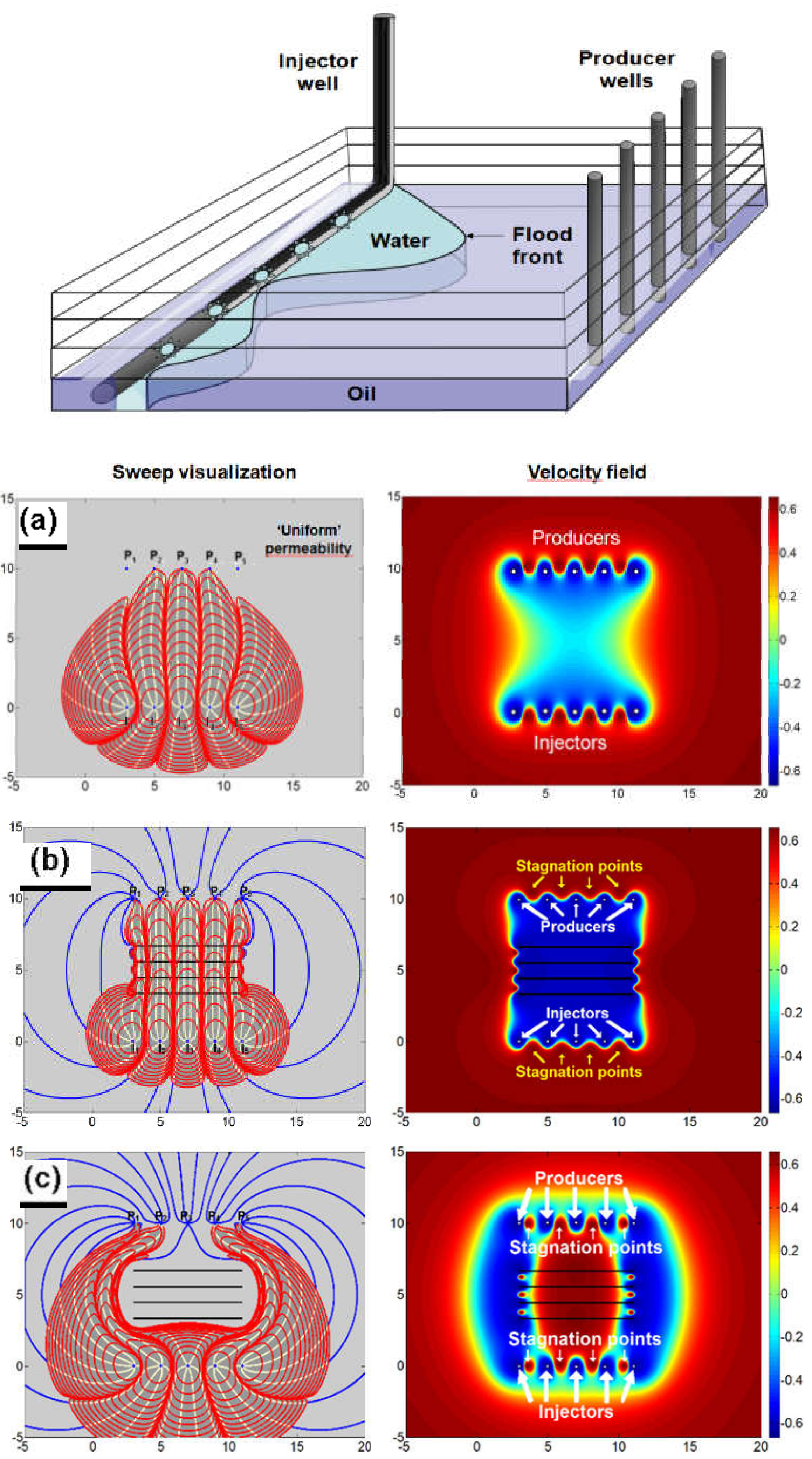
4. Application
4.1. Flow in Fractured Reservoirs
4.2. Field Application: Flow Near Hydraulic Fractures
4.3. Augmented Solution for Flow Near Hydraulic Fractures with Natural Fractures
4.4. Comparison of Results Augmented and Earlier Solution
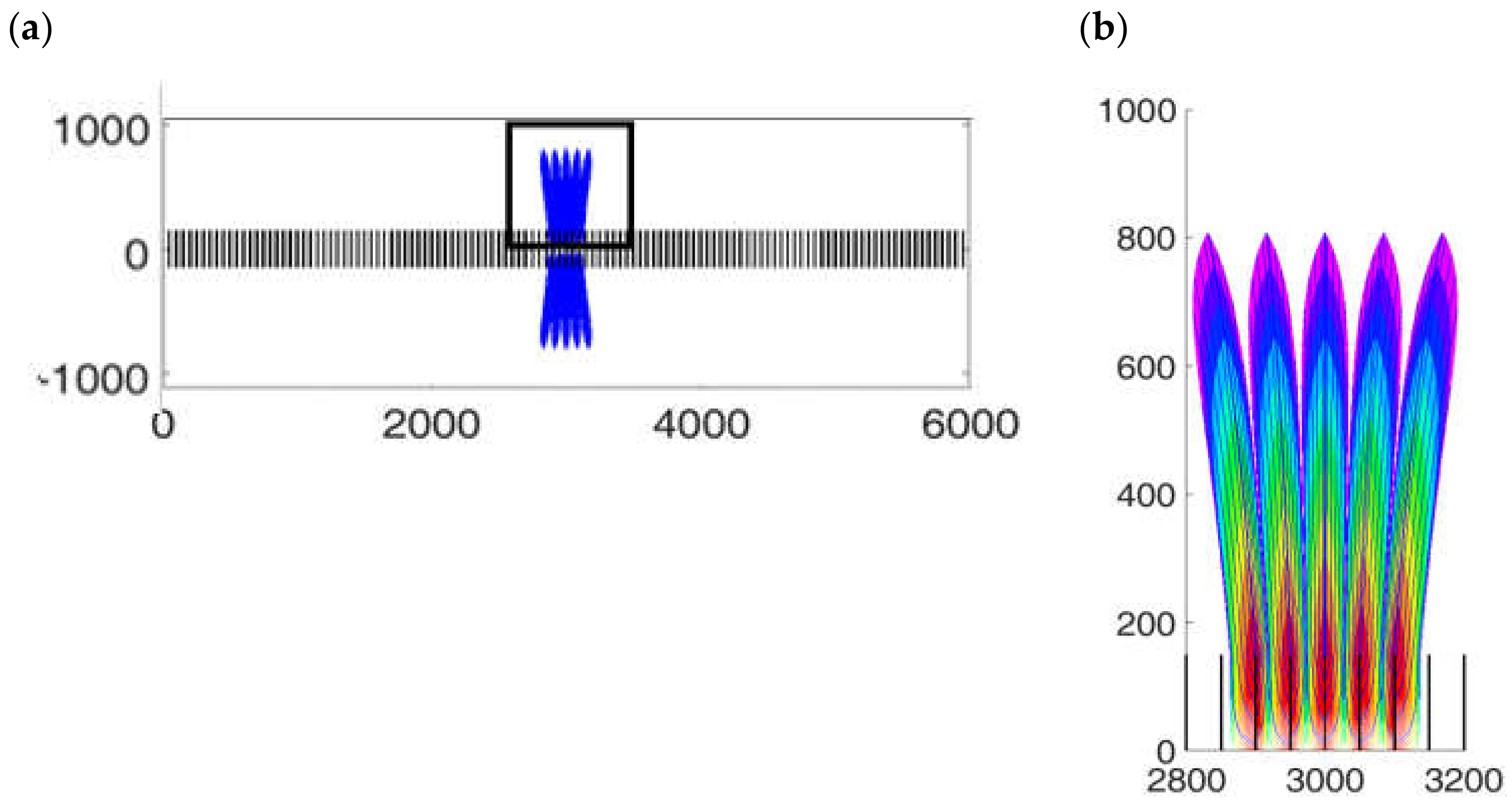
4.5. Verification
5. Discussion
5.1. Effect of Permeability Contrast
5.2. Model Strengths and Weaknesses
6. Conclusions
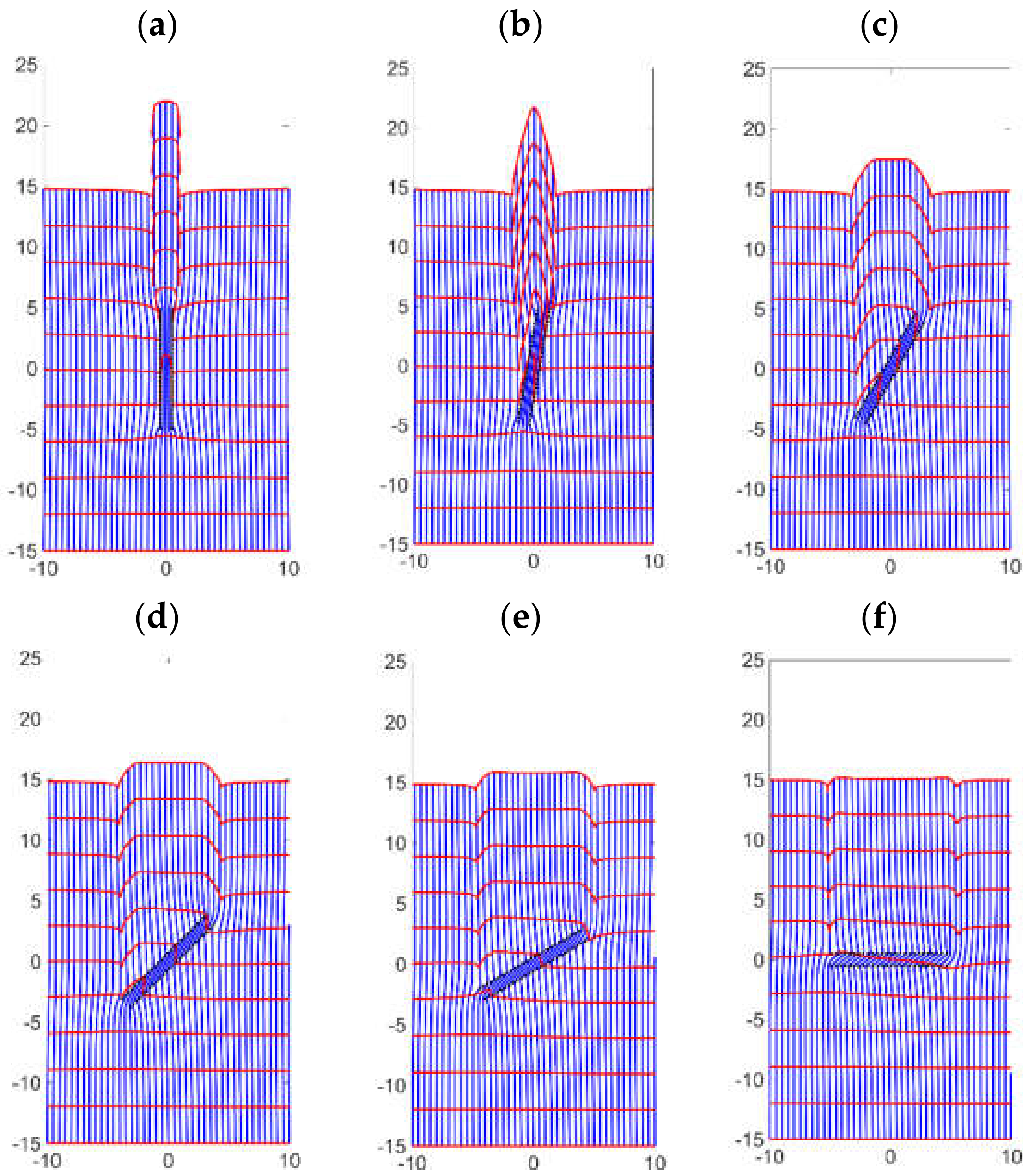
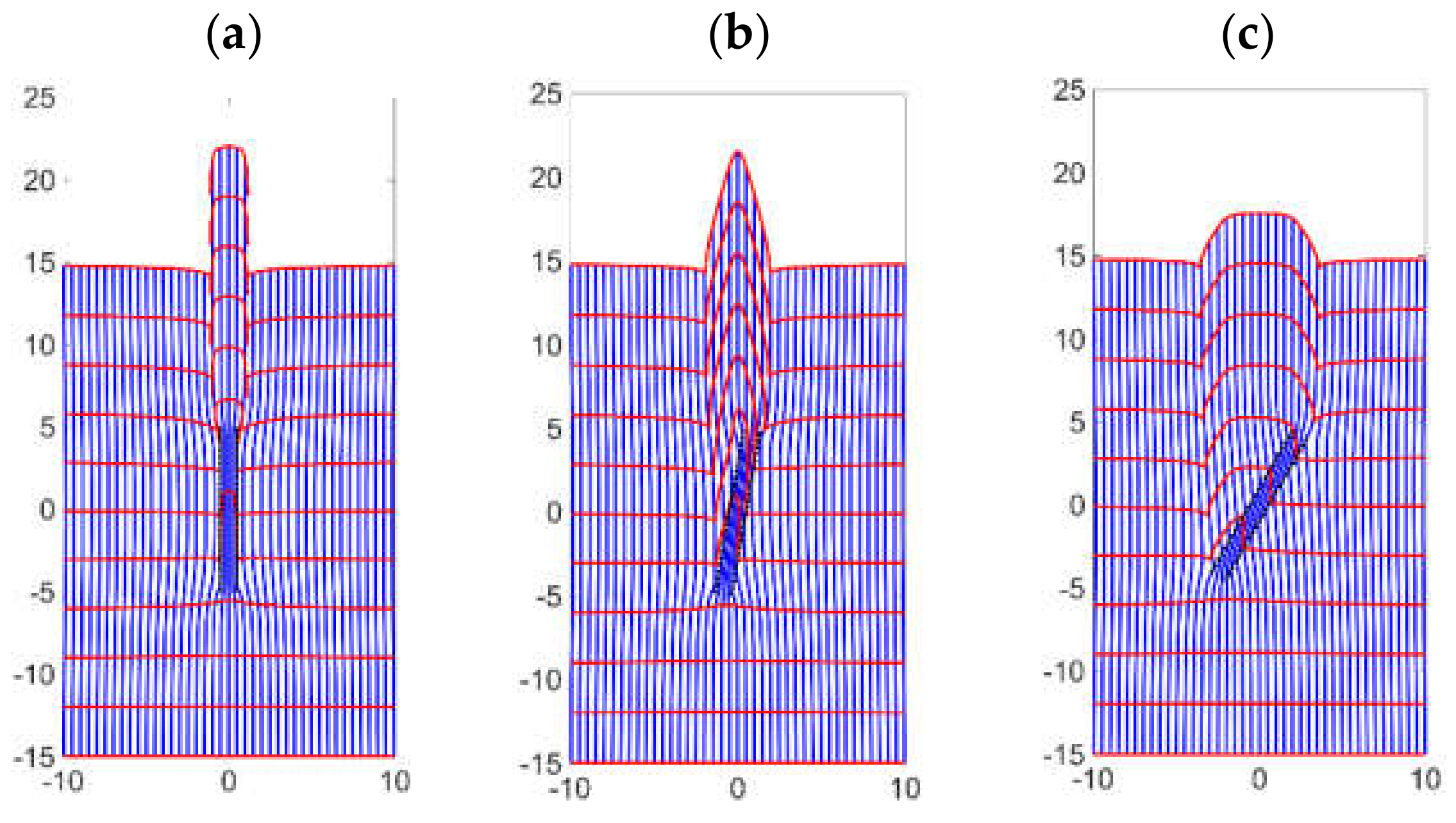
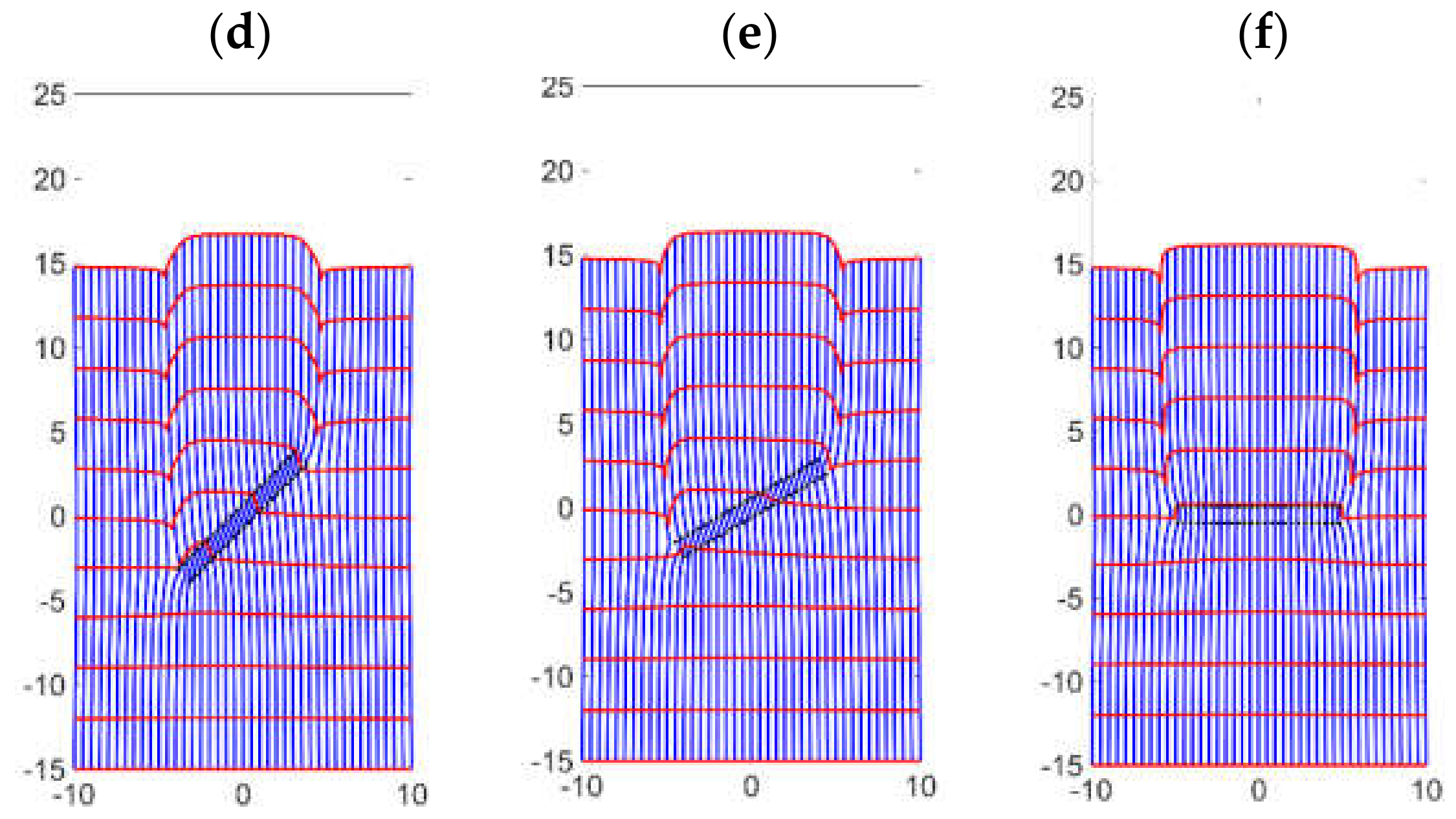
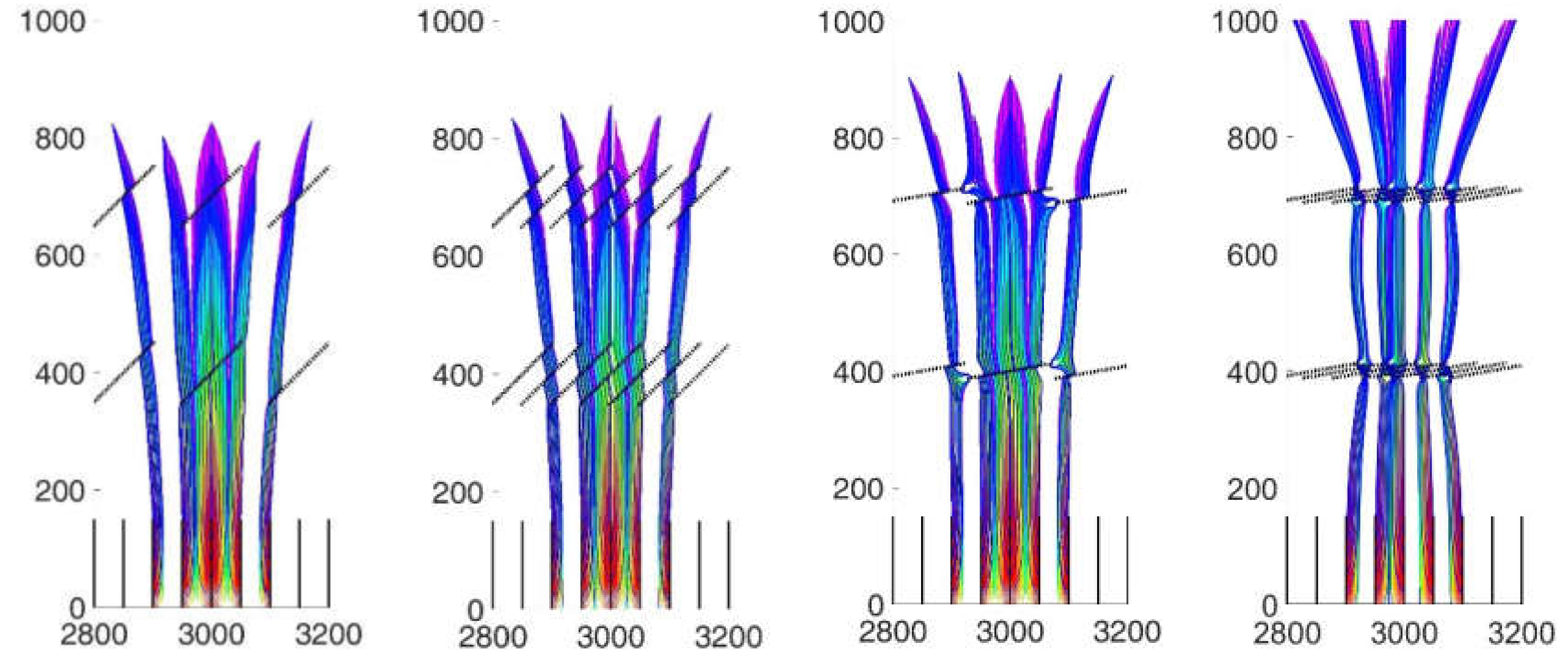
- Areal doublets can be used to model the flow in high conductivity flow channels such as the natural fractures in porous media. The natural fractures (areal doublets) distort the DRV and locally increase the velocity while modeling the flow in porous media (Figure 16).
- The modified areal doublet algorithm in Equation (12) yields a more realistic result for fractures oriented at a high angle with respect to the direction of fluid flow (Figure 16d).
- The augmented solution in the present study avoids the branch cuts and therefore provides an efficient method to model the flow paths of fluids in naturally fractured porous media.
Author Contributions
Funding
Conflicts of Interest
References
- Karimi-Fard, M.; Durlofsky, L.J.; Aziz, K. An efficient discrete-fracture model applicable for general-purpose reservoir simulators. Soc. Pet. Eng. 2004. [Google Scholar] [CrossRef]
- Moridis, G.J.; Blasingame, T.A.; Freeman, C.M. Analysis of mechanisms of flow in fractured tight-gas and shale-gas reservoirs. In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, Lima, Peru, 1–3 December 2010. [Google Scholar] [CrossRef] [Green Version]
- Olorode, O.; Freeman, C.M.; Moridis, G.; Blasingame, T.A. High-resolution numerical modeling of complex and irregular fracture patterns in shale-gas reservoirs and tight gas reservoirs. SPE Reserv. Eval. Eng. 2013, 16. [Google Scholar] [CrossRef]
- Sun, J.; Hu, K.; Wong, J.; Hall, B.; Schechter, D. Investigating the effect of improved fracture conductivity on production performance of hydraulic fractured wells through field case studies and numerical simulations. Soc. Pet. Eng. 2014. [Google Scholar] [CrossRef]
- Van Harmelen, A.; Weijermars, R. Complex analytical solutions for flow in hydraulically fractured hydrocarbon reservoirs with and without natural fractures. Appl. Math. Model. 2018, 56, 137–157. [Google Scholar] [CrossRef]
- Khanal, A.; Weijermars, R. Modeling flow and pressure fields in porous media with high conductivity flow channels and smart placement of branch cuts for variant and invariant complex potentials. Fluids 2019, 4, 154. [Google Scholar] [CrossRef] [Green Version]
- Weijermars, R.; van Harmelen, A.; Zuo, L. Controlling flood displacement fronts using a parallel analytical streamline simulator. J. Pet. Sci. Eng. 2016, 139, 23–42. [Google Scholar] [CrossRef]
- Strack, O.D.L. Groundwater Mechanics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Weijermars, R.; van Harmelen, A. Breakdown of doublet re-circulation and direct line drives by far-field flow: Implications for geothermal and hydrocarbon well placement. Geophys. J. Int. 2016, 206, 19–47. [Google Scholar] [CrossRef] [Green Version]
- Holzbecher, E. Streamline visualization of potential flow with branch cuts, with applications to groundwater. J. Flow Vis. Image Process. 2018, 25, 119–144. [Google Scholar] [CrossRef]
- Walton, I.; Mclennan, J. The role of natural fractures in shale gas production. Eff. Sustain. Hydraul. Fract. 2013, 327–356. [Google Scholar] [CrossRef]
- Aguilera, R. Effect of fracture compressibility on gas-in-place calculations of stress-sensitive naturally fractured reservoirs. SPE Reserv. Eval. Eng. 2008, 11, 307–310. [Google Scholar] [CrossRef]
- Kolawole, O.; Ispas, I. Interaction between hydraulic fractures and natural fractures: Current status and prospective directions. J. Petrol. Explor Prod. Technol. 2019. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Yu, W.; Wu, K.; Weijermars, R. Assessment of production interference level due to fracture hits using diagnostic charts. Soc. Pet. Eng. 2020. [Google Scholar] [CrossRef]
- Weijermars, R.; Van Harmelen, A. Advancement of sweep zones in waterflooding: Conceptual insight and flow visualizations of oil-withdrawal contours and waterflood time-of-flight contours using complex potentials. J. Pet. Explor. Prod. Technol. 2017, 7, 785–812. [Google Scholar] [CrossRef] [Green Version]
- Khanal, A.; Weijermars, R. Visualization of drained rock volume (DRV) in hydraulically fractured reservoirs with and without natural fractures using complex analysis methods (CAMs). Pet. Sci. 2019, 16, 550–577. [Google Scholar] [CrossRef] [Green Version]
- Olson, J.E. Multi-fracture propagation modeling: Applications to hydraulic fracturing in shales and tight gas sands. In Proceedings of the the 42nd U.S. Rock Mechanics Symposium (USRMS), San Francisco, CA, USA, 1 January 2008. [Google Scholar]
- Cipolla, C.L.; Lewis, R.E.; Maxwell, S.C.; Mack, M.G. Appraising unconventional resource plays: Separating reservoir quality from completion effectiveness. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 1 January 2011. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The behavior of naturally fractured reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Kazemi, H.; Merrill, L.S., Jr.; Porterfield, K.L.; Zeman, P.R. Numerical simulation of water-oil flow in naturally fractured reservoirs. SPE J. 1976, 6, 317–326. [Google Scholar] [CrossRef]
- March, R.; Elder, H.; Doster, F.; Geiger, S. Accurate dual-porosity modeling of co2 storage in fractured reservoirs. In Proceedings of the 2017 SPE Reservoir Simulation Conference, Montgomery, TX, USA, 20–22 February 2017. [Google Scholar] [CrossRef]
- Geiger, S.; Matthai, S.K.; Niessner, J.; Helmig, R. Black-oil simulations for three-component, three-phase flow in fractured porous media. SPE J. 2009. [Google Scholar] [CrossRef]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of an efficient embedded discrete fracture model for 3D compositional reservoir simulation in fractured reservoirs. SPE J. 2014, 19, 289–303. [Google Scholar] [CrossRef] [Green Version]
- Parsegov, S.G.; Nandlal, K.; Schechter, D.S.; Weijermars, R. Physics-driven optimization of drained rock volume for multistage fracturing: Field example from the Wolfcamp formation, Midland Basin. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018. [Google Scholar] [CrossRef] [Green Version]
- Weijermars, R.; Khanal, A. High-resolution streamline models of flow in fractured porous media using discrete fractures: Implications for upscaling of permeability anisotropy. Earth-Sci. Rev. 2019, 194, 399–448. [Google Scholar] [CrossRef]
- Weijermars, R.; Khanal, A.; Zuo, L. Fast models of hydrocarbon migration paths and pressure depletion based on complex analysis methods (CAM): Mini-review and verification. Fluids 2020, 5, 7. [Google Scholar] [CrossRef] [Green Version]
- Zuo, L.; Weijermars, R. Rules for flight paths and time of flight for flows in heterogeneous isotropic and anisotropic porous media. Geofluids 2017, 2017, 5609571. [Google Scholar] [CrossRef] [Green Version]
- Weijermars, R. Improving well productivity—Ways to reduce the lag between the diffusive and convective time of flight in shale wells. J. Pet. Sci. Eng. 2020, in press. [Google Scholar]




| Quantity | Value | Units | Symbol |
|---|---|---|---|
| Matrix Porosity | 0.1 | n | |
| Center of the line element | 0 | m | zc |
| Length | 10 | m | L |
| Tilt angle | 0 | ° | β |
| Strength | 0.01 | m4 s−1 | m(t) |
| Height | 1 | m | H |
| Polarity | (a) 90°, (b) 45°, (c) 10°, (d) 0° | ° | θ |
| Attributes of Reservoir and Hydraulic Fractures | |||||||
|---|---|---|---|---|---|---|---|
| Reservoir height | 60 ft (18.3 m) | ||||||
| Porosity | 4.4% | ||||||
| Hydraulic fracture half-length | 150 ft (45.7 m) | ||||||
| Residual oil saturation | 0.25 | ||||||
| Initial Strength (m0) | 8.47 ft2/day (0.79 m2/day) | ||||||
| Formation volume factor (B) | 1.05 RB/STB | ||||||
| Attributes of Areal Doublets (Natural Fractures) | |||||||
| Figure | Length | Width | Height (ft) | No. of natural fractures | Orientation (with respect to wellbore) | Strength (ft4/day) | Permeability Contrast Ratio |
| 15a | 150 ft (45.7 m) | 3 ft (0.91 m) | 60 ft (18.3 m) | 6 | 45° | 6 × 103 ft4/day 51.8 m4/day | 7.87 |
| 15b | 150 ft (45.7 m) | 3 ft (0.91 m) | 60 ft (18.3 m) | 14 | 45° | 6 × 103 ft4/day 51.8 m4/day | 7.87 |
| 15c | 150 ft (45.7 m) | 3 ft (0.91 m) | 60 ft (18.3 m) | 6 | 10° | 60 × 103 ft4/day 518 m4/day | 78.68 |
| 15d | 150 ft (45.7 m) | 3 ft (0.91 m) | 60 ft (18.3 m) | 14 | 10° | 60 × 103 ft4/day 51.8 m4/day | 78.68 |
| Natural Fracture Attributes | Symbol | Value |
|---|---|---|
| Natural fracture width (m) | W | 5 |
| Natural fracture length (m) | L | 5 |
| Natural fracture height (m) | H | 1 |
| Natural fracture angle to far-field flow | α | (a) 90° (b) 60° (c) 0° |
| Porosity | n | 0.1 |
| Effective far-field flow rate (m/s) | ux/n | 3.12 × 10−8 |
| Effective natural fracture strength (m4/s) | υ/n | 2.97 × 10−6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weijermars, R.; Khanal, A. Flow in Fractured Porous Media Modeled in Closed-Form: Augmentation of Prior Solution and Side-Stepping Inconvenient Branch Cut Locations. Fluids 2020, 5, 51. https://doi.org/10.3390/fluids5020051
Weijermars R, Khanal A. Flow in Fractured Porous Media Modeled in Closed-Form: Augmentation of Prior Solution and Side-Stepping Inconvenient Branch Cut Locations. Fluids. 2020; 5(2):51. https://doi.org/10.3390/fluids5020051
Chicago/Turabian StyleWeijermars, Ruud, and Aadi Khanal. 2020. "Flow in Fractured Porous Media Modeled in Closed-Form: Augmentation of Prior Solution and Side-Stepping Inconvenient Branch Cut Locations" Fluids 5, no. 2: 51. https://doi.org/10.3390/fluids5020051
APA StyleWeijermars, R., & Khanal, A. (2020). Flow in Fractured Porous Media Modeled in Closed-Form: Augmentation of Prior Solution and Side-Stepping Inconvenient Branch Cut Locations. Fluids, 5(2), 51. https://doi.org/10.3390/fluids5020051





