1. Introduction
Undoubtedly, one of the most hazardous cases of hydrodynamic loading on ships, offshore and coastal structures, as well as on the novel wind and wave energy conversion systems originates from slamming phenomena [
1,
2,
3,
4]. The dominant characteristics of these phenomena are the typically large velocities and accelerations of the water particles hitting the structure violently and the impulsive hydrodynamic pressures exerted on it. Careless design of structures exposed to this kind of loading may lead to devastating effects. These phenomena may be categorized in water entry problems, wave impact problems and green water loading.
Wave impact problems lead unavoidably to mixed boundary value problems (bvp). This means that different type of conditions should hold in different portions of the boundary. The impacted region is governed by a Neumann condition and the free-moving free surface by a Dirichlet condition. The most common encountered problems associated with the hydrodynamic slamming are the water entry problems [
5,
6,
7,
8]. A typical example in naval engineering is the bow slamming of a ship navigating in a rough sea. The mathematical formulation of relevant problems involves a single free surface which is penetrated suddenly by a solid.
A more complicated configuration is that of a steep wave colliding with a structure. Breaking waves may be idealized leading to what we call “steep wave”, by assuming a totally flat free surface and a vertical wave front. This rectangular formation, which extends longitudinally to semi-infinite, collides with the structure with a specific velocity, exerting high impulsive loads depending on the instantaneous contact line between the solid and the water. This category of problems is more complicated than the water entry problems as it involves two free surfaces. There are few analytical solutions to relevant formulations. The impact on a vertical plate was investigated by approximating the cross section of the plate as a degenerate ellipse, making use of the special Mathieu functions [
9]. This study was further expanded by introducing an open rectangular section on the plate, which allowed the water to escape the plate during impact [
10]. The bvp needed a special treatment as it involved triple trigonometrical series [
11]. Of great significance in the ocean is the hydrodynamic loading exerted on cylinders. Clearly, cylinders constitute the most important structural components of floating structures as they are used either as pontoons or as vertical axisymmetric pillars supporting the deck. Research on such an important subject has been conducted recently and results were presented for the hydrodynamic loading and the pressure impulse exerted on the cylinder by determining the actual contact line between the cylinder and the wave front at every time instant [
12].
Wave breaking in the open ocean is of major concern for offshore platforms and for floating wind turbines [
13,
14] as it could lead to critical failures of crucial structural elements. There are several studies focusing on the hydrodynamic pressures exerted on a wall by a breaking wave. Breaking criteria and categorization of breaker types depend of the physical parameters of the problem related to the shape of the structure [
15]. However, sometimes, the limiting state of one type to another is rather unclear. The vast majority of the reported results rely on numerical simulations [
16,
17,
18,
19,
20,
21]. The intensity of this phenomenon is strongly affected by the relative distance between the breaking point and the wall. This distance is of paramount importance, as it affects directly the shape of the breaker, the amount of the entrapped/entrained air and the water depth in front of the wall, just before the impact. The roughness of the wall affects the maximum pressures. Different boundary conditions hold on the impacted region of the wall, depending in its characteristics, impermeable, porous or perforated etc. [
22]. The presence of the wall strongly affects the dynamics of the phenomenon, as the wave trough just in front of it, suddenly moves upwards with typically large velocities [
23]. The location of the structure relative to the breaking point also strongly influences the peak pressure and the analogous rise time [
24].
Fundamental results on relevant subjects have been provided by experimental studies as well. Large-scale regular wave tests have shown that greater pressures were exerted on a vertical wall than on a slopping, while the impulse owing to the impact can reach up to 30% of the total impulse on the wall [
25]. Wave breaking is rather a localized phenomenon as for example during the flip-through impact, the trough moving upwards with large velocities, and the crest of the breaking wave focus towards a point on the wall [
26]. It has been shown that the first contact point is, more or less, in the vicinity of the still water level and the pulsation of the air pocket due to the compression leads to an oscillating behavior of the pressure record versus time [
27]. Apart from a single cylinder and a vertical wall, more complicated structures were studied as well, e.g., a vertical wall with a horizontal cantilever slab just above it [
28]. Due to the first impact of the breaking wave on the wall, the jet formed escaped upwards with great accelerations straight impacting the slab above the wall.
The significance of the air entrapment has been thoroughly investigated, as it affects directly the dynamics of the impact. Even though the large air pockets which may be entrapped during the overturning of the wave tend to reduce the maximum impact pressure on the wall, an effect known as “cushioning”, the time needed for the air to compress and afterwards expand, elongates the duration of the impact leading to a possible increase of the total impulse on the wall [
29]. A sophisticated modelling of the air pocket has been suggested by substituting a 2D air-pocket by a 3D square pillar with specific width, length and height. The compression of the air-pocket can be simulated via a spring of stiffness
[
30].
An interesting result is that, during a sequence of identical breaking waves, the pressure profile was found to vary significantly, in contrast to the total impulse, leading to the idea of “kinetic mass”, a mass of water of certain geometry replacing the actual wave [
31]. For calculating the pressure–impulse distribution, we need to know the breaker location and the shape of the wave close to the wall. For distances larger than the half the wave height, it can be shown that the wave parameters are not so important [
32]. The steeper the wave, the more localized the impact region, as proven by the velocity profile [
33]. Studies have been conducted to compare the results for impacts occurring in shallow waters and deep waters which shew that despite the fact that the walls or the breakwaters locate close to the coast, and the offshore structures are in deep water it was concluded that when the features of the wave kinematic and the impact zone are comparable in the shallow and deep water, so are the impact loads, regardless the water depth [
34].
In contrast, few studies have dealt with this problem analytically, basically due to the mathematical difficulties arising for the solution of a mixed bvp. In Reference [
35], a breaking wave hitting briefly and violently the wall was considered, including two different impacted regions, with several impacting velocities and zero pressure in the air pocket. From the mathematical point of view, the solution method assumed a cosine-dependent Neumann condition on the wall and a Dirichlet condition in the air-pocket. The pressure impulse model was extended in [
36] by considering that, during impact, the entrapped air firstly decelerates the water and thereafter causes the water to move backwards, a phenomenon called “bounce-back”. It should be noted that the impulse exerted on the wall was attributed to the loss of the horizontal momentum of the wave because of the impact. Finally, a noticeable feature that should be mentioned is that the pressure impulse on the wall is not zero in the bed [
37].
This study is structured as follows:
Section 2 formulates the complete bvp.
Section 3 describes the perturbation method used in this study, which allows us to expand the total velocity potential in a series including a leading order and higher order terms.
Section 4 presents the mathematical analysis used to solve the bvp for the leading order of the potential.
Section 5 deals with the hydrodynamic pressure calculation on the wall and also discusses the way in which the singularity of the free surface in the intersection with the wall was tackled in this research. In
Section 6, we cite some results in terms of the first order velocity potential, the velocity distribution on the wall, the hydrodynamic pressures and the free surface elevation. Finally, the conclusions are drawn in
Section 7.
2. The Mixed-Type Hydrodynamic Impact bvp
The hydrodynamic impact problem under consideration is investigated with the aid of the schematic representation of
Figure 1. The impacted wall is hit by a breaking wave, which is greatly idealized in the following manner: (i) The upper part of the wave collides with the impermeable wall with steady velocity
. (ii) During impact, a cavity is formed that extends between
, according to the notations and the Cartesian coordinate system of the problem shown in
Figure 1. The width of the cavity is considered negligible and is assumed that is contained by air. Air compression effects are omitted. The flow is assumed to be incompressible, inviscid, and irrotational. The elevation of the free surface (free-surface disturbance) is denoted by
and is determined relative to
.
Within the linearized realm of the potential theory, the investigated hydrodynamic impact is governed by the following bvp:
Clearly, the velocity potential is denoted by and the problem is set into the two-dimensional (2D) space. Equation (1) is the Laplace equation that should hold in the entire liquid field, Equation (2) is the Neumann condition on the impacted part of the wall, while Equation (3) is the dynamic boundary condition on the front of the liquid in the cavity. No kinematic condition is considered in the liquid front of the cavity and accordingly no disturbance is taken into consideration. Note that Equation (3) is directly imposed on the wall, due to the negligible width of the cavity. Further, Equation (4) is the bottom condition, Equations (5) and (6) are respectively the linearized kinematic and dynamic boundary conditions on the free surface at and finally, Equation (7) is the far-field condition, which implies that any disturbance caused by the collision with the wall should vanish at infinity.
3. Perturbation Analysis
The problem is considered at the very early stages of the impact. Using the small-time approximation, we are allowed to expand the original governing set of Equations (1)–(7) into a sequence of perturbation systems. Clearly, the perturbation parameter is the time variable
, which is assumed indefinitely small. The perturbation series for the velocity potential and the wave elevation are taken in the form
Conditions (5) and (6) hold on the unknown boundary (interface between the liquid and the air)
. To cope with this issue and to convert the conditions on the fixed boundary of the undisturbed free surface, the relevant equations are expanded using a Taylor series around
.
Using Equations (8) and (9), Equations (10) and (11) are transformed into
Clearly, Equations (12) and (13) correspond to Equations (5) and (6). Higher order terms are accordingly omitted. For employing the perturbation analysis, we assume that . Hence, the bvp is composed by Equations (1)–(4), (7), (12) and (13) and equating like powers of , we obtain the perturbation systems at and , in terms of the leading- and the higher-order potentials and , respectively. Clearly, the derivation of through the associated system dictates the solution of the leading order problem.
3.1. The Leading Order Problem
The elevation
is obtained from Equation (12) after equating powers of
as
3.2. The Higher Order Problem
The elevation
is obtained from Equation (12) after equating powers of
as
Clearly, higher order problems are omitted. The evaluation of dictates the solution of the leading order bvp for . The elevations and are detached from the bvps and they can be obtained explicitly from the potentials. The solution of the higher order mixed bvp in terms of and is left for a future endeavor.
4. Solution for the Leading Order Mixed bvp
The leading order of the velocity potential is obtained from the solution of Equations (14)–(19). Using separable solutions for the Laplace equation, and taking into account Equations (17)–(19), it follows that
Expansion (28) satisfies Equations (14) and (17)–(19). The remaining Equations (15) and (16) determine a bvp of mixed type, which using Equation (28) yields
Both series of Equations (29) and (30) are divergent at
. This dual trigonometrical series [
38,
39], reveals a singularity for the velocity, explicitly at
. Letting
and
, the system of Equations (29) and (30) becomes identical with the one reported and analyzed by Sneddon [
40] (pp.151, 152), namely
for the special case
. Note that
herein is a constant. The solution to this problem is taken directly from Sneddon (p. 158), which reads
where
denotes the
th degree Legendre Polynomial and
The constant
yields from
Substituting the constant value for
into the above formulas, does not simplify significantly the computations. Without loss of generality, we may assume that
. All the elliptic integrals employed in this research are calculated using MATLAB’s [
41] built-in function “integral”, which allows the efficient approximation of improper integrals. The differentiations and accordingly the sought expansion coefficients
are treated numerically as well.
Figure 2 shows a relative oscillating behavior for the expansion coefficients for
and a progressive decrease to zero for higher modes. This implies a fast convergence for the solution sought. For the test cases examined herein, the computations employed nearly 200 modes, which secured a convergence of four significant digits for the velocity potential.
5. Hydrodynamic Pressure Distribution and Free-Surface Elevation
The pressure distribution in the liquid field is obtained from the linear term of the Bernoulli’s equation
The pressure exerted exactly on the wall, can be simply calculated by substituting in Equation (37). It is important to mention that due to the uncoupling of the potential from time using the perturbation series expansion, the pressure is literally calculated for a specific wave shape that hits the wall at a specific time instant.
The free-surface elevation is obtained from Equation (20), using again
, as
Letting next
, Equation (38) is cast into the time dependent form
It should be mentioned that Equation (39) is divergent explicitly on the wall at
. That has been verified numerically given that the expansion coefficients are also obtained numerically to cope with the mixed bvp involved. For a solid impermeable wall, the corresponding series that provides the free-surface elevation yields a closed-form analytical solution [
42], which also grows indefinitely at
. From the physical point of view, the mathematical singularity could be attributed to the water jet that is formed at the instant of impact. King and Needham [
42] investigated the problem of the sudden acceleration of an impermeable wall (in 2D) that bounds a volume of liquid, initially at rest and they showed that the liquid run-up on the wall is obtained from
where
is a parameter that expresses the ratio between the wall acceleration to the gravitational acceleration. Clearly, the series in Equation (40) yields a unique solution which is singular as
, namely explicitly on the wall. To cope with the singular asymptotic behavior at
, King and Needham [
42] assumed two regions: (i) an outer region (
), where the expansion for the free-surface elevation (relied on the small-time approximation) is valid and (ii) an inner region (
), where the magnitude of the previously neglected terms of the Euler momentum equations they used are of the same magnitude as those retained. In the latter case they applied a different kind of expansion. In detail, the assumed expansion reads
where
and
denote respectively the first and second order free-surface elevations in the inner region, while
is the time.
The assumptions taken by King and Needham [
42] could be used in the present formulation, provided that the sums of Equations (38) and (40) exhibit the same behavior for
. The variations of the concerned sums relative to the mode number are shown in
Figure 3. Both sums grow indefinitely with the mode number and eventually become infinite. Although evident differences are observed, it can be easily deduced that they nearly coincide, and they become indistinguishable for large truncation of the sums. The wavy trend of the mixed bvp sum of Equation (38), is attributed to the values of the expansion coefficients
. Accordingly, the mixed bvp methodology discussed in the present is enhanced with King and Needham’s [
42] asymptotic analysis formulas explicitly for
.
In accord with the aforementioned discussion, the free-surface elevation can be approximated by
Following the asymptotic expansion suggested by King and Needham [
42], one gets for the inner region
Expression (43) has no singularity neither for
or
. In order to derive the complete expression for the free-surface elevation in the inner region, one finds
6. Results
The leading order velocity potential derived in
Section 4, exhibits several interesting characteristics.
Figure 4 shows that the wave impact velocity affects directly the potential distribution. In detail, the greater the velocity, the wider the curve is.
Further,
Figure 5 shows that the velocity potential far from the free surface
, is not identical even in the same impacted region and is strongly influenced by the air cavity position. In both
Figure 4 and
Figure 5, one can easily observe the semi-elliptical shape of the potential in the impacted region. Beyond it, in the air pocket cavity, is equal to zero, satisfying explicitly the Dirichlet dynamic boundary condition on the wall.
Figure 6 shows the velocity profiles connected with the test cases included in
Figure 4. In the impacted region the velocity is constant, while in the air pocket region a rapid decrease close to zero is observed. Furthermore, an evident discontinuity occurs at
, i.e., at the point where the formed cavity ends up, revealing a clear singularity for the velocity. It should be made clear that the observed singularity does not mean that the liquid penetrates the wall. In contrast, the singularity is evidence of jet formation.
Figure 7 and
Figure 8 depict the profiles of the hydrodynamic pressure distributions in a liquid field of
. The hydrodynamic pressure exhibits, as expected, the same pattern with the velocity potential. This assumption is validated by the 3D graph of
Figure 7, where the vertical semi-elliptical configuration and the zero pressure in the air pocket are evident. Moreover, one can easily observe the exponential decrease of the pressure with the distance from the wall.
The contours of the hydrodynamic pressure (that correspond to
Figure 7) are shown in
Figure 8. The isobaric lines testify that the highest pressures occur in the wave impact zone.
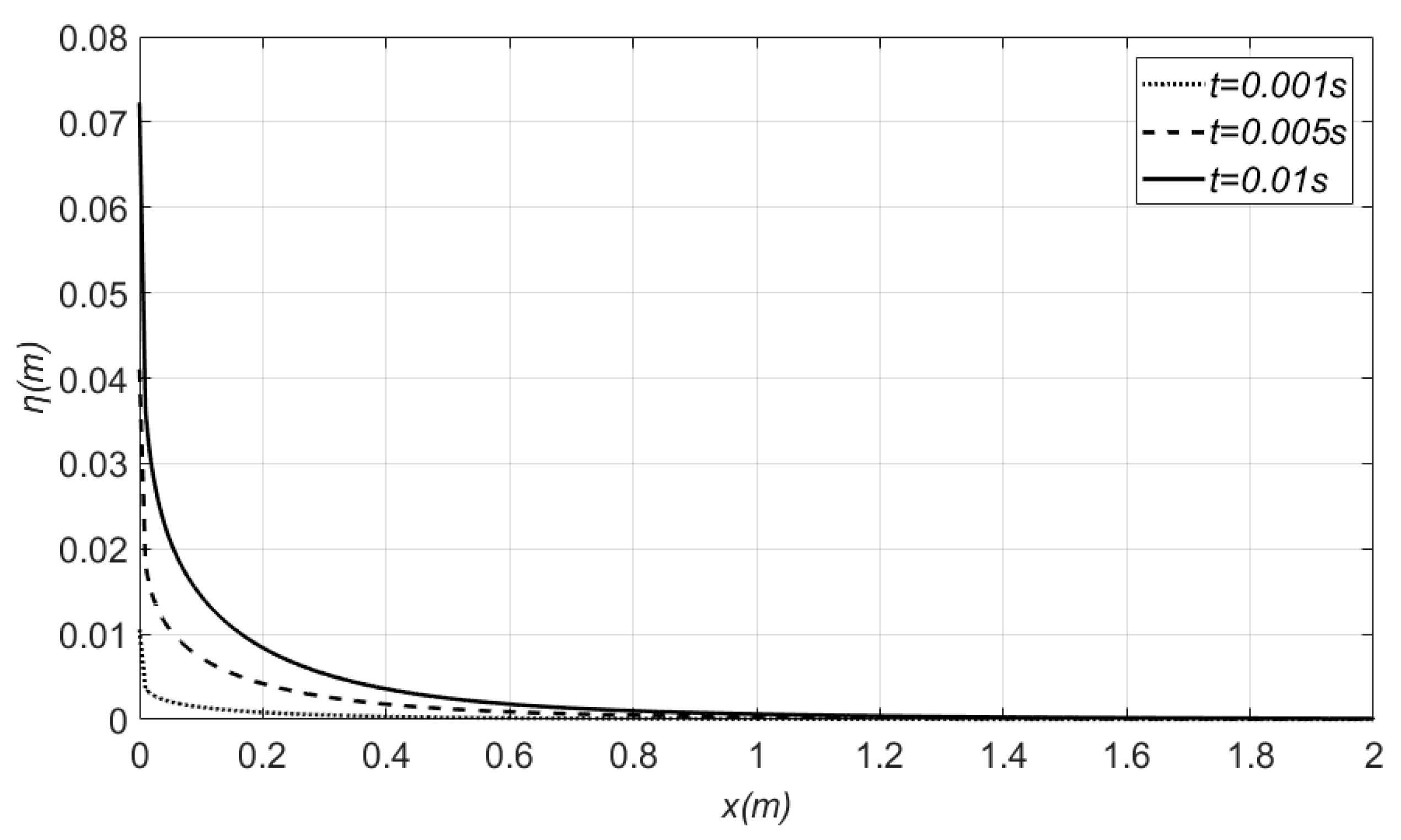
Figure 9 shows that the portion of the water, which collides with the wall, in the region of the free surface, is characterized by a greater run-up on the wall, as time evolves. Finally,
Figure 10 depicts the free-surface elevation for three different test cases. The wave run-up increases as the velocity is increased, a result which is totally reasonable. Nevertheless, an interesting result deduced from both figures is that for distance from the wall greater than
, the free surface is calm and coincides with the undisturbed level.
7. Conclusions
The present study treated the 2D problem of a plunging-like breaking wave impacting an impermeable wall. Linear potential theory was used along with the small-time approximation in order to eliminate the time-dependence from the solution. A perturbation method was used to satisfy the kinematic and the dynamic boundary conditions of the free surface on a fixed boundary, i.e., the still water level. The governing bvp of mixed type is solved analytically for the leading order of the velocity potential. The Neumann boundary condition on the impacted region and the Dirichlet condition beyond that must be satisfied, leading to a dual trigonometric series problem. The solution provided is based on the assumptions that the pressure in the cavity is zero and the compression effects are neglected. The singularity occurred in the intersection point of the free surface and the wall was tackled by adjusting the theory presented in the seminal paper of King and Needham [
42].
Numerical results are cited in terms of the velocity potential, velocity profiles, hydrodynamic pressure distributions for several impacting velocities and air cavity positions. Figures for the free-surface elevations are also provided showing the deformation over time and over the wave impact velocities. The main outcome of this research is that the peak pressure is situated in the middle of the impacted region of the wall. Further, the presence of the air pocket significantly affects the pressure distribution on the wall, even in the same impacted region, especially for increasing depth, and for the same hitting velocity. An interesting result is that for relative long distances from the impacted region, no deformation of the free-surface occurs.
It is the intention of the authors to extend this study by (i) considering a time varying intersection point a on the wall and (ii) solving the higher-order perturbation problem that is formulated via Equations (21)–(27). Clearly, the reasonable outcomes of the study should be validated against experimental measurements.