Three-Dimensional Convective Planforms for Inclined Darcy-Bénard Convection
Abstract
:1. Introduction
2. Governing Equations and Stability Analysis
3. Results and Discussion
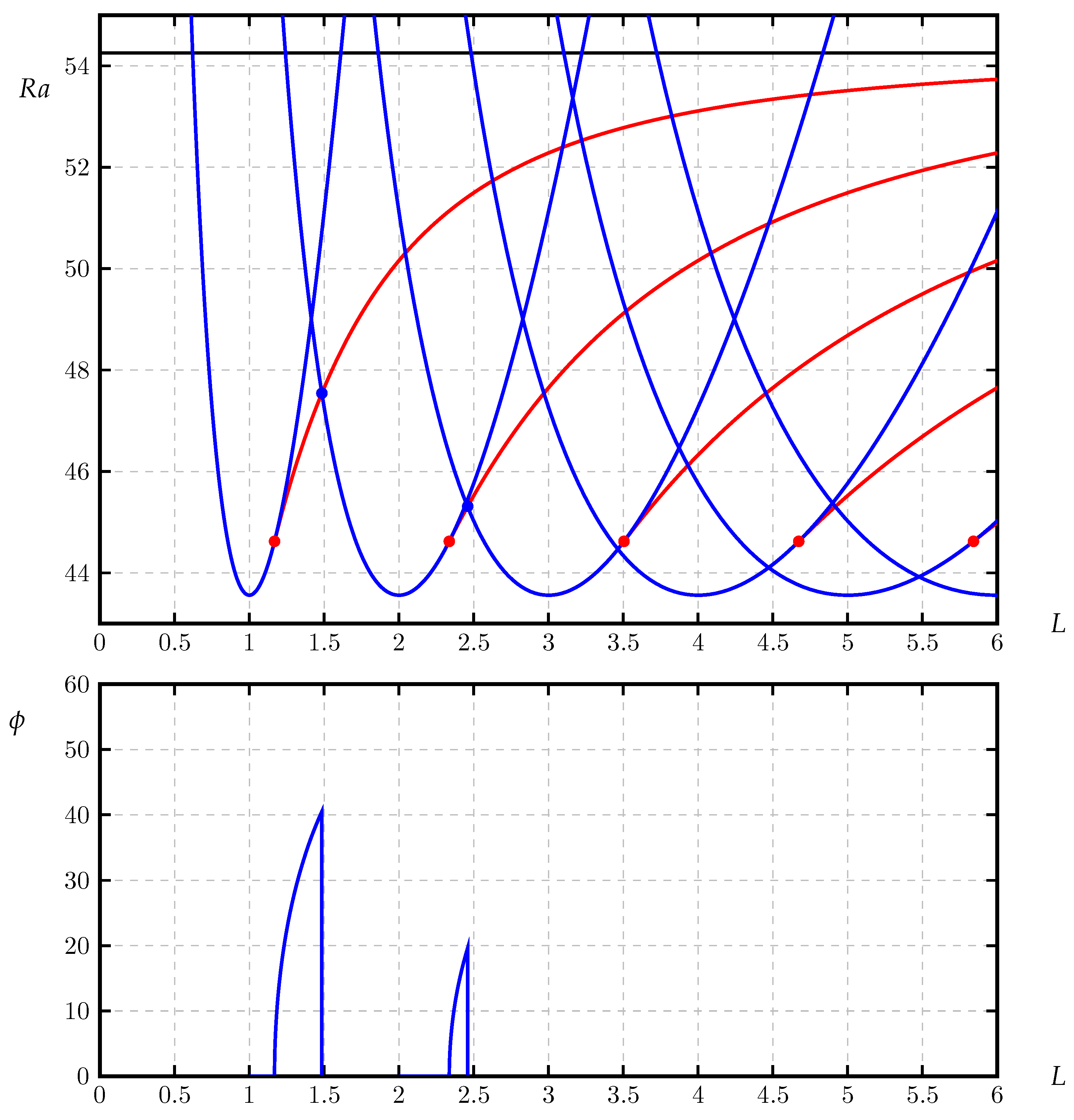
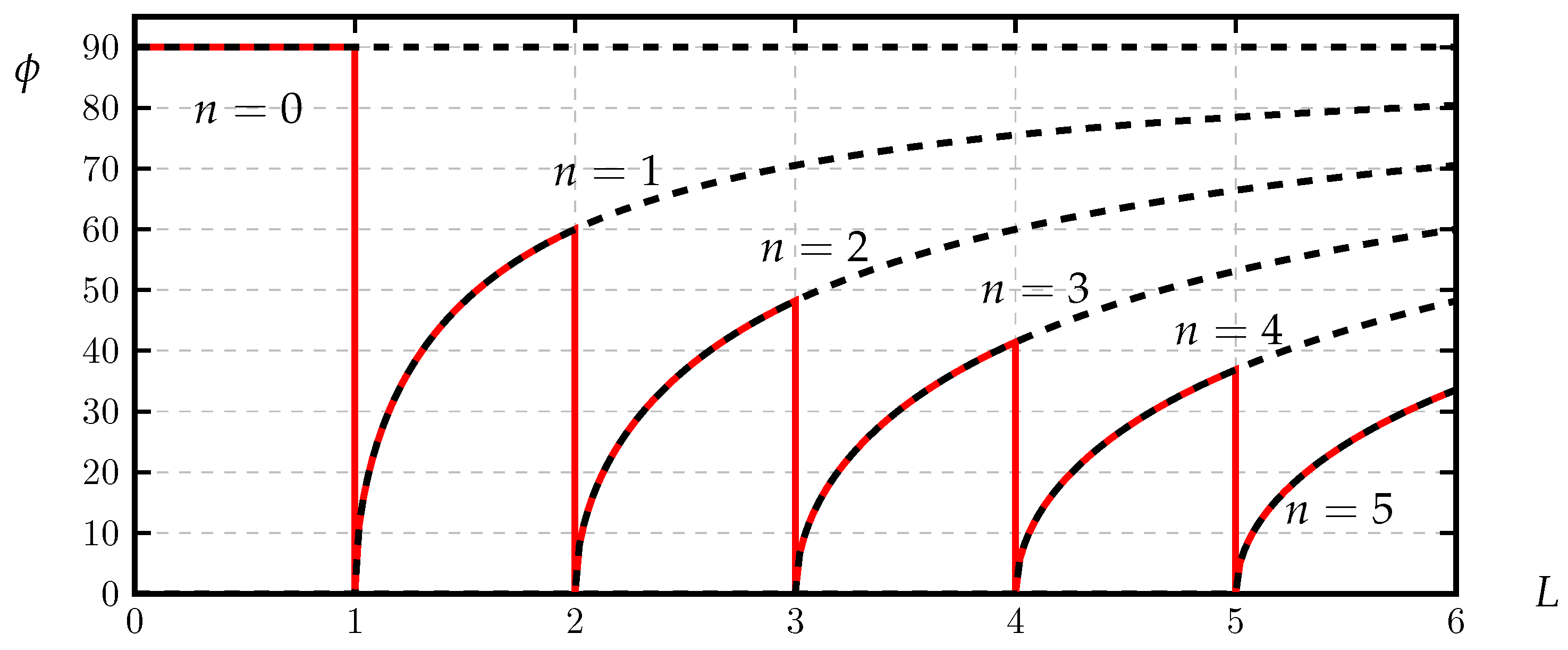
3.1. Sample Neutral Curves
3.2. The Modal Map
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Latin letters | |
| imaginary constant | |
| particular integral coefficients for | |
| complementary function coefficient | |
| particular integral coefficients for | |
| d | height of the channel |
| reduced pressure and temperature | |
| g | gravity |
| k | wave number |
| K | permeability |
| L | channel aspect ratio |
| differential operators in Equation (A41) | |
| m | wave number |
| n | number of rolls |
| N | number of intervals |
| p | pressure |
| Darcy-Rayleigh number | |
| right hand sides in Equation (A41) | |
| t | time |
| u | Darcy velocity along the layer |
| v | Darcy velocity across the layer |
| w | spanwise Darcy velocity |
| x | coordinate along the layer |
| y | coordinate across the layer |
| z | spanwise coordinate |
| Greek letters | |
| inclination angle | |
| coefficient of cubical expansion | |
| temperature difference | |
| temperature | |
| thermal diffusivity | |
| exponential growth rate | |
| dynamic viscosity | |
| reference density | |
| orientation of oblique roll | |
| Other symbols | |
| terms in series expansion | |
| i | imaginary component |
| r | real component |
| differentiation with respect to y |
Appendix A
References
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Bories, S.A.; Combarnous, M.A. Natural convection in a sloping porous layer. J. Fluid Mech. 1973, 57, 63–79. [Google Scholar] [CrossRef]
- Weber, J.E. Thermal convection in a tilted porous layer. Int. J. Heat Mass Transf. 1975, 18, 474–475. [Google Scholar] [CrossRef] [Green Version]
- Gill, A.E. A proof that convection in a porous vertical slab is stable. J. Fluid Mech. 1939, 35, 545–547. [Google Scholar] [CrossRef]
- Lewis, S.; Bassom, A.P.; Rees, D.A.S. The stability of vertical thermal boundary layer flow in a porous medium. Eur. J. Mech. B Fluids 1995, 14, 395–408. [Google Scholar]
- Straughan, B. A nonlinear analysis of convection in a porous vertical slab. Geophys. Astrophys. Fluid Dyn. 1988, 42, 269–275. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Bassom, A.P. Onset of Darcy-Bénard convection in an inclined porous layer heated from below. Acta Mech. 2000, 144, 103–118. [Google Scholar] [CrossRef]
- Postelnicu, A.; Rees, D.A.S. The onset of convection in an anisotropic porous layer inclined at a small angle from the horizontal. Int. Commun. Heat Mass Transf. 2001, 28, 641–650. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Postelnicu, A. The onset of convection in an inclined anisotropic porous layer. Int. J. Heat Mass Transf. 2001, 44, 4127–4138. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Postelnicu, A.; Storesletten, L. The onset of Darcy-Forchheimer convection in inclined porous layers heated from below. Transp. Porous Media 2006, 64, 15–23. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Storesletten, L.; Postelnicu, A. The onset of convection in an inclined anisotropic porous layer with oblique principle axes. Transp. Porous Media 2006, 62, 139–156. [Google Scholar] [CrossRef]
- Barletta, A.; Rees, D.A.S. Local thermal non-equilibrium analysis of the thermoconvective instability in an inclined porous layer. Int. J. Heat Mass Transf. 2015, 83, 327–336. [Google Scholar] [CrossRef] [Green Version]
- Barletta, A.; Storesletten, L. Thermoconvective instabilities in an inclined porous channel heated from below. Int. J. Heat Mass Transf. 2011, 54, 2724–2733. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Barletta, A. Linear instability of the isoflux Darcy-Bénard problem in an inclined porous layer. Transp. Porous Media 2011, 87, 665–678. [Google Scholar] [CrossRef]
- Barletta, A.; Rees, D.A.S. Linear instability of the Darcy-Hadley flow in an inclined porous layer. Phys. Fluids 2012, 24, 074104. [Google Scholar] [CrossRef] [Green Version]
- Barletta, A.; Celli, M. The Horton-Rogers-Lapwood problem for an inclined porous layer with permeable boundaries. Proc. Royal Soc. A 2018, 474, 20180021. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Celli, M.; Barletta, A. Onset of buoyancy driven convection in an inclined porous layer with an isobaric boundary. Int. J. Heat Mass Transf. 2019, 132, 782–788. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Bassom, A.P. The inclined Wooding problem. Transp. Porous Media 2018, 125, 465–482. [Google Scholar] [CrossRef]
- Wen, B.; Chini, G.P. On Moderate-Rayleigh-number convection in an inclined porous layer. Fluids 2019, 4, 101. [Google Scholar] [CrossRef] [Green Version]
- Riley, D.S.; Winters, K.H. A numerical bifurcation study of natural convection in a tilted two-dimensional porous cavity. J. Fluid Mech. 1990, 215, 309–329. [Google Scholar] [CrossRef]
- Beck, J.L. Convection in a box of porous material saturated with fluid. Phys. Fluids 1972, 15, 1377–1383. [Google Scholar] [CrossRef] [Green Version]
- Guerrero-Martínez, F.J.; Karimi, N.; Ramos, E. Numerical modelling of multiple steady-state convective modes in a tilted porous medium heated from below. Int. Commun. Heat Mass Transf. 2018, 92, 64–72. [Google Scholar] [CrossRef] [Green Version]

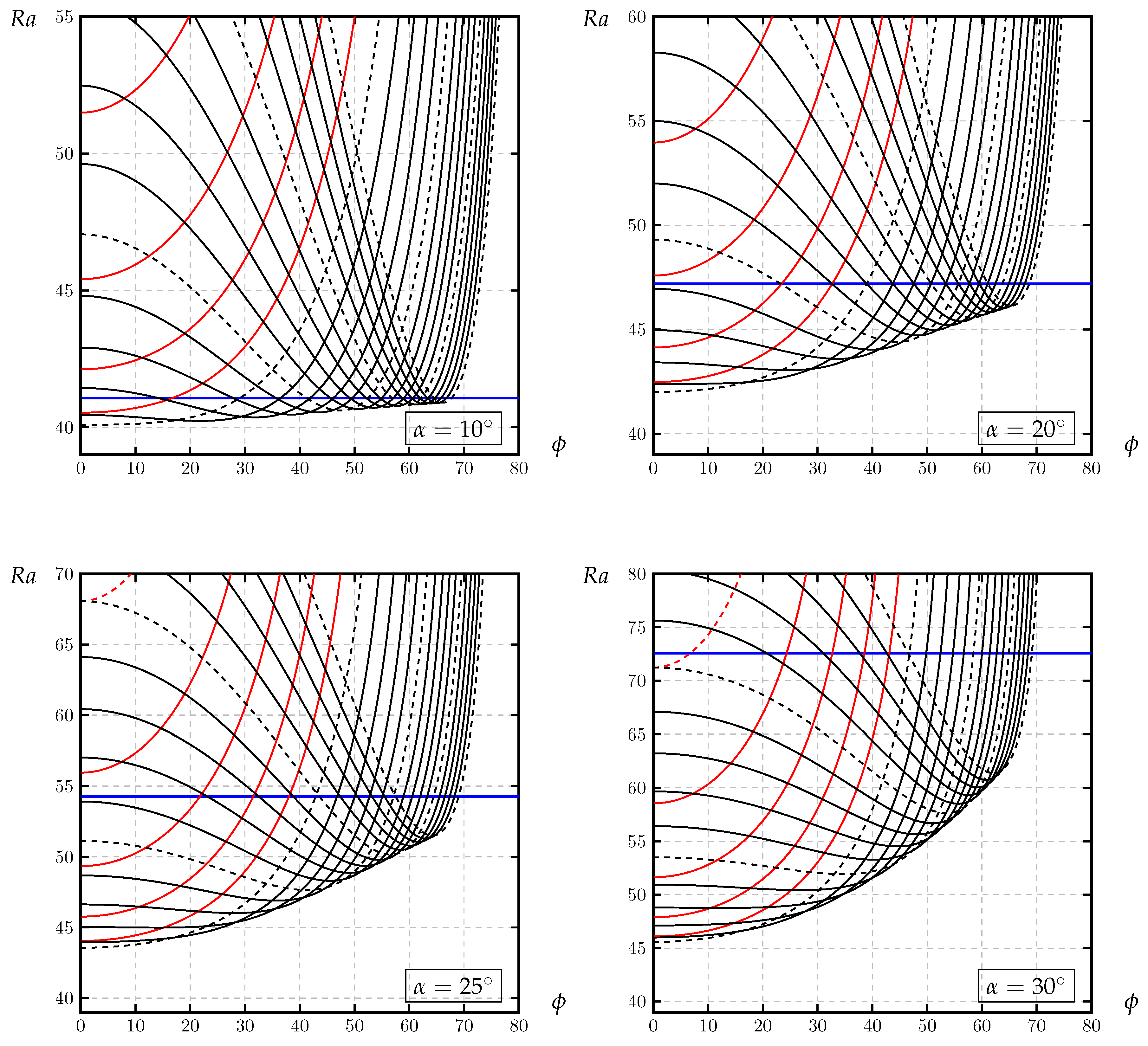

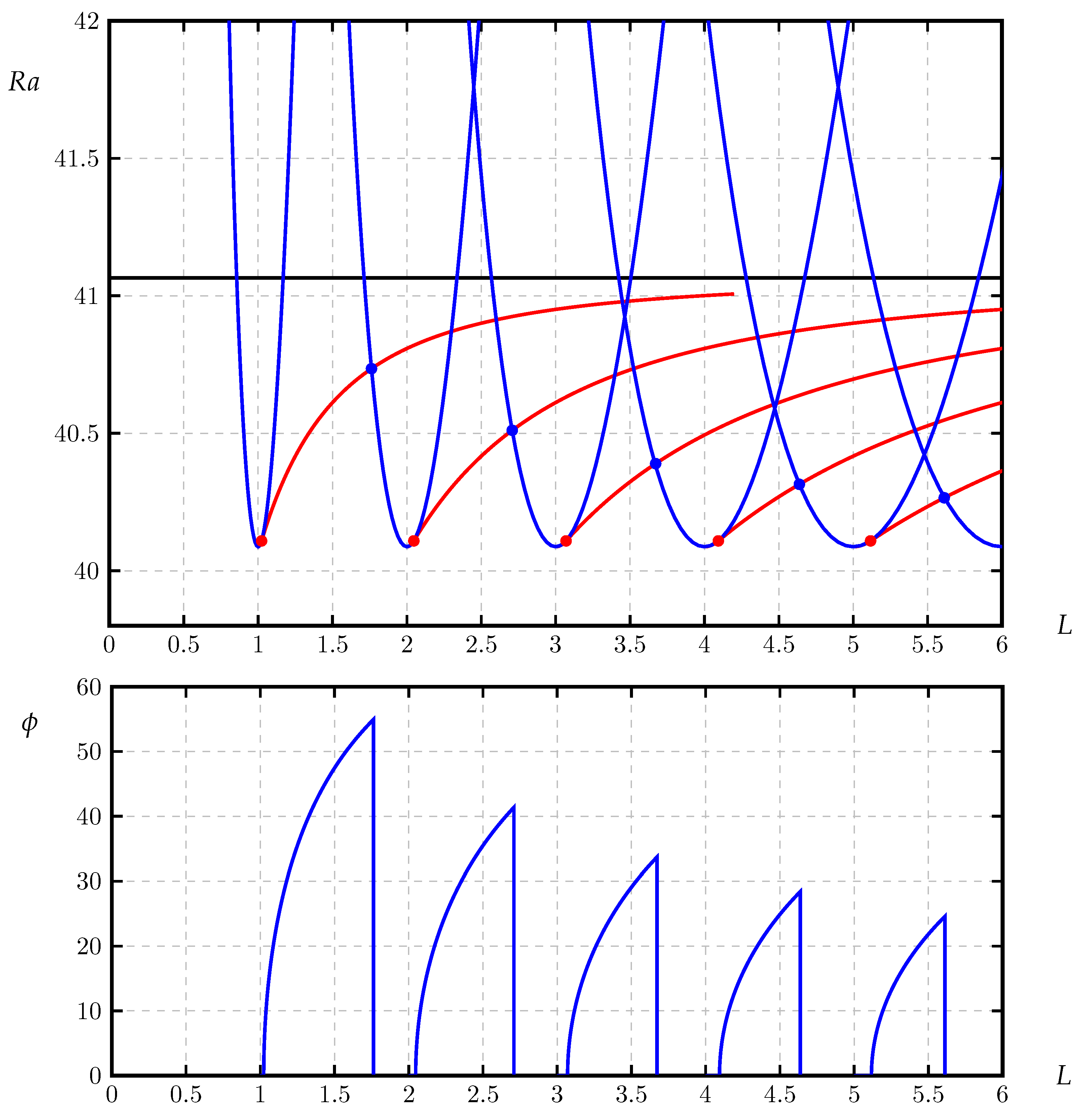
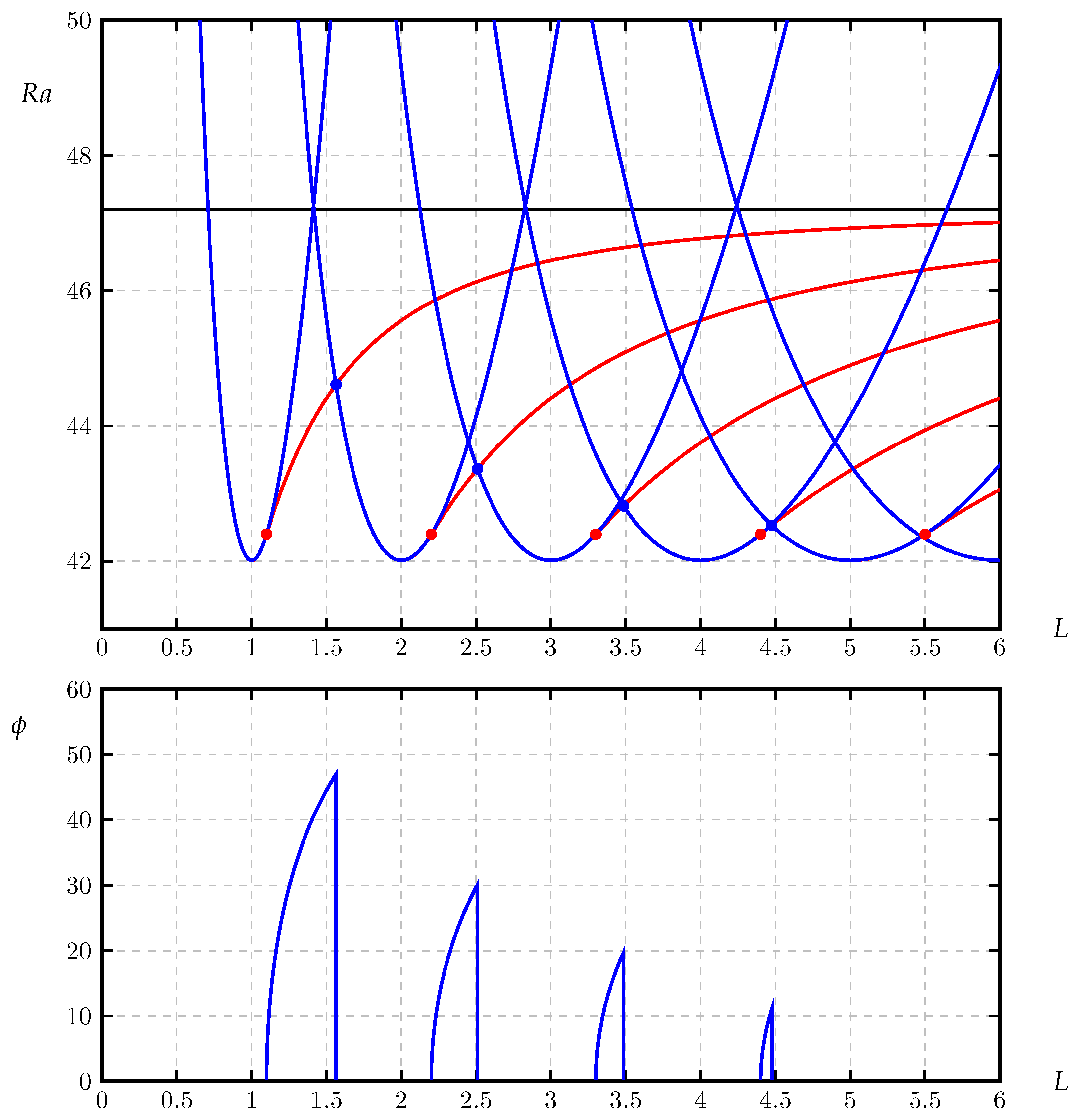

| N | Error | Error | ||
| 25 | 0.000 163 16 | 45.024 341 41 | 0.000 201 46 | |
| 50 | 0.000 010 24 | 45.024 152 58 | 0.000 012 63 | |
| 100 | 0.000 000 65 | 45.024 140 74 | 0.000 000 79 | |
| 200 | 0.000 000 04 | 45.024 140 00 | 0.000 000 05 | |
| 400 | 0.000 000 00 | 45.024 139 95 | 0.000 000 00 | |
| 800 | 0.000 000 00 | 45.024 139 95 | 0.000 000 00 | |
| n | (Degrees) | |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 10 | ||
| 20 | ||
| 50 | ||
| 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rees, D.A.S.; Barletta, A. Three-Dimensional Convective Planforms for Inclined Darcy-Bénard Convection. Fluids 2020, 5, 83. https://doi.org/10.3390/fluids5020083
Rees DAS, Barletta A. Three-Dimensional Convective Planforms for Inclined Darcy-Bénard Convection. Fluids. 2020; 5(2):83. https://doi.org/10.3390/fluids5020083
Chicago/Turabian StyleRees, D. Andrew S., and Antonio Barletta. 2020. "Three-Dimensional Convective Planforms for Inclined Darcy-Bénard Convection" Fluids 5, no. 2: 83. https://doi.org/10.3390/fluids5020083
APA StyleRees, D. A. S., & Barletta, A. (2020). Three-Dimensional Convective Planforms for Inclined Darcy-Bénard Convection. Fluids, 5(2), 83. https://doi.org/10.3390/fluids5020083