1. Introduction
A few parts of human arterial system can be used in representative models for hemodynamics: the heart, the proximal and abdominal aorta, the left coronary artery and the carotid bifurcation [
1]. The above mentioned human vessels exhibit flow characteristics that can be detected in most of the vascular system. Blood flow inside these vessels is of great importance since it is frequently related to disease and affected by many parameters [
2,
3,
4]. Blood vessels are divided into five categories: capillaries which are in intimate contact with the tissues, arteries, arterioles, veins and venules [
5]. The arteries are under various flow and pressure conditions in order to be conformed with the changing hemodynamic demands.
Blood is connected to oxygen and nutrients delivery to the body tissues as well as with the removal of tissue waste products [
6]. Blood is approximately four times more viscous than water and consists of a complex mixture of ions, proteins, lipoproteins and cells [
5]. In addition, it is constantly deformed under the effect of shear stress. Red blood cells (RBCs) are major components of blood due to their significant effect on hemodynamics and the performing biological functions. Remarkable deformability is exhibited by the RBCs partly due to their circular biconcave shapes while 35%–
of the blood volume in the human circulatory system is occupied [
7]. Moreover, the assumption of constant viscosity cannot be made of blood, which is typically considered as a non-Newtonian fluid. An indication of the non-Newtonian behavior of blood is demonstated at very low shear rates when aggregations of red blood cells are formed [
8]. In addition, the non-Newtonian behavior of blood is also exhibited in small branches and capillaries. This is caused due to the reduction of the effective viscosity through the tube, as a cell-free skimming layer is formed at the walls due to the squeeze of cells. Since RBCs are small semi-rigid particles, they increase the blood viscosity and affect its rheology [
9]. Therefore, the fluid inside the human vessels contains semi-rigid particles and their microrotation cannot be neglected [
10]. As a result, blood rheological properties cannot be described by the classical Newtonian theory or simple viscoelastic models.
In order to interpret the behaviour of blood inside the human vascular system, the micropolar fluids theory is adopted in this study [
11,
12]. In this theory, micromorphic geometrical characteristics, deformation phenomena and the intrinsic movement of the material particles are taken into account. Micropolar theory involves fluids that are containing microelements and possessing internal microstructure. Micropolar fluids represent a category of fluids showing micro-rotational phenomena and micro-rotational inertia. In addition, they can support couple stresses, surface and body couples [
13]. Moreover, they possess a microstructure, as they contain non-deformable solid particles, randomly oriented, suspended in a viscous medium [
14]. The aforementioned microstructure gives rise to a certain degree of polarity [
15]. The microstructure within the fluid acts as an additional factor affecting the fluid behavior in various flows. The internal particles may possess varying size and shape, shrink, change or expand of their geometry. Additionally, they can move independently of bulk flow and rotate individually, apart from the rotation of the fluid [
15].
The rheology of blood is constantly changing since the diameter of the arteries are continuously changing. Consequently, microelements that are carried by the blood are compressed as the diameter of the arteries is minimized. This gives rise to collision effects as well as enhanced friction among the microelements [
16]. Furthermore, as the diameter of the arteries changes the viscosity of the blood is also changes due to its microelements, such as RBCs, that are carried by the blood [
17]. Changes in the viscosity of the blood lead to changes in its velocity profiles [
18].
Over decades, cholesterol plaque may be accumulated in the walls of the carotid. Consequently, carotid’s flow path may eventually narrow by the growing plaque. Therefore, increased possibility for a sudden blood clot in the carotid artery can cause a stroke due to the interruption of blood flow. Furthermore, cholesterol plaque fragments may also navigated by the carotid artery into the brain. The latter can cause temporary blindness by blocking blood flow in an artery supplying the eye. It is well known that the deposition of the cholesterol plaque on the arteries is affected by the fluid flow conditions [
19,
20,
21]. For this reason the blood flow inside the human carotid artery is analyzed using a micropolar fluid model.
Blood flow under normal and disease conditions is an important field of study. Better understanding of the rheology of the human vascular system can be provided by simulations of blood flow in the arterial network system. Consequently, innovative methods in biomedicine could be used with enhanced efficiency [
22,
23]. The blood flow in the human arterial system can be considered as a biofluid dynamics problem. It should be noticed that remarkable differences under a specific fluid flow can be occurred when different numerical models (Newtonian, Non-Newtonian) are taken into consideration [
24]. In this study, the hemodynamics of a representative artery model, namely the carotid artery, is investigated. This artery is very a significant blood vessel since it supplies the brain, the neck and the face with the sufficient quantity of blood in order to maintain their fundamental functions [
25,
26]. Carotid artery is located along the sides of the neck and divided into the internal and the external carotid artery. Brain blood is supplied by the internal carotid artery, while the face and neck are supplied through the external carotid artery.
In the present study, the effect of the vortex viscosity, that directly affect the micropolarity of the blood flow inside a humans’ carotid model is investigated. In addition, the results are compared with the Newtonian fluid model. The governing equations of micropolar fluid flow as well as the simulation details are presented in
Section 2. Results for different values of the micropolar parameters are presented in
Section 3 and compared to the Newtonian fluid model case. Finally, discussion of findings and most important conclusions from the study are presented in
Section 4 and
Section 5, respectively.
3. Results
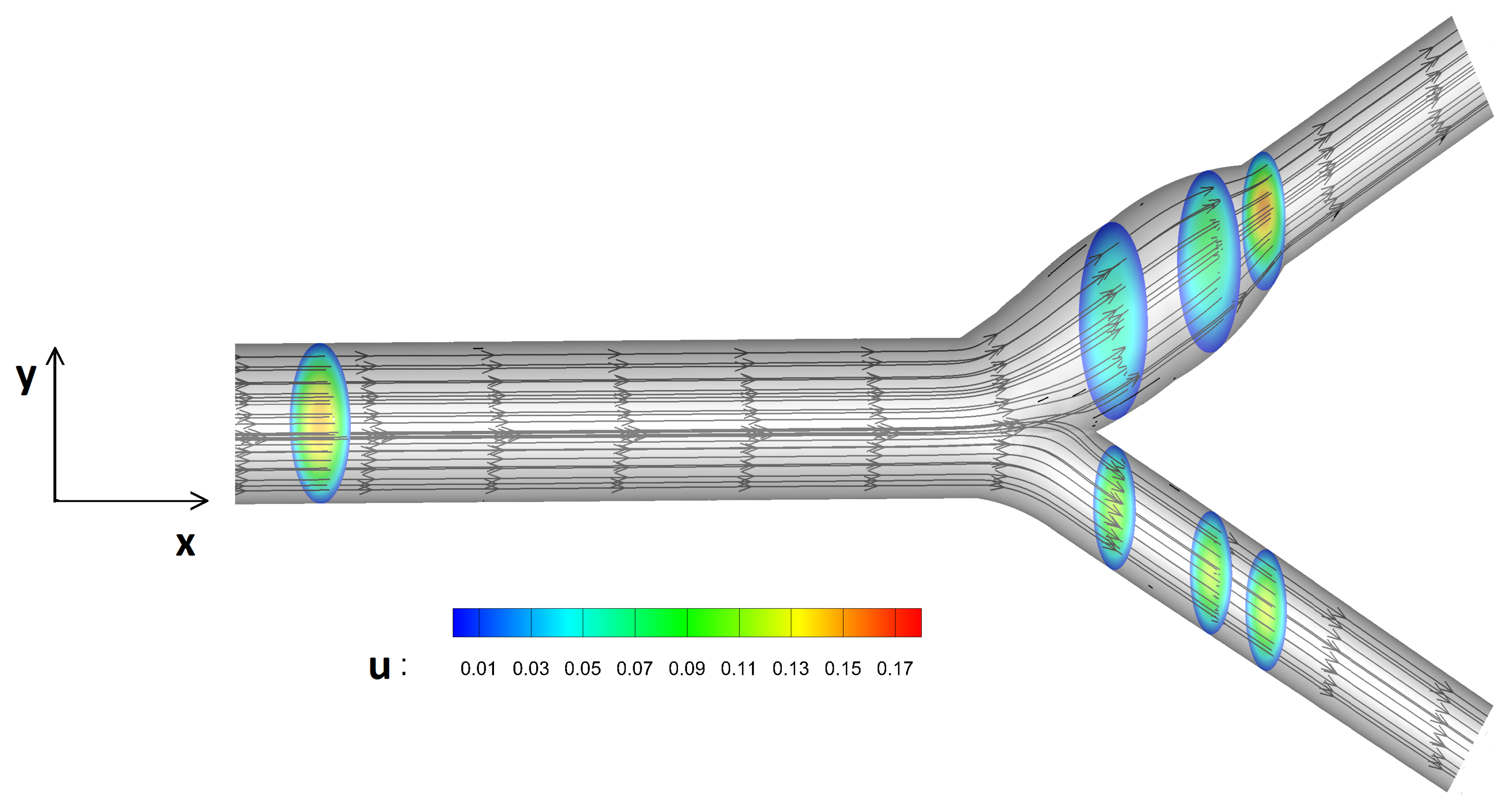
In this study, blood flow under different levels of micropolarity is compared against the Newtonian fluid model. Streamlines as well as velocity contours are presented in
Figure 6. The blood flow is moved towards the common artery and its velocity is divided into two streams after the bifurcation.
The profiles of streamwise and angular velocities for the Newtonian and the micropolar representative case of
are presented in
Figure 7a,b along the location
. As the fluid flow is fully developed the streamwise velocity profile is parabolic for both Newtonian and micropolar fluid (
Figure 7a). Although the micropolar fluids belongs to a class of non-Newtonian fluids, no flattening in the velocity profile due to the shear thinning effect is observed. Differences of angular velocity between the Newtonian and two representative micropolar cases (i.e.,
and
) are presented in
Figure 7b. It should be noticed that in the case of the Newtonian fluid, no angular velocity is observed. On the other hand, as the vortex viscosity
increases, the angular velocity is increased (
Figure 7b). The velocity in the center of the carotid is higher in the case of
micropolarity (i.e.,
) than in the Newtonian one. The velocity at the center of the tube for each micropolar case
scaled by the Newtonian one is presented in
Figure 7c. As
m increases, higher centerline velocities compared to the Newtonian case are observed (
Figure 7c). On the other hand, the velocity of the fluid near the walls of the carotid is decreased (
Figure 7d) in all of the simulated cases as compared to the Newtonian case. Furthermore, as the vortex viscosity
increases, the velocity of the fluid near the walls is decreased, as is depicted in
Figure 7d.
In this study, the velocity difference between the micropolar cases as
m increases and the Newtonian fluid is investigated in order to examine its variability between the two kind of fluid models. This difference is defined as:
where,
is the velocity of the corresponding micropolar case and
is the velocity of the Newtonian case. The percentage difference of the shear stress between the micropolar cases and the Newtonian fluid in the carotid wall is defined as:
where,
is the shear stress in the carotid walls of the corresponding micropolar case and
is the shear stress in the carotid’s walls of the Newtonian case. The angular velocity as a consequence of micropolarity are studied in terms of percentage difference between the base micropolar case of
and the cases with higher
m. This difference is defined as:
where,
is the angular velocity of the corresponding micropolar case and
is the angular velocity of the micropolar case where
.
The
among the different values of the vortex viscosity
and the Newtonian fluid
is presented in
Figure 8a. As the micropolar parameter
is increased the velocity of blood in the center of the carotid’s tube is also increased compared to the Newtonian fluid, as is depicted in
Figure 8. On the other hand, blood velocity is decreased in the walls of the artery with the increase of
m. Consequently, it is novelty found that the increased micropolarity of the blood leads to an acceleration of the flow in the middle of the carotid and a deceleration of the flow near the boundaries. It should be noticed also that this different
m trend is reversed at
as it is compiled for the profiles of
Figure 8a. This mark the thickness of micropolar boundary layer and corresponds to the maximum
value as it is shown in
Figure 7b.
The deceleration of the flow near the walls leads to a decrease in the shear stress. The rate in which
is decreased as the vortex viscosity is increased it is depicted in
Figure 8b. As the vortex viscosity increased, a linear decrease of
is observed. Although the decrease of
in the micropolar case of
is marginally, in the case of
micropolarity reaches ≈2.5%. It should be noticed that this is a very significant results since low shear stress values in the walls of the vessels may be connected with the accumulation of plaque.
At the center of the carotid tube the flow is increased approximately by
for the case of
, while the flow is decelerated approximately by
near the boundaries as compared to the Newtonian case. Thus, an overall difference of about
may be recorded for the higher
m. This effect is caused due to the enhanced contribution by the angular velocity that is occurred with the increase of the vortex viscosity
in the middle of carotid tube, as is depicted in
Figure 9. In the representative case of
,
is increased about
near the in the center of carotid tube while this increase is about
near the carotid walls compared to the case of
(
Figure 9).
is increased at the center while is decreased in the boundary of the carotid as is presented in
Figure 8a. The differerence of
in the center and the boundary of the tube is almost a linear function of
m, as described by the following equations:
It should be noticed that the decrease of
in the boundary is steeper compared to the increase of the
in the carotid’s center, as is depicted in
Figure 10.
The
x component of distribution of
along the specified locations of the internal carotid artery ( see
Figure 1) for the representative micropolar cases of
and
is presented in
Figure 11. Many differences in the fluid flow compared to the Newtonian one due to the geometry and the micropolarity of the fluid are found as the flow moves towards to the internal carotid. In the monitoring position
, increased fluid flow in the side of the divider wall in all micropolar cases compared to the Newtonian one is observed (
Figure 11a). As the vortex viscosity
is increased,
is decreased in the side of the divider wall. Significant changes in the fluid flow profile among the representative cases of
Figure 11a are observed. A difference in the range of
% to
is found as
m changes from
to
that occurs in different sides of the vessel depending on
m. In the case of
, increased fluid flow compared to the Newtonian one from the side of the divider wall till
is observed. On the other hand, marginally decreased of the fluid flow compared to the Newtonian one for
is observed. As the vortex viscosity increased, the fluid flow difference is increased by
and approximately by
in the center of the tube for
and
, respectively. It should be noticed that as the vortex viscosity is increased
, the fluid flow difference is significantly decreased compared to the Newtonian one for
till the outer wall of the internal carotid. This reduction is approximately
with
micropolar fluid.
As the fluid moves towards the internal carotid, the profile of the flow presents significant changes as it is depicted in
Figure 11b for the location
. In the case of
,
is increased in the carotid boundaries while is decreased in the center of the tube. As the vortex viscosity is increased, a parabolic
is established. It should be noticed that the increase of
m have a significant effect in the parabolic profile of
. An increase of
m leads to minimization in the flattening of the parabolic flow. Although
is increased in the center of the tube, it is decreased in the same way close to both divider and outer walls of the carotid internal artery (
Figure 11b).
When flow reaches the monitoring location
, only small changes are observed from location
(
Figure 1). In the case of
, the decrease of the flow in the center of the tube is minimized while in the cases of
and
the flattening of the parabolic flow difference is eliminated (
Figure 11c).
is increased in the center of the tube by
and
while is decreased in the boundaries by
and
in the cases of
and
(
Figure 11c), respectively.
At the last monitoring location
of the internal carotid, negative values of
width wise of the carotid tube are observed in the case of
. Higher values of
m, leads to increased
compared to the Newtonian one in the center of the tube (
Figure 11d). On the other hand, the flow is decreased by
and
at both the divider and outer walls for the case of
and
, respectively. It should be noticed that the decrease in the flow for the cases of
and
in the measurement location
is smaller as compared along the measurement location
. From the above it is obvious that as the diameter of the artery is decreased, the differences due to
m are reduced from about 4% to
.
Since no angular velocity is presented in the Newtonian fluid, all the cases are compared to the base case of
. In the measurement position
the angular velocity of the micropolar fluid presents significant changes in the center of the tube as the vortex viscosity increases as it is depicted in
Figure 12a. Due to its definition
at r = 0. The maximum value of
reaches
near the center of the tube for both cases. On the other hand, in the case of
a steeper increase in
is observed compared to the case of
.
In the monitoring position
, a completely different evolution of the angular velocity compared to the position
is observed. A steeper difference of
between the cases of
and
is found, as it is depicted in
Figure 12b. It should be noticed that the differences are more pronounced compared to the location
. In addition, differences in the maximum
are observed in the center of the tube.
As the flow moves and reaches the position
, no significant changes compared to the measurement position
are observed, as it is depicted in
Figure 12c. In the final monitoring position (i.e., position 44’), no significant change in the profile of
for both cases compared with the positions 22 and
is observed. On the other hand, the values of
are decreased, as it is shown in
Figure 12d. The maximum values for
are
and
for the cases of
and
, respectively. Based on the results from
Figure 12, it is clear that the profile of the angular velocity is affected by the geometry.
4. Discussion
In the past, non-Newtonian effects have only been considered in small arteries with diameter smaller than 100
m [
34]. On the other hand, the behavior of blood presents significant differences as flows through the vascular system of the human. This is caused by the substances that are carried by it, such as red blood cells. These substances are highly deformable [
35], especially when the diameter of the capillaries change [
36]. Furthermore, red blood cells can create aggregations [
37]. In this study, several simulations are performed in order to investigate the microrotation effect of the carried elements in the micropolar blood flow inside a human carotid model [
15]. The comparison between different kind of fluids indicate the variations in the fluid flow that can occur.
An increase in the vortex viscosity of the micropolar fluid is found to lead to an increase in blood velocity in the center of the carotid tube while the velocity is decreased near its boundaries as compared to the Newtonian fluid, as it is depicted in
Figure 8. Consequently, the boundary layer thickness is increase as the vortex viscosity is increased. In addition, the shear stress on the carotid wall is decreased as the vortex viscosity increases compared to a Newtonian flow. Therefore, the micropolarity of the fluid plays an important role in the distribution of the flow inside human vessels. In addition, accumulation of particles on the surface of the vessels is connected to low values of the shear stress on the vessel walls [
38]. This is very significant result since smaller shear stress near the boundaries of the vessels compared to a Newtonian fluid will enhance the deposition of those elements potentially reducing the vessel area available to blood flow, as well as affecting the mechanical properties of the artery walls.
A significant effect is induced by the interaction among the carried elements. Given the fact that blood velocity is increased in the center of the carotid tube and it is decelerated near the walls, as compared to a Newtonian fluid, with the increase of the vortex viscosity, it seems that the angular motion of those microelements has decreased the collisions among them in the center of the tube. On the other hand, increased collisions among the microelements and the walls of the carotid are occurring [
16].
in the center of the carotid tube is linearly increased with the increase of the vortex viscosity
m and linearly decreased in the boundaries, as is depicted in
Figure 10. The slope of decrease is steeper compared the one of increase. Consequently, as the vortex viscosity increases, the difference between
and
will increase.
The geometry is a crucial parameter for the development of the flow. Based on the results in the internal carotid artery (
Figure 11), under small values of
m, the
is decreased. The same result is presented in recent studies [
16,
24] where the fluid flow inside ligament tissues was investigated. Consequently, in small arteries and especially in arterioles the micropolarity of the fluid is a parameter that decreases the
. This is caused due to the small diameter of arteries and arterioles, as the blood cannot sustain the angular motion of the micro-elements.
Micropolarity of the fluid seems to play significant role in the distribution of the flow. As the flow advances through the arteries, the flattening of the parabolic profile of
is affected by the vortex viscosity and geometry. Based on
Figure 11, flattening of the parabolic profile of
may be occurred inside the arteries under small values of the vortex viscosity.
The magnitude of the angular velocity is affected by the micropolarity of the fluid. As the vortex viscosity increases, the angular velocity is increased. It should be noticed that the profile of
is affected by the geometry. Differences in
may occur in different radial directions of the carotid, as is depicted in
Figure 12. These differences may be increased in complex geometries such as the human vascular system.