Partially Averaged Navier-Stokes: A (k-ω)/(k-ε) Bridging Model
Abstract
:1. Introduction
2. Mathematical Model and Method of Solution
3. Results and Discussion
3.1. Wall-Bounded Flows: Backward-Facing Step
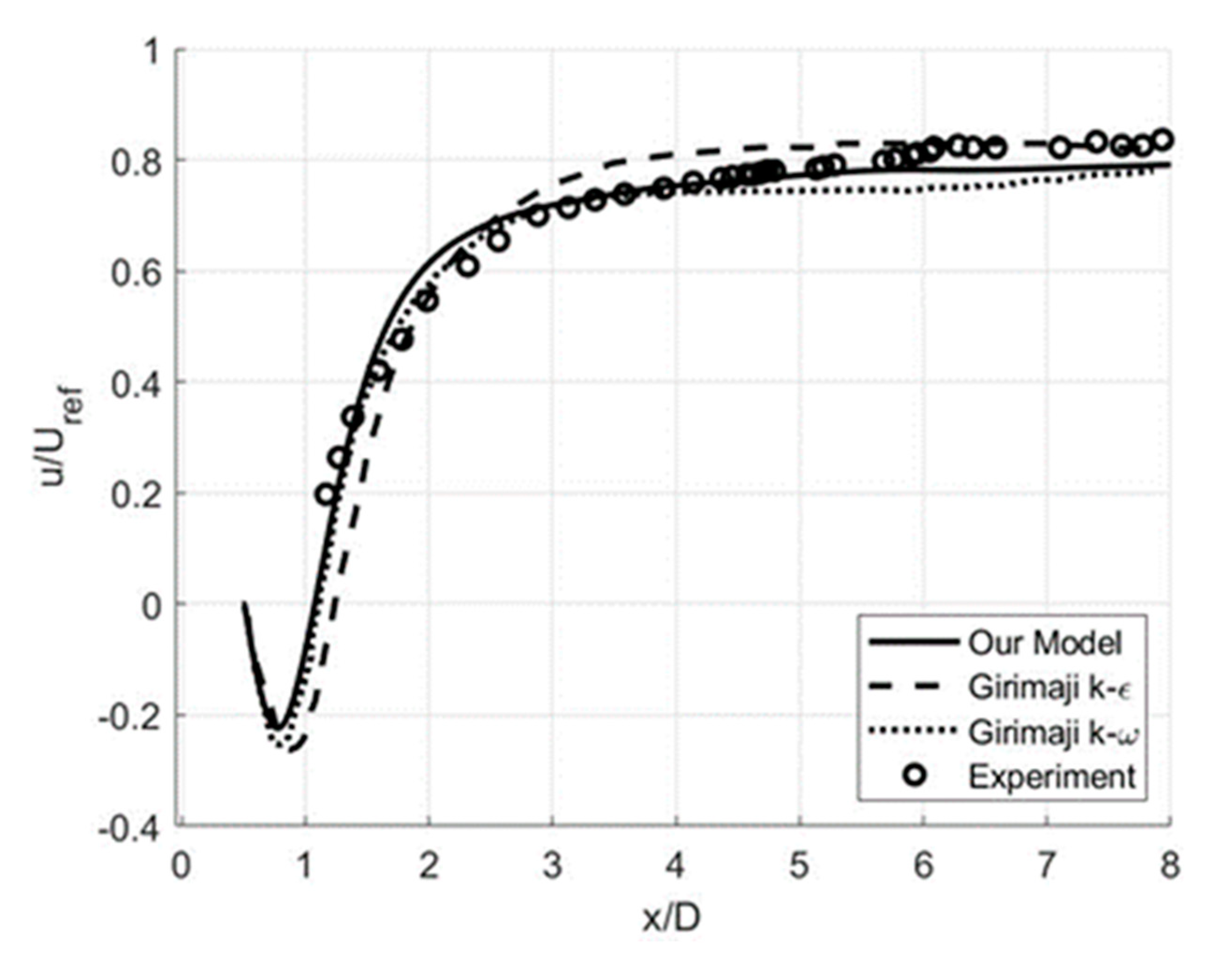
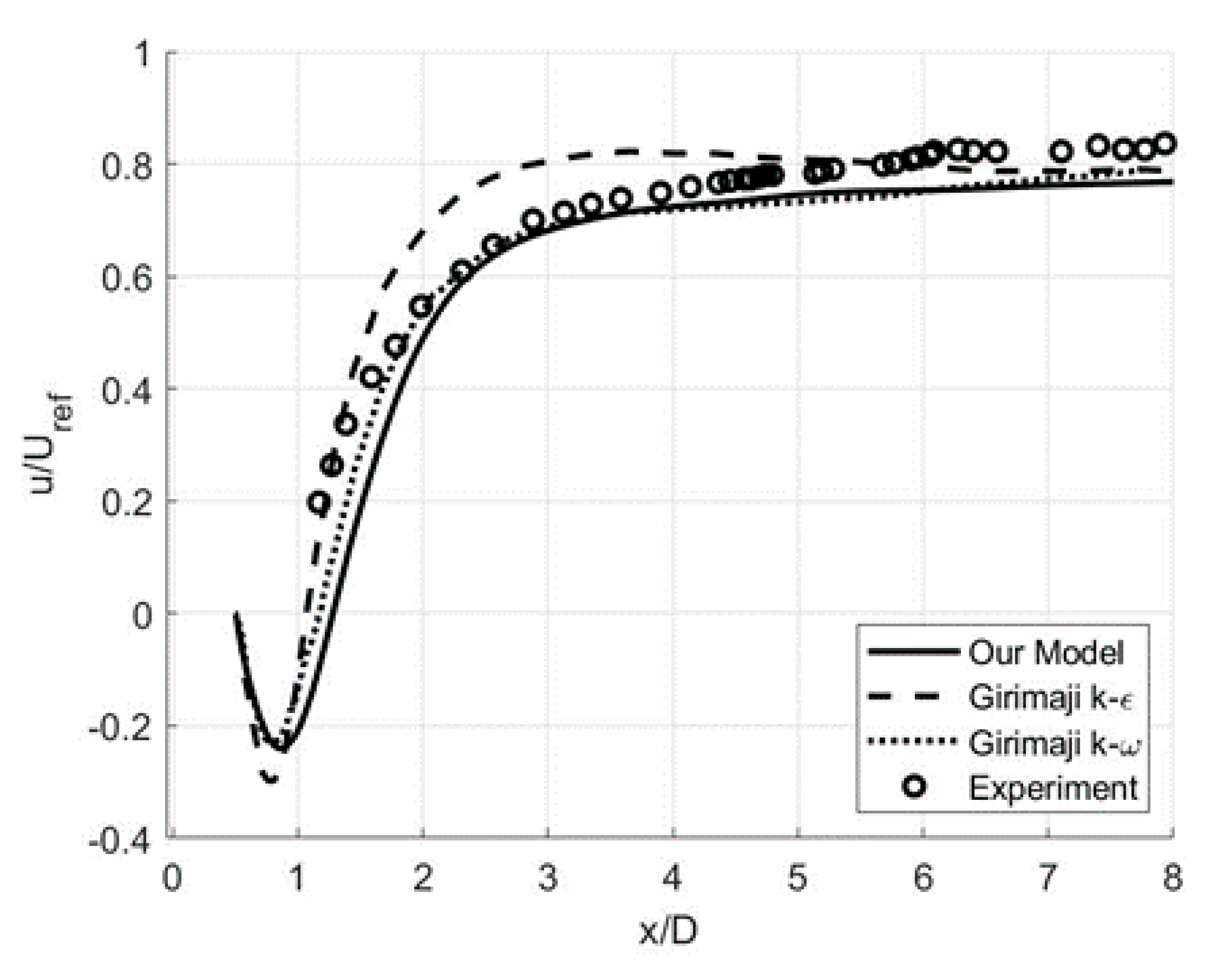
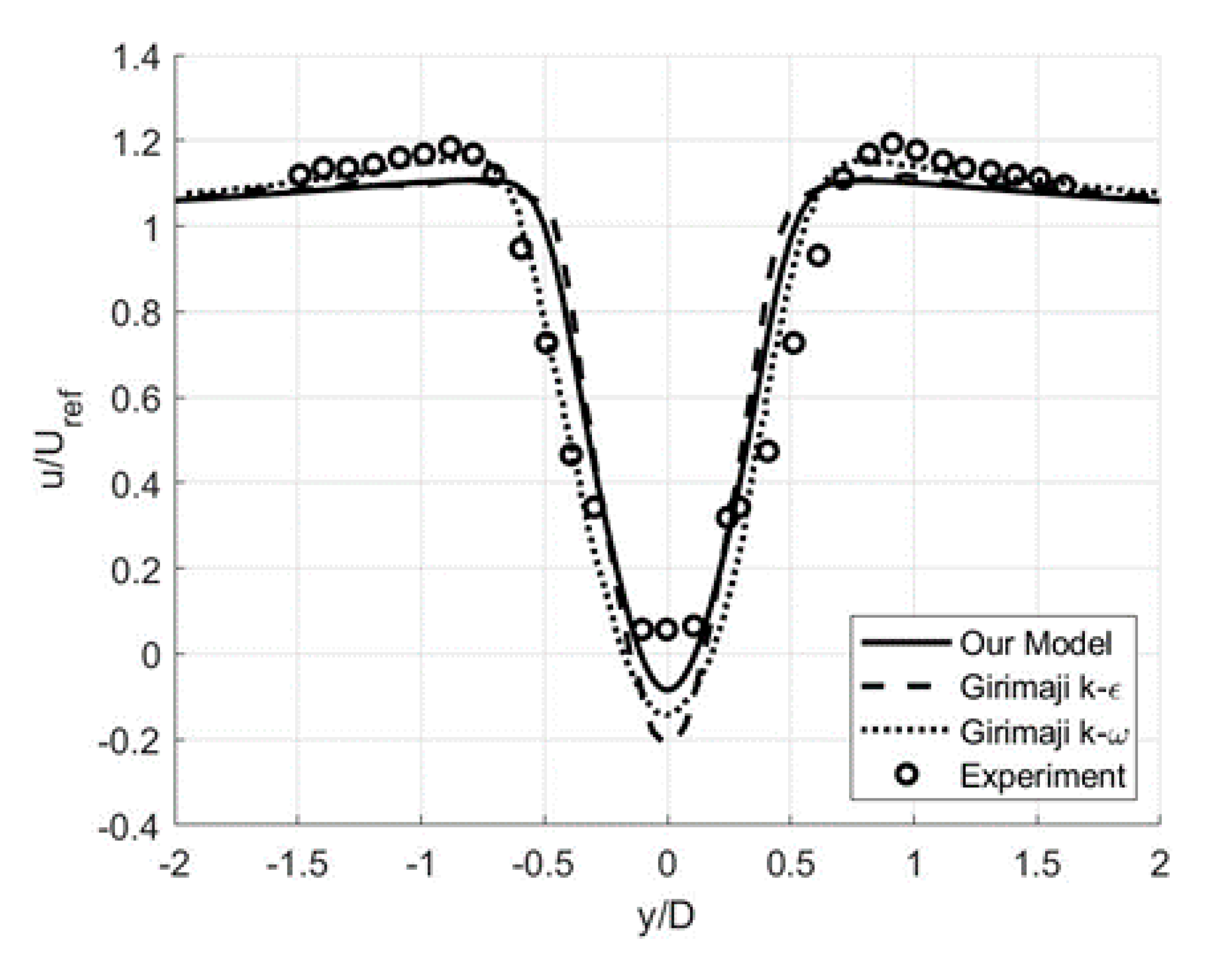
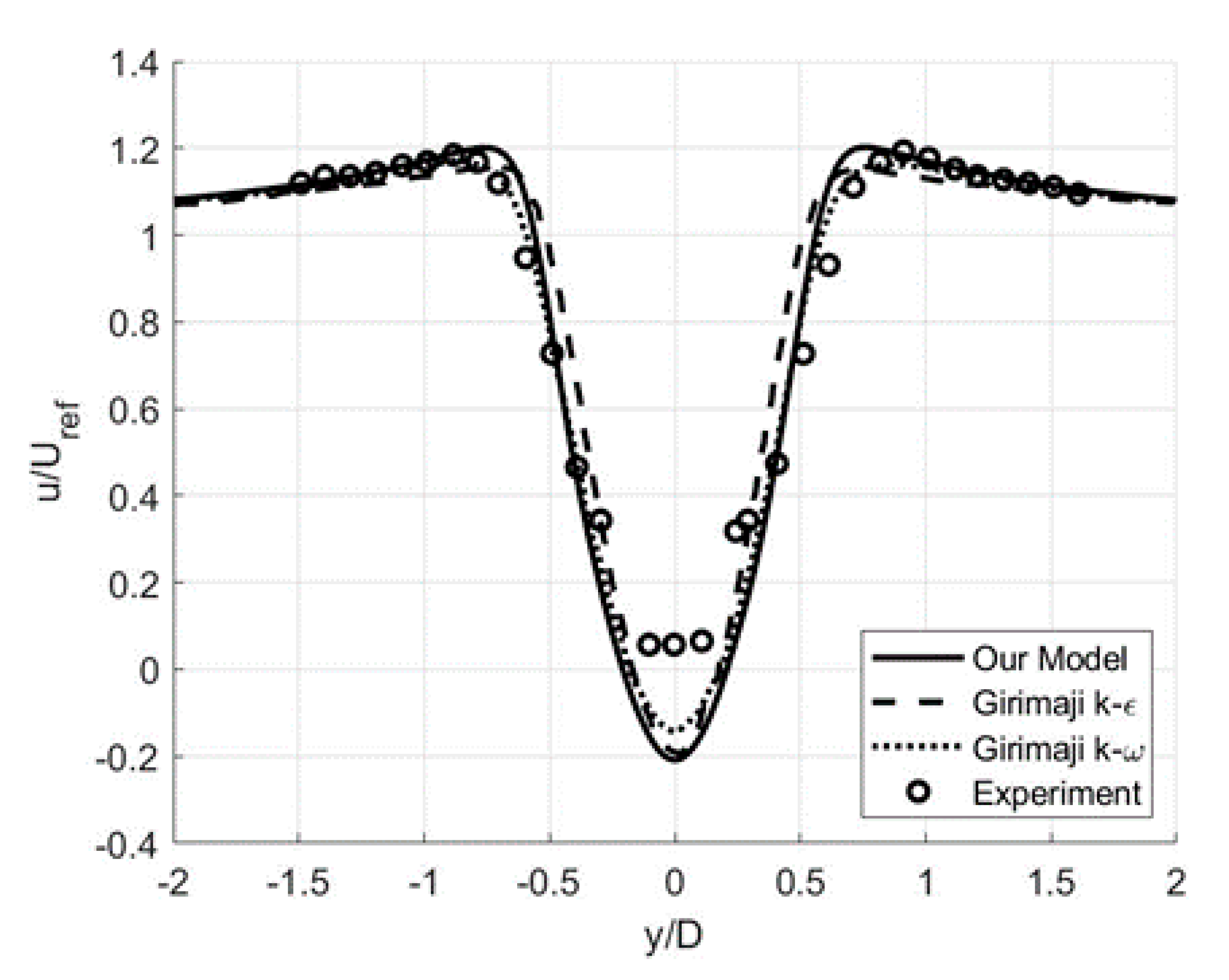
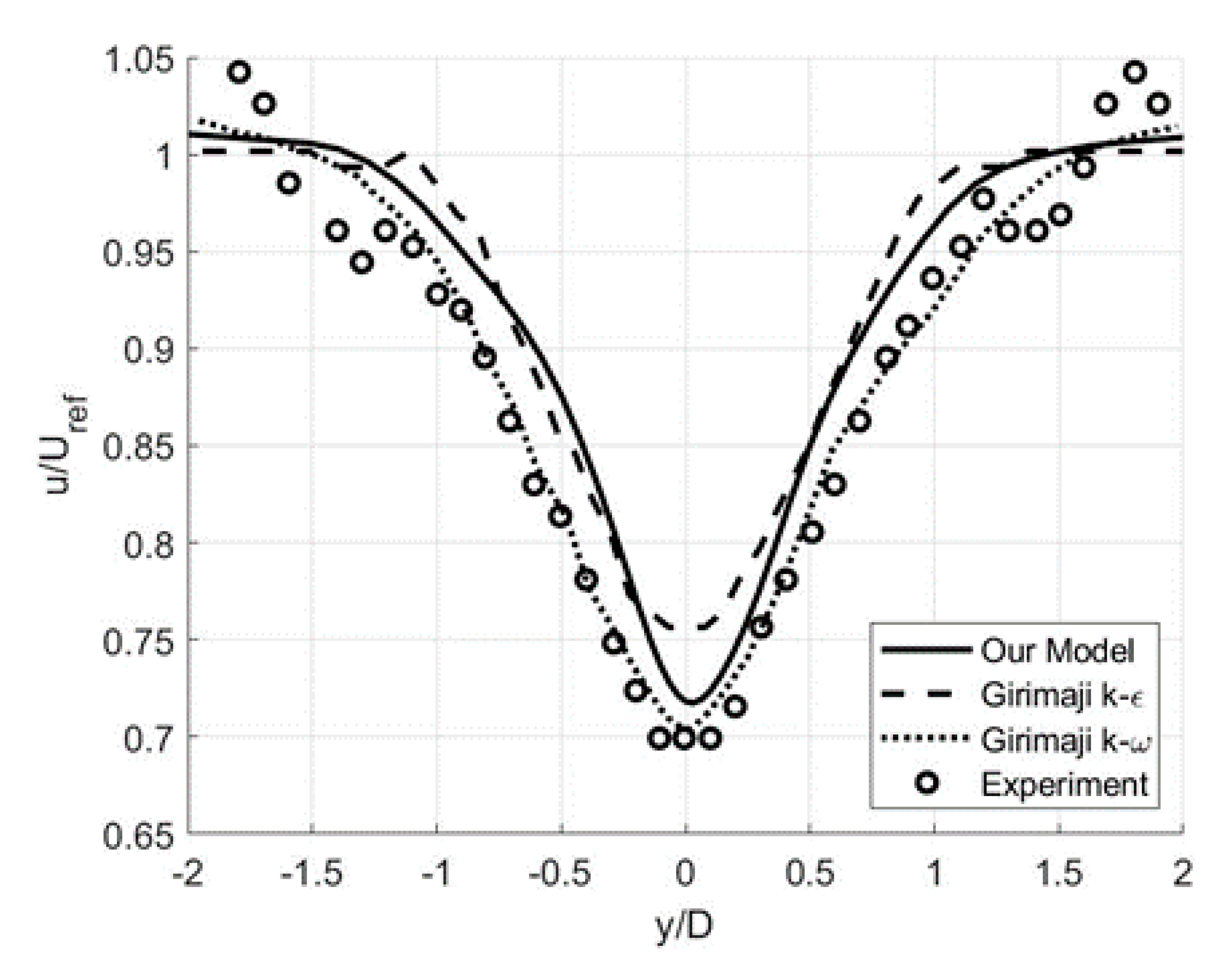
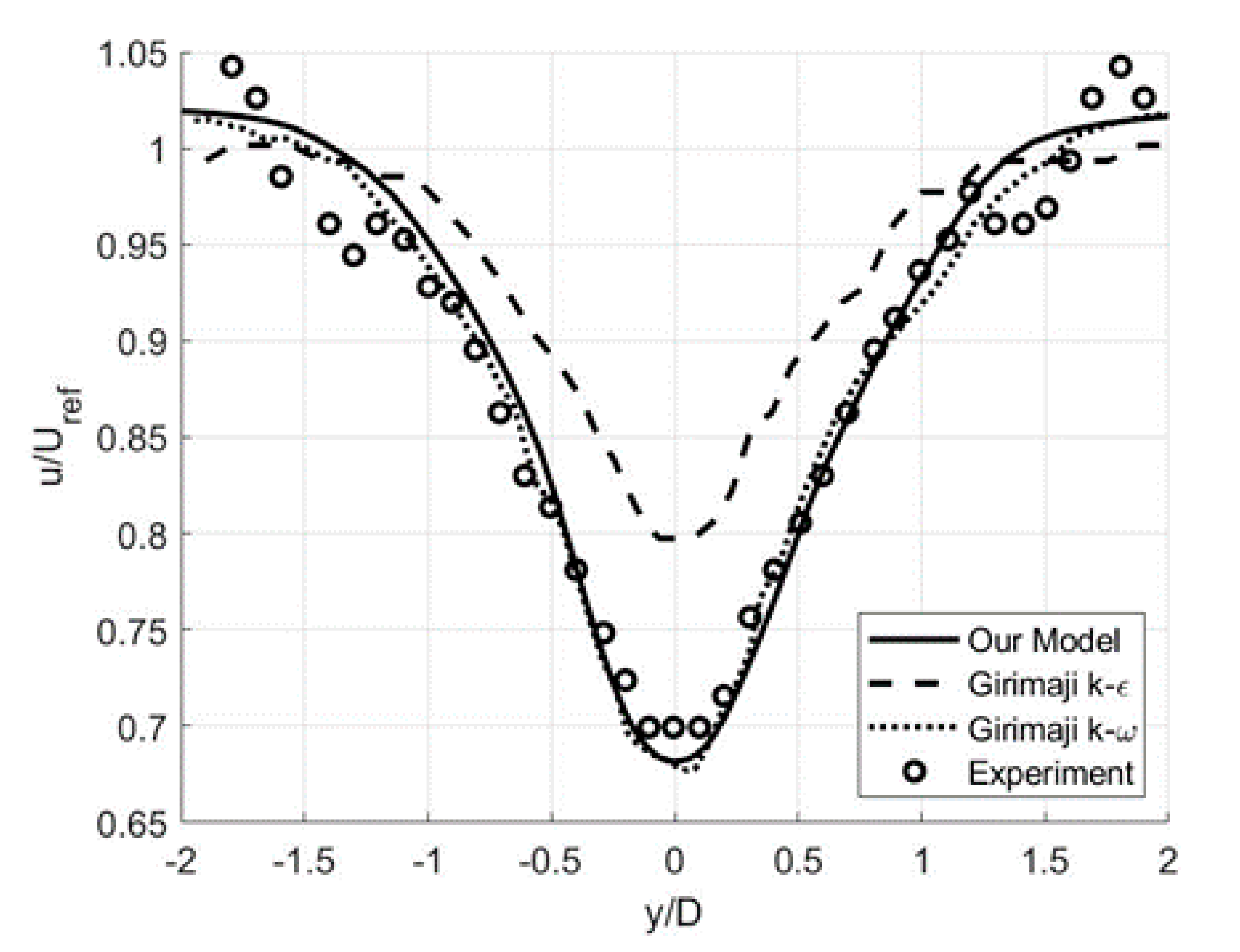
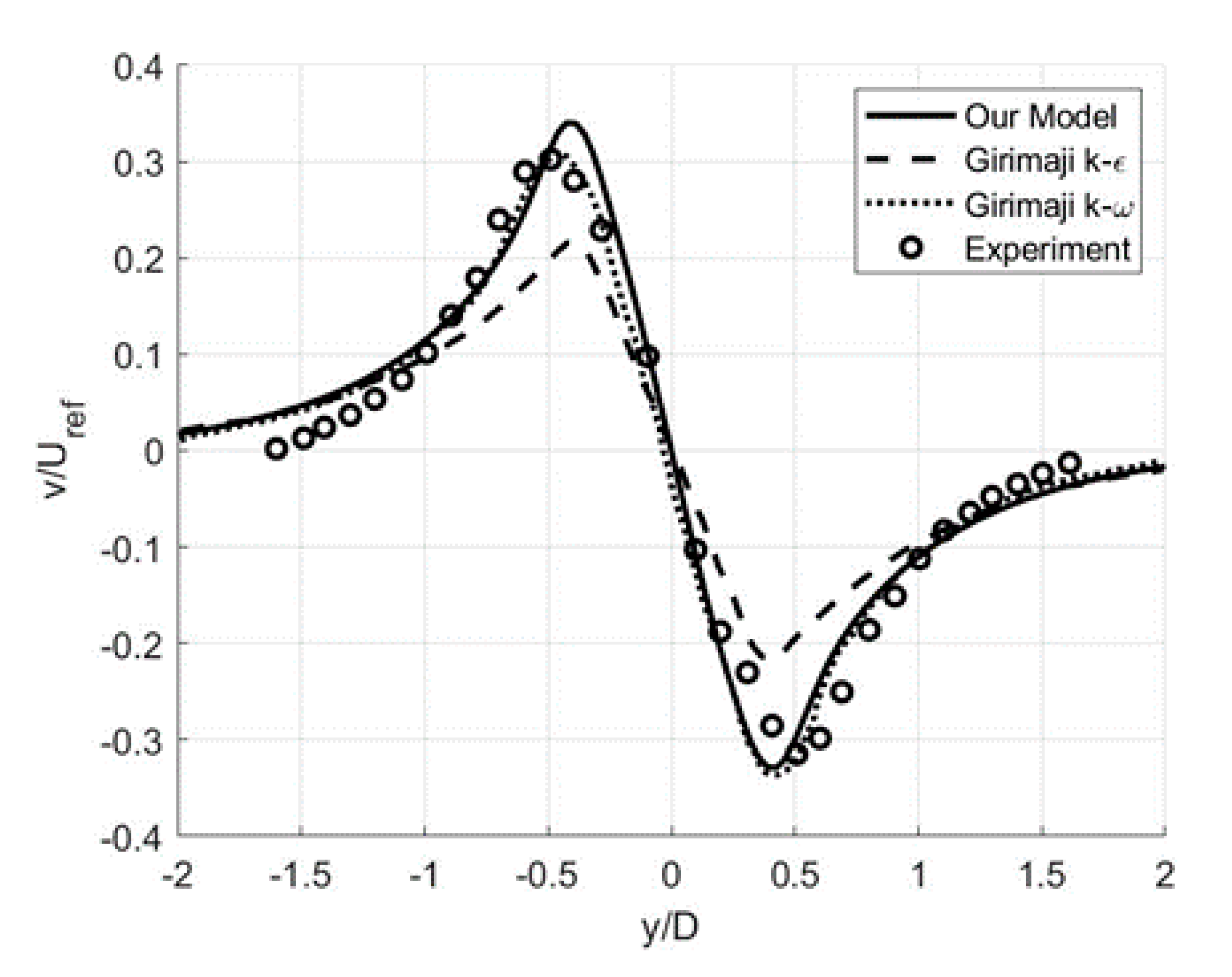
3.2. Free-Shear Flows: Circular Cylinder
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Speziale, C.G. Turbulence Modeling for Time-Dependent RANS and VLES: A Review. AIAA J. 1998, 36, 173–184. [Google Scholar] [CrossRef]
- Le, H.; Moin, P.; Kim, J. Direct Numerical Simulation of Flow over a Backward Facing Step. J. Fluid Mech. 1997, 330, 349–374. [Google Scholar] [CrossRef] [Green Version]
- Kolmogorov, A.N. A Refinement of Previous Hypotheses Concerning the Local Structure of Turbulence in a Viscous Incompressible Fluid at High Reynolds Number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef] [Green Version]
- Spalding, D.B. Kolmogorov’s two-equation model of turbulence. Proc. R. Socoety London Math. Phys. Eng. Sci. 1991, 434, 211–216. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. Mon. Weather. Rev. 1963, 93, 99–164. [Google Scholar] [CrossRef]
- Moin, P.; Kim, J. Numerical Investigation of Turbulent Channel Flow. J. Fluid Mech. 1982, 118, 341–377. [Google Scholar] [CrossRef] [Green Version]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.M. A Dynamic Subgrid-Scale Eddy Viscosity Model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef] [Green Version]
- Germano, M. From RANS to DNS: Towards a Bridging Model. ERCOFTAC Series, 7. In Direct and Large-Eddy Simulation III; Voke, P.R., Sandham, N.D., Kleiser, L., Eds.; Kluwer Academic Publishers: Berlin, Germany, 1999; pp. 225–236. [Google Scholar]
- Spalart, P.R.; Jou, W.-H.; Strelets, M.; Allmaras, S.R. Comments on the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach. In Advances in DNS/LES, 1st AFOSR Int. Conf. On DNS/LES, Aug. 4–8, 1997; Greyden Press: Columbus, OH, USA, 1997. [Google Scholar]
- Squires, K.D.; Frosythe, J.R.; Spalart, P.R. Detached-Eddy Simulation of the Separated Flow Around a Forebody Cross-section. In ERCOFTAC Series, 16 “Direct and Large-Eddy Simulation IV”; Geurts, B.J., Friedrich, R., Metais, O., Eds.; Kluwer Academic Press: Berlin, Germany, 2001; Volume 8, pp. 481–500. [Google Scholar]
- Deck, S. Zonal-Detached-Eddy Simulation of the flow around a high-lift configuration. AIAA J. 2005, 43, 2372–2384. [Google Scholar] [CrossRef] [Green Version]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A.K. A new version of Detached-Eddy Simulation, resistant to ambiguous grid densities. Theor. Comp. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A. A hybrid RANS-LES model with delayed DES and wall-modeled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Girimaji, S. Partially Averaged Navier-Stokes Model for Turbulence: A Reynolds Averaged Navier-Stokes to Direct Numerical Simulation Bridging Method. J. Appl. Mech. 2006, 73, 413–421. [Google Scholar] [CrossRef]
- Frendi, A.; Tosh, A.; Girimaji, S. Flow Past a Backward Facing Step: Comparison of PANS, DES, and URANS Results with Experiments. Int. J. Comput. Methods Eng. Sci. Mech. 2006, 8, 23–38. [Google Scholar] [CrossRef]
- Girimaji, S.; Lakshmipathy, S. Partially Averaged Navier-Stokes Method for Turbulent Flows: K-ω Model Implementation. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Jones, W.; Launder, B. The Prediction of Laminarization with a Two-Equation Model of Turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the Scale-Determining Equation for Advanced Turbulence Models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Batten, P.; Goldberg, U.; Chakravarthy, S. LNS-An Approach Towards Embedded LES. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
- Speziale, C.G. Computing non-Equilibrium Flows with Time-Dependent RANS and VLES. In Proceedings of the 15th ICNMFD, Monterey, CA, USA, 24–28 June 1996. [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- OpenFOAM: The OpenFOAM Foundation. Available online: https://openfoam.org (accessed on 29 July 2020).
- Gmesh: A Three-Dimensional Finite Element Mesh Generator with Built-in Pre- and Post-Processing Facilities. Available online: https://gmsh.info/ (accessed on 29 July 2020).
- Harrison, C. Partially Averaged Navier-Stokes: A Bridging Model. Master’s Thesis, The University of Alabama in Huntsville, Huntsville, AL, USA, 2020. [Google Scholar]
- Driver, D.; Seegmiller, H. Features of a Reattaching Turbulent Shear Layer in Divergent Channel Flow. AIAA J. 1985, 23, 163–171. [Google Scholar] [CrossRef]
- Cantwell, B.; Coles, D. An Experimental Study of Entrainment and Transport in the Turbulent Near Wake of a Circular Cylinder. J. Fluid Mech. 1983, 136, 321–374. [Google Scholar] [CrossRef] [Green Version]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frendi, A.; Harrison, C. Partially Averaged Navier-Stokes: A (k-ω)/(k-ε) Bridging Model. Fluids 2020, 5, 129. https://doi.org/10.3390/fluids5030129
Frendi A, Harrison C. Partially Averaged Navier-Stokes: A (k-ω)/(k-ε) Bridging Model. Fluids. 2020; 5(3):129. https://doi.org/10.3390/fluids5030129
Chicago/Turabian StyleFrendi, Abdelkader, and Christopher Harrison. 2020. "Partially Averaged Navier-Stokes: A (k-ω)/(k-ε) Bridging Model" Fluids 5, no. 3: 129. https://doi.org/10.3390/fluids5030129
APA StyleFrendi, A., & Harrison, C. (2020). Partially Averaged Navier-Stokes: A (k-ω)/(k-ε) Bridging Model. Fluids, 5(3), 129. https://doi.org/10.3390/fluids5030129




