The Propagation of Nonlinear Internal Waves under the Influence of Variable Topography and Earth’s Rotation in a Two-Layer Fluid

Abstract

A nonlinear equation of the Korteweg–de Vries equation usually describes internal solitary waves in the coastal ocean that lead to an exact solitary wave solution. However, in any real application, there exists the Earth’s rotation. Thus, an additional term is required, and consequently, the Ostrovsky equation is developed. This additional term is believed to destroy the solitary wave solution and form a nonlinear envelope wave packet instead. In addition, an internal solitary wave is commonly disseminated over the variable topography in the ocean. Because of these effects, the Ostrovsky equation is retrieved by a variable-coefficient Ostrovsky equation. In this study, the combined effects of both background rotation and variable topography on a solitary wave in a two-layer fluid is studied since internal waves typically happen here. A numerical simulation for the variable-coefficient Ostrovsky equation with a variable topography is presented. Two basic examples of the depth profile are considered in detail and sustained by numerical results. The first one is the constant-slope bottom, and the second one is the specific bottom profile following the previous studies. These indicate that the combination of variable topography and rotation induces a secondary trailing wave packet.

1. Introduction

The classical example of an equation yielding solitary wave equations is the Korteweg–de Vries (KdV) equation. The KdV Equation (1), which is acknowledged as a model for weakly nonlinear long waves, was first derived by Korteweg and de Vries [1] by conducting long one-dimensional wave generating at a constant depth of a shallow water channel. They found solitary wave solutions [2]. Assuming that the topography is uniform or the depth of the water, h, is constant, the outcome is:

$$\begin{array}{c}\hfill A_t+c{A}_x+\mu A{A}_x+\lambda A_{xxx}=0.\end{array}$$

(1)

Equation (1) is known as a partial differential equation (PDE), with x and t variables. Here, $A(x,t)$ is denoted as the amplitude of the wave, while x and t are space and time variables. Both $\mu$ and $\lambda$ are the coefficients of the nonlinear and dispersive terms, respectively, which are determined by the characteristics of the distinct physical system. However, the effect of variable topography has to be considered when obtaining the mathematical model as waves propagate over variable depths in many physical problems. These effects are believed to generate a long trailing tail behind a wave, besides the topographical dispersion and other more subtle circumstances. The detailed analysis and the appropriate model of the solitary wave propagated over a variable topography were accomplished by Johnson [3] and Grimshaw [4,5] in the context of the variable-coefficient Korteweg–de Vries (vKdV) equation. The further theory behind the solitary waves with the effects of variable topography on the free-surface and the internal solitary waves’ configuration is well-developed [6,7,8].

Moreover, although the KdV equation is known to be a good model for internal solitary waves in the coastal ocean, the wave is supplemented with the additional effects of the Earth’s rotation, and the new equation, the so-called Ostrovsky equation, is obtained [9]. Numerous numerical experiments of this equation have proven that the Earth’s rotation tends to restrain the formation of internal solitary waves, as it does not support the solitary wave solution. This additional term generated a new persistent feature known as the envelope nonlinear wave packet [10,11]. This is due to a disintegration of the solitary-like initial condition caused by the dispersion of the inertia-gravity wave, which has the slowest absolute speed of all emitted radiation. An observation of an oceanic nonlinear internal wave packet affected by the Earth’s rotation was done by Grimshaw et al. [12]. The simplest model of the Ostrovsky equation is given by:

$$\begin{array}{c}\hfill {(A_t+c{A}_x+\mu A{A}_x+\lambda A_{xxx})}_x=\gamma A.\end{array}$$

(2)

The non-local term on the right-hand side in Equation (2) represents the rotational effect, and when $\gamma =0$, Equation (2) is reduced to (1). $A(x,t)$ is the amplitude of the modal function $\varphi \left(z\right)$, determined by:

$$\begin{array}{c}\hfill {\{{\rho }_0{(c-u_0)}^2{\varphi }_z\}}_z+{\rho }_0{N}^2\varphi =0,\mathrm{for}-h<z<0,\\ \hfill \varphi =0,\mathrm{at}z=-h,{(c-u_0)}^2{\varphi }_z=g\varphi ,\mathrm{at}z=0,\end{array}$$

which also is used to determine the linear phase speed, c. Here, ${\rho }_0\left(z\right)$ is the background density where ${\rho }_0{N}^2=-g{\rho }_{0z}$ and $u_0\left(z\right)$ represent the background current. The coefficients of Equation (2) are given by general uttering for the KdV equation. Thus, the coefficients $\mu$ and $\lambda$ are given by:

$$\begin{array}{cc}\hfill I\mu & =3{\int }_{-h}^0{\rho }_0{(c-u_0)}^2{\varphi }_z^{3}dz,\hfill \\ \hfill I\lambda & ={\int }_{-h}^0{\rho }_0{(c-u_0)}^2{\varphi }^{2}dz,\hfill \end{array}$$

(3)

where I is:

$$I=2{\int }_{-h}^0{\rho }_0(c-u_0){\varphi }_z^{2}dz.$$

(4)

The Earth’s rotation is defined by $\gamma$,

$$\begin{array}{cc}\hfill & I\gamma =f^2{\int }_{-h}^0{\rho }_0\mathsf{\Phi }{\varphi }_{z}dz,\mathrm{and}\hfill \\ \hfill & {\rho }_0(c-u_0)\mathsf{\Phi }={\rho }_0(c-u_0){\varphi }_z-{\left({\rho }_0{u}_0\right)}_z\varphi ,\hfill \end{array}$$

(5)

where f is the Coriolis parameter. The linear dispersion relation of the Equation (2) for the sinusoidal waves $sin(kX-\omega t)$ of wavenumber k, and frequency $\omega$, is given by:

$$\begin{array}{c}\hfill \omega =\frac{\gamma }{k}-\lambda k^3,\end{array}$$

Thus, the phase speed and the group velocity are stated by:

$$\begin{array}{c}\hfill \mathrm{Phase} \mathrm{Speed}:c=\frac{\omega }{k}=\frac{\gamma }{k^2}-\lambda k^2.\end{array}$$

(6)

$$\begin{array}{c}\hfill \mathrm{Group} \mathrm{Velocity}:c_g=\frac{d\omega }{dk}=-\frac{\gamma }{k^2}-3\lambda k^2.\end{array}$$

(7)

According to the dispersion relation shows in Figure 1, we can see some gap in the linear spectrum in the KdV case ($\gamma =0$) for all $c>0$, where the solitary waves can occur and steady solitary waves diverge from $k=0$. Meanwhile, there is no such gap for the phase speed of the Ostrovsky Equation (2) and hence, the solitary waves solution could not be supported. It is believed that the rotational term eliminates the spectral gap in which the solitary waves are expected to occur [13]. A theoretical analysis, numerical simulations and a series of laboratory experiments are used to evoke the formation of the nonlinear wave packet in the Equation (2) from the initial KdV solitary wave [14]. Recent theoretical studies have shown that the evolution of the leading nonlinear wave packet from Equation (2) is represented by an extended nonlinear Schrodinger equation. The recent numerical study on the Ostrovsky equation for the case with $\lambda \gamma >0$, and background current, $u_0=0$, which is common for internal and surface waves, has found the unsteady envelope solitary wave solution [13]. However, it is possible to have a case with $\lambda \gamma <0$, known as the anomalous case in sufficiently strong shear and found the steady envelope solitary wave solution [15,16].

Nonetheless, the internal solitary waves usually generates over the variable topography, and show some impressive effect of deformation and evolution of the internal solitary waves. The combination effects of the background rotation and variable topography leads to the development of the variable-coefficient Ostrovsky equation [17,18,19,20]. It is believed that the effects of the rotation and topography can led significant impact on the internal solitary waves propagation in the realistic oceanic situations. Grimshaw and et al. [17] presented numerical simulations of this problem, together with the analogous simulations of a certain cross section of the South China Sea. Moreover, there are several researches that demonstrated the effects of the rotation and background topography on the internal undular in the past few years [18,21,22].

In this paper, we analyze the same scenario when the variable topography and rotational effects are all considered, using the solitary wave solution as the initial condition. Here, we intend to identify the topography and rotational effects on the solitary waves in two-layer fluid. Our main interest here is for the normal case where $\lambda \gamma >0$, which is believed to destroy the solitary wave and form the unsteady wave packet. First, we shall describe our problem formulation for the two-layer fluid in Section 2. The pseudospectral method is used as the numerical method to solve our mathematical model. Then, in Section 3, we shall present our numerical simulations. Finally, we conclude our findings in Section 4.

2. Problem Formulation

The KdV Equation (1) is replaced by the vKdV Equation (8) when the topography is varied. However, there are many versions of the derivation of the vKdV equation, depending on the physical problems under consideration. The vKdV equation for the water waves, where $Q=c$ was first derived by Johnson [3] and by Grimshaw [23] for the internal waves (see Grimshaw et al. [8] for a recent review). Following [8], the general equation of the vKdV equation is written as:

$$\begin{array}{c}\hfill A_t+c\left(x\right)A_x+\frac{c\left(x\right)Q_x\left(x\right)}{2Q\left(x\right)}A+\mu \left(x\right)A{A}_x+\lambda \left(x\right)A_{xxx}=0.\end{array}$$

(8)

Similarly, when the Earth’s rotation is taken into account, in the existence of a slowly changing slope where the fluid depth h, background current $u_0\left(z\right)$ and density ${\rho }_0\left(z\right)$ differ gradually in the horizontal direction with x, the Ostrovsky Equation (2) is now replaced by:

$$\begin{array}{c}\hfill {\{A_t+c\left(x\right)A_x+\frac{c\left(x\right)Q_x\left(x\right)}{2Q\left(x\right)}A+\mu \left(x\right)A{A}_x+\lambda \left(x\right)A_{xxx}\}}_x=\gamma \left(x\right)A.\end{array}$$

(9)

Equation (9) is known as the variable-coefficient Ostrovsky equation [17,18,19,20]. Equation (9) is reduced to (2) when all coefficients are constant in x as h is constant. Since the modal equation now depends also parametrically on x, and so $\mu$, $\lambda$, $\gamma$, c, and Q are also in terms of x where $Q\left(x\right)$ is the linear magnification factor given by:

$$\begin{array}{c}\hfill Q=I{c}^2.\end{array}$$

(10)

It is appropriate to make the transformation,

$$B=\sqrt{Q}A,\tau =\int \frac{dx}{c},X=\tau -t,$$

(11)

and Equation (9) is replaced by:

$$\begin{array}{c}\hfill {\{B_{\tau }+\nu \left(\tau \right)B{B}_X+\delta \left(\tau \right)B_{XXX}\}}_X=\sigma \left(\tau \right)B,\end{array}$$

(12)

where

$$\nu \left(\tau \right)=\frac{\mu }{c\sqrt{Q}},\delta \left(\tau \right)=\frac{\lambda }{c^3},\mathrm{and}\sigma \left(\tau \right)=\gamma c.$$

(13)

Here, the coefficients $\nu$ and $\delta$ are functions of $\tau$ alone which are decided by the properties of the basic state of the fluids, $h\left(\tau \right)$. Generally, we denote $A(x,t)=A(X,\tau )$ and $h\left(x\right)=h\left(\tau \right)$ where the depth varies slowly in the propagation of x-direction. While $\tau$ is described as a variable along the spatial path of the waves, it can also represent “time”. Likewise, although X is a temporal variable, we also can indicate it as a “space” variable in a reference frame moving with speed, c.

Like the KdV equation, Equation (12) in the absence of the rotational effect is integrable and has a solitary wave solution. We revisited the decay of the initial KdV solitary waves for the case when the depth, h, is constant as the initial condition. A solitary wave solution is given by:

$$B(X,\tau )=asec{h}^2\left(k(X-c\tau )\right),c=\frac{\nu a}{3}=4\delta k^2.$$

(14)

Here, the speed, c, is proportional to the wave amplitude, a, or to the square of the wave number, $k^2$, which means that the solitary waves propagate with a speed that increases with the amplitude of the waves. This means that the smaller amplitude waves are wider and travel slower than the larger ones. The wave propagation for the water surface in the absence of the rotational background has been studied previously in [24,25]. However, in the real world problems, the internal waves often propagate in the two-layer fluids and one would expect similarity for other similar density stratification. The discussion about wave propagating over two-layer fluid in the presence of the rotational effect is discussed in the next section.

Two-Layer Fluid

Internal waves is a common phenomenon near the coastal areas and the two-layer fluid is a typical model to describe the internal waves. The interaction between the waves in the two-layer fluid and coastal structures has been studied by many researchers [8,12,17,19,26,27]. The wave propagation over the two-layer fluid has been studied by [27] using an extended KdV (eKdV) equation. In this paper, we examine the generation of the internal solitary waves in the two-layer fluid flow over a varying topography region in the presence of the background rotation. Thus, the appropriate mathematical model for this problem is the variable-coefficient Ostrovsky equation. For interfacial waves in the two-layer fluid, consider the constant density ${\rho }_1$ and ${\rho }_2$ in the upper layer and lower layer, hence $N^2=0$. The height of the upper layer is denoted by $H_1$, and $H_2=H-H_1$ is the depth of the fluid in the lower layer where H is the total depth. For simplicity, consider that ${\rho }_2\approx {\rho }_1$, which is the normal situation in the ocean. We replaced the free boundary with a rigid boundary so that the upper boundary condition for $\varphi \left(z\right)$ becomes just $\varphi \left(0\right)\approx 0$, the so called rigid-lid approximation typically used for the internal waves. Assuming that there is no background flow ($u_0\left(z\right)=0$) and setting ${\rho }_0=1$, then we obtain:

$$\begin{array}{cc}\hfill \varphi & =\frac{z+H}{H_2},\mathrm{for}-H<z<-H_1,\hfill \\ \hfill \varphi & =\frac{-z}{H_1},\mathrm{for}-H_1<z<0,\hfill \end{array}$$

(15)

and

$$\begin{array}{c}\hfill c=\sqrt{\frac{g^{\prime }{H}_1{H}_2}{H_1+H_2}},\mathrm{and}I=\frac{2cH}{H_1{H}_2}.\end{array}$$

(16)

Hence, the coefficients $\mu$, $\lambda$, and $\gamma$ from the Equations (3) and (5) are

$$\mu =\frac{3c(H_1-H_2)}{2H_1{H}_2},\lambda =\frac{c{H}_1{H}_2}{6},\mathrm{and}\gamma =\frac{f^2}{2c}.$$

(17)

Noted that, for such interface waves, the nonlinear coefficient $\mu$, is negative when $H_1<H_2$ for the normal oceanic situation (where the interface is closer to the free surface than the bottom), and positive in the opposite case. Unlike for the surface water waves, where $\mu$ always remains positive. In the case where $H_1\approx H_2$, $\mu$ is nearly vanished and it is significant to suggest higher-order non-linearity in order to balance the dispersion. The linear magnification factor (10) is given by:

$$Q=\frac{2H_2{[\frac{\left(H_1{H}_2\right)}{H_1+H_2}]}^{3/2}}{H_1^2}.$$

(18)

Substitute Equation (18) into (13), the coefficients of wave propagation over uneven bottom in the two-layer fluid can be written as:

$$\nu \left(\tau \right)=\frac{3(H_1-H_2)\sqrt{2}}{4H_1{H}_2\sqrt{\frac{H_2{\left(\frac{H_1{H}_2}{H_1+H_2}\right)}^{3/2}}{H_1^2}}},\delta \left(\tau \right)=\frac{H_1+H_2}{6},\mathrm{and}\sigma \left(\tau \right)=\frac{f^2}{2}.$$

(19)

Then, the simulations of the variable-coefficient Ostrovsky equation over a bottom with a constant and varying slope following the previous researches is shown in the next section. The numerical solution of this equation has been solved using the Fourier Pseudospectral method in the time-like phase variable X. The calculation uses a periodic domain in X that diverges within runs, but is sufficient enough to prevent major problems in the evolving wave solution. The numerical resolution is in the order of $▵\tau =0.001$ and infinite interval of $-1200<X<1200$. We use larger $\sigma$ in our simulations, where the Coriolis parameter is $f\approx 1$ to diminish computational time and emphasize the role of the rotation.

3. Results and Discussions

The wave propagation over a bottom with a constant and varying slope on a water surface has been studied before but at that time the background rotation is neglected. Thus, the aim of this paper is to distinguish the formation of the solitary waves as it propagates through the varying depth region in two-layer fluid in the presence of the rotational effect. Here, we consider the formation and propagation of the solitary waves traveled for three different cases of depth similar to [25] but this time the depth, h, is now divided into two layers, $H_1$ and $H_2$, where $H_1$ is considered constant for all $\tau$ and $H_2$ varies according to the given bottom profile. Here, we focus on the case when $\mu >0$ and hence, $H_1$ is always greater than $H_2$. For the first case, we consider the depth, $H_2$, to be constant, where the variable-coefficient Ostrovsky is reduced to the Ostrovsky equation. Noted that the small initial wave amplitude did not really apparent when the rotation term is added, as the amplitude of the wave packet is reduced as the energy of the soliton is decreased. Therefore, the initial amplitude, $a_0=3$ is applied for all cases in this study. The numerical solutions of Equation (12) are shown in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. The KdV solitary wave solution from (14) is used as the initial condition where:

$$B(X,0)=3sec{h}^2\left(kX\right),k=\sqrt{\frac{\nu }{4\delta }}.$$

As can be seen in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, the initial solitary wave immediately disintegrated into Poincare waves and ultimately the leading disturbance formed a wave packet.

3.1. Case 1: Constant Variable

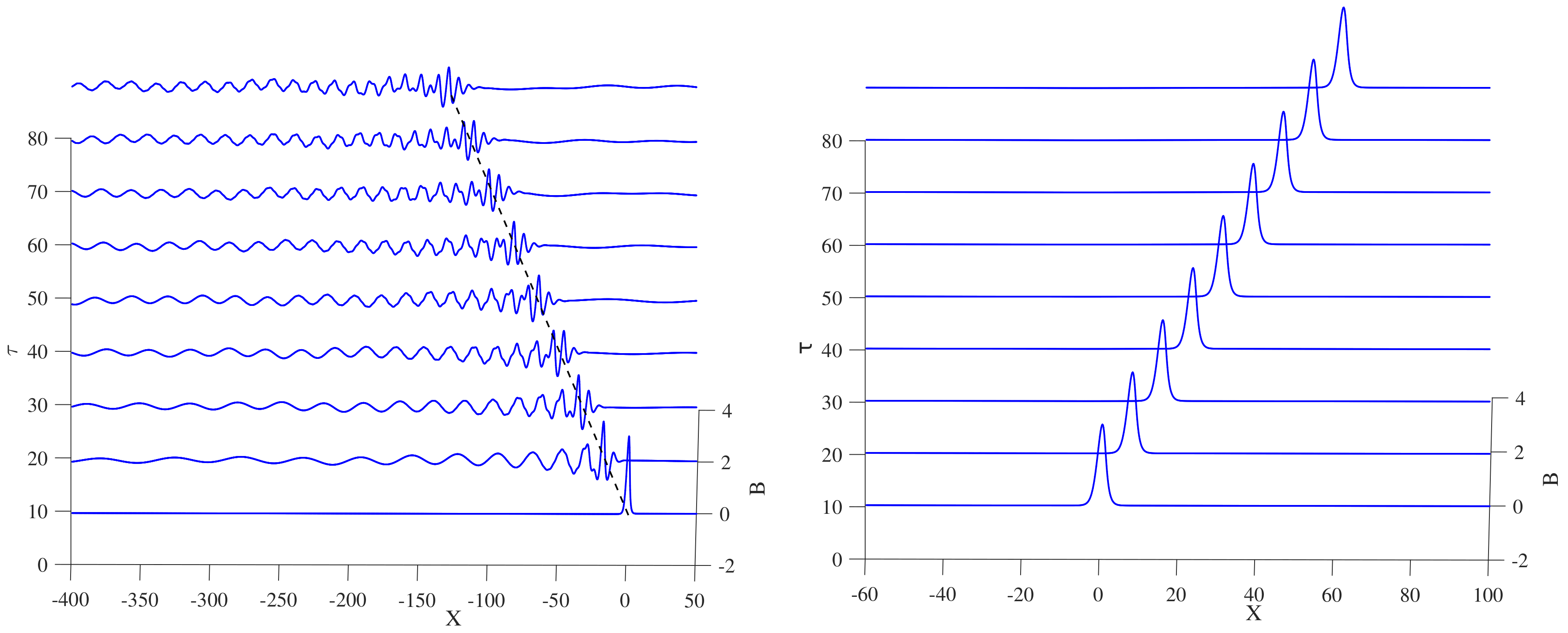
Figure 2 shows the solution of solitary waves with the initial amplitude $a_0=3$ released in the infinite interval of $-1200<X<1200$. In this example, we analyze the wave propagation when the rotational effect has been set to $f=1$ and $f=0.01$. From Figure 2, as the water depth is constant and f is $0.01$, the rotational term on the right hand side of Equation (12) becomes too small and eventually the Ostrovsky equation is reduced to the normal KdV equation where the wave maintain its shape and move at a constant speed which is in a good agreement with previous study [28].

From Equation (14), the constant speed for the solitary waves over a surface water is $1.5$ and in the two-layer fluid is ≈0.78. The numerically determined speed of the solitary waves in the absence of background rotation for each $\tau =10$ is shown in

Table 1. Numerically determined speed, c over a constant depth in the absence of the background rotation.

	Water Surface			Two Layer Fluid
$\mathit{\tau }$	$\mathit{X}$	$\mathit{a}$	$\mathit{c}$	$\mathit{X}$	$\mathit{a}$	$\mathit{c}$
10	15.01464844	2.97306900	1.50146484	7.83691406	2.99955300	0.78369141
20	30.10253906	2.99604300	1.50512695	15.60058594	2.99844000	0.78002930
30	45.04394531	2.99206100	1.50146484	23.36425781	2.99665700	0.77880859
40	60.13183594	2.98092200	1.50329590	31.12792969	2.99420400	0.77819824
50	75.07324219	2.99984300	1.50146484	39.03808594	2.99380000	0.78076172
60	90.01464844	2.97241500	1.50024414	46.80175781	2.99634800	0.78002930

. From the Table, we can see that for the both cases of water surface and two-layer fluid, when $f=0$, the speed, c is reduced as total depth of the water is deeper.

3.2. Case 2: Rapidly Varying Depth

Next, we will discuss the wave propagation over various topography when the variable topography is being considered. Figure 3 shows the wave propagation for every $\tau =10$ when the depth $H_2\left(\tau \right)$ decreases rapidly. The detailed amplitude variations are determined by the rapidly changing bottom profile. The depth profile is taken as:

$$\begin{array}{cc}\hfill H_2\left(\tau \right)& =\left\{\begin{array}{ccc}\hfill h_0=1& :& \tau <50\hfill \\ \hfill h_1=0.7& :& \tau >50,\hfill \end{array}\right.\hfill \end{array}$$

(20)

The right Figure 3 shows the time series plot of the wave amplitude, B propagates over rapidly decreasing depth in the absence of the rotational term, $\sigma =0$ in the range of $-50\le X\ge 200$. It is not until $\tau >50$ where the total depth is $2.2$, that the coefficients in (12) begin to change significantly. It shows that the topography plays significant effects on the incident waves as the solitary waves begin to fission into two solitons followed by an oscillatory tail. This process has been demonstrated numerically and experimentally by [29] while the analytical explanation was done by [3,30]. The number of solitons formed, N is obtained by $N=1+[(\sqrt{8Z+1}-1)/2]$, where Z is the ratio of coefficients determined by:

$$Z=\frac{{\nu }_{+}{\delta }_{-}}{{\nu }_{-}{\delta }_{+}}.$$

(21)

The solitary waves disintegrate into several different sizes of the solitary waves when it travels rapidly from a constant depth to another shallower constant depth. It follows that, if $h_0>h_1$, then, $Z>0$ and $N\ge 2$. Hence, at least one more solution is formed. This is due to the nonlinear effects that ultimately contributes to the steepening and thus, the dispersive effects will be invoked. Here, the leading solitary waves split from a trailing wave which initially carries the speed c before the steepening and fissioning arises. Then, this leading solitary wave propagates adiabatically with the local solitary wave speed, $c+\nu a/3$, where a is the local amplitude (see (14)). It is believed that, in the absence of the rotational effect, the amplitude of the waves is increased and propagated faster as the speed of the waves is increased from ≈0.78 to ≈1.24 at $\tau =60$.

In comparison, the inclusion of rotational effects, $\sigma \ne 0$, generates the wave formation shown in the left Figure 3. Here, the rotational term included has destroyed the solitary wave solution and nonlinear envelope wave packet is formed instead. The incident solitary wave still experiences a fissioning process after $\tau >50$ similar to that seen in the right Figure 3 although the number of wave scattered in the packet and the wave amplitude have reduced due to the energy lost in the initial waves to a larger amplitude trailing wave. This trailing wave develops as it generates up the slope and eventually steepens to form a secondary wave packet positioned at $X=-110$ at $\tau =60$. As for the wave propagation over rapidly increasing depth, the depth profile is taken as:

$$\begin{array}{cc}\hfill H_2\left(\tau \right)& =\left\{\begin{array}{ccc}\hfill h_0=1& :& \tau <50\hfill \\ \hfill h_1=1.3& :& \tau >50,\hfill \end{array}\right.\hfill \end{array}$$

(22)

Figure 4 shows the wave propagation over rapidly increasing depth. Similarly, the solitary wave is decayed and forms a wave packet in the existence of background rotation, $\sigma \ne 0$. Meanwhile, when the background rotation is omitted ($\sigma =0$), there is no fission of solitary waves observed after $\tau >50$, where the waves move into the deeper region, $h_0<h_1$, as the waves disintegrated and formed a radiation tail. Here, no further solitons are composed when $N=1$ [3,7]. Here, the speed is reduced to ≈0.65 at $\tau =60$. At this time, the amplitude of the trailing tail for both $\sigma =0$ and $\sigma \ne 0$ is slightly less than in the previous case, as the waves just happen to develop. The cross-section formation of wave propagation over a constant and rapidly decreasing and increasing depth at $\tau =90$ in the presence of a rotational effect is shown in Figure 5.

Figure 5 shows the time series of the wave amplitude at the selected range $-400<X<-50$. It is not until $\tau >50$ where the wave begins to change accordingly. As it generates up the slope, it encounters a fissioning process. The initial shoaling process generates a trailing tail as discussed, but it is quite small and obscured by the fissioning. We can clearly see that the amplitude of the waves is increase in (b) and as amplitude is higher, the waves is larger and narrower. In contradiction, when the depth is rapidly increase (c), the amplitude of the waves is decreased and hence, the waves is smaller and wider. Both cases are in a good agreement with the previous study except that the solitary waves is decayed and formed a wave packet. This is due to rotational effect on the right hand side of Equation (12).

This compelling new feature, which was not previously disclosed, is caused by a combination of the background rotation and variable topography. The incident waves undergo a fissioning process close to that shown in the right panels of Figure 3 and Figure 4, even though the number of the scattered waves in the packet and the rate at which it happened does depend on $a_0$. This is due to the waves being smaller when the rotation is inserted since the energy in the initial wave vanishes as discussed in the previous section. Considering that the dispersive packet is more refined when the initial waves used is large, hence, the leading solitary waves are essentially larger. Even though the background topography effect seems not so apparent when the rotation is added, it still has shown some dynamics in the formation of waves. In fact, the effect of Earth’s rotation gives an immense effect as the solitary waves has transformed into nonlinear wave packet.

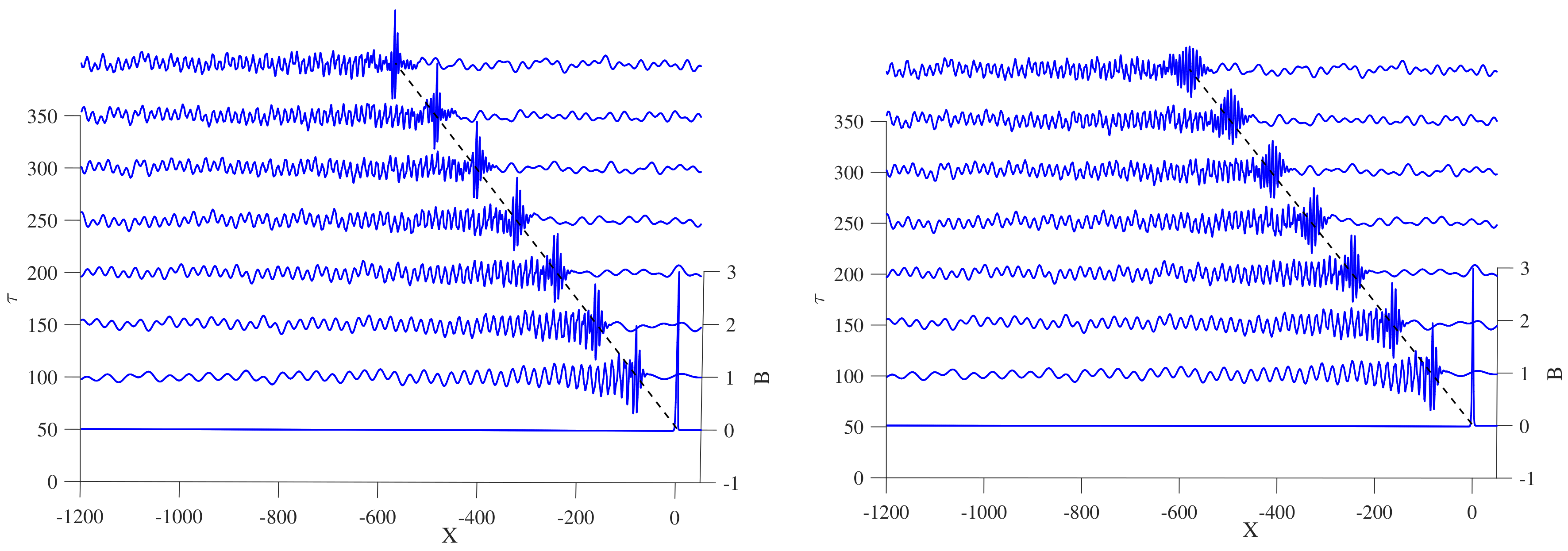
3.3. Case 3: Slowly Varying Slope

Next, we will take the opposite situation, in which the coefficients $\nu \left(\tau \right)$ and $\delta \left(\tau \right)$ in (19) are varying slowly in which the solitary waves is generates over a gradually changing topography. The depth profile, $H_2\left(\tau \right)$ is given by:

$$H_2\left(\tau \right)=\left\{\begin{array}{ccc}\hfill 1.0& :& \tau <100\hfill \\ \hfill {(1-\frac{\alpha (\tau -100)}{2})}^2& :& 100<\tau <334.60,\alpha =0.0009\hfill \\ \hfill 0.8& :& \tau >334.60\hfill \end{array}\right.$$

(23)

Figure 6 shows the numerical simulation of the propagation of the solitary waves over a slowly shallower and deeper region for every $\tau =50$. As can be seen, the amplitude of the wave packet increases adiabatically when propagating over a slowly shallower region and vice versa. As expected, the number of the waves inside the envelope wave packet is fewer as the amplitude is higher and vice versa. Here, the depth profile, $H_2\left(\tau \right)$ for slowly decreasing slope is taken as:

$$H_2\left(\tau \right)=\left\{\begin{array}{ccc}\hfill 1.0& :& \tau <100\hfill \\ \hfill {(1+\frac{\alpha (\tau -100)}{2})}^2& :& 100<\tau <312.10,\alpha =0.0009\hfill \\ \hfill 1.2& :& \tau >312.10\hfill \end{array}\right.$$

(24)

The details comparison of the wave packet formation when propagating over a slowly increasing and decreasing depth at $\tau =350$ is shown in Figure 7. There is a valid agreement that the amplitude of the wave is higher and narrower as the topography is shallower. Again, there is an excellent agreement with [7]. Similar to the previous case of the internal solitary wave propagating over a rapidly varying depth, the amplitude of the wave packet adiabatically increases while it is on the increasing slope and reduces when it enters the decreasing slope region. The amplitude of the transformed wave packet propagates after the slope is slightly less than the amplitude of the initial internal solitary waves for every case. 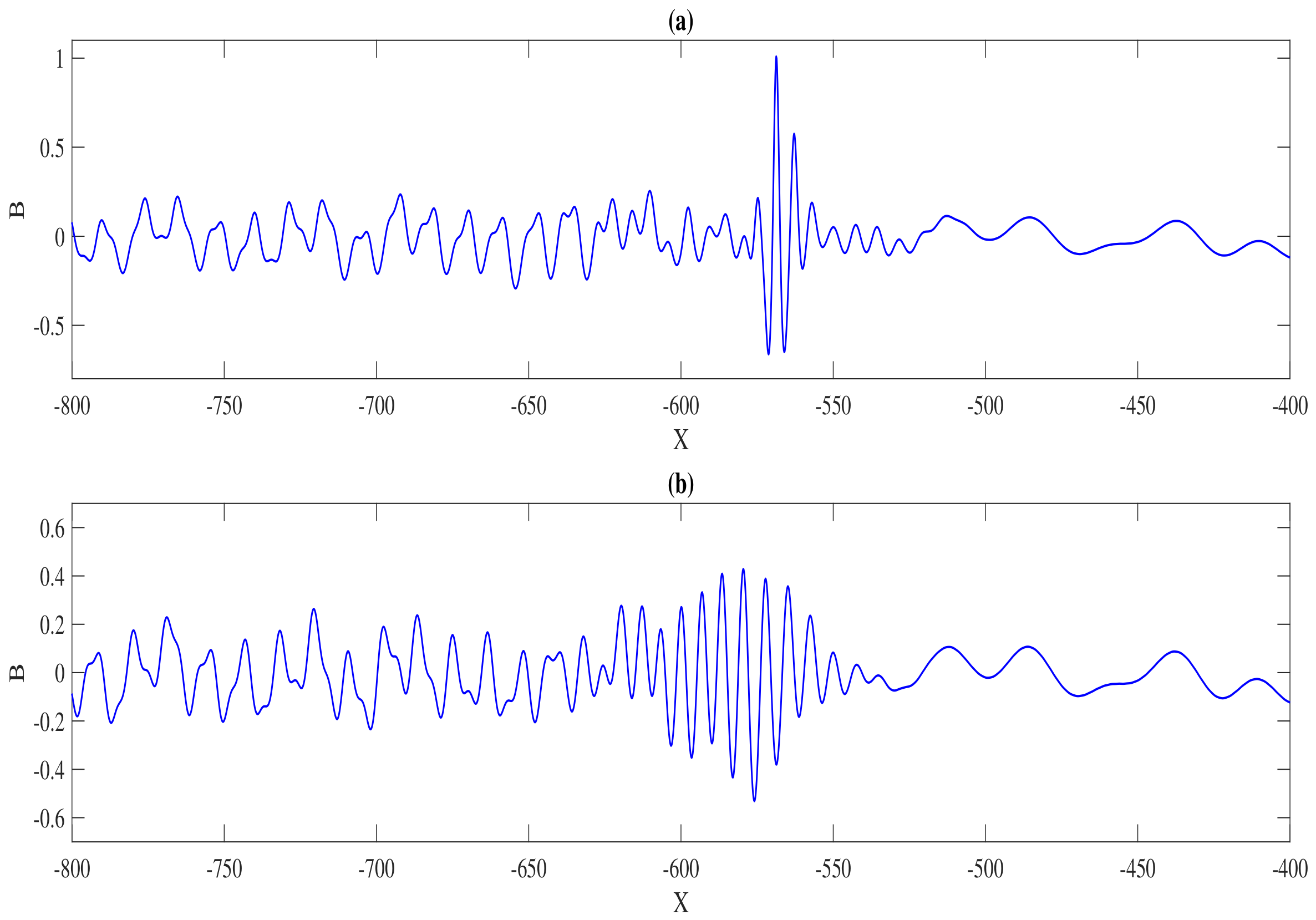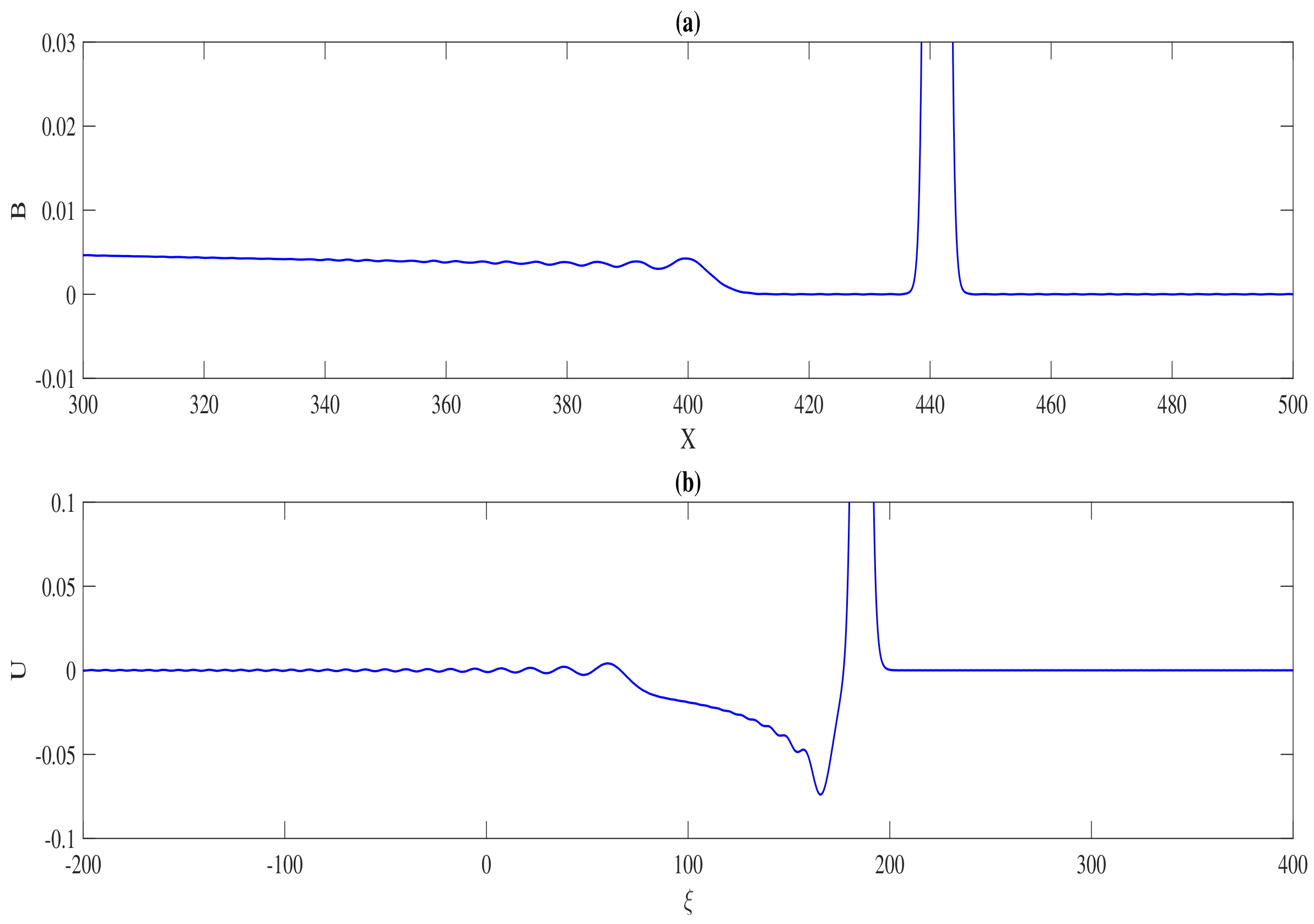Meanwhile, the solitary waves typically deforms adiabatically in the absence of rotational effect, $\sigma \ne 0$, and there is a non-adiabatic response regardless of the small variation of the bottom slope in the form of an extended small amplitude secondary structure or a shelf, which can have a positive or negative polarity that travel behind the solitary waves [7]. This trailing shelf which happened to disintegrate into the secondary solitary waves is parallel to the soliton fission process on a much larger temporal scale. The cross-section of this trailing shelf structure at $\tau =350$ is shown in Figure 9 which happened to be similar to the case found in the water surface [24,25]. The normalized soliton amplitude $a\left(X\right)/a_0$ seems to not depend on the initial amplitude, $a_0$, when it evolves on the gradually changing slope but, slowly increases or decreases with distance, X according to the hyperbolic law. However, its amplitude remains unchanged and the transformed internal solitary waves continues to propagate with constant velocity once it reaches another constant depth region. However, when $\sigma \ne 0$, the trailing shelf is then disturbed by the formation of the wave packet in the presence of Earth’s rotation.

4. Conclusions

In this research, the solitary wave propagates over a bottom with a constant and varying slope is tested and the configuration for both rapidly and slowly changes of depth is studied. The numerical simulations discussed in this research convince that the rotational term in vKdV equation destroyed the initial KdV solitary waves and generated a new structure known as the nonlinear wave packet. The cases when rotation is neglected proved that the propagation structure produces a single steadily generating solitary wave of depression. Previous studies on vKdV equation for the water waves by [7] have found that the variable topography tends to break the solitary waves into a secondary solitons when propagating through rapidly decreasing depth, but no fission observed as the waves traveled through rapidly increasing depth. Furthermore, the waves amplitude is begun to increase and move faster after the depth rapidly decreases. In contradiction, the amplitude of the solitary waves is decrease hence travel slower as the depth rapidly increases. As for varying depth, the amplitude of the waves increases and decreases adiabatically when propagating through slowly increasing and decreasing depth. In the context of the original vKdV equation, computational modeling has proven the theoretical assumptions for a relatively low bottom slope, when the asymptotic principle applies. In these cases, a very strong agreement was found between the theoretical results and numerical evidences, both for the flat bottom profile and changing bottom profile, which provide a constant amplitude of the soliton propagation.

Similarly, for this study, when the background rotation is added, the waves propagates accordingly with the vKdV case but rather than a single solitary wave, the wave is generated in the form of unsteady packet-like structure instead. However, if the forcing is small, $f=0.01$, the former relation holds and the impact of the rotation is narrow. However, if the forcing is large, $f=1$, then the rotational effect is dominant as can see in Figure 2. As for varying depth cases, the leading waves of the trailing shelf wave packet can be interpreted as a secondary solitary wave reconciling with the soliton fission described earlier. In this circumstance, the rotational effect tends to be dominant, while the topography effect is partially suppressed, since the variance of the nonlinear coefficient $\nu$ and $\delta$ did not seem to have a substantial influence on the subsequent evolution, although the amplitude of the envelope tends to change. We also believe that the amplitude of the wave packet formed will reduce from the initial amplitude $a_0$ as the energy of the soliton gradually decreases by the permanent radiation of the small-amplitude waves caused by the rotational effect, while the KdV soliton keeps its amplitude unchanged when propagating over a constant depth. For this reason, the small value of $a_0$ chosen, will affect the formation of the wave packets as the wave packet solution arises has a very small amplitude, and will take a very long time to appear. Furthermore, the amplitude varies with $\sigma$ [13]. At higher latitudes and in deeper water, $\sigma$ increases, therefore, the rotational effects can also be expected to increase. Hence, the waves become smaller and wider. Besides, the larger amplitudes of the envelope wave packet formed has a small number of waves contained in the trailing shelf and vice versa which can be clearly seen in Figure 7. We indicate that the simulations use Equation (12) for the process model. The application of our findings to real oceanic conditions involves a transition back to the physical variables. Nonetheless, for all cases, the obtained findings have shown that they are in a good accession with observational studies on the evolution of the internal solitary waves in the deep basin of the South China Sea (SCS) [31,32], where the rotational effects were found to be significant.