Analysis of Hydraulic Mixing Efficiency in Widespread Models of Micromixers
Abstract
:1. Introduction
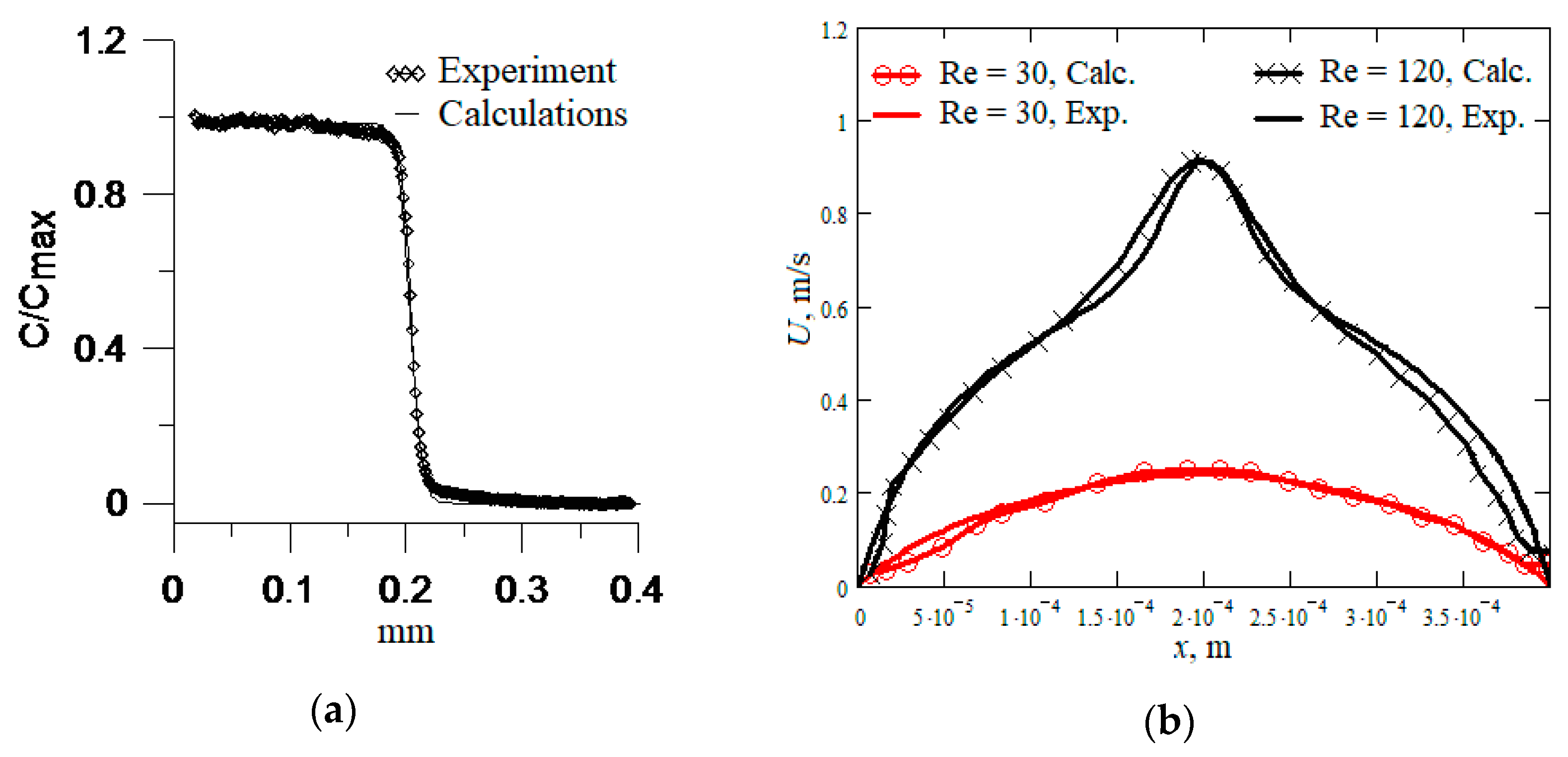
2. Mathematical Model and Numerical Computation Method
3. Results
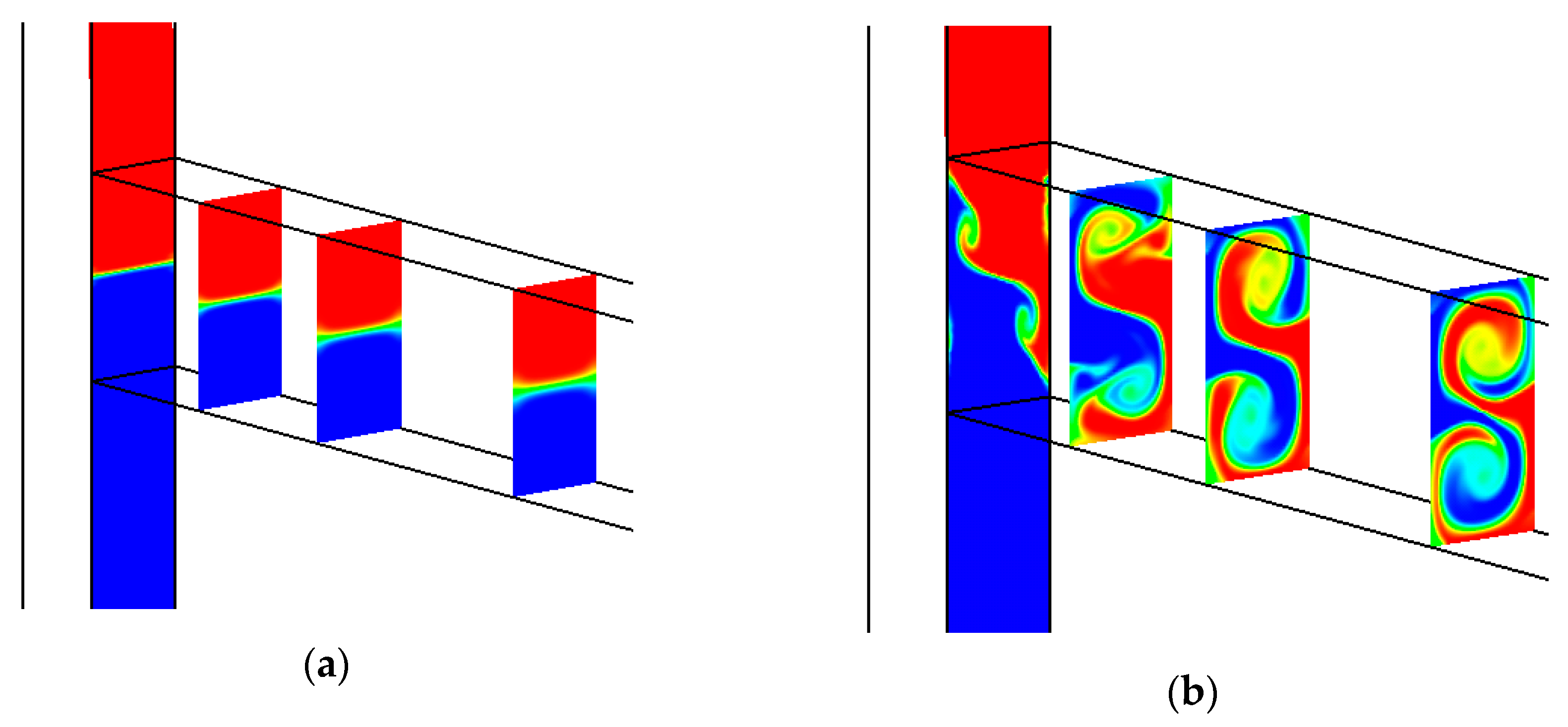
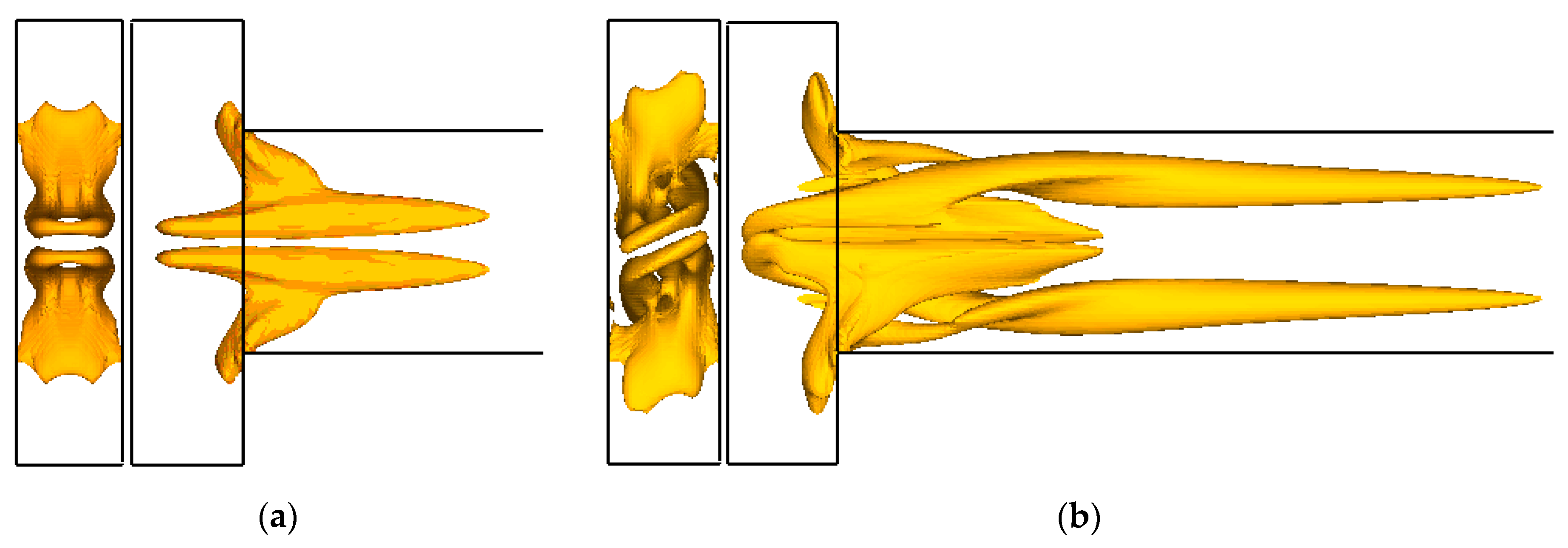
3.1. Flow Analysis in a Basic T Micromixer
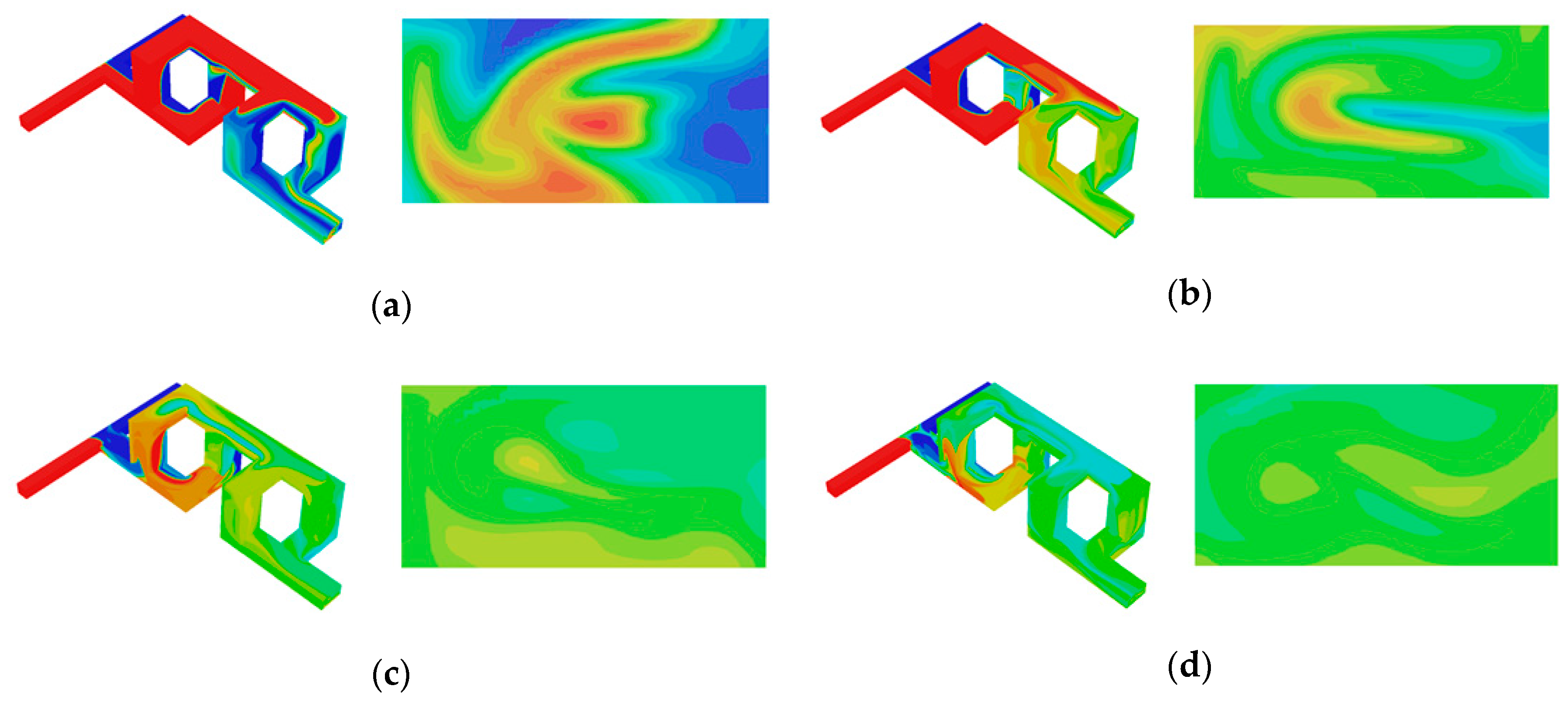
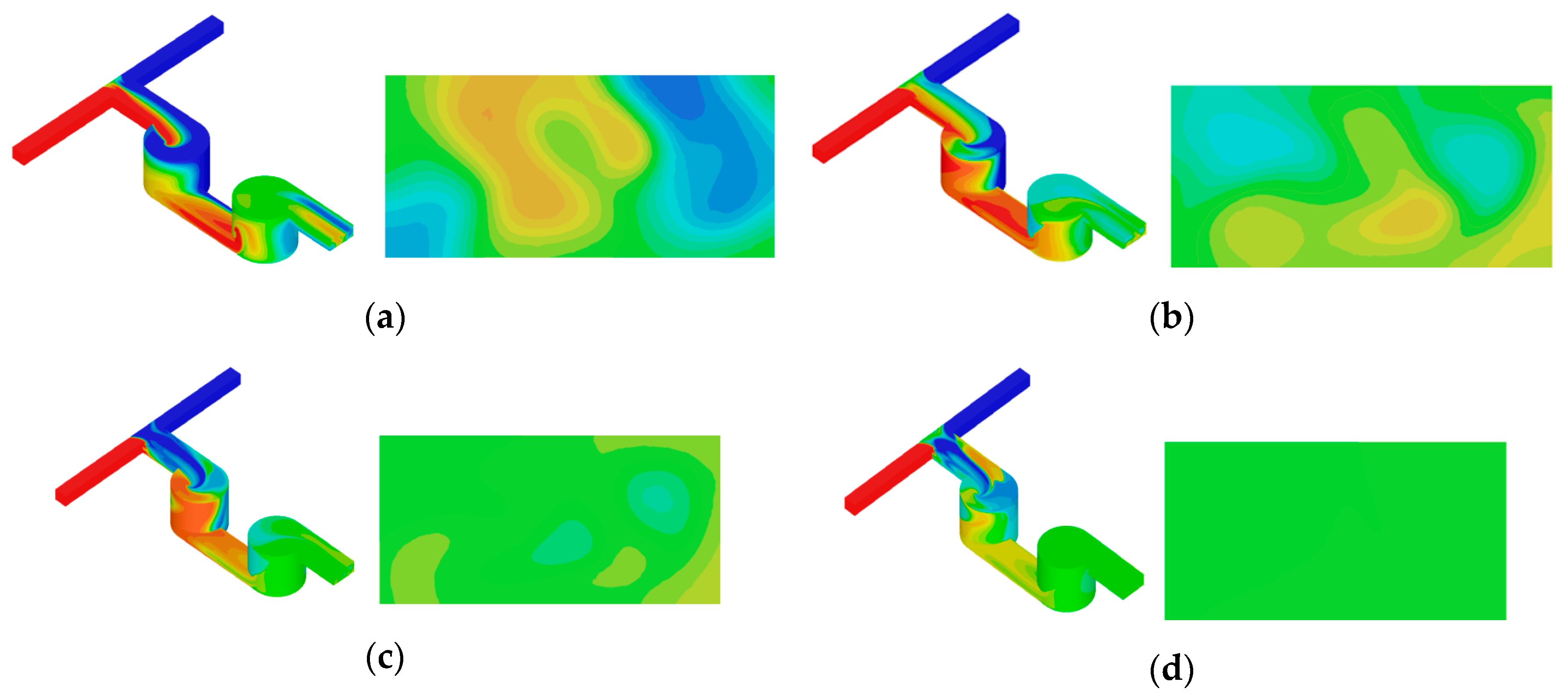
3.2. Flow Analysis in Micromixer No. 2
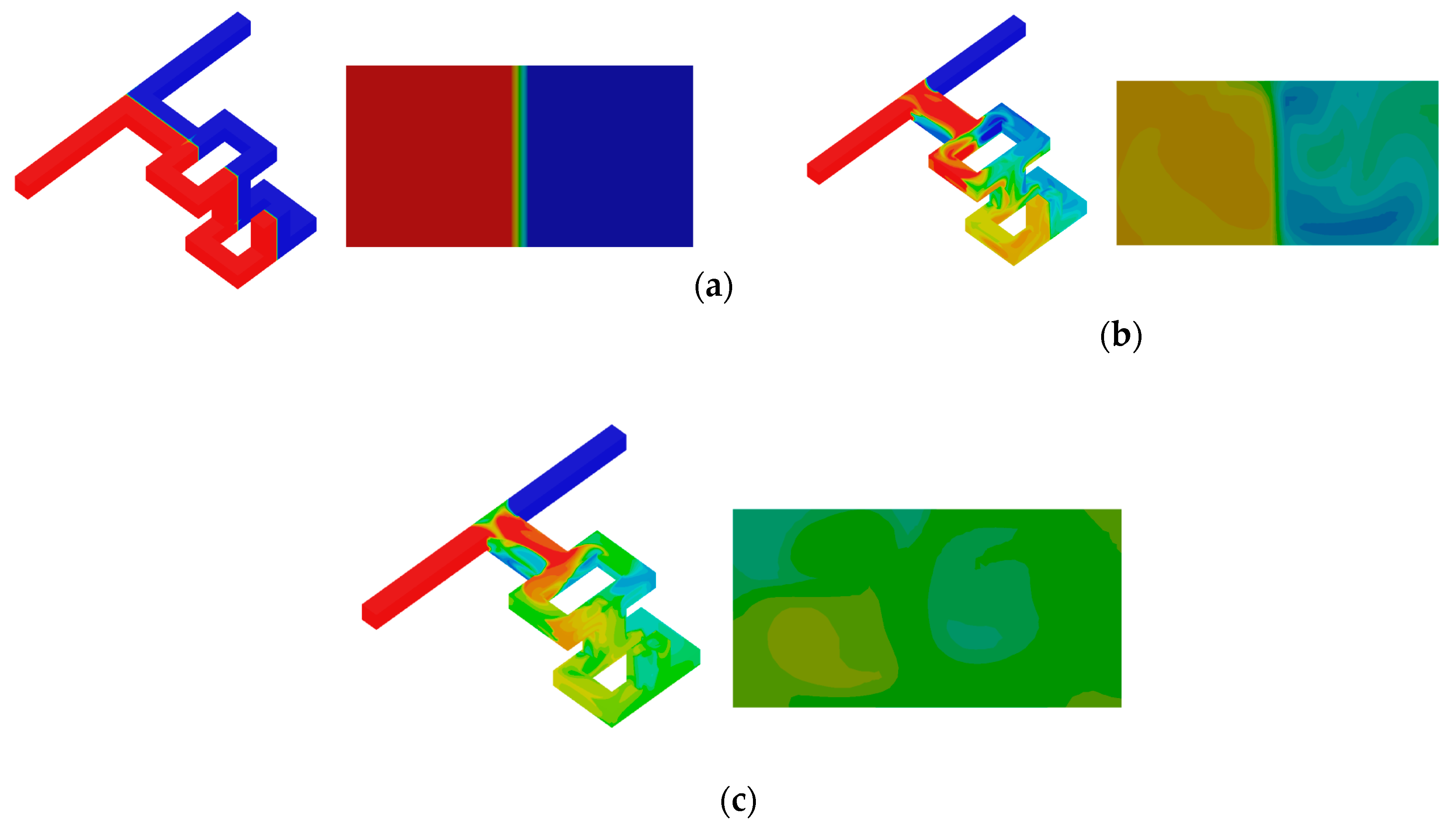
3.3. Flow Analysis in Micromixer No. 3
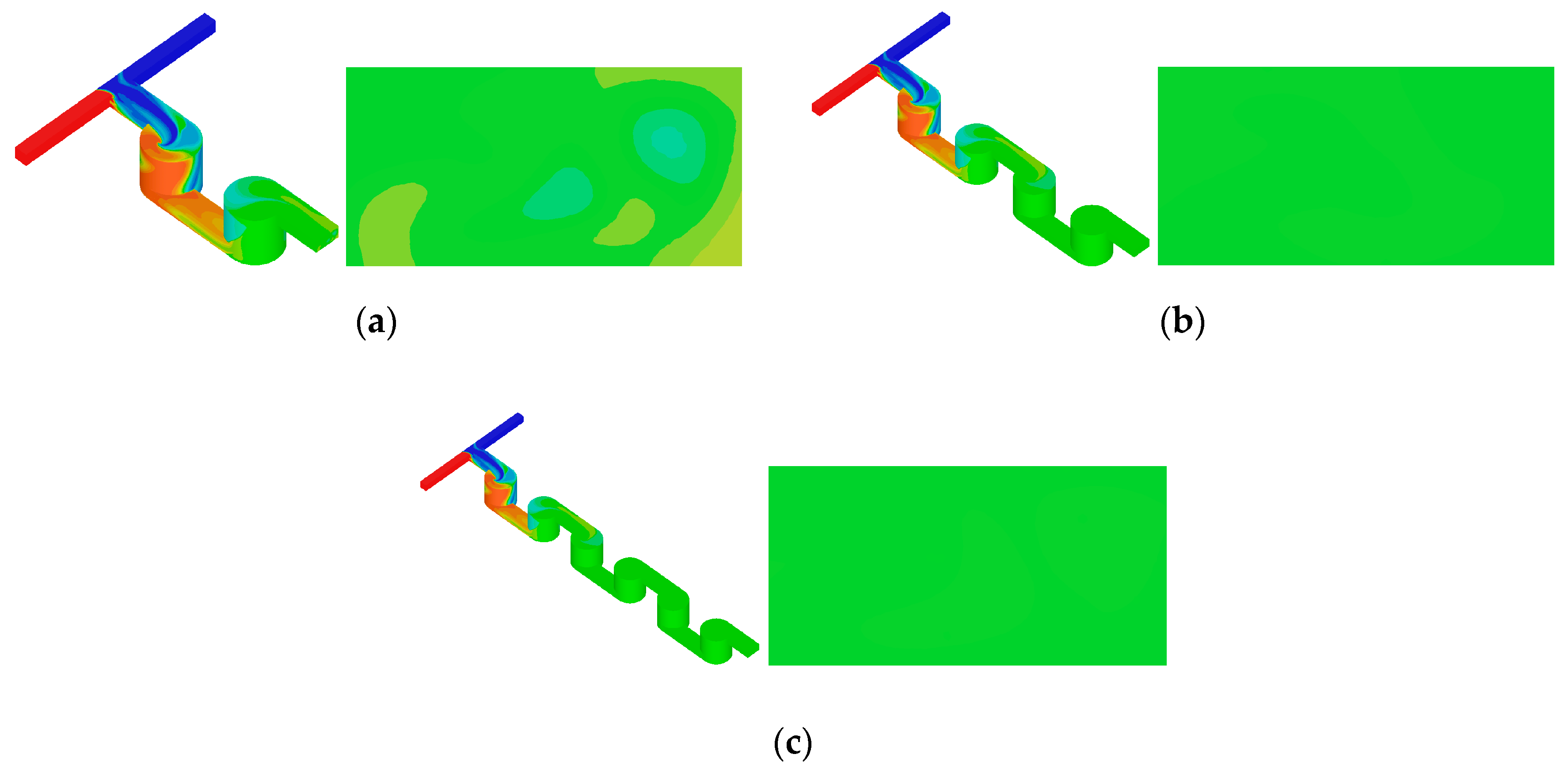
3.4. Flow Analysis in Micromixer No. 4
4. Discussions
5. Conclusions
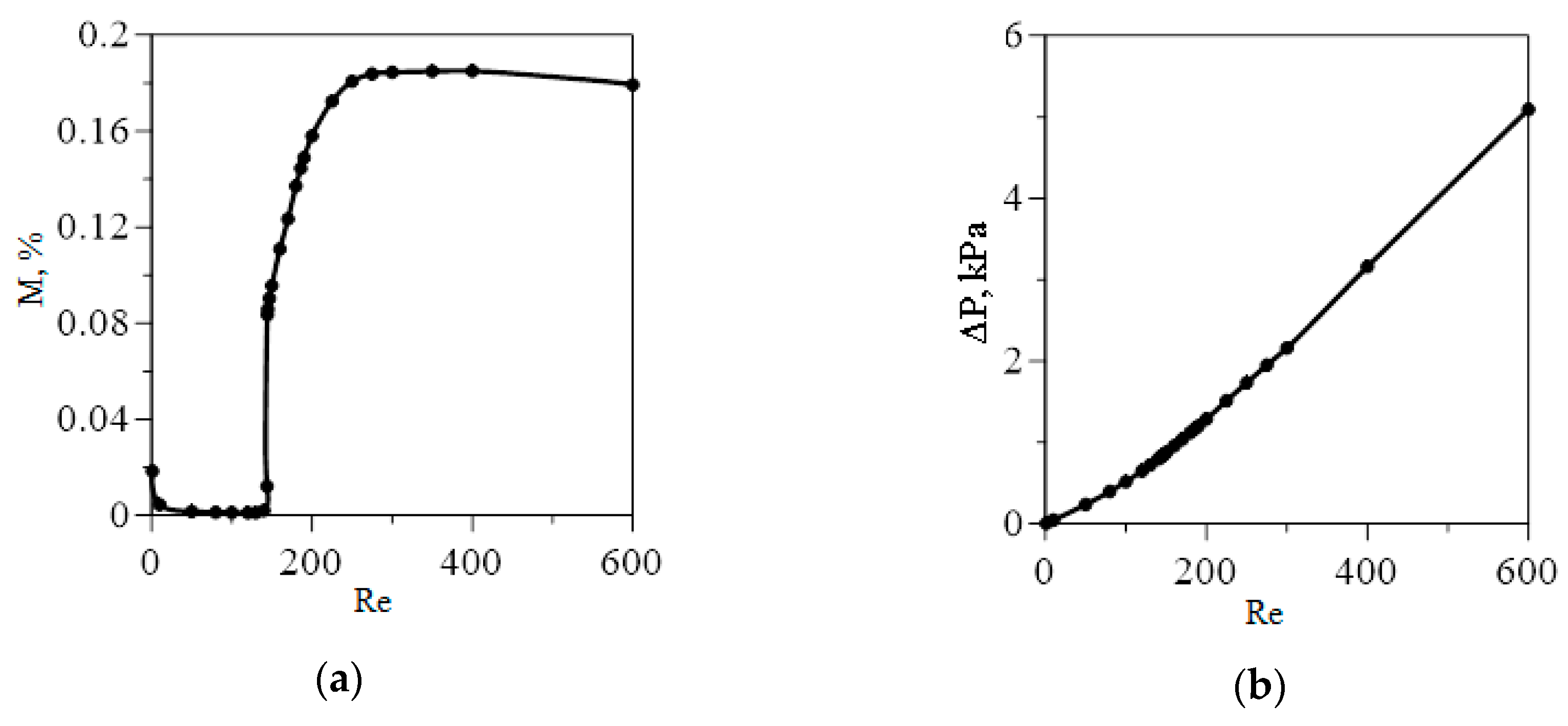
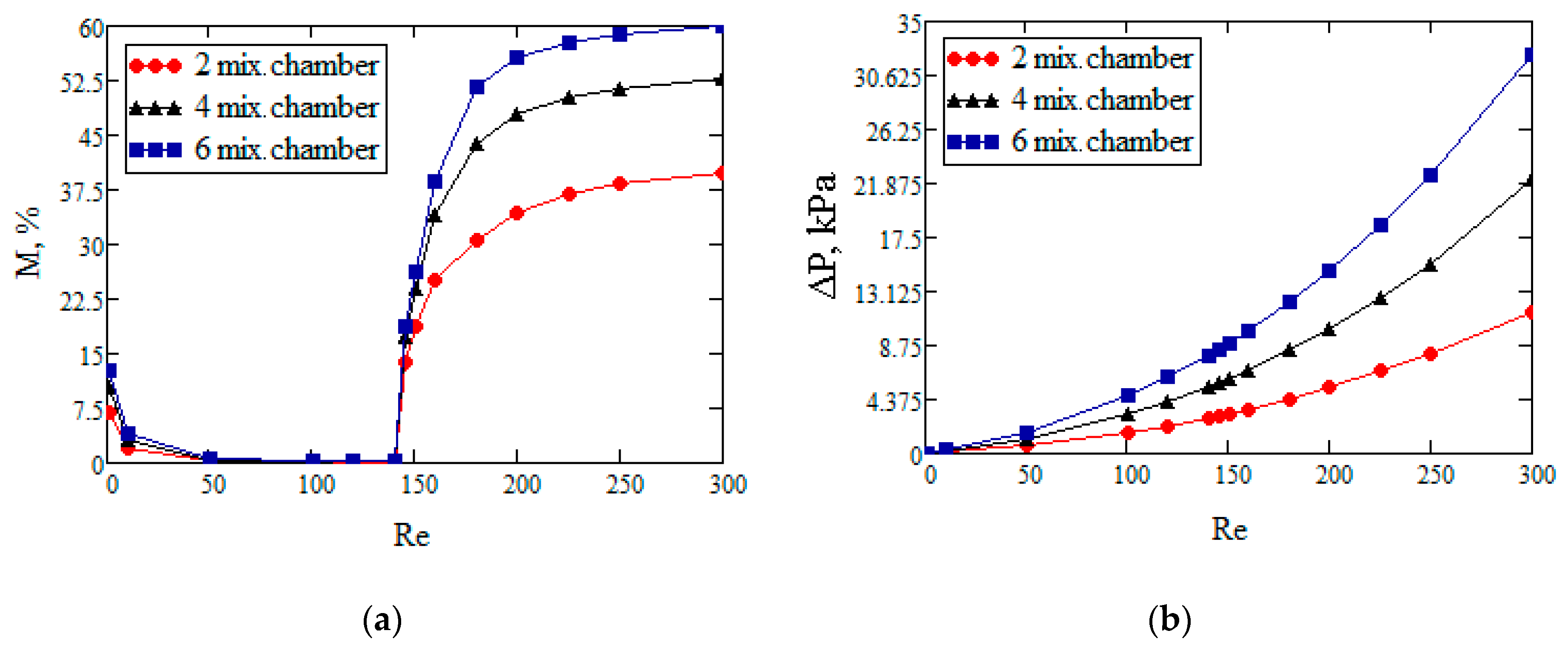
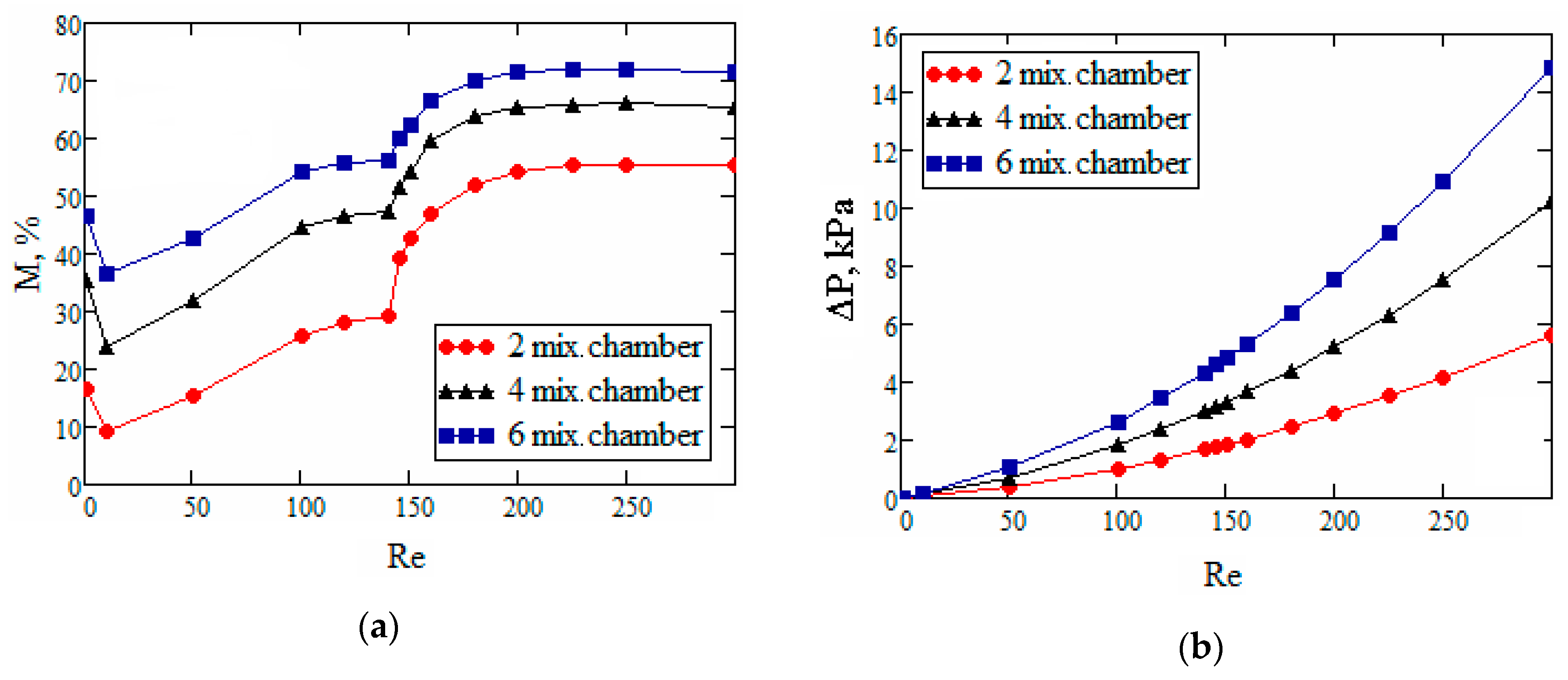
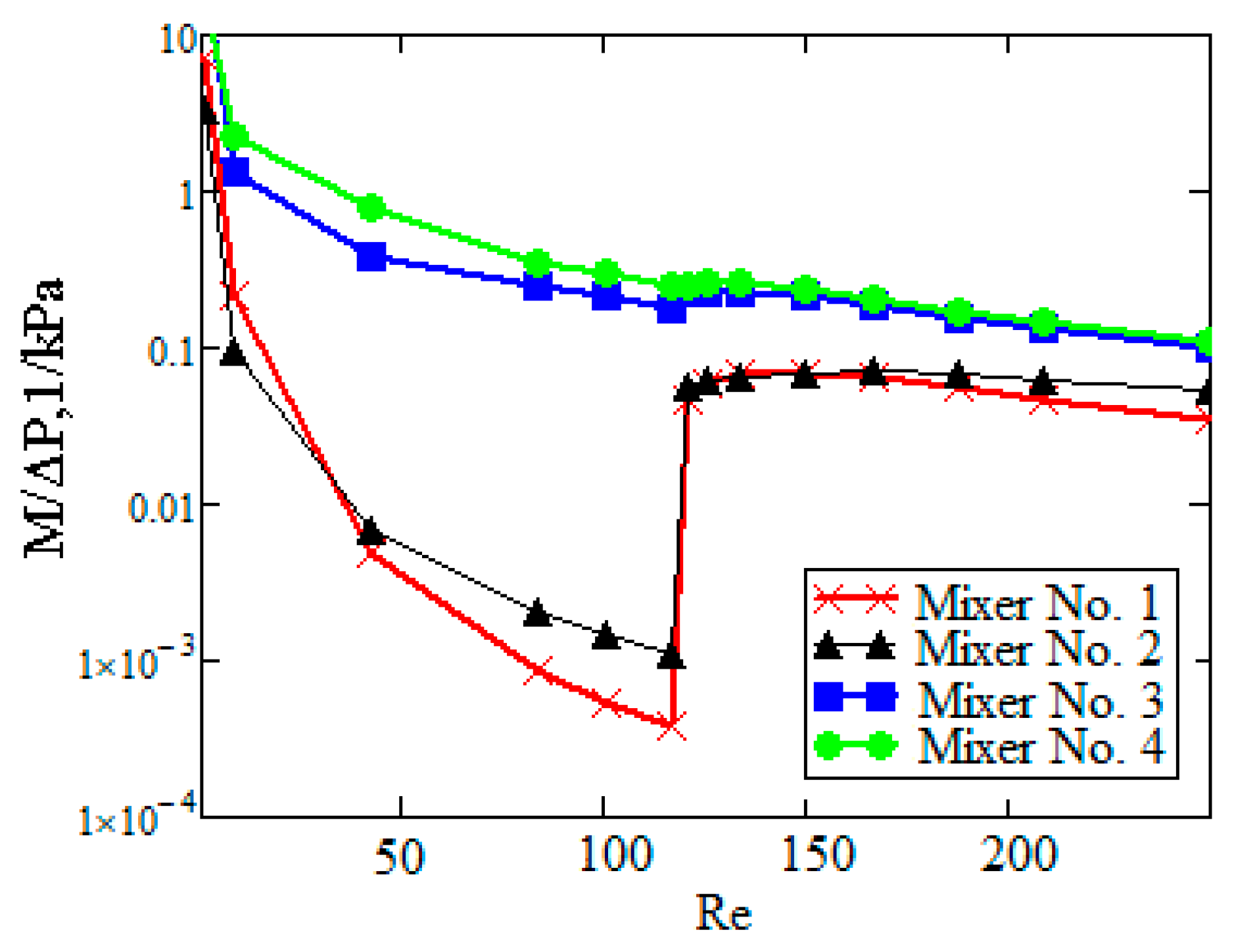
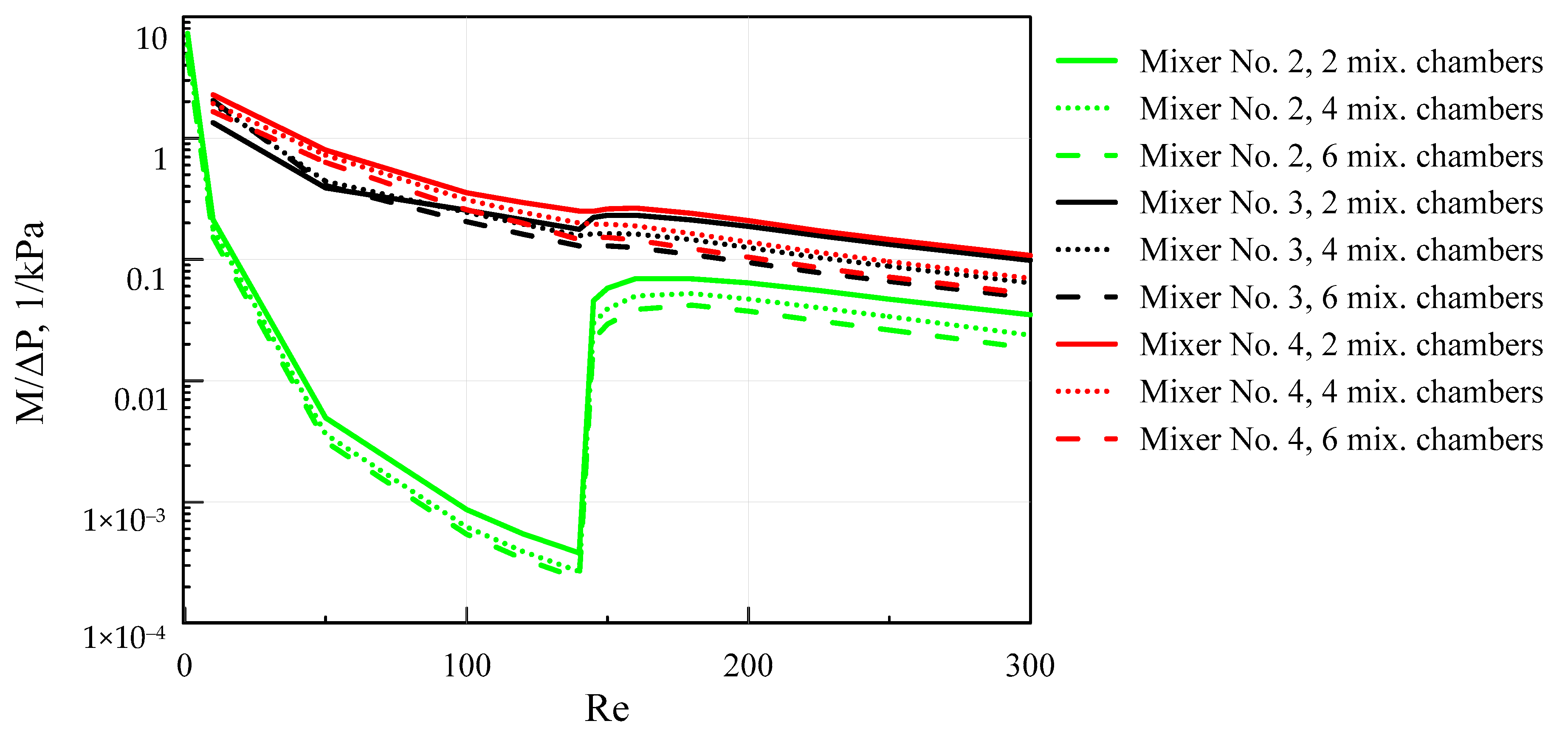
- The normalized mixing efficiency decreases with an increase in the Re number for all the considered mixers.
- It is shown that the maximum normalized mixing efficiency in the entire range of Re numbers was noted for mixer No. 4, in which a vortex-based intensification of mixing occurs due to the flow swirling in cylindrical chambers. This mixer allows mixing the fluids 600 times more efficiently than a straight T-mixer, while all other conditions being equal.
- Mixer No. 3, which implements the flow multiplication principle, is inferior in terms of normalized mixing efficiency to mixer No. 4 by about 1.5 times. At the same time, this mixer is much more difficult to manufacture due to its complicated geometric configuration.
- It was shown that mixer No. 2, which implements, the principle of alternating split and recombine of the flow, has a minimum normalized mixing efficiency. This mixer allows increasing the mixing efficiency by only 1.5 times compared to the straight T-mixer.
- It is established that in addition to the mixer geometric configuration, the flow mode has a determining effect on mixer performance efficiency. It is shown that for all the considered mixers, at Re > 145, the flow regime is rearranged to form a two-vortex S-shaped structure that increases the mixing efficiency tenfold without an additional increase in pressure loss. From a practical perspective, this flow mode is the most effective for any micromixer.
Author Contributions
Funding
Conflicts of Interest
References
- Tabeling, P. Introduction to Microfluidics; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Karnidakis, G.; Beskok, A.; Aluru, N. Microflows and nanoflows. Interdiscip. Appl. Math. 2005, 29, 817. [Google Scholar]
- Elvira, K.S.; Solvas, X.C.; Wootton, R.C.; de Mello, A.J. The past, present and potential for microfluidic reactor technology in chemical synthesis. Nat. Chem. 2013, 11, 905–915. [Google Scholar] [CrossRef] [PubMed]
- Yew, M.; Ren, Y.; Koh, K.S.; Sun, C.; Snape, C. A Review of State-of-the-Art Microfluidic Technologies for Environmental Applications: Detection and Remediation. Global Chall. 2018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Convery, N.; Gadegaard, N. 30 years of microfluidics. Micro Nano Eng. 2019, 2, 76–91. [Google Scholar] [CrossRef]
- Shestopalov, I.; Tice, J.D.; Ismagilov, R.F. Multi-step synthesis of nanoparticles performed on millisecond time scale in a microfluidic droplet-based system. Lab Chip. 2004, 4, 316–321. [Google Scholar] [CrossRef] [Green Version]
- Tsai, T.T.; Shen, S.W.; Cheng, C.M.; Chen, C.F. Paper-based tuberculosis diagnostic devices with colorimetric gold nanoparticles. Sci. Technol. Adv. Mater. 2013, 14. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.; Martinez, A.W.; Gong, J. Paper-based ELISA. Angew. Chem. 2010, 122, 4881–4884. [Google Scholar] [CrossRef] [Green Version]
- Martinez, A.W.; Phillips, S.T.; Whitesides, G.M. Three-dimensional microfluidic devices fabricated in layered paper and tape. Proc. Natl. Acad. Sci. USA 2008, 105, 19606–19611. [Google Scholar] [CrossRef] [Green Version]
- Tawfik, D.S.; Griffiths, A.D. Man-made cell-like compartments for molecular evolution. Nat. Biotechnol. 1998, 16, 652–656. [Google Scholar] [CrossRef]
- Karnik, R. Microfluidic mixing. In Encyclopedia of Microfluidics and Nanofluidics; Li, D., Ed.; Springer: Cham, Switzerland, 2008; pp. 1177–1186. [Google Scholar]
- Jeong, G.; Chung, S.; Kim, C.; Lee, S. Applications of micromixing technology. Analyst 2010, 135, 460–473. [Google Scholar] [CrossRef]
- Gaozhe, C.; Xue, L.; Zhang, H.; Lin, J. A Review on Micromixers. Micromachines 2017, 8, 274. [Google Scholar]
- Kwang-Yong, K.; Mubashshir, A.A.; Arshad, A. Passive Micromixers; MDPI: Basel, Switzerland, 2018; p. 166. [Google Scholar]
- Stroock, A.D.; Dertinger, S.K.; Whitesides, G.M.; Ajdari, A. Patterning flows using grooved surfaces. Anal. Chem. 2002, 74, 5306–5312. [Google Scholar] [CrossRef] [PubMed]
- Bökenkamp, D.; Desai, A.; Yang, X.; Tai, Y.C.; Marzluff, E.M.; Mayo, S.L. Microfabricated Silicon Mixers for Submillisecond Quench-Flow Analysis. Anal. Chem. 1998, 70, 232–236. [Google Scholar] [CrossRef]
- Gobby, D.P.; Angeli, A. Mixing characteristics of T-type microfluidic mixers. Micromech. Microeng. 2001, 11, 126–132. [Google Scholar] [CrossRef]
- Engler, M.; Kockmann, N.; Kiefer, T.; Woias, P. Numerical and experimental investigations on liquid mixing in static micromixers. Chem. Eng. J. 2004, 101, 315–322. [Google Scholar] [CrossRef]
- Telib, H.; Manhart, M.; Iollo, A. Analysis and Low-Order Modeling of the Inhomogeneous Transitional Flow inside a TMixer. Phys. Fluids 2004, 16, 2717–2731. [Google Scholar] [CrossRef]
- Bothe, D.; Stemich, C.; Warnecke, H.J. Fluid mixing in a T-shaped micromixer. Chem. Eng. Sci. 2006, 61, 2950–2958. [Google Scholar] [CrossRef]
- Dreher, S.; Kockmann, N.; Woias, P. Characterization of laminar transient flow regimes and mixing in T-shaped micromixers. Heat Transf. Eng. 2009, 30, 91–100. [Google Scholar] [CrossRef]
- Galletti, C.; Roudgar, M.; Brunazzi, E.; Mauri, R. Effect of inlet conditions on the engulfment pattern in a T-shaped micro-mixer. Chem. Eng. J. 2012, 185, 300–313. [Google Scholar] [CrossRef]
- Lobasov, A.S.; Minakov, A.V. Density effect on the mixing efficiency and flow modes in T-shaped micromixers. MATEC Web Conf. 2017, 115. [Google Scholar] [CrossRef] [Green Version]
- Lobasov, A.S.; Minakov, A.V. Analyzing mixing quality in a T-shaped micromixer for different fluids properties through numerical simulation. Chem. Eng. Process. 2018, 124, 11–23. [Google Scholar] [CrossRef] [Green Version]
- Lobasov, A.S.; Minakov, A.V.; Kuznetsov, V.V.; Rudyak, V.Y.; Shebeleva, A.A. Investigation of mixing efficiency and pressure drop in T-shaped micromixers. Chem. Eng. Process. 2018, 134, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.S.; Lee, S.H.; Kwon, T.H.; Ahn, C.H. A serpentine laminating micromixer combining splitting/recombination and advection. Lab Chip 2005, 5, 739–747. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Long, M.; Sprague, M.; Grimes, A.; Rich, B.; Khine, M. A simple three dimensional vortex micromixer. Appl. Phys. Lett. 2009, 94. [Google Scholar] [CrossRef]
- Park, J.; Kim, D.; Kang, T.; Kwon, T. Improved serpentine laminating micromixer with enhanced local advection. Microfluid. Nanofluid. 2008, 4, 513–523. [Google Scholar] [CrossRef]
- Wang, L.; Yang, J. An overlapping crisscross micromixer using chaotic mixing principles. J. Micromech. Microeng. 2006, 16, 2684. [Google Scholar] [CrossRef]
- Hossain, S.; Husain, A.; Kim, K.-Y. Optimization of Micromixer with Staggered Herringbone Grooves on Top and Bottom Walls. Eng. Appl. Comp. Fluid Mech. 2011, 5, 506–516. [Google Scholar] [CrossRef] [Green Version]
- Hossain, S.; Ansari, M.A.; Husain, A.; Kim, K.-Y. Analysis and optimization of a micromixer with a modified Tesla structure. Chem. Eng. J. 2010, 158, 305–314. [Google Scholar] [CrossRef]
- Afzal, A.; Kim, K.-Y. Passive split and recombination micromixer with convergent–divergent walls. Chem. Eng. J. 2012, 203, 182–192. [Google Scholar] [CrossRef]
- Karvelas, E.; Liosis, C.; Benos, L.; Karakasidis, T.; Sarris, I. Micromixing Effciency of Particles in Heavy Metal Removal Processes under Various Inlet Conditions. Water 2019, 11, 1135. [Google Scholar] [CrossRef] [Green Version]
- Liosis, C.; Karvelas, E.; Karakasidis, T.; Sarris, I. Numerical study of magnetic particles mixing in waste water under an external magnetic field. J. Water Supply Res. Tech. AQUA 2020, 69, 266–275. [Google Scholar] [CrossRef]
- Karvelas, E.G.; Koubogiannis, D.G.; Hatziapostolou, A.; Sarris, I.E. The effect of anode bed geometry on the hydraulic behaviour of PEM fuel cells. Renew. Energy 2016, 93, 269–279. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Methods for Solving Problems of Heat Exchange and Fluid Dynamics; Energoatomizdat: Moscow, Russia, 1984; p. 152, [Russian translation]. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer Science + Business Media Inc.: Berlin, Germany, 2002; p. 423. [Google Scholar]
- Chen, H.; Meiners, J.C. Topologic mixing on a microfluidic chip. Appl. Phys. Lett. 2004, 84, 2193–2195. [Google Scholar] [CrossRef]
- Garstecki, P.; Fuerstman, M.J.; Fischbach, M.A.; Sia, S.K.; Whitesides, G.M. Mixing with bubbles: A practical technology for use with portable microfluidic devices. Lab Chip 2006, 6, 207–212. [Google Scholar] [CrossRef]
- Chung, Y.-C.; Hsu, Y.-L.; Jen, C.-P.; Lud, M.-C.; Lin, Y.-C. Design of passive mixers utilizing microfluidic self-circulation in the mixing chamber. Lab Chip 2004, 4, 70–77. [Google Scholar] [CrossRef]
- Hoffmann, M.; Schluter, M.; Rabiger, N. Experimental investigation of liquid-liquid mixing in T-shaped micro-mixers using μ-LIF and μ-PIV. Chem. Eng. Sci. 2006, 61, 2968–2976. [Google Scholar] [CrossRef]
- Lobasov, A.; Minakov, A.; Rudyak, V.; Yagodnitsina, A.; Bilsky, A. Micro-LIF and Numerical Investigation of Mixing in Microchannel. J. Sib. Fed. Univ. Tech. technol. 2013, 6, 15–27. [Google Scholar]





| Boundary | Mass Flow Rate (Qin) (mg/s) | Pressure (pa) | Passive Scalar (φ) |
|---|---|---|---|
| Inlets | 0.2, 2, 10, 20, 24, 28, 29, 30, 32, 36, 40, 45, 50, 60 | Zero gradient | 1 |
| Outlet | Zero gradient | 0 | 0 |
| Walls | 0 | Zero gradient | Zero gradient |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minakov, A.V.; Lobasov, A.S.; Shebeleva, A.A.; Shebelev, A.V. Analysis of Hydraulic Mixing Efficiency in Widespread Models of Micromixers. Fluids 2020, 5, 211. https://doi.org/10.3390/fluids5040211
Minakov AV, Lobasov AS, Shebeleva AA, Shebelev AV. Analysis of Hydraulic Mixing Efficiency in Widespread Models of Micromixers. Fluids. 2020; 5(4):211. https://doi.org/10.3390/fluids5040211
Chicago/Turabian StyleMinakov, Andrey V., Alexander S. Lobasov, Anna A. Shebeleva, and Alexander V. Shebelev. 2020. "Analysis of Hydraulic Mixing Efficiency in Widespread Models of Micromixers" Fluids 5, no. 4: 211. https://doi.org/10.3390/fluids5040211
APA StyleMinakov, A. V., Lobasov, A. S., Shebeleva, A. A., & Shebelev, A. V. (2020). Analysis of Hydraulic Mixing Efficiency in Widespread Models of Micromixers. Fluids, 5(4), 211. https://doi.org/10.3390/fluids5040211





