Decoding the Relationships between Body Shape, Tail Beat Frequency, and Stability for Swimming Fish
Abstract
:1. Introduction
2. Methods
2.1. Fluid–Structure Interaction
2.2. Body Construction
2.3. Material Model and Driving Torque
2.4. Body Coordinate System
2.5. Computational Implementation
3. Results
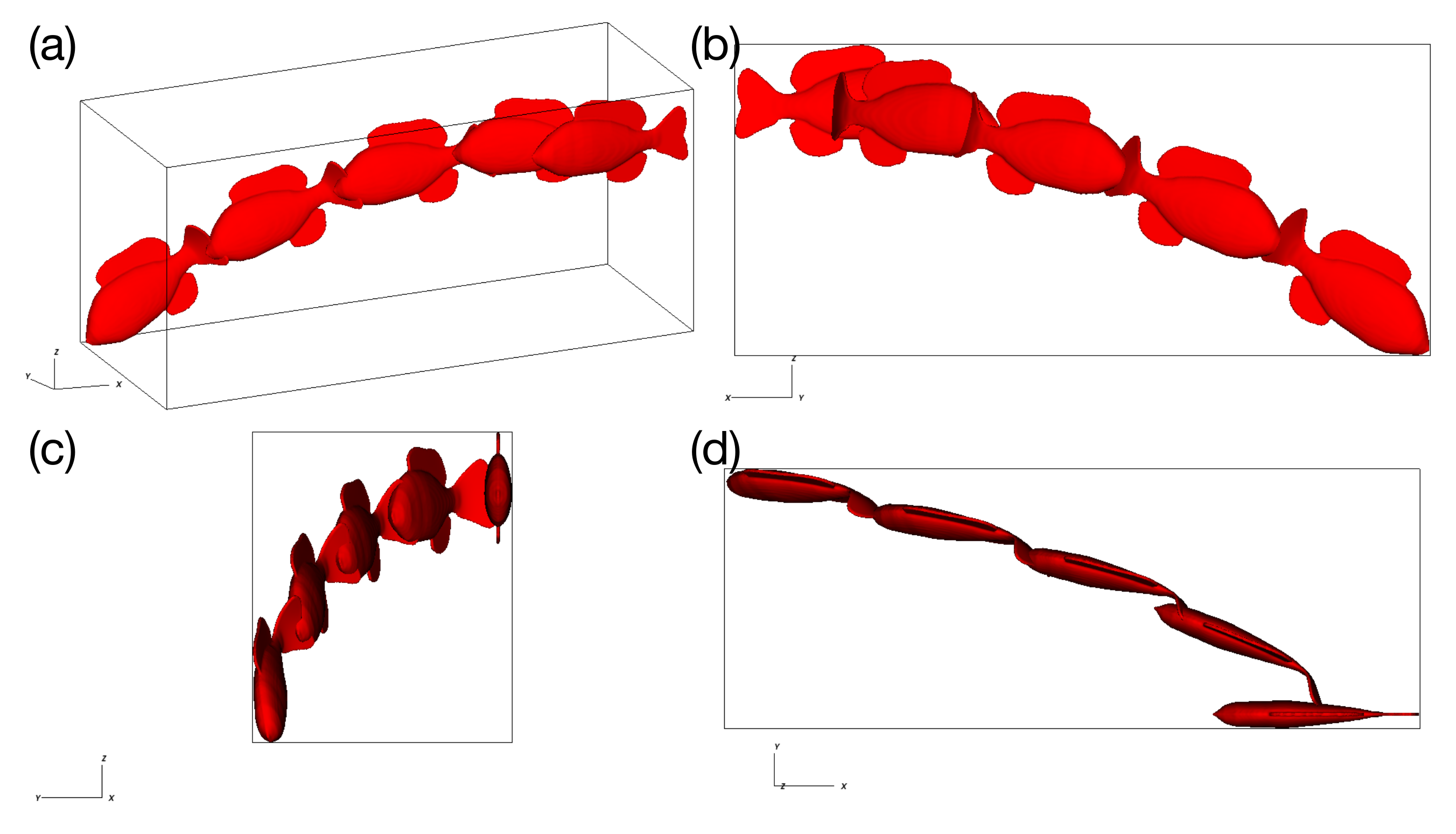
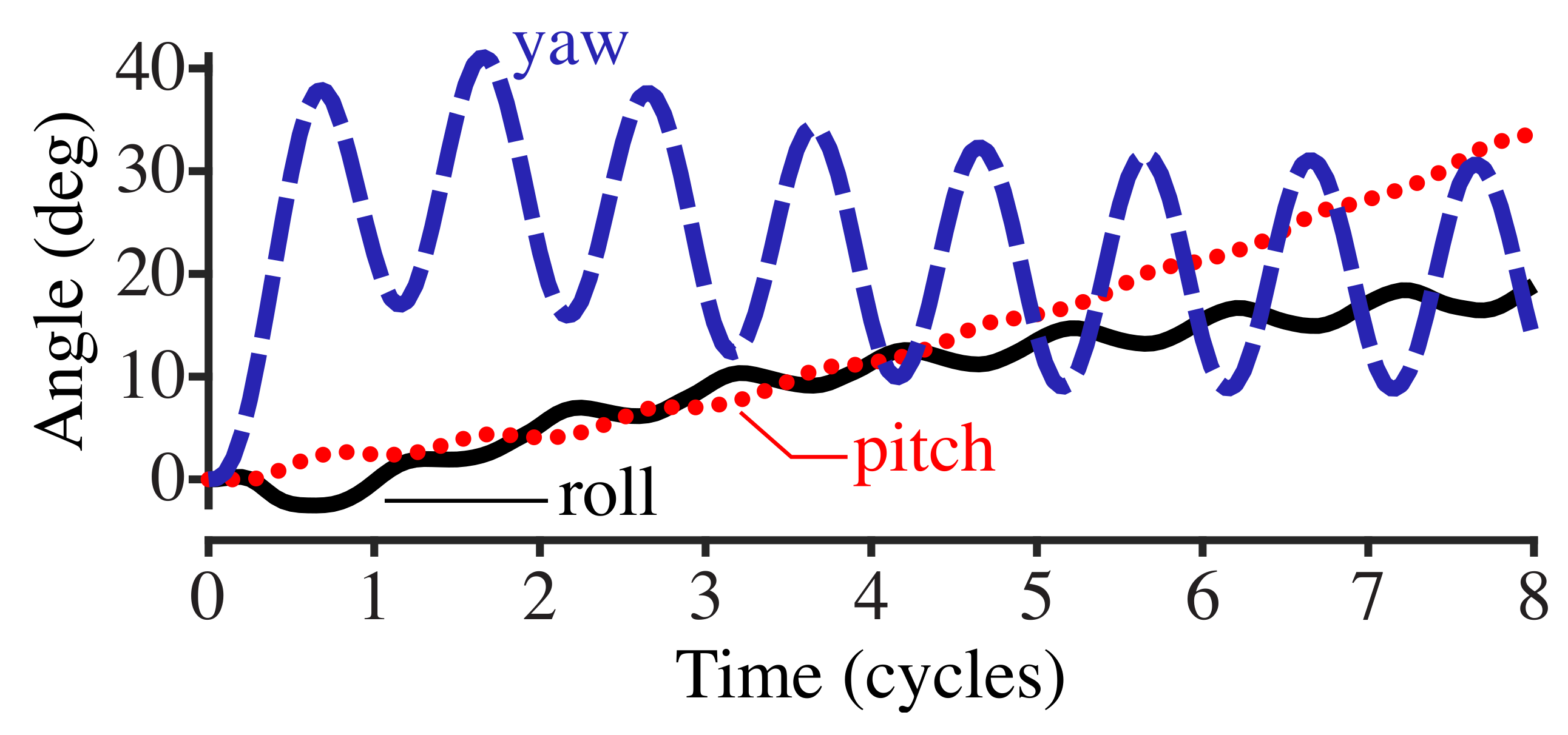
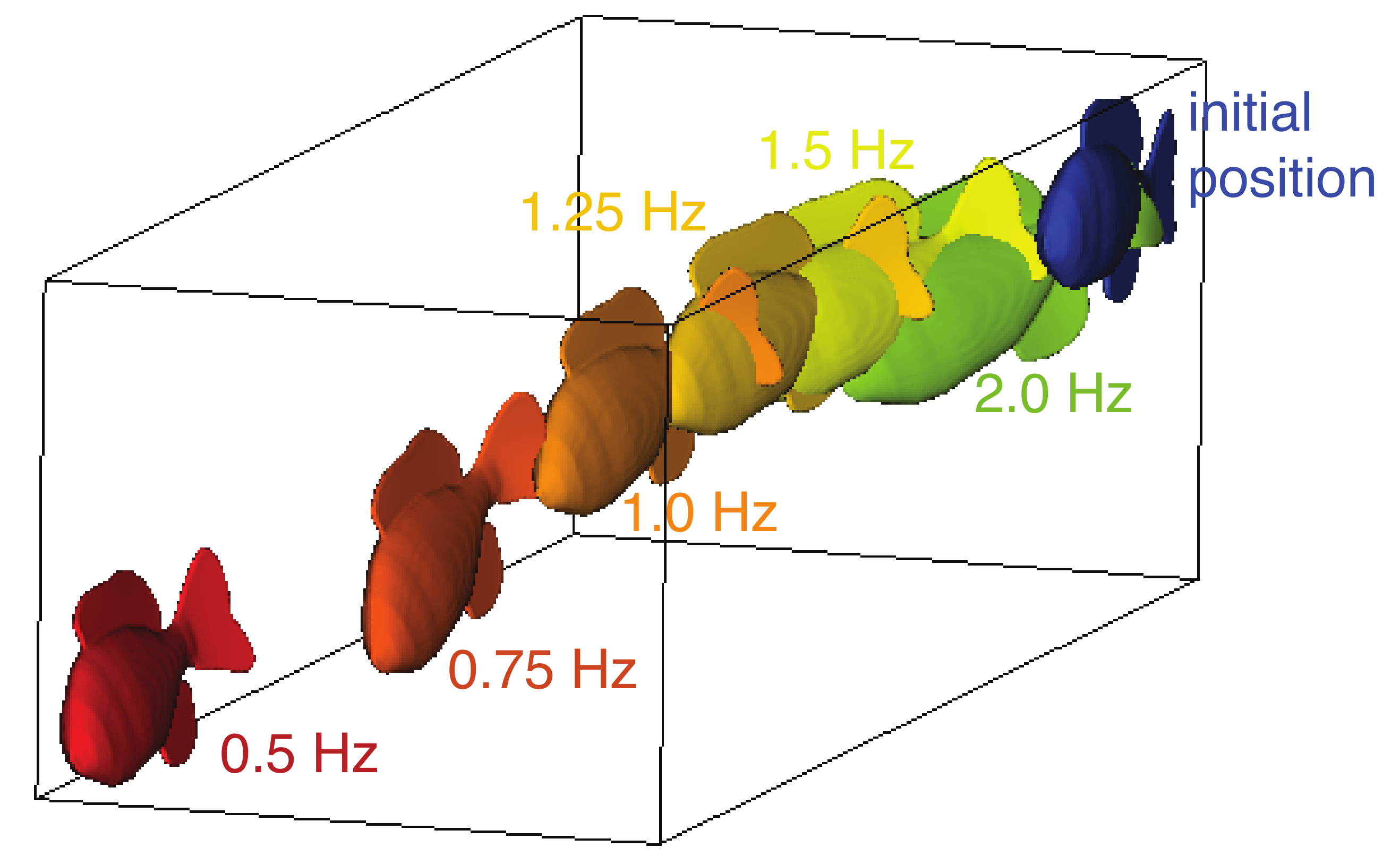
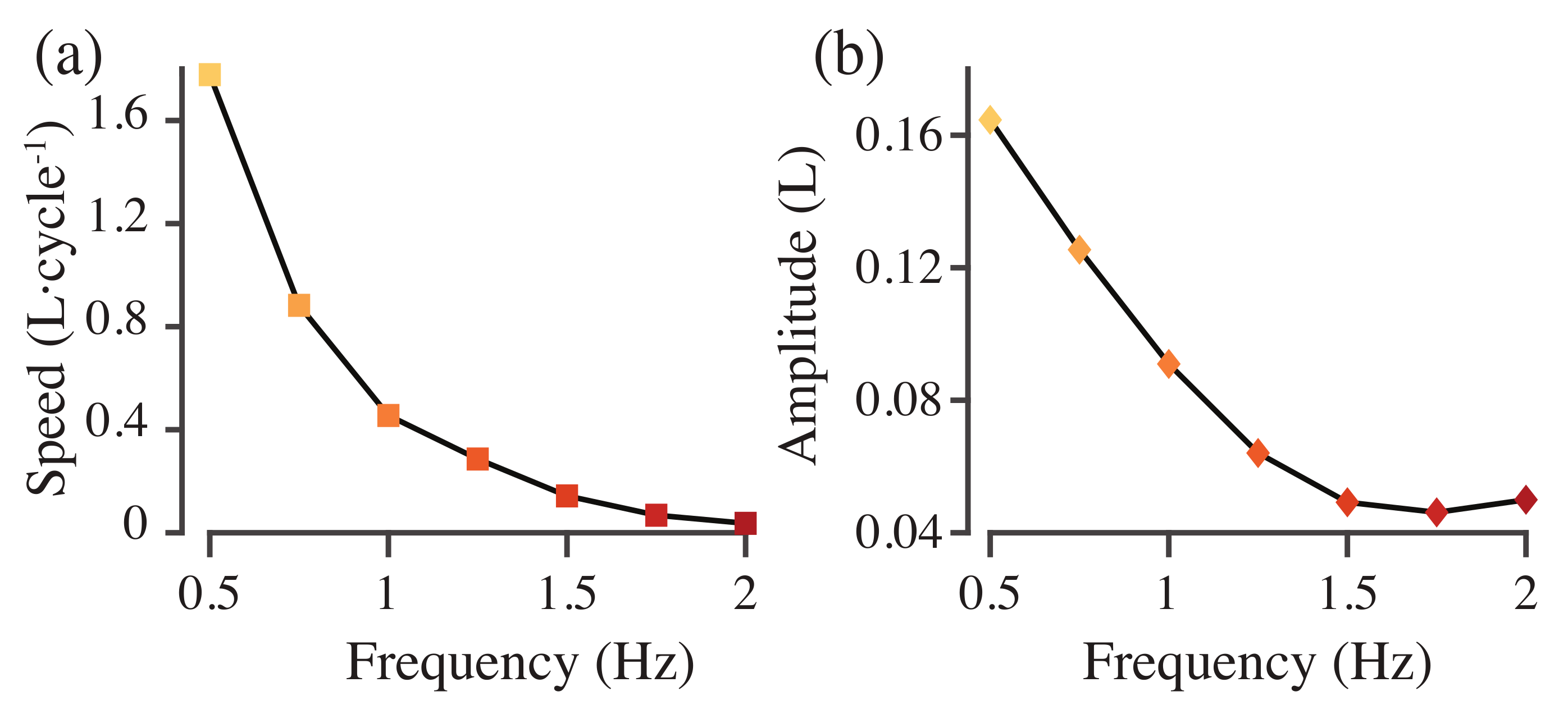
3.1. Unconstrained Swimming
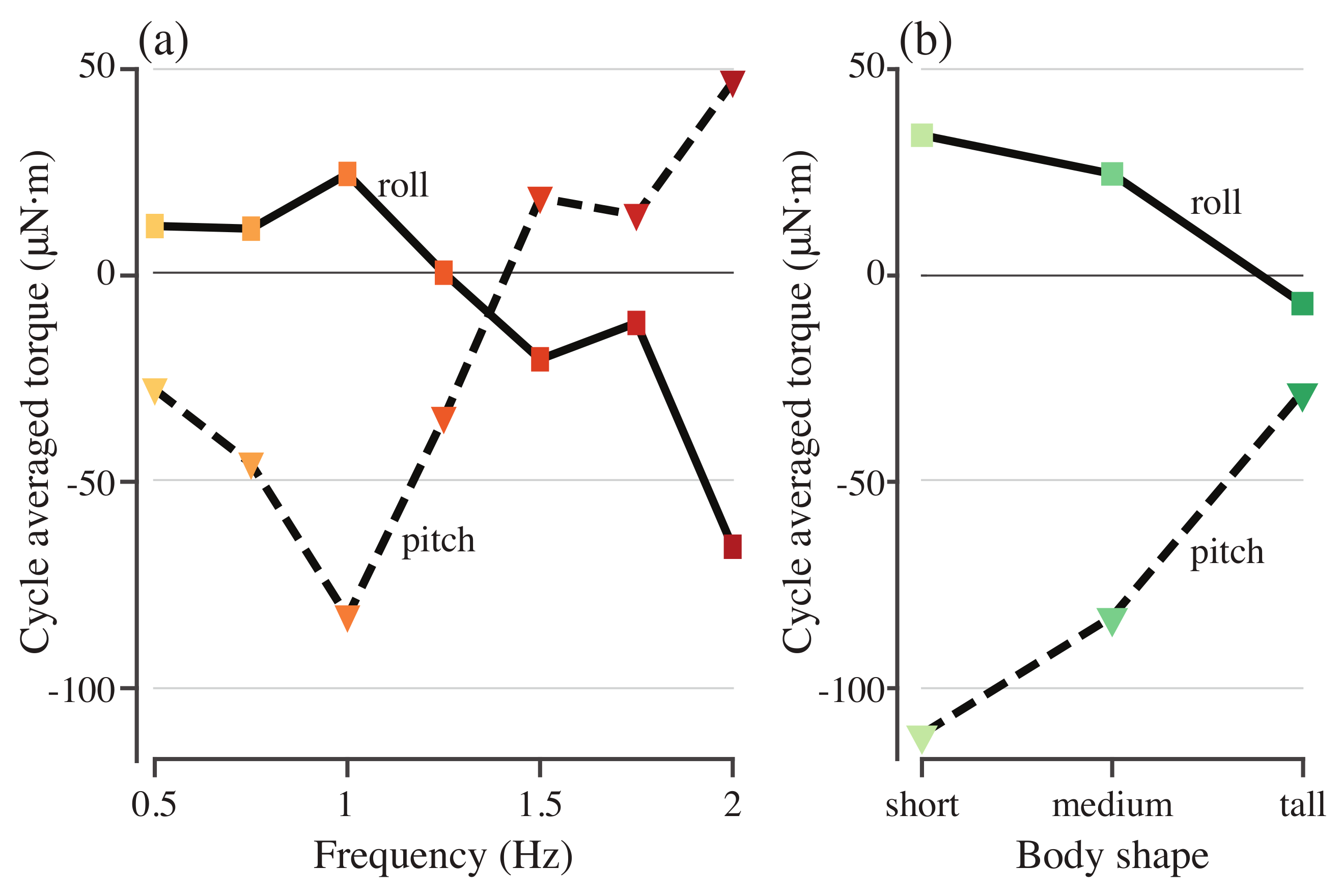
3.2. Stabilizing Torque
3.3. Varying Body Shape
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Videler, J.J. Fish Swimming; Chapman and Hall: London, UK, 1993. [Google Scholar]
- Webb, P.W. Control of Posture, Depth, and Swimming Trajectories of Fishes. Integr. Comp. Biol. 2002, 42, 94–101. [Google Scholar] [CrossRef] [PubMed]
- Standen, E.M.; Lauder, G.V. Hydrodynamic Function of Dorsal and Anal Fins in Brook Trout (Salvelinus Fontinalis). J. Exp. Biol. 2007, 210, 325–339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tytell, E.D. Median fin function in bluegill sunfish, Lepomis macrochirus: Streamwise vortex structure during steady swimming. J. Exp. Biol. 2006, 209, 1516–1534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Webb, P.W.; Weihs, D. Hydrostatic Stability of Fish with Swim Bladders: Not All Fish Are Unstable. Can. J. Zool. 1994, 72, 1149–1154. [Google Scholar] [CrossRef]
- Webb, P.W. Stability and Maneuverability. In Fish Biomechanics; Academic Press: San Diego, CA, USA, 2005; Volume 23, pp. 281–332. [Google Scholar]
- Lauder, G.V.; Madden, P.G.A.; Mittal, R.; Dong, H.; Bozkurttas, M. Locomotion with Flexible Propulsors: I. Experimental Analysis of Pectoral Fin Swimming in Sunfish. Bioinspiration Biomimetics 2006, 1, S25–S34. [Google Scholar] [CrossRef]
- Standen, E.M. Pelvic Fin Locomotor Function in Fishes: Three-Dimensional Kinematics in Rainbow Trout (Oncorhynchus Mykiss). J. Exp. Biol. 2008, 211, 2931–2942. [Google Scholar] [CrossRef] [Green Version]
- Tytell, E.D.; Standen, E.M.; Lauder, G.V. Escaping Flatland: Three-Dimensional Kinematics and Hydrodynamics of Median Fins in Fishes. J. Exp. Biol. 2008, 211, 187–195. [Google Scholar] [CrossRef] [Green Version]
- Bartol, I.K.; Gordon, M.S.; Webb, P.; Weihs, D.; Gharib, M. Evidence of Self-Correcting Spiral Flows in Swimming Boxfishes. Bioinspir. Biomim. 2008, 3, 014001. [Google Scholar] [CrossRef] [Green Version]
- Trinci, G.; Harvey, G.L.; Henshaw, A.J.; Bertoldi, W.; Hölker, F. Life in Turbulent Flows: Interactions between Hydrodynamics and Aquatic Organisms in Rivers. Wiley Interdiscip. Rev. Water 2017, 4, e1213. [Google Scholar] [CrossRef]
- Guckenheimer, J.M.; Holmes, P.J. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Stevens, L.M.; Blob, R.W.; Mayerl, C.J. Ontogeny, Morphology and Performance: Changes in Swimming Stability and Turning Performance in the Freshwater Pleurodire Turtle, Emydura Subglobosa. Biol. J. Linn. Soc. 2018, 125, 718–729. [Google Scholar] [CrossRef]
- Tytell, E.D.; Hsu, C.Y.; Williams, T.L.; Cohen, A.H.; Fauci, L.J. Interactions between Internal Forces, Body Stiffness, and Fluid Environment in a Neuromechanical Model of Lamprey Swimming. Proc. Natl. Acad. Sci. USA 2010, 107, 19832–19837. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hamlet, C.; Fauci, L.J.; Tytell, E.D. The Effect of Intrinsic Muscular Nonlinearities on the Energetics of Locomotion in a Computational Model of an Anguilliform Swimmer. J. Theor. Biol. 2015, 385, 119–129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoover, A.P.; Cortez, R.; Tytell, E.D.; Fauci, L.J. Swimming Performance, Resonance, and Shape Evolution in Heaving Flexible Panels. J. Fluid Mech. 2018, 847, 386–416. [Google Scholar] [CrossRef] [Green Version]
- Hamlet, C.; Santhanakrishnan, A.; Miller, L.A. A Numerical Study of the Effects of Bell Pulsation Dynamics and Oral Arms on the Exchange Currents Generated by the Upside-down Jellyfish Cassiopea Xamachana. J. Exp. Biol. 2011, 214, 1911–1921. [Google Scholar] [CrossRef] [Green Version]
- Hoover, A.; Miller, L. A Numerical Study of the Benefits of Driving Jellyfish Bells at Their Natural Frequency. J. Theor. Biol. 2015, 374, 13–25. [Google Scholar] [CrossRef]
- Hoover, A.P.; Griffith, B.E.; Miller, L.A. Quantifying Performance in the Medusan Mechanospace with an Actively Swimming Three-Dimensional Jellyfish Model. J. Fluid Mech. 2017, 813, 1112–1155. [Google Scholar] [CrossRef]
- Battista, N.A.; Baird, A.J.; Miller, L.A. A Mathematical Model and MATLAB Code for Muscle-Fluid-Structure Simulations. Integr. Comp. Biol. 2015, 55, 901–911. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Guy, R.D.; Mulloney, B.; Zhang, Q.; Lewis, T.J. Neural Mechanism of Optimal Limb Coordination in Crustacean Swimming. Proc. Natl. Acad. Sci. USA 2014, 111, 13840–13845. [Google Scholar] [CrossRef] [Green Version]
- Miller, L.A.; Peskin, C.S. When Vortices Stick: An Aerodynamic Transition in Tiny Insect Flight. J. Exp. Biol. 2004, 207, 3073–3088. [Google Scholar] [CrossRef] [Green Version]
- Jones, S.; Laurenza, R.; Hedrick, T.L.; Griffith, B.E.; Miller, L.A. Lift vs. Drag Based Mechanisms for Vertical Force Production in the Smallest Flying Insects. J. Theor. Biol. 2015, 384, 105–120. [Google Scholar] [CrossRef] [Green Version]
- Mittal, R.; Iaccarino, G. Immersed Boundary Methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef] [Green Version]
- Peskin, C.S. The Immersed Boundary Method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef] [Green Version]
- Griffith, B.E.; Patankar, N.A. Immersed methods for fluid–structure interaction. Annu. Rev. Fluid Mech. 2020, 52, 421–448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Griffith, B.E.; Luo, X. Hybrid Finite Difference/Finite Element Immersed Boundary Method. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2888. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McHenry, M.J.; Pell, C.A.; Long, J.H. Mechanical Control of Swimming Speed: Stiffness and Axial Wave Form in Undulating Fish Models. J. Exp. Biol. 1995, 198, 2293–2305. [Google Scholar] [PubMed]
- Diebel, J. Representing Attitude: Euler Angles, Unit Quaternions, and Rotation Vectors. Matrix 2006, 58, 1–35. [Google Scholar]
- IBAMR. IBAMR: An Adaptive and Distributed-Memory Parallel Implementation of the Immersed Boundary Method. 2014. Available online: https://github.com/IBAMR/IBAMR (accessed on 21 September 2020).
- Griffith, B.E.; Hornung, R.D.; McQueen, D.M.; Peskin, C.S. An Adaptive, Formally Second Order Accurate Version of the Immersed Boundary Method. J. Comput. Phys. 2007, 223, 10–49. [Google Scholar] [CrossRef]
- Lighthill, M.J. Aquatic Animal Propulsion of High Hydromechanical Efficiency. J. Fluid Mech. 1970, 44, 265–301. [Google Scholar] [CrossRef]
- Lucas, K.N.; Lauder, G.V.; Tytell, E.D. Airfoil-like Mechanics Generate Thrust on the Anterior Body of Swimming Fishes. Proc. Natl. Acad. Sci. USA 2020. [Google Scholar] [CrossRef]
- Lauder, G.V.; Tytell, E.D. Hydrodynamics of Undulatory Propulsion. Fish Physiol. 2005, 23, 425–468. [Google Scholar]
- Zelenin, P.V.; Grillner, S.; Orlovsky, G.N.; Deliagina, T.G. The Pattern of Motor Coordination Underlying the Roll in the Lamprey. J. Exp. Biol. 2003, 206, 2557–2566. [Google Scholar] [CrossRef] [Green Version]
- Ullén, F.; Deliagina, T.G.; Orlovsky, G.N.; Grillner, S. Spatial Orientation in the Lamprey. 1. Control of Pitch and Roll. J. Exp. Biol. 1995, 198, 665–673. [Google Scholar]
- Summers, A.P.; Long, J.H. Skin and Bones, Sinew and Gristle: The Mechanical Behavior of Fish Skeletal Tissues. In Fish Physiology; Shadwick, R.E., Lauder, G.V., Eds.; Elsevier: Amsterdam, The Netherland, 2005; Volume 23, pp. 141–177. [Google Scholar]
- Tytell, E.D.; Carr, J.A.; Danos, N.; Wagenbach, C.; Sullivan, C.M.; Kiemel, T.; Cowan, N.J.; Ankarali, M.M. Body Stiffness and Damping Depend Sensitively on the Timing of Muscle Activation in Lampreys. Integr. Comp. Biol. 2018, 58, 860–873. [Google Scholar] [CrossRef] [PubMed]
- Long, J.H.; Adcock, B.; Root, R.G. Force Transmission via Axial Tendons in Undulating Fish: A Dynamic Analysis. Comp. Biochem. Physiol. A 2002, 133, 911–929. [Google Scholar] [CrossRef]
- Coughlin, D.J.; Valdes, L.; Rome, L.C. Muscle Length Changes during Swimming in Scup: Sonomicrometry Verifies the Anatomical High-Speed Cine Technique. J. Exp. Biol. 1996, 199, 459–463. [Google Scholar]
- Shadwick, R.E.; Gemballa, S. Structure, Kinematics, And Muscle Dynamics In Undulatory Swimming. In Fish Biomechanics; Shadwick, R.E., Lauder, G.V., Eds.; Elsevier Academic Press: San Diego, CA, USA, 2006; Volume 23, pp. 241–280. [Google Scholar]
- Gemballa, S.; Vogel, F. The Spatial Arrangement of White Muscle Fibers and Myoseptal Tendons in Fishes. Comp. Biochem. Physiol. A 2002, 133, 1013–1037. [Google Scholar] [CrossRef]
- Root, R.G.; Courtland, H.W. Swimming Fish and Fish-like Models: The Harmonic Structure of Undulatory Waves Suggests That Fish Actively Tune Their Bodies. In International Symposium on Unmanned Untethered Submersible Technology; University of New Hampshire-Marine Systems Engineering Laboratory: Durham, NH, USA, 1999; pp. 378–388. [Google Scholar]
- Flammang, B.E.; Alben, S.; Madden, P.G.A.; Lauder, G.V. Functional Morphology of the Fin Rays of Teleost Fishes. J. Morphol. 2013, 274, 1044–1059. [Google Scholar] [CrossRef] [Green Version]
- Flammang, B.E.; Lauder, G.V. Caudal Fin Shape Modulation and Control during Acceleration, Braking and Backing Maneuvers in Bluegill Sunfish, Lepomis Macrochirus. J. Exp. Biol. 2009, 212, 277–286. [Google Scholar] [CrossRef] [Green Version]
- Alben, S.; Witt, C.; Baker, T.V.; Anderson, E.; Lauder, G.V. Dynamics of Freely Swimming Flexible Foils. Phys. Fluids 2012, 24, 051901. [Google Scholar] [CrossRef] [Green Version]



| Quantity | Symbol | Reference Value |
|---|---|---|
| Fish length | L | 10 cm |
| Fish height | h | 5.5 cm |
| Elastic Modulus | E | Pa |
| Poisson ratio | ||
| Spring constant | Pa | |
| Max force magnitude | N | |
| Numerical timestep | s | |
| Domain width | W | 0.6 m |
| Grid stepsize | h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoover, A.P.; Tytell, E. Decoding the Relationships between Body Shape, Tail Beat Frequency, and Stability for Swimming Fish. Fluids 2020, 5, 215. https://doi.org/10.3390/fluids5040215
Hoover AP, Tytell E. Decoding the Relationships between Body Shape, Tail Beat Frequency, and Stability for Swimming Fish. Fluids. 2020; 5(4):215. https://doi.org/10.3390/fluids5040215
Chicago/Turabian StyleHoover, Alexander P., and Eric Tytell. 2020. "Decoding the Relationships between Body Shape, Tail Beat Frequency, and Stability for Swimming Fish" Fluids 5, no. 4: 215. https://doi.org/10.3390/fluids5040215
APA StyleHoover, A. P., & Tytell, E. (2020). Decoding the Relationships between Body Shape, Tail Beat Frequency, and Stability for Swimming Fish. Fluids, 5(4), 215. https://doi.org/10.3390/fluids5040215





