1. Introduction
The problem of wavefield behind a moving source is well-known in various domains of modern physics and, in particular, in the dynamics of the atmosphere and ocean [
1]. The brightest and deepest for understanding rich physics is the example of ship waves, first considered in the works of Lord Kelvin [
2,
3,
4,
5]. At the turn of the 20th century, Kelvin and his followers created the basis for many works developing the classical results (e.g., [
6,
7]).
Patterns of phases of linear waves can be constructed in a relatively simple and general way [
8]. In what follows, we assume a motionless source and the flow velocity
directed along the
axis in the positive direction. We restrict ourselves to the case of two-dimensional waves, which include surface water waves, Rossby waves, and internal gravity waves in a depth-limited ocean (atmosphere). Stationarity condition in the reference frame associated with the source
allows one to determine the transverse component of the wave vector
by specifying the longitudinal component
k, which is usually associated with the size of the source. The phase
at an arbitrary point
is determined from the condition of stationarity (
1), i.e., for the conditional extremum of the function
The Lagrange multiplier
t in (
2) can be interpreted as the propagation time of a wave packet with a constant group velocity [
9], since the conditional extremum of the phase
is realized at
The isophases provide a visual picture of the distribution of the wave troughs and crests in a stationary wake created by the source. Note that the straightforward implementation of this approach can lead to non-physical results when the wave pattern appears where it should not be. The reason for this may be the arbitrariness of the choice of the sign of the phase . Formally, and are equal in rights. Usually, they refer to the principle of causality for choosing the sign of the phase and linking it with the positiveness of the time t.
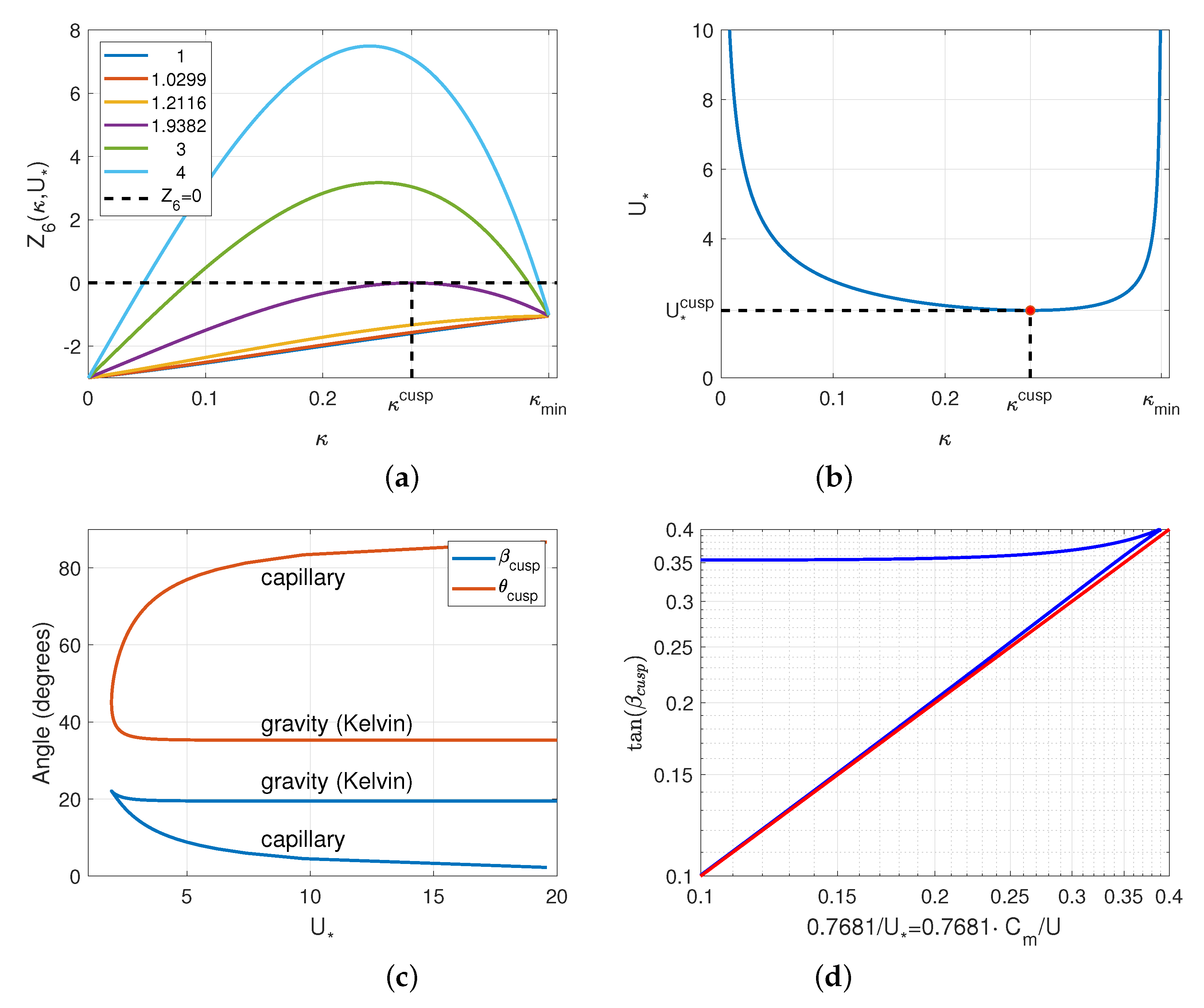
The situation becomes somewhat more complicated when the stationarity condition (
1) has two (or more) solutions. Lord Rayleigh [
10] considered one of such cases for standing gravity–capillary waves on the surface of running water. For the flow speed higher than the minimum wave velocity
(phase and group speeds are the same) the Equation (
1) has two roots corresponding to “slow” gravitational and “fast” capillary waves. The group velocities of these waves relative to a stationary source have opposite signatures: the energy of capillary waves runs upstream, while the energy of the gravitational waves lags behind. Rayleigh [
10] accounted for this feature in the one-dimensional problem while discussed the solution for the two-dimensional case “by analogy”.
The group velocity of waves is considered as an essential quantity of energy transfer since works of Hamilton [
11]. It does not enter explicitly into the well-known expressions for the classic Kelvin’s solution of pure gravity ship waves [
3,
4]. The Lighthill [
8] interpretation of the Kelvin angle operates with a fixed ratio of
, thus emphasizing the physical difference of the phase and group propagation. This fact alone results in the occurrence of the universal stationary wake patterns in the form of arcs of chevron.
The dispersion of pure capillary waves (
) is positive, i.e., group velocity is larger than the phase one, and the corresponding wave patterns are not so peculiar as the Kelvin wake ones with their two systems of transverse and divergent waves. In a sense, the wave patterns look trivial. This visual simplicity disappears when passing to gravity–capillary waves where the above wave patterns represent asymptotics at very short and very long waves. The “intermediate” (in words of [
12]) range of gravity–capillary waves turns out to be rich in non-trivial kinematic and dynamical effects. Two characteristic scales, minima of phase and group velocities, provide the dimensionless quantities of the Mach numbers. The “phase Mach number”
demarcates gravity and capillary branches of the ship wake. At relatively high
singularities of the phase patterns of the ship wake arise as cusps resembling the well-known gussets of Kelvin. A new family of cusps emerges as a feedback of the wave speed minimum, that is, as a result of the coupling of gravity and capillarity effects. The “group Mach number”
(
is minimal group velocity of gravity–capillary waves) forms a cone where diverging capillary and gravity waves cannot enter. This Mach cone is observed in laboratory and field experiments, e.g., ([
13]).
The reference solution approach [
9,
14] resolves the problem of assessment of wake amplitudes under quite mild physical assumptions including wave caustics. At loci of the group velocity minima this method predicts the effect of quasi-dispersion [
14], i.e., slow decay of wave amplitude with distance from the source. The observability of this effect is questionable under typical scales of wake but still worth to be mentioned in the context of the previously used asymptotic approaches (e.g., [
13,
15]) and the effect of the “group Mach” [
13].
In contrast to the “point-wise” estimates of wave amplitudes with conventional asymptotic approaches (e.g., the stationary phase method), the reference solution method describes an evolution of a finite perturbation of elliptic shape. Thus, the effect of the shape on the wake patterns can be discussed with explicit formulas in hand.
In
Section 2 the mathematical and physical background for the problem of gravity–capillary waves on running water is presented. The corresponding solutions will be formulated in
Section 3 for phase patterns and asymptotic dependencies of wave amplitudes. Discussion of
Section 4 is devoted to general aspects of the problem of linear wave propagation and their implications in geophysical hydrodynamics.
3. Results
In this section, we present illustrations of the above theoretical analysis for different parameters. The dimensionless speed , the Mach number related to the minimum of phase speed, determines characteristic wave patterns. Dimensionless coordinates make distributions of wave phases and amplitudes universal, i.e., independent of the nature of fluids. The dimensionless variable wavenumber can be treated as the inverse Bond number with wavelength as a characteristic scale. In our discussion of results, we mostly focus on an intermediate range of waves where both gravity and capillarity effects are equally important. For illustrations of wave phase patterns, we choose characteristic values of the current speed:
- 1
The phase speed of the first Wilton resonance [
20];
- 2
The phase speed of the minimum group velocity;
- 3
The threshold value of the isophase cusps;
- 4
as a case when families of gravity and capillary branches essentially overlap.
When discussing wave amplitude distributions, we consider just three cases of the above list, avoiding a special case of wave caustics and superposition of different wave systems (gravity and capillary).
3.1. Phase Patterns at Different Speeds of Current
3.1.1. The First Wilton Resonance
A stationary wave pattern appears when the current speed exceeds the minimal phase speed of waves, i.e., for
. One can start illustrations with the case of the first Wilton resonance [
20]. Wavelengths of the Wilton harmonics for water waves
cm and
cm correspond to rather small excess of the current speed over the minimal speed
, i.e.,
.
Figure 3a shows two systems of waves. Below, we refer to waves running upstream and shown by red isolines as a capillary family. Their downstream counterparts of gravity family are given in blue. The two families are independent at this current speed, that is, their domains are not overlapping. The demarcation line of the families, the asymptote (
17), is shown in magenta. The classic Kelvin cone is given by a black solid line for reference.
The cone of “group Mach” is shown in cyan. It is wider than the Kelvin cone (black lines).
3.1.2. The Minimum of the Group Velocity
The case of minimal group velocity shows nothing new in the phase distributions. This is the threshold value of
when the inner Mach cone emerges and the condition of anomalous wave dispersion (
52) starts to be satisfied. The “group Mach” cone is still essentially larger than the Kelvin one.
3.1.3. Cusps of Isophases at
As mentioned above, the case of the appearance of singularities of isophases is of special interest. All the characteristic cones (demarcation—magenta, “group Mach” and Kelvin’s one are well separated.
3.1.4. Merging Wave Systems. Inner Mach’s cone
The domains of gravity and capillary families continue to be separated by the demarcation lines up to
when the fan waves match the classic Kelvin cone. At slightly lower
, the domains of capillary and gravity families start to overlap. While the capillary family isophases remain smooth, the gravity family curves form two types of cusps that correspond to two roots of (
20) and (
21). The longer wave cusp can be naturally related to the well-known caustics of the Kelvin wake of pure gravity waves. The shorter wave cusps (fan waves in words of [
15]) are genetically related to the capillarity effect as it has been noted by Moissy and Rabaud [
13]. Asymptotically, when
this Mach cone is shrinking as (
24). The dimensionless wavenumbers at the cone are limited by maximal value
when the denominator of (
21) vanishes. This wavenumber corresponds to the minimum of the group velocity of gravity–capillary waves as noted above. Thus, the inner cone of the anomalous dispersion (
25) and (
52) always remains inside the cone of capillary cusps.
3.2. Wake Amplitudes
The reference solution method provides analytical solutions (
40)–(42) that can be easily converted to graphics. Presenting these figures, the authors are trying to accompany them by comments on possible physical effects governing the amplitude distributions.
The key amplitude factor
D depends on two variables: the wavenumber
that is determined by wave direction
at a given speed
(
16) and the distance along the ray expressed by time
or phase
. The first remark to be made is the presence of two terms
A and
B in the expression of
D (
40): the first term on the right-hand side is proportional to phase
in power 4 while the second one is just squared phase. Thus, vanishing of
A qualitatively changes asymptotical behavior along wave rays (with distance from the source), while vanishing the term
can lead to an extremum of amplitudes both as functions of distance and angle, and rather peculiar distributions of amplitudes in the ship wake.
The second remark concerns the demarcation line
where amplitudes of wake vanish as it is seen from (
40)–(42):
are singular in this case. The observability of this effect is an interesting point for experimentalists.
In this paper, we present distributions of wave amplitudes for relatively low speeds when these amplitudes are governed by the only wave system at a given coordinate point that is for
. At higher speeds after singularity occurrence, two (or even three) wave systems can be easily superimposed as it has been done for pure gravity waves in [
9]. Here, we restrict ourselves by the simplest case. Note that in this case there is no similarity with the case of pure gravity waves where two different overlapping wave systems (divergent and transversal) always co-exist irrespectively to the current speed value.
3.2.1. Wakes of Circular Sources
For the circular shape of the source when , wave amplitudes (terms ) do not depend on angle explicitly. While wavenumber depends on monotonically basic features of distributions can be investigated qualitatively.
Figure 4 shows the amplitude factor
in (
35) as function of dimensionless coordinates
, that is, a relative decrease of particular wave harmonics with the distance along a ray. Wave patterns are shown in two columns: the left panels are zoomed images of the right ones. Colorbars are scaled by the exponent
n of
.
At the low speed of the first Wilton resonance
(
Figure 4a,b), the isolines of amplitudes in the wake resemble slightly distorted circles. The amplitude vanishes at the demarcation line
. It decays approximately 15 times on the scale of the right panel of
Figure 4 about 5 m.
Figure 4c,d likely reflects an effect of the group velocity minimum. The source produces a sort of bulldozing pattern with a mushroom-shaped front and a track along the axis behind. The amplitude decay is minimal near the current axis: only 6 times at a distance of about 30 m (
) along the axis versus 30 times at oblique directions.
At higher threshold speed
(
Figure 4e,f), the capillary waves propagating upstream show slower decay than their gravity counterparts. The high amplitudes are concentrated near the “group Mach” cone (cyan lines). Amplitudes of the gravity waves inside this cone appear almost one order lower than in the previous case at the same distances.
3.2.2. Wakes of Elliptic Sources
The reference solution method, in contrast to its asymptotic counterparts, accounts for the shape of the initial perturbation. These are bandwidth parameters
in formulas for wave amplitudes defined by (
39) and their reciprocal values
that characterize the initial perturbation dimension in the coordinate space. For correct comparison, two pairs of the bandwidth parameters that satisfy an evident condition
have been chosen, i.e., two elliptic distributions of equal square areas in the coordinate and wavenumber spaces.
Figure 5 shows wave patterns for two sets of the shape parameters for two values of dimensionless speed
.
Case
(
Figure 5a,b,e,f) presents a source for which its along-current size is 4 times shorter than its front size. This source demonstrates a pronounced bulldozing effect. For
(minimum of group velocity), the mushroom pattern is larger than for the circular source (cf.
Figure 4c,d) and the track is essentially narrower. For higher speed
, a similar mushroom-shaped pattern is seen near the Mach cone (cyan lines).
Narrow source with high length-beam ratio
shows peculiar features in
Figure 5c,d,g,h. For
(minimum of group velocity), the wake appears larger than in other cases (circle and wide sources). For
, the wake perturbations are concentrating near the Mach angle and strongly decaying both to the short capillary waves and to the interior of the Kelvin angle of gravity waves.
It would be interesting to verify the above estimates of the wave amplitude patterns experimentally.
4. Discussion and Conclusions
The gravity–capillary waves play a special role in ocean studies. One of the issues is the remote sensing applications. Satellite altimeters (Ka- and Ku-band) and other space- and airborne systems operate in the intermediate range of wavelength where the effects of gravity and capillarity compete on equal terms. This is a reason for focusing on the specific range of scales and/or relatively low dimensionless speed of . In this case, wave patterns differ dramatically from the well-known pictures of pure gravity waves with the classic Kelvin cone.
We started with the analysis of the gravity–capillary wave kinematics following the conventional approach developed in previous works (e.g., [
1,
21,
22,
23]). The feature of our approach is in the scale choice. The wave Bond number
provides a useful reference
for capillary (
) and gravity (
) families of the ship wake in wavenumber and coordinate spaces. The counterpart of the Froude number, dimensionless speed of current
, is exploited for specifying a variety of patterns of gravity–capillary waves.
Parameters of wave patterns are specified analytically, thus extending the results of recent works (e.g., [
13,
24]). In particular, analytical expressions for parameters of cusps of isophases are presented (e.g., (
22)–(
24)) and related to phase and group velocity extremes, and characteristic angles (see
Figure 1).
The analytical expressions for the wake amplitudes are derived with the reference solutions approach for the first time. The “phase Mach” cone is shown to be invisible because of vanishing amplitudes along the demarcation line of gravity and capillary families. On the contrary, the “group Mach” cone is emphasized by the effect of quasi-dispersion of two-dimensional waves when the corresponding dispersion factor (
51) vanishes. This is in line with the analytical and experimental results of Moissy and Rabaud [
13]. The amplitude effect of the “group Mach” cone is demonstrated for a limited range of dimensionless speed
when cusps are absent. It is natural to assume that the presence of the merging waves at the cusps enhances this effect and emphasizes the “group Mach” effect at higher speeds.
The reference solution approach goes beyond the point-wise paradigm of its asymptotic counterparts (e.g., stationary phase approach), thus accounting for the effect of the source shape. The corresponding estimates have been carried out for elliptic sources of different orientation. The bulldozing effect of the shapes on the wake has been demonstrated in
Figure 5 fairly well.