Effects of Inflow Condition on RANS and LES Predictions of the Flow around a High-Rise Building
Abstract
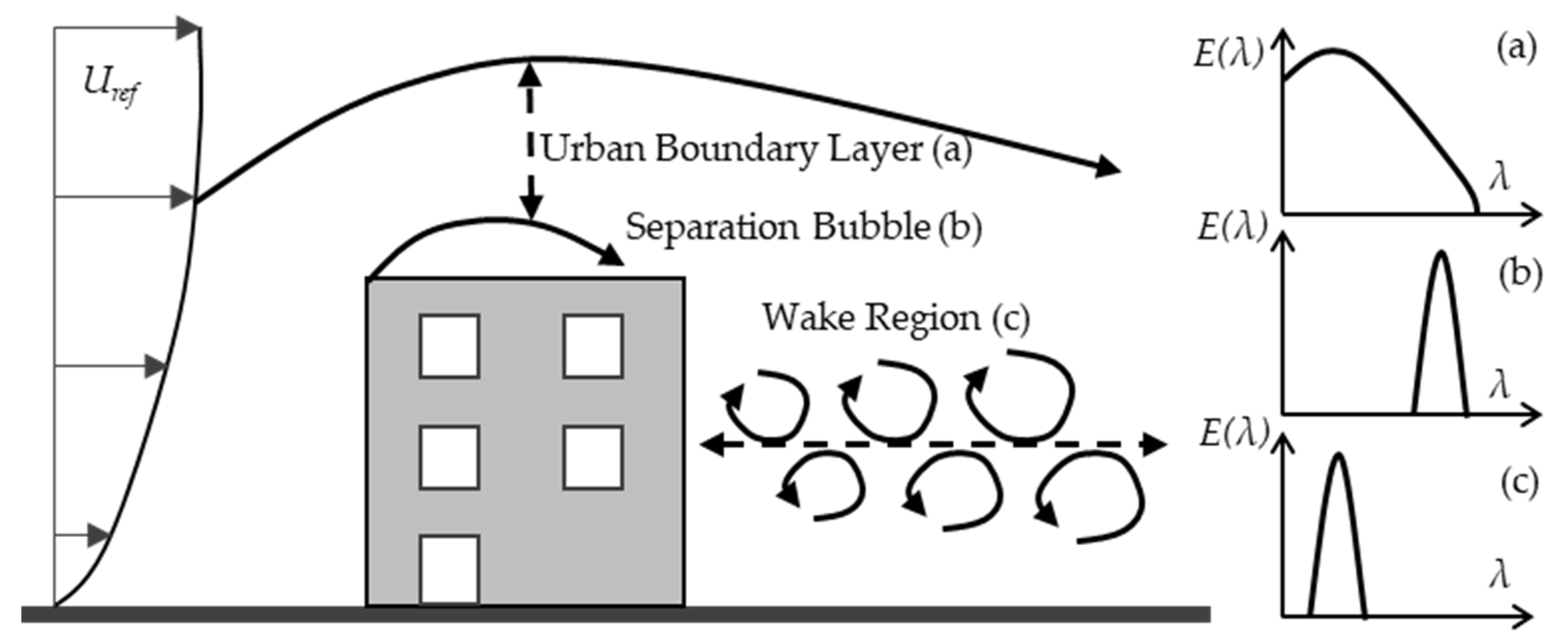
1. Introduction
- To assess the mean wind velocity and turbulence intensity in the roof region, at the pedestrian level, and in the wake region of a high-rise building.
- To evaluate the adequacy of steady-state RANS simulations for predicting the flow features.
- To evaluate the advantages of LES data for predicting more advanced flow statistics.
- To assess the role of the turbulent inflow in the flow field for RANS and LES.
2. Methodology
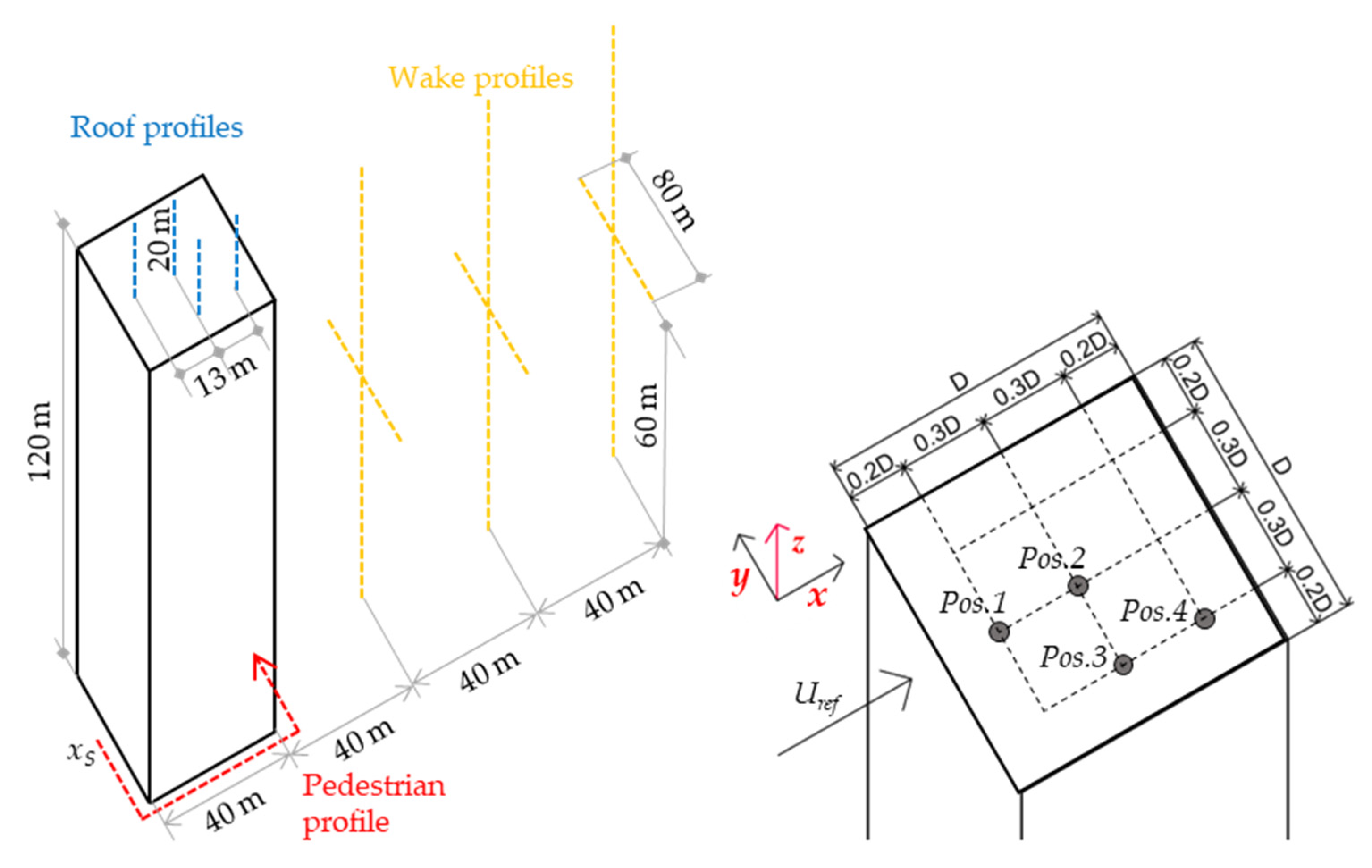
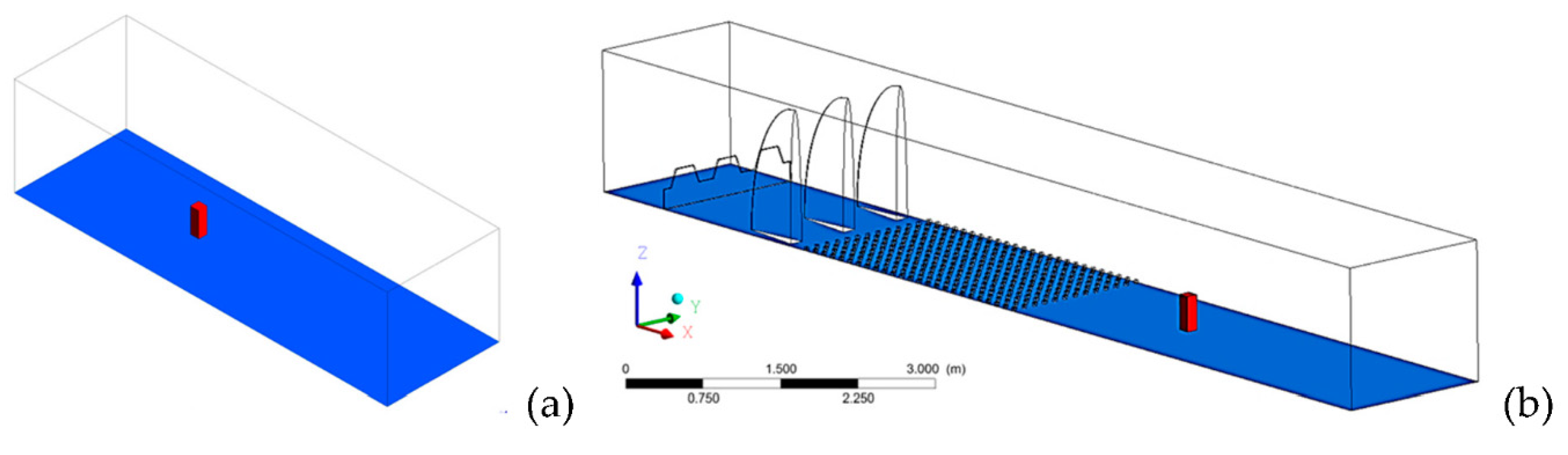
2.1. High-Rise Building Model and Computational Domains
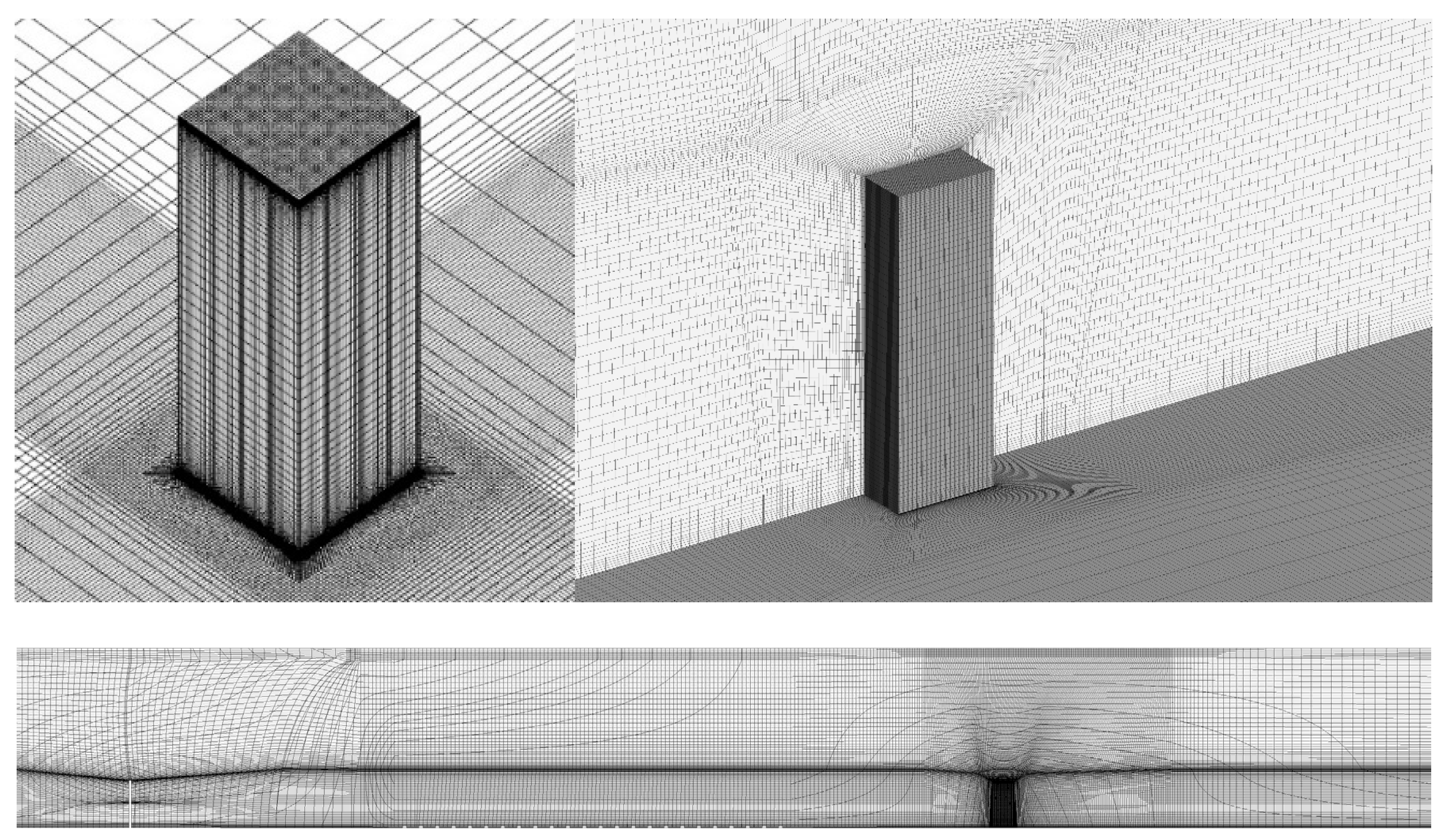
2.2. Numerical Setup
3. Results
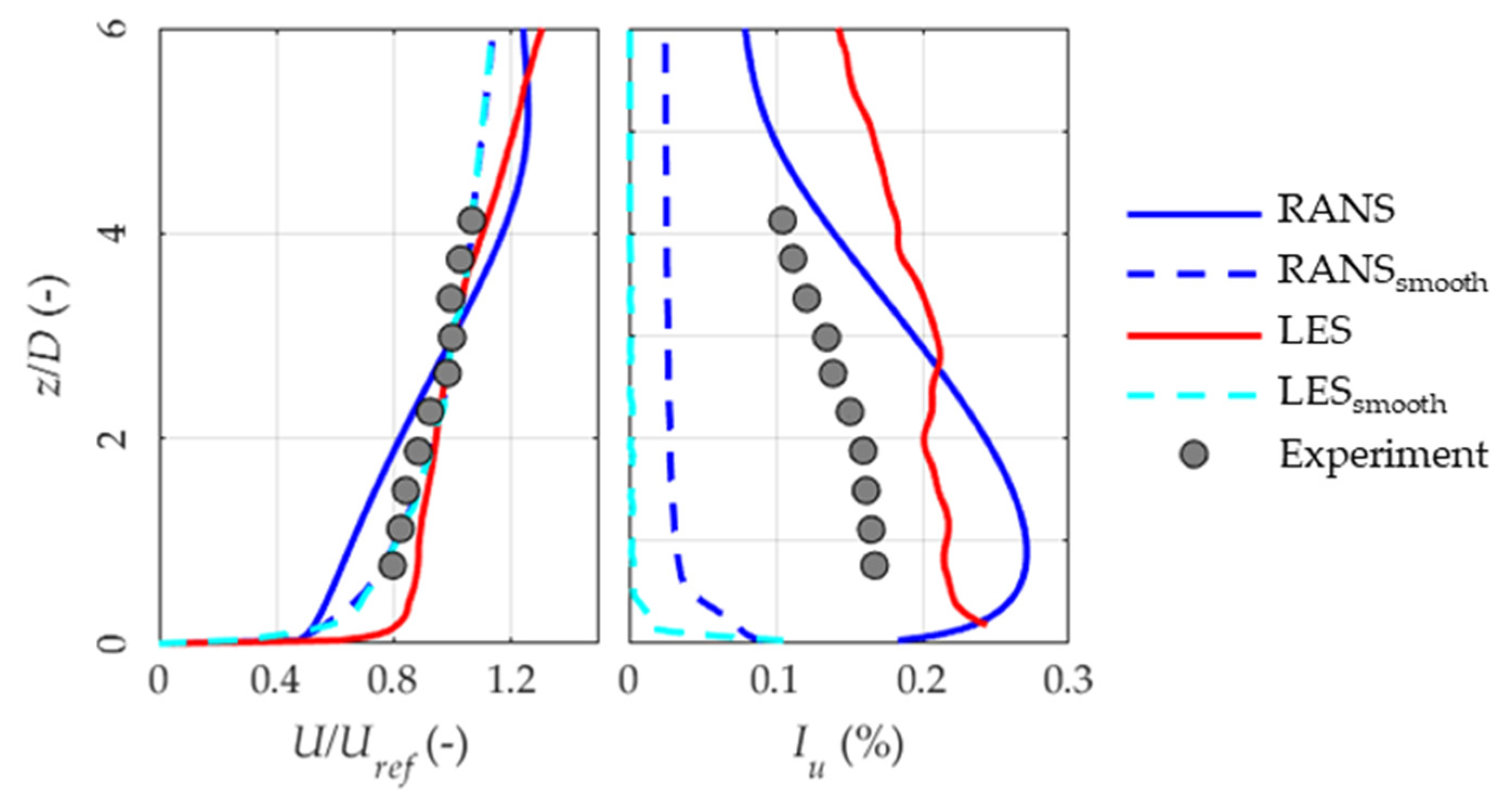
3.1. Inflow Profile as Modeled
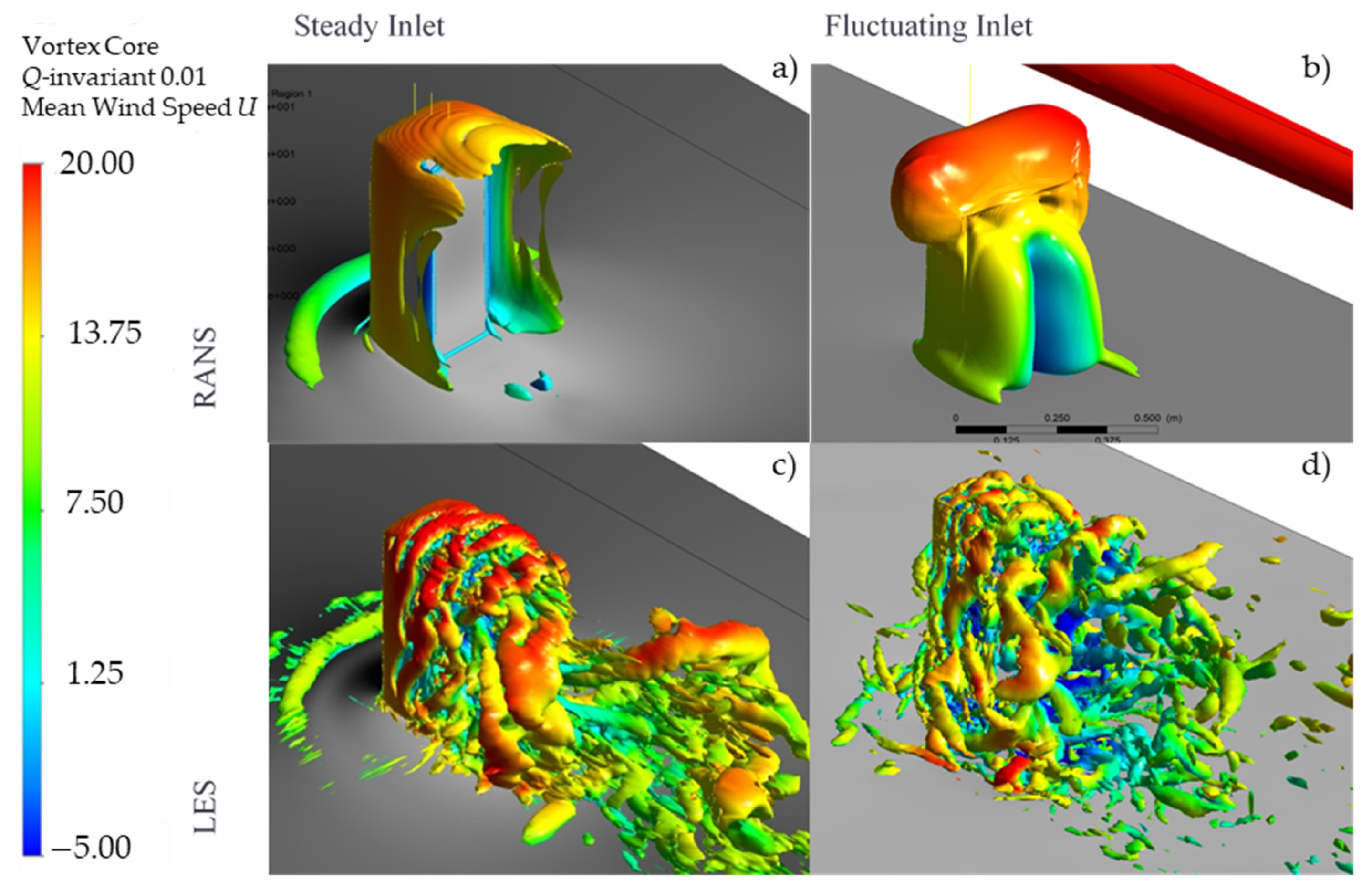
3.2. Numerical Flow Pattern
3.3. RANS and LES Overprediction of the Roof Region
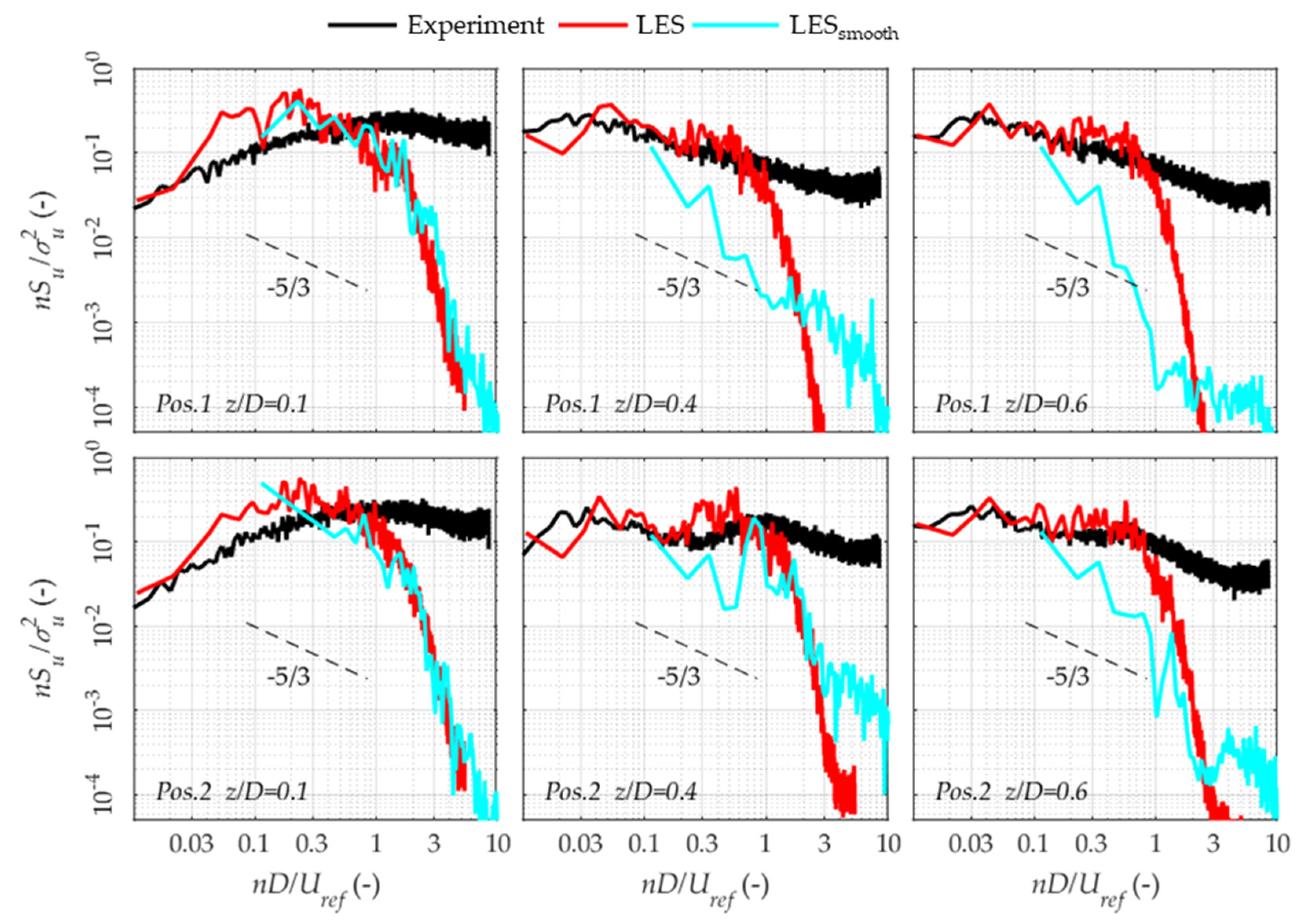
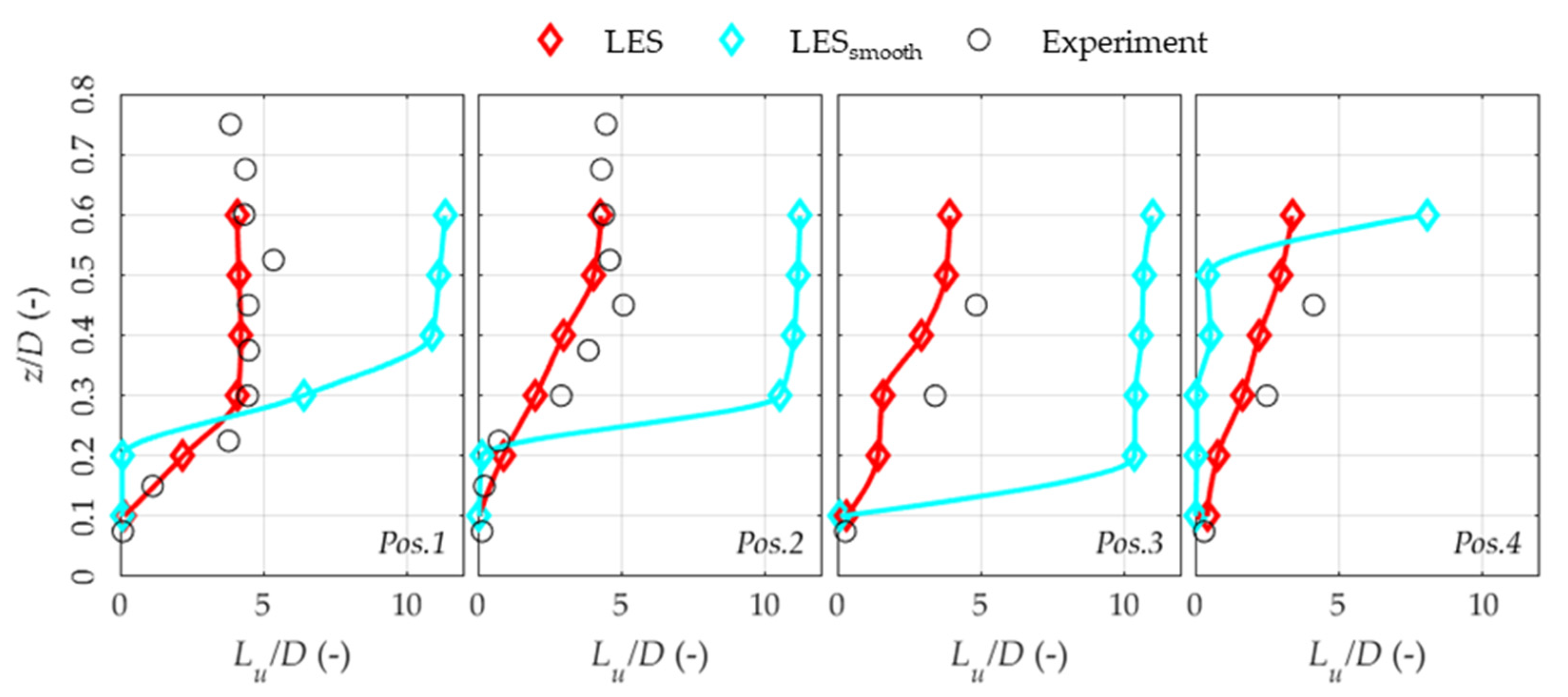
3.4. The Role of Turbulent Inflow in LES Prediction
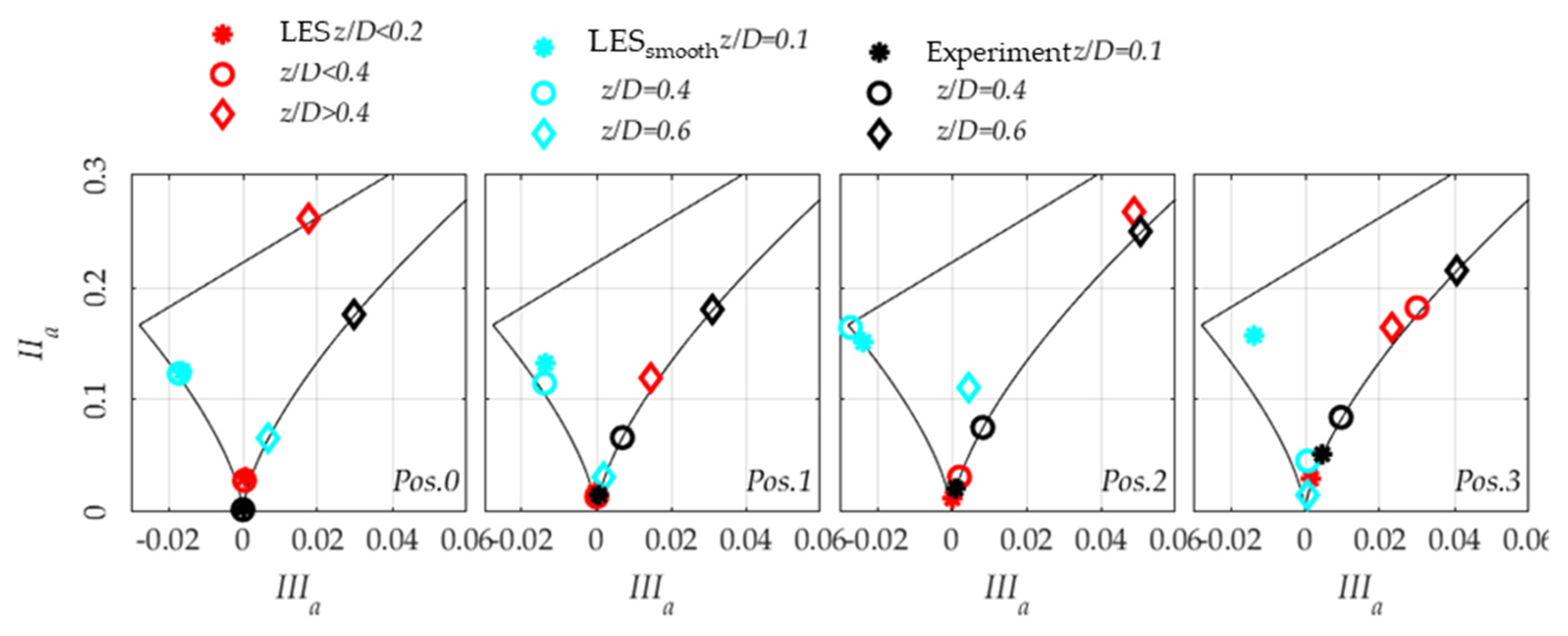
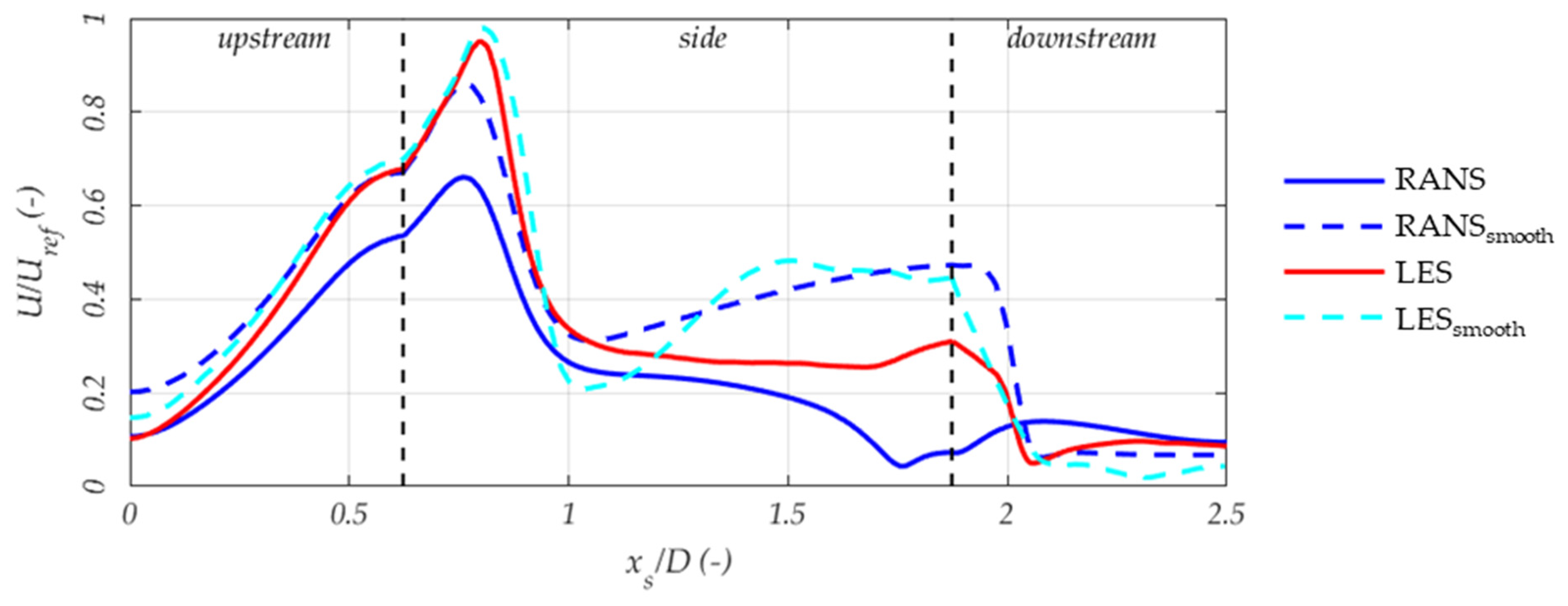
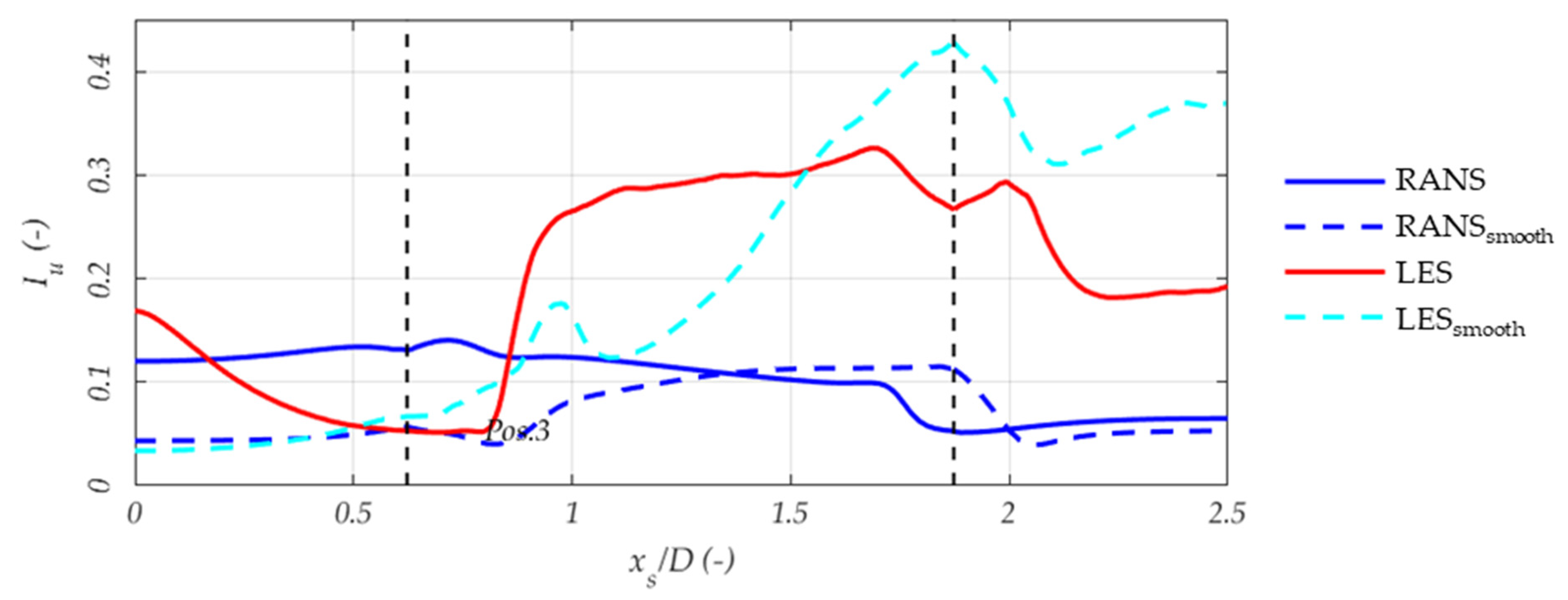
3.5. RANS over LES Prediction at Pedestrian Level
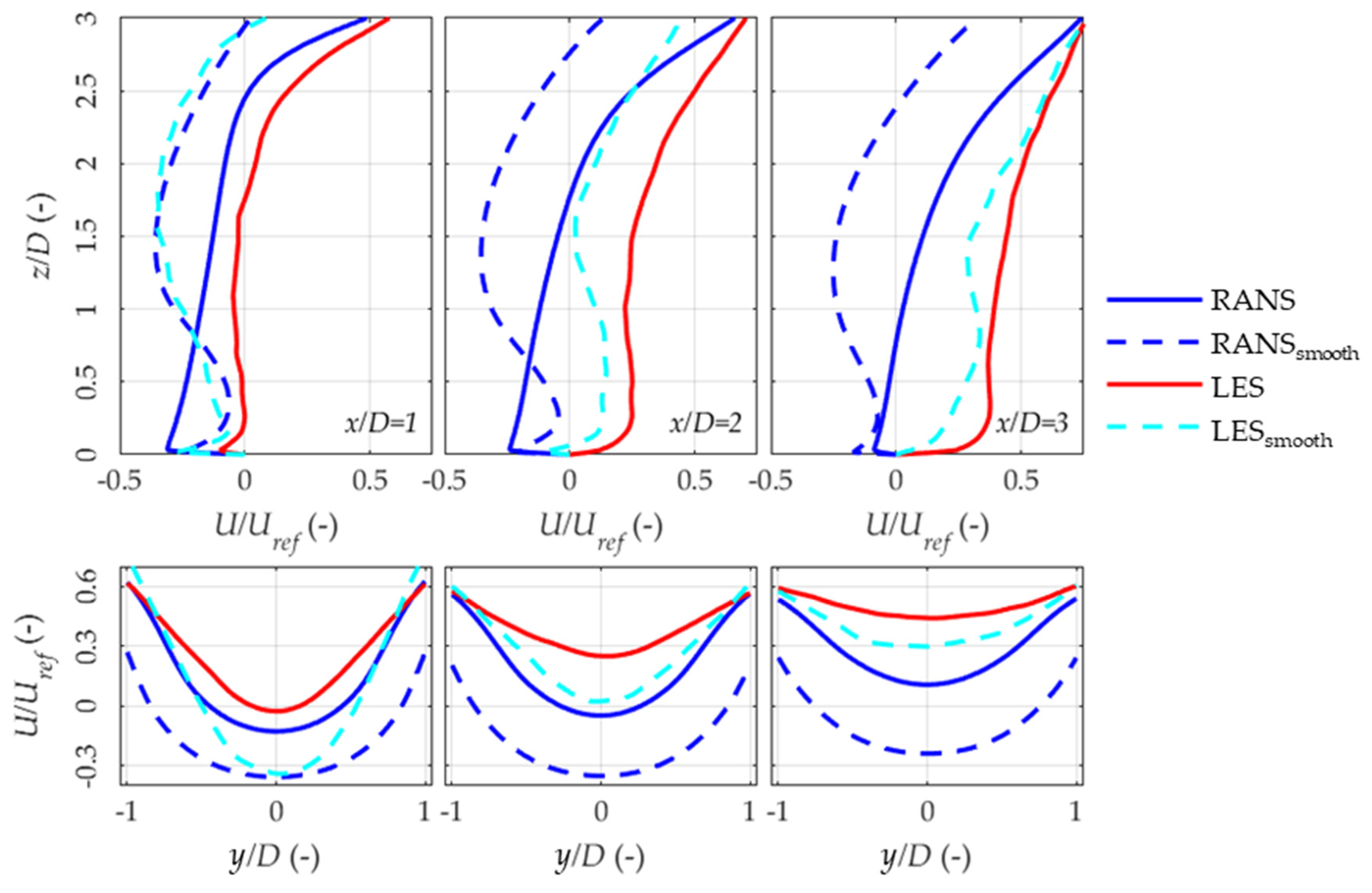
3.6. RANS over LES Prediction in the Wake Region
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haan, F.L.; Kareem, A. Anatomy of Turbulence Effects on the Aerodynamics of an Oscillating Prism. J. Eng. Mech. 2009, 135, 987–999. [Google Scholar] [CrossRef]
- Piringer, M.; Joffre, S.; Baklanov, A.; Christen, A.; Deserti, M.; De Ridder, K.; Emeis, S.; Mestayer, P.; Tombrou, M.; Middleton, D.; et al. The surface energy balance and the mixing height in urban areas—Activities and recommendations of COST-Action 715. Bound.-Layer Meteorol. 2007, 124, 3–24. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlunzen, K.H.; Carissimo, B. The COST 732 Best Practice Guideline for CFD simulation of flows in the urban environment: A summary. Int. J. Environ. Pollut. 2011, 44, 419. [Google Scholar] [CrossRef]
- Franke, J.; Hirsch, C.; Jensen, A.G.; Krüs, H.W.; Schatzmann, M.; Westbury, P.S.; Miles, S.D.; Wisse, J.A.; Wright, N.G. Recommendations on the use of CFD in wind engineering. In Proceedings of the COST Action C14, Impact of Wind and Storm on City Life Built Environment, Brussels, Belgium, 5–7 May 2004. [Google Scholar]
- Blocken, B. Computational Fluid Dynamics for urban physics: Importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef]
- Blocken, B. 50 years of Computational Wind Engineering: Past, present and future. J. Wind Eng. Ind. Aerodyn. 2014, 129, 69–102. [Google Scholar] [CrossRef]
- Baker, C.J. Wind engineering—Past, present and future. J. Wind Eng. Ind. Aerodyn. 2007, 95, 843–870. [Google Scholar] [CrossRef]
- Tamura, T. Towards practical use of LES in wind engineering. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1451–1471. [Google Scholar] [CrossRef]
- Blocken, B. LES over RANS in building simulation for outdoor and indoor applications: A foregone conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar] [CrossRef]
- Toja-Silva, F.; Kono, T.; Peralta, C.; Lopez-Garcia, O.; Chen, J. A review of computational fluid dynamics (CFD) simulations of the wind flow around buildings for urban wind energy exploitation. J. Wind Eng. Ind. Aerodyn. 2018, 180, 66–87. [Google Scholar] [CrossRef]
- Stathopoulos, T.; Alrawashdeh, H. Urban Wind Energy: A Wind Engineering and Wind Energy Cross-Roads. In Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2019; pp. 3–16. [Google Scholar]
- Bontempo, R.; Manna, M. The axial momentum theory as applied to wind turbines: Some exact solutions of the flow through a rotor with radially variable load. Energy Convers. Manag. 2017, 143, 33–48. [Google Scholar] [CrossRef]
- Moeini, R.; Weston, P.; Tricoli, P.; Dinh, T.Q.; McGordon, A.; Hughes, D. Enhancement of Reliability in Condition Monitoring Techniques in Wind Turbines. In Proceedings of the 2019 23rd International Conference on Mechatronics Technology, ICMT 2019, Fisciano, Italy, 23–26 October 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019. [Google Scholar]
- Vita, G.; Shu, Z.; Jesson, M.; Quinn, A.; Hemida, H.; Sterling, M.; Baker, C. On the assessment of pedestrian distress in urban winds. J. Wind Eng. Ind. Aerodyn. 2020, 203, 104200. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; van Beeck, J.P.A.J. Pedestrian-level wind conditions around buildings: Review of wind-tunnel and CFD techniques and their accuracy for wind comfort assessment. Build. Environ. 2016, 100, 50–81. [Google Scholar] [CrossRef]
- Aly, A.M.; Bitsuamlak, G. Aerodynamics of ground-mounted solar panels: Test model scale effects. J. Wind Eng. Ind. Aerodyn. 2013, 123, 250–260. [Google Scholar] [CrossRef]
- Kakimpa, B.; Hargreaves, D.M.; Owen, J.S. An investigation of plate-type windborne debris flight using coupled CFD-RBD models. Part I: Model development and validation. J. Wind Eng. Ind. Aerodyn. 2012. [Google Scholar] [CrossRef]
- Kakimpa, B.; Hargreaves, D.M.; Owen, J.S. An investigation of plate-type windborne debris flight using coupled CFD-RBD models. Part II: Free and constrained flight. J. Wind Eng. Ind. Aerodyn. 2012. [Google Scholar] [CrossRef]
- Bourriez, F.; Sterling, M.; Baker, C. Windborne debris trajectories in tornado-like flow field initiated from a low-rise building. J. Wind Eng. Ind. Aerodyn. 2020. [Google Scholar] [CrossRef]
- Hang, J.; Li, Y.; Sandberg, M.; Buccolieri, R.; Di Sabatino, S. The influence of building height variability on pollutant dispersion and pedestrian ventilation in idealized high-rise urban areas. Build. Environ. 2012, 56, 346–360. [Google Scholar] [CrossRef]
- Kim, J.J.; Baik, J.J. Effects of inflow turbulence intensity on flow and pollutant dispersion in an urban street canyon. J. Wind Eng. Ind. Aerodyn. 2003, 91, 309–329. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Zajic, D.; Di Sabatino, S.; Dimitrova, R.; Hedquist, B.; Dallman, A. Flow, turbulence, and pollutant dispersion in urban atmospheres. Phys. Fluids 2010, 22, 1–20. [Google Scholar] [CrossRef]
- Sanderse, B.; Pijl, S.P.; Koren, B. Review of computational fluid dynamics for wind turbine wake aerodynamics. Wind Energy 2011, 14, 799–819. [Google Scholar] [CrossRef]
- Prospathopoulos, J.M.; Politis, E.S.; Rados, K.G.; Chaviaropoulos, P.K. Evaluation of the effects of turbulence model enhancements on wind turbine wake predictions. Wind Energy 2011, 14, 285–300. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Porté-Agel, F. Atmospheric Turbulence Effects on Wind-Turbine Wakes: An LES Study. Energies 2012, 5, 5340–5362. [Google Scholar] [CrossRef]
- Moeini, R.; Entezami, M.; Ratkovac, M.; Tricoli, P.; Hemida, H.; Hoeffer, R.; Baniotopoulos, C. Perspectives on condition monitoring techniques of wind turbines. Wind Eng. 2019. [Google Scholar] [CrossRef]
- Tanner, K.; Mackenzie, N.; Jones, R.; Lee, Y.K. Aeroacoustic Assessment of Facades. In Proceedings of the ACOUSTICS 2016, Brisbane, Australia, 9–11 November 2016; New Zealand Acoustics: Brisbane, Australia, 2016; p. 11. [Google Scholar]
- Zhiyin, Y. Large-eddy simulation: Past, present and the future. Chin. J. Aeronaut. 2015, 28, 11–24. [Google Scholar] [CrossRef]
- Ricci, A.; Burlando, M.; Repetto, M.P.; Blocken, B. Simulation of urban boundary and canopy layer flows in port areas induced by different marine boundary layer inflow conditions. Sci. Total Environ. 2019. [Google Scholar] [CrossRef]
- Hertwig, D.; Efthimiou, G.C.; Bartzis, J.G.; Leitl, B. CFD-RANS model validation of turbulent flow in a semi-idealized urban canopy. J. Wind Eng. Ind. Aerodyn. 2012, 111, 61–72. [Google Scholar] [CrossRef]
- García-Sánchez, C.; Van Tendeloo, G.; Gorlé, C. Quantifying inflow uncertainties in RANS simulations of urban pollutant dispersion. Atmos. Environ. 2017, 161, 263–273. [Google Scholar] [CrossRef]
- Baniotopoulos, C.C.; Borri, C.; Stathopoulos, T. Environmental Wind Engineering and Design of Wind Energy Structures; Springer: New York, NY, USA, 2011; Volume 531, p. 352. [Google Scholar]
- Flay, R.G.J. Bluff body aerodynamics. In Advanced Structural Wind Engineering; Springer: Tokyo, Japan, 2013; pp. 59–84. ISBN 9784431543374. [Google Scholar]
- Irwin, P.A. Bluff body aerodynamics in wind engineering. J. Wind Eng. Ind. Aerodyn. 2008, 96, 701–712. [Google Scholar] [CrossRef]
- Hemida, H.; Šarkić Glumac, A.; Vita, G.; Kostadinović Vranešević, K.; Höffer, R. On the Flow over High-rise Building for Wind Energy Harvesting: An Experimental Investigation of Wind Speed and Surface Pressure. Appl. Sci. 2020, 10, 5283. [Google Scholar] [CrossRef]
- Šarkić Glumac, A.; Hemida, H.; Höffer, R. Wind energy potential above a high-rise building influenced by neighboring buildings: An experimental investigation. J. Wind Eng. Ind. Aerodyn. 2018, 175, 32–42. [Google Scholar] [CrossRef]
- Vita, G. The Effect of Turbulence in the Built Environment on Wind Turbine Aerodynamics. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2020. [Google Scholar]
- Lund, T.S.; Wu, X.; Squires, K.D. Generation of Turbulent Inflow Data for Spatially-Developing Boundary Layer Simulations. J. Comput. Phys. 1998, 140, 233–258. [Google Scholar] [CrossRef]
- Ozmen, Y.; Baydar, E.; van Beeck, J.P.A.J. Wind flow over the low-rise building models with gabled roofs having different pitch angles. Build. Environ. 2016, 95, 63–74. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; Volume 1, ISBN 0521598869. [Google Scholar]
- Van Driest, E.R. On Turbulent Flow near a Wall. J. Aeronaut. Sci. 1956, 23, 1007–1011. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Ansys Inc. ANSYS CFX-Solver Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Hemida, H.; Šarkic, A.; Höffer, R. Interference effect of high-rise buildings for wind energy extraction; wind tunnel and numerical investigations. In Proceedings of the 14th International Conference on Wind Engineering, Porto Alegre, Brazil, 21–26 June 2015. [Google Scholar]
- Vita, G.; Šarkić-Glumac, A.; Hemida, H.; Salvadori, S.; Baniotopoulos, C. On the Wind Energy Resource above High-Rise Buildings. Energies 2020, 13, 3641. [Google Scholar] [CrossRef]
- Baker, C.J. The turbulent horseshoe vortex. J. Wind Eng. Ind. Aerodyn. 1980, 6, 9–23. [Google Scholar] [CrossRef]
- Meroney, R.N.; Leitl, B.M.; Rafailidis, S.; Schatzmann, M. Wind-tunnel and numerical modeling of flow and dispersion about several building shapes. J. Wind Eng. Ind. Aerodyn. 1999, 81, 333–345. [Google Scholar] [CrossRef]
- Nakamura, Y.; Ohya, Y. Vortex shedding from square prisms in smooth and turbulent flows. J. Fluid Mech. 1986, 164, 77–89. [Google Scholar] [CrossRef]
- Buresti, G. Elements of Fluid Dynamics; Imperial College Press: London, UK, 2012; ISBN 1848168896. [Google Scholar]
- Zdravkovich, M.M. Flow around Circular Cylinders; Oxford University Press: Oxford, UK, 1997; ISBN 0198563965. [Google Scholar]
- Nakamura, Y. Bluff-body aerodynamics and turbulence. J. Wind Eng. Ind. Aerodyn. 1993, 49, 65–78. [Google Scholar] [CrossRef]
- Hemida, H. Large-eddy simulation of the above roof flow of a high-rise building for micro-wind turbines. In Proceedings of the 11th UK Conference on Wind Engineering, Nottingham, UK, 11–12 November 2014. [Google Scholar]
- IEC 61400-2:2013 Wind Turbines—Part 2: Small Wind Turbines; International Electrotechnical Commission: Geneve, Switzerland, 2013.
- Ledo, L.; Kosasih, P.B.; Cooper, P. Roof mounting site analysis for micro-wind turbines. Renew. Energy 2011, 36, 1379–1391. [Google Scholar] [CrossRef]
- Jovanović, J. The Statistical Dynamics of Turbulence; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004. [Google Scholar]
- Bearman, P.W.; Morel, T. Effect of free stream turbulence on the flow around bluff bodies. Prog. Aerosp. Sci. 1983, 20, 97–123. [Google Scholar] [CrossRef]
- Bottema, M. A method for optimisation of wind discomfort criteria. Build. Environ. 2000, 35, 1–18. [Google Scholar] [CrossRef]
- Jacob, J.; Sagaut, P. Wind comfort assessment by means of large eddy simulation with lattice Boltzmann method in full scale city area. Build. Environ. 2018, 139, 110–124. [Google Scholar] [CrossRef]







| Gust Wind Speed | xS/D | RANS | RANSsmooth | LES | LESsmooth |
|---|---|---|---|---|---|
| 0.7 | 12.01 | 14.54 | 15.96 | 16.93 | |
| 1.5 | 1.74 | 8.52 | 5.73 | 10.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vita, G.; Salvadori, S.; Misul, D.A.; Hemida, H. Effects of Inflow Condition on RANS and LES Predictions of the Flow around a High-Rise Building. Fluids 2020, 5, 233. https://doi.org/10.3390/fluids5040233
Vita G, Salvadori S, Misul DA, Hemida H. Effects of Inflow Condition on RANS and LES Predictions of the Flow around a High-Rise Building. Fluids. 2020; 5(4):233. https://doi.org/10.3390/fluids5040233
Chicago/Turabian StyleVita, Giulio, Simone Salvadori, Daniela Anna Misul, and Hassan Hemida. 2020. "Effects of Inflow Condition on RANS and LES Predictions of the Flow around a High-Rise Building" Fluids 5, no. 4: 233. https://doi.org/10.3390/fluids5040233
APA StyleVita, G., Salvadori, S., Misul, D. A., & Hemida, H. (2020). Effects of Inflow Condition on RANS and LES Predictions of the Flow around a High-Rise Building. Fluids, 5(4), 233. https://doi.org/10.3390/fluids5040233








