Reduced Order Models for the Quasi-Geostrophic Equations: A Brief Survey
Abstract
:1. Introduction
1.1. Reduced Order Models (ROMs)
| Algorithm 1 ROM Strategy |
|
1.2. ROMs for the Quasi-Geostrophic Equations
2. Quasi-Geostrophic Equations (QGE)
3. Full Order Model (FOM)
3.1. Finite Difference Methods for the QGE
3.2. Finite Volume Methods for the QGE
3.3. Pseudospectral and Spectral Methods for the QGE
3.4. Finite Element Methods for the QGE
4. Reduced Order Models (ROMs)
4.1. Galerkin Reduced Order Model (G-ROM)
4.2. ROM Closure Models
4.2.1. Under-Resolved ROMs Require Closure Models
- Black box ROM closure models: These models consider the true closure model as a black box, i.e., the specific form of is not determined. Instead, one first postulates a model form for , i.e., , and then determines the parameters of the model form , either by using available data or physical insight.
- Mathematical ROM closure models: These models use filtering/averaging (e.g., with respect to space, time, or initial conditions) to determine the specific form of the true ROM closure term . As in the black box ROM closure models, one postulates a model form for , i.e., . However, the mathematical ROM closure modeling utilizes data for the specific form of to determine the ROM closure model .
4.2.2. Large Eddy Simulation ROM Closure Models
4.2.3. Machine Learning ROM Closure Models
- The ROM coefficients in a given time window were extracted from the high-resolution FOM data by projecting the snapshots onto the ROM modes.
- The LSTM neural network was used to construct an ML-ROM that mapped the old ROM coefficients to the ROM coefficients at the new time step .
5. Numerical Results
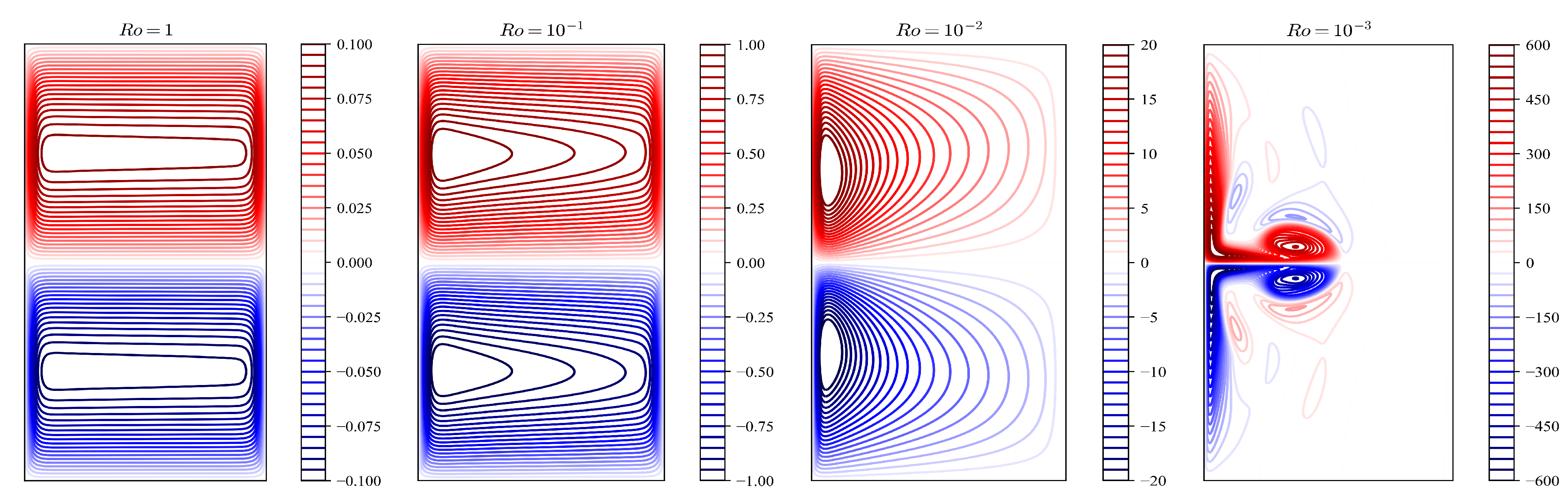
5.1. Regimes
5.2. Test Problem Setup
5.3. Criteria
5.4. FOM Snapshot Generation
5.5. ROM Numerical Investigation
5.5.1. Resolved, Reconstructive Regime
5.5.2. Resolved, Predictive Regime
5.5.3. Under-Resolved, Reconstructive Regime
5.5.4. Under-Resolved, Predictive Regime
5.5.5. Computational Cost
5.5.6. Summary
- For our test problem, the resolved regime requires ROMs that have a large dimension (i.e., ) in both the reconstructive and the predictive regimes.
- In the realistic, under-resolved regime, the LES-ROM is orders of magnitude more accurate than the G-ROM in both the reconstructive and the predictive regimes.
- The LES-ROM in the under-resolved regime (i.e., with ) is significantly more accurate and dramatically more efficient than the G-ROM in the resolved regime (i.e., with ).
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Hesthaven, J.S.; Rozza, G.; Stamm, B. Certified Reduced Basis Methods for Parametrized Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Holmes, P.; Lumley, J.L.; Berkooz, G. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Quarteroni, A.; Manzoni, A.; Negri, F. Reduced Basis Methods for Partial Differential Equations: An Introduction; Springer: Berlin/Heidelberg, Germany, 2015; Volume 92. [Google Scholar]
- Benner, P.; Gugercin, S.; Willcox, K. A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Rev. 2015, 57, 483–531. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Noack, B.R.; Morzynski, M.; Tadmor, G. Reduced-Order Modelling for Flow Control; Springer: Berlin/Heidelberg, Germany, 2011; Volume 528. [Google Scholar]
- Taira, K.; Hemati, M.S.; Brunton, S.L.; Sun, Y.; Duraisamy, K.; Bagheri, S.; Dawson, S.T.M.; Yeh, C.A. Modal analysis of fluid flows: Applications and outlook. AIAA J. 2020, 58, 998–1022. [Google Scholar] [CrossRef]
- Mou, C.; Liu, H.; Wells, D.R.; Iliescu, T. Data-Driven Correction Reduced Order Models for the Quasi-Geostrophic Equations: A Numerical Investigation. Int. J. Comput. Fluid Dyn. 2020, 34, 147–159. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Mohebujjaman, M.; Rebholz, L.G.; Iliescu, T. Data-Driven Filtered Reduced Order Modeling of Fluid Flows. SIAM J. Sci. Comput. 2018, 40, B834–B857. [Google Scholar] [CrossRef] [Green Version]
- Star, S.K.; Stabile, G.; Belloni, F.; Rozza, G.; Degroote, J. Extension and comparison of techniques to enforce boundary conditions in finite volume POD-Galerkin reduced order models for fluid dynamic problems. arXiv 2019, arXiv:1912.00825. [Google Scholar]
- Couplet, M.; Sagaut, P.; Basdevant, C. Intermodal energy transfers in a proper orthogonal decomposition-Galerkin representation of a turbulent separated flow. J. Fluid Mech. 2003, 491, 275. [Google Scholar] [CrossRef]
- Hess, M.W.; Quaini, A.; Rozza, G. Reduced basis model order reduction for Navier–Stokes equations in domains with walls of varying curvature. Int. J. Comput. Fluid Dyn. 2020, 34, 119–126. [Google Scholar] [CrossRef] [Green Version]
- Pitton, G.; Quaini, A.; Rozza, G. Computational reduction strategies for the detection of steady bifurcations in incompressible fluid-dynamics: Applications to Coanda effect in cardiology. J. Comput. Phys. 2017, 344, 534–557. [Google Scholar] [CrossRef] [Green Version]
- Skitka, J.; Marston, J.B.; Fox-Kemper, B. Reduced-Order Quasilinear Model of Ocean Boundary-Layer Turbulence. J. Phys. Oceanogr. 2020, 50, 537–558. [Google Scholar] [CrossRef] [Green Version]
- Cushman-Roisin, B.; Beckers, J.M. Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Majda, A.J.; Wang, X. Nonlinear Dynamics and Statistical Theories for Basic Geophysical Flows; Cambridge University Press: Cambridge, UK, 2006; p. xii+551. [Google Scholar]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Charney, J.G.; Fjörtoft, R.; Neumann, J.V. Numerical Integration of the Barotropic Vorticity Equation. Tellus 1950, 2, 237–254. [Google Scholar] [CrossRef] [Green Version]
- Majda, A.J.; Shefter, M.G. Nonlinear instability of elementary stratified flows at large Richardson number. Chaos Interdiscip. J. Nonlinear Sci. 2000, 10, 3–27. [Google Scholar] [CrossRef] [PubMed]
- Majda, A.J.; Shefter, M.G. Elementary stratified flows with instability at large Richardson number. J. Fluid Mech. 1998, 376, 319–350. [Google Scholar] [CrossRef]
- Majda, A.J.; Embid, P. Averaging over fast gravity waves for geophysical flows with unbalanced initial data. Theor. Comput. Fluid. Dyn. 1998, 11, 155–169. [Google Scholar] [CrossRef]
- Embid, P.F. Averaging over fast gravity waves for geophysical flows with arbitary. Commun. Partial. Differ. Equ. 1996, 21, 619–658. [Google Scholar] [CrossRef]
- Embid, P.F.; Majda, A.J. Low Froude number limiting dynamics for stably stratified flow with small or finite Rossby numbers. Geophys. Astro. Fluid. 1998, 87, 1–50. [Google Scholar] [CrossRef]
- Majda, A.J.; Grote, M.J. Model dynamics and vertical collapse in decaying strongly stratified flows. Phys. Fluids. 1997, 9, 2932–2940. [Google Scholar] [CrossRef] [Green Version]
- Dijkstra, H.A. Dynamical Oceanography; Springer: Berlin, Germany, 2008; p. xvi+407. [Google Scholar]
- Pedlosky, J. Geophysical Fluid Dynamics, 2nd ed.; Springer: Berlin, Germany, 1992. [Google Scholar]
- Greatbatch, R.J.; Nadiga, B.T. Four-gyre circulation in a barotropic model with double-gyre wind forcing. J. Phys. Oceanogr. 2000, 30, 1461–1471. [Google Scholar] [CrossRef]
- Holm, D.D.; Nadiga, B.T. Modeling mesoscale turbulence in the barotropic double-gyre circulation. J. Phys. Oceanogr. 2003, 33, 2355–2365. [Google Scholar] [CrossRef] [Green Version]
- Nadiga, B.T.; Margolin, L.G. Dispersive-dissipative eddy parameterization in a barotropic model. J. Phys. Oceanogr. 2001, 31, 2525–2531. [Google Scholar] [CrossRef] [Green Version]
- Foster, E.L.; Iliescu, T.; Wang, Z. A finite element discretization of the streamfunction formulation of the stationary quasi-geostrophic equations of the ocean. Comput. Methods Appl. Mech. Eng. 2013, 261, 105–117. [Google Scholar] [CrossRef] [Green Version]
- Monteiro, I.O.; Manica, C.C.; Rebholz, L.G. Numerical study of a regularized barotropic vorticity model of geophysical flow. Numer. Methods Partial. Differ. Equ. 2015, 31, 1492–1514. [Google Scholar] [CrossRef]
- San, O.; Iliescu, T. A stabilized proper orthogonal decomposition reduced-order model for large scale quasigeostrophic ocean circulation. Adv. Comput. Math. 2015, 41, 1289–1319. [Google Scholar] [CrossRef] [Green Version]
- San, O.; Staples, A.E.; Wang, Z.; Iliescu, T. Approximate deconvolution large eddy simulation of a barotropic ocean circulation model. Ocean Model. 2011, 40, 120–132. [Google Scholar] [CrossRef] [Green Version]
- Medjo, T.T. Numerical Simulations of a Two-Layer Quasi-Geostrophic Equation of the Ocean. SIAM J. Numer. Anal. 2000, 37, 2005–2022. [Google Scholar] [CrossRef]
- Medjo, T.T. Multi-layer quasi-geostrophic equations of the ocean with delays. Discret. Contin. Dyn. Syst. Ser. B 2008, 10, 171. [Google Scholar]
- Shevchenko, I.; Berloff, P. Multi-layer quasi-geostrophic ocean dynamics in eddy-resolving regimes. Ocean Model. 2015, 94, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Phillips, N.A. The general circulation of the atmosphere: A numerical experiment. Q. J. R. Meteorol. Soc. 1956, 82, 123–164. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational Design of the Basic Dynamical Processes of the UCLA General Circulation Model. In General Circulation Models of the Atmosphere; Elsevier: Amsterdam, The Netherlands, 1977; Volume 17, pp. 173–265. [Google Scholar] [CrossRef]
- Collins, S.N.; James, R.S.; Ray, P.; Chen, K.; Lassman, A.; Brownlee, J. Grids in numerical weather and climate models. In Climate Change and Regional/Local Responses; IntechOpen: Rijeka, Croatia, 2013. [Google Scholar] [CrossRef] [Green Version]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Modular Ocean Model (MOM)—Geophysical Fluid Dynamics Laboratory. Available online: https://www.gfdl.noaa.gov/mom-ocean-model/# (accessed on 9 November 2020).
- Maulik, R.; San, O. Dynamic modeling of the horizontal eddy viscosity coefficient for quasigeostrophic ocean circulation problems. J. Ocean Eng. Sci. 2016, 1, 300–324. [Google Scholar] [CrossRef] [Green Version]
- Maulik, R.; San, O. A novel dynamic framework for subgrid scale parametrization of mesoscale eddies in quasigeostrophic turbulent flows. Comput. Math. Appl. 2017, 74, 420–445. [Google Scholar] [CrossRef]
- San, O.; Staples, A.E.; Iliescu, T. Approximate Deconvolution Large Eddy Simulation of a Stratified Two-Layer Quasigeostrophic Ocean Model. Ocean Model. 2013, 63, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, S.D. Kelvin wave propagation along straight boundaries in C-grid finite-difference models. J. Comput. Phys. 2013, 255, 639–659. [Google Scholar] [CrossRef] [Green Version]
- Campin, J.M.; Heimbach, P.; Losch, M.; Forget, G.; Adcroft, A.; Menemenlis, D.; Hill, C.; Jahn, O.; Scott, J.; Mazloff, M.; et al. MITgcm/MITgcm: Mid 2020 Version. 2020. Available online: https://zenodo.org/record/3967889/export/xd#.X-087RYRVPY (accessed on 9 November 2020).
- Thuburn, J.; Ringler, T.D.; Skamarock, W.C.; Klemp, J.B. Numerical representation of geostrophic modes on arbitrarily structured C-grids. J. Comput. Phys. 2009, 228, 8321–8335. [Google Scholar] [CrossRef] [Green Version]
- Ringler, T.D.; Thuburn, J.; Klemp, J.B.; Skamarock, W.C. A unified approach to energy conservation and potential vorticity dynamics for arbitrarily-structured C-grids. J. Comput. Phys. 2010, 229, 3065–3090. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Ringler, T.D.; Gunzburger, M. A co-volume scheme for the rotating shallow water equations on conforming non-orthogonal grids. J. Comput. Phys. 2013, 240, 174–197. [Google Scholar] [CrossRef]
- Chen, Q.; Ju, L. Conservative finite-volume schemes for the quasi-geostrophic equation on coastal-conforming unstructured primal–dual meshes. Q. J. R. Meteorol. Soc. 2018, 144, 1106–1122. [Google Scholar] [CrossRef] [Green Version]
- Randall, D.A. Geostrophic adjustment and the finite-difference shallow-water equations. Mon. Weather Rev. 1994, 122, 1371–1377. [Google Scholar] [CrossRef]
- Nadiga, B. Nonlinear evolution of a baroclinic wave and imbalanced dissipation. J. Fluid Mech. 2014, 756, 965–1006. [Google Scholar] [CrossRef] [Green Version]
- San, O.; Staples, A.E. An efficient coarse grid projection method for quasigeostrophic models of large-scale ocean circulation. Int. J. Multiscale Comput. Eng. 2013, 11, 463–495. [Google Scholar] [CrossRef] [Green Version]
- Phillips, N.A. An example of non-linear computational instability. Atmos. Sea Motion 1959, 501, 504. [Google Scholar]
- Orszag, S.A. On the elimination of aliasing in finite-difference schemes by filtering high-wavenumber components. J. Atmos. Sci. 1971, 28, 1074. [Google Scholar] [CrossRef] [Green Version]
- Abernathey, R.; Rocha, C.B.; Poulin, F.; Jansen, M. pyqg: v0.1.4. 2015. Available online: https://zenodo.org/record/32539#.X-09JhYRVPY (accessed on 9 November 2020).
- Hogg, A.M.C.; Dewar, W.K.; Killworth, P.D.; Blundell, J.R. A Quasi-Geostrophic Coupled Model (Q-GCM). Mon. Weather Rev. 2003, 131, 2261–2278. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Fundamentals in Single Domains; Scientific Computation; Springer: Berlin, Germany, 2006. [Google Scholar]
- Frigo, M.; Johnson, S.G. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef] [Green Version]
- Foster, E.L. Finite Elements for the Quasi-Geostrophic Equations of the Ocean. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2013. [Google Scholar]
- Galán del Sastre, P. Estudio Numérico Del Atractor en Ecuaciones de Navier-Stokes Aplicadas a Modelos de Circulación Del océano. Ph.D. Thesis, Universidad Complutense de Madrid, Madrid, Spain, 2004. [Google Scholar]
- Kim, T.Y.; Park, E.J.; Shin, D.W. A C0-discontinuous Galerkin method for the stationary quasi-geostrophic equations of the ocean. Comput. Meth. Appl. Mech. Engrg. 2016, 300, 225–244. [Google Scholar] [CrossRef]
- Shin, D.W.; Kang, Y.; Park, E.J. C0-discontinuous Galerkin methods for a wind-driven ocean circulation model: Two-grid algorithm. Comput. Meth. Appl. Mech. Engrg. 2018, 328, 321–339. [Google Scholar] [CrossRef]
- Fix, G. Finite element models for ocean circulation problems. SIAM J. Appl. Math. 1975, 29, 371–387. [Google Scholar] [CrossRef]
- LeProvost, C.; Bernier, C.; Blayo, E. A comparison of two numerical methods for integrating a quasi-geostrophic multilayer model of ocean circulations: Finite element and finite difference methods. J. Comput. Phys. 1994, 110, 341–359. [Google Scholar] [CrossRef]
- Temam, R. Navier–Stokes Equations: Theory and Numerical Analysis; American Mathematical Society: Providence, RI, USA, 2001; Volume 2. [Google Scholar]
- Medjo, T.T. Mixed Formulation of the Two-Layer Quasi-Geostrophic Equations of the Ocean. Numer. Methods Partial. Differ. Equ. Int. J. 1999, 15, 489–502. [Google Scholar] [CrossRef]
- Cascon, J.M.; Garcia, G.C.; Rodriguez, R. A Priori and A Posteriori Error Analysis for a Large-Scale Ocean Circulation Finite Element Model. Comput. Methods Appl. Mech. Eng. 2003, 192, 5305–5327. [Google Scholar] [CrossRef]
- Kim, T.Y.; Iliescu, T.; Fried, E. B-spline based finite-element method for the stationary quasi-geostrophic equations of the ocean. Comput. Methods Appl. Mech. Eng. 2015, 286, 168–191. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Kim, T.Y. Spline-based finite-element method for the stationary quasi-geostrophic equations on arbitrary shaped coastal boundaries. Comp. Meth. Appl. Mech. Eng. 2016, 299, 144–160. [Google Scholar] [CrossRef]
- Al Balushi, I.; Jiang, W.; Tsogtgerel, G.; Kim, T.Y. Adaptivity of a B-spline based finite-element method for modeling wind-driven ocean circulation. Comp. Meth. Appl. Mech. Eng. 2018, 332, 1–24. [Google Scholar] [CrossRef]
- Kim, D.; Kim, T.Y.; Park, E.J.; Shin, D.W. Error estimates of B-spline based finite-element methods for the stationary quasi-geostrophic equations of the ocean. Comp. Meth. Appl. Mech. Eng. 2018, 335, 255–272. [Google Scholar] [CrossRef]
- Rotundo, N.; Kim, T.Y.; Jiang, W.; Heltai, L.; Fried, E. Error analysis of a B-spline based finite-element method for modeling wind-driven ocean circulation. J. Sci. Comput. 2016, 69, 430–459. [Google Scholar] [CrossRef]
- Crommelin, D.T.; Majda, A.J. Strategies for model reduction: Comparing different optimal bases. J. Atmos. Sci. 2004, 61, 2206–2217. [Google Scholar] [CrossRef] [Green Version]
- Galán del Sastre, P.; Bermejo, R. Error estimates of proper orthogonal decomposition eigenvectors and Galerkin projection for a general dynamical system arising in fluid models. Numer. Math. 2008, 110, 49–81. [Google Scholar] [CrossRef]
- Franzke, C.; Majda, A.J.; Vanden-Eijnden, E. Low-order stochastic mode reduction for a realistic barotropic model climate. J. Atmos. Sci. 2005, 62, 1722–1745. [Google Scholar] [CrossRef]
- Kondrashov, D.; Berloff, P. Stochastic modeling of decadal variability in ocean gyres. Geophys. Res. Lett. 2015, 42, 1543–1553. [Google Scholar] [CrossRef]
- Kondrashov, D.; Chekroun, M.D.; Berloff, P. Multiscale Stuart-Landau emulators: Application to wind-driven ocean gyres. Fluids 2018, 3, 21. [Google Scholar] [CrossRef] [Green Version]
- Rahman, S.M.; Ahmed, S.E.; San, O. A dynamic closure modeling framework for model order reduction of geophysical flows. Phys. Fluids 2019, 31, 046602. [Google Scholar] [CrossRef] [Green Version]
- Selten, F.M. An efficient description of the dynamics of barotropic flow. J. Atmos. Sci. 1995, 52, 915–936. [Google Scholar] [CrossRef] [Green Version]
- Selten, F.M. Baroclinic empirical orthogonal functions as basis functions in an atmospheric model. J. Atmos. Sci. 1997, 54, 2099–2114. [Google Scholar] [CrossRef]
- Selten, F.M. A statistical closure of a low-order barotropic model. J. Atmos. Sci. 1997, 54, 1085–1093. [Google Scholar] [CrossRef]
- Strazzullo, M.; Ballarin, F.; Mosetti, R.; Rozza, G. Model Reduction for Parametrized Optimal Control Problems in Environmental Marine Sciences and Engineering. SIAM J. Sci. Comput. 2018, 40, B1055–B1079. [Google Scholar] [CrossRef]
- Rahman, S.M.; Pawar, S.; San, O.; Rasheed, A.; Iliescu, T. A nonintrusive reduced order modeling framework for quasigeostrophic turbulence. Phys. Rev. E 2019, 100, 053306. [Google Scholar] [CrossRef] [Green Version]
- San, O.; Maulik, R. Extreme learning machine for reduced order modeling of turbulent geophysical flows. Phys. Rev. E 2018, 97, 042322. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Nolan, P.J.; Ross, S.D.; Mou, C.; Iliescu, T. Lagrangian Data-Driven Reduced Order Modeling Using Finite Time Lyapunov Exponents. Fluids 2020, 5, 189. [Google Scholar] [CrossRef]
- Perotto, S.; Reali, A.; Rusconi, P.; Veneziani, A. HIGAMod: A Hierarchical IsoGeometric Approach for MODel reduction in curved pipes. Comput. Fluids 2017, 142, 21–29. [Google Scholar] [CrossRef]
- Caiazzo, A.; Iliescu, T.; John, V.; Schyschlowa, S. A numerical investigation of velocity-pressure reduced order models for incompressible flows. J. Comput. Phys. 2014, 259, 598–616. [Google Scholar] [CrossRef]
- Volkwein, S. Proper Orthogonal Decomposition: Theory and Reduced-Order Modelling; Lecture Notes; University of Konstanz: Konstanz, Germany, 2013. [Google Scholar]
- Mou, C.; Koc, B.; San, O.; Rebholz, L.G.; Iliescu, T. Data-Driven Variational Multiscale Reduced Order Models. Comput. Methods Appl. Mech. Engrg. 2021, 373, 113470. [Google Scholar] [CrossRef]
- Berselli, L.C.; Iliescu, T.; Layton, W.J. Mathematics of Large Eddy Simulation of Turbulent Flows; Scientific Computation; Springer: Berlin, Germany, 2006; p. xviii+348. [Google Scholar]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; p. xxxiv+771. [Google Scholar]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows, 3rd ed.; Scientific Computation; Springer: Berlin, Germany, 2006; p. xxx+556. [Google Scholar]
- Pinkus, A. N-Widths in Approximation Theory; Springer: Berlin, Germany, 2012; Volume 7. [Google Scholar]
- Ohlberger, M.; Rave, S. Reduced basis methods: Success, limitations and future challenges. arXiv 2015, arXiv:1511.02021. [Google Scholar]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison. Comput. Meth. Appl. Mech. Eng. 2012, 237–240, 10–26. [Google Scholar] [CrossRef] [Green Version]
- Smagorinsky, J.S. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Maulik, R.; San, O.; Rasheed, A.; Vedula, P. Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 2019, 858, 122–144. [Google Scholar] [CrossRef] [Green Version]
- Pawar, S.; San, O.; Rasheed, A. Deep Learning Based Sub-Grid Scale Closure for LES of Kraichnan Turbulence. APS 2019, G17-007. Available online: https://ui.adsabs.harvard.edu/abs/2019APS..DFDG17007P/abstract (accessed on 9 November 2020).
- Lee, K.; Carlberg, K.T. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. J. Comput. Phys. 2020, 404, 108973. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, S.E.; San, O.; Rasheed, A.; Iliescu, T. A long short-term memory embedding for hybrid uplifted reduced order models. Phys. D Nonlinear Phenom. 2020, 409, 132471. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, S.; Rahman, S.M.; San, O.; Rasheed, A. LSTM based nonintrusive ROM of convective flows. APS 2019, L10-003. Available online: https://ui.adsabs.harvard.edu/abs/2019APS..DFDL10003A/abstract (accessed on 9 November 2020).
- Parish, E.J. Machine Learning Closure Modeling for Reduced-Order Models of Dynamical Systems; Technical Report; Sandia National Lab. (SNL-CA): Livermore, CA, USA, 2019. [Google Scholar]
- Rahman, S.M.; San, O.; Rasheed, A. A hybrid approach for model order reduction of barotropic quasi-geostrophic turbulence. Fluids 2018, 3, 86. [Google Scholar] [CrossRef] [Green Version]
- Cummins, P.F. Inertial gyres in decaying and forced geostrophic turbulence. J. Mar. Res. 1992, 50, 545–566. [Google Scholar] [CrossRef]
- Daescu, D.N.; Navon, I.M. A dual-weighted approach to order reduction in 4DVAR data assimilation. Mon. Weather Rev. 2008, 136, 1026–1041. [Google Scholar] [CrossRef] [Green Version]
- Kaercher, M.; Boyaval, S.; Grepl, M.A.; Veroy, K. Reduced basis approximation and a posteriori error bounds for 4D-Var data assimilation. Optim. Eng. 2018, 19, 663–695. [Google Scholar] [CrossRef] [Green Version]
- Maday, Y.; Patera, A.T.; Penn, J.D.; Yano, M. A parameterized-background data-weak approach to variational data assimilation: Formulation, analysis, and application to acoustics. Int. J. Num. Meth. Engng. 2015, 102, 933–965. [Google Scholar] [CrossRef] [Green Version]
- Popov, A.A.; Mou, C.; Iliescu, T.; Sandu, A. A multifidelity ensemble Kalman filter with reduced order control variates. arXiv 2020, arXiv:2007.00793. [Google Scholar]
- Ştefănescu, R.; Sandu, A.; Navon, I.M. POD/DEIM reduced-order strategies for efficient four dimensional variational data assimilation. J. Comput. Phys. 2015, 295, 569–595. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Du, J.; Fang, F.; Pain, C.C.; Li, J. Parameterised non-intrusive reduced order methods for ensemble Kalman filter data assimilation. Comput. Fluids 2018, 177, 69–77. [Google Scholar] [CrossRef]
- Zerfas, C.; Rebholz, L.G.; Schneier, M.; Iliescu, T. Continuous data assimilation reduced order models of fluid flow. Comput. Meth. Appl. Mech. Eng. 2019, 357, 112596. [Google Scholar] [CrossRef] [Green Version]











| Relative Energy Content | 90% | 95% | 99% |
|---|---|---|---|
| 2D flow past a cylinder | 2 | 4 | 6 |
| QGE | 77 | 152 | 380 |
| r | 10 | 20 | 40 | 80 | 120 |
|---|---|---|---|---|---|
| Relative error | 2.009 × 10 | 7.377 × 10 | 4.595 × 10 | 2.999 × 10 | 1.493 × 10 |
| Relative energy content |
| r | 10 | 20 | 40 | 80 | 120 |
|---|---|---|---|---|---|
| Relative error | 2.030 × 10 | 1.015 × 10 | 5.115 × 10 | 3.892 × 10 | 2.619 × 10 |
| Relative energy content |
| r | G-ROM | LES-ROM |
|---|---|---|
| 10 | 2.009 × 10 | 1.074 × 10 |
| 15 | 5.569 × 10 | 6.780 × 10 |
| 20 | 7.377 × 10 | 2.784 × 10 |
| r | G-ROM | LES-ROM |
|---|---|---|
| 10 | 2.030 × 10 | 1.622 × 10 |
| 15 | 2.880 × 10 | 2.385 × 10 |
| 20 | 1.015 × 10 | 1.266 × 10 |
| FOM CPU time | 2.19 × 10 s | ||||||
| G-ROM CPU time | 2.69 × 10 s | 4.80 × 10 s | 4.58 × 10 s | 1.32 × 10 s | 6.45 × 10 s | ||
| LES-ROM CPU time | 3.22 × 10 s | 3.85 × 10 s | 5.07 × 10 s | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mou, C.; Wang, Z.; Wells, D.R.; Xie, X.; Iliescu, T. Reduced Order Models for the Quasi-Geostrophic Equations: A Brief Survey. Fluids 2021, 6, 16. https://doi.org/10.3390/fluids6010016
Mou C, Wang Z, Wells DR, Xie X, Iliescu T. Reduced Order Models for the Quasi-Geostrophic Equations: A Brief Survey. Fluids. 2021; 6(1):16. https://doi.org/10.3390/fluids6010016
Chicago/Turabian StyleMou, Changhong, Zhu Wang, David R. Wells, Xuping Xie, and Traian Iliescu. 2021. "Reduced Order Models for the Quasi-Geostrophic Equations: A Brief Survey" Fluids 6, no. 1: 16. https://doi.org/10.3390/fluids6010016
APA StyleMou, C., Wang, Z., Wells, D. R., Xie, X., & Iliescu, T. (2021). Reduced Order Models for the Quasi-Geostrophic Equations: A Brief Survey. Fluids, 6(1), 16. https://doi.org/10.3390/fluids6010016





