Flow Structures on a Planar Food and Drug Administration (FDA) Nozzle at Low and Intermediate Reynolds Number
Abstract
:1. Introduction
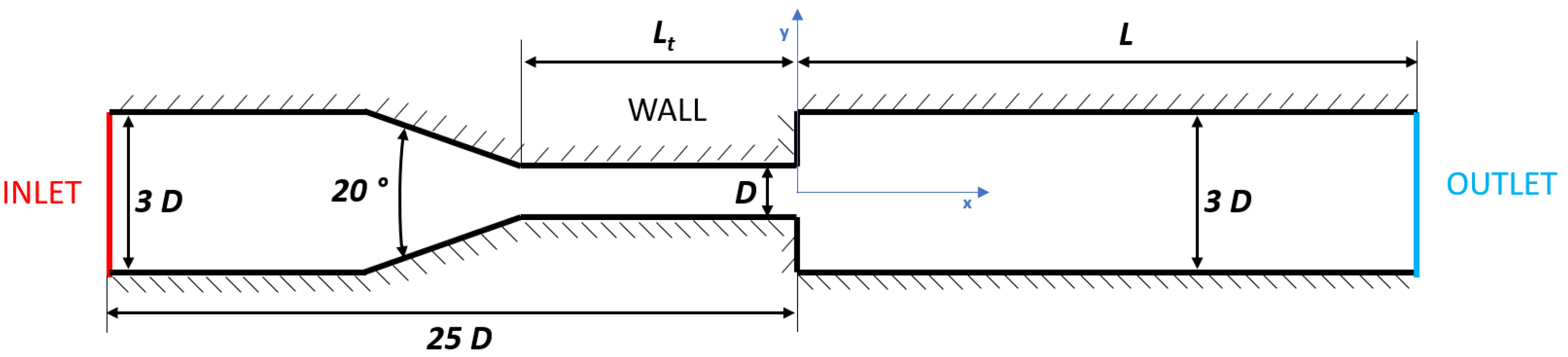
2. Geometry Description and Numerical Simulations
3. Methodology
3.1. Linear Stability Analysis
3.2. Higher-Order Dynamic Mode Decomposition
4. Results
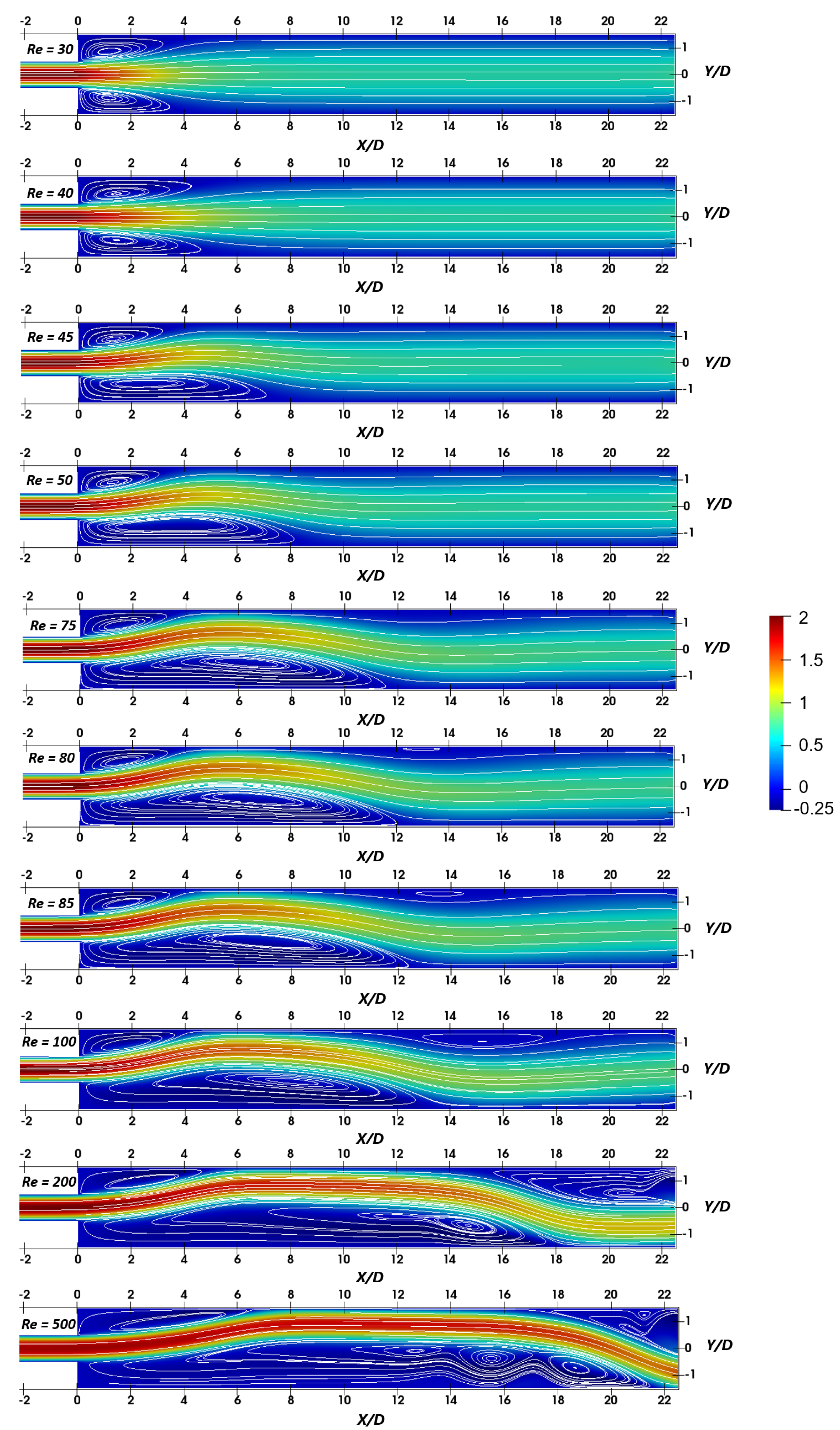
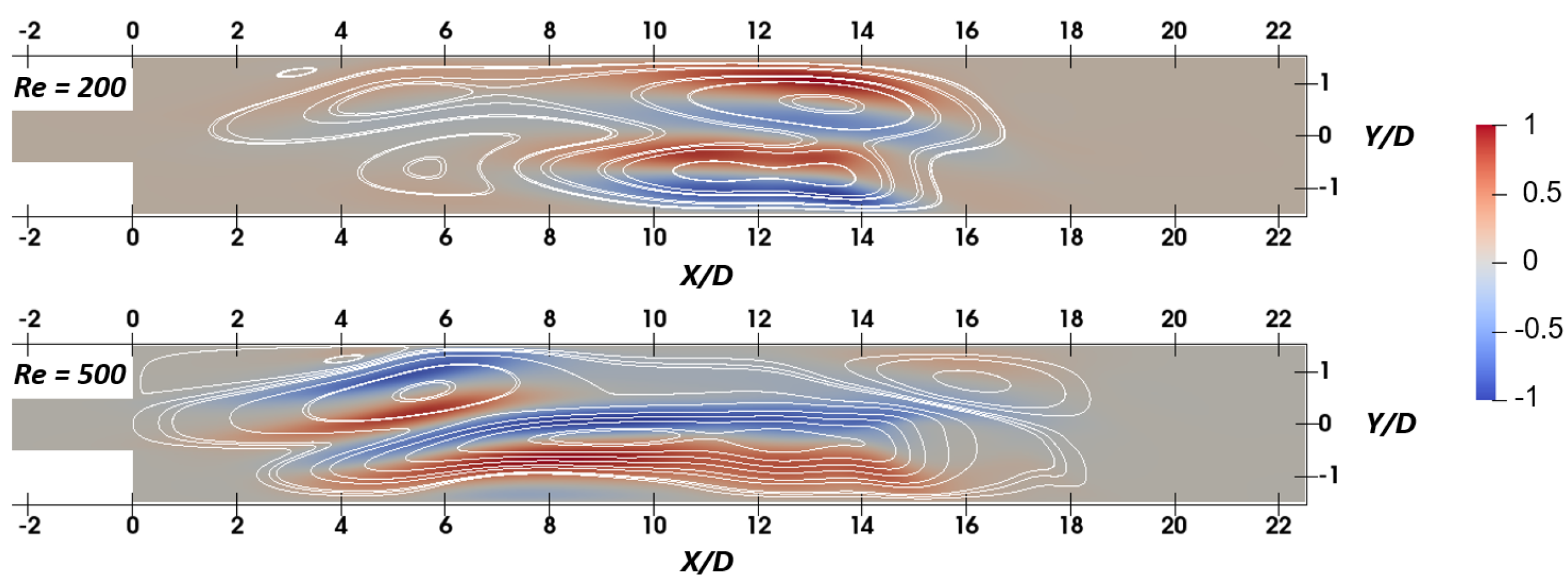
4.1. Flow Topology
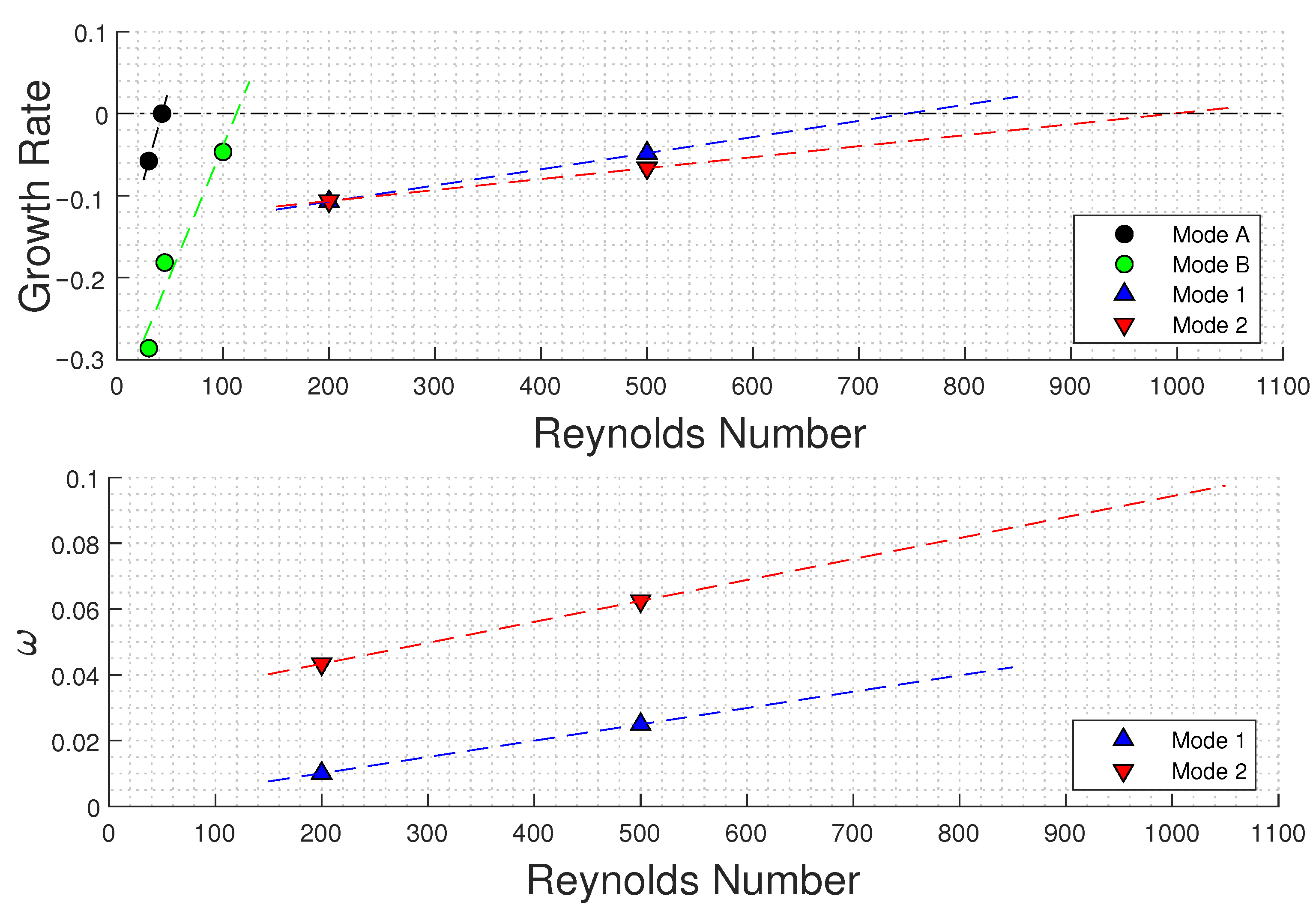
4.2. Linear Stability Analysis
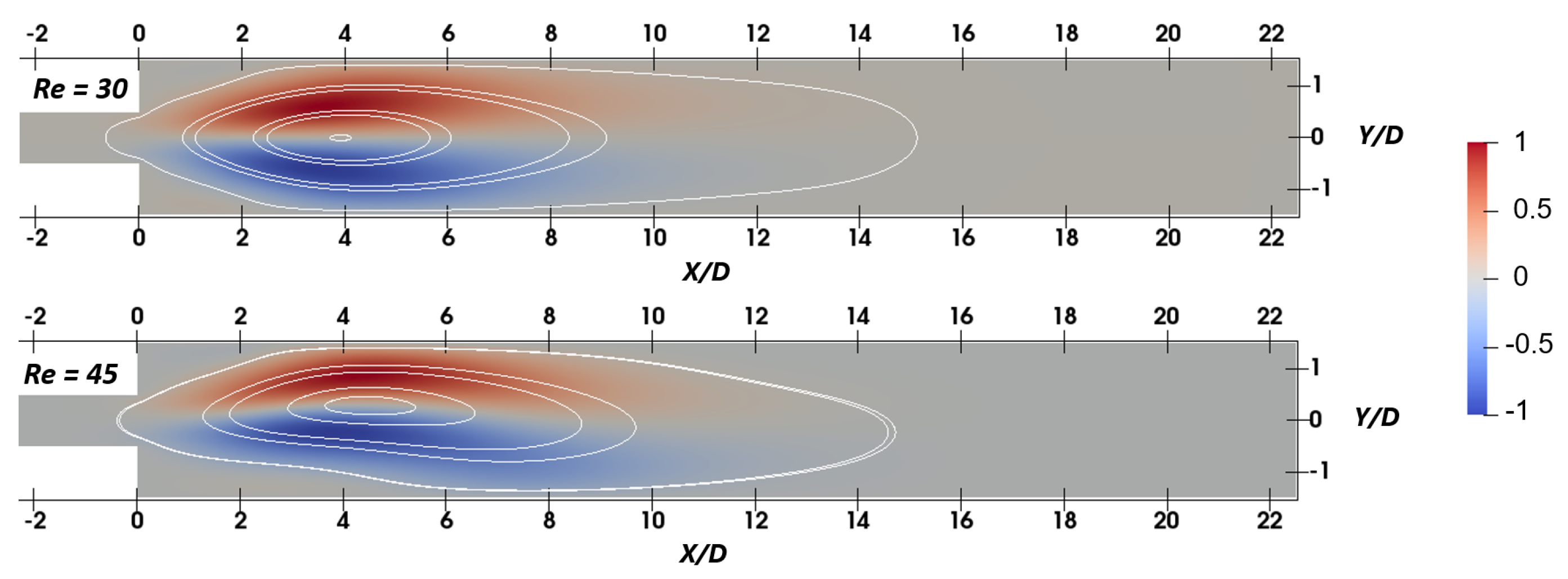
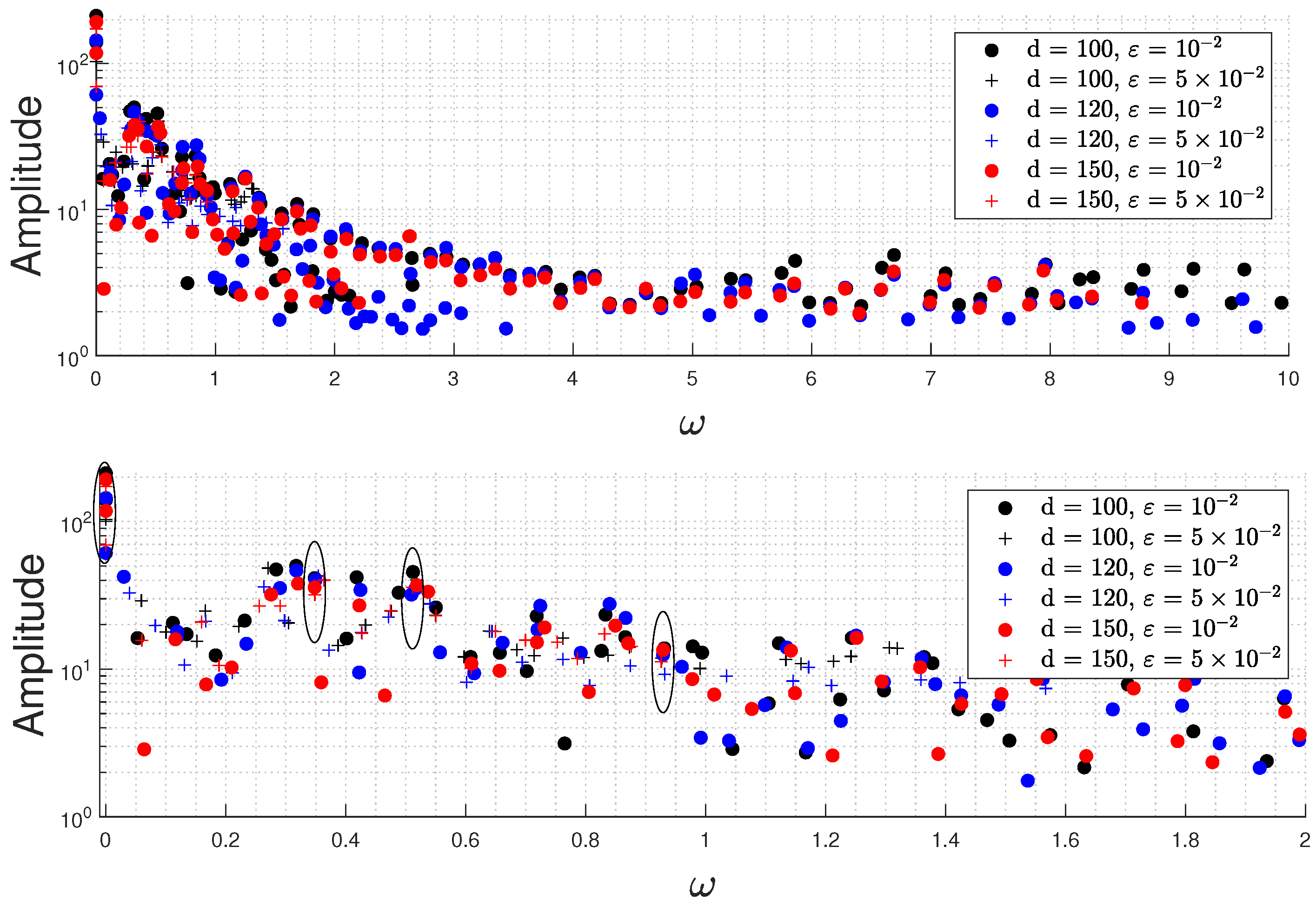
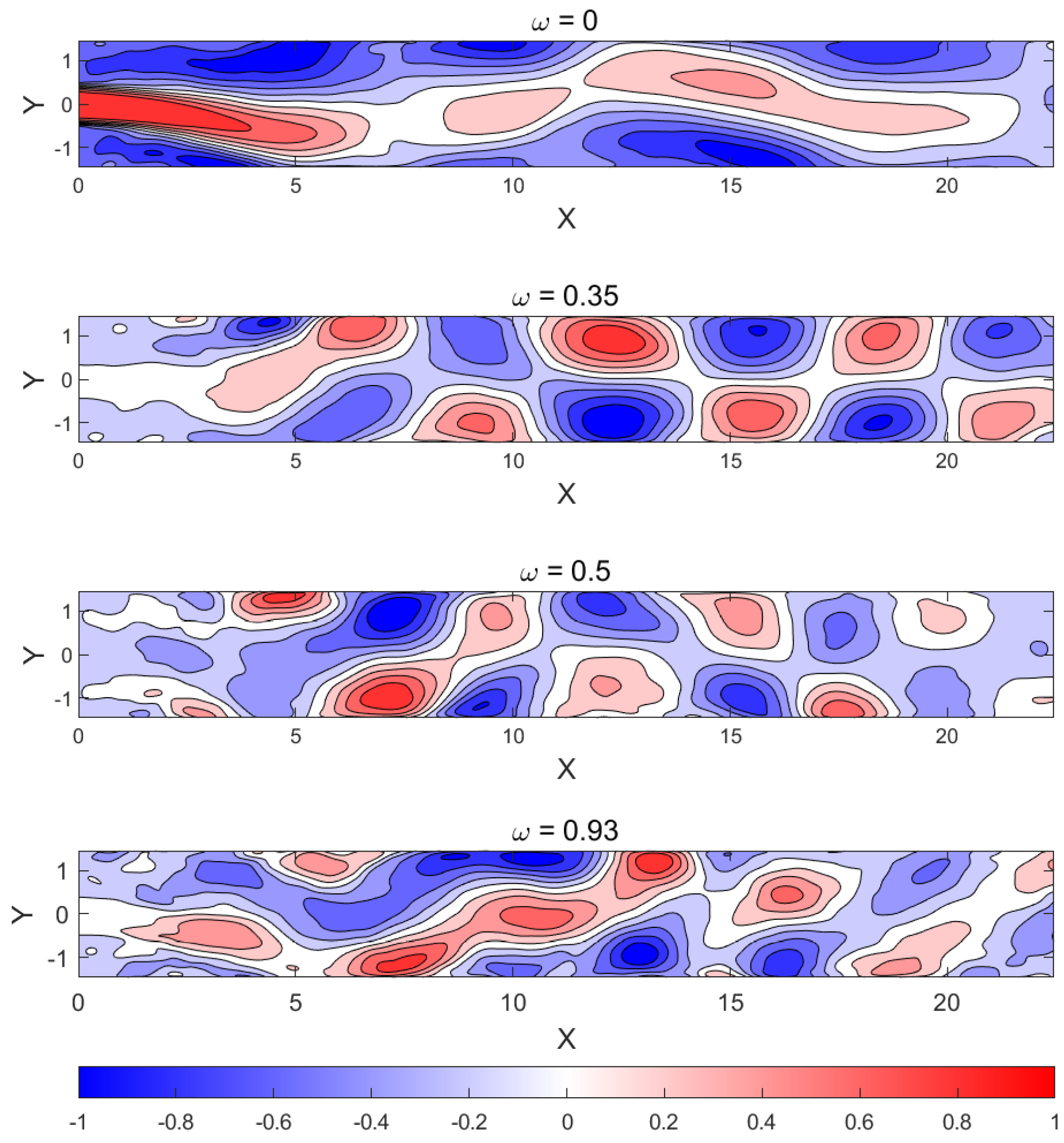
4.3. Flow Structures in the Unsteady Flow
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Malinauskas, R.A.; Hariharan, P.; Day, S.W.; Herbertson, L.H.; Buesen, M.; Steinseifer, U.; Aycock, K.I.; Good, B.C.; Deutsch, S.; Manning, K.B.; et al. FDA benchmark medical device flow models for CFD validation. ASAIO J. 2017, 63, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, A.; Tanabe, M.; Onishi, K.; Kitamura, T.; Okinaka, T.; Ito, M.; Nakano, T. Intravascular Hemolysis in Aortic Stenosis. Intern. Med. 2004, 43, 935–938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ha, H.; Lantz, J.; Ziegler, M.; Casas, B.; Karlsson, M.; Dyverfeldt, P.; Ebbers, T. Assessment of turbulent viscous stress using ICOSA 4D Flow MRI for prediction of hemodynamic blood damage. Sci. Rep. 2016, 6, 39773. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- FDA’s Critical Path Initiative. Available online: https://www.fda.gov/science-research/science-and-research-special-topics/critical-path-initiative (accessed on 30 November 2020).
- Bergersen, A.W.; Mortensen, M.; Valen-Sendstad, K. The FDA nozzle benchmark: In theory there is no difference between theory and practice, but in practice there is. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3150. [Google Scholar] [CrossRef] [Green Version]
- Hariharan, P.; Giarra, M.; Reddy, V.; Day, S.W.; Manning, K.B.; Deutsch, D.; Stewart, S.F.C.; Myers, M.R.; Berman, M.R.; Burgreen, G.W.; et al. Multilaboratory Particle Image Velocimetry analysis of the FDA benchmark nozzle model to support validation of Computational Fluid Dynamics simulations. J. Biomech. Eng. 2011, 133, 041002. [Google Scholar] [CrossRef] [Green Version]
- Bhushan, S.; Walters, D.K.; Burgreen, G.W. Laminar, turbulent, and transitional simulations in benchmark cases with cardiovascular device features. Cardiovasc. Eng. Technol. 2013, 4, 408–426. [Google Scholar] [CrossRef]
- Chabannes, V.; Prud’Homme, C.; Szopos, M.; Tarabay, R. High order finite element simulations for fluid dynamics validated by experimental data from the FDA benchmark nozzle model. arXiv 2017, arXiv:1701.02179. [Google Scholar]
- Janiga, G. Large eddy simulation of the FDA benchmark nozzle for a Reynolds number of 6500. Comput. Biol. Med. 2014, 47, 113–119. [Google Scholar] [CrossRef] [PubMed]
- Stewart, S.F.C.; Hariharan, P.; Paterson, E.G.; Burgreen, G.W.; Reddy, V.; Day, S.W.; Malinauskas, R.A. Results of FDA’s First Interlaboratory Computational Study of a Nozzle with a Sudden Contraction and Conical Diffuser. Cardiovasc. Eng. Technol. 2013, 4, 374–391. [Google Scholar] [CrossRef]
- Stewart, S.F.C.; Paterson, E.G.; Burgreen, G.W.; Hariharan, P.; Giarra, M.; Reddy, V.; Day, S.W.; Manning, K.B.; Deutsch, S.; Berman, M.R.; et al. Assessment of CFD Performance in Simulations of an Idealized Medical Device: Results of FDA’s First Computational Interlaboratory Study. Cardiovasc. Eng. Technol. 2012, 3, 139–160. [Google Scholar] [CrossRef]
- Abad, N.; Vinuesa, R.; Schlatter, P.; Andersson, M.; Karlsson, M. Simulation strategies for the Food and Drug Administration nozzle using Nek5000. AIP Adv. 2020, 10, 025033. [Google Scholar] [CrossRef]
- Delorme, Y.T.; Anupindi, K.; Frankel, S.H. Large eddy simulation of FDAs idealized medical device. Cardiovasc. Eng. Technol. 2013, 4, 392–407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fehn, N.; Wall, W.A.; Kronbichler, M. Modern discontinuous Galerkin methods for the simulation of transitional and turbulent flows in biomedical engineering: A comprehensive LES study of the FDA benchmark nozzle model. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zmijanovic, V.; Mendez, S.; Moureau, V.; Nicoud, F. About the numerical robustness of biomedical benchmark cases: Interlaboratory FDA’s idealized medical device. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e02789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jain, K. Efficacy of the FDA nozzle benchmark and the lattice Boltzmann method for the analysis of biomedical flows in transitional regime. Med. Biol. Eng. Comput. 2020, 58, 1817–1830. [Google Scholar] [CrossRef]
- Manchester, E.L.; Xu, X.Y. The effect of turbulence on transitional flow in the FDA’s benchmark nozzle model using large-eddy simulation. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3389. [Google Scholar] [CrossRef] [PubMed]
- Le Clainche, S. Prediction of the optimal vortex in synthetic jets. Energies 2019, 12, 1635. [Google Scholar] [CrossRef] [Green Version]
- Le Clainche, S.; Vega, J.M. Higher Order Dynamic Mode Decomposition. SIAM J. Appl. Dyn. Syst. 2017, 16, 882–925. [Google Scholar] [CrossRef] [Green Version]
- Jotkar, M.; Govindarajan, R. Two-dimensional modal and non-modal instabilities in straight-diverging-straight channel flow. Phys. Fluids 2019, 31, 014102. [Google Scholar] [CrossRef]
- Barkley, D.; Blackburn, H.M.; Sherwin, S.J. Direct optimal growth analysis for timesteppers. Int. J. Numer. Methods Fluids 2008, 57, 1435–1458. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ferrer, E.; Martínez-Cava, A.; Zheng, Y.; Valero, E. Enhanced stability of flows through contraction channels: Combining shape optimisation and linear stability analysis. Phys. Fluids 2019, 31, 074109. [Google Scholar] [CrossRef] [Green Version]
- Fischer, P.F.; Lottes, J.W.; Kerkemeier, S.G. nek5000 Web Page. Available online: http://nek5000.mcs.anl.gov (accessed on 30 November 2020).
- Nourani, A.; Vinuesa, R.; Brandt, L.; Schlatter, P. Aspect ratio effect on particle transport in turbulent duct flows. Phys. Fluids 2017, 28, 115103. [Google Scholar] [CrossRef] [Green Version]
- Vinuesa, R.; Negi, P.S.; Atzori, M.; Hanifi, A.; Henningson, D.S.; Schlatter, P. Turbulent boundary layers around wing sections up to Rec= 1,000,000. Int. J. Heat Fluid Flow 2018, 72, 86–99. [Google Scholar] [CrossRef] [Green Version]
- Alleborn, N.; Nandakumar, K.; Raszillier, H.; Durst, F. Further contributions on the two-dimensional flow in a sudden-expansion flow. J. Fluid Mech. 1997, 330, 169–188. [Google Scholar] [CrossRef]
- Battaglia, F.; Tavener, S.J.; Kulkarni, A.K.; Merkle, C.L. Bifurcation of low Reynolds number flows in symmetric channels. AIAA J. 1997, 35, 99–105. [Google Scholar] [CrossRef]
- Fani, A.; Camarri, S.; Salvetti, M. Stability analysis and control of the flow in a symmetric channel with a sudden expansion. Physics Fluids 2012, 24, 084102. [Google Scholar] [CrossRef]
- Gómez, F.; Le Clainche, S.; Paredes, P.; Hermanns, M.; Theofilis, V. Four decades of studying global linear instability: Problems and challenges. AIAA J. 2012, 50, 2731–2743. [Google Scholar] [CrossRef] [Green Version]
- Theofilis, V. Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 2003, 39, 249–315. [Google Scholar] [CrossRef]
- Gómez de Segura, G.; García-Mayoral, R. Turbulent drag reduction by anisotropic permeable substrates analysis and direct numerical simulations. J. Fluid Mech. 2019, 875, 124–172. [Google Scholar] [CrossRef] [Green Version]
- Barkley, D.; Henderson, R.D. Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluids Mech. 1996, 322, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Peplinski, A.; Schlatter, P.; Fischer, P.F.; Henningson, D.S. Stability Tools for the Spectral-Element Code Nek5000: Application to Jet-in-Crossflow. In Spectral and High Order Methods for Partial Differential Equations; Azaïez, M., El Fekih, H., Hesthaven, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Schmid, P. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Le Clainche, S.; Moreno, R.; Taylor, P.; Vega, J.M. New Robust Method to Study Flight Flutter Testing. J. Aircr. 2018, 56, 1–8. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M.; Soria, J. Higher Order Dynamic Mode Decomposition for noisy experimental data: Flow structures on a Zero-Net-Mass-Flux jet. Exp. Therm. Fluid Sci. 2017, 88, 336–353. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M. Higher Order Dynamic Mode Decomposition to identify and extrapolate flow patterns. Phys. Fluids 2017, 29, 084102. [Google Scholar] [CrossRef]
- Le Clainche, S.; Izbassarov, D.; Rosti, M.; Brandt, L.; Tammisola, O. Coherent structures in the turbulent channel flow of an elastoviscoplastic fluid. J. Fluid Mech. 2020, 888. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M. Analyzing nonlinear dynamics via data-driven dynamic mode decomposition-like methods. Complexity 2018, 2018, 6920783. [Google Scholar] [CrossRef]
- Le Clainche, S.; Ferrer, E. A Reduced Order Model to Predict Transient Flows around Straight Bladed Vertical Axis Wind Turbines. Energies 2018, 11, 566. [Google Scholar] [CrossRef] [Green Version]
- Le Clainche, S.; Rosti, M.; Brandt, L. Flow structures and shear-stress predictions in the turbulent channel flow over an anisotropic porous wall. J. Phys. Conf. Ser. 2020, 1522, 012016. [Google Scholar] [CrossRef]
- Vega, J.M.; Le Clainche, S. Higher Order Dynamic Mode Decomposition and Its Applications; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corrochano, A.; Xavier, D.; Schlatter, P.; Vinuesa, R.; Le Clainche, S. Flow Structures on a Planar Food and Drug Administration (FDA) Nozzle at Low and Intermediate Reynolds Number. Fluids 2021, 6, 4. https://doi.org/10.3390/fluids6010004
Corrochano A, Xavier D, Schlatter P, Vinuesa R, Le Clainche S. Flow Structures on a Planar Food and Drug Administration (FDA) Nozzle at Low and Intermediate Reynolds Number. Fluids. 2021; 6(1):4. https://doi.org/10.3390/fluids6010004
Chicago/Turabian StyleCorrochano, Adrián, Donnatella Xavier, Philipp Schlatter, Ricardo Vinuesa, and Soledad Le Clainche. 2021. "Flow Structures on a Planar Food and Drug Administration (FDA) Nozzle at Low and Intermediate Reynolds Number" Fluids 6, no. 1: 4. https://doi.org/10.3390/fluids6010004
APA StyleCorrochano, A., Xavier, D., Schlatter, P., Vinuesa, R., & Le Clainche, S. (2021). Flow Structures on a Planar Food and Drug Administration (FDA) Nozzle at Low and Intermediate Reynolds Number. Fluids, 6(1), 4. https://doi.org/10.3390/fluids6010004





