Comparison of Techniques for the Estimation of Flow Parameters of Fan Inflow Turbulence from Noisy Hot-Wire Data ^†

Abstract

Turbulence parameters, in particular integral length scale (ILS) and turbulence intensity (Tu), are key input parameters for various applications in aerodynamics and aeroacoustics. The estimation of these parameters is typically performed using data obtained via hot-wire measurements. On the one hand, hot-wire measurements are affected by external disturbances resulting in increased measurement noise. On the other hand, commonly applied turbulence parameter estimators lack in robustness. If not addressed correctly, both issues may impede the accuracy of the turbulence parameter estimation. In this article, a procedure consisting of several signal processing steps is presented to filter non-turbulence related disturbances from the unsteady velocity data. The signal processing techniques comprise time- and frequency-domain approaches. For the turbulence parameter estimation, two different models of the turbulence spectra—the von Kármán model and the Bullen model—are fitted to match the spectrum of the measured data. The results of several parameter estimation techniques are compared. Computational Fluid Dynamics (CFD) data are used to validate the estimation techniques and also to assess the influence of the variation in window size on the estimated parameters. Additionally, hot-wire data from a high-speed fan rig are analyzed. ILS and Tu are assessed at several radial positions for two fan speeds. It is found that most techniques yield similar values for ILS and Tu. The comparison of the fitted spectra with the spectra of the measured data shows a good agreement in most cases provided that a sufficiently fine frequency resolution is applied. The ratio of ILS and Tu of the velocity components in longitudinal and transverse direction allows the assessment of flow-isotropy. Results indicate that the turbulence is anisotropic for the investigated flow fields.

1. Introduction

The pursuit for green solutions for the aircraft industry includes not only low greenhouse gas emissions, but also quieter airplanes. Regulations and restrictions of aircraft noise emissions have become increasingly stringent over the past decades [1,2]. The engines of a modern aircraft are critical noise sources during approach and take-off [3,4].

In a modern Ultra-High By-pass Ratio (UHBR) turbofan engine, the fan stator interaction noise is the main contributor to the total engine noise emissions at both take-off and approach conditions. Therefore, there is great interest from industry and the science to better understand fan noise mechanisms in order to develop solutions for quieter engines. Broadband interaction noise sources, which arise due to the interaction of turbulence with the leading edges of both rotor and stator blades, are major contributors to the overall noise of a fan [5,6]. While the wake turbulence is generally thought to be the most critical turbulence components, ingested, background, and boundary layer turbulence can also be relevant for certain configurations.

In order to fully understand fan broadband noise generation, the full characterization of relevant turbulence components is necessary. Turbulence parameters like turbulence length scale and turbulence intensity describe the statistically averaged behavior of the turbulent flow structures. Both these parameters are known to have heavy influence on airfoil aerodynamics. Some examples are boundary layer thickness and laminar to turbulent transition [7], turbine aerodynamics [8], heat transfer [9,10], and especially noise excitation of an airfoil or a fan stage [11,12,13,14].

The objective of this study is to identify the most suitable technique for the estimation of turbulence parameters, namely, the turbulence integral length scale and the turbulence intensity (which can be understood as a normalized turbulent kinetic energy (TKE)). Commonly, methods for fan broadband noise prediction are based on analytic models [14,15,16,17], synthetic turbulence methods [18,19], and scale-resolving techniques [6,20,21]. They depend on turbulence parameters, which can include boundary layer thickness, turbulence integral length scale, and flow turbulence kinetic energy of the inlet flow or/and of the flow at the fan interstage section. The output of those techniques is sensitive to these input parameters. Therefore, a high accuracy of the estimated turbulence parameters is a key requirement for reliable noise prediction. In this work, turbulence intensity and turbulence integral length scale are determined from hot-wire anemometry data.

Hot-wire anemometry is a time-demanding and -sensitive measurement technique. Hot-wire probes consists of thin wires, which typically are about $2.8$ mm long and 9–12.5 $\mathsf{\mu }$m in diameter [22], and are placed directly in the flow, where they affect the flow field intrusively. The flow field is spatially sampled by traversing the probe in radial direction. If the whole duct cross section evaluation is desired, the probe is traversed additionally in circumferential direction.

One of many complications of hot-wire anemometry is its sensitivity to external disturbances. Two sources of disturbance are of particular importance: electrical disturbances and excitation of vibrations at the base of the probe caused by vibrations of the fan rig. The former are typically due to the electrical power supply and other electrical peripheral equipment and are usually easier to filter, as they often consist of periodic signals with few harmonic frequencies. The impact of the second disturbance source is more complicated, because the vibrations of the test rig act at the base of the probe and lead to vibrations of the entire setup consisting of traverse, probe and wire. The excitation spectrum consists of tonal and broadband components, which superpose the turbulent velocity spectrum. Furthermore, resonances of the wire and/or the probe system can be excited by the broadband excitation of the fan rig vibrations.

In this article, a procedure consisting of several signal processing steps is presented to filter non-turbulence related disturbances from the unsteady velocity data. Besides that, the results of different techniques for turbulence parameter estimation (i.e., turbulence integral length scale and turbulence intensity) are compared, most of which utilize models of the turbulence spectrum. This paper is structured as follows.

−

Section 2 succinctly describes fundamentals of turbulence, the length-scale problematic and the integral length scale, as well as two theoretical models of the turbulence spectrum.

−

Section 3 introduces the signal processing procedure to filter disturbances from noisy measurement data.

−

Section 4 assesses the performance of each applied estimator using synthetic data superposed with representative disturbances. Further analysis is performed with CFD data where the flow field in a turbine blade passage was simulated and turbulence parameters are estimated downstream of the blade. The impact of window size of the power spectrum estimator is also assessed by using CFD and experimental data.

−

Section 5 describes the experimental setup.

−

Section 6 shows experimental data and results are discussed.

−

Section 7 ends the paper with conclusions and remarks.

2. A Succinct Overview of Essential Turbulence Properties

Turbulence is a complex, interdisciplinary, and vast field of investigation. As stated by Tennekes [23] “…turbulence theory suffers from the absence of sufficiently powerful mathematical methods. This lack of tools makes all theoretical approaches to problems in turbulence trial-and-error affairs”. In addition to that, because of the strong non-deterministic (or stochastic) behavior of turbulence, the use of statistical tools is one of few options that allows the extraction of useful information from the unsteady flow velocity data. In this study, the term “unsteady” data makes reference to a time-series signal with sampling frequency of at least several kilo-Hertz.

According to Hinze [24] and Tennekes [23]: “…turbulence is a multiple length scale problem. Scales are bounded from above (large scales) by the dimensions of the flow-field and bounded from below (small scales) by the diffusive action of molecular viscosity. That is the reason spectral analyses of turbulent motions are so useful.” That is, in a turbulent flow-field a broad range of turbulent structures are present, ranging from big to small scales. When however, the turbulence is found in the so called “equilibrium”, the big structures break down into smaller ones. The energy of big scales are transferred to smaller ones, and so forth. This process keeps going up to a limit, when the scales are tiny enough to disperse their energy into thermal dissipation due to viscosity.

There is, therefore, the need to set a metric to quantify (in some sense) the size in average of the turbulence structures. A metric frequently used is the turbulence integral length scale (ILS). In few words, this metric tries to estimate the average size of the most energetic scales (eddies) in a given turbulent flow. Its formulation is reviewed in the following section.

2.1. Turbulence Integral Length Scale—ILS

The turbulence integral length scale is computed by the integral of the spatial velocity coherence function:

$$\mathsf{\Lambda }={\int }_{-\infty }^{\infty }\rho \left(r\right)dr,$$

(1)

where $\rho \left(r\right)$ is the cross-correlation coefficient between two points distanced by r in a flow field. In order to determine the spatial correlation defined in Equation (1) experimentally, simultaneous measurements from two probes are required and their distance apart has to be varied. Due to physical constraints, this kind of measurement is oft not adopted, or even not possible to be performed. Alternatively, the spatial correlation is estimated from the temporal autocorrelation by assuming the Taylor’s hypothesis [24]. It is also referred as the “frozen-turbulence” assumption. The integral time scale (ITS, ${\tau }_l$) can be therefore computed by the temporal autocorrelation coefficient following:

$${\mathsf{\tau }}_1={\int }_{-\infty }^{\infty }{r}_{11}\left(\mathsf{\tau }\right)d\mathsf{\tau },$$

(2)

where the autocorrelation coefficient $r_{11}\left(\mathsf{\tau }\right)$ is computed from the unsteady velocity signal $u\left(t\right)$:

$$r_{11}\left(\mathsf{\tau }\right)=\frac{\overline{u\left(t\right)u(t-\mathsf{\tau })}}{\overline{u^2}}=\frac{R_{11}\left(\mathsf{\tau }\right)}{R_{11}\left(0\right)}.$$

(3)

The overbar refers to the time-averaged value. Last, the ILS can be estimated under Taylor’s hypothesis by:

$${\mathsf{\Lambda }}_1={\mathsf{\tau }}_1{U}_0,$$

(4)

where $U_0$ refers to the average flow speed.

From another perspective, the autocorrelation function can also be estimated by the inverse Fourier transform of the PSD $S_{11}\left(f\right)$ of the unsteady velocity $u\left(t\right)$:

$$r_{11}\left(\mathsf{\tau }\right)=\frac{1}{\overline{u^2}}{\int }_{-\infty }^{\infty }{S}_{11}\left(f\right)e^{j2\pi ft}df.$$

(5)

However, it is known from the Parseval Theorem [25] that:

$$R_{11}\left(0\right)={\int }_{-\infty }^{\infty }{S}_{11}\left(f\right)df,$$

(6)

and

$$S_{11}\left(0\right)={\int }_{-\infty }^{\infty }{R}_{11}\left(\mathsf{\tau }\right)d\mathsf{\tau },$$

(7)

and then, the integral time scale can be calculated by:

$${\mathsf{\tau }}_1=\frac{S_{11}\left(0\right)}{\overline{u^2}}.$$

(8)

where

$$\overline{u^2}={\int }_{-\infty }^{\infty }{S}_{11}\left(f\right)df.$$

(9)

By assuming Taylor’s hypothesis, we finally obtain:

$${\mathsf{\Lambda }}_1={\mathsf{\tau }}_1{U}_0=\frac{S_{11}\left(0\right)U_0}{\overline{u^2}}.$$

(10)

2.2. Integral Length Scale under the Hypothesis of Homogeneous and Isotropic Turbulence (HIT)

Hinze [24] states: “Usually the condition of isotropy is defined, rather briefly, by the invariance under rotation of the coordinate system and under reflection with respect to the coordinate planes of the statistically averaged properties of the turbulence.” A more precise definition is rather given by Batchelor [26]: “In isotropic turbulence the joint-probability distribution of the velocities at any arbitrarily chosen n points in space is invariant under arbitrary rotations of the configuration as formed by the n points and by the various direction vectors, and under reflection of the configuration with respect to any plane.” A deeper analysis of HIT is, nonetheless, outside the extension of this present study. Rather, the eventual flow isotropy is assessed by the ratio of the integral length scale of both longitudinal and transverse velocity components, as well as the ratio of the turbulence intensity of these components. With the aim to reduce complexity, the spectrum models used in this study are based on the assumption of HIT.

In order to assess the integral length scale (ILS) under the HIT turbulence assumption, the velocity PSD can be described according to Roach [27] by:

$$\frac{4\overline{u^2}{\mathsf{\Lambda }}_1}{S_{11}\left(f\right)U_0}=1+{\left(\frac{2\pi f{\mathsf{\Lambda }}_1}{U_0}\right)}^2,$$

(11)

and therefore:

$${\mathsf{\Lambda }}_1={\left. [\frac{S_{11}\left(f\right)U_0}{4\overline{u^2}}\right]}_{f\to 0},$$

(12)

while for the transverse velocity component it is given by:

$${\mathsf{\Lambda }}_2={\left. [\frac{S_{22}\left(f\right)U_0}{2\overline{v^2}}\right]}_{f\to 0}.$$

(13)

Note that there is a factor 2 between these two scales. This is in agreement with the theoretical relation, given by Hinze [24] (Equations (3)–(74) and (3)–(75)), between the longitudinal and transverse integral scales for HIT, i.e., ${\mathsf{\Lambda }}_2={\mathsf{\Lambda }}_1/2$.

Equations (12) and (13) can be easily checked by setting $f=0$ (or correspondingly ${\widehat{k}}_n=0$) onto Equations (17) and (20), as an example. This will be later introduced in Section 2.4. At this point an attuned reader might ask her- or himself why Equations (10) and (12) are similar, except by the factor 4 dividing Equation (12). In fact a PSD at $f=0$ has a different meaning as for the nearby frequency bins $f\to 0$. The first represents, physically speaking, the Root Mean Square (RMS) of the signal. The latter, however, is essentially the power density of the low-frequency band of the PSD. This fact is (from the authors’ understanding) not modeled by synthetic turbulence models under HIT assumption, although observed on measured turbulence data.

2.3. Turbulence Intensity—Tu

The turbulence intensity according to [24,27] for the longitudinal velocity component is obtained by:

$$T{u}_x=\frac{u_{rms}}{U_0}=\frac{\sqrt{\overline{u^2}}}{U_0},$$

(14)

where often $\overline{u^2}$ is obtained from Equation (9). The same principle holds for the transverse velocity component:

$$T{u}_y=\frac{v_{rms}}{U_0}=\frac{\sqrt{\overline{v^2}}}{U_0}.$$

(15)

Equation (14) can be applied directly to the time-series velocity signal, or with the help of Equation (9), where if necessary, a frequency band-width of the signal can be selected in order to eliminate frequency bands potentially contaminated with noise or any other non-turbulence related sources.

2.4. Isotropic and Homogeneous Turbulence Spectrum Models

2.4.1. The Two-Parameters von Kármán Spectrum Model

A turbulence model commonly adopted in the literature of turbo-machinery is the von Kármán. The two-dimensional energy spectra of the longitudinal and transverse velocity components are described [24,28] as:

$$E_{11}=\frac{\overline{u^2}{\mathsf{\Lambda }}_1}{\pi }\frac{1}{{(1+{\widehat{k}}_n^2)}^{5/6}},$$

(16)

$$E_{22}=\frac{\overline{u^2}{\mathsf{\Lambda }}_1}{2\pi }\frac{1+\frac{8}{3}{\widehat{k}}_n^2}{{(1+{\widehat{k}}_n^2)}^{11/6}},$$

(17)

where the subscripts 11 and 22 refer for the longitudinal and transverse velocity components, respectively. ${\widehat{k}}_n$ is the normalized wave-number given by:

$${\widehat{k}}_n=\widehat{k}(f,n,{\mathsf{\Lambda }}_1)=\frac{2\pi f}{v_0{k}_e(n,{\mathsf{\Lambda }}_1)},$$

and

$$k_e(n,{\mathsf{\Lambda }}_1)=\frac{\sqrt{\pi }\mathsf{\Gamma }(n+1/2)}{{\mathsf{\Lambda }}_1\mathsf{\Gamma }\left(n\right)}.$$

$\mathsf{\Gamma }\left(n\right)$ stands for the Gamma function of order n. For the von Kármán spectrum n has be set to 1/3. Turbulence velocity PSD is then defined by:

$$S_{ii}\left(f\right)=\frac{4\pi }{U_0}{E}_{ii},$$

(18)

where the subscript ‘ii’ refers to the respective velocity component.

2.4.2. The Three-Parameter Bullen Spectrum Model

The Bullen spectrum model [29,30] can be seen as a generalization of the von Kármán spectrum, where the spectral slope towards high frequencies can be set by the parameter n. When $n=1/3$ the Bullen spectrum becomes identically the von Kármán spectrum. The two-dimensional energy spectra of the longitudinal and transverse velocity components are given by:

$$E_{11}=\frac{\overline{u^2}{\mathsf{\Lambda }}_1}{\pi }\frac{1}{{(1+{\widehat{k}}_n^2)}^{n+1/2}},$$

(19)

$$E_{22}=\frac{\overline{u^2}{\mathsf{\Lambda }}_1}{2\pi }\frac{1+2(n+1){\widehat{k}}_n^2}{{(1+{\widehat{k}}_n^2)}^{n+3/2}}.$$

(20)

2.5. Spectrum Test Case

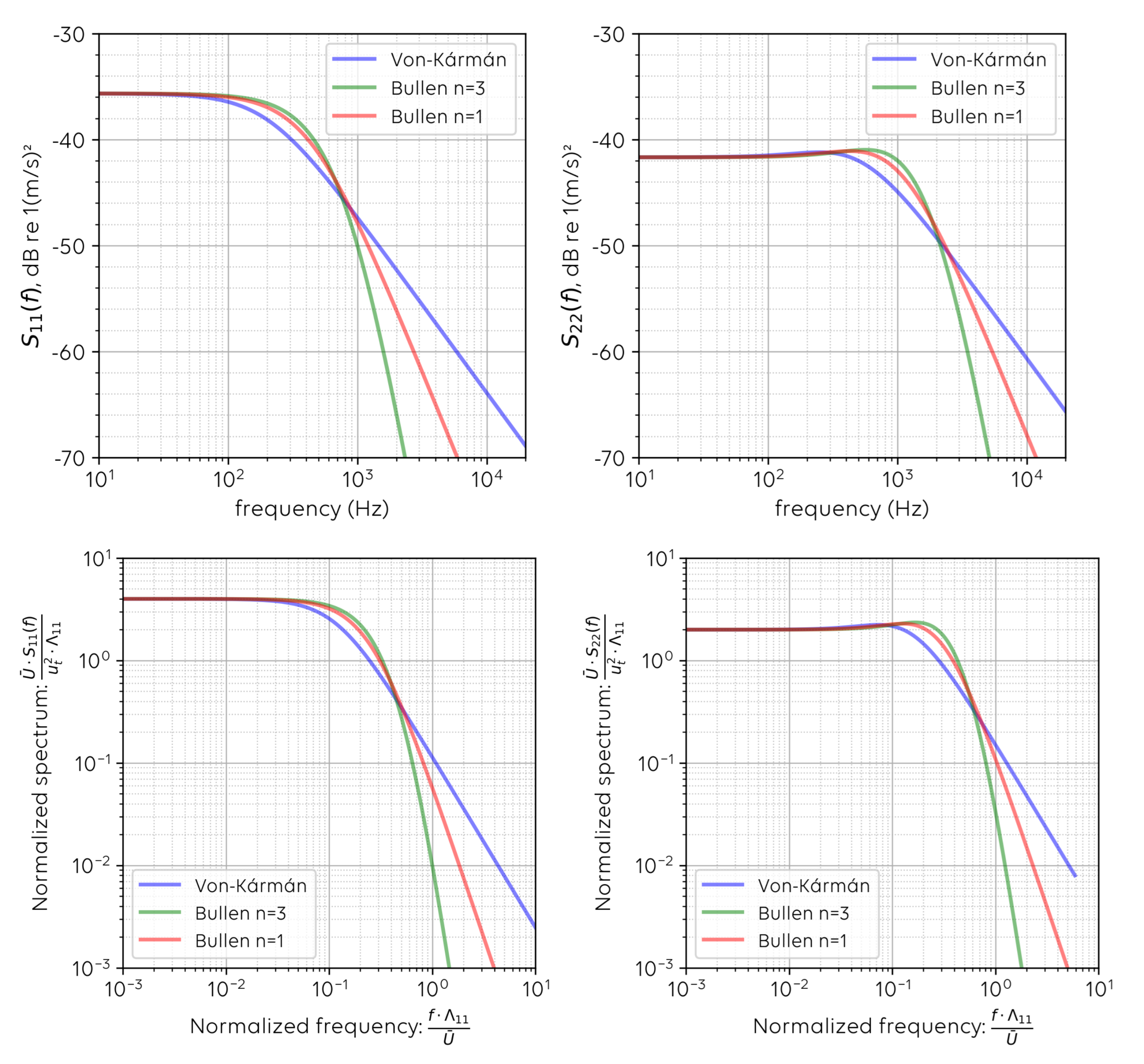
Figure 1 displays a test case for both synthetic spectrum models, along with both transverse and longitudinal velocity components. Non-normalized and normalized plots are shown. The Bullen spectrum is displayed with two examples of slope coefficients: $n=1$ and $n=3$. In these two examples, the Bullen spectra experience a steeper slope at high frequencies when contrasted to the von Kármán spectrum.

3. Signal Processing Techniques and Turbulence Parameter Estimation

The proposed signal processing chain of this work covers all the steps from the raw velocity signals from the hot-wires, up to the final estimated turbulence parameters. The following Section 3.1 and Section 3.2 describe the preprocessing of the signal and removal of the dominant parts of disturbances. Later on, three somewhat different techniques are used to estimate turbulence parameters: A maximum likelihood estimation technique is succinctly described in Section 3.5. Two PSD fit techniques are introduced in Section 3.3 and Section 3.4.

3.1. Data Resampling and Cyclostationary Analysis

The velocity signals measured by the hot-wire anemometer are first linearly resampled using adaptive resampling technique. It uses the fan shaft trigger as reference. A constant 2048 samples per fan revolution is achieved through data resampling. This produces a new sampling frequency that lies between 200 and 210 kHz, depending on the fan speed. Data is then decimated by a factor of four, which produces a final sampling frequency of around 50 kHz. A cyclostationary analysis [31,32] is then performed, which separates the rotor-coherent and -incoherent signal parts. On one hand, tones observed in the PSD, often originated from blade passing frequency (BPF), or vibrations of the test rig are expected to be rotor-coherent. On the other hand, the turbulence (broadband part of the signal) is expected to be incoherent with the rotating fan. The incoherent part of the signal (broadband—CyS2) is thus used as input for the following steps of the proposed signal processing chain.

3.2. Low Frequency Disturbance Removal

This technique was first implemented and presented by Mark [33]. In that work, a hot-wire probe was fixed onto an airplane wing and flight turbulence data were recorded. The investigation of the autocorrelation function of the hot-wire data revealed the presence of a low frequency component in the signals. Further investigation concluded that this disturbance has a Non-Gaussian distribution. This art of distortion was interpreted as “wind gusts”, i.e., slow oscillations in the velocity signals, and should not be originated from turbulence. In our study, after analyzing a reasonable large hot-wire data set recorded in the inlet of turbo-machines, we observed a similar phenomenon, as observed by Mark [33].

Mark [33] described this event as the superposition of two random processes: A low frequency process (or slow oscillations, associated to “wind gusts”), and turbulence, which is characterized by a higher frequency process (or fast oscillations). Mathematically, it can be described by:

$$\begin{array}{cc}\hfill w\left(t\right)& =w_s\left(t\right)+w_f\left(t\right)\hfill \\ \hfill & =w_s\left(t\right)+{\sigma }_f\left(t\right)z\left(t\right),\hfill \end{array}$$

(21)

where ${\sigma }_f\left(t\right)z\left(t\right)\ge 0$, $E\left\{z\left(t\right)\right\}=\overline{z\left(t\right)}=0$ and $E\left\{z^2\left(t\right)\right\}=\overline{z^2\left(t\right)}=1$. In Equation (21), $w\left(t\right)$ refers to the measured signal, $w_s\left(t\right)$ to the “slow” (low frequency) component, and $w_f\left(t\right)$ the “fast” one. Mark [33] assumes that $z\left(t\right)$ is a Gaussian stationary process and that ${\sigma }_f\left(t\right)$ is a stationary random process. Furthermore, ${\sigma }_f\left(t\right)z\left(t\right)\ge 0$, ${\sigma }_f\left(t\right)$ is not necessarily a Gaussian process. Crucial for this analysis is the assumption that $w_s\left(t\right)$ and $w_f\left(t\right)$ are statistically independent. By assuming that, the autocorrelation and the PSD can be assessed by:

$$R_w\left(\mathsf{\tau }\right)=R_{w_s}\left(\mathsf{\tau }\right)+R_{w_f}\left(\mathsf{\tau }\right),$$

(22)

and

$$S_w\left(f\right)=S_{w_s}\left(f\right)+S_{w_f}\left(f\right).$$

(23)

The technique proposed by Mark [33] was incorporated into the proposed signal processing chain according to the following steps:

−

Data resampling using the one pulse-per-rev shaft-trigger signal;

−

The cyclostationary analysis and the CyS2 component (broadband rotor-incoherent part of the signal) selected as data input data;

−

The PSD is estimated via Welch’s method [25,34] and frequency limited to $f=5$ kHz. The reason for that is the high contamination of the hot-wire signals at this frequency band, as will be later shown.

−

The autocorrelation function is therefore estimated by the inverse Fourier transform of the PSD obtained in the previous step. The outcome is thus used as input for the low-frequency removal technique.

By following the guidelines suggested by Mark [33], the “slow-component” of the autocorrelation function $R_{w_s}\left(\mathsf{\tau }\right)$ can be interpolated by a polynomial of order 2 or 3. Figure 2 left and middle plots show an example of the interpolation using experimental data. Note that this result agrees with the observations from Mark [33]. The orange curve in Figure 2 (CyS2 Component) is used as input source data and stands for the autocorrelation function $R_w\left(\mathsf{\tau }\right)$. $R_{w_s}\left(\mathsf{\tau }\right)$ (blue curve) represents the outcome of an polynomial interpolation of order 3 to $R_w\left(\mathsf{\tau }\right)$. The black curve refers to $R_{w_f}\left(\mathsf{\tau }\right)$. The difference in falling time of the black curve “fast-components” and the blue curve “slow-component” is evidently seen in Figure 2, middle plot. Finally, the right-hand plot of Figure 2 shows the PSD of each component: raw signal, CyS2 component ($S_w\left(f\right)$), and the turbulence resultant component $S_{w_f}\left(f\right)$.

3.3. L-1 Norm Spectrum Fit

The principle of the fit technique is to adjust a synthetic turbulence PSD in order to match the estimated PSD from experimental data. An appropriate turbulence spectrum model has to be selected based on the characteristics of the flow field. In this study, as shown in Section 2.4 the Bullen and the von Kármán turbulence spectra were chosen. These models are constrained by the HIT assumption. The validity of the HIT assumption can be drawn by assessing eventual differences in the spectra fit of both velocity components. If different values for turbulence intensity and/or integral length scale are obtained for the two velocity components, the flow is potentially anisotropic at that measured position.

The optimization problem is formulated by:

$$\begin{array}{cc}\hfill \underset{\overline{u^2},{\mathsf{\Lambda }}_1,n\in \mathbb{R}}{argmin}\left|\right|& S\left(f\right)-S_{11}(f,\overline{u^2},{\mathsf{\Lambda }}_1,n,U_0){\left|\right|}_1,\hfill \end{array}$$

(24)

where $S\left(f\right)$ is the estimated PSD from experimental data. In this case it is used the output PSD “$S_{wf}$ Spectrum” resulted from from the previous technique by removing low frequency disturbances. Equation (24) describes the longitudinal velocity component. The transverse component is obtained analogously. If the Bullen model is selected, the optimal n is automatically adjusted. Otherwise, if the von Kármán model is chosen, then n is fixed at $1/3$.

The selection of the norm as for the objective criterion is another critical step of this minimization problem. Aiming the minimization of the residual power, the L2-norm is often used for a typical least-squared-fit (LSF) problem. In this study though, the L1-norm is rather used in order to weight more the broadband part of the signal, and reduce the importance of eventual points distanced from the synthetic spectrum. A classic example would be tonal components. These are known to not be related to turbulence [24,35]. The impact of the selected norm is again shortly discussed in Section 4. The use of the L1-norm provides robustness for the technique against tonal components. These are frequently present in turbo machinery data [22,36,37]. If tones are not removed from the PSD, this could lead to strong discrepancies in the estimated turbulence intensity (or equivalently the TKE).

3.4. L-1 Norm Spectrum Fit with Constraint

The difference between this fit technique to the previous one is that now a constraint added to the minimization problem has to be met. The new formulation is addressed as follows:

$$\begin{array}{cc}\hfill \underset{\overline{u^2},{\mathsf{\Lambda }}_1,n\in \mathbb{R}}{argmin}\left|\right|& S\left(f\right)-S_{11}(f,\overline{u^2},{\mathsf{\Lambda }}_1,n,U_0){\left|\right|}_1\hfill \\ \hfill \mathrm{subjected}\mathrm{to}& {\mathsf{\Lambda }}_1={\left. [\frac{S\left(f\right)U_0}{4\overline{u^2}}\right]}_{f\to 0}\hfill \end{array}$$

(25)

i.e., the variables $\overline{u^2}$ and ${\mathsf{\Lambda }}_1$ now meet a physical restriction governed by Equation (12). This constraint reduces by one the degree of freedom of this optimization problem, as the variable ${\mathsf{\Lambda }}_1$ is now a function of the variable $\overline{u^2}$ and other parameters. This constraint can make the method more stable, i.e., helping on finding the solution of the problem, in particular when the input data set is strongly embedded with noise.

3.5. Maximum Likelihood Estimator—von Kármán Turbulence Model

The maximum likelihood estimator (MLH) technique applied to turbulence parameter estimation was described by Mark [30]. The MLH technique is a robust statistical tool [25,34] to estimate parameters of a pre-defined model from data contaminated with noise. For the reader’s convenience, the formulation proposed by Mark [30] applied to the von Kármán turbulence model is briefly shown as follows. The application of the MLH with the Bullen model was also described by Mark [29], yet it is outside the scope of this study.

The two essential equations to be resolved for the MLH problem are given by:

$$\overline{u^2}\mathsf{\Lambda }=\frac{1}{N}\sum _{j=1}^N\frac{S_j}{F_j\left(\mathsf{\Lambda }\right)},$$

(26)

$$\sum _{j=1}^N\left\{\left. [\frac{d}{d\mathsf{\Lambda }}ln{F}_j\left(\mathsf{\Lambda }\right)\right]\left. [\frac{S_j}{F_j\left(\mathsf{\Lambda }\right)}-\frac{1}{N}\sum _{i=1}^N\frac{S_i}{F_i\left(\mathsf{\Lambda }\right)}\right]\right\}=0.$$

(27)

Indices $i,j$ in $S_i$, $S_j$, $F_i$, $F_j$ stand for the $i^{th}$ or $j^{th}$ frequency bin of the frequency vector ($f_k\triangleq \frac{k{f}_s}{N},k=0,1,2,\dots ,N$), where the estimated PSD $S\left(f_k\right)$ is evaluated, $f_s$ stands for the sampling frequency, and N is the window size. For simplicity, the same notation proposed by Mark [30] was used. $G_j$ and $F_j$ are auxiliary functions, which are defined by

$$G_j\left(\mathsf{\Lambda }\right)\triangleq \frac{d}{d\mathsf{\Lambda }}ln{F}_j\left(\mathsf{\Lambda }\right),$$

which solutions for each velocity component are thus as follows:

Longitudinal spectrum $S_{11}\left(f\right)$:

$$F_{\widehat{k}}\left(\mathsf{\Lambda }\right)\equiv F(\widehat{k},\mathsf{\Lambda })=\frac{2}{U_0}\frac{2}{{(1+{\widehat{k}}^2)}^{5/6}},$$

(28)

$$G_{\widehat{k}}\left(\mathsf{\Lambda }\right)\equiv \frac{d}{d\mathsf{\Lambda }}lnF(\widehat{k},\mathsf{\Lambda })=-\frac{2}{U_0}\frac{1}{\mathsf{\Lambda }}\frac{\frac{5}{3}{\widehat{k}}^2}{1+{\widehat{k}}^2}.$$

(29)

Transverse spectrum $S_{22}\left(f\right)$:

$$F_{\widehat{k}}\left(\mathsf{\Lambda }\right)\equiv F(\widehat{k},\mathsf{\Lambda })=\frac{2}{U_0}\frac{1+\frac{8}{3}{\widehat{k}}^2}{{(1+{\widehat{k}}^2)}^{11/6}},$$

(30)

$$G_{\widehat{k}}\left(\mathsf{\Lambda }\right)\equiv \frac{d}{d\mathsf{\Lambda }}lnF(\widehat{k},\mathsf{\Lambda })=\frac{2}{U_0}\frac{1}{\mathsf{\Lambda }}\frac{\frac{5}{3}{\widehat{k}}^2(1-\frac{8}{3}{\widehat{k}}^2)}{(1+{\widehat{k}}^2)(1+\frac{8}{3}{\widehat{k}}^2)}.$$

(31)

Equation (27) has to be solved first, as it is a function only of the PSD $S_i\triangleq S\left(f_i\right)$ of measured data and the von Kármán spectrum model. Equation (27) is essentially a minimization problem that has to be solved numerically. As a result of this step, the turbulence integral length scale $\mathsf{\Lambda }$, which was found by optimizing the equations shown above, is then used for the subsequent solution of Equation (26).

Note that Equation (26) searches for the optimal $\overline{u^2}$ by meeting the power of the modeled turbulence PSD to the power of the estimated PSD from experimental data $S\left(f\right)$. A clear drawback of this approach is that the presence of disturbances (such as those described in Section 4) strongly bias the estimated parameters. As explained in Section 3.3 and Section 3.4, the spectral fitting techniques are more robust and thus more appropriated for distorted signals, foremost against tonal noise. The difference in performance of every technique is further analyzed in the test cases by using synthetic, numerical, and experimental data.

4. Test Cases

This section describes how each turbulence parameter estimation technique performs under relatively clean turbulence spectrum and under different sources of distortion. For this test, the von Kármán spectrum was used as primary clean and reference spectrum. The three different sources of noise added are described as follows:

(1)

White noise with standard-deviation equals to 2 and filtered with a low-pass filter with a cut-off frequency $f_c=250$ Hz was added to the PSD (see Figure 3, left plot).

(2)

Harmonic tones with fundamental frequency at 160 Hz and harmonics up to the 7th order with decreasing amplitude were generated. These tones were combined with noise disturbances from the previous item (1) and added to the spectrum. The aim was to synthesize BPF tones in the spectrum, which are often seen in turbulence measurements in turbomachinery [36,37], shown in Figure 3, center plot.

(3)

Around 15 dB in power narrow-band random noise was added directly to the spectrum in the frequency band from 0 to 17 Hz. The original disturbance observed in the low frequency band is not straight forward to be generated, due to its non-Gaussian origin [33,38]. In this test though, a simple addition directly in the PSD in the low frequency band was performed. All these 3 sources of distortion combined are displayed in Figure 3, right plot.

Each PSD was then normalized by the power of the initial PSD (noise free) after the addition of distortions. This should reduce offset in the turbulent kinetic energy of the spectrum introduced by the added synthetic distortions. The PSD shown as the gray thick curves in Figure 3, labeled as “Noisy Spectrum”, is the used as input for the signal processing technique. The dashed black curve (“$S_{wf}$ Spectrum”) refers to the outcome of the low frequency removal technique. This PSD is thus used as input for each parameter estimating technique. In Figure 3, the green curve (Bullen model) and the blue curve (von Kármán model) were fitted following the formulation presented by Equation (24). The Bullen model (red curve) was fitted with constraints as described in Section 3.4. The purple curve represents the outcome achieved with the Maximum Likelihood technique, as introduced in Section 3.5.

Note the fact that after adding such distortions (or noise) to the turbulence spectrum, and afterwards normalizing it to conserve its energy, its associated turbulence parameters do not hold the same. The spectral shape has naturally changed, and therefore slightly different values for turbulence intensity and integral length scale are expected. The MLH technique converged to different values when compared to all three fit techniques (purple curve in Figure 3). This bias observed is due to the presence of tones in the spectrum. This test shows how each technique behaves with different types of distortions embedded in the turbulence signal. Furthermore, the fit technique (both with and without constraints: blue, green and red curves) seems to be robust against the presence of tones in the turbulence spectrum, as mentioned in Section 3.3.

4.1. Test with CFD Data

An additional test of the techniques was performed for data from an unsteady computational fluid dynamics (CFD) simulation. A Large Eddy Simulation (LES) of a T106C cascade low-pressure turbine was performed with an exit Mach number of 0.65, Reynolds number of 80,000, and laminar inflow. This operating condition produces a laminar separation in the aft section of the suction side, as seen in Figure 4. This simulation was performed and reported by Bergmann et al. in [39] and cordially made available by Christian Morsbach from the Numeric Methods department of the DLR in Cologne for the purpose of this current study. The blade chord length is $c=93$ mm and the stagger angle is equal to 30.7 degrees.The data analyzed in this work were extracted from the axial slices marked with black dots, labeled “Wake cut”, only the slice on the right-hand side of this figure. The y-axis at this cut spans from −0.07 m (upper part) to −0.14 m (bottom part) comprising 60 measurement points. Simulated data were sampled at $f_s\approx 1$ MHz with 163.5 thousand samples, which gives approx. 0.165 s of simulation time. All power spectral densities (PSD) were calculated using the Welch’s method with 50% window-overlap with Hanning window type [25,34]. The limitation in data size makes the use of nonparametric power spectral density estimators like the Welch method especially challenging, which requires a certain amount of data in order to allow averaging windows.

The instantaneous velocity field at this plane is plotted in Figure 5, on the left. The thick dot plotted on all figures shows a selected probe position, which will be further analyzed in the next section. The turbulence intensity profile is plotted in the center of Figure 5, which was directly calculated via the definition given by Equation (14) from the power spectral density in solid lines, and using a von Kármán model (estimated via the fit technique described in Section 3.3) in dashed lines. The same color standard is applied to show the results for the turbulence integral length scale, on the right-side of Figure 5. The solid lines show the results obtained using the definition in Equation (10). The dashed lines represent the integral length scale obtained using the von Kármán model fit. Inside the blade wake, at $y\approx -0.095$ m, as expected, the turbulence levels are higher and the turbulence length scales are slightly smaller, this last observation made possible only with the fitted von Kármán spectrum. Note that the results obtained for the integral length scale calculated using the definition (solid lines) oscillate from point to point and do not follow a trend. The reason for that observation could be associated with the poor quality of this estimator based on a single bin of the estimated power spectral density. This phenomenon will be better discussed in the following section. This contrasts with the result obtained from a von Kármán model fit, which seems to reach a minimum roughly at the middle of the blade wake.

4.2. Impact of Window Size on Turbulence Parameter Estimation

The following sessions show the impact of the choice in window size in the nonparametric spectral estimation of Welch’s method [25,34] on the parameter estimation techniques proposed in this work. Both data sets from CFD as well as from hot-wire measurements are analyzed.

4.2.1. CFD Data

Figure 6 shows the power spectral density (PSD) of the velocity at the point marked in Figure 5 at $y\approx -0.10$ m. On the left side, both longitudinal (red) and transverse (blue) velocity components are shown. The continuous lines represent the estimated spectrum (fade out line was calculated with a four times larger window size, and therefore higher frequency resolution, compared to the darker curve). Dashed lines represent the fitted von Kármán spectrum using the fit technique as described in Section 3.3 (fit without constraints). From the estimated PSD of both velocity components (solid lines) it is possible to observe some tones around 3 kHz–8 kHz. These tones are understood to be caused by vortex shedding, which is illustrated in Figure 4. The von Kármán spectrum represents the longitudinal velocity component (red curve) well, including the spectrum decay rate, from 10 kHz to 20 kHz. For the transverse component (blue curve), however, at the low frequency region $f<2$ kHz, the PSD levels are lower than the fitted von Kármán spectrum. This is followed by a levels raise at $f=2$ kHz, which is not expected by the model. A possible reason for that could be the presence of tones in this region, which are injecting energy in this frequency band. The spectral slope matches again well with the von Kármán model (−5/3 slope).

The impact of window size on the PSD estimation is assessed and first depicted in Figure 6, on the right-hand side. The largest window size plotted comprises $L=2^{17}=$131,072 samples. As only 163,500 samples are available, these results (with 50% window overlap) in only 2 blocks to be averaged. When $L=2^{11}=2048$, 160 blocks are available to be averaged, with the penalty of lower frequency resolution (higher frequency step/ bin). For the largest window size, due to the reduced number of blocks, the variance of the spectrum is naturally higher, as well as the interval of confidence [25,34]. In this specific case, an “optimal” window size probably lies along the blue and orange curves. The term “optimal” refers to the typical problem in spectral analysis, that is often hard to find the optimal trade-off between window size, number of blocks to be averaged and frequency resolution. Non-parametric spectral estimators normally require a good amount of data in order to allow enough blocks to be averaged, which is not the case for this particular test case. Because of the simulation grid size and computational limits, this spectrum can be assumed to be well-resolved/ realistic up to $f\approx 100$ kHz. For $f>100$ kHz a steeper spectral slope is observed, which is not expected to be turbulence related.

Figure 7 shows the impact of window size on the parameter estimation of turbulence intensity (left) and integral length scale (center) for all four cases: calculated using the definition under Taylor’s hypothesis as in Equations (10) and (14); the fit techniques as introduced in Section 3.3 “fit v1” and Section 3.4 “fit v2”. Finally, the maximum likelihood is also displayed. In the case for the integral length scale, the results from a fifth technique are plotted labeled as “Enhanced definition”, which is based on Equation (12) including the assumption of homogeneous and isotropic turbulence (HIT).

The results for the estimated turbulence intensity (Figure 7, left plot) are inside a range of ~$4\%$ for a window size in the range of $2^{12}<L<2^{16}$. Interestingly, the maximum likelihood estimator technique follows the black curve (using the definition) perfectly in shape, having only a small offset of ~$0.3\%$ in intensity level. When the window size is increased, the fit techniques (both fit v1 and v2, respectively, curves blue and red) tend to decrease the estimated turbulence level, whereas the other way around is observed using the maximum likelihood technique as well as the definition. On the other hand, for the integral length scale (Figure 7, center plot) all techniques seem to be robust against the choice of window size. The exception holds when using the definition for such estimations. It is clear from this result how the output is dependent on the data window size. The reason for this can be better understood by the result shown on the right-side of Figure 7.

One of the problems of using the definition as in Equation (10) is that only one point of the estimated PSD is used in order to estimate the integral length scale, in this case $S\left(0\right)$. On one hand, because of a lack of frequency resolution at low frequency and variance in the spectrum estimation (typical problem in power spectral estimation [25,34]), the absolute value of the PSD at one specific point varies depending on the window size. On the other hand, when an average value over a frequency range is used, as in Equation (12), this value tends to stay more constant compared to a single point, as the energy inside a frequency range is less dependent on the window size as the PSD value of a single frequency bin. The advantage of using this approach has also been reported by El-Gabry et al. [40]. This behaviour is plotted in Figure 7, right-hand side. There, the average of the spectrum for $f<1$ kHz divided by $S\left(0\right)$ is shown. When this ratio is equal to 4, Equations (10) and (12) deliver the exact same value for the integral length scale, what could also be interpreted as the turbulence data relating potentially to homogeneous and isotropic turbulence (HIT). As shown, the ratio oscillates around 4 for small window sizes ($L<2^{13}$) and then random values are observed for higher window sizes. This result helps to understand why the result obtained for the estimated integral length scale using the definition has a great variance and dependence on the window size.

4.2.2. Experimental Data from Hot-Wire

A similar analysis as performed in Section 4.2.1 is now presented—but using experimental data obtained from hot-wire measurements in the inlet of a fan test rig. A more detailed specification of the instrumentation capabilities of the hot-wire anemometer will be introduced in Section 5. The data were acquired with $f_s=192$ kHz sampling frequency and 10s measurement time. Figure 8 shows the PSD of the longitudinal velocity component. The selected point is the same as shown in Section 3.2. On the left-hand side, the impact of window size is seen when the PSD is estimated using the CyS2 component (resulting from the cyclostationary analysis, corresponding to the rotor-incoherent part of the signal). On the right-hand side of Figure 8, the window size is varied and its impact on the low-frequency distortion removal technique is addressed. In this case, for $L>2^{15}$ the technique was not able to reduce effectively the energy content of the signal for $f<100$ Hz. However, $L=2^{13}$ (representing a frequency resolution of $\mathsf{\Delta }f=7.2$ Hz) seems to be an optimal window size, which is the same used as in the result displayed in Figure 2. The performance of the low frequency distortion removal technique has a direct influence on the turbulence integral length scale estimation, when calculated via definition or via the HIT assumption (which takes the average value at the low-frequency part of the PSD, as shown in Section 2.2).

Figure 9 portrays an analogous analysis as in Figure 7 but with experimental data. The estimators seem to be more stable for small window sizes ($L\lesssim 2^{14}$) in the sense that their output values do not change considerably with window size variation. For the turbulence intensity estimation (left plot), the black line (“Definition”) used the “$S_{wf}$ spectrum” as input, which was frequency limited at $f=5$ kHz. This possibly explains why its levels lie approx. 25% lower than the values obtained with the fitting techniques. When the turbulence intensity is computed from the raw signal instead, the turbulence intensity is equal to 1.9% for this test case. This higher value is due to the presence of disturbances (tones, low frequency disturbances, etc). The Maximum Likelihood (MLH) technique converged only when $L<2^{14}$. Numbers obtained with the three methods delivered similar results for the turbulence intensity.

Regarding the turbulence integral length scale, as in Figure 9 (center plot), the reason for the estimated integral length scale exponential growth for $L{\ge }^{14}$ for both “Enhanced definition” and “fit v2” might be associated to the fact, that the low-frequency disturbance removal technique also does not achieve good results in terms of removing the very low frequency energy from the signal. This results in a higher level of the PSD at low frequencies, what leads to an over-estimation of the integral length scale. As the “fit v1” technique does not contain a constraint regarding the low frequency part of the spectrum (as shown in Section 3.3), its results are not considerably affected by the high energy content at very low frequencies, and therefore, less sensitive to the window size variation. Another result worth mentioning is the one obtained using the “Enhanced definition” as in Section 2.2 (black curve). The outcomes for small window sizes ($L\gtrsim 2^{14}$) are comparable with the ones obtained using the von Kármán model. The advantage of this technique is that it does not assume any turbulence spectrum model, only the HIT assumption.

Finally, on the right-hand side of Figure 9, the low-frequency content ratio of the PSD is again analyzed. As observed, the ratio is far from the value 4. This means if the integral length scale would be calculated via definition under the assumption of Taylor’s hypothesis, as in Equation (10), a great deviation would be expected when compared with the result obtained with Equation (12), under the assumption of HIT. This deviation is due to the contamination in the low frequency part of the PSD.

5. Hot-Wire Measurement Setup

The experimental aerodynamic data set used in this study were acquired at the Universal Fan Facility for Acoustics (UFFA) of AneCom AeroTest in Wildau, Germany. The measurement campaign was carried out inside the frame of the EU project TurboNoiseBB. An overview of the measurement campaign can be found in [16]. Tests were performed on the ACAT1 transonic 20 bladed fan. At design point, the fan produces a pressure ratio of about 1.42. The modular fan rig is 864 mm (34 inches) in diameter and powered by an 18 MW motor. The fan inlet is found in a big room where air is sucked from the outside through a chimney. A more precise description of the test facility can be found in [41,42].

The hot-wire probe comprised two wires in x-wire configuration. The probe was mounted in a radial traverse (Figure 10, left) allowing measurements ranging from near-wall to up to 160 mm inside the channel. Figure 10, right, shows a cross section of the AneCom UFFA test rig. The red line sketches approximately the axial position of the measurement plane, as well as the radial traverse path of the hot-wire probe. Further information about the DLR’s hot-wire technique capabilities are found in [22,36,37].

The hot-wire data were recorded for 10 s at 192 kHz sampling rate for each measurement position. A one pulse-per-rev trigger signal was simultaneously recorded. In this work, two fan speeds were selected for analysis: ${\eta }_1\approx$ 3800 RPM, with $U_0\approx$ 83 m/s (M = 0.24) and ${\eta }_2\approx$ 6840 RPM, with $U_0\approx$ 166 m/s (M = 0.48).

6. Experimental Results

This section begins with the analysis of each parameter estimation technique using experimental data. Measurements outside the boundary-layer (lower turbulence levels, higher noise) and inside (higher turbulence levels, lower noise) are used. In this context, the term noise is used to denote all components that are not turbulence related, such as tones, low-frequency disturbance, etc. The PSD of experimental data was estimated via Welch method, Hanning window, 50% overlap and band-with limited to 5 kHz for all cases. Subsequently, this PSD was used as input data for all parameter estimation techniques.

6.1. Power Spectral Density—PSD

Figure 11 shows a collection of measured points performed both inside and outside of the turbulent boundary layer. The colors used were kept the identical as in earlier plots. The thicker gray curve instances the estimated PSD from raw hot-wire velocity data. The estimated turbulence integral length scale and turbulence intensity are plotted inside the legend of each figure. The dashed black curve refers, as previously, to the PSD of the broadband components (Cys2 part of the signal after a cyclostationary analysis), low-frequency distortions filtered out and band-width limited to 5 kHz. In order to reduce legend space, the label “von Kármán fit” was shortened to “VK fit” and “Bullen fit” to “B. fit”.

On the top plots, the raw spectrum is relatively clean for the longitudinal component (left), but some spurious noise starts emerging at $f>1$ kHz for the transverse component (left). This is probably due to the higher turbulence levels in the left plot, which leads to a more favorable signal-to-noise ratio (SNR). Despite this, all techniques, except the MLH technique that did not converge for the transverse component, converged to comparable values of turbulence levels and integral length scale. At this point, it is important to further discuss the slope of the spectra at high-frequency band. This slope at higher frequencies of the PSD of the raw data is noticeably steeper than the von Kármán spectrum (blue and purple curves). Different reasons can be attributed to the origin of this phenomenon: If the slope is indeed turbulence related, thus the von Kármán spectrum fails to correctly represent PSD obtained from experimental data. On the other hand, this steeper slope can also be related to the measurement technique, in this case more precisely the diameter of the hot-wires used in this measurement campaign.

Polacsek et al. [20] showed for this same data set, that the band-width limitation of the hot-wires could explain this steeper slope. This results in an attenuation of the measured unsteady velocity signals at high frequency. In other words, the steeper slope could be attributed to band-width limitation of the measurement technique, rather than to the physics of turbulence. Considering that no systematic study concerning the effect of the wire thickness was performed, uncertainties regarding the noticed differences in spectral slope at higher frequency remains. The previous study performed using CFD data in Section 4 showed that the slope of the von Kármán spectrum reasonably captured the observed slope of the simulation data.

Figure 11 (center plots) shows the results of a measured position outside of the turbulent boundary layer, where strong tones are observed in the raw data, alongside with a high power distortion occurring for $f>5$ kHz. The cyclostationary analysis succeeded in removing the tonal components from the raw data. The combination of this technique and the turbulence spectrum fit led to realistic turbulence parameters that likely represent the turbulent field at the respective measurement position.

The bottom plots of Figure 11 depict the results for measurements outside the boundary layer, in which strong energy content is seen in the low frequency band of the PSD. In spite of that, the outcome of all techniques pointed towards similar values for the longitudinal velocity component. Note that the turbulence intensity computed directly from the raw PSD is ~2%, although for the other methods this level lies at ~1%. In other words, an error of ~100% in the estimated turbulence intensity would have occurred when no signal conditioning had been applied to the raw signal. The “fit v2” and MLH techniques did not give reasonable results for the transverse velocity component. A possible reason could be the remaining contamination in the “$S_{wf}$ spectrum”. A plateau is theoretically expected at lower frequency band in the spectrum, which is not observed in this case. The estimated turbulence intensity was once more approximately half of the obtained from the raw data.

6.2. Results for Varying Probe Insertion Depths

Selected results for five probe insertion depths are depicted in Figure 12. The normalization of the spectra allows a comparison of all spectra from different measurement points, regardless of the velocity, turbulence level, and integral length scale. It is also an approximated way of validating whether the estimated parameters turbulence intensity and integral length scale are (approximately) correct. A von Kármán spectrum is alongside plotted as reference, since it is commonly used to model turbulence in turbomachinery applications. The normalization follows Hinze [24] and the normalization is shown on each respective axis label.

For the lower fan speed ${\eta }_1\approx$ 3800 RPM (see Figure 12, top plots), the normalized spectra from measurement points inside the turbulent boundary layer (5, 10 and 30 mm) are similar. An exception holds due to discrepancies at high frequencies. The presence of tones and distortions in the signal make it especially challenging not only to the turbulence parameters estimators, but also to judge the similarity in spectral shapes.This holds especially for measurements points outside of the turbulent boundary layer (70 and 90 mm). When all spectra cluster approximately together, it means the turbulence parameters should (potentially) be estimated precisely.

Figure 12 bottom plots depict the same probe insertion depths and velocity components, but now for a higher fan speed ${\eta }_2\approx$ 6840 RPM. Disturbances in the data are as expected stronger at this fan speed. Nonetheless, all spectra roughly cluster together. The spectral slope from experimental data is once more steeper than the von Kármán spectrum. The explanation for that is still as previously discussed.

In Figure 13, the turbulence intensity plotted for several radial positions together with the normalized axial velocity. The latter works as an indicator of the velocity profile and boundary layer in the radial direction. Both plots on left- and right-hand sides refer to the longitudinal velocity component. Inside the legend, the label “improved” refers to the turbulence intensity estimated directly by integrating the “$S_{wf}$ spectrum”, that means, there is no spectral modeling behind it. All techniques cluster to a narrow range of values. Higher turbulence intensity values were obtained when computing it directly from raw data. This was observed for both rotor speeds and can be explained by the strong distortions present in the raw signals. This fact is particularly evident for ${\eta }_2$ on Figure 11 center plots, where the discrepancy compared to all estimators is enormous.

Figure 14 portrays the estimated turbulence integral length scale computed from the longitudinal and transverse velocity components and both fan speeds. The thicker line (blue and red) inside the shaded area shows the more likely value. It was determined by analyzing the spectral fits of all techniques separately. The shaded range gives an idea of an interval of confidence. This region comprises the outcome of all techniques regarding the estimated turbulence integral length scale. This was not calculated using statistical tools specifically designed for that, as such analysis is beyond the scope of this study.

In addition to the fit and the MLH techniques, the integral length scale was additionally calculated from the “$S_{wf}$ spectrum” via Equation (12) and from raw data via Equation (10). For measurements near to the duct wall, where a favorable SNR is observed, i.e., higher turbulence intensity and relatively low distortion, all techniques met to comparable values. On the other hand, as the probe further traveled into the flow, the confidence interval increasingly widened due to the reduction of the SNR. It means, lower turbulence levels and higher contamination in the signals.

The fitting techniques were used onto both longitudinal and transverse velocity components. Differences in the estimated turbulence parameters of both velocity components can either indicate that the spectra of each velocity component experienced significantly different levels of contamination. Another hypothesis is that the HIT assumption is less suitable in some regions of the flow. The ratio of the integral length scale as well as the turbulence intensity of both velocity components are depicted in Figure 15. The thick and red line indicates the respective ratio for the case of HIT. By looking at the velocity component ratios for both integral length scale and turbulence intensity, the data set analyzed seems to be anisotropic at all measurement positions. It is important to highlight that the integral length scale of the transverse component has numbers ranging from roughly 2 to 5 times the longitudinal component for deeper probe insertion depths. This is markedly away from HIT.

7. Conclusions

The current work compared a few different techniques to extract turbulence parameters from noise-free and strongly distorted hot-wire unsteady velocity data. Turbulence parameters analyzed are the integral length scale (ILS) and the turbulence intensity (Tu; or turbulent kinetic energy (TKE)). The turbulence spectrum models Bullen and von Kármán (Figure 1) were selected to estimate turbulence parameters from noisy experimental data. What sets both turbulence spectra apart is that the Bullen model features an adjustable spectral slope at high frequencies.

The low-frequency disturbance removal technique was first used to remove wind gusts from hot-wire data installed on an airplane wing, as reported by Mark [33], and now it was applied on turbomachinery inflow turbulence data. The similar behaviour of the autocorrelation function is observed in fan inflow instationary data, interpreted by Mark [33] as wind gusts. The application of this technique allows removing the non-turbulence power content from the low frequency part of the power spectral density. As the integral length scale is directly affected by this part of the PSD, if no data conditioning is applied, strong deviation in the estimation of the integral length scale is observed.

For the first synthetic test case (Figure 3, left plot) with weak noise added to it, all techniques behaved similarly and estimated the turbulence parameters properly. In the second test case though, the addition of harmonic tones to the spectrum deteriorated the performance of the MLH estimator technique. The reason for this phenomenon is that this technique works by matching the power of the synthetic turbulence spectrum to the input spectrum (the noisy one obtained from experimental data). Therefore, if any non-turbulence related components are present in the spectrum, such as tones, this will bias its output values. In this case, the turbulence intensity was more noticeably biased by it. Apart of the MLH, all the fit techniques excelled well on both estimating the initial integral length scale and the turbulence intensity. For the third and last synthetic test case, as in the right-hand side of Figure 3, stronger white noise and low frequency noise were added to the clean turbulence spectrum. The low-frequency removal technique confirmed to work, as well the fitting techniques. The MLH was once more biased by the strong tones found in the spectrum. This biased the turbulence parameters estimated by this technique.

In Section 4.1, downstream turbulence data from a LES simulation of a turbine blade were analyzed with the introduced estimator techniques. Both turbulence intensity and integral length scale were estimated from the CFD data using both the definition, as well as the fit technique with a von Kármán spectrum model. The results obtained for the turbulence intensity with both approaches were similar within a range of ~10%. The highest deviation was observed in the region close to the center of the wake, where few tones were present in the spectra. These tones are believed to be related to vortex-shedding. The energy of these tones contributes to the calculation of turbulence intensity using the definition equation, but not via fit techniques. This might explain the deviation observed.

The profile of the turbulence intensity curve against the probe position in the flow is coherent with what would be expected, as it increases monotonically until reaching a maximum value, which is referred to as the center of the wake (minimum flow velocity), and then it starts decreasing again. The integral length scale however, when estimated via the proposed fit technique with the help of a von Kármán spectrum, follows a shape that behaves approximately inverse as the turbulence intensity curve. That means, the curve over the probe position reaches a minimum where the turbulence intensity finds its maximum. The integral length scale tends to increase the further the probe is from the center of the blade wake. This trend was however not observed when the integral length scale was estimated via the definition. The curve profile over probe position, instead, has a slightly oscillatory behavior and does not follow a trend, what makes one believe that this might be attributed to the poor performance of such parameter estimator.

The impact of window size of the nonparametric power spectral density estimator Welch method in the estimated turbulence parameters was assessed in Section 4.2. Both simulated data and experimental data were tested. For the CFD test case, the results for both turbulence intensity and integral length scale were not affected considerably by the change of window size, when kept in a range of approximately $2^{12}<L<2^{16}$. The result for turbulence intensity for both fit techniques (with and without constraints) started to drop for $L>2^{16}$, what was not observed for the maximum likelihood technique and the calculated value according to the definition. The reason for this could be associated with lack of blocks to be averaged (leading to high variance in the spectrum) and also the higher (proportionally speaking) amount of spectral points at high frequency compared to the low-frequency area. This effect seems to have a stronger impact on the fit technique at high frequencies, leading to a poor fit at low frequency. In other words, the model spectrum follows more precisely the high-frequency range (less bias) than the low-frequency range of the spectrum (higher bias), as the higher frequency part of the spectrum is proportionally more sampled than the low frequency. A similar behavior was observed when using hot-wire data, as in Figure 8.

The influence of window size on the estimated integral length scale was shown to be negligible. The fit technique without constraints (“fit v1”) combined with the von Kármán spectrum performed the best keeping a stable output independent of the window size. This was observed for both CFD data and experimental data. The fit with constraints and the “Enhanced definition” had a poor performance for higher window size ($L\gtrsim 2^{14}$) using experimental data due to the poor performance of the low frequency disturbance removal technique, when a large window size is selected. Finally, the ratio ${\left. [\frac{S_{11}\left(f\right)}{S_{11}\left(0\right)}\right]}_{f\to 0}$ was analyzed in order to assess the deviation from Equations (10) and (12). When this ratio is equal to 4, both of them deliver the exact same value for the integral length scale, what could also be interpreted as the turbulence data refers potentially to homogeneous and isotropic turbulence (HIT). The deviation from 4 in this case however, in the understanding of the authors, is related to the poor performance of the integral length scale estimator according to the definition, as in Equation (10).

All estimation techniques performed similarly when tested with data measured inside the turbulent boundary layer (Figure 11 top plots). The reason for that is the higher turbulence intensity and lower distortion levels. The Bullen spectrum captured more precisely the experimental spectral slope. The von Kármán spectrum features a fixed spectral slope, which is less steep as the observed from the experimental spectra. It is not clear whether this indicates that the Bullen turbulence spectrum is more suitable than the von Kármán for this data set. The steeper slope may not be due to the turbulence physics as examined in Section 6.1. The subsequent test with the hot-wire probe inside the free stream, i.e., outside of the turbulent boundary layer, as in middle and bottom plots of Figure 11 was strongly affected by distortions, similar as the ones reviewed in the synthetic test case: high energy content at low frequency band, and tones probably because of hot-wire element and/or probe vibration, etc. The cyclostationary technique was able to separate the majority of the tonal components embedded in the measured data; as did the low-frequency removal technique when filtering out distortions from the spectrum at the low-frequency band. The removed part refers to the “slow” part of the autocorrelation function.

The normalized spectra plots from Figure 12 show that all spectra experience a similar von Kármán-like spectral shape, although the strong contamination that some of them contain. This analysis reveals that the turbulence parameters even if they could not be precisely estimated, they have the same order of magnitude of what would be expected as the correct values.

Comparing the estimated turbulence intensity side-by-side from all techniques, Figure 13 shows the outcome for the longitudinal velocity component, and for two different fan speeds. All techniques met roughly in the same range. When these results are compared with the one from the raw spectrum, a noticeable discrepancy is observed. For the high fan speed case, the turbulence intensity computed directly from raw data was ~3% inside the channel, although the models suggested that values might lie below 0.3%. This refers to a difference of one order of magnitude.

Last, the analysis of the turbulence intensity ratio of both longitudinal and transverse velocity components allowed an isotropy assessment. The same ratio was also performed for the integral length scale. Several hot-wire insertion depths were analyzed, as shown in Figure 15. As discovered, the inflow seems to be anisotropic at all measured points, notably outside the turbulent boundary layer. There the turbulence integral length scale of the transverse component reached over 4 times the longitudinal one. The ratio of turbulence of both velocity components did not meet value one. When the ratio is equal to one, this indicates potential isotropic turbulence. Indeed, the turbulence intensity outside the turbulent boundary layer is stronger in the transverse direction comparing to the longitudinal direction. On the other hand, inside the turbulent boundary layer the opposite is observed. Despite the use of HIT spectrum models (von Kármán and Bullen) to characterize potentially anisotropic turbulence, the outcome of this work seem to be plausible and allow the estimation and assessment of flow turbulence parameters with some degree of reliability.