Computational Fluid Dynamics Using the Adaptive Wavelet-Collocation Method
Abstract
:1. Introduction
2. External Flow
2.1. Development and Implementation of Techniques to Resolve External-Flow Using the AWCM
2.1.1. Immersed Boundary Methods
2.1.2. Body-Fitted Grid on General Curvilinear Co-Ordinate Systems
2.1.3. Level Set Methods Using the AWCM Solver
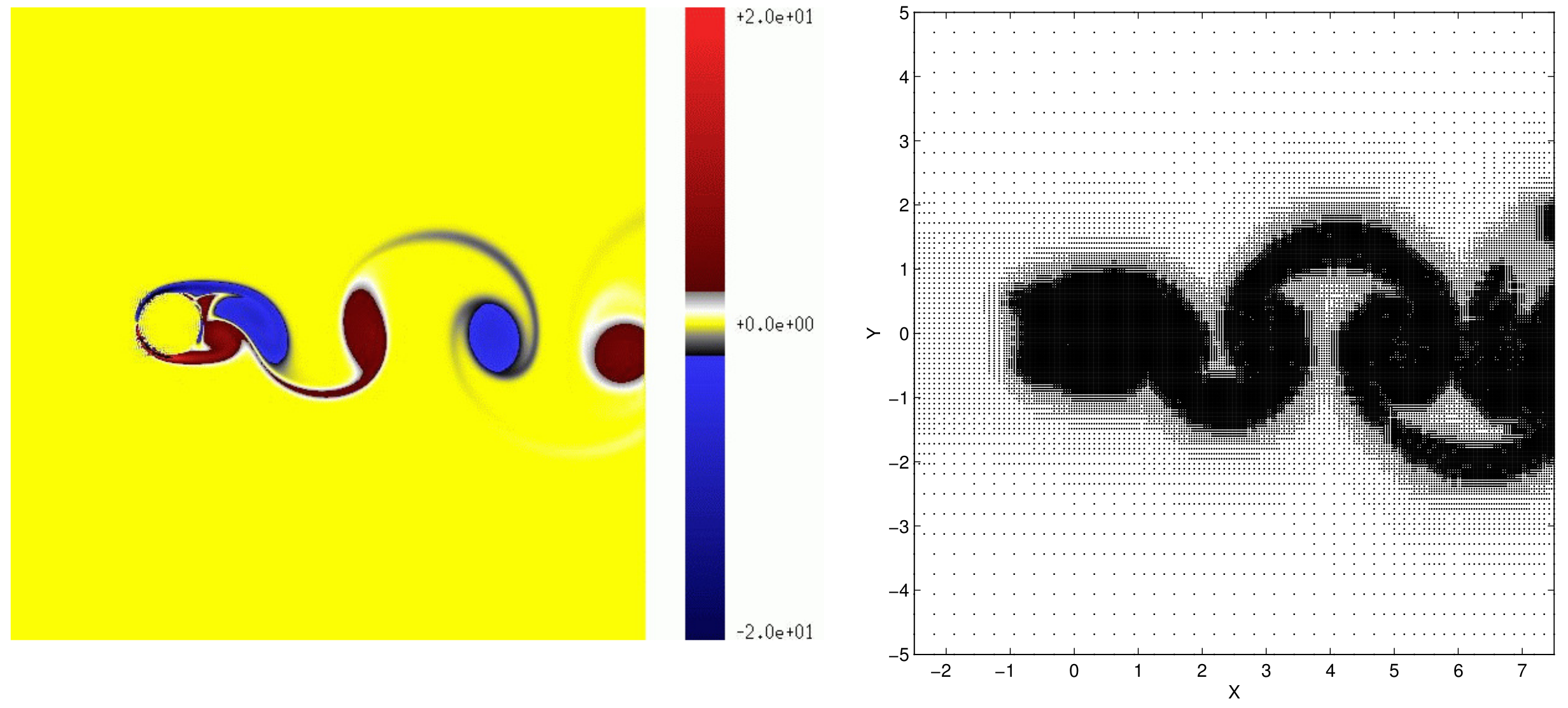
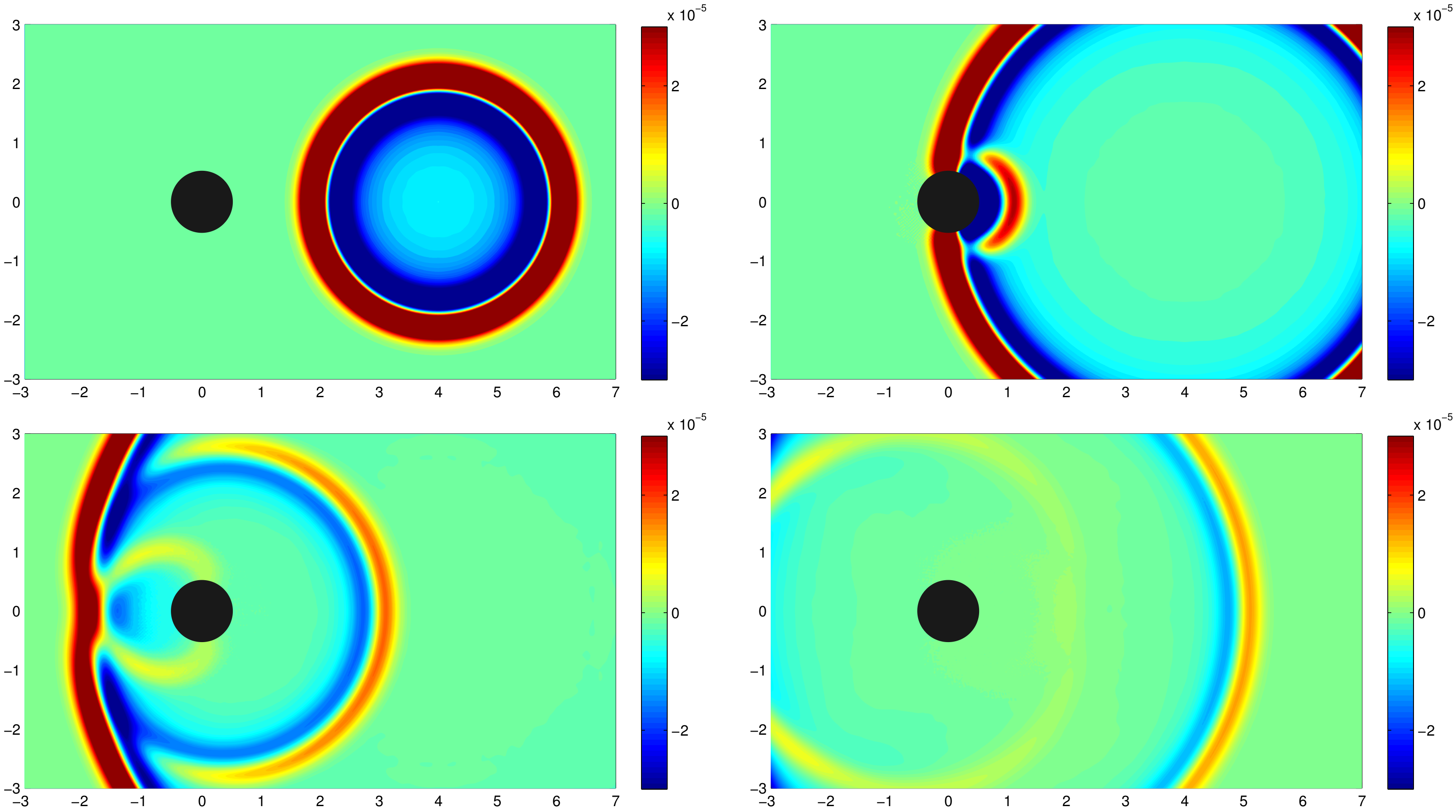
2.2. Application of AWCM to Study External Flows
3. Physics Exploration
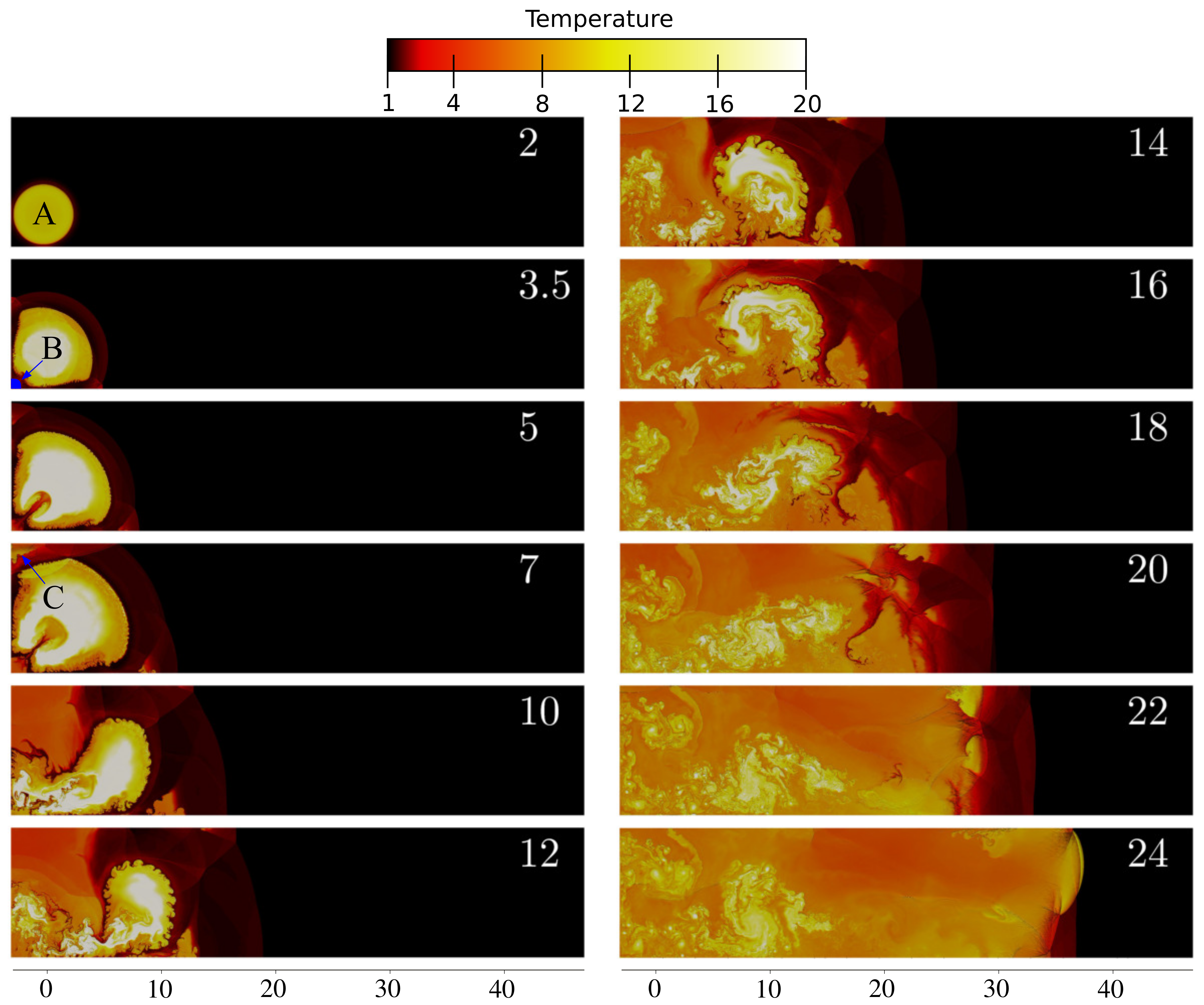
3.1. Detonation Initiation and Hot Spot Characterization
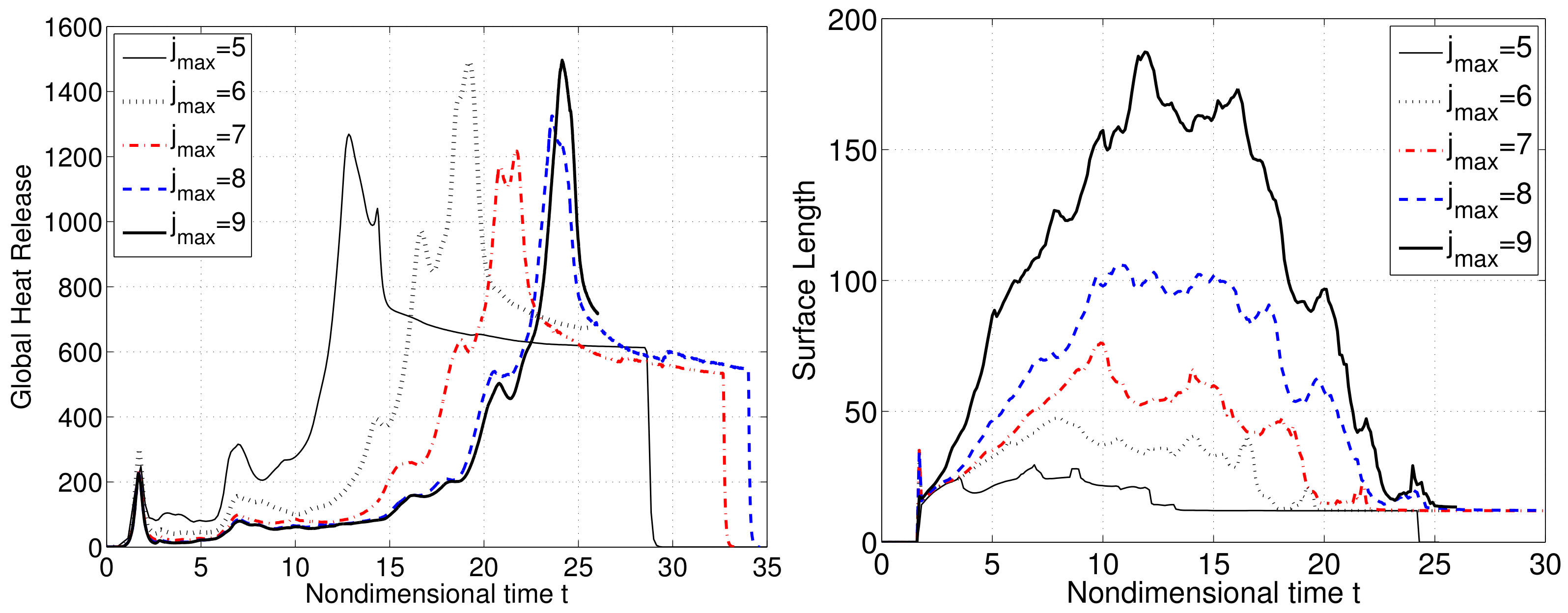
3.2. Fluid Instabilities
3.3. Heat and Mass Transfer
3.4. Supersonic Channel Flow
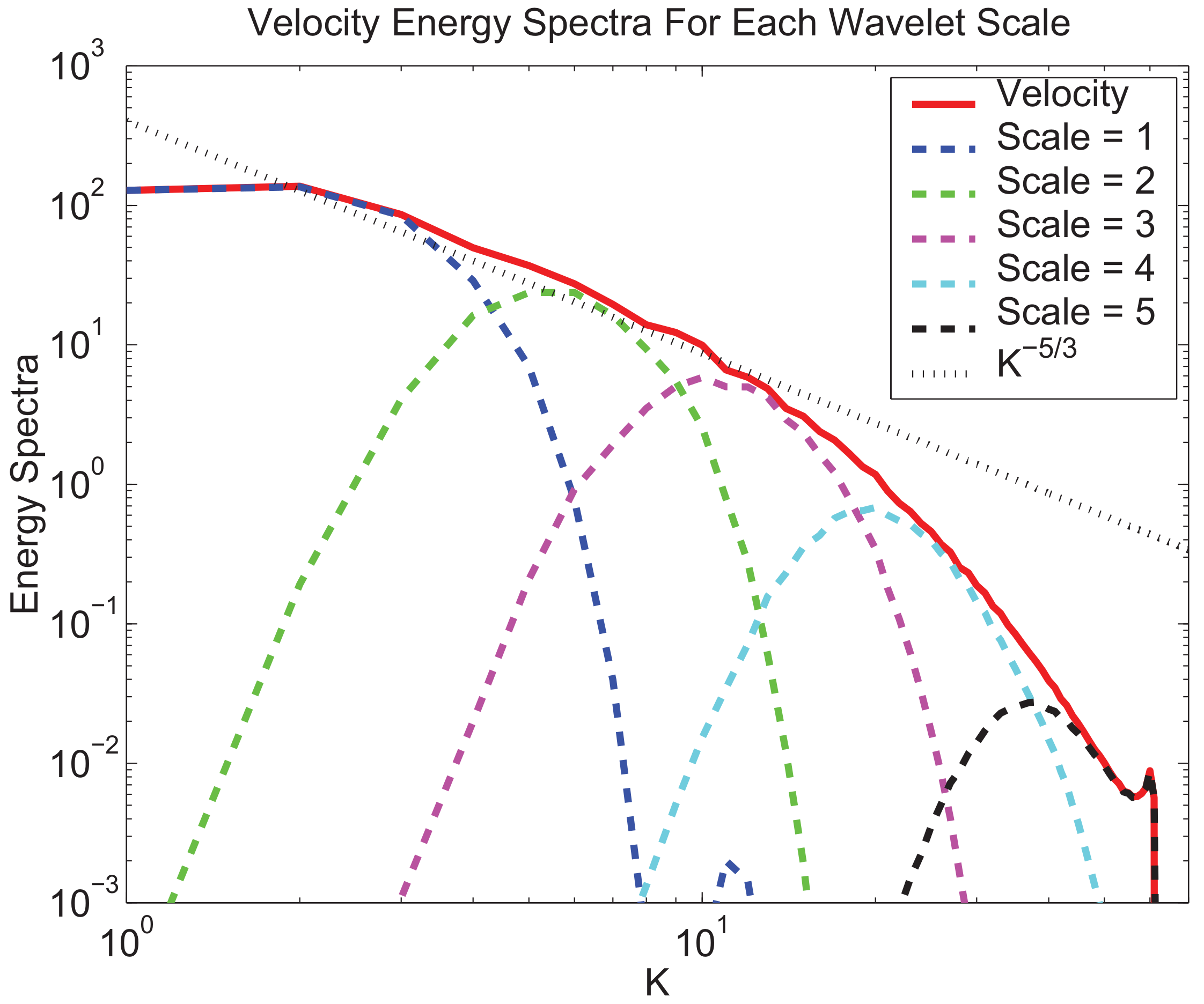
4. Turbulence Modeling
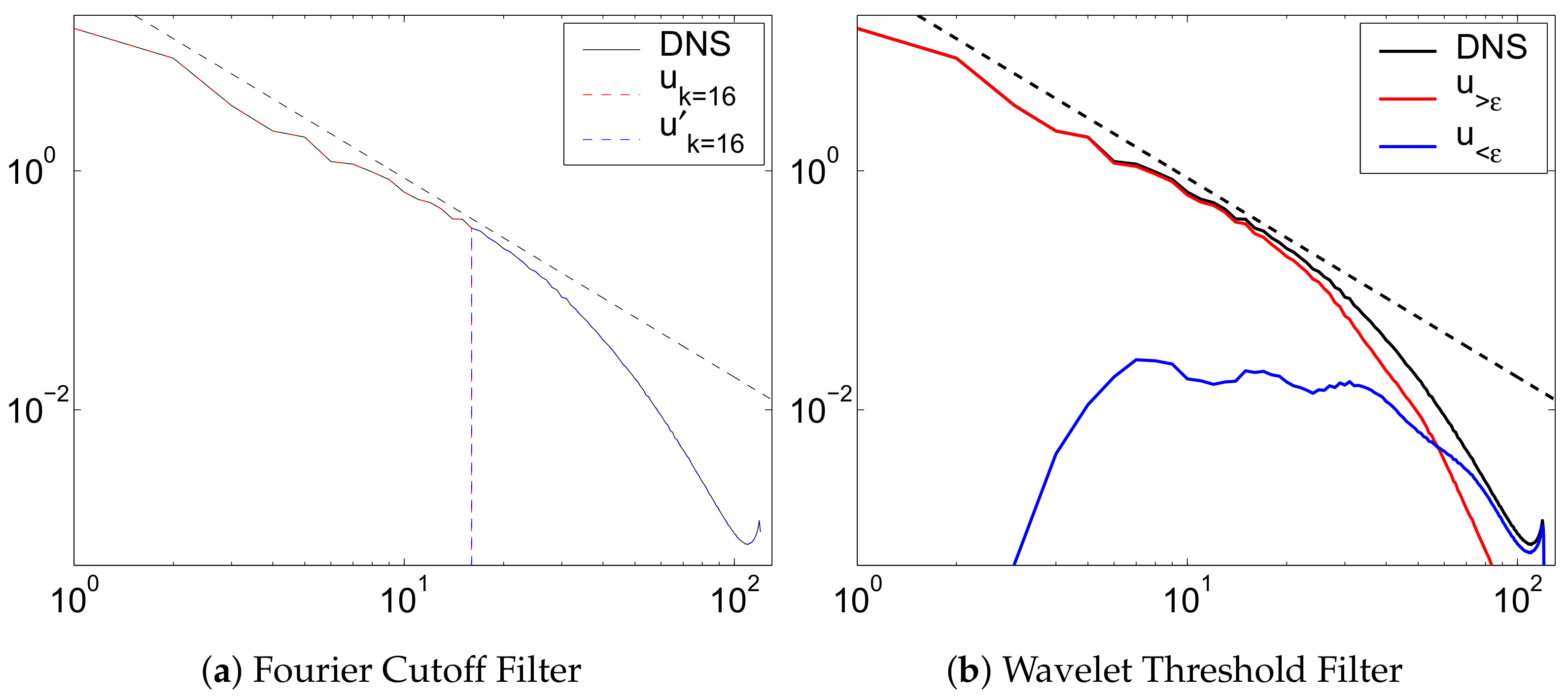
4.1. Physics-Based Adaptive Simulation—Hybrid WA-DNS/CVS/WA-LES
4.2. WA-URANS
4.3. WA-DDES
- 1.
- It is more flexible and improves accuracy by mitigating the log-layer mismatch of the mean flow quantities with considerably smaller mean threshold and more precise control of the relative resolution of fluctuating components using more physically relevant scales based on the turbulence intensity instead of relying on instantaneous or mean flow scales;
- 2.
- The use of a larger fluctuating threshold results in fewer adaptive grid points with a priori known turbulence resolution.
- 1.
- Supersonic plane channel flow—Compared with the WA-LES, WA-DDES successfully achieved accuracy indicated by the threshold and efficiency in terms of degrees of freedom. In addition, WA-DDES resolved the typical log-layer match issue encountered in attached flows using the conventional non-adaptive DDES method;
- 2.
- Subsonic channel flow with periodic hill constrictions and massive flow separation—WA-DDES was found to be in good agreement with the DNS data. Compared with WA-URANS, a great improvement was gained in terms of the separation bubble size as well as mean velocity and turbulent stress profiles. Besides, a very high compression ratio of 99.9% was achieved with the adaptive mesh size being only less than 8.0% of the non-adaptive DNS grid, while the finest allowed wavelet grid resolution was even higher than the DNS;
- 3.
- Supersonic flow over a compression ramp inducing the shock wave-turbulent boundary layer interaction—Analogous to the subsonic channel flow case, compared with WA-URANS, significant improvement was gained in terms of the prediction of the shock-induced separation bubble. Compared with the reference experimental and DNS data, mean velocity and mass flux turbulence intensities were in acceptable agreement.
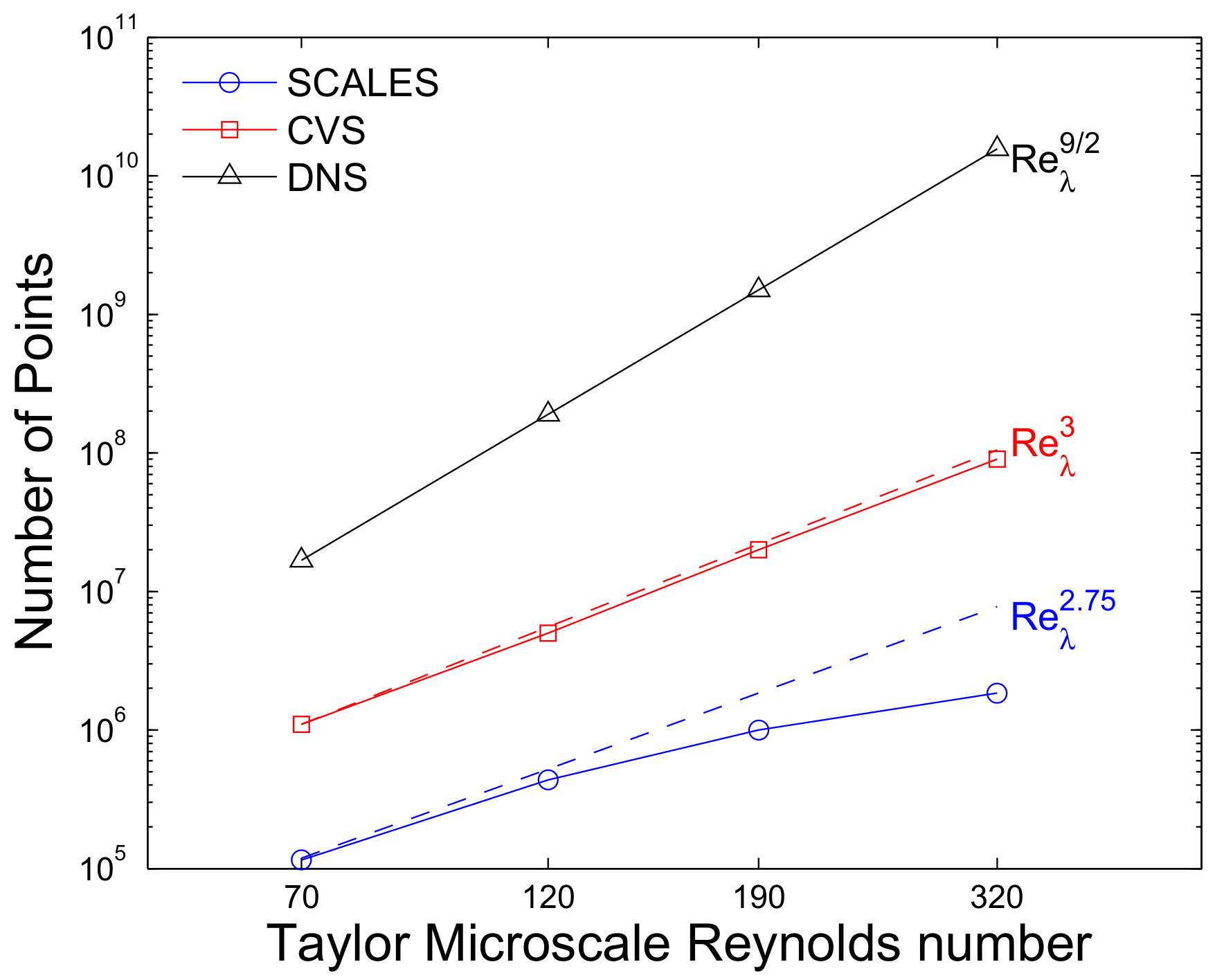
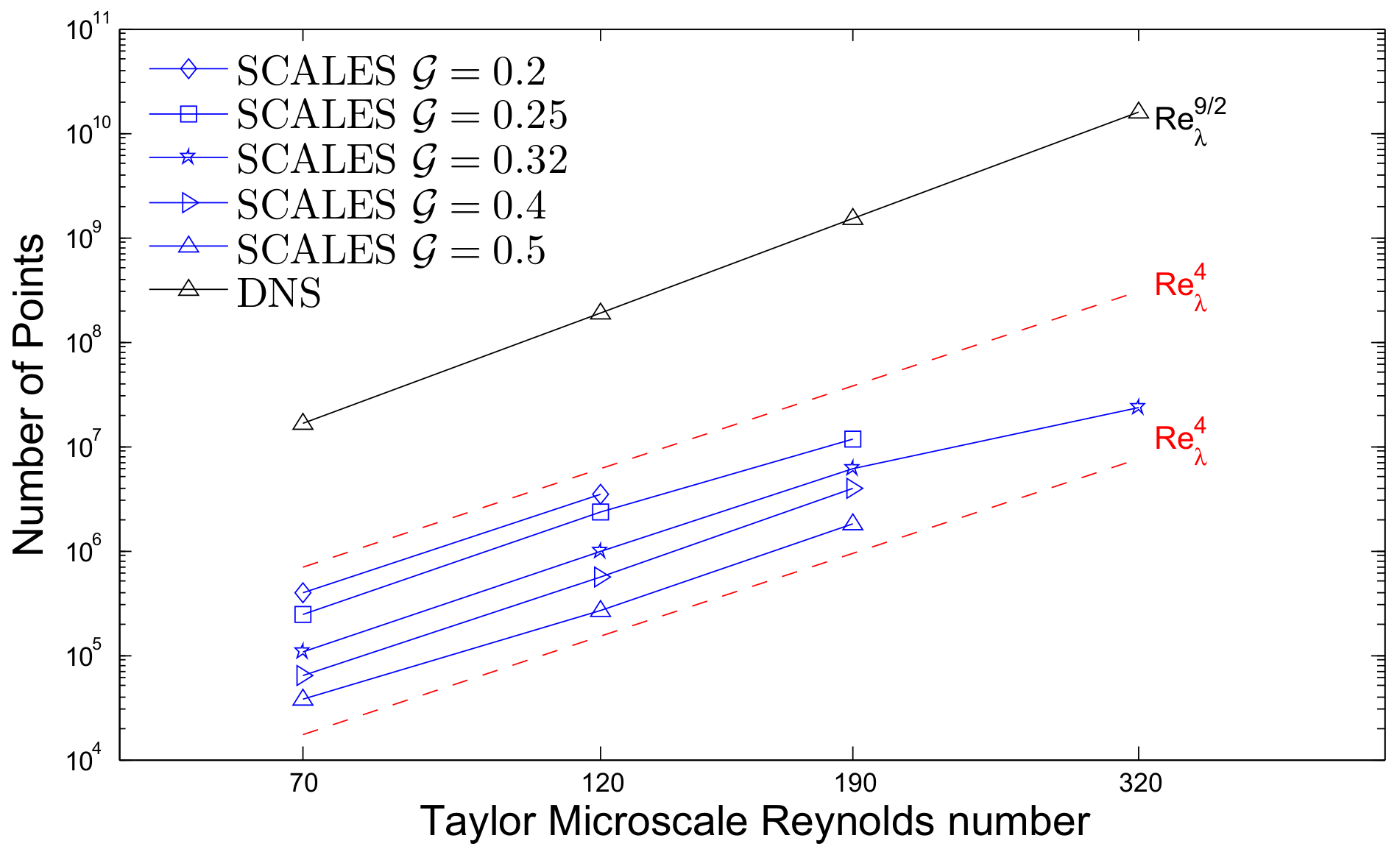
4.4. Reynolds Scaling of WA-DNS, CVS, WA-LES
5. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Schneider, K.; Vasilyev, O.V. Wavelet methods in computational fluid dynamics. Annu. Rev. Fluid Mech. 2010, 42, 473–503. [Google Scholar] [CrossRef] [Green Version]
- Vasilyev, O.V.; Bowman, C. Second-Generation Wavelet Collocation Method for the Solution of Partial Differential Equations. J. Comput. Phys. 2000, 165, 660–693. [Google Scholar] [CrossRef] [Green Version]
- Vasilyev, O.V.; Kevlahan, K.R. Hybrid wavelet collocation–Brinkman penalization for complex geometry flows. Int. J. Numer. Methods Fluids 2002, 40, 531–538. [Google Scholar] [CrossRef]
- Brown-Dymkoski, E.; Kasimov, N.; Vasilyev, O.V. A characteristic based volume penalization method for general evolution problems applied to compressible viscous flows. J. Comput. Phys. 2014, 262, 344–357. [Google Scholar] [CrossRef] [Green Version]
- Brown-Dymkoski, E.; Vasilyev, O.V. Adaptive-Anisotropic Wavelet Collocation Method on general curvilinear coordinate systems. J. Comput. Phys. 2017, 333, 414–426. [Google Scholar] [CrossRef] [Green Version]
- Shervani-Tabar, N.; Vasilyev, O.V. Stabilized conservative level set method. J. Comput. Phys. 2018, 375, 1033–1044. [Google Scholar] [CrossRef]
- Souopgui, I.; Wieland, S.A.; Yousuff Hussaini, M.; Vasilyev, O.V. Space-time adaptive approach to variational data assimilation using wavelets. J. Comput. Phys. 2016, 306, 253–268. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Vasilyev, O.V. Nonreflecting boundary conditions based on nonlinear multidimensional characteristics. Int. J. Numer. Methods Fluids 2010, 62, 24–55. [Google Scholar] [CrossRef]
- Devine, K.; Boman, E.; Heaphy, R.; Hendrickson, B.; Vaughan, C. Zoltan Data Management Services for Parallel Dynamic Applications. Comput. Sci. Eng. 2002, 4, 90–97. [Google Scholar] [CrossRef]
- Boman, E.G.; Catalyurek, U.V.; Chevalier, C.; Devine, K.D. The Zoltan and Isorropia Parallel Toolkits for Combinatorial Scientific Computing: Partitioning, Ordering, and Coloring. Sci. Program. 2012, 20, 129–150. [Google Scholar] [CrossRef]
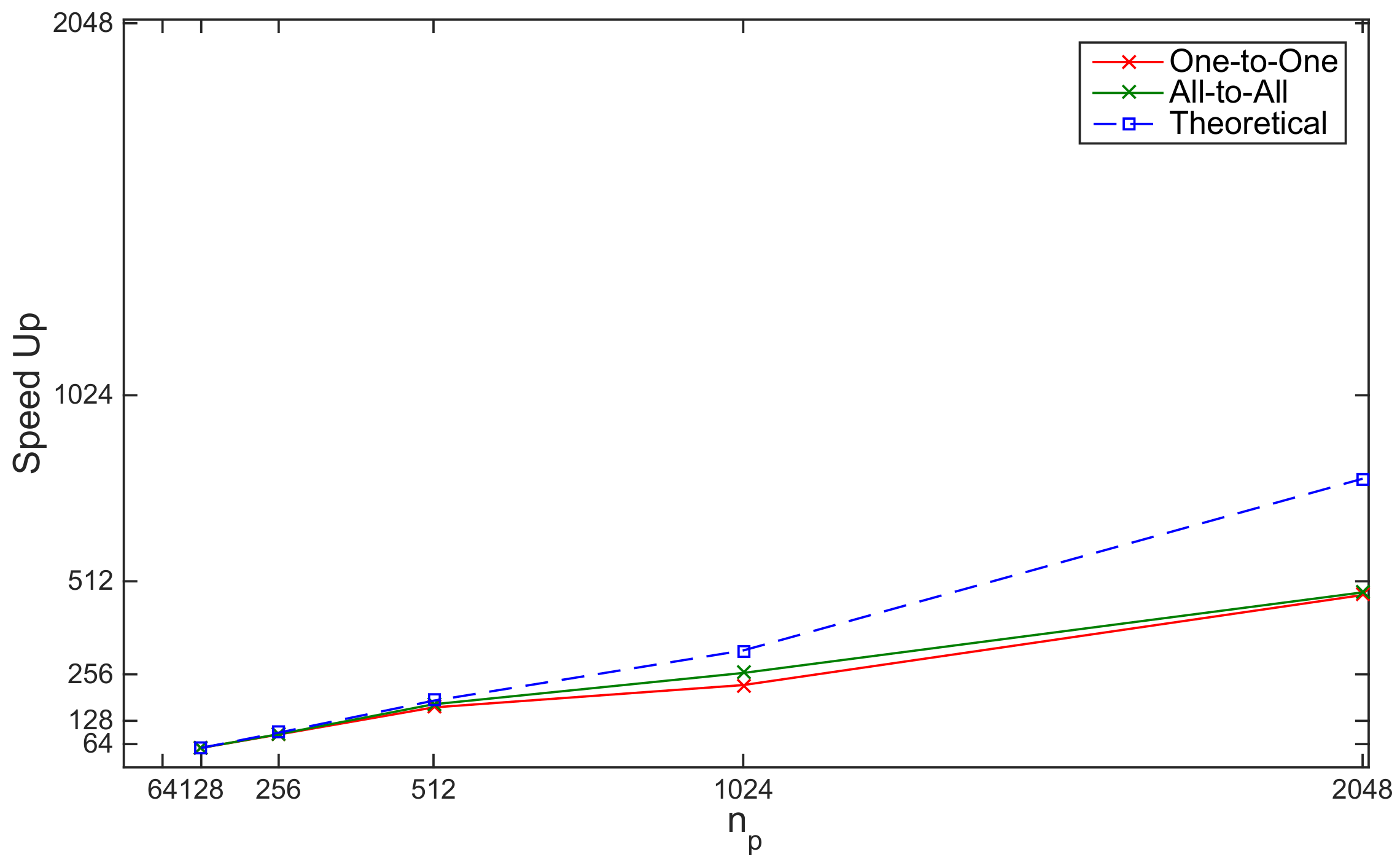
- Nejadmalayeri, A.; Vezolainen, A.; Brown-Dymkoski, E.; Vasilyev, O.V. Parallel adaptive wavelet collocation method for PDEs. J. Comput. Phys. 2015, 298, 237–253. [Google Scholar] [CrossRef] [Green Version]
- Kevlahan, N.K.; Vasilyev, O.V. An adaptive wavelet collocation method for fluid-structure interaction at high reynolds numbers. SIAM J. Sci. Comput. 2005, 26, 1894–1915. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Vasilyev, O.V. A Brinkman penalization method for compressible flows in complex geometries. J. Comput. Phys. 2007, 227, 946–966. [Google Scholar] [CrossRef]
- Reckinger, S.M.; Vasilyev, O.V.; Fox-Kemper, B. Adaptive volume penalization for ocean modeling. Ocean Dyn. 2012, 62, 1201–1215. [Google Scholar] [CrossRef]
- Reckinger, S.M.; Vasilyev, O.V.; Fox-Kemper, B. Adaptive wavelet collocation method on the shallow water model. J. Comput. Phys. 2014, 271, 342–359. [Google Scholar] [CrossRef] [Green Version]
- De Stefano, G.; Vasilyev, O.V. Wavelet-based adaptive simulations of three-dimensional flow past a square cylinder. J. Fluid Mech. 2014, 748, 433–456. [Google Scholar] [CrossRef] [Green Version]
- De Stefano, G.; Nejadmalayeri, A.; Vasilyev, O.V. Wall-resolved wavelet-based adaptive large-eddy simulation of bluff-body flows with variable thresholding. J. Fluid Mech. 2016, 788, 303–336. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V.; Brown-Dymkoski, E. Wavelet-based adaptive unsteady Reynolds-averaged turbulence modelling of external flows. J. Fluid Mech. 2018, 837, 765–787. [Google Scholar] [CrossRef]
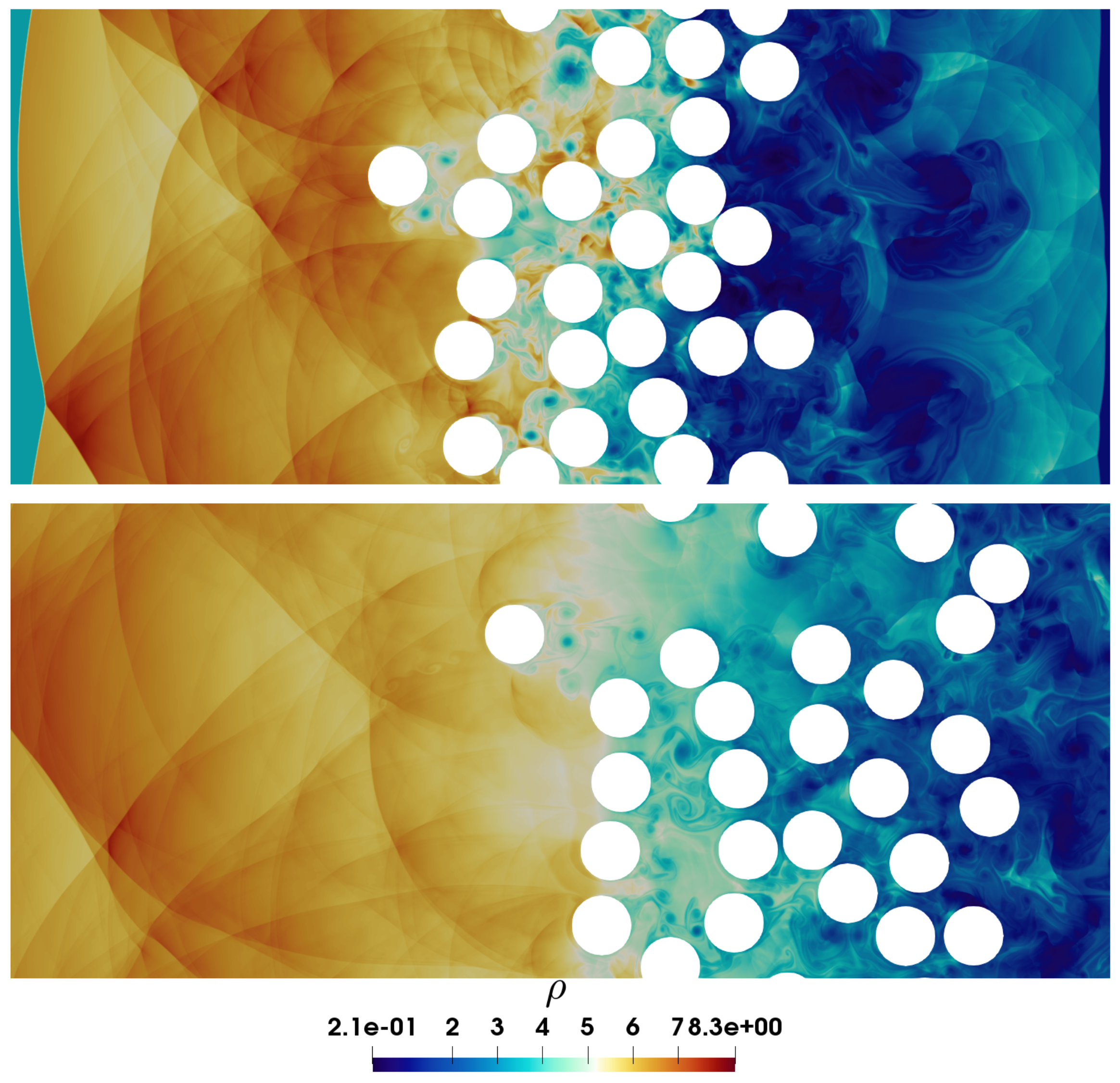
- Mehta, Y.; Jackson, T.; Zhang, J.; Balachandar, S. Numerical investigation of shock interaction with one-dimensional transverse array of particles in air. J. Appl. Phys. 2016, 119, 104901. [Google Scholar] [CrossRef]
- Mehta, Y.; Neal, C.; Jackson, T.L.; Balachandar, S.; Thakur, S. Shock interaction with three-dimensional face centered cubic array of particles. Phys. Rev. Fluids 2016, 1, 054202. [Google Scholar] [CrossRef]
- Mehta, Y.; Neal, C.; Salari, K.; Jackson, T.; Balachandar, S.; Thakur, S. Propagation of a strong shock over a random bed of spherical particles. J. Fluid Mech. 2018, 839, 157–197. [Google Scholar] [CrossRef]
- Mehta, Y.; Salari, K.; Jackson, T.; Balachandar, S. Effect of Mach number and volume fraction in air-shock interacting with a bed of randomly distributed spherical particles. Phys. Rev. Fluids 2019, 4, 014303. [Google Scholar] [CrossRef]
- Mehta, Y.; Jackson, T.; Balachandar, S. Pseudo-turbulence in inviscid simulations of shock interacting with a bed of randomly distributed particles. Shock Waves 2020, 30, 49–62. [Google Scholar] [CrossRef]
- Regele, J.D.; Vasilyev, O.V. An Adaptive Wavelet-Collocation Method for Shock Computations. Int. J. Comput. Fluid Dyn. 2009, 23, 503–518. [Google Scholar] [CrossRef]
- Hosseinzadeh-Nik, Z.; Subramaniam, S.; Regele, J.D. Investigation and quantification of flow unsteadiness in shock-particle cloud interaction. Int. J. Multiph. Flow 2018, 101, 186–201. [Google Scholar] [CrossRef] [Green Version]
- Goetsch, R.J.; Regele, J.D. Discrete element method prediction of particle curtain properties. Chem. Eng. Sci. 2015, 137, 852–861. [Google Scholar] [CrossRef]
- Mehta, Y.; Goetsch, R.J.; Regele, J.D. Particle resolved direct numerical simulations using the adaptive wavelet collocation method to study shock interacting with moving, colliding particles. J. Comput. Phys. 2021. under review. [Google Scholar]
- Kassoy, D.R.; Kuehn, J.A.; Nabity, M.W.; Clarke, J.F. Detonation initiation on the microsecond time scale: DDTs. Combust. Theory Model. 2008, 12, 1009–1047. [Google Scholar] [CrossRef]
- Regele, J.D.; Kassoy, D.R.; Vasilyev, O.V. Effects of high activation energies on acoustic timescale detonation initiation. Combust. Theory Model. 2012, 16, 650–678. [Google Scholar] [CrossRef] [Green Version]
- Kurtz, M.D.; Regele, J.D. Acoustic timescale characterisation of a one-dimensional model hot spot. Combust. Theory Model. 2014, 18, 532–551. [Google Scholar] [CrossRef]
- Kurtz, M.D.; Regele, J.D. Acoustic timescale characterization of symmetric and asymmetric multidimensional hot spots. Combust. Theory Model. 2014, 18, 711–729. [Google Scholar] [CrossRef]
- Reinbacher, F.; Regele, J.D. Influence of smooth temperature variation on hotspot ignition. Combust. Theory Model. 2018, 22, 110–130. [Google Scholar] [CrossRef]
- Regele, J.D.; Kassoy, D.R.; Vezolainen, A.; Vasilyev, O.V. Indirect detonation initiation using acoustic timescale thermal power deposition. Phys. Fluids 2013, 25, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Regele, J.D.; Kassoy, D.R.; Aslani, M.; Vasilyev, O.V. Evolution of detonation formation initiated by a spatially distributed, transient energy source. J. Fluid Mech. 2016, 802, 305–332. [Google Scholar] [CrossRef] [Green Version]
- Aslani, M.; Regele, J.D. Numerical simulation of finite disturbances interacting with laminar premixed flames. Combust. Theory Model. 2018, 22, 812–833. [Google Scholar] [CrossRef]
- Reckinger, S.J.; Livescu, D.; Vasilyev, O.V. Adaptive wavelet collocation method simulations of Rayleigh-Taylor instability. Phys. Scr. 2010, 2010, 014064. [Google Scholar] [CrossRef] [Green Version]
- Reckinger, S.J.; Livescu, D.; Vasilyev, O.V. Comprehensive numerical methodology for direct numerical simulations of compressible Rayleigh-Taylor instability. J. Comput. Phys. 2016, 313, 181–208. [Google Scholar] [CrossRef]
- Wei, T.; Livescu, D. Late-time quadratic growth in single-mode Rayleigh-Taylor instability. Phys. Rev. E 2012, 86, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Alam, J.M.; Kevlahan, N.K.; Vasilyev, O.V.; Hossain, Z. A multiresolution model for the simulation of transient heat and mass transfer. Numer. Heat Transf. Part B Fundam. 2012, 61, 147–170. [Google Scholar] [CrossRef] [Green Version]
- Ghia, U.; Ghia, K.N.; Shin, C.T. High-Re Solutions for Incompressible Flow Using the Navier-Stokes Equations and a Multigrid Method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Botella, O.; Peyret, R. Benchmark spectral results on the lid-driven cavity flow. Comput. Fluids 1998, 27, 421–433. [Google Scholar] [CrossRef]
- De Stefano, G.; Brown-Dymkoski, E.; Vasilyev, O.V. Wavelet-based adaptive large-eddy simulation of supersonic channel flow. J. Fluid Mech. 2020, 901. [Google Scholar] [CrossRef]
- Farge, M.; Rabreau, G. Transformee en ondelettes pour detecter et analyser les structures coherentes dans les ecoulements turbulents bidimensionnels. C. R. Acad. Sci. Paris 1988, II, 1479–1486. [Google Scholar]
- Fröhlich, J.; Schneider, K. Numerical simulation of decaying turbulence in an adaptive wavelet basis. Appl. Comput. Harmon. Anal. 1996, 3, 393–397. [Google Scholar] [CrossRef] [Green Version]
- Kevlahan, N.K.R.; Alam, J.; Vasilyev, O.V. Scaling of space-time modes with Reynolds number in two-dimensional turbulence. J. Fluid Mech. 2007, 570, 217–226. [Google Scholar] [CrossRef] [Green Version]
- Farge, M.; Schneider, K.; Kevlahan, N. Non-Gaussianity and coherent vortex simulation for two-dimensional Nurbulence using an adaptive orthogonal wavelet basis. Phys. Fluids 1999, 11, 2187–2201. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, D.E.; Vasilyev, O.V. Stochastic coherent adaptive large eddy simulation method. Phys. Fluids 2004, 16, 2497–2513. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V. A fully adaptive wavelet-based approach to homogeneous turbulence simulation. J. Fluid Mech. 2012, 695, 149–172. [Google Scholar] [CrossRef]
- Nejadmalayeri, A.; Vezolainen, A.; De Stefano, G.; Vasilyev, O.V. Fully adaptive turbulence simulations based on Lagrangian spatio-temporally varying wavelet thresholding. J. Fluid Mech. 2014, 749, 794–817. [Google Scholar] [CrossRef] [Green Version]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Sweldens, W. The lifting scheme: A custom-design construction of biorthogonal wavelets. Appl. Comput. Harmon. Anal. 1996, 3, 186–200. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, D.E.; Vasilyev, O.V.; Kevlahan, N.K. CVS and SCALES simulation of 3-D isotropic turbulence. J. Turbul. 2005, 6, 1–20. [Google Scholar] [CrossRef]
- Vasilyev, O.V.; De Stefano, G.; Goldstein, D.E.; Kevlahan, N.K. Lagrangian dynamic SGS model for stochastic coherent adaptive large eddy simulation. J. Turbul. 2008, 9, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Vasilyev, O.V. Hybrid adaptive wavelet collocation-Brinkman penalisation method for unsteady RANS simulations of compressible flow around bluff bodies. In Proceedings of the 36th AIAA Fluid Dynamics Conference, San Francisco, CA, USA, 5–8 June 2006; Collection of Technical Papers. Volume 1, pp. 730–739. [Google Scholar] [CrossRef] [Green Version]
- Ge, X.; Vasilyev, O.V.; De Stefano, G.; Yousuff Hussaini, M. Wavelet-Based Adaptive Unsteady Reynolds-Averaged Navier–Stokes Simulations of Wall-Bounded Compressible Turbulent Flows. AIAA J. 2020, 58, 1529–1549. [Google Scholar] [CrossRef]
- Ge, X.; Vasilyev, O.V.; Hussaini, M.Y. Wavelet-based adaptive delayed detached eddy simulations for wall-bounded compressible turbulent flows. J. Fluid Mech. 2019, 873, 1116–1157. [Google Scholar] [CrossRef]
- Nejadmalayeri, A.; Vezolainen, A.; Vasilyev, O.V. Reynolds number scaling of coherent vortex simulation and stochastic coherent adaptive large eddy simulation. Phys. Fluids 2013, 25, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Nejadmalayeri, A.; Vasilyev, O.V.; Vezolainen, A. Computational Complexity of Adaptive LES with Variable Fidelity Model Refinement. In Direct and Large-Eddy Simulation IX; Fröhlich, J., Kuerten, H., Geurts, B.J., Armenio, V., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 149–153. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehta, Y.; Nejadmalayeri, A.; Regele, J.D. Computational Fluid Dynamics Using the Adaptive Wavelet-Collocation Method. Fluids 2021, 6, 377. https://doi.org/10.3390/fluids6110377
Mehta Y, Nejadmalayeri A, Regele JD. Computational Fluid Dynamics Using the Adaptive Wavelet-Collocation Method. Fluids. 2021; 6(11):377. https://doi.org/10.3390/fluids6110377
Chicago/Turabian StyleMehta, Yash, Ari Nejadmalayeri, and Jonathan David Regele. 2021. "Computational Fluid Dynamics Using the Adaptive Wavelet-Collocation Method" Fluids 6, no. 11: 377. https://doi.org/10.3390/fluids6110377
APA StyleMehta, Y., Nejadmalayeri, A., & Regele, J. D. (2021). Computational Fluid Dynamics Using the Adaptive Wavelet-Collocation Method. Fluids, 6(11), 377. https://doi.org/10.3390/fluids6110377





