Abstract
We perform high-resolution numerical simulations of three-dimensional dynamics of an elongated bubble in a microchannel at moderate Reynolds numbers up to 1800. For this purpose, we use the coupled Brinkman penalization and volume of fluid methods implemented in the open-source framework Basilisk. The new results are validated with available experimental data and compared with previous numerical and theoretical predictions. We extend existing results to regimes with significant inertia, which are characterized by intense deformations of the bubble, including cases with azimuthal symmetry breaking. Various dynamical features are analyzed in terms of their spatiotemporal characteristics, such as frequencies and wavelengths of the bubble surface undulations and vortical structures in the flow.
1. Introduction
Understanding the flow of viscous liquid containing gas bubbles is a classical and challenging problem in multiphase fluid dynamics. It has attracted much attention in the literature because of its importance in numerous applications in areas such as the miniaturization of technologies [1,2,3,4], enhanced oil recovery [5], biomedical research [6,7,8,9], cooling of microcircuits [10,11,12], chemical microreactors [13,14,15], and numerous others.
In this work, we use supercomputer simulations to investigate the dynamics of an elongated air bubble in viscous flow in a water-filled microchannel, the so-called Taylor flow. Particular attention is paid to the regimes with substantial inertia when the bubble motion is strongly time-dependent and is associated with the loss of axial symmetry.
The main object of interest in the study of Taylor flow is the thickness and the shape of the thin layer between the bubble and the tube wall, and the bubble velocity relative to the bulk flow velocity. The film plays a crucial role in many processes that are important for technological applications. It strongly affects the heat transfer from the walls to the bulk liquid [16]. If there is a mass transfer between the bubble and the bulk fluid, it is also dependent sensitively on the film thickness [17]. It becomes therefore very important to understand the precise shape and dynamics of the thin film, and computational studies of Taylor flow must be careful to resolve the film with a fine-enough mesh [18]. Other features of the flow which are of interest from a practical point of view are the vortical structures within and around the bubble. The reason is that strong vorticity helps mixing of matter and enhances heat transfer processes between the tube wall and the bulk fluid.
Fundamental studies of the Taylor bubble began with the work of Taylor [19], who measured the bubble velocity (more precisely, the relative excess velocity , where is the bubble velocity, is the mean flow velocity in the carrier fluid) as a function of the capillary number for , where is the dynamic viscosity of the bulk fluid and is the surface tension coefficient. The dependence was shown to follow at very small values of Ca (note that this dependence has been corrected later by Bretherton [20] to follow ) and to deviate substantially from this form at any reasonably large Ca. Taylor’s data have subsequently been correlated by a different dependence in [21], where the authors also proposed the relation for the film thickness h relative to the capillary radius r given by . Further empirical extensions of this correlation to include the effects of inertia can be found in [22].
Experimental measurements of the film thickness in the Taylor flow have been carried out in [21,22,23]. The measurements require significant spatial resolution (hundreds of nanometers) and, at high flow speeds, additionally require good temporal resolution due to the large frequency of oscillations (several kilohertz) of the bubble shape. We note that, if the film thickness becomes too small, even locally during the oscillations, it may result in the rupture of the film [24]. Simulations of this phenomenon require modifications of the underlying model to include the effects of disjoining pressure and contact angles, which is outside the scope of our work.
The first theoretical analysis of the Taylor flow was carried out by Bretherton [20]. He assumed axially symmetric steady-state flow and, using the standard assumptions of lubrication theory, calculated the relative excess velocity as a function of the capillary number. The relationship between the film thickness and the capillary number was found to be . This prediction was used as the leading term in the empirical expression of [21] at small Ca.
In recent work [25], a more general theory of the steady-state axially symmetric shape of the bubble that includes the effects of inertia as well as of viscosity and surface tension was developed. This work substantially extends the prior results [19,20,21,22]. New theoretical predictions are in good agreement with the experiments, and as we show in the sections below, their predictions are also in good agreement with our numerical simulations in parameter regimes corresponding to the steady or quasi-steady dynamics of the bubble.
The presence of a thin liquid layer between the bubble and the capillary wall makes the Taylor bubble a multiscale phenomenon, which poses a challenge not only for the theory and experiment but also for numerical simulations. The details of the computational difficulties depend on the relative role of the viscosity, capillarity, and inertia. First, when the inertial effects are significant, the bubble shape undergoes substantial deformations that evolve in a highly complex manner, resulting sometimes in the bubble breakup into smaller bubbles that shed from the back side. Second, the thin liquid layer between the bubble and the walls undergoes strong wavy deformations. These deformations must be resolved in numerical simulations, which is nearly impossible without adaptive meshes. Third, accurate calculation of the complex deforming surface of the bubble requires proper numerical techniques for capturing interface evolution. Finally, due to the extreme multiscale nature of the phenomenon, substantial computational resources are required to simulate the bubble dynamics, especially at high Reynolds numbers when inertial effects are significant.
In previous simulations of the Taylor flow [23,26,27], the commercial software Ansys Fluent and open-source OpenFOAM were used. They both use the volume of fluid (VOF) method to track the free interface. The authors were able to predict the bubble shape in various regimes ranging from steady states at small Reynolds numbers to axially symmetric unsteady oscillations at moderate Reynolds numbers. In some cases, their simulations indicated breaking of the axial symmetry [26], but such regimes have not been explored in detail. It must be pointed out that the efficiency of a numerical algorithm is influenced by the structure of the computational mesh used, whether it is fixed or adaptive. Since the Taylor bubble is in constant motion and can deform substantially, we must require that the mesh used is refined near the bubble, especially in the thin film near the wall. The problem of mesh adaptation becomes quite serious if the length of the microchannel is much longer than the smallest scale of the flow, that of the thin film. In our case, the channel length is up to 30 times larger than the channel diameter and 2200 times larger than the film thickness. In [23,26,27], a fixed grid was used, while [28,29] used adaptive meshes. In recent work [30], the authors carry out three-dimensional simulations of the Taylor flow accounting for the presence of surfactants. Again, a uniform Cartesian mesh was used. The inertial effects considered were relatively small such that strongly unsteady or non-axisymmetric structures were not observed.
Our analysis focuses on high-resolution three-dimensional simulations of the Taylor flow. The simulations are carried out using the numerical algorithm we proposed in [31], which is implemented in the open-source software Basilisk [32]. It allows for highly accurate simulations using effective mesh adaptation to resolve all multiscale features of the flow, especially the thin-film flow between the bubble and the wall. Our choice of geometry and flow conditions follows [23] for the purpose of validation and comparison with their experiments and simulations. We compare our results also with the numerical results of other researchers for a wide range of capillary and Reynolds numbers.
In addition to the cases with relatively small Reynolds numbers when the bubble shape remains quasi-steady and axisymmetric, we also investigated highly unstable regimes corresponding to large Reynolds numbers at which the bubble deformations are substantial and the film thickness oscillates at high frequencies undergoing strong undulatory motion. The frequency analysis of both the thickness and various characteristic points of the bubble is performed using the Fourier spectral analysis, which allows us to identify characteristic frequencies of the flow. At relatively large Reynolds numbers, we also identified a symmetry-breaking transition from the axisymmetric oscillations to asymmetric oscillations and analyzed the nature of the resultant shapes and the physical origin of the observed features.
The remainder of the paper is organized as follows. In Section 2, we explain the problem setting, formulate the main questions, introduce the governing equations, and briefly describe the numerical method used for solving the governing equations. Section 4 and Section 5 contain the results of three-dimensional numerical simulations for a range of conditions corresponding both to axially symmetric and asymmetric shapes of the bubble. In these sections, comparisons with the experiments and prior work are presented, and the observed dynamics are explained in terms of the oscillation characteristics of the bubble and of the thin film between the bubble and the tube wall. In Section 5, we also illustrate the flow around the bubble visualizing the vortical structures constructed using one of the techniques of vortex identification. Concluding remarks are given in Section 6.
2. The Problem Formulation
We consider the situation depicted schematically in Figure 1. A cylindrical tube of diameter d contains a viscous fluid flowing from left to right with mean velocity . The fluid contains a bubble of a sufficiently large size such that it has an elongated shape filling most of the cross section of the tube and forming a thin film of thickness h near the tube wall. The densities and dynamic viscosities of the fluid and bubble are and , respectively.
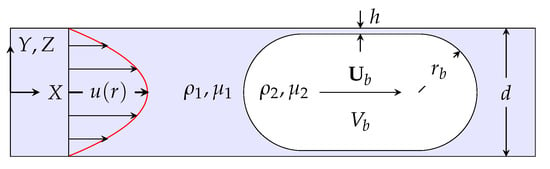
Figure 1.
Schematics of the fluid flow with a bubble in a cylindrical tube. The bubble volume is denoted as , and the radii of the end caps are . The velocity profile is initially parabolic everywhere, and and is set to be parabolic at the left end of the tube at all times. In what follows, the film thickness h is nondimensionalized by the tube diameter as .
As known from experiments, the bubble generally moves with a velocity that is larger than , with the difference depending on various parameters of the problem. The bubble dynamics depends on the Reynolds and capillary numbers of the flow, defined as
where is the surface tension coefficient, as well as on the density and viscosity ratios of the fluids, the bubble size, and the tube diameter. Our goal in this work is to investigate the three-dimensional dynamics of the bubble in various flow conditions corresponding to a wide range of Re and Ca. The effects of gravity are neglected assuming that the tube diameter is small in the sense that the corresponding Bond number is small, i.e., , where , and g is gravitational acceleration.
One of the primary quantities of interest in this flow is the film thickness relative to the tube diameter, . When buoyancy and inertial effects are negligible ( and ), the flow is in a visco-capillary regime [21] governed by the viscous and capillary forces, and then, the thickness of the film depends only on Ca. In the lubrication theory of Bretherton [20], it is found that for a small ,
For larger values of Ca, viscous effects become important and lead to thickening of the film, which also leads to an increase in the bubble velocity relative to the mean flow velocity . Aussillous and Quéré [21] proposed an empirical correlation that extended (2) to larger values of Ca as
This relation is determined by fitting against Taylor’s experimental data [19], and hence, it is referred to as the Taylor law. The correlation (3) is valid for Ca from about to about 2. Note that a more general correlation that also includes the dependence on Reynolds and Weber numbers was obtained in [22]. In comparisons below, we use Expression (3).
With an increase in the Reynolds number, the inertial effects become comparable with viscous and capillary effects, and the Correlations (2) and (3) become inaccurate. The influence of inertia on the thickness of the liquid film of an elongated bubble was studied analytically, numerically, and experimentally in [21,23,25,33]. In [25,33], the non-monotonic, U-shaped behavior of the film thickness is observed, such that at high the thickness decreases up to , then increases at . Additionally, the influence of inertia elongates the bubble nose and modifies the bubble tail from the almost spherical shape to the flat one [23,34]. Near the tail, the thickness can oscillate and the oscillation amplitude increases with Re, leading to difficulties with measurements of the thickness.
There is a useful relationship between the film thickness and the bubble velocity that follows from the basic mass conservation. Assuming steady flow, the mass conservation leads to
where is the diameter of the bubble and is the average velocity of the liquid film. If the thin liquid film is further assumed stagnant in the visco-capillary regime, i.e., , the dimensionless film thickness is related to the flow and bubble velocities as [35]:
This relationship is used further below to estimate the mean thickness of the film and to compare with other, more direct, measurements of the thickness from the simulation results.
3. Governing Equations and the Numerical Method
Here, we describe the governing equations, the initial and boundary conditions, and the numerical method used to solve the equations. The numerical method is based on the algorithm implemented in the open source software Basilisk, and its detailed description is reported in our recent work [31].
The governing equations are based on the Navier–Stokes equations for incompressible Newtonian fluids that are modified to handle multiphase flows containing solid boundaries to treat all phases as a single fluid. The equations are given by
where is the velocity vector, t is time, is density, is the dynamic viscosity, p is pressure, and is the viscous stress tensor. The last equation above, (7), describes the advection of a scalar field , which is the volume fraction of the carrier fluid 1. This equation is used to track the fluid interface evolution. In the pure liquid, , and in the gas, . The source terms and are the surface tension force (so-called continuum surface force) and a penalization term due to the presence of solids. Their inclusion in the Navier–Stokes equations allows for a volume representation of interfacial effects at fluid–fluid or fluid–solid boundaries [31].
In particular, the continuum surface force is given by [36]
where is the surface total curvature, is the Dirac distribution used to represent the interfacial localization of the surface tension, is the unit normal vector to the interface, and is the average density of the two fluid phases.
The presence of solids, either as inclusions or as boundaries (as in the present problem) is modeled via their representation as porous media with vanishing permeability [37,38]. The Brinkman penalization term
is added to the momentum equation as the body force, where is the solid volume fraction, is the penalization coefficient, and is the local velocity of the solid. In our case, the solid is a fixed cylinder so that . The penalization coefficient is taken as , where number [31].
The local averaged density and dynamic viscosity of the fluids are calculated via the volume fraction of fluid 1 and the field using interpolation:
where subscript 3 refers to the solid phase. This definition ensures the following: and inside solids ( and any ); and inside fluid 1 ( and ); and and inside fluid 2 ( and ). The tube inner wall is modeled as a perfectly wet surface so that the fictitious volume fraction of fluid 1 inside the solid is taken as .
The equations above are solved using the open-source software Basilisk [32], which uses the Cartesian grid with adaptive mesh refinement (AMR) and the volume of fluid method (VOF). The AMR technique allows us to obtain highly resolved accurate simulation results for problems involving various interfaces. The fluid volume fraction is tracked using the geometric VOF method [39] which is conservative and non-diffusive. It allows one to simulate multiphase flows with complex topological changes with accurate interface representation. A detailed analysis of the method can be found in [31].
For the boundary conditions at the inlet, , we use a prescribed parabolic velocity profile with a given mean, , and a zero pressure gradient. At the outlet, , the pressure is set to zero, and the homogeneous Neumann condition on velocity is set. At the walls, the no-slip condition is set.
As the initial condition, a parabolic velocity profile is taken for the whole fluid domain including the bubble. The bubble is assumed to be a cylinder with two spherical caps on the ends with radius . The presence of the bubble in the flow makes the pressure field distinct from that of the usual Poiseuille flow and follows from the governing equations to conform to the given velocity field and the geometry of the bubble.
4. Simulation Results: Axially Symmetric Motion
In this and the following sections, we consider various regimes of the flow focusing on the axisymmetric situations first in this section and nonsymmetric cases in the next.
The following geometric parameters and fluid properties are used. The tube diameter is mm. The fluids correspond to air in the bubble and water as the carrier fluid. The water density , air density , water viscosity , air viscosity , and surface tension . The results are presented in dimensionless form using the diameter of the channel d, the mean velocity , and the water density as scales of the corresponding variables and parameters. The dimensionless versions of coordinates and the channel length L are , respectively.
The simulations below cover the ranges of and of , which correspond to a wide range of scales for the film thickness, the smallest scale that must be accurately resolved in the simulations. The level of refinement of the adaptive grid is chosen to provide sufficient resolution of the film thickness (see Table 1). The bubble size and the tube length over which the computations are carried out are much larger than the small scales of the thin-film flow. In our simulations, the ratio reaches 900–2200, so that extremely wide range of scales are involved in this multiscale problem. All simulations reported are three dimensional and have been obtained on Skoltech’s Arkuda cluster that has Intel(R) Xeon(R) CPU E5-2698 v4 (40 cores at GHz). To give an idea of the computational cost, case AW4, for example, required 120,000 CPU hours and took about 25 days on 200 cores.

Table 1.
Parameters and flow properties for the first five cases AW1 to AW5. Simulation results (indicated as BPM, for Brinkman Penalization Method) are compared with the experiments of Khodaparast et al. [23]. Here, is the mean velocity at the inflow, is the mean velocity of the bubble, is the dimensionless averaged thickness, l is the dimensionless channel length, is the maximum level of refinement, and is the number of cells for the film resolution that is required to satisfy .
We first consider the problem of the bubble motion when the capillary number Ca is relatively small. This allows us, in particular, to verify the bubble shape with experiments and previous numerical simulations. For this purpose, we take the parameters shown in Table 1, which correspond to ([23], Appendix: cases 18–22). Various cases in Table 1 will be referred to as AW1–AW5 below. The capillary number Ca in the table is computed based on the present simulation results. The smallest mesh size is controlled by the maximum level of refinement as .
Next, we investigate the bubble shape and its oscillation characteristics, its velocity, and the film thickness for the cases shown in Table 1.
4.1. The Bubble Shape
In Figure 2, the bubble shapes are shown at different times and at various values of Ca. Our results (black curves) are compared with the experimental data and two-dimensional axisymmetric numerical simulations from [23], which were obtained using ANSYS Fluent [40] and OpenFOAM [41]. In [23], the authors used structured orthogonal non-uniform fixed grids consisting of 50 cells in the radial direction. The core region was resolved using 40 uniform cells, while the film region was gradually refined using 10 cells and achieved a maximum aspect ratio of about 30. The same grids were used in OpenFOAM and ANSYS Fluent, and no appreciable differences were observed.
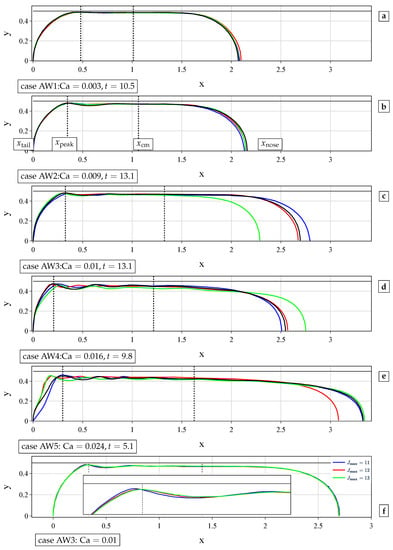
Figure 2.
(a–e) Comparison of the experimental [23] (blue) and numerical (red: ANSYS Fluent [23], green: OpenFOAM [23], and black: present work) results of air–water interfaces in the tube with diameter μm. The results from [23] are reproduced with the authors’ permission. (f) Convergence of the bubble profile with the mesh refinement for case AW3. Three levels of refinement are considered: . The inset is the zoom-in of the top-left part of the profile.
While axisymmetric simulations are sufficient for the cases in Figure 2a–c, for large Ca numbers (see Figure 2d), the bubble shape becomes more complex and the differences between the axisymmetric simulations and experiment become more pronounced. The results of OpenFOAM simulations in Figure 2b,c and ANSYS Fluent in Figure 2b,d show noticeable discrepancies with the experiments in terms of the volume (hence the mass) of the bubble. The likely reasons for these large errors may be first that the meshes used were too crude and second that the flow was actually not axisymmetric. The present results agree relatively well with the experiments for all of the cases shown. When using courser meshes, we could also observe larger errors in the mass conservation.
At the beginning of the simulations, the bubble undergoes some shape oscillations due to the choice of initial conditions, but they eventually damp, and the bubble reaches a steady or a quasi-steady state for cases of Figure 2a–c. Importantly, in Figure 2e, the bubble does not reach a steady state, and the oscillations lead to breaking of the axial symmetry (see also Figure 8e–h below). Similar symmetry breaking was also seen in ([26], Figure 14).
We also use this example of Figure 2 to demonstrate the grid convergence. Figure 2f shows the profile of the bubble for case AW3 computed at three different levels of the mesh refinement: . This particular case AW3 is chosen because of its axisymmetric and stationary bubble shape. The profiles are first close to each other for all of the cases and second converge with the increase in . Note that, with , the film thickness is covered with only 3 mesh cells. With , the number of cells is , respectively, which improves the accuracy. We mention that the authors of [42] recommend taking at least five grid points in the liquid film in the radial direction. While such a recommendation is always subjective and dependent on the required accuracy, we indeed find that even with only three cells in the film, the prediction is rather accurate for case AW3 (see the inset of Figure 2f). For more unsteady and unstable situations, better refinement may be needed.
In Figure 3, we compare our simulations with a theoretical model of Magnini et al. [25], where the authors studied steady-state undulations on the surface of the Taylor bubble. The classical axisymmetric Bretherton model was extended to account for the effects of inertia and of the curvature of the channel wall. Note that, in [25], the Reynolds number was defined based on the bubble velocity rather than the mean velocity. Hence, there is a difference of factor with our definition. The comparison shown in Figure 3 indicates that both the steady-state theory and the present simulations are in good agreement with each other as well as with experiment.
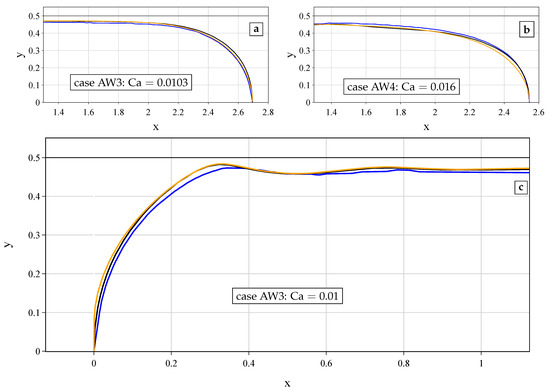
Figure 3.
Comparison of the profiles of the front (a,b) and back (c) shapes of the bubble computed by the present method (black), predicted theoretically (orange, calculated following the formulation of [25]) and measured experimentally (blue, [23]). Relatively stable cases AW3 and AW4 are considered. The results from [23] are reproduced with the permission of the authors.
4.2. Film Thickness and Its Dynamics
Here, we analyze the dynamics of the film by looking at how its thickness varies in space and time. Usually, the thickness of the flat region of the film is taken as the film thickness. However, at the largest capillary numbers, it is not possible to identify this region. For large capillary numbers, various methods for estimating the film thickness have been proposed: (1) as an average value in the region far from the nose of the bubble [23], (2) as the average thickness between the coordinates of the first peak and the center of mass of the bubble [26], and (3) as an estimate by (4) [35]. Here, we analyze the minimum , average , and estimated thicknesses, as shown in Table 1 and in Figure 4 below.
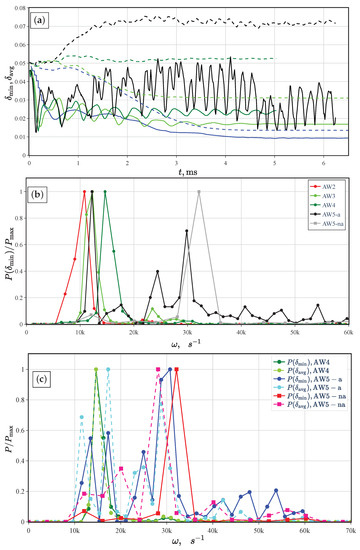
Figure 4.
(a) The dimensionless film thicknesses (solid) and (dashed) as functions of time t. Different cases are marked by the following colors for (a) and (b): AW1 (  ), AW2 (
), AW2 (  ), AW3 (
), AW3 (  ), AW4 (
), AW4 (  ), and AW5(
), and AW5(  ). AW2 is similar to AW3 and hence is omitted in (a). (b) The filtered power spectrum of the minimum thickness, , for cases AW2–AW5. The signals of case AW5 are split into axial ( ms) and non-axial ( ms) indicated by the circle and square marks, respectively. (c) The spectrum comparison of and for AW4–AW5 cases.
). AW2 is similar to AW3 and hence is omitted in (a). (b) The filtered power spectrum of the minimum thickness, , for cases AW2–AW5. The signals of case AW5 are split into axial ( ms) and non-axial ( ms) indicated by the circle and square marks, respectively. (c) The spectrum comparison of and for AW4–AW5 cases.
 ), AW2 (
), AW2 (  ), AW3 (
), AW3 (  ), AW4 (
), AW4 (  ), and AW5(
), and AW5(  ). AW2 is similar to AW3 and hence is omitted in (a). (b) The filtered power spectrum of the minimum thickness, , for cases AW2–AW5. The signals of case AW5 are split into axial ( ms) and non-axial ( ms) indicated by the circle and square marks, respectively. (c) The spectrum comparison of and for AW4–AW5 cases.
). AW2 is similar to AW3 and hence is omitted in (a). (b) The filtered power spectrum of the minimum thickness, , for cases AW2–AW5. The signals of case AW5 are split into axial ( ms) and non-axial ( ms) indicated by the circle and square marks, respectively. (c) The spectrum comparison of and for AW4–AW5 cases.
The average thickness at some fixed time is determined from the numerical computation of coordinates of the first peak at the back of the bubble, ; the center of mass, ; and the bubble volume, , between cross sections through these points:
Something similar has also been presented in [26]. These cross sections are shown in Figure 2d as dotted lines.
The average thickness tends smoothly toward stationary values for cases AW1–AW4 at ms (Figure 4a). The minimum thickness oscillates strongly at the beginning and then attenuates. In case AW5, the average film thickness increases to and the bubble elongates (Figure 2d). The minimum thickness oscillates around certain average value, and its amplitude does not decay. The minimum and average thicknesses are time-averaged to obtain , . The estimated thickness is obtained from velocity values. All of these quantities are presented in Table 2.

Table 2.
The minimum, ; time-averaged, ; and estimated from (4), thicknesses, , and dominant frequencies, , for .
Since oscillations of are observed for cases AW2–AW5, to extract dominant frequencies in the signal, Fourier analysis is performed with a high-pass filter to cut-off parasitic low frequencies. It is found that, in cases AW2–AW4, there is one dominant frequency that coincides with the dominant frequency of (see Table 2). The dynamics of case AW5 can be divided into three distinct stages: (1) a transition regime, when the initial cylindrical bubble deforms to take an elongated shape; (2) axially symmetric oscillations occur (AW5-a); and (3) the axial symmetry breaks, and a three-dimensional dynamic structure emerges (AW5-na). AW5 contains both axially symmetric and asymmetric oscillations, and the first stage contains a series of frequencies, but thereafter, only one dominant frequency remains. In all cases, it is observed that the dominant frequency slightly increases with velocity.
In Figure 4c, the dominant frequencies for and of AW4 and AW5 are compared. For AW4, the dominant frequency remains the same for both ’s, while for AW5, the spectrum of is shifted to the left. Three dominant frequencies for average thickness in case AW5-a can be seen: s−1, with the third one here being the sum of the first two. As seen in Figure 4a, there are low-frequency oscillations, which then transform to a high-frequency signal (AW5-na). Indeed, it is confirmed by the spectrum in Figure 4c, where the low-frequencies fade and only one dominant frequency remains, s−1. A similar spectrum is observed for . Hence, the consistency in and spectra is observed.
To provide some insight into the origin of the observed frequencies, we estimate the frequencies from the dispersion relation for water waves with dominant capillary effects,
where is the frequency of the waves; is their wavenumber, with being the wavelength; and H the fluid depth. We estimate the latter as the film thickness for waves on the film and as for oscillations at the back of the bubble.
In Table 2, we show various properties of the bubble oscillation for cases AW1 to AW5, including the dominant frequencies of the oscillations. Case AW1 does not exhibit any appreciable sustained oscillations, while for the other cases we observe the following. Cases AW2–AW4, which are not too unstable, have frequencies of about (10 to 16) , while case AW5 has two dominant frequencies of about (12 and 30) . A possible explanation of the physical origin of these frequencies may be as follows. At relatively small Reynolds numbers of cases AW2–AW4, the oscillations of the thin layer are the result of the forcing due to the strong oscillations of the back of the bubble. They arise in the back and propagate along the layer damping toward the front of the bubble. Their frequency can be estimated from (13) using and mm as . This is close to the numerical values shown in Table 2 in all cases. Two frequencies of case AW5 could be explained as one coming from the same origin as in the previous cases and the other arising from the instability of the thin layer itself. The instability may be caused by the influence of the strong flow of the gas inside the bubble relative to the layer or, again, by the oscillations at the back of the bubble. If this is indeed the case, the second frequency can be estimated from the same dispersion relation (13) using μm now instead of infinity. The wavelength of the ripples in Figure 2d can be estimated as mm with the corresponding wavenumber mm−1, which gives , which is close to the second dominant frequency of (AW5-na) and of in Figure 4 and Figure 7, respectively. Hence, the arguments above appear to provide a plausible mechanism for the observed frequencies.
Therefore, we may conclude that, at relatively small Reynolds numbers, the undulations of the film are purely the result of the oscillations of the bubble tail, while at larger Reynolds numbers, there is an additional frequency due to the waves on the thin film arising because of its instability, which is excited either by the tail oscillations or by the relative motion of the gas in the bubble. The gas motion may excite waves on the film akin to the wind-driven waves on the free surface of water when the wind speed exceeds certain critical value. Further and more detailed calculations may be required to confirm and elucidate the precise mechanisms of the ripple formation on the thin film.
In Figure 5, we compare the dimensionless minimum, average, and estimated thicknesses of the film depending on the capillary number Ca with the results of experiments and numerical simulations [23,26] and an empirical correlation from [21]. The experimental and empirical results fall between and . Note that the experimental data in [26] were based on the experiments of [23], with the only difference being in the method of thickness measurements. Specifically, [23] defined the thickness as that in the uniform region while [26] defined it as given by (12). For , a good agreement is seen between the results of both numerical simulations and experiments. At larger Ca, the experimental and all numerical results show systematic deviation from Taylor’s law (3). The reason is the increased importance of inertial effects even at relatively small capillary numbers, since the Weber number and the Reynolds number are relatively large. In [21], the authors introduced a non-dimensional number , which is equal to for an air–water system and tube diameter mm. According to [21], for low-viscosity liquids and high F numbers, the relationship deviates from Taylor’s law, and for the air–water system, Taylor’s law applies only for . The numerical simulations with OpenFOAM with flexCLV (2D, 3D) [26] and our present results () are within the margin of error of experiments. The thickness calculated numerically using interFOAM in 2D is slightly larger than that in experiments. The minimum thickness grows substantially slower in comparison with the experimental results and the empirical correlation. We point out that the thickness obtained using (4) is very close to the results of experiments of Khodaparast et al. [23] even for large Ca.
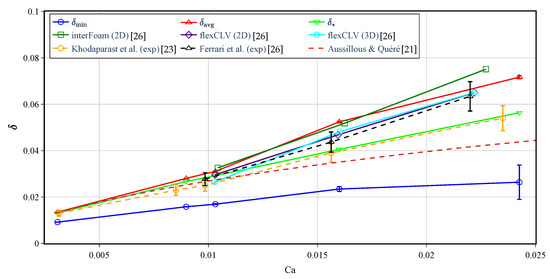
Figure 5.
Comparison of the dimensionless minimum , average (12), and estimated (4) thicknesses versus the capillary number with the results of numerical simulations in OpenFOAM [23,26], experiments [23,26], and empirical correlation of [21]. Note that the experimental results in [26] are based on [23], but the film thickness is estimated using (12). The minimum thickness, , gives an idea of the range of deviation from the average. The error bar for the present results is calculated as a standard deviation of the corresponding thickness.
4.3. Bubble Velocity and Its Oscillations
The bubbles in a microchannel move faster than the average velocity of the fully developed flow. Bretherton has shown [20] that, within the lubrication theory approximation at small Ca, the speed of the bubble exceeds the mean flow speed according to
Comparisons of our numerical predictions with this relation as well as with the experiments and previous simulations are shown in Figure 6. The simulations are seen to somewhat overestimate the velocity in comparison with the experiments in [23]. This is consistent with the results on the film thickness shown in Figure 5 which shows that the film thickness in numerical simulations is larger than that in the experiments. Recall, that (4) shows that the larger thickness corresponds to larger bubble velocity. The interFOAM (2D) shows the largest discrepancy with the experiment. The Bretherton model (14) is also seen to overestimate the velocity. However, note that the Bretherton’s equation is strictly valid only at small Ca and small Re, such as and , as suggested in [25].
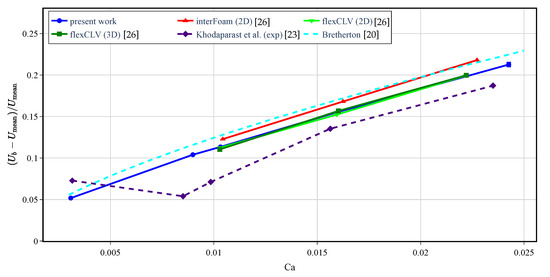
Figure 6.
Comparison of the relative excess of the average bubble velocity over the mean flow velocity, , versus capillary number in the present work with the results of the numerical simulations in [26], experiment of [23], and Bretherton’s theory [20].
Finally, we look at the oscillations of various characteristic points of the bubble (Figure 7) and check if they are consistent with the oscillation characteristics of the film discussed earlier. The position of the tail , first peak , and center of mass oscillate in time, but the bubble nose moves with practically constant velocity. Therefore, the first three coordinates are considered relative to and are denoted as , , and , correspondingly (Figure 7a). The center of mass reaches a plateau during the time ms. In Figure 7b, it is seen that, at the beginning, there is one dominant frequency (solid line). Subsequently, the second independent frequency of about (28 to 32) (dashed line) appears. These frequencies are consistent with those of the film thickness oscillations in Figure 4c (see also Table 2).
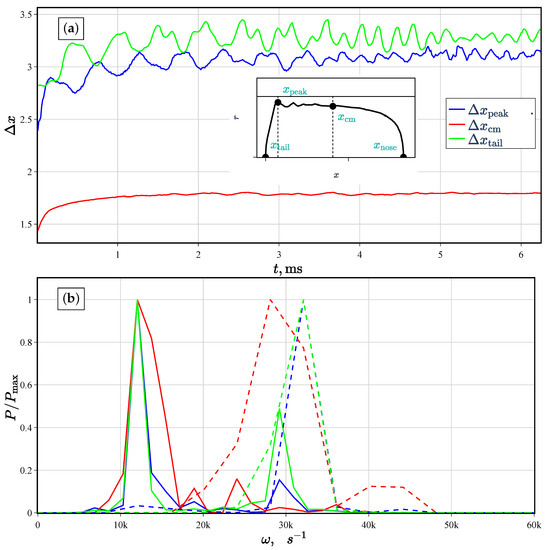
Figure 7.
(a) Positions of the first peak (  ), the bubble center of mass (
), the bubble center of mass (  ), and the tail (
), and the tail (  ) relative to the position of the bubble nose for case AW5. (b) The power spectrum of for axisymmetric oscillations at times ms (solid line) and after symmetry breaking at ms (dashed line).
) relative to the position of the bubble nose for case AW5. (b) The power spectrum of for axisymmetric oscillations at times ms (solid line) and after symmetry breaking at ms (dashed line).
 ), the bubble center of mass (
), the bubble center of mass (  ), and the tail (
), and the tail (  ) relative to the position of the bubble nose for case AW5. (b) The power spectrum of for axisymmetric oscillations at times ms (solid line) and after symmetry breaking at ms (dashed line).
) relative to the position of the bubble nose for case AW5. (b) The power spectrum of for axisymmetric oscillations at times ms (solid line) and after symmetry breaking at ms (dashed line).
5. Simulation Results: Breaking of Axial Symmetry
In this section, we discuss highly resolved three-dimensional simulations of the bubble dynamics for cases AW5 to AW8 (Table 3) at which the bubble deformations are substantially larger than in the previous cases. In [21], the authors observed that increasing the Reynolds number Re at a constant capillary number Ca leads to a longer nose of the bubble and flatter tail. Numerical simulations are consistent with this observation (see Figure 2 and Figure 8). What is important in cases AW5-8 is that the bubble axial symmetry breaks, leading to the formation of wavy structures in the azimuthal direction in the back of the bubble.

Table 3.
Summary of the final velocities of the bubble and the average thicknesses. Here, is the mean velocity at the inflow, is the mean velocity of the bubble, is the dimensionless averaged thickness, and is the number of cells for the film resolution. For all cases AW5–AW8, the volume of the bubble is fixed, . The dimensionless channel length l is taken as 30, and the maximum level of refinement is taken as 13. Note that the bubble velocity and film thickness for cases AW7 and AW8 (indicated by superscript ‘*’) are taken at times ms, respectively. At these times, the bubble approaches but may be somewhat short of its final dynamic state.

Figure 8.
The isometric view of the bubble evolution in case AW5. The color indicates the magnitude of the velocity. Until ms, the oscillations are axially symmetric and then gradually become asymmetric.
Figure 8 displays the observed shape at various times for the least unstable case AW5, with the color indicating the velocity magnitude. Early on in this regime, only axial deformations of the bubble are observed with the thin layer of the carrier fluid between the bubble and the wall exhibiting ripples that are weak near the head of the bubble but increase in strength toward the back. Strong sloshing-like oscillations of the back end of the bubble are seen until about ms, after which the axial symmetry breaks exhibiting period-3 waves in the azimuthal direction. These waves move back and forth between the tube walls and the center with some “spilling” along the wall, which is seen as the ripples on the thin film. The waves are initially radially symmetric (Figure 8a–d), but eventually the radial symmetry breaks, forming three humps along the azimuthal direction (see Supplementary Movie S1).
The waves at the back of the bubble can be interpreted as arising due to the kind of sloshing caused by the relative motion of the bubble and the wall (see [43] for a related qualitative analysis). With this viewpoint, we expect to see various modes determined roughly by Bessel functions in the radial direction and sinusoidal functions in the azimuthal direction. The latter is responsible for the observed asymmetric shapes at the tail and consequently in the film region near the tail. The fundamental mode of the oscillation is radially symmetric and corresponds to our cases AW1–AW4. The radial wavelength of these modes can be estimated as the tube diameter as we have estimated before. Higher modes have shorter wavelength and are asymmetric as we saw in cases AW5–AW6. Of course, these are crude qualitative arguments that are confirmed only by estimates of the frequencies and wavelengths in the simulations versus predictions of the linear dispersion relation (for infinite space rather than for a cylindrical domain, which would have been more appropriate). More detailed and careful analysis of stability is likely to be rather complicated in view of the complex geometry of the flow. However, the above estimates may serve as certain guides in the future development of a more in-depth modeling of the phenomena.
In Figure 9, we show the more unstable cases AW6 to AW8 at four different times for each case. What we notice in these cases is that the instability of the bubble back is stronger, increasing with the case number. Not only is the amplitude of the sloshing-like oscillations of the back larger, but also the number of maxima/minima in the azimuthal direction (azimuthal mode number) increases. The dynamics is highly complex and irregular at saturation. It is also relatively concentrated toward the tail of the bubble (see Supplementary Movie S2).
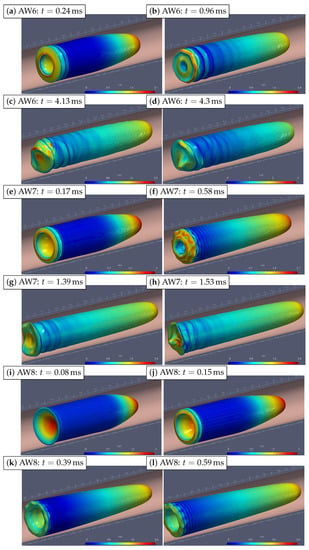
Figure 9.
The isometric view of the bubble evolution for cases AW6 (a–d), AW7 (e–h), and AW8 (i–l). The color indicates the magnitude of the velocity.
Figure 10 shows the back view of the bubble for the cases AW6 to AW8 at various times that show clearly how various azimuthal modes arise and nonlinear patterns form.
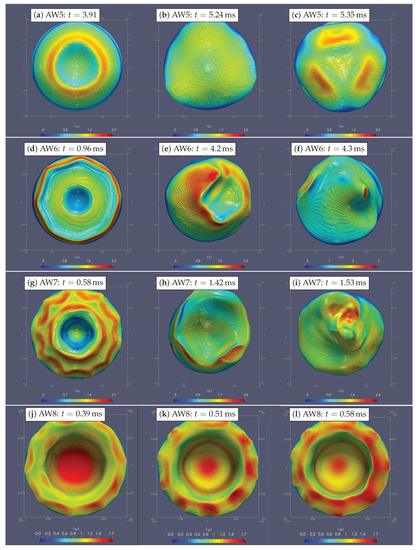
Figure 10.
The tail side view of the bubble for cases AW5–AW8, where asymmetric oscillations are shown at different times.
Figure 11 shows how the number of corners increases with increasing Re. The numerical study is conducted for a wide range of the Reynolds numbers . The symmetrical oscillations are observed up to about . The asymmetric oscillations are subsequently generated with simple modes; then, at larger times, they go over to more complex modes. It was observed that the mode numbers start at 3 for and reach about 10 at . The duration of existence of the simple modes is shortened as Re increases.
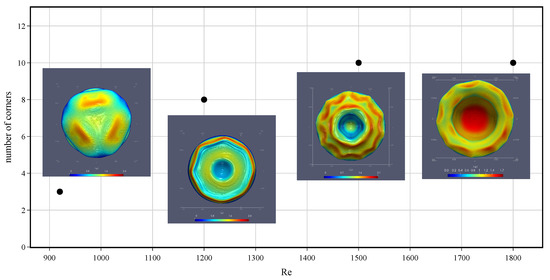
Figure 11.
Number of corners on the tail of the bubble versus the Reynolds number.
Vortical Structures
In order to visualize the flow structure around and downstream of the bubble in various cases considered above, here, we apply the technique of vortex identification proposed in [44]. We note up front that there exists no unique way of identifying vortices in a general flow. In fact, this is still a topic of active research, as evidenced by numerous recent publications. We refer the reader to the review article [45] and to [46], in which the existing methods are analyzed and compared with each other. Even though the criterion of [44] that we use here is perhaps not the most justified of the existing methods, it is relatively simple to use and allows for some useful insight into the coherent vortical structures that exist in the flow under consideration.
In this subsection, the vortices in cases AW5 and AW8 are described and contrasted in connection with the results in previous sections. As mentioned before, due to high Reynolds numbers, and 1800, these cases produce axially asymmetric structures that should somehow be reflected in the vortex field.
In Figure 12 and Figure 13, the visualized vortex structures based on the criterion are shown. We recall the definition and basic ideas behind the criterion. Let , where is the rate of the strain tensor and is the vorticity tensor. The criterion defines a vortex core as a connected region, where has two negative eigenvalues. That is, if eigenvalues of W are sorted as , then in the vortical structure, the second eigenvalue must be negative.
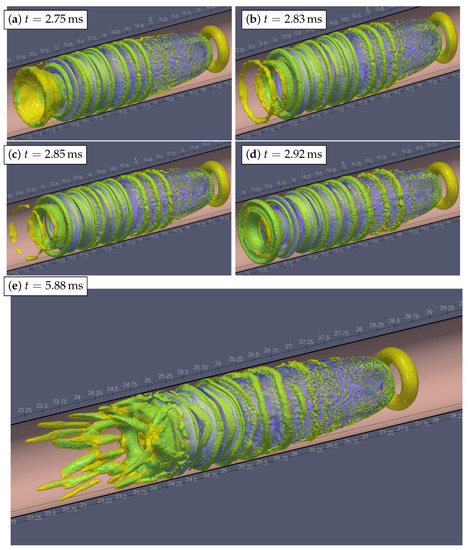
Figure 12.
The vortex structure for case AW5. The color corresponds to isosurfaces of (yellow) and (green).
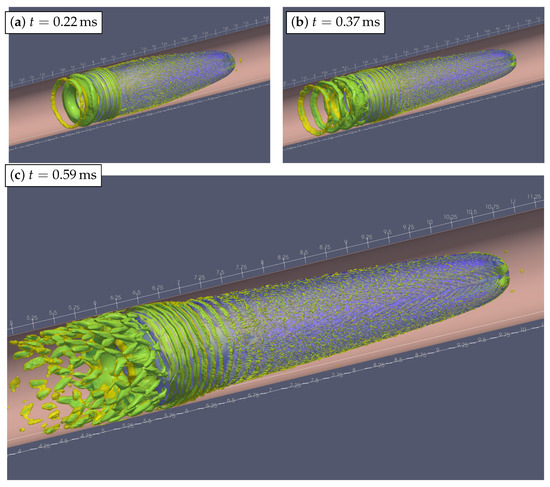
Figure 13.
The vortex structure for case AW8. The color corresponds to isosurfaces of (yellow) and (green).
The criterion is based on the following arguments. One can deduce from the Navier–Stokes equations that [44]
The physical intuition behind the criterion is that, in the vortex core, the pressure is expected to have a local minimum in a plane perpendicular to the vortex axis, and it must not be affected by the first two terms in the above equation, the first of which is the rate of change of (irrotational straining) following the fluid particle and the second is due to viscosity. In that case, . The existence of a local minimum of p implies that has two positive eigenvalues. Therefore, must have two negative eigenvalues. With the ordering indicated above, this requires that .
Isosurfaces of and are shown in Figure 12 and Figure 13. There is a toroidal vortex in front of the bubble in Figure 12 the origin of which can be understood if we move into a coordinate system attached to the bubble. In that frame of reference, the flow velocity is , and therefore, there is a radial position r at which the relative velocity vanishes, . This is the position of the toroidal vortex core. In this regard, see also [19,47,48]. The oscillations at the back of the drop lead to the formation of two kinds of vortices: (i) the main one has a truncated cone shape, and the vortex decays with time and reappears with a new cycle of oscillations; (ii) secondary vortices are seen as ring shape oscillations propagating along the drop and decaying in the middle of the drop. In Figure 13, the toroidal vortex is harder to see due to the choice of the levels of used for the visualization. With a different level surface, the torus becomes more clear. The present choice is made to more clearly illustrate the vortical stuctures around and at the back of the bubble. The dynamics of the vortical structures can be further observed in Supplementary Movie S3.
6. Conclusions
In this work, we studied the dynamics of the Taylor flow—the motion of an elongated bubble in a viscous flow in a microchannel. The analysis was conducted by performing high-resolution three-dimensional numerical simulations using the authors’ extension of the Basilisk software [31]. The solver employs adaptive mesh refinement to resolve fine dynamical features associated with the thin liquid layer between the bubble and the tube wall. The simulations have been performed for a wide range of Reynolds and capillary numbers such that both steady-state and highly unsteady shapes of the bubble are covered. The steady-state and time-dependent axisymmetric results have been validated against available experiments, numerical simulations, and theoretical models.
At relatively large Reynolds numbers, the bubble is found to be highly unsteady and to undergo strong deformations that may lead to asymmetric shapes of the bubble. By analyzing the Fourier spectra of the shape oscillations, we found that the frequency and wavelength of the bubble-surface undulations appear to be controlled by two distinct physical mechanisms. First, at sufficiently small Reynolds numbers, when the bubble velocity is close to the mean velocity, the back side of the bubble oscillates with a certain frequency. These oscillations are transmitted to the film preserving the same frequency. Second, when the Reynolds number is large enough, the bubble oscillations become so strong that the second independent frequency appears. We attribute this frequency to the thin layer instability under the influence of the gas flow in the bubble or caused by the perturbations coming from the backside oscillations. The estimates of the frequencies based on the linear dispersion relation for the surface waves following these physical ideas are found to be consistent with the data obtained from the simulations.
We also analyzed in detail how the bubble shape becomes asymmetric with azimuthal structures appearing in it as the Reynolds number increases. The breaking of axial symmetry yields complex irregular shapes of the bubble back and very strong oscillations. The linear modes that appear early in the simulations have mode numbers that increase with increasing Reynolds number.
Finally, we analyzed the vortical structures that arise in various regimes using the criterion of vortex identification. Isosurfaces of demonstrate the generation of a toroidal vortex near the nose of the bubble that is stationary relative to the bubble nose. This structure is consistent with predictions in earlier works. Elongated bubbles at large Reynolds numbers oscillate forming ring vortices around the bubble, which propagate along the bubble surface.
Supplementary Materials
The following movies are available online at https://www.mdpi.com/article/10.3390/fluids6110389/s1, Movie S1: AW5-ux.mp4, Movie S2: AW6.mp4, Movie S3: AW5-Lambda2.mp4.
Author Contributions
Conceptualization, E.L.S., O.A.R. and A.R.K.; formal analysis, E.L.S., O.A.R. and A.R.K.; funding acquisition, A.R.K.; investigation, E.L.S., O.A.R. and A.R.K.; project administration, A.R.K.; supervision, A.R.K.; writing—original draft, E.L.S.; writing—review and editing, E.L.S., O.A.R. and A.R.K. All authors have read and agreed to the published version of the manuscript.
Funding
A.R.K. and O.A.R. were partially supported by the Russian Foundation for Basic Research (Grant No. 20-51-00004).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data were generated at Skoltech. The derived data supporting the findings of this study are available from the corresponding author Kasimov A.R. upon request.
Acknowledgments
We are grateful to the authors of [23], especially Mirco Magnini, for sharing their experimental data. We acknowledge the use of Zhores [49] for obtaining the results presented in this paper. We also acknowledge the use of Skoltech’s Arkuda cluster for obtaining the results presented in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gravesen, P.; Branebjerg, J.; Jensen, O.S. Microfluidics-a review. J. Micromech. Microeng. 1993, 3, 168. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, S.; Yuan, D.; Alici, G.; Nguyen, N.T.; Warkiani, M.E.; Li, W. Fundamentals and applications of inertial microfluidics: A review. Lab Chip 2016, 16, 10–34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shang, L.; Cheng, Y.; Zhao, Y. Emerging droplet microfluidics. Chem. Rev. 2017, 117, 7964–8040. [Google Scholar] [CrossRef] [PubMed]
- Anna, S.L. Droplets and bubbles in microfluidic devices. Annu. Rev. Fluid Mech. 2016, 48, 285–309. [Google Scholar] [CrossRef]
- Le, N.N.H.; Sugai, Y.; Nguele, R.; Sreu, T. Bubble size distribution and stability of CO2 microbubbles for enhanced oil recovery: Effect of polymer, surfactant and salt concentrations. J. Dispers. Sci. Technol. 2021, 42, 1974873. [Google Scholar]
- Grotberg, J.B. Respiratory fluid mechanics and transport processes. Annu. Rev. Biomed. Eng. 2001, 3, 421–457. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Chen, Y.; Tang, H.; Zong, N.; Jiang, X. Microfluidics for biomedical analysis. Small Methods 2020, 4, 1900451. [Google Scholar] [CrossRef]
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical research. Nature 2014, 507, 181–189. [Google Scholar] [CrossRef]
- Rodríguez-Rodríguez, J.; Sevilla, A.; Martínez-Bazán, C.; Gordillo, J.M. Generation of microbubbles with applications to industry and medicine. Annu. Rev. Fluid Mech. 2015, 47, 405–429. [Google Scholar] [CrossRef]
- Dang, B.; Bakir, M.S.; Sekar, D.C.; King, C.R., Jr.; Meindl, J.D. Integrated microfluidic cooling and interconnects for 2D and 3D chips. IEEE Trans. Adv. Packag. 2010, 33, 79–87. [Google Scholar] [CrossRef]
- van Erp, R.; Soleimanzadeh, R.; Nela, L.; Kampitsis, G.; Matioli, E. Co-designing electronics with microfluidics for more sustainable cooling. Nature 2020, 585, 211–216. [Google Scholar] [CrossRef]
- Gilmore, N.; Timchenko, V.; Menictas, C. Microchannel cooling of concentrator photovoltaics: A review. Renew. Sustain. Energy Rev. 2018, 90, 1041–1059. [Google Scholar] [CrossRef]
- Bojang, A.A.; Wu, H.S. Design, fundamental principles of fabrication and applications of microreactors. Processes 2020, 8, 891. [Google Scholar] [CrossRef]
- Song, H.; Chen, D.L.; Ismagilov, R.F. Reactions in Droplets in Microfluidic Channels. Angew. Chem. Int. Ed. 2006, 45, 7336–7356. [Google Scholar] [CrossRef] [Green Version]
- Tanimu, A.; Jaenicke, S.; Alhooshani, K. Heterogeneous catalysis in continuous flow microreactors: A review of methods and applications. Chem. Eng. J. 2017, 327, 792–821. [Google Scholar] [CrossRef]
- Bandara, T.; Nguyen, N.T.; Rosengarten, G. Slug flow heat transfer without phase change in microchannels: A review. Chem. Eng. Sci. 2015, 126, 283–295. [Google Scholar] [CrossRef] [Green Version]
- Nirmal, G.M.; Leary, T.F.; Ramachandran, A. Mass transfer dynamics in the dissolution of Taylor bubbles. Soft Matter 2019, 15, 2746–2756. [Google Scholar] [CrossRef]
- Fletcher, D.F.; Haynes, B.S. CFD simulation of Taylor flow: Should the liquid film be captured or not? Chem. Eng. Sci. 2017, 167, 334–335. [Google Scholar] [CrossRef]
- Taylor, G.I. Deposition of a viscous fluid on the wall of a tube. J. Fluid Mech. 1961, 10, 161–165. [Google Scholar] [CrossRef]
- Bretherton, F.P. The motion of long bubbles in tubes. J. Fluid Mech. 1961, 10, 166–188. [Google Scholar] [CrossRef]
- Aussillous, P.; Quéré, D. Quick deposition of a fluid on the wall of a tube. Phys. Fluids 2000, 12, 2367–2371. [Google Scholar] [CrossRef]
- Han, Y.; Shikazono, N. Measurement of the liquid film thickness in micro tube slug flow. Int. J. Heat Fluid Flow 2009, 30, 842–853. [Google Scholar] [CrossRef]
- Khodaparast, S.; Magnini, M.; Borhani, N.; Thome, J.R. Dynamics of isolated confined air bubbles in liquid flows through circular microchannels: An experimental and numerical study. Microfluid. Nanofluidics 2015, 19, 209–234. [Google Scholar] [CrossRef]
- Rosengarten, G.; Harvie, D.; Cooper-White, J. Contact angle effects on microdroplet deformation using CFD. Appl. Math. Model. 2006, 30, 1033–1042. [Google Scholar] [CrossRef]
- Magnini, M.; Ferrari, A.; Thome, J.R.; Stone, H.A. Undulations on the surface of elongated bubbles in confined gas-liquid flows. Phys. Rev. Fluids 2017, 2, 084001. [Google Scholar] [CrossRef]
- Ferrari, A.; Magnini, M.; Thome, J.R. A Flexible Coupled Level Set and Volume of Fluid (flexCLV) method to simulate microscale two-phase flow in non-uniform and unstructured meshes. Int. J. Multiph. Flow 2017, 91, 276–295. [Google Scholar] [CrossRef]
- Li, W.; Luo, Y.; Zhang, J.; Minkowycz, W. Simulation of single bubble evaporation in a microchannel in zero gravity with thermocapillary effect. J. Heat Transf. 2018, 140, 112403. [Google Scholar] [CrossRef]
- Afkhami, S.; Leshansky, A.; Renardy, Y. Numerical investigation of elongated drops in a microfluidic T-junction. Phys. Fluids 2011, 23, 022002. [Google Scholar] [CrossRef] [Green Version]
- Chaves, I.; Duarte, L.; Coltro, W.; Santos, D. Droplet length and generation rate investigation inside microfluidic devices by means of CFD simulations and experiments. Chem. Eng. Res. Des. 2020, 161, 260–270. [Google Scholar] [CrossRef]
- Batchvarov, A.; Kahouadji, L.; Magnini, M.; Constante-Amores, C.R.; Shin, S.; Chergui, J.; Juric, D.; Craster, R.; Matar, O.K. Effect of surfactant on elongated bubbles in capillary tubes at high Reynolds number. Phys. Rev. Fluids 2020, 5, 093605. [Google Scholar] [CrossRef]
- Sharaborin, E.L.; Rogozin, O.A.; Kasimov, A.R. The Coupled Volume of Fluid and Brinkman Penalization Methods for Simulation of Incompressible Multiphase Flows. Fluids 2021, 6, 334. [Google Scholar] [CrossRef]
- Popinet, S.; collaborators. Basilisk. 2013–2021. Available online: http://basilisk.fr (accessed on 12 September 2021).
- Kreutzer, M.T.; Kapteijn, F.; Moulijn, J.A.; Kleijn, C.R.; Heiszwolf, J.J. Inertial and interfacial effects on pressure drop of Taylor flow in capillaries. AIChE J. 2005, 51, 2428–2440. [Google Scholar] [CrossRef]
- Edvinsson, R.K.; Irandoust, S. Finite-element analysis of Taylor flow. AIChE J. 1996, 42, 1815–1823. [Google Scholar] [CrossRef]
- Goldsmith, H.; Mason, S. The flow of suspensions through tubes. II. Single large bubbles. J. Colloid Sci. 1963, 18, 237–261. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Angot, P.; Bruneau, C.H.; Fabrie, P. A penalization method to take into account obstacles in incompressible viscous flows. Numer. Math. 1999, 81, 497–520. [Google Scholar] [CrossRef]
- Vasilyev, O.; Kevlahan, N.R. Hybrid wavelet collocation–Brinkman penalization method for complex geometry flows. Int. J. Numer. Methods Fluids 2002, 40, 531–538. [Google Scholar] [CrossRef]
- López-Herrera, J.; Ganan-Calvo, A.; Popinet, S.; Herrada, M. Electrokinetic effects in the breakup of electrified jets: A Volume-Of-Fluid numerical study. Int. J. Multiph. Flow 2015, 71, 14–22. [Google Scholar] [CrossRef] [Green Version]
- ANSYS, Inc. ANSYS Fluent Tutorial Guide, Release 14.5. 2011. Available online: http://www.ansys.com (accessed on 27 October 2021).
- The OpenFOAM Foundation. OpenFOAM, Release 2.1.1. 2012. Available online: https://cfd.direct/openfoam/user-guide (accessed on 27 October 2021).
- Gupta, R.; Fletcher, D.F.; Haynes, B.S. On the CFD modelling of Taylor flow in microchannels. Chem. Eng. Sci. 2009, 64, 2941–2950. [Google Scholar] [CrossRef]
- Polonsky, S.; Shemer, L.; Barnea, D. The relation between the Taylor bubble motion and the velocity field ahead of it. Int. J. Multiph. Flow 1999, 25, 957–975. [Google Scholar] [CrossRef] [Green Version]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Epps, B. Review of vortex identification methods. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 989. [Google Scholar]
- Haller, G. Can vortex criteria be objectivized? J. Fluid Mech. 2021, 908, 937. [Google Scholar] [CrossRef]
- Thulasidas, T.; Abraham, M.; Cerro, R. Flow patterns in liquid slugs during bubble-train flow inside capillaries. Chem. Eng. Sci. 1997, 52, 2947–2962. [Google Scholar] [CrossRef]
- Heil, M. Finite Reynolds number effects in the Bretherton problem. Phys. Fluids 2001, 13, 2517–2521. [Google Scholar] [CrossRef]
- Zacharov, I.; Arslanov, R.; Gunin, M.; Stefonishin, D.; Bykov, A.; Pavlov, S.; Panarin, O.; Maliutin, A.; Rykovanov, S.; Fedorov, M. “Zhores”—Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology. Open Eng. 2019, 9, 512–520. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).