Development of a Scalable Thermal Reservoir Simulator on Distributed-Memory Parallel Computers

Abstract

Reservoir simulation is to solve a set of fluid flow equations through porous media, which are partial differential equations from the petroleum engineering industry and described by Darcy’s law. This paper introduces the model, numerical methods, algorithms and parallel implementation of a thermal reservoir simulator that is designed for numerical simulations of a thermal reservoir with multiple components in three-dimensional domain using distributed-memory parallel computers. Its full mathematical model is introduced with correlations for important properties and well modeling. Efficient numerical methods (discretization scheme, matrix decoupling methods, and preconditioners), parallel computing technologies, and implementation details are presented. The numerical methods applied in this paper are suitable for large-scale thermal reservoir simulations with dozens of thousands of CPU cores (MPI processes), which are efficient and scalable. The simulator is designed for giant models with billions or even trillions of grid blocks using hundreds of thousands of CPUs, which is our main focus. The validation part is compared with CMG STARS, which is one of the most popular and mature commercial thermal simulators. Numerical experiments show that our results match commercial simulators, which confirms the correctness of our methods and implementations. SAGD simulation with 7406 well pairs is also presented to study the effectiveness of our numerical methods. Scalability testings demonstrate that our simulator can handle giant models with billions of grid blocks using 100,800 CPU cores and the simulator has good scalability.

1. Introduction

Reservoir simulations play critical roles in reservoir management, as simulators provide one way to validate production plans in the early stages and to predict future oil and gas production. Many simulators have been developed and applied over the past decades, such as CMG STARS and Eclipse. Those simulators have been widely used in reservoir management. For example, CMG STARS is the most popular thermal reservoir simulator, which has been developed for around 40 year. It has been applied worldwide in various thermal recovery processes, such as in situ combustion, CSS (Cyclic Steam Stimulation) and SAGD (Steam-Assisted Gravity Drainage). When multiple chemicals are considered in a model, more physics features are applied, or if the geological model is complex, a simulator may take very long to complete one simulation. A model may be run dozens of times to match history and to optimize oil production so the long running time reduces the productivity of reservoir engineers. Acceleration of simulations is important to oil and gas industry.

Reservoir simulation is an interdisciplinary research topic, which involves petroleum modeling, applied mathematics, computational methods, and computer sciences. It has been studied for decades, and various models and methods have been proposed [1]. Crookston et al. [2] proposed a simple two-dimensional model, which handled three-phase flow and vaporization–condensation effects. Grabowski and his collaborators developed a sequential implicit method for thermal reservoir model [3]. Coats was a pioneer in reservoir simulations, and he developed models and numerical methods for black oil model, compositional model and thermal model, including in situ combustion mode [4]. In [4], a general four-phase multicomponent in situ combustion model was proposed by Coats, which was improved later by Rubin [5]. Zhu et al. proposed new upscaling methods for their simulators [6,7]. There are a few popular numerical schemes for thermal and compositional models, such as variable substitution [4] methods and pseudo-equilibrium ratio (PER) methods [2]. The variable substitution method changes variables, such as temperature and saturation, depending on the phase status, while the PER method assumes phases do not disappear and modifies the K-value calculation formula. Both methods have been employed in simulator development. Another scheme was also proposed by Mifflin et al. [8], which utilized global variables, such as pressure, moles, and energy as unknowns. For the global variable scheme, phase status is computed after obtaining the global variables. Numerical methods and algorithms were proposed by Barua [9] to improve the nonlinear system and linear system. A key to reservoir simulations is to develop effective solution techniques, especially preconditioners. Many preconditioners have been proposed to accelerate the solution of linear systems, such as constrained pressure residual (CPR) methods [10,11]; multiple level preconditioners [12]; multi-stage methods [13]; CPR-FP, CPR-FPF, and CPR-FFPF methods [14]; and FASP (fast auxiliary space preconditioners) [15,16]. Parallel computers have more memory and better performance, which provide excellent approaches to accelerate reservoir simulations [17,18,19,20,21,22,23,24,25,26,27,28]. Wang [29,30] implemented a fully implicit equation-of-state compositional simulator for distributed-memory parallel computers, and large-scale reservoir models were simulated [31]. Reservoir models with millions of grid blocks on parallel computers were reported [32]. Killough [33] reviewed the parallel reservoir models and parallel computing technologies. Saudi Aramco developed new-generation massively-parallel reservoir simulator [34,35,36,37]. Zhang et al. developed a scalable general-purpose platform for parallel adaptive finite element methods and adaptive finite volume methods [38,39], which was applied to reservoir simulations [40].

This paper introduces our work on developing a parallel thermal simulator, including a mathematical model and numerical methods. The simulator works for three-dimensional domain and has three phases: water, oil, and gas. The model has one water component, arbitrary oil components, and arbitrary non-condensable gas components. Here, water is assumed to stay in the water and gas phases. Oil components have two types: heavy oil components and light components. The heavy oil components stay in oil phase only but the light oil components exist in oil phase and gas phase. The distribution of water and light oil in gas phase is determined by pressure, temperature, K-values and composition of water, and light oil and non-condensable gas components. This paper gives full mathematical details of a thermal model, including mass conservation law, energy conservation law, phase equilibrium calculation, density, viscosity, enthalpy, relative permeability, and well modeling. Numerical methods are introduced, especially physics-based preconditioning methods, including decoupling methods and preconditioners. In the numerical experiment section, our simulator is compared with CMG STARS (a popular commercial reservoir simulator), and results show that they match very well, from which we can conclude our implementations are correct. Furthermore, numerical testings show that our numerical methods are effective. From the scalability testings, we can see that the thermal simulator has good scalability, and it can compute large-scale thermal reservoir models. A scalable simulator enables us to run large models and to calculate a model in shorter simulation time. Furthermore, as we can use hundreds of computation nodes and lots of memory, we can model physical problems in a much smaller scale, such as nanoscale.

The structure of the paper is as follows. In Section 2, the thermal reservoir model is introduced and the equations for various properties are presented. In Section 3, numerical methods and parallel computing approaches are proposed. In Section 4, numerical experiments are carried out to validate our results against commercial simulator, CMG STARS, and to show the scalability of the parallel thermal simulator.

2. Mathematical Model

Most simulators share the same theory framework [1,41,42,43,44]. For the sake of completeness, the mathematical model of the thermal simulator is introduced here, and the models are almost the same as in [1,41,42,43,44,45]. Some content of this section is borrowed from our previous paper [1,44], CMG STARS [41], and the textbook  in [45]. In [1], the following assumptions were made: water component exists in water and gas phases; all oil components exist in oil and gas phases, which means all oil components are light oil; non-condensable gas components exist in gas phase only; and all three phases co-exist during the entire simulation. Furthermore, the PER method is applied to one light oil component only, in which the light oil is the one has the largest molecular weight. In this paper, different assumptions are made: the water component exists in water and gas phases, heavy oil components exist in oil phase only, light oil components exist in both oil and gas phases, and non-condensable gas components exist in gas phase. Gas phase appearance and disappearance are allowed. Depending on the input, arbitrary oil components and non-condensable gas components are allowed.

2.1. Darcy’s Law

The fluid is assumed to be Darcy flow, and the Darcy’s law is applied to model the velocity of a fluid phase, which defines the relation among permeability, viscosity, saturation, pressure difference, gravity, and temperature. The thermal model has three phases, water phase (w), oil phase (o), and gas phase (g) [1,45]:

$$\begin{array}{c}\begin{array}{cc}\hfill {\overrightarrow{u}}_w& =-\frac{k_{rw}}{{\mu }_w}\overrightarrow{k}\left(\nabla p_w-{\gamma }_w\nabla z\right)\hfill \\ \hfill {\overrightarrow{u}}_o& =-\frac{k_{ro}}{{\mu }_o}\overrightarrow{k}\left(\nabla p_o-{\gamma }_o\nabla z\right)\hfill \\ \hfill {\overrightarrow{u}}_g& =-\frac{k_{rg}}{{\mu }_g}\overrightarrow{k}\left(\nabla p_g-{\gamma }_g\nabla z\right).\hfill \end{array}\end{array}$$

(1)

Here, ${\overrightarrow{u}}_{\alpha }$ is velocity, $k_{r\alpha }$ is relative permeability, ${\mu }_{\alpha }$ is viscosity, $\overrightarrow{k}$ is permeability, $p_{\alpha }$ is pressure, and z is depth.

2.2. Mass Conservation Equations

For a multi-phase multicomponent reservoir model, we use $x_{c,\alpha }$, $n_{c,\alpha }$, and $n_{\alpha }$ to denote the mole fraction of a component in the $\alpha$-phase, the mole number of a component in the phase, and the total mole number of the phase, respectively [1,45]. Then, the mole fraction of a component in a phase is defined as

$$\begin{array}{c}{x}_{c,\alpha }=\frac{n_{c,\alpha }}{n_{\alpha }}.\end{array}$$

(2)

If only water exists in the water phase, $x_w=1$. If the gas phase exists, it may contains water, light oil, and non-condensable gas components. Here, y is employed to note gas mole fraction,

$$\begin{array}{c}{\mathsf{\sum }}_c^{N_{c,g}}{y}_c=1,\end{array}$$

(3)

where $N_{c,g}$ is total chemicals in gas phase. Moreover, if the oil phase exists, x is employed to note oil mole fraction,

$$\begin{array}{c}{\mathsf{\sum }}_c^{N_{c,o}}{x}_c=1,\end{array}$$

(4)

where $N_{c,o}$ is total chemicals in oil phase.

A component c may exist in several phases, so its mass at a reservoir is summation of masses in all phases, which is written as below [45]:

$$\begin{array}{c}\frac{\partial }{\partial t}\left(\varphi {\mathsf{\sum }}_{\alpha }^{N_{\alpha }}{\rho }_{\alpha }{S}_{\alpha }{x}_{c,\alpha }\right)=-\nabla ·\left({\mathsf{\sum }}_{\alpha }^{N_{\alpha }}{\rho }_{\alpha }{S}_{\alpha }{\overrightarrow{u}}_{\alpha }\right)+{\mathsf{\sum }}_{\alpha }^{N_{\alpha }}{q}_{\alpha ,well}{x}_{c,\alpha },\end{array}$$

(5)

where ${\rho }_{\alpha }$ is density and $q_{\alpha ,well}$ is well rate.

The water, oil, and gas saturation have the following constraint:

$$S_w+S_o+S_g=1.$$

(6)

2.3. Energy Conservation Equation

The energy conservation equation for a thermal reservoir model [45] is described as

$$\begin{array}{c}\begin{array}{cc}& \frac{\partial }{\partial t}\left(\varphi ({\rho }_w{S}_w{U}_w+{\rho }_o{S}_o{U}_o+{\rho }_g{S}_g{U}_g)+(1-\varphi )U_r\right)\hfill \\ \hfill =& \nabla ·\left(K_T\nabla T\right)-\nabla ·\left({\rho }_w{H}_w{\overrightarrow{u}}_w+{\rho }_o{H}_o{\overrightarrow{u}}_o+{\rho }_g{H}_g{\overrightarrow{u}}_g\right)\hfill \\ & +(q_{w,well}{H}_w+q_{o,well}{H}_o+q_{g,well}{H}_g)-Q_{loss},\hfill \end{array}\end{array}$$

(7)

where U denotes the internal energy and H is enthalpy. This equation considers fluid energy, rock heat energy, heat conduct, heat loss, and energy changes through wells. The heat conduction is noted by $K_T$, the bulk thermal conductivity, which is a combination of liquid and rock, where a linear mixing rule is applied [41],

$$\begin{array}{c}{K}_T=\varphi \left[S_w{K}_w+S_o{K}_o+S_g{K}_g\right]+(1-\varphi )K_r.\end{array}$$

(8)

In the equation, $K_w,K_o,K_g,K_r$ denote thermal conductivities for water phase, oil phase, gas phase, and rock, respectively. This rule is also called simple mixing rule (CMG STARS) [41]. A more complicated model is also available [41].

Note that there are different ways to model rock internal energy: $(1-\varphi )U_r$. In the above equation, the porosity, $\varphi$, is a function of pressure and temperature, and $U_r$ is a function of temperature, so the rock internal energy is a function of pressure and temperature. This method assumes the volume of a grid block does not change but $(1-\varphi )$ changes depending on pressure and temperature. Another way is to assume the rock volume, $(1-\varphi )$, does not change, even if $\varphi$ changes during the simulation. This method preserves the rock energy and mass. The second method is applied as the default method by us and CMG STARS [41]. A heat loss term is modeled by the semi-analytical method developed by Vinsome et al. [46].

2.4. Capillary Pressure

Capillary pressure $P_c$ is the pressure difference between two phases, which are usually functions of saturation [45]:

$$\begin{array}{c}{p}_w=p_o-p_{cow}\left(S_w\right),p_g=p_o+p_{cog}\left(S_g\right),\end{array}$$

(9)

from which we can see if we know the oil phase pressure, water saturation, and gas saturation, the water phase pressure and the gas phase pressure can be computed.

2.5. Phase Equilibrium Constraints

The K-value (or an equilibrium ratio) is defined as the ratio of the mole fractions of a component in two phases (gas phase vs. water phase and gas phase vs. oil phase in this paper):

$$\begin{array}{c}{K}_{c,{\alpha }_1,{\alpha }_2}=\frac{x_{c,{\alpha }_1}}{x_{c,{\alpha }_2}}.\end{array}$$

(10)

Here, a K-value of water component and light oil component is a function of pressure and temperature, which is calculated using the following method:

$$\begin{array}{c}K=\left(\frac{{kv}_1}{p}+{kv}_{2}p+{kv}_3\right)exp\left(\frac{{kv}_4}{T-{kv}_5}\right).\end{array}$$

(11)

The K-value is valid only if the gas phase exists. Furthermore, each chemical has different parameters. The five parameters are user input.

In our thermal model, the calculations of K-values are modified, where the PER (Pseudo-Equilibrium Ratios) method [2,47] is applied for water and light oil,

$$\begin{array}{c}{K^{*}}_W=K_W^{*}(p,T)=\left(\frac{S_w}{S_w+ϵ}\right)K_W(p,T),\end{array}$$

(12)

$$\begin{array}{c}{K^{*}}_{O,i}=K_{O,i}^{*}(p,T)=\left(\frac{S_o}{S_o+ϵ}\right)K_{O,i}(p,T).\end{array}$$

(13)

In calculations of pseudo K-values, $ϵ$ is a small number of the order of $0.0001$. The water phase and oil phase exist through the entire simulation. However, the gas phase is allowed to disappear. The gas phase mole fraction for the oil components and water component are functions of $p,T,S_w,S_g$.

2.6. Phase Changes

Gas phase is allowed to reappear and disappear, which has to be checked and determined in each Newton iteration. The K-value only validates when gas phase exists.

When gas phase exists, its saturation, $S_g$, is positive. If a non-positive gas saturation is detected, then gas phase disappears. $S_g$ is set to 0.

When gas phase does not exist, $S_g$ is 0. If the following relationship is detected:

$$\begin{array}{c}{\mathsf{\sum }}_i{y}_i>1,\end{array}$$

(14)

then gas phase reappears. A small gas saturation is set, such as ${10}^{-3}$. A cell type boolean variable is applied to store the gas phase status.

2.7. Compressibility Factor of Real Gas

The gas phase mole density is calculated as

$${\rho }_g={\rho }_g(p,T,S_w,S_o,x_i,y_i)=\frac{p}{Z·R·T},$$

where Z is calculated by EOS equation.

In the thermal model, the Redlich–Kwong EOS [48] is used to calculate the Z factor.

$$\begin{array}{c}A=A(p,T)=0.427480\left(\frac{p}{p_{crit}}\right){\left(\frac{T_{crit}}{T}\right)}^{2.5},\end{array}$$

(15)

$$\begin{array}{c}B=B(p,T)=0.086640\left(\frac{p}{p_{crit}}\right)\left(\frac{T_{crit}}{T}\right),\end{array}$$

(16)

where p is pressure, T is temperature, $p_{crit}$ is critial pressure, and $T_{crit}$ is critical temperature. These represent the user input for a gas component, which is determined by a lab.

In addition, the following mixing method is applied:

$$\begin{array}{c}a=\mathsf{\sum }_i{y}_i{T}_{crit,i}\sqrt{\frac{T_{crit,i}}{p_{crit,i}}},\end{array}$$

(17)

$$\begin{array}{c}b=\mathsf{\sum }_i{y}_i\frac{T_{crit,i}}{p_{crit,i}},\end{array}$$

(18)

$$\begin{array}{c}{T}_{crit}={\left(\frac{a^2}{b}\right)}^{\frac{2}{3}},\end{array}$$

(19)

$$\begin{array}{c}{p}_{crit}=\frac{T_{crit}}{b}.\end{array}$$

(20)

Then, after we have the coefficients A and B, the compressibility factor of real gas satisfies the equation [41]

$$\begin{array}{c}{Z}^3-Z^2+(A-B-B^2)Z-AB=0.\end{array}$$

(21)

This cubic equation has three roots, in which the biggest real root is chosen [45]. The Z factor is a function of p, T, $S_g$, $S_w$, $x_i$, and $y_i$.

2.8. Density

The water component and oil components have the same equation:

$$\begin{array}{c}\rho =\rho (p,T)={\rho }_{ref}exp(cp(p-p_{ref})-c{t}_1(T-T_{ref})\end{array}$$

(22)

$$\begin{array}{c}-\frac{c{t}_2}{2}(T^2-T_{ref}^2)+cpt(p-p_{ref})(T-T_{ref}))\end{array}$$

(23)

where ${\rho }_{ref}$ is the reference density of a component at the reference temperature, $T_{ref}$, and pressure, and $p_{ref}$, $cp$, $c{t}_1$, $c{t}_2$, and $cpt$ are parameters. The density of oil phase, ${\rho }_o$, which is mixture of multiple oil components, is calculated as

$$\begin{array}{c}\frac{1}{{\rho }_o}=\mathsf{\sum }_i^{n_{co}}\frac{x_i}{{\rho }_{o,i}}.\end{array}$$

(24)

2.9. Viscosity

There are a few ways to calculate viscosity, such as table input and analytical correlations. For the table input method, interpolations are required to calculate the viscosity of a component or a phase at a given temperature. In the following, an analytical method is introduced for oil, water, and gas.

The viscosity of oil component in oil phase and water component in water phase has the same formula, which is a function of temperature,

$$\begin{array}{c}\mu =aviscexp\left(\frac{bvisc}{T}\right),\end{array}$$

(25)

where $avisc$ and $bvisc$ are parameters. The viscosity of oil phase is computed by a mixing rule,

$$\begin{array}{c}ln\left({\mu }_o\right)=\mathsf{\sum }_i^{n_{c,o}}x\left[i\right]ln\left({\mu }_{O_i}\left(T\right)\right).\end{array}$$

(26)

The viscosity of a component in gas phase is calculated as

$$\begin{array}{c}\mu =\mu \left(T\right)=avg·T^{bvg},\end{array}$$

(27)

where $avg$ and $bvg$ are parameters. The gas phase viscosity is calculated as

$$\begin{array}{c}{\mu }_g={\mu }_g(p,T,S_w,S_g,x_i,y_i)=\frac{{\mathsf{\sum }}_i^{n_{c,g}}{\mu }_{g,i}·y_i\sqrt{M_i}}{{\mathsf{\sum }}_i^{n_{c,g}}{y}_i\sqrt{M_i}},\end{array}$$

(28)

where $M_i$ is molecular weight of i-th component.

2.10. Porosity

Porosity is the ratio of the pore volume to the bulk volume, which changes as pressure and temperature change. A total compressibility of porosity [45] is defined as

$$\begin{array}{c}{\varphi }_c={\varphi }_c(p,T)=cpor(p-p_{ref})-ctpor(T-T_{ref})+cptpor(p-p_{ref})(T-T_{ref}),\end{array}$$

(29)

which defines a function of pressure and temperature. There are two ways to model porosity, linear, and exponential. Linear model is described as

$$\begin{array}{c}\varphi =\varphi (p,T)={\varphi }_{ref}·(1+{\varphi }_c),\end{array}$$

(30)

and exponential model is described as

$$\begin{array}{c}\varphi =\varphi (p,T)={\varphi }_{ref}·e^{{\varphi }_c}.\end{array}$$

(31)

The linear model is applied by default.

2.11. Relative Permeabilities

There are two ways for calculating relative permeabilities: The first one is to use analytical correlations, and the second one is to use input tables. The water phase relative permeability, $k_{rw}$, is a function of $S_w$ (and/or temperature):

$$\begin{array}{c}{k}_{rw}=k_{rw}\left(S_w\right).\end{array}$$

(32)

The gas phase relative permeability, $k_{rg}$, is a function of $S_g$ (and/or temperature):

$$\begin{array}{c}{k}_{rg}=k_{rg}\left(S_g\right).\end{array}$$

(33)

Sometime temperature is considered, a set of relative permeabilities are provided for each temperature. Furthermore, a reservoir model may have several rock types, and each rock type has one set of relative permeabilities.

Several models are available [49,50,51,52] to calculate oil phase relative permeability, $k_{ro}$. In this paper, the Stone’s model II method [53] is applied, which is defined as

$$\begin{array}{c}{k}_{ro}=k_{ro}(S_w,S_g)=k_{rocw}\left[\left(\frac{k_{row}\left(S_w\right)}{k_{rocw}}+k_{rw}\left(S_w\right)\right)\left(\frac{k_{rog}\left(S_g\right)}{k_{rocw}}+k_{rg}\left(S_g\right)\right)-k_{rw}\left(S_w\right)-k_{rg}\left(S_g\right)\right],\end{array}$$

(34)

where $k_{rocw}$ is the oil–water relative permeability to oil at connate water saturation, $krog$ is the oil–gas relative permeability to oil, and $krow$ is the oil–water relative permeability to oil.

2.12. Energy

There are a few ways to model enthalpy (energy), such as a gas-based model and a liquid-based model. Here, the gas-based model is introduced. The enthalpy of a gas component is calculated as follows [41]:

$$\begin{array}{c}{H}_{g,i}=H_{g,i}\left(T\right)={\int }_{T_{ref}}^T\left(cpg{1}_i+cpg{2}_i·t+cpg{3}_i·t^2+cpg{4}_i·t^3+cpg{5}_i·t^4\right)dt,\end{array}$$

(35)

$cpg{1}_i$, $cpg{2}_i$, $cpg{3}_i$, $cpg{4}_i$, and $cpg{5}_i$ are constants for component i. The gas phase enthalpy can be calculated by a weighted mean with gas mole fractions $y_i$:

$$\begin{array}{c}{H}_g=\mathsf{\sum }_i^{N_{c,g}}{y}_i{H}_{g,i}.\end{array}$$

(36)

For the oil and water components, vaporization is considered, which can be calculated by

$$H_{v,i}=\left\{\begin{array}{cccc}\hfill & hv{r}_i·{(T_{crit,i}-T)}^{e{v}_i},\hfill & \hfill & T<T_{crit,i};\hfill \\ \hfill & 0,\hfill & \hfill & T>=T_{crit,i};\hfill \end{array}\right.$$

(37)

However, if an oil component is heavy oil, which stays as liquid (oil phase), the vaporization energy is zero. The enthalpy of a liquid component is calculated as

$$\begin{array}{c}{H}_i=H_{g,i}-H_{v,i}.\end{array}$$

(38)

where $H_{g,i}$ is the enthalpy of component i in the gas phase. The water phase enthalpy is

$$\begin{array}{c}{H}_w=H_{g,w}-H_{v,w}.\end{array}$$

(39)

The enthalpy of oil phase is

$$\begin{array}{c}{H}_o=\mathsf{\sum }_i^{n_{c,o}}{x}_i(H_{g,O_i}-H_{v,O_i}).\end{array}$$

(40)

The internal energy for oil, gas, and water phases [41] are calculated as

$$\begin{array}{c}{U}_{\alpha }=U_{\alpha }\left(T\right)=H_{\alpha }-p/{\rho }_{\alpha },\alpha =w,o,g\end{array}$$

(41)

For rock, a similar formula is used:

$$\begin{array}{c}{U}_r=U_r\left(T\right)=c{p}_{r,1}(T-T_{ref})+\frac{c{p}_{r,2}}{2}(T^2-T_{ref}^2).\end{array}$$

(42)

The internal energy for rock has a unit of energy per unit volume, while others have energy per mole. As mentioned above, there are two ways to calculate the volume of rock. The following equation defines relationship among bulk volume $V_b$, rock volume $V_r$, and pore volume $V_p$,

$$\begin{array}{c}{V}_b=V_r+V_p,\end{array}$$

(43)

where $V_p$ is calculated by porosity correlations and $V_r$ is used when calculating the internal energy of rock. The first one assumes the volume of rock (non-null) does not change, which is noted as constant rock. It assumes that $V_r$ is constant, which preserves rock mass and heat, and $V_b$ changes as $V_r$ changes. The second one assumes that the volume of the grid block does not change, which is noted as constant bulk. It means $V_b$ is constant and $V_r$ ($V_r=V_b-V_p$) changes as $V_p$ changes. The default method is the first one, rock constant.

2.13. Well Modeling

Peaceman’s model is adopted for well modeling. A well may have different directions, such as vertical and horizontal, and it may have many perforations, each of which belongs to a grid cell (block). Each perforation has its own properties, such as well index, rates, and mobility. Each well has its own properties, such as well rates and bottom hole pressure. For a perforation, its well rate for phase $\alpha$, $Q_{\alpha }$, is calculated by the following formula [54]:

$$\begin{array}{c}{Q}_{\alpha ,well}=WI\frac{{\rho }_{\alpha }{k}_{r\alpha }}{{\mu }_{\alpha }}\left(p_b-p_{\alpha }-{\gamma }_{\alpha }g(z_{bh}-z)\right),\end{array}$$

(44)

where WI is the well index and mobility, $\frac{k_{r\alpha }}{{\mu }_{\alpha }}$, is explicit or implicit. Explicit means its value is from the last time step, while implicit means its value is from the last Newton iteration. Well rate can also be calculated using a third method, unweighted method,

$$\begin{array}{c}{Q}_{\alpha ,well}=WI\left(p_b-p_{\alpha }-{\gamma }_{\alpha }g(z_{bh}-z)\right),\end{array}$$

(45)

where $WI$ is user input value. A well index defines the relationship among a well bottom hole pressure, a flow rate, and a grid block pressure. $p_b$ is the bottom hole pressure defined at the reference depth z, $z_{bh}$ is the depth of the perforation in grid cell, and $p_{\alpha }$ is the phase pressure in grid block m. Well index can be read from modeling file and it can also be calculated using analytical method. For a vertical well, it can be defined as

$$\begin{array}{c}WI=\frac{2\pi h_3\sqrt{k_{11}{k}_{22}}}{ln\left(\frac{r_e}{r_w}\right)+s}*\mathtt{frac}*\mathtt{ff},\end{array}$$

(46)

where $r_e$ is equivalent radius, $\mathtt{frac}$ is well fraction, and $\mathtt{ff}$ is completion factor. Horizontal well is defined similarly. We should mention that well modeling is the most complicated part in reservoir simulations and various operation constraints can be defined, such as fixed bottom hole pressure, fix liquid, and gas rate constraints and thermal constraints.

2.13.1. Fixed Bottom Hole Pressure

When the fixed bottom hole pressure condition is applied to a well, the well equation is written as

$$\begin{array}{c}{p}_b=c,\end{array}$$

(47)

where c is pressure and is a constant. The bottom hole pressure is defined at a reference depth or a grid block. If neither is provided, the grid block containing the first perforation serves as the reference grid block.

2.13.2. Fixed Rates

Fixed rate constraints are commonly used, including fixed oil rate, fixed water rate, fixed gas rate, and fixed liquid rate (oil and water). The rate can be reservoir rate or surface rate. The volume of a fluid in reservoir condition can be obtained easily. However, the volume of a fluid in surface condition requires a flash calculation to determine the distribution in oil, water, and gas phases. There are two ways to separate phase: segregated method and PT-flash method. The segregated method is easy but the PT-flash is tricky. The segregated method is the default. For phase $\alpha$, its fixed rate constraint is described by the following equation:

$$\begin{array}{c}\mathsf{\sum }_m{\left(Q_{\alpha ,well}\right)}_m=c,\end{array}$$

(48)

where c is a constant rate and known. The fixed liquid rate is written as

$$\begin{array}{c}\mathsf{\sum }_m{\left(Q_{w,well}\right)}_m+\mathsf{\sum }_m{\left(Q_{o,well}\right)}_m=c,\end{array}$$

(49)

The fixed total fluid rate is written as

$$\begin{array}{c}\mathsf{\sum }_m{\left(Q_{w,well}\right)}_m+\mathsf{\sum }_m{\left(Q_{o,well}\right)}_m+\mathsf{\sum }_m{\left(Q_{g,well}\right)}_m=c,\end{array}$$

(50)

2.14. Boundary Conditions

A no-flow boundary condition is applied to fluid, which is coupled with each mass conservation equation. For the energy conservation equation, heat loss to underburden and overburden is considered, which is modeled by a semi-analytical method [46]. Each well may have multiple constraints, which is user input. They are determined and switched dynamically during the simulations.

2.15. Initial Conditions

A few initial methods are supported. The easiest one is to use explicit initial conditions, such as pressure, temperature, mole fraction, and saturation. Another one uses the gravity average, in which the pressure is calculated by depth difference to reference depth (grid block). The saturation, mole fractions, and temperature can be computed or be given by user input.

3. Numerical Methods

In our previous previous work, a few reservoir simulators and their numerical methods have been reported [14,55,56]. The simulators share similar methods, such as time discretization scheme, spatial discretization scheme, decoupling method, linear solver, and preconditioners [14]. For the sake of completeness, the numerical methods are introduced in this section. There are two main sets of unknowns: natural variables and overall variables. The natural variables use pressure, temperature, saturation, and mole fractions. The overall variables use pressure, temperature, and overall mole fractions. Phase changes have to be checked in each nonlinear iteration and time step if we use natural variables. When liquid and gas phases co-exist, temperature and pressure are not independent, and only one variable is required, such as pressure or temperature. Some researchers applied the variable substitution trick to switch unknowns and to save computation. To overall variables, phase status is determined after obtaining solutions. In this paper, a fully implicit method is employed, which is friendly to large time step and to accuracy. However, it is possible to apply some techniques to speed simulation, such as adaptive methods.

In this paper, one additional equation is adopted, when enables us to treat pressure and temperature as independent variables through the entire simulation, which only introduces a little more computation but simplifies the numerical treatment and linear systems.

3.1. Spatial Discretization

The natural variables are applied as unknowns, which are also called Type A variables, including pressure, temperature, saturations, and mole fractions (oil components in oil phase and non-condensable gas in gas phase). The variables do not change during the simulation. However, depending on the gas phase status, one constrained equation is switched. If gas phase exist, the following equation is applied:

$$\mathsf{\sum }_i{y}_i=1.$$

(51)

If gas phase does not exist, the following equation is switched:

$$S_g=0.$$

(52)

The status of gas phase has to be checked block by block in each Newton iteration.

When fluids move in a reservoir, there may be fluid exchange in two neighboring grid blocks, which is described by transmissibility. Assuming $d(d=x,y,z)$ is a space direction and A be the area of a face in the d direction, the transmissibility $K_{\alpha ,d}$ for phase $\alpha (\alpha =o,w,g)$ is defined as

$$T_{\alpha ,d}=\frac{KA}{\mathsf{\Delta }d}\times \frac{K_{r\alpha }}{{\mu }_{\alpha }}{\rho }_{\alpha },$$

(53)

where $\mathsf{\Delta }d$ is the grid block length in the d direction, K is the absolute permeability, $K_{r\alpha }$ is the relative permeability of phase $\alpha$, ${\mu }_{\alpha }$ is the viscosity of phase $\alpha$, and ${\rho }_{\alpha }$ is the mole density of phase $\alpha$. The transmissibility is defined on each face of a grid block. If a face is an internal face shared shared by two grid blocks, its value is the same for these two blocks. If the face is a boundary face, the transmissibility is zero, as the no-flow boundary condition is applied. Different weighting schemes must be applied to average different properties at an interface. The left part, $\frac{KA}{\mathsf{\Delta }d}$, is geometric properties, and the harmonic averaging method is applied. The right part, $\frac{K_{r\alpha }}{{\mu }_{\alpha }}{\rho }_{\alpha }$, relies on fluid properties, and the upstream averaging method is applied [45]. The upstream finite difference method is employed to discretize the model.

3.2. Linear Solver

The Jacobian matrix from Newton method is highly ill-conditioned, and the Krylov subspace solvers are applied to solve the linear system $Ax=b$. The key to an effective solution method is to choose a proper preconditioner M, which should be easy to setup and effective. In our previous work, a family of scalable CPR-type methods [14] has been developed for reservoir simulations, which have been applied to black oil model, compositional, in situ combustion, and the general thermal model in this paper. The unknowns are numbered grid block by grid block and the resulted matrix in each iteration is block-wise,

$$A=\left(\begin{array}{cccc}{A}_{11}\hfill & \cdots \hfill & \cdots \hfill & A_{1n}\hfill \\ A_{21}\hfill & A_{22}\hfill & \cdots \hfill & A_{2n}\hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill \\ A_{n1}\hfill & A_{n2}\hfill & \cdots \hfill & A_{nn}\hfill \end{array}\right),$$

(54)

where each sub-matrix $A_{ij}$ is a square matrix. In-house distributed-memory matrix, vector, and their operations have been developed, such as adding entries, assembling, getting sub-matrix (for CPR-type preconditioners), factorization, sparse BLAS, and point-wise and block-wise matrices. Base on these operations, internal parallel solvers, such as GMRES, LGMRES, CG, and BICGSTAB, and preconditioners, such as RAS, AMG, CPR-FP, CPR-PF, CPR-FPF, ILU(k), and ILUT, have been implemented.

3.3. Decoupling Methods

A proper decoupling method is critical to the success of the CPR-type preconditioners. In general, the decoupling method is applied before applying the CPR-type preconditioners, which converts the original linear system to an equivalent linear system,

$$\left(D^{-1}A\right)x=D^{-1}b.$$

(55)

Several decoupling methods have been proposed, such as Quasi-IMPES, True-IMPES [57], Alternate Block Factorization (ABF) [58], full row sum (FRS), and dynamic row sum (DRS) [59] methods. The idea of ABF method is simple, which is defined as

$$D_{abf}=diag(A_{11},A_{22},\cdots ,A_{nn}).$$

(56)

It converts the block diagonal part to identity matrix. This method requires to calculate the inverse of each diagonal part, and the matrix–matrix multiplications are performed for each sub-matrix. The FRS decoupling method is described as

$$D_{frs}^{-1}=diag(D_1,D_2,\cdots ,D_n),$$

(57)

where,

$$D_i=\left(\begin{array}{cccc}1& 1& \cdots & 1\\ 0& 1& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots \\ 0& \cdots & 1& 0\\ 0& 0& 0& 1\end{array}\right).$$

(58)

The diagonal part and the first row are 1 and all other locations are 0, which means to add the all rows to the first row. The DFS decoupling method is a simplified version of the FRS method, and details can be read in [59].

The Guass–Jordan elimination (Gauss elimination; GJE) method [1] has been used to solve linear systems. Its idea is to convert $\left[D\left|A\right|b\right]$ to an equivalent linear system $\left[I|\tilde{A}|\tilde{b}\right]$ by Gauss–Jordan elimination method, and the $\tilde{b}$ is the final solution. In this paper, it is adopted as a decoupling method and is applied grid block by grid block to turn the diagonal matrices to identity matrix. Pivoting technique is used and only row reordering is involved. Since the decoupling is processed block by block, no communication is required, which is friendly to parallel computing. The GJE decoupling is more efficient than the ABF method. These decoupling methods are naturally parallel, and they have ideal scalability for parallel computing.

When the CPR-type preconditioners are applied to reservoir simulations, it is important to keep the pressure matrix positive definite. The FRS method helps to enhance this property, from which the CPR-type preconditioners can benefit. In the first stage, FRS or DRS methods are applied; then, ABF or GJE methods are used as the second stage. In this case, two-stage decoupling methods are developed, which are noted as FRS + ABF, FRS + GJE, DRS + ABF, and DRS + GJE.

3.4. Preconditioners

Several scalable CPR-type preconditioners have been proposed [14], such as CPR-FP, CPR-PF, CPR-FPF, and CPR-FFPF methods. According to our practices, the CPF-FPF method, which is a three-stage preconditioner, is effective for black oil model and thermal model. The first step is to solve an approximate solution using restricted additive Schwarz (RAS) method, the third step is to solve the sub-problem by algebraic multi-grid method (AMG), the fifth step is to get an approximate solution again using restricted additive Schwarz method, and the second step and the forth step are to calculate residual.

It is well-known that the RAS method is scalable for parallel computing. Parallel AMG method is also scalable. The default overlap of the RAS method is 1. If it’s 0, then it is equivalent to block Jacobi method. When there are too many MPI processes, we may increase the overlap to maintain convergence of the preconditioner, such as 2 and 3. However, more communications are introduced in the setup phase of the RAS method, which needs to construct a local sub-problem by requesting more entries of the distributed matrix from other MPI processes. The sub-problem in each MPI process (CPU core) from RAS method is solved by ILUT by default, which can also be solved by ILU(k) or block ILU(k) [14]. The size of the lower triangular matrix and the upper triangular matrix can be reduced by dropping small entries or using smaller p for ILUT and k for ILUK, and the convergence of ILU methods should be well balanced. The recommended level (k) for ILUK is 1. The AMG is from Hypre [60].

We should mention here that the RAS method requires very few communications. In each solution phase, it requires some off-process component information of the right-hand side. After this, no communication is required. In parallel computing, the RAS method has ideal scalability. If overlap 0 is applied, there is no communication during the solution phase. The AMG method also has good scalability. In addition, the decoupling methods are local, which means there is no communication. We can see that the solution methods here are designed for parallel computing and good scalability is ensured.

3.5. Parallel Computing

The key to scalability is to partition the given grid in a proper way. The partitioning method should minimize the total communications and maximal communication per MPI. Furthermore, each sub-grid should be connected with a few other sub-grids. In our simulator, two methods are supported. The first one is a graph partitioning method, which sees each grid as a dual graph. The dual graph models communication patterns. When the grid is partitioned, we make sure the cut edges are minimized, which makes sure communications are minimized. The package ParMETIS provides excellent partitioning speed and quality. The second method is to use geometry-based method. In our simulator, an in-house Hilbert space-filling curve method is implemented, which maps all grid blocks to $(0,1)$. Then, the interval is partitioned into m sub-intervals, and each interval is assigned to one MPI process. Grid blocks belong to the same interval belong to the same MPI process.

The grid partition determines the grid distribution and communication pattern, which is the key to scalability. Furthermore, each MPI forms its own part of the Jacobian system. The grid partition also determines the scalability of RAS method and its convergence. Assuming that non-overlapped RAS is chosen, then each MPI extracts a diagonal matrix from its local Jacobian system. If overlapped RAS is applied, then neighbors of each local diagonal matrix is determined by the matrix structure, which is from the grid partition. We can see that the grid partition is the key to simulator scalability and solver scalability.

If we keep the grid unchanged, then each sub-grid keeps the same, which means the communication pattern does not change. The pattern can be saved and attached to the grid. When communications are required, each sub-grid knows where to send data, where to receive data, and how much data should be exchanged. By storing the communication pattern, the communication operations are easy to perform. When we compute sparse matrix vector multiplication, a similar communication pattern can be computed and attached to a matrix.

In parallel simulation, a large data file may be read and written to initialize the reservoir and to save results. In our simulator, the MPI-IO is applied to read and write in parallel. The simplest way to do this is to save a grid data in one file, such as pressure and saturation. The read and write operations are easy to implement. Another way is to save data in multiple column format. For example, the first column is pressure, the second one is density, and the third one is temperature. It is easy for MPI-IO to handle the formatted data file. In our implementation, we assume each column has a length of 20 letters, so we can compute the offset in relative easy way, where the offset is required by MPI-IO.

4. Numerical Studies

Numerical experiments are presented here, which occupy a few sections. The first section validates our results against CMG STARS, which is the most widely applied thermal simulator. The purpose is to prove the correctness of our numerical methods, models, and implementation. The second section studies numerical performance of our methods. The third section tests the scalability of our thermal simulator using some giant models. In the following sections, each MPI runs on one core, and the number of MPI processes is the same as the number of CPU cores. A better way is each MPI runs on one CPU and multiple threads run on the multi-cores. In our simulator, the OpenMP is disabled by default. The reason we disable OpenMP is that efficient usage of OpenMP requires us to change a lot of codes, especially that the solver needs major re-factorization, which is our future work.

4.1. Validation

This section has two validation models. The first one has water heavy oil. The second one has water, heavy oil, light oil, and non-condensable gas (NCG). They are created to validate if our results match commercial simulator when equivalent models are used, where CMG STARS is employed. The CMG STARS is the most popular thermal simulator.

4.1.1. Heavy Oil

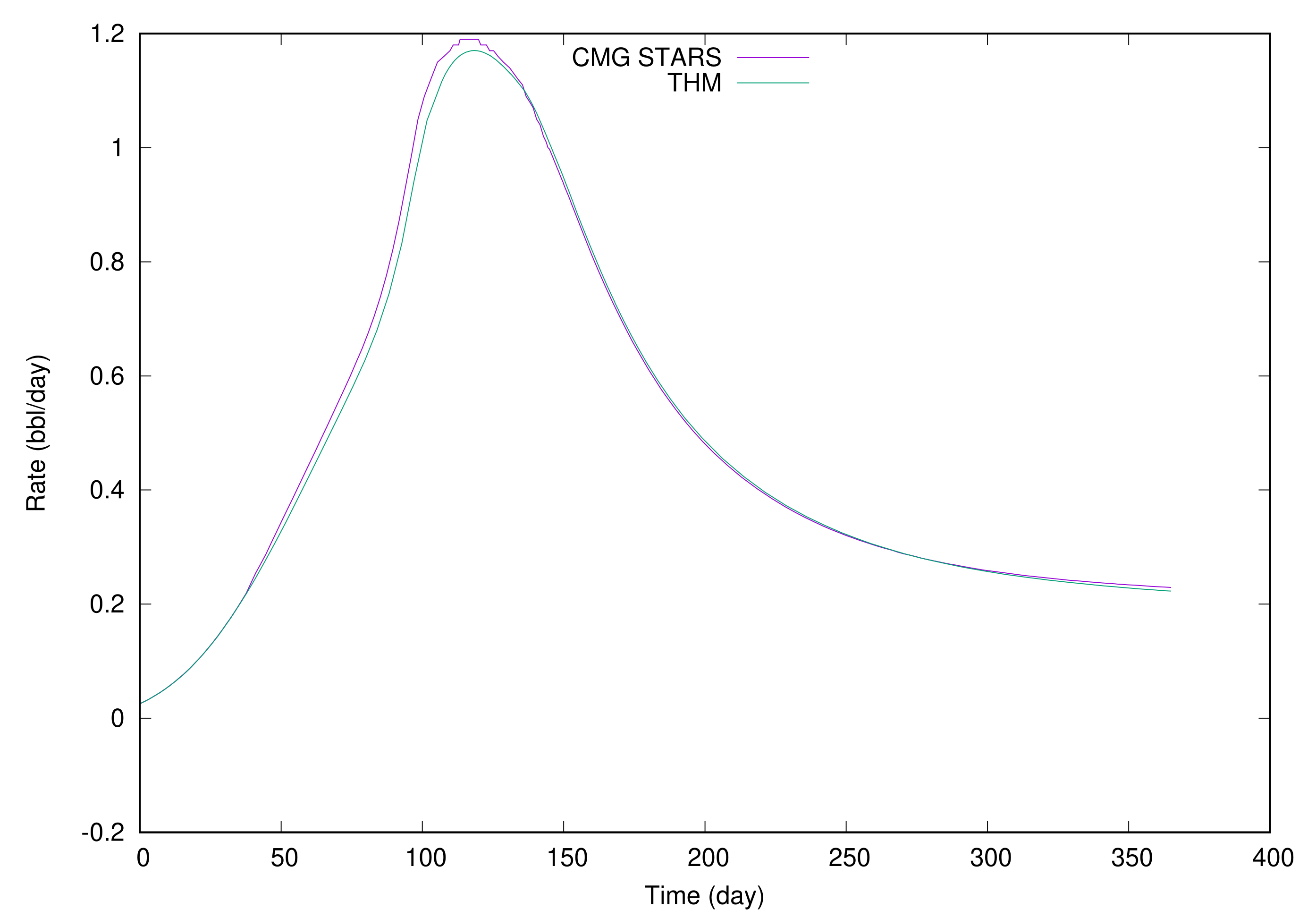
Example 1.

This model has water and one heavy oil component. The heavy oil component stays in oil phase only. It has three vertical wells: one injection well at (1,1) and two production wells at (9, 1) and (5, 5).

Table 1. Oil–water relative permeability for Example 1.

${\mathit{S}}_{\mathit{w}}$	${\mathit{k}}_{\mathbf{rw}}$	${\mathit{k}}_{\mathbf{row}}$
0.45	0.0	0.4
0.47	0.000056	0.361
0.50	0.000552	0.30625
0.55	0.00312	0.225
0.60	0.00861	0.15625
0.65	0.01768	0.1
0.70	0.03088	0.05625
0.75	0.04871	0.025
0.77	0.05724	0.016
0.80	0.07162	0.00625
0.82	0.08229	0.00225
0.85	0.1	0.0

and

Table 2. Liquid–gas relative permeability for Example 1.

${\mathit{S}}_{\mathit{l}}$	${\mathit{k}}_{\mathbf{rg}}$	${\mathit{k}}_{\mathbf{rog}}$
0.45	0.2	0.0
0.55	0.14202	0.0
0.57	0.13123	0.00079
0.60	0.11560	0.00494
0.62	0.10555	0.00968
0.65	0.09106	0.01975
0.67	0.08181	0.02844
0.70	0.06856	0.04444
0.72	0.06017	0.05709
0.75	0.04829	0.07901
0.77	0.04087	0.09560
0.80	0.03054	0.12346
0.83	0.02127	0.15486
0.85	0.01574	0.17778
0.87	0.01080	0.20227
0.90	0.00467	0.24198
0.92	0.00165	0.27042
0.94	0.0	0.30044
1.0	0.0	0.4

show the oil–water relative permeability curve and liquid–gas relative permeability curve. Here, the capillary pressures are ignored.

Table 3. Property data for Example 1.

Properties	HO
$M\left(\mathrm{lb}/\mathrm{lbmole}\right)$	600
${\rho }_{ref}\left({\mathrm{lbmole}/\mathrm{ft}}^3\right)$	0.10113
$cp(1/\mathrm{psi})$	$5\times {10}^{-6}$
$c{t}_1(1/{}^{\circ }\mathrm{F})$	$3.8\times {10}^{-4}$
$cpg1(\mathrm{Btu}/({}^{\circ }\mathrm{F}·\mathrm{lbmol}))$	300
$avisc\left(\mathrm{cp}\right)$	2
$bvisc\left({}^{\circ }\mathrm{F}\right)$	5728.2
Properties	Water
$M\left(\mathrm{lb}/\mathrm{lbmole}\right)$	18.02
$p_{crit}\left(\mathrm{psi}\right)$	3206.2
$T_{crit}\left({}^{\circ }\mathrm{F}\right)$	705.4
${\rho }_{ref}\left({\mathrm{lbmole}/\mathrm{ft}}^3\right)$	3.464
$cp(1/\mathrm{psi})$	$3.999\times {10}^{-6}$
$c{t}_1(1/{}^{\circ }\mathrm{F})$	$4\times {10}^{-4}$
$cpg1(\mathrm{Btu}/({}^{\circ }\mathrm{F}·\mathrm{lbmol}))$	7.613
$hvr(\mathrm{Btu}/({{}^{\circ }\mathrm{F}}^{ev}·\mathrm{lbmol}))$	1657.0
$ev$	0.38
$avg(\mathrm{cp}/{}^{\circ }\mathrm{F})$	$1.13\times {10}^{-5}$
$bvg$	1.075
$avisc\left(\mathrm{cp}\right)$	0.0047352
$bvisc\left({}^{\circ }\mathrm{F}\right)$	2728.2
$k{v}_1\left(\mathrm{psi}\right)$	$1.7202\times {10}^6$
$k{v}_2(1/\mathrm{psi})$	0
$k{v}_3$	0
$k{v}_4\left({}^{\circ }\mathrm{F}\right)$	−6869.59
$k{v}_5\left({}^{\circ }\mathrm{F}\right)$	−376.64

presents chemical properties.

Table 4. Well data for Example 1.

Well Conditions
Injector	water $\left(\mathrm{bbl}/\mathrm{day}\right)$	100
	wi $(\mathrm{ft}·\mathrm{md})$	${10}^4$
	tinjw ${(}^{\circ }\mathrm{F})$	450
	steam quality	0.0
Producer 1	bhp $\left(\mathrm{psi}\right)$	17
	wi $(\mathrm{ft}·\mathrm{md})$	${10}^4$
Producer 2	bhp $\left(\mathrm{psi}\right)$	17
	wi $(\mathrm{ft}·\mathrm{md})$	${10}^4$

shows well data, including well index and operations.

Table 5. Initial condition data for Example 1.

Initial Condition
$k_{x,y,z}\left(\mathrm{md}\right)$	313, 424, 535
$\varphi$	0.3
${\varphi }_c$	$5\times {10}^{-4}$
$p\left(\mathrm{psi}\right)$	4000
$T{(}^{\circ }\mathrm{F})$	125
$S_{w,o,g}$	0.45, 0.55, 0.
x	0.6, 0.4

gives initial conditions. The simulation period is 365 days and the initial time step is ${10}^{-3}$ day. The model is small, and its grid dimension is $9\times 5\times 4$. The grid size is $29.17ft\times 29.17ft\times 10ft$. The standard Newton method is applied to solve the nonlinear system, in which the termination tolerance is ${10}^{-6}$ and the maximal iterations are 10. The linear solver is BICGSTAB and the preconditioner is CPR-FPF, in which the tolerance is 0.0001 and the maximal iterations are 100. The GJE decoupling method is applied to the linear systems. All wells apply the implicit modeling. Each perforation of the production wells is heated at ${10}^6$ Btu/day. Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show bottom hole pressure and liquid rates, which are compared with CMG STARS.

Figure 1 is the bottom hole pressure of the injection well. In this figure, the results from our simulator are marked as “THM” and the results from CMG STARS are marked as “CMG STARS”. From now on, all results are marked the same way. From Figure 1, we can see that the bottom hole pressures from two simulator match exactly. In the beginning, the bottom hole pressures change dramatically. Figure 2 is the water rate of the injection well. The model has an injection rate of 100 bbl/day. Figure 2 shows that both simulators have the correct injection rates and the error is small.

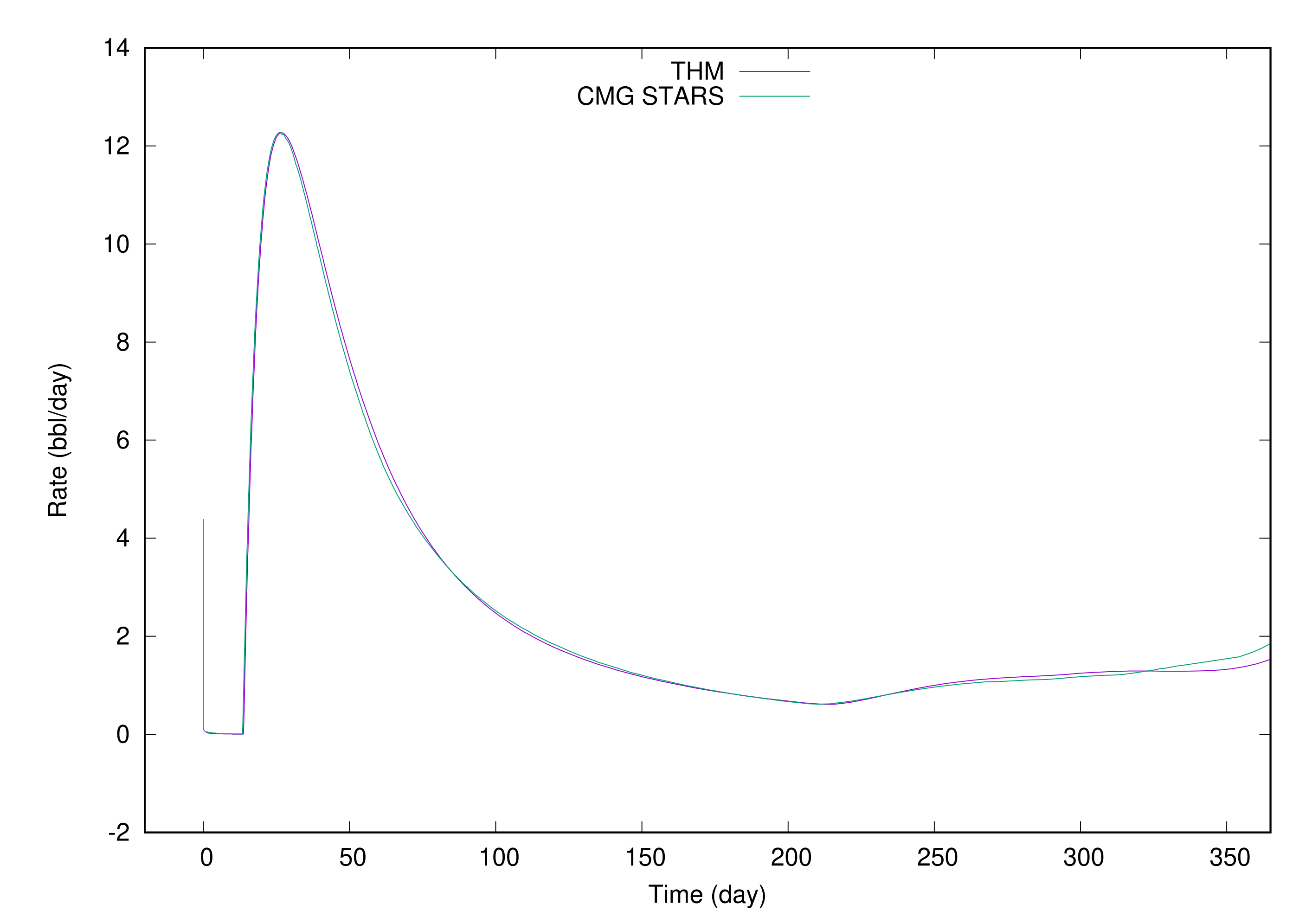
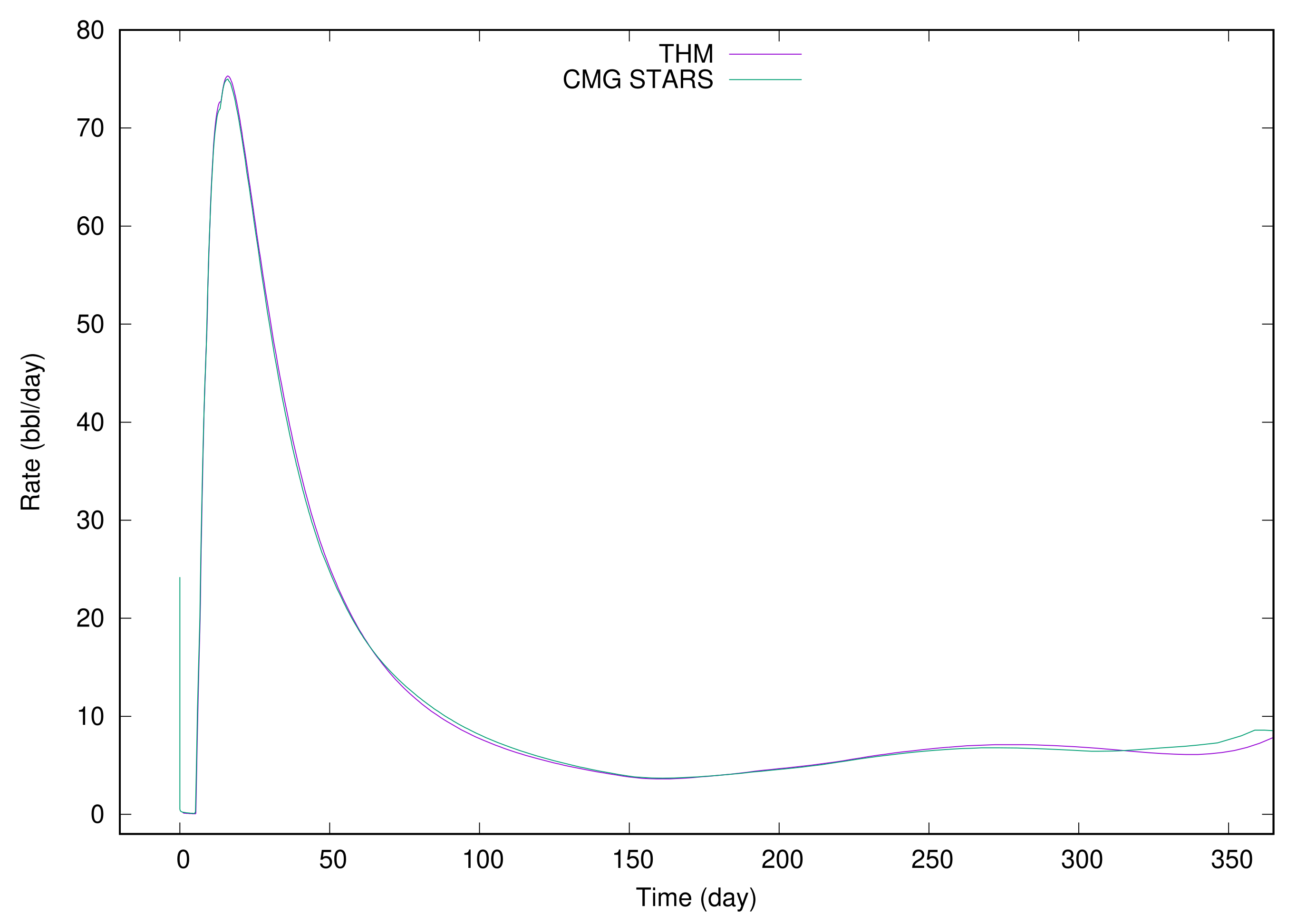
Figure 3, Figure 4 and Figure 5 show the water production rate of the first production well, the water production rate of the second production well, and the total water production rate of all production wells. All three figures show that our simulator has the same results as CMG STARS in the early stage. However, as each simulator has its own internal numerical tunings, the curves have slight differences, which are totally acceptable in real production. Figure 6, Figure 7 and Figure 8 are the oil production rate of the first production well, the oil production rate of the second production well, and the total oil production rate of all production wells. Again, we can see that our results match CMG STARS. In this example, we can conclude that our results match CMG STARS very well, which confirms our methods and implementation are correct.

4.1.2. Light Oil and Non-Condensable Gas

Example 2.

This model has water, one heavy oil component, one light oil component, and two non-condensable gas (NCG) components. The water and heavy oil component have the same properties as Example 1.

Table 6. Light oil property data for Example 2.

Properties	Light Oil
$M(\mathrm{lb}/\mathrm{lbmole})$	250
$p_{crit}\left(\mathrm{psi}\right)$	225
$T_{crit}\left({}^{\circ }\mathrm{F}\right)$	800
${\rho }_{ref}(\mathrm{lbmole}/{\mathrm{ft}}^3)$	0.2092
$cp(1/\mathrm{psi})$	$5\times {10}^{-6}$
$c{t}_1(1/{}^{\circ }\mathrm{F})$	$3.8\times {10}^{-4}$
$cpg1(\mathrm{Btu}/({}^{\circ }\mathrm{F}·\mathrm{lbmol}))$	247.5
$hvr(\mathrm{Btu}/({{}^{\circ }\mathrm{F}}^{ev}·\mathrm{lbmol}))$	657.0
$ev$	0.38
$avg(\mathrm{cp}/{}^{\circ }\mathrm{F})$	$5\times {10}^{-5}$
$bvg$	0.9
$avisc\left(\mathrm{cp}\right)$	0.287352
$bvisc\left({}^{\circ }\mathrm{F}\right)$	3728.2
$k{v}_1\left(\mathrm{psi}\right)$	$7.9114\times {10}^4$
$k{v}_2(1/\mathrm{psi})$	0
$k{v}_3$	0
$k{v}_4\left({}^{\circ }\mathrm{F}\right)$	−1583.71
$k{v}_5\left({}^{\circ }\mathrm{F}\right)$	−446.78

and

Table 7. NCG property data for Example 2.

Properties	N2	Isert
$M\left(\mathrm{lb}/\mathrm{lbmole}\right)$	28	40.8
$p_{crit}\left(\mathrm{psi}\right)$	730	500
$T_{crit}\left({}^{\circ }\mathrm{F}\right)$	−181	−232
$cpg1(\mathrm{Btu}/({}^{\circ }\mathrm{F}·\mathrm{lbmol}))$	6.713	7.44
$cpg2(\mathrm{Btu}/({}^{\circ }{\mathrm{F}}^2·\mathrm{lbmol}))$	−$4.883\times {10}^{-7}$	−0.0018
$cpg3(\mathrm{Btu}/({}^{\circ }{\mathrm{F}}^3·\mathrm{lbmol}))$	$1.287\times {10}^{-6}$	$1.975\times {10}^{-6}$
$cpg4(\mathrm{Btu}/({}^{\circ }{\mathrm{F}}^4·\mathrm{lbmol}))$	$-4.36\times {10}^{-10}$	$-4.78\times {10}^{-10}$
$avg(\mathrm{cp}/{}^{\circ }\mathrm{F})$	$2.1960\times {10}^{-4}$	$2.1267\times {10}^{-4}$
$bvg$	0.721	0.702

provide data for light oil component and NCG.

Table 8. Well data for Example 2.

Well Conditions
Injector	water $\left(\mathrm{bbl}/\mathrm{day}\right)$	100
	wi $(\mathrm{ft}·\mathrm{md})$	${10}^4$
	tinjw ${(}^{\circ }\mathrm{F})$	450
	steam quality	0.3
Producer 1	bhp $\left(\mathrm{psi}\right)$	17
	wi $(\mathrm{ft}·\mathrm{md})$	$2\times {10}^4$
Producer 2	bhp $\left(\mathrm{psi}\right)$	17
	wi $(\mathrm{ft}·\mathrm{md})$	$3\times {10}^4$
Producer 3	bhp $\left(psi\right)$	17
	wi $(\mathrm{ft}·\mathrm{md})$	$4\times {10}^4$
Producer 4	bhp $\left(\mathrm{psi}\right)$	17
	wi $(\mathrm{ft}·\mathrm{md})$	$5\times {10}^4$

and

Table 9. Initial data for Example 2.

Initial Condition
$k_{x,y,z}\left(\mathrm{md}\right)$	313, 424, 535
$\varphi$	0.3
${\varphi }_c$	$5\times {10}^{-4}$
$p\left(\mathrm{psi}\right)$	4000
$T{(}^{\circ }\mathrm{F})$	125
$S_{w,o,g}$	0.4, 0.5, 0.1
x	0.6, 0.4
y	0.2, 0.7

present well data and initial conditions. It has five vertical wells: one injection well in the center (5, 5), and four production wells in four corners, (1, 1), (1, 9), (9, 1), and (9, 9). The grid dimension is $9\times 9\times 4$, and the grid size is $29.17ft\times 29.17ft\times 10ft$. The standard Newton method is applied to solve the nonlinear system, in which the termination tolerance is 0.0001 and the maximal iterations are 10. The linear solver is BICGSTAB and the preconditioner is CPR-FPF, in which the tolerance is 0.0001 and the maximal iterations are 100. The GJE decoupling method is applied to the linear systems. All wells apply the implicit modeling. Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 present bottom hole pressure for injection well and fluid rates, including water rate, oil rate, and gas rate. As each production well has similar results, only results from the first production well are reported. All results are compared with CMG STARS.

Example 1 has only one oil component, which stays in oil phase only, while this example has light oil component and non-condensable gas components. Example 1 has no gas production. Furthermore, under reservoir conditions, gas may or may not appear. The physics of this example is more complicated. Figure 9 is the bottom hole pressure of the injection well, and from the curves, we can see that our results match the CMG STARS simulator. Figure 10 and Figure 11 are water production rate of the first production well and the total water production rate of all production wells. Again, a good match can be observed. Figure 12 and Figure 13 are the oil production rate of the first production well and the total oil production rate of all production wells. Figure 14 and Figure 15 are the gas production rate of the first production well and the total gas production rate of all production wells. These figures show that our results match CMG STARS very well, which confirms our methods and implementation are correct.

4.2. Numerical Performance

Example 3.

This example tests a SAGD model with 25 well pairs, which includes one water component, one heavy component, one light component, and two inert gase components, and their properties are the same as Example 2. The grid dimension is $100\times 100\times 6$ and gird size is $10ft\times 10ft\times 1ft$. The simulation time is 200 days and the maximal time step is 10 days. The Newton tolerance is ${10}^{-3}$ and its maximal iterations are 15. The linear solver is BICGSTAB, its tolerance is also ${10}^{-3}$ and its maximal iterations are 60. GJE is the decoupling method. All injectors operate at 3 bbl/day water injection with steam quality of 0.2 and temperature of 450 F . All producers operate at bottom hole pressure of 2000 psi and steam trap temperature difference of 20 F. summaries of our simulator are shown in

Table 10. Numerical summaries of Example 3.

CPU Cores	# Time Steps	# Newton	# Linear Solver	Avg. Linear	Time
4	96 (4)	314	5587	17.80	1420.63
8	100 (6)	338	6157	18.22	816.69
16	101 (4)	326	6215	19.06	558.22

. As the model is small, only one computing node is employed.

Table 10 provides numerical summaries for time steps (and time cut), total Newton iterations, total linear solver iterations, average linear iterations per Newton iteration, and total simulation time at different CPU cores (MPIs). The RAS method solves a smaller local problem on each CPU core, and the parallel AMG method balances scalability and convergence rate. As expected, when more CPU cores (MPIs) are used, time steps and linear iterations increase. Regardless, the results show that our numerical methods are effective, which can solve a time step in less than 4 Newton iterations and solve a linear system in less than 20 iterations. When more CPU cores are used, the simulation time is cut, which shows that parallel computing is a powerful tool for reservoir simulation.

Example 4.

This example tests one water component, one heavy component, and one light component. SAGD process with 756 well pairs is simulated. The grid has a dimension of $60\times 220\times 85$ and size of $20ft\times 10ft\times 1ft$. All wells are horizontal wells along x direction, if the index of y direction of a grid block equals to 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67, 71, 75, 79, 83, 87, 91, 95, 99, 103, 107, 111, 115, 119, 123, 127, 131, 135, 139, 143, 147, 151, 155, 159, 163, 167, 171, 175, 179, 183, 187, 191, 195, 199, 203, 207, 211, or 215, and the index of z direction equals to 4, 10, 16, 22, 28, 34, 40, 46, 52, 58, 64, 70, 76, or 82, then an injection well is defined. For example, (1:60, 3, 10) defines an injection well at (3,10) of $yz$-plane, and its perforations are from 1 to 60. This defines 756 injection wells. A production well is defined two blocks under an injection well. Therefore, 756 well pairs and total 1512 wells are defined in the model. All injection wells operate at 10 bbl/day water injection, with a steam quality of 0.2 and temperature of 450 F. All production wells operate at fixed bottom hole pressure of 100 psi. Each perforation of an injection well is heated at rate of ${10}^5$ btu/day. The simulation time is 100 days. Eight CPU cores (8 MPIs) are employed. The Newton tolerance is 0.0001 and its maximal iterations are 15. The linear solver is BICGSTAB, its tolerance is also 0.0001, and its maximal iterations are 100. Different preconditioners and decoupling methods are employed.

Table 11. Numerical summary of Example 4.

Preconditioner	Decoupling	Time Steps	# Newton	# Linear Solver
CPR-FP	NONE	NA	NA	NA
CPR-FP	FRS	NA	NA	NA
CPR-FP	DRS	NA	NA	NA
CPR-FP	ABF	NA	NA	NA
CPR-FP	GJE	101 (12)	598	8856
CPR-FP	DRS + ABF	NA	NA	NA
CPR-FP	DRS + GJE	95 (10)	559	8090
CPR-FP	FRS + ABF	NA	NA	NA
CPR-FP	FRS + GJE	96 (10)	552	7608
CPR-PF	NONE	NA	NA	NA
CPR-PF	FRS	NA	NA	NA
CPR-PF	DRS	NA	NA	NA
CPR-PF	ABF	125 (15)	738	18,680
CPR-PF	GJE	105 (10)	585	11,263
CPR-PF	DRS + ABF	103 (9)	563	12,642
CPR-PF	DRS + GJE	109 (11)	636	12,947
CPR-PF	FRS + ABF	NA	NA	NA
CPR-PF	FRS + GJE	109 (12)	640	13,050
CPR-FPF	NONE	NA	NA	NA
CPR-FPF	FRS	NA	NA	NA
CPR-FPF	DRS	NA	NA	NA
CPR-FPF	ABF	NA	NA	NA
CPR-FPF	GJE	97 (10)	566	7887
CPR-FPF	DRS + ABF	NA	NA	NA
CPR-FPF	DRS + GJE	97 (10)	566	7813
CPR-FPF	FRS + ABF	NA	NA	NA
CPR-FPF	FRS + GJE	97 (10)	559	7666

shows numerical summaries.

Table 11 presents preconditioners, decoupling methods, total time steps and time cuts, total Newton iterations, and total linear iteration. Here, NA means the combination fails to simulate the model. The CPR-FP and the CPR-PF are two-stage CPR preconditioner and the CPR-FPF is a three-stage CPR preconditioner. From the table, we can see the simulations fail if no decoupling method is used. Furthermore, FRS or DRS does not work for thermal reservoir simulations. The ABF decoupling method works very well for black oil simulation, where temperature does not change. Here, the ABF method fails two cases out of three cases while the GJE method works for all cases. Even when the ABF method works with the CPR-PF preconditioner, the GJE decoupling method has much less time steps, Newton iterations, and linear iterations. It is clear that the GJE decoupling works much better than the ABF method. For CPR-FP and CPR-FPF preconditioners, two stage decoupling methods improve the efficiency of Newton method and linear solver. The results clearly show that a proper decoupling method is critical to the success of linear solver and CPR-type preconditioners. The GJE decoupling and the FRS+GJE decoupling work better than the ABF decoupling.

Example 5.

This example tests one water component, one heavy component and one light component. SAGD process with 7406 well pairs (14,812 wells, 7406 injectors, and 7406 producers) is simulated. The grid has a dimension of $60\times 2200\times 85$, 11 million grid blocks, and size of $20ft\times 10ft\times 2ft$. All wells are horizontal wells along x direction. All injection wells operate at 5 bbl/day water injection, with a steam quality of 0.2 and temperature of 450 F. All production wells operate at fixed bottom hole pressure of 300 psi. All wells are modeled by implicit method. The model file has around 185,000 lines. The simulation time is 100 time steps due to system running time limit. The initial time step is ${10}^{-6}$ days. 10 nodes and 200 CPU cores (200 MPIs) are employed on Niagara, Compute Canada. The Newton tolerance is ${10}^{-3}$ and its maximal iterations are 15. The linear solver is BICGSTAB, its tolerance is also 0.0001 and its maximal iterations are 100. The maximal changes in a time step for pressure, saturation, mole fraction and temperature are 500 psi, 0.1, 0.1, and 15 F. Numerical summaries are shown by

Table 12. Numerical summaries of Example 5.

Preconditioner	Decoupling	Time Steps	# Newton	# Linear Solver
CPR-FP	GJE	100	284	1245
CPR-FP	FRS + GJE	100	267	1194
CPR-PF	GJE	100	299	1540
CPR-PF	FRS + GJE	100	282	1183
CPR-FPF	GJE	100	308	1801
CPR-FPF	FRS + GJE	100	298	1255

.

Table 12 shows that all tests pass. The Newton method converges in around three iterations, while linear solver converges in four to five iterations in average. For a specific preconditioner, the FRS + GJE decoupling method is always better than the GJE method. When two-stage decoupling method FRS + GJE is applied, less Newton iterations and linear iterations are required.

4.3. Scalability

The parallel computers from Compute Canada are employed. The Niagara supercomputer consists of 1500 nodes, and each node has 40 Intel Skylake cores at 2.4 GHz, for a total of 60,000 cores. Each node has 202 GB (188 GiB) RAM, and EDR Infiniband network is used to communicate. The Cedar supercomputer has a hybrid architecture, which uses Intel E5-2683 v4 “Broadwell” at 2.1 Ghz, E5-2650 v4 at 2.2 GHz, Intel E7-4809 v4 “Broadwell” at 2.1 Ghz, and Intel Platinum 8160F “Skylake” at 2.1 Ghz. It has a total of 58,416 CPU cores for computation, and 584 GPU devices.

A Cray XC30 supercomputer is also employed. Each computation node contains two 2.7 GHz, 12-core Intel E5-2697 v2 CPUs, and 64 GB of memory is shared between the two processors. The memory bandwidth is ~103 Gb/s. The memory access is nonuniform access (NUMA): each processor owns a single NUMA region of 32 GB. Accessing its own region has a lower latency than accessing the other NUMA region. Also, these 24 cores compete the memory channels. The Aries interconnect connects all computation nodes in a Dragonfly topology.

Example 6.

This example studies a large thermal model with a grid dimension of $360\times 400\times 1600$, 230 million grid blocks. Twelve nodes and up to 192 CPU cores are employed using the Niagara supercomputer. The Newton method is applied with a tolerance of ${10}^{-6}$ and maximal iterations of 10. The linear solver is BICGSTAB with a tolerance of ${10}^{-5}$ and maximal iterations of 100. The preconditioner is the CPR-FPF method.

Table 13. Summary of Example 6.

CPU Cores	Total Time (s)	Solver Time (s)	Overall Speedup	Memory (GB)
24	2448.78	927.92	1.00 (100%)	1945.92
48	1094.55	380.40	2.24 (112%)	1959.28
96	545.20	194.81	4.49 (112%)	1970.83
192	291.88	107.32	8.38 (105%)	1994.25

presents running time and memory used. Figure 16 shows the scalability.

Table 13 shows total time, linear solver time, speedup and total memory, from which we can see that huge amount of memory is required. The simulation is not possible for desktop computers. The running time and Figure 16 show the simulator, linear solver, and preconditioner have good scalability.

Example 7.

This example studies a large thermal model with a grid dimension of $1080\times 2000\times 1600$, 3.46 billion grid blocks and the resulted linear systems have 17.3 billion unknowns. 360 nodes are employed using the Cedar supercomputer. The Newton method is applied with a tolerance of ${10}^{-10}$ and maximal iterations of 10. The linear solver is BICGSTAB with a tolerance of ${10}^{-10}$ and maximal iterations of 100. The preconditioner is the CPR-FPF method with GJE decoupling.

Table 14. Summary of Example 7.

CPU Cores	Total Time (s)	Solver Time (s)	Overall Speedup	Memory (GB)
2880 (360 × 8)	1247.74	996.76	1.00 (100%)	30,101.46
5760 (360 × 16)	757.70	578.32	1.65 (82.5%)	33,490.12

presents running time and memory used.

Table 14 shows that the simulator, linear solver, and preconditioner have excellent scalability. This example proves that our thermal simulator can handle extreme large-scale models. If more computing resources are available, a larger model can be simulated. Our linear solver and preconditioner can solve linear systems with dozens of billions of unknowns. In an ideal case, when the size of MPIs doubles, the simulation time should be cut by half and the ideal speedup should be 2. This example shows a speedup of 1.65 and an efficiency of 82.5%, and we believe the reason is that when more CPU cores are used in one node, these processors compete memory and computing, which reduces the effective memory communication bandwidth. Therefore, the speedup is reduced.

Example 8.

This example studies a large thermal model with a grid dimension of $1440\times 2000\times 1600$, 4.6 billion grid blocks and the resulted linear systems have 23 billion unknowns; 1024 nodes are employed. The Newton method is applied with a tolerance of 0.0001 and maximal iterations of 10. The linear solver is BICGSTAB with a tolerance of ${10}^{-3}$ and maximal iterations of 100. The preconditioner is the CPR-FPF method with GJE decoupling.

Table 15. Summary of Example 8.

CPU Cores	Total (s)	Solver (s)	Solver Speedup	Overall Speedup	Memory (GB)
2048	793.68	594.70	1.00 (100%)	1.00 (100%)	43,090.70
4096	419.45	305.93	1.94 (97.0%)	1.89 (94%)	41,542.27
6144	293.85	213.48	2.78 (92.7%)	2.70 (90%)	45,118.68
12,288	168.97	118.23	5.03 (83.0%)	4.70 (78%)	44,063.20

presents running time and memory used and Figure 17 shows the scalability.

Table 15 shows overall time, linear solver time, linear solver speedup, overall speedup, and total memory. When 4096 and 6144 cores are used, the scalabilities are 1.89 and 2.7, respectively, while the best scalabilities should be 2 and 3. In this case, the parallel efficiencies are 94% and 90%, which are good for parallel numerical simulations. However, this example shows linear solver has better speedup and parallel efficiency. If special optimization techniques are applied, such as multi-level load balancing that considers the architecture of the system and multi-layer communications, the communication volume and latency will be reduced and scalability can be improved. When 12,288 cores are employed, each node runs 12 cores and 12 MPIs, and each processor uses its 6 cores. In this case, memory access may be an important issue, which may reduce the effective memory bandwidth of each MPI and increase computation time.

Example 9.

This example studies a simplified problem with a grid dimension of 216 billion grid blocks. The linear solver is BICGSTAB and the preconditioner is the RAS method.

Table 16. Summary of Example 9.

CPU Cores	Total (s)	Solver (s)	Solver Speedup	Overall Speedup	Memory (GB)
8192	472.64	240.15	1.00 (100%)	1.00 (100%)	252,194.32
16,384	249.68	130.52	1.84 (92.0%)	1.89 (94.5%)	255,154.24
24,576	169.84	88.58	2.71 (90.4%)	2.78 (92.7%)	258,981.60
49,152	96.53	51.97	4.62 (77.0%)	4.89 (81.5%)	269,806.56
98,304	55.77	31.89	7.53 (62.8%)	8.47 (70.6%)	289,981.44

presents running time and memory used for 4096 computation nodes.

Table 17. Summary of Example 9.

CPU Cores	Total (s)	Solver (s)	Solver Speedup	Overall Speedup	Memory (GB)
8400	456.68	229.65	1.00 (100%)	1.00 (100%)	252,915.14
16,800	237.28	121.62	1.89 (94.4%)	1.92 (96.2%)	255,850.05
25,200	161.45	82.23	2.79 (93%)	2.83 (94.1%)	259,589.53
50,400	93.97	50.54	4.54 (75.7%)	4.86 (80.9%)	270,134.15
100,800	54.16	30.94	7.42 (61.8%)	8.43 (70.2%)	290,869.03

presents running time and memory used for 4200 computation nodes. Each node uses 2, 4, 6, 12, and 24 cores. Figure 18 is the speedup curve.

Table 16 and Table 17 show numerical summaries, including CPU cores, total simulation time, solver time, speedup, and memory usage. The first table uses 4024 computation nodes, and the second table uses 4200 computation nodes. The tables and curves show our parallel simulator has good scalability and efficiency. To the best of our knowledge, this is the largest thermal model, and it uses the most CPU cores for thermal reservoir simulation.

5. Conclusions

This paper introduces a parallel thermal simulator on distributed-memory parallel computers, where MPI is employed for communications. The simulator is designed to handle giant models with billions of grid blocks using hundreds of thousands of CPU cores. Its mathematical models and numerical methods are presented. Numerical experiments are carried out to verify the methods and implementations, which show that our simulator can match commercial software and it has excellent scalability, and it can handle extremely large-scale reservoir models.