Pressure Change for Single- and Two-Phase Non-Newtonian Flows through Sudden Contraction in Rectangular Microchannel
Abstract
:1. Introduction
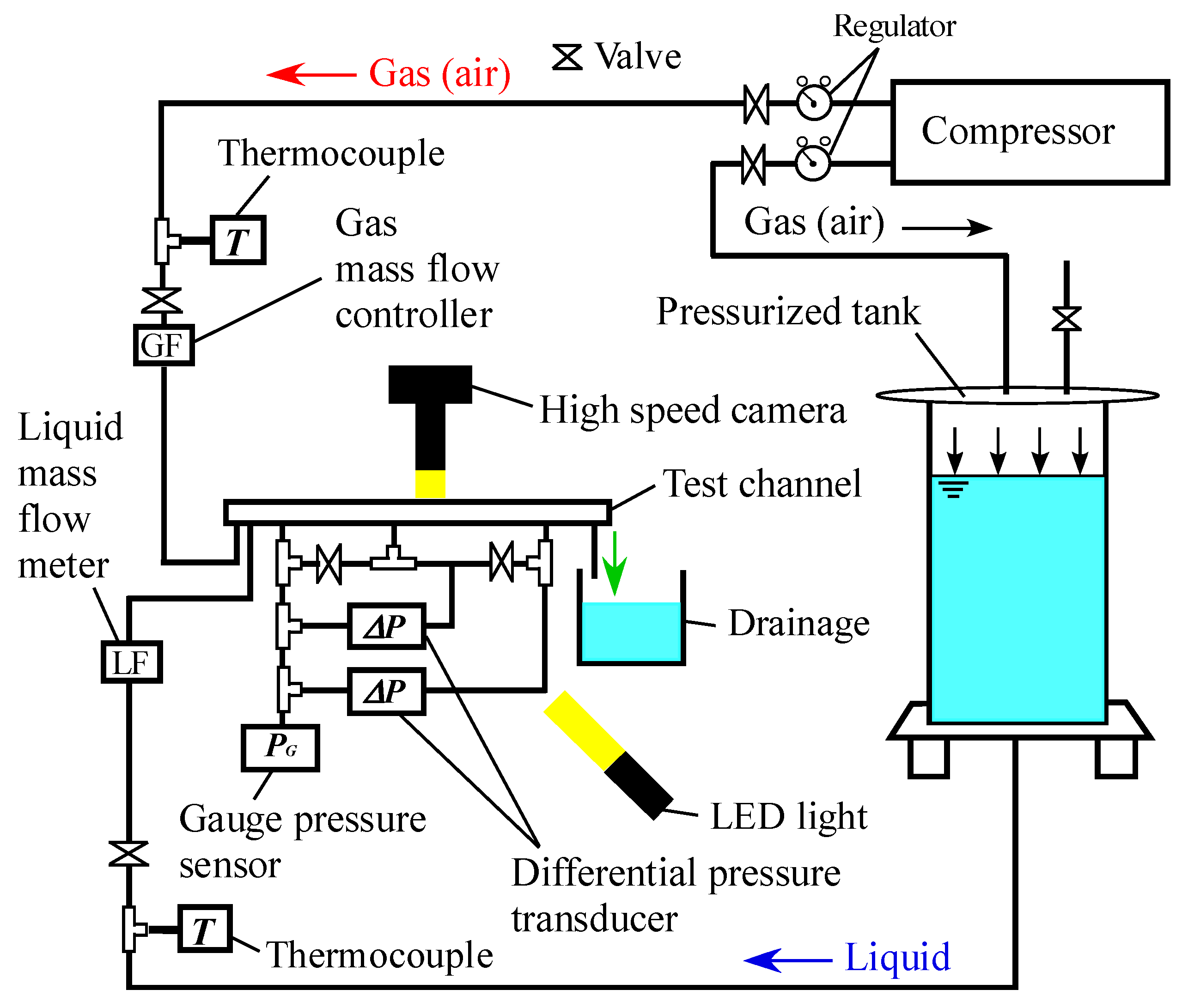
2. Experiments
2.1. Test Apparatus
2.2. Test Liquids and Flow Conditions
2.3. Data Reduction for Pressure Change through Contraction
3. Results and Discussions
3.1. Single-Phase Liquid Flow
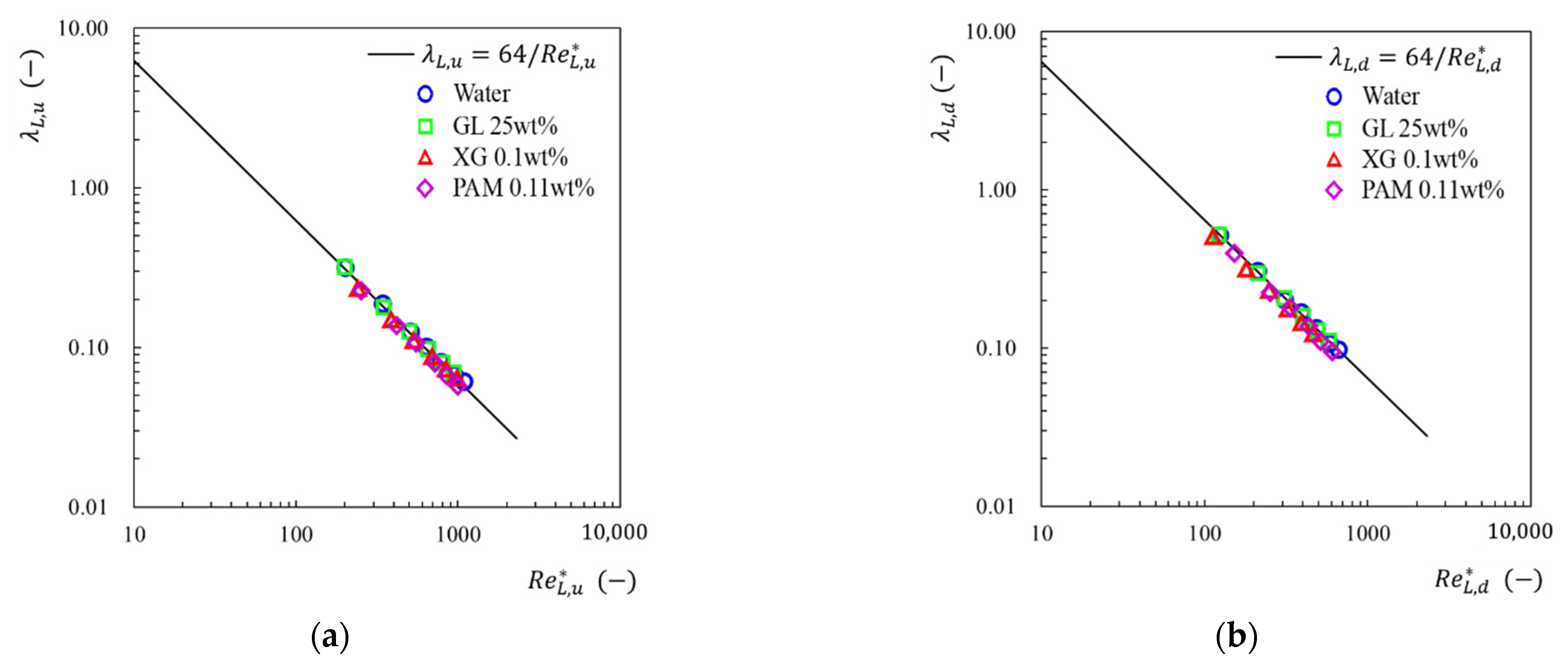
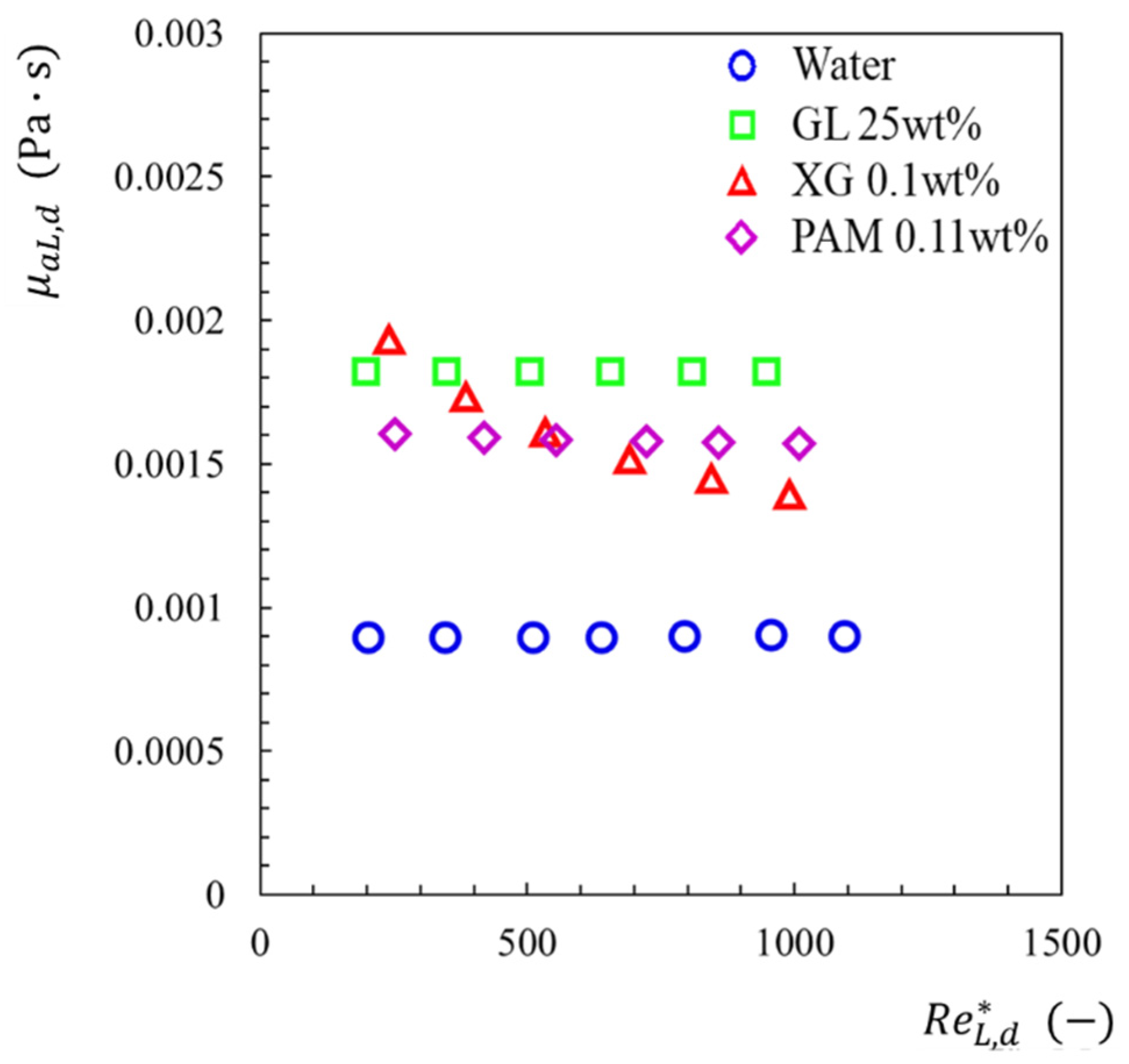
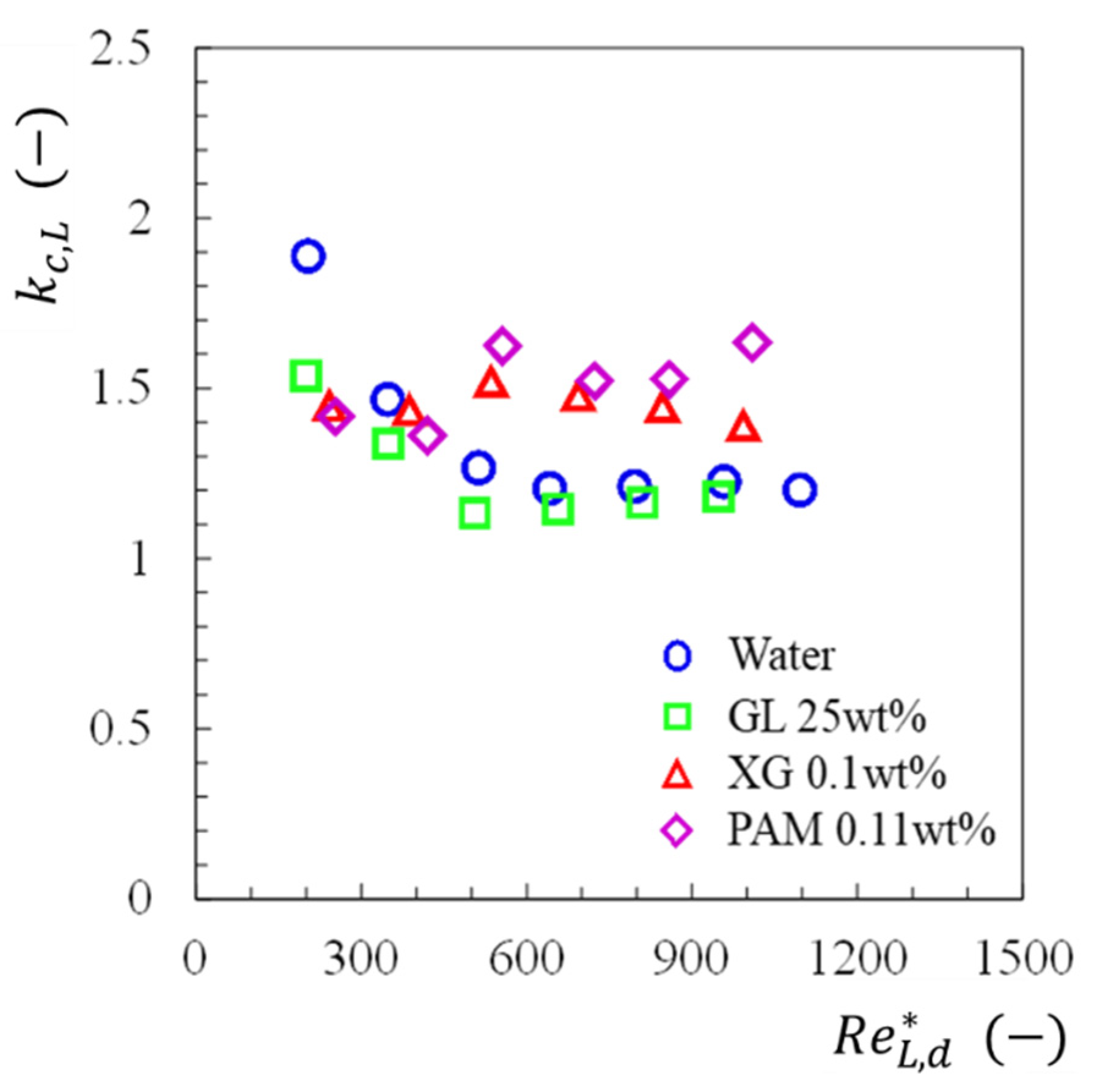
3.1.1. Friction Factor in the Straight Channel
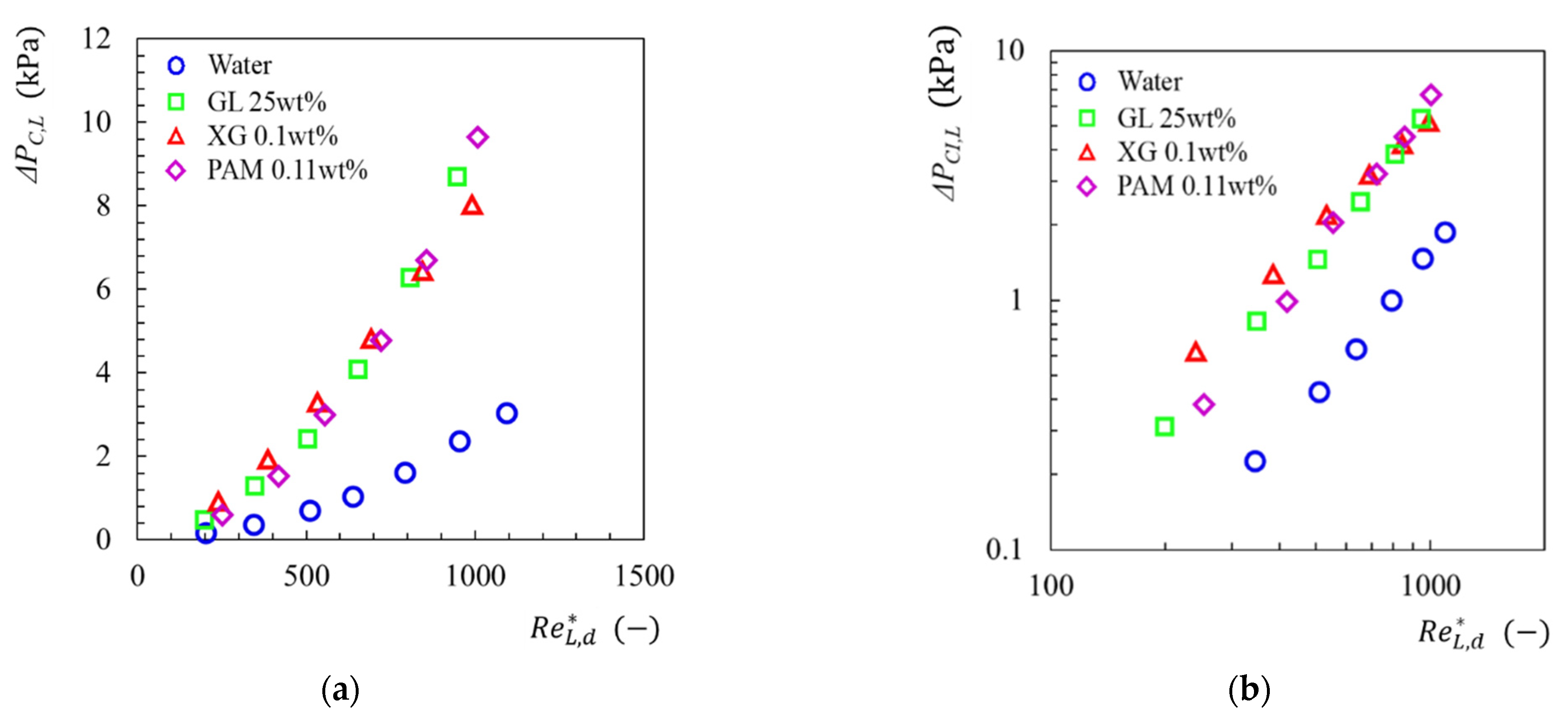
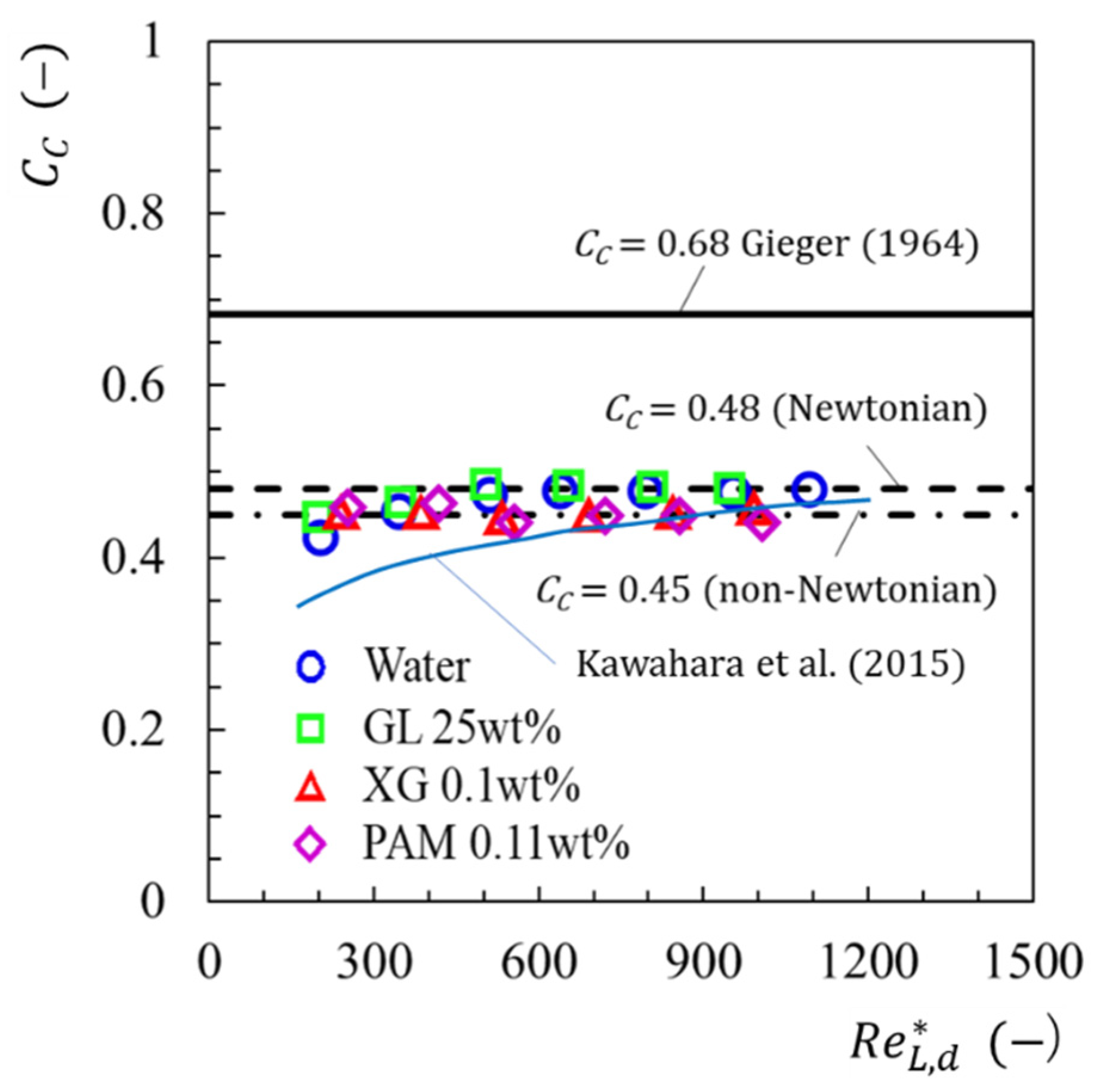
3.1.2. Pressure Change across Sudden Contraction
3.2. Two-Phase Flow
3.2.1. Flow Pattern
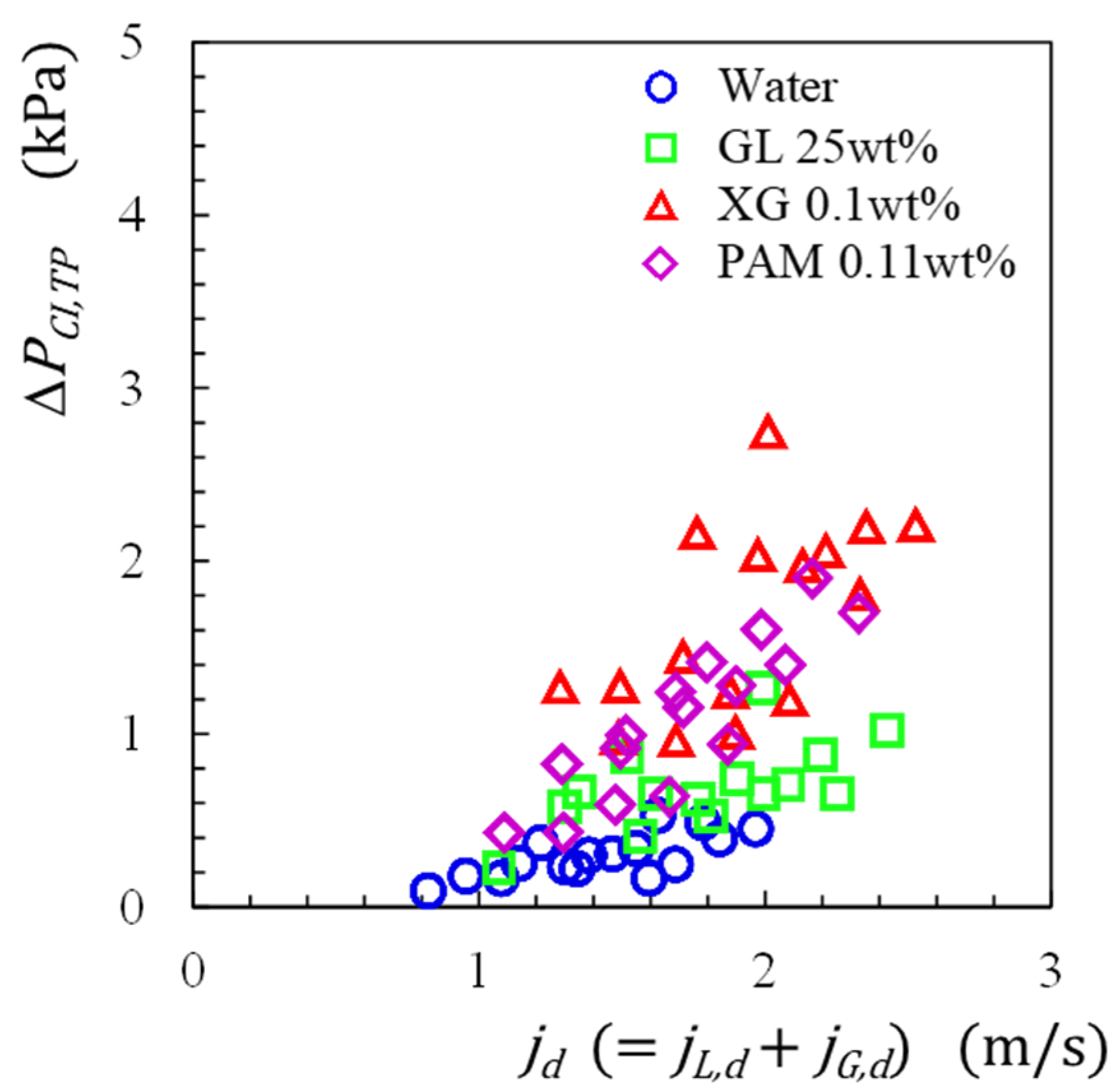
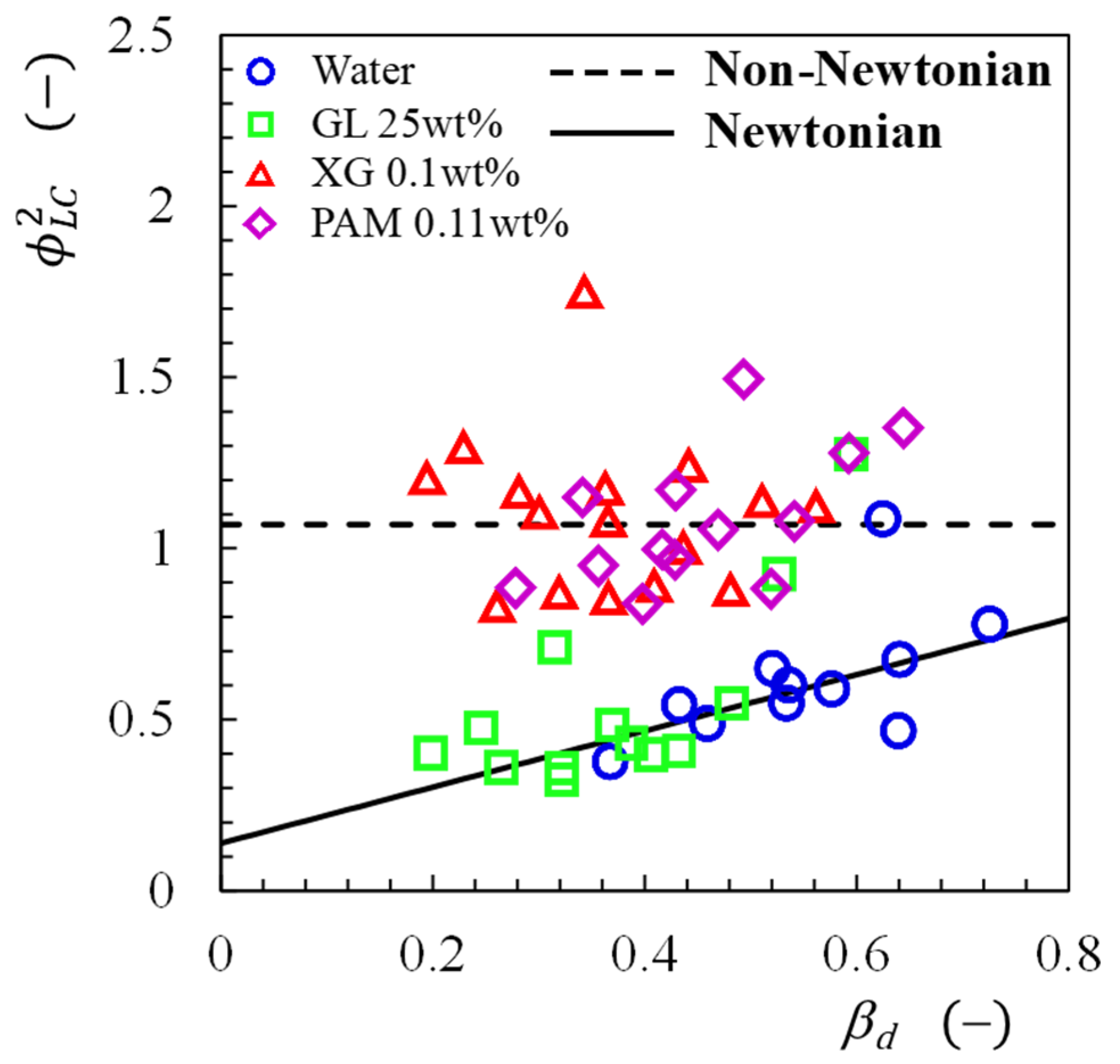
3.2.2. Two-Phase Pressure Change across Sudden Contraction
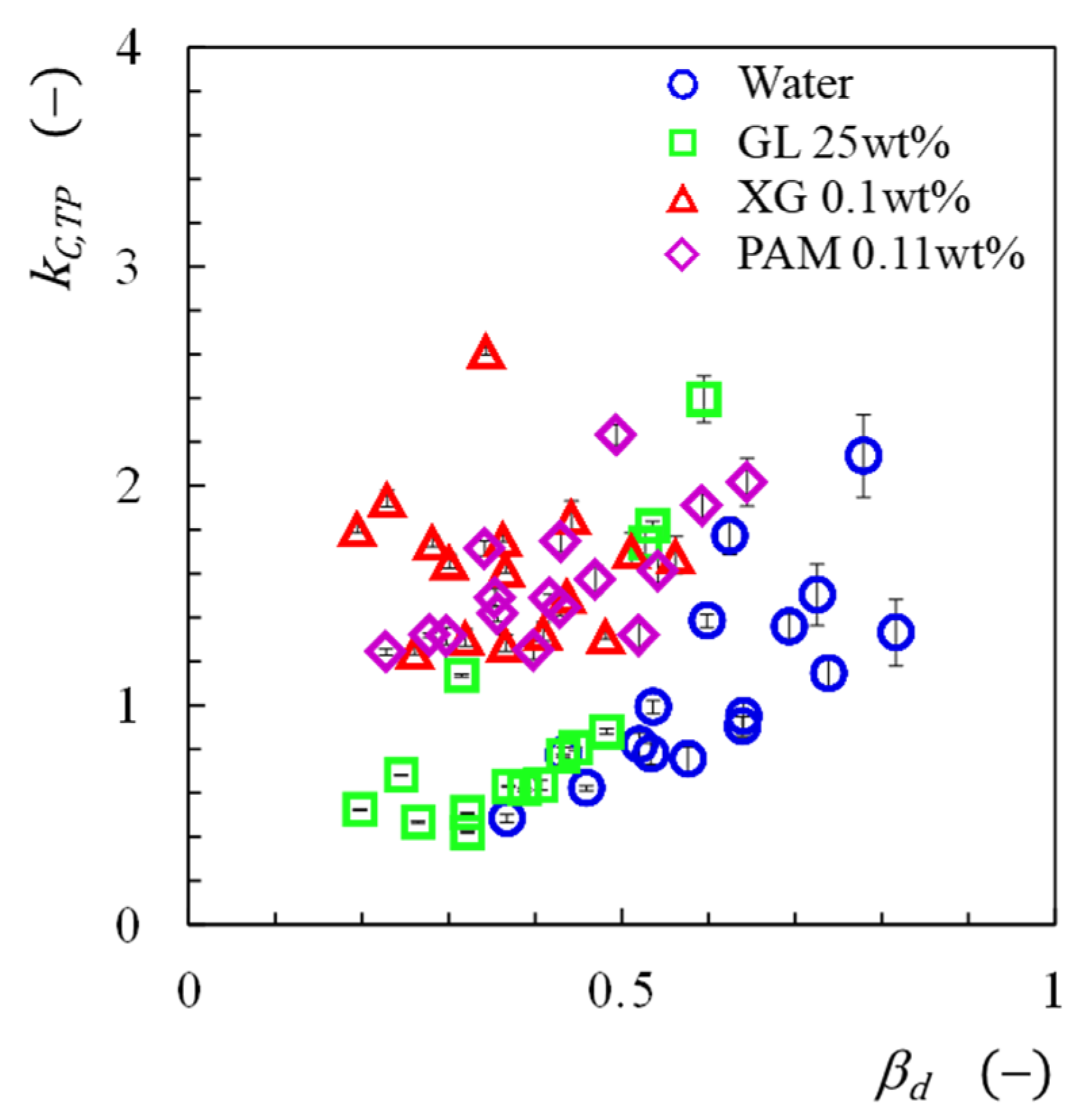
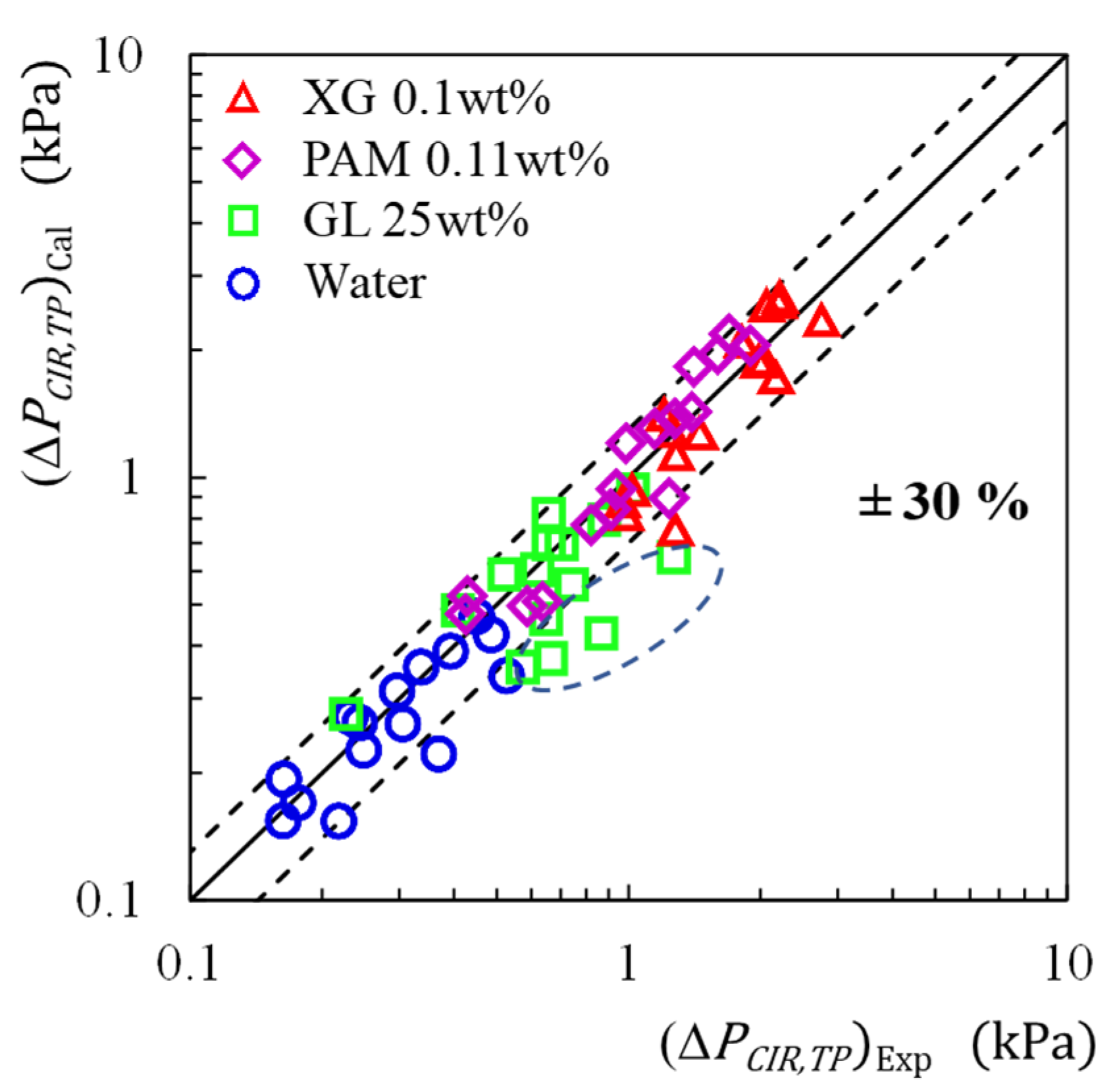
3.2.3. Correlation of Two-Phase Pressure Change
4. Conclusions
4.1. Single-Phase Flow
- Regardless of the test liquid, the sudden contraction pressure drop, ΔPCI,L, for single-phase liquid flows increased as the average flow velocity increased. The magnitude relation of ΔPCI,TP at the same flow velocity was PAM 0.11 wt% > XG 0.1 wt% > GL 25 wt% > distilled water.
- The contraction coefficient obtained in this single-phase liquid experiment was considerably smaller than the value according to Gieger’s equation developed in a conventionally sized channel. In addition, the coefficients of the non-Newtonian fluids were slightly smaller than those of Newtonian fluids.
4.2. Two-Phase Flow
- Slug or bubble flow patterns were observed in the straight channel part upstream and downstream of the contraction. The size and/or length of the bubble and liquid film thickness around the bubble depend on the liquid properties.
- The sudden contraction pressure change ΔPC,TP increased with the total gas and liquid volumetric flux, jd, irrespectively of the test liquids.
- The magnitude of the ΔPC,TP was affected by the pseudoplasticity and elasticity of the liquid phase, and the magnitude at the same flow velocity was XG system > PAM system > GL system > distilled water system.
- The calculated values of ΔPC,TP by a newly developed correlation were in agreement with the experimental values within ± 30% of the relative error.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.-C.; Tseng, C.-Y.; Chen, I.Y. A new correlation and the review of two-phase flow pressure change across sudden expansion in small channels. Int. J. Heat Mass Transf. 2010, 53, 4287–4295. [Google Scholar] [CrossRef]
- Jähnisch, K.; Baerns, M.; Hessel, V.; Ehrfeld, W.; Haverkamp, V.; Lowe, H.; Wille, C.; Guber, A. Direct fluorination of toluene using elemental fluorine in gas/liquid microreactors. J. Fluor. Chem. 2000, 105, 117–128. [Google Scholar] [CrossRef]
- Yen, T.J.; Fang, N.; Zhang, X.; Lu, G.Q.; Wang, C.Y. A micro methanol fuel cell operating at near room temperature. Appl. Phys. Lett. 2003, 83, 4056–4058. [Google Scholar] [CrossRef]
- Qu, W.; Mudawar, I. Flow boiling heat transfer in two-phase microchannel heat sinks—II. Annular two-phase flow model. Int. J. Heat Mass Transf. 2003, 46, 2773–2784. [Google Scholar] [CrossRef]
- Abdelall, F.F.; Hahm, G.; Ghiaasiaan, S.M.; Abdel-Khalik, S.I.; Jeter, S.S.; Yoda, M.; Sadowski, D.L. Pressure drop caused by abrupt flow area changes in small channels. Exp. Therm. Fluid Sci. 2005, 29, 425–434. [Google Scholar] [CrossRef]
- Chalfi, T.Y.; Ghiaasiaan, S.M. Pressure drop caused by flow area changes in capillaries under low flow conditions. Int. J. Multiph. Flow 2008, 34, 2–12. [Google Scholar] [CrossRef]
- Chen, I.Y.; Chu, M.-C.; Liaw, J.-S.; Wang, C.-C. Two-phase flow characteristics across sudden contraction in small rectangular channels. Exp. Therm. Fluid Sci. 2008, 32, 1609–1619. [Google Scholar] [CrossRef]
- Chen, I.Y.; Tseng, C.-Y.; Lin, Y.-T.; Wang, C.-C. Two-phase flow pressure change subject to sudden contraction in small rectangular channels. Int. J. Multiph. Flow 2009, 35, 297–306. [Google Scholar] [CrossRef]
- Kawahara, A.; Mansour, M.H.; Sadatomi, M.; Law, W.Z.; Kurihara, H.; Kusumaningsih, H. Characteristics of gas–liquid two-phase flows through a sudden contraction in rectangular microchannels. Exp. Therm. Fluid Sci. 2015, 66, 243–253. [Google Scholar] [CrossRef]
- Sontti, S.G.; Atta, A. CFD analysis of Taylor bubble in a co-flow microchannel with Newtonian and non-Newtonian liquid. Ind. Eng. Chem. Res. 2017, 56, 7401–7412. [Google Scholar] [CrossRef]
- Alves, M.A.; Oliveira, P.J.; Pinho, F.T. Numerical methods for viscoelastic fluid flows. Annual Review of Fluid Mechanics. Annu. Rev. Fluid Mech. 2021, 53, 509–541. [Google Scholar] [CrossRef]
- Mansour, M.H.; Kawahara, A.; Sadatomi, M. Experimental investigation of gas–non-Newtonian liquid two-phase flows from T-junction mixer in rectangular microchannel. Int. J. Multiph. Flow 2015, 72, 263–274. [Google Scholar] [CrossRef]
- Kawahara, A.; Yonemoto, Y.; Arakaki, Y. Pressure drop for gas and polymer aqueous solution two-phase flows in horizontal circular microchannel. Flow Turbul. Combust. 2020, 105, 1325–1344. [Google Scholar] [CrossRef]
- Boger, D.V.; Cable, P.J. An anomalous effect in the measurement of normal stresses in polyacrylamide solutions. Rheol. Acta 1977, 16, 322–323. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Farooqi, S.I.; Richardson, J.F. Isothermal two-phase flow of air and aqueous polymer solutions in a smooth horizontal pipe. Chem. Eng. Res. Des. 1984, 62, 22–32. [Google Scholar]
- Sousa, R.G.; Reithmuller, M.L.; Pinto, A.M.F.R.; Campos, J.B.L.M. Flow around individual Taylor bubbles rising in stagnant polyacrylamide (PAA) solutions. J. Non-Newton. Fluid Mech. 2006, 135, 16–31. [Google Scholar] [CrossRef]
- Farooqi, S.I.; Richardson, J.F. Rheological behaviour of Kaolin suspensions in water and water glycerol Mixtures. Trans. Inst. Chem. Eng. 1980, 58, 116–124. [Google Scholar]
- Kozicki, W.; Chou, C.H.; Tiu, C. Non-Newtonian flow in ducts of arbitrary cross-sectional shape. Chem. Eng. Sci. 1966, 21, 665–679. [Google Scholar] [CrossRef]
- Geiger, G.E. Sudden Contraction Losses in Single and Two-Phase Flow. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 1964. [Google Scholar]
- Garstecki, P.; Fuerstman, M.J.; Stone, H.A.; Whitesides, G.M. Formation of droplets and bubbles in a microfluidic T-junction—Scaling and mechanism of break-up. Lab Chip 2006, 2, 437–446. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.H.; Li, S.W.; Tan, J.; Luo, G.S. Correlations of droplet formation in T-junction microfluidic devices: From squeezing to dripping. Microfluid. Nanofluidics 2008, 5, 711–717. [Google Scholar] [CrossRef]
- Chisholm, D. Two-Phase Flow in Pipelines and Heat Exchangers; George Godwin: London, UK; New York, NY, USA, 1983. [Google Scholar]
- Collier, J.G.; Thome, J.R. Convective Boiling and Condensation; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Schmidt, J.; Friedel, L. Two-phase flow pressure drop across sudden contractions in duct areas. Int. J. Multiph. Flow 1997, 23, 283–299. [Google Scholar] [CrossRef]






| Authors | Cross–Section of Test Channels (Shape: ○ Circular, □ Rectangular) (Dimension in mm) | Test Fluids (Gas–Liquid) |
|---|---|---|
| Abdellal et al. (2008) | ○ 1.6 --> ○ 0.84 | Air–water |
| Chalfi et al. (2008) | ||
| Chen et al. (2008) | □ 3 × 9 --> ○ 3 □ 3 × 6 --> ○ 3 | |
| Chen et al. (2009) | □ 2 × 4 --> ○ 2 □ 2 × 6 --> ○ 2 □ 4 × 4 --> ○ 2 □ 4 × 6 --> ○ 2 | |
| Kawahara et al. (2015) | □ 0.53 × 0.23 --> □ 0.27 × 0.23 □ 0.78 × 0.23 --> □ 0.27 × 0.23 | Nitrogen gas–water Nitrogen gas–ethanol 49 wt% aqueous solution Nitrogen gas–ethanol Nitrogen gas–HFE7200 |
| Channels | W (mm) | H (mm) | Dh (mm) | sA (−) |
|---|---|---|---|---|
| Upstream | 0.99 | 0.50 | 0.66 | 0.49 |
| Downstream | 0.49 | 0.50 | 0.50 |
| Test Liquids | rL (kg/m3) | sL (N/m) | K (Pa × sn) | n (−) | (du/dy)y=0 (1/s) |
|---|---|---|---|---|---|
| Distilled water | 997 | 0.072 | 8.97 × 10−4 | 1.00 | - |
| GL 25 wt% | 1058 | 0.063 | 1.82 × 10−3 | 1.00 | - |
| XG 0.1 wt% | 998 | 0.073 | 3.47 × 10−2 | 0.70 | 1400–52,000 |
| PAM 0.11 wt% | 998 | 0.073 | 1.85 × 10−3 | 0.98 | 1060–41,400 |
| Test Liquids | jL,d (m/s) | jG,d (m/s) | ReG,d | |
|---|---|---|---|---|
| Distilled water | 0.29–0.85 | 0.48–1.30 | 183–532 | 20–50 |
| GL 25 wt% | 0.61–1.53 | 0.38–1.07 | 197–497 | 20–50 |
| XG 0.1 wt% | 0.83–1.64 | 0.39–1.07 | 208–506 | 20–50 |
| PAM 0.11 wt% | 0.59–1.40 | 0.41–1.07 | 205–490 | 20–50 |
| Correlations | Distilled Water | GL 25 wt% | XG 0.1 wt% | PAM 0.11 wt% | ||||
|---|---|---|---|---|---|---|---|---|
| em (%) | erms (%) | em (%) | erms (%) | em (%) | erms (%) | em (%) | erms (%) | |
| Chisholm (1983) | 191 | 206 | 194 | 211 | 83 | 90 | 102 | 108 |
| Collier-Thome (1994) | −25 | 29 | −25 | 31 | −53 | 55 | −48 | 51 |
| Schmidt-Friedel (1997) | −36 | 40 | −25 | 33 | −54 | 56 | −52 | 554 |
| Abdelall et al. A (2005) | −29 | 40 | 8 | 39 | −23 | 27 | −27 | 31 |
| Abdelall et al. B (2005) | −26 | 35 | 33 | 50 | −17 | 19 | −22 | 29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toshimitsu, M.; Yonemoto, Y.; Kawahara, A. Pressure Change for Single- and Two-Phase Non-Newtonian Flows through Sudden Contraction in Rectangular Microchannel. Fluids 2021, 6, 440. https://doi.org/10.3390/fluids6120440
Toshimitsu M, Yonemoto Y, Kawahara A. Pressure Change for Single- and Two-Phase Non-Newtonian Flows through Sudden Contraction in Rectangular Microchannel. Fluids. 2021; 6(12):440. https://doi.org/10.3390/fluids6120440
Chicago/Turabian StyleToshimitsu, Masaki, Yukihiro Yonemoto, and Akimaro Kawahara. 2021. "Pressure Change for Single- and Two-Phase Non-Newtonian Flows through Sudden Contraction in Rectangular Microchannel" Fluids 6, no. 12: 440. https://doi.org/10.3390/fluids6120440
APA StyleToshimitsu, M., Yonemoto, Y., & Kawahara, A. (2021). Pressure Change for Single- and Two-Phase Non-Newtonian Flows through Sudden Contraction in Rectangular Microchannel. Fluids, 6(12), 440. https://doi.org/10.3390/fluids6120440






