Dynamic Stall Characteristics of Pitching Swept Finite-Aspect-Ratio Wings
Abstract
:1. Introduction
2. Experimental Setup
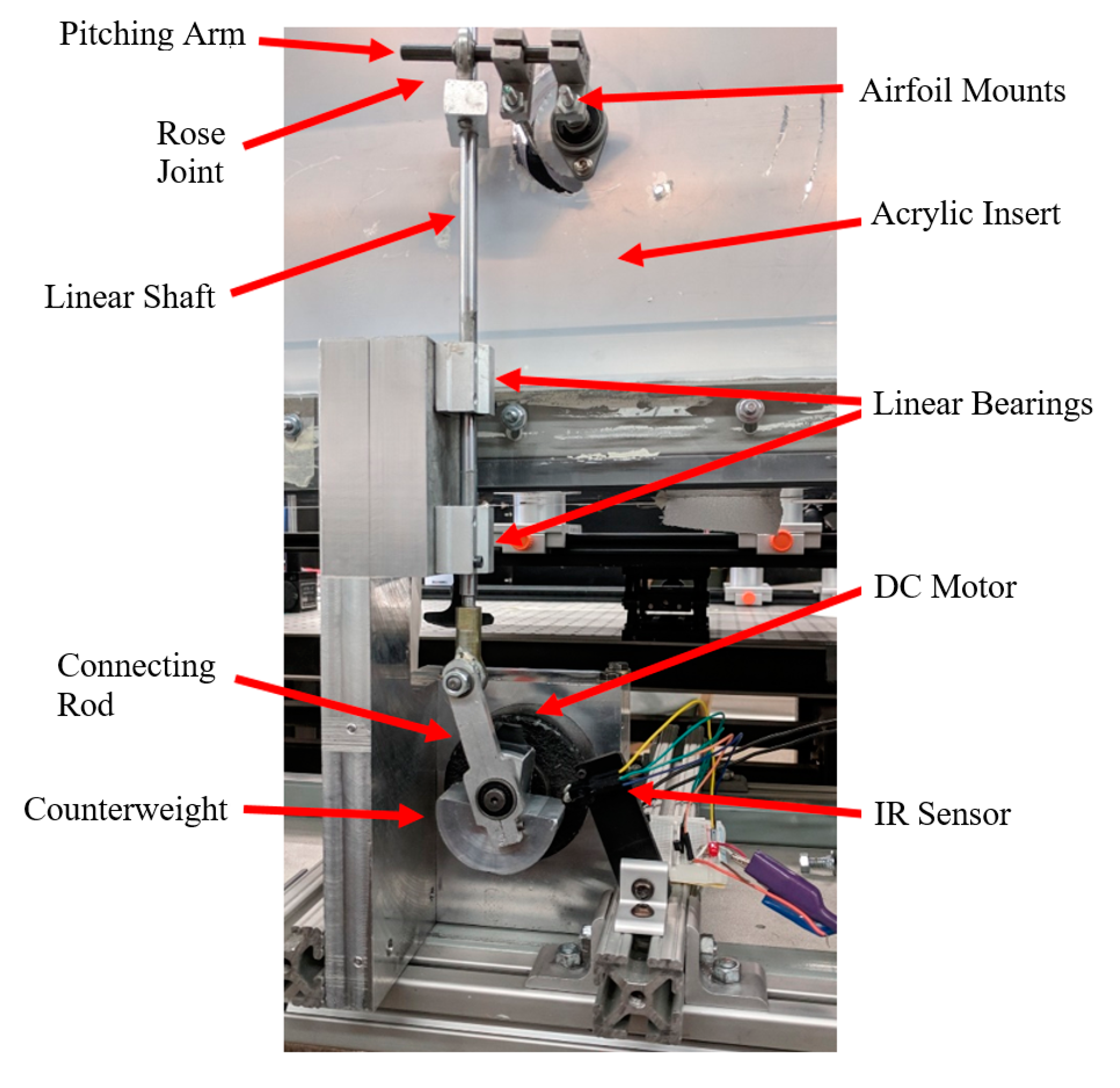
2.1. Wings and Actuator Design
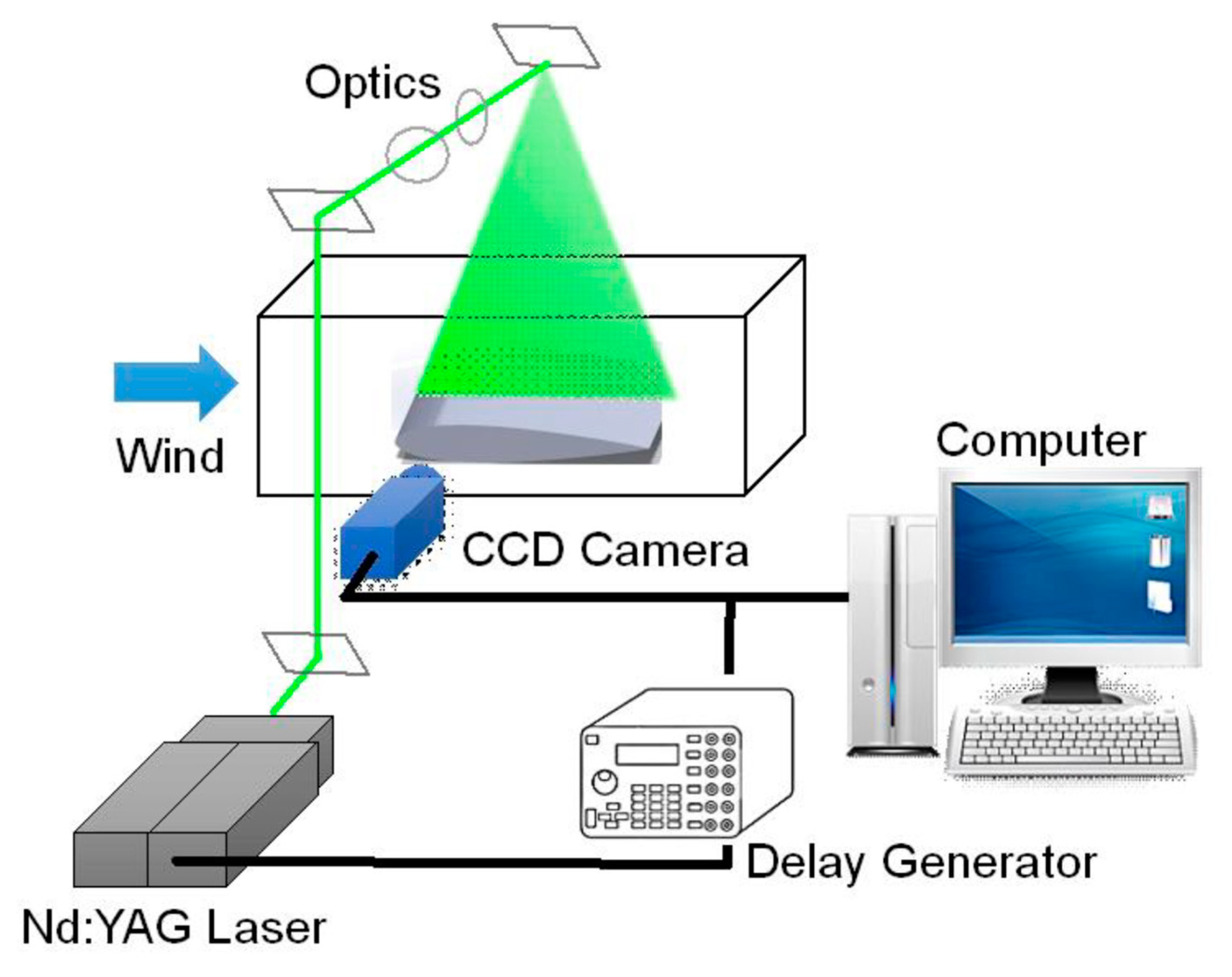
2.2. Particle Image Velocimetry
2.3. Pressure Sensitive Paint (Turbo PSP)
2.4. Synchronous Triggering Design for PSP Experiment
2.5. Flow Parameters during PIV and PSP Testing Campaigns
3. Results and Discussion
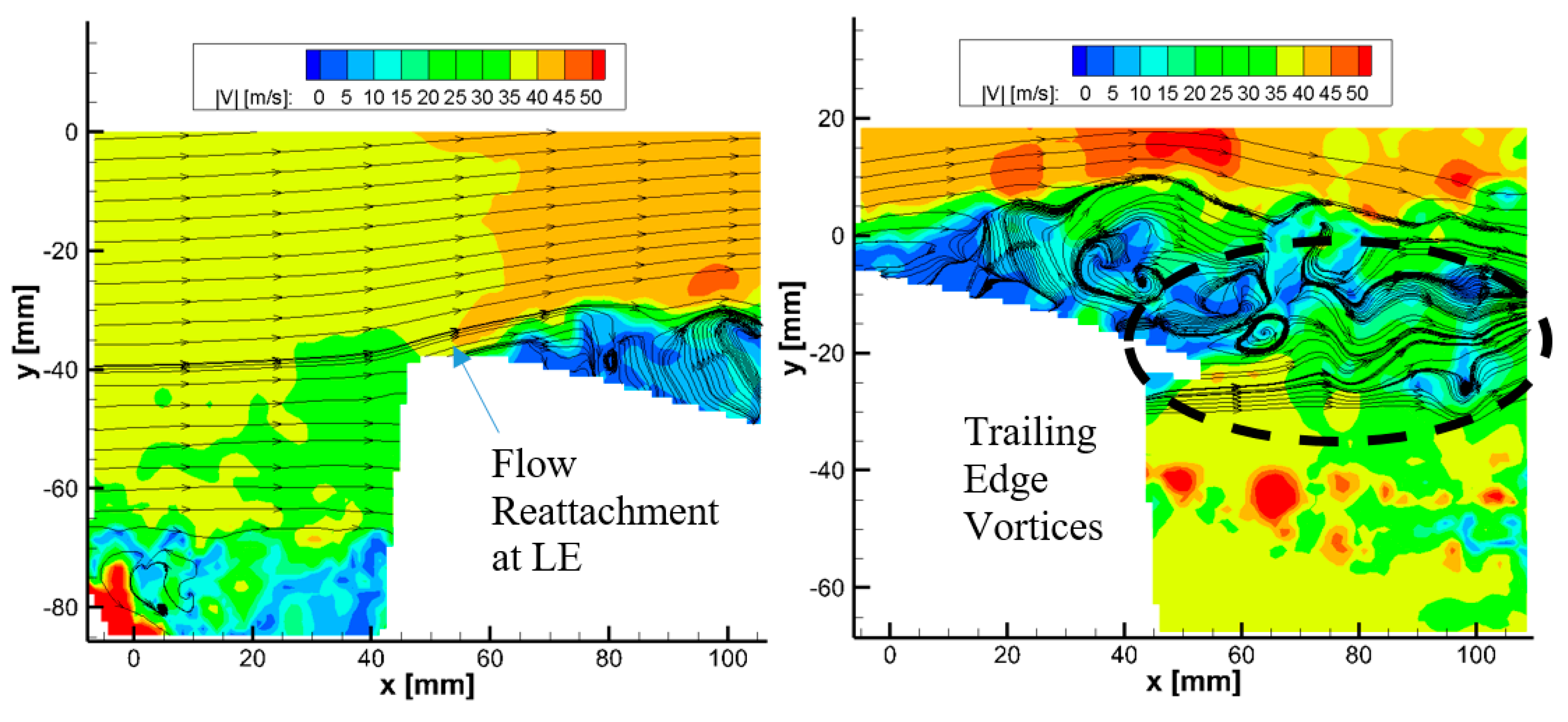
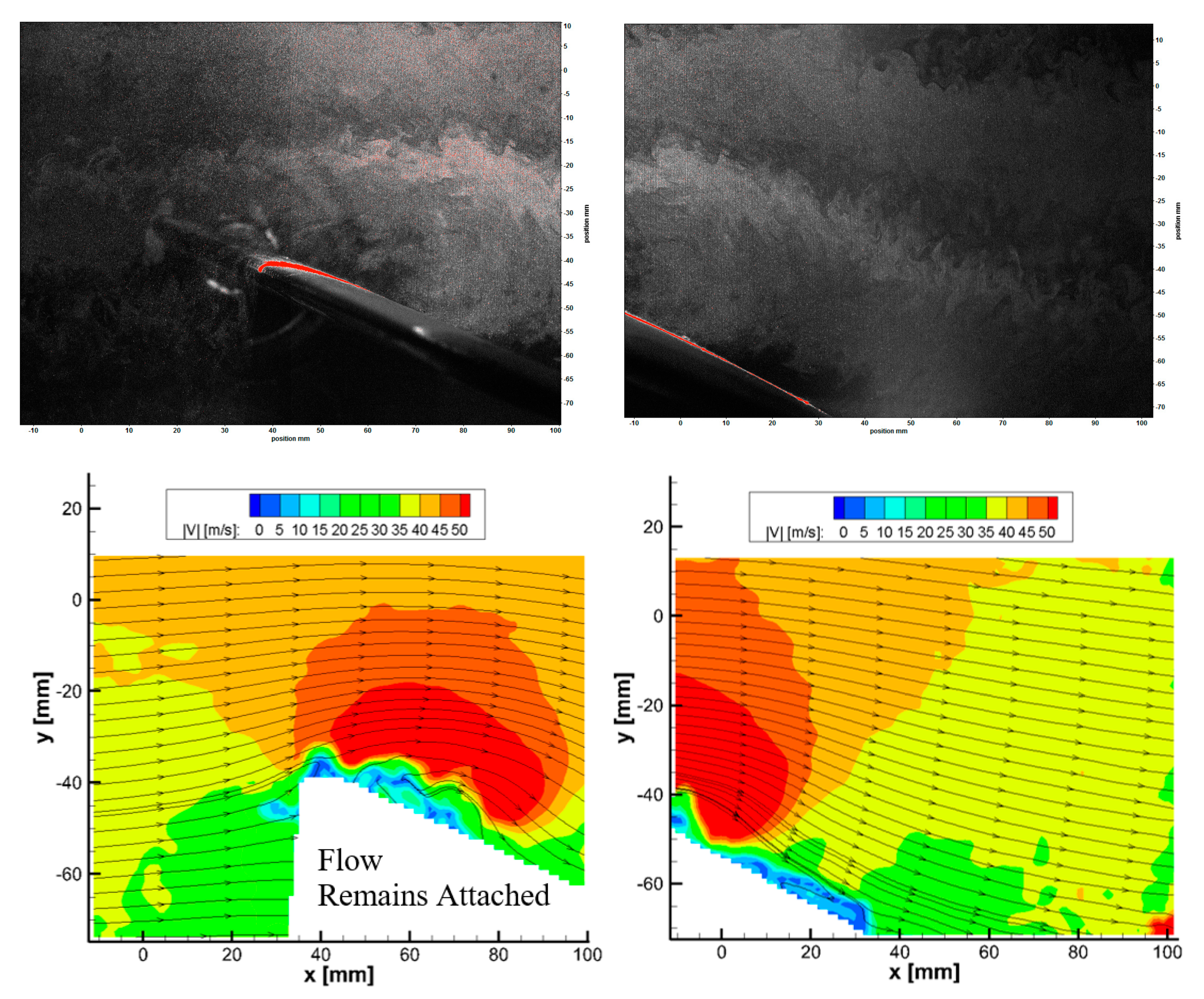
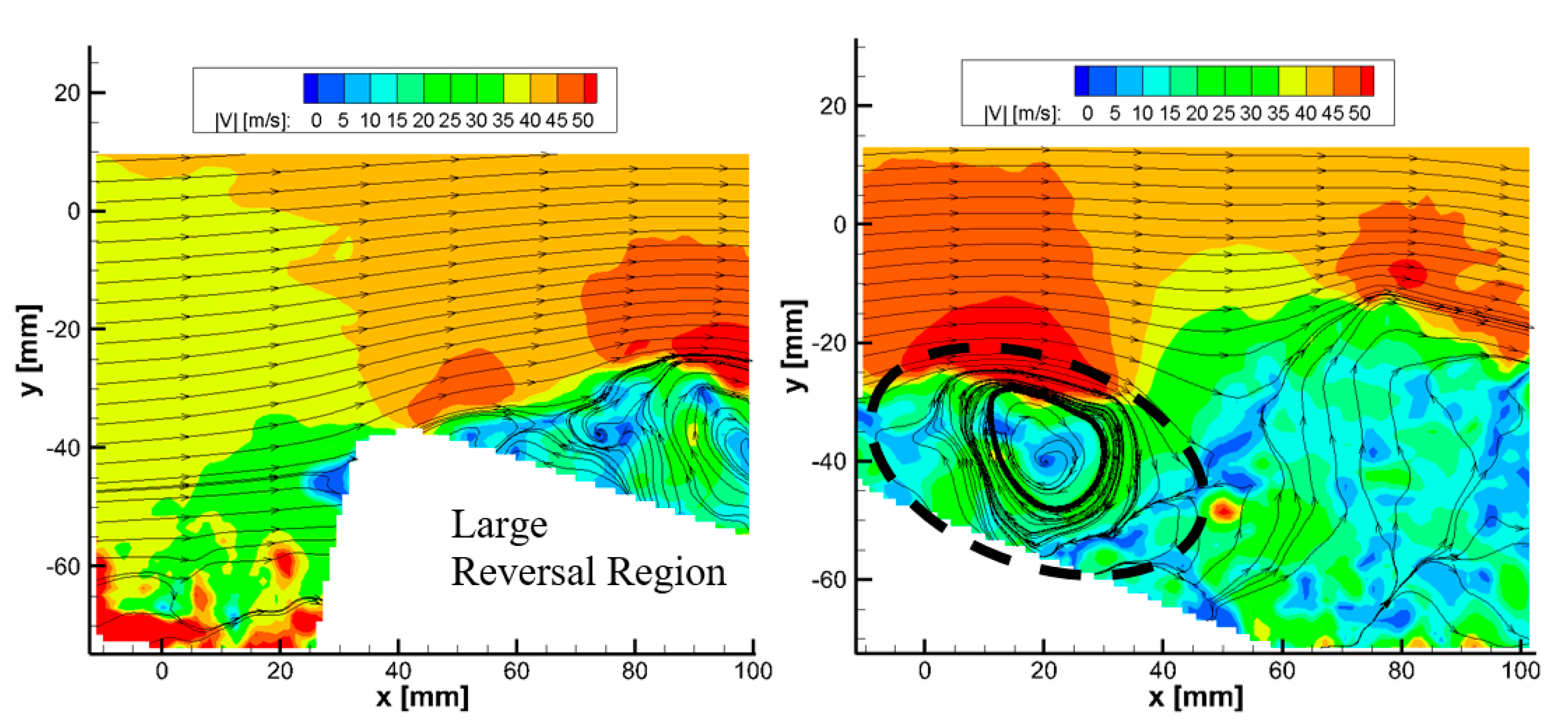
3.1. Flow Structure over Unswept Pitching Wing, Λ = 0°
3.2. Flow Structure over Swept Pitching Wing, Λ = 15°
3.3. Flow Structure over Swept Pitching Wing, Λ = 30°
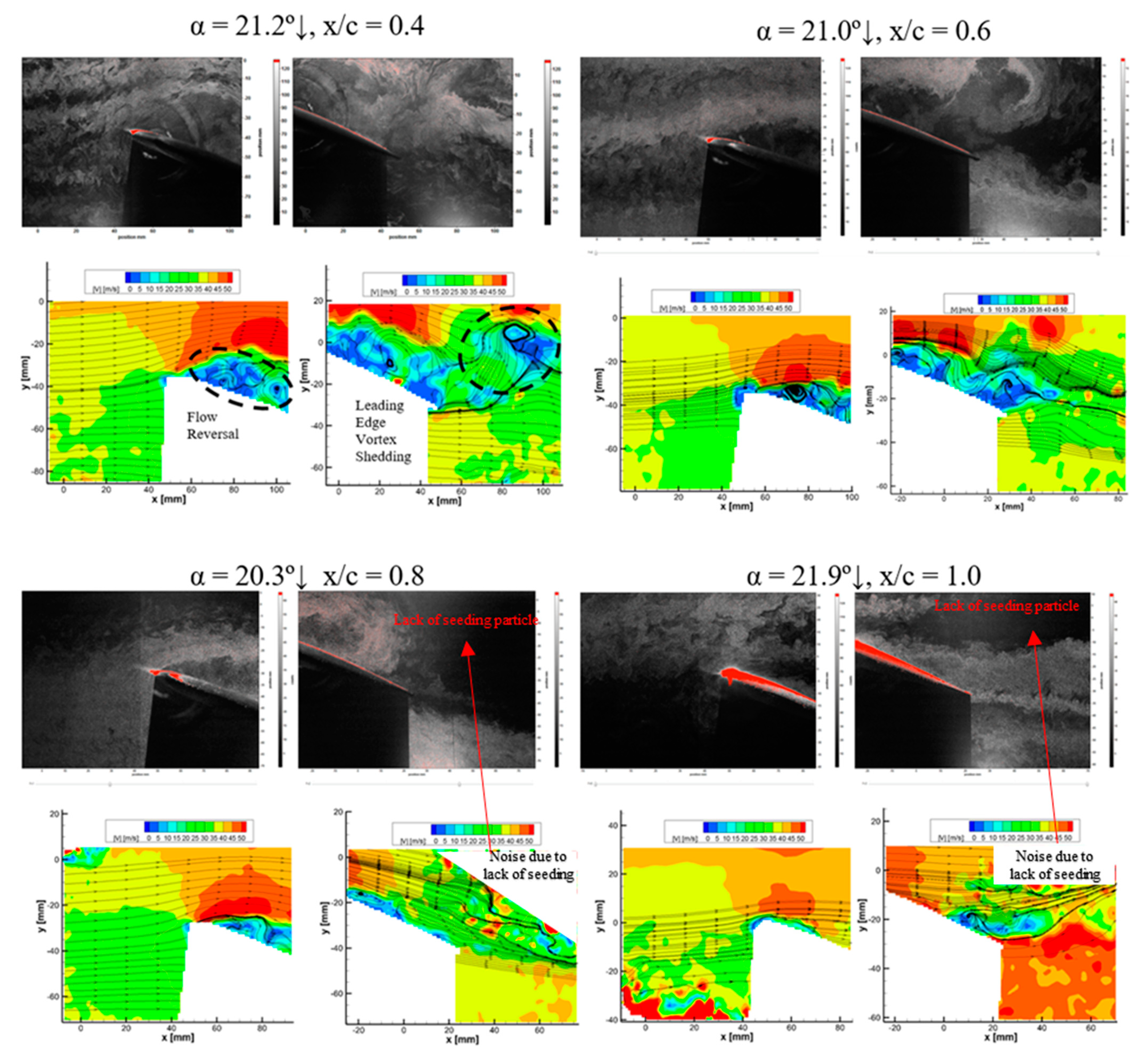
3.4. Dynamic Stall Behaviours at Various Spans forUnswept Pitching Wing, Λ = 0°
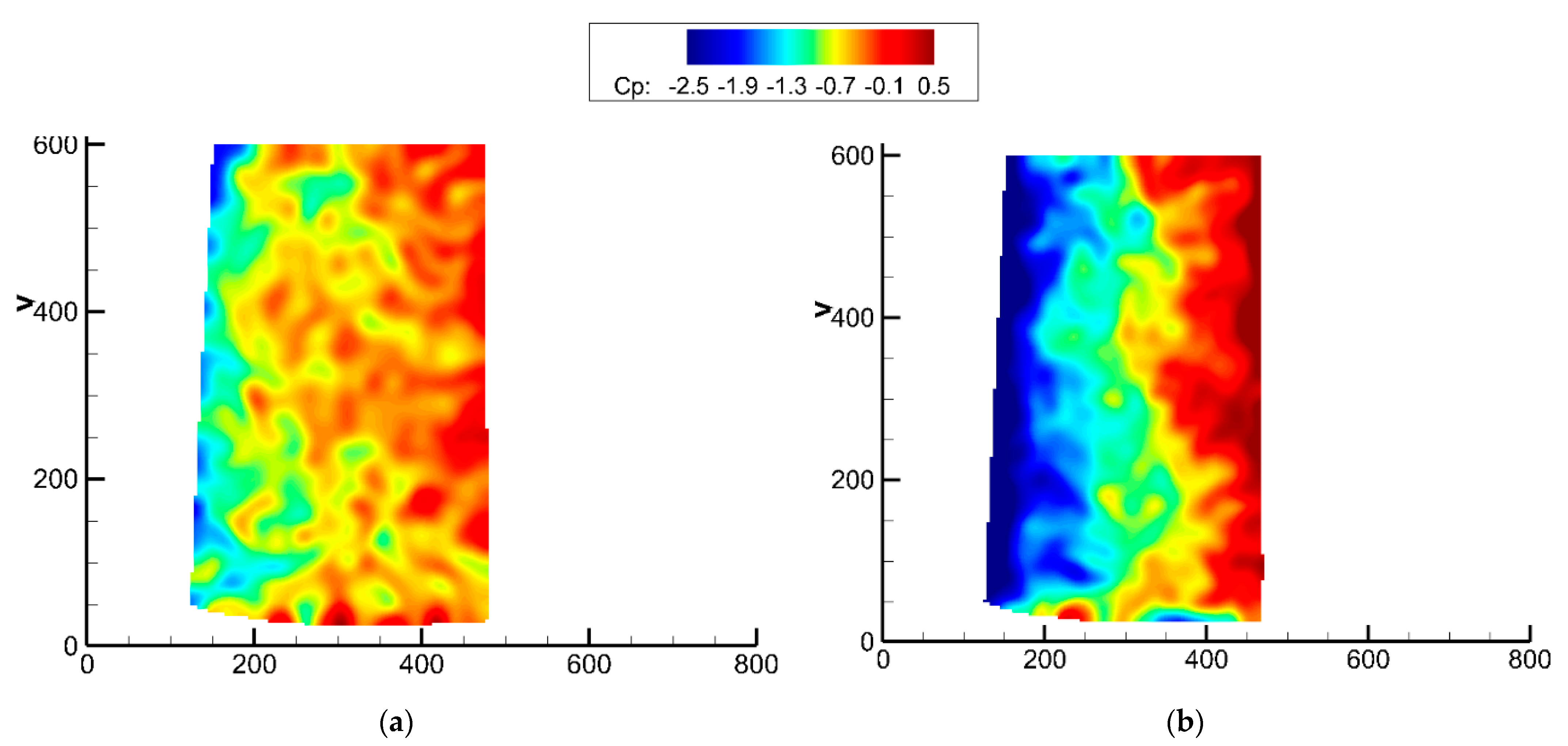
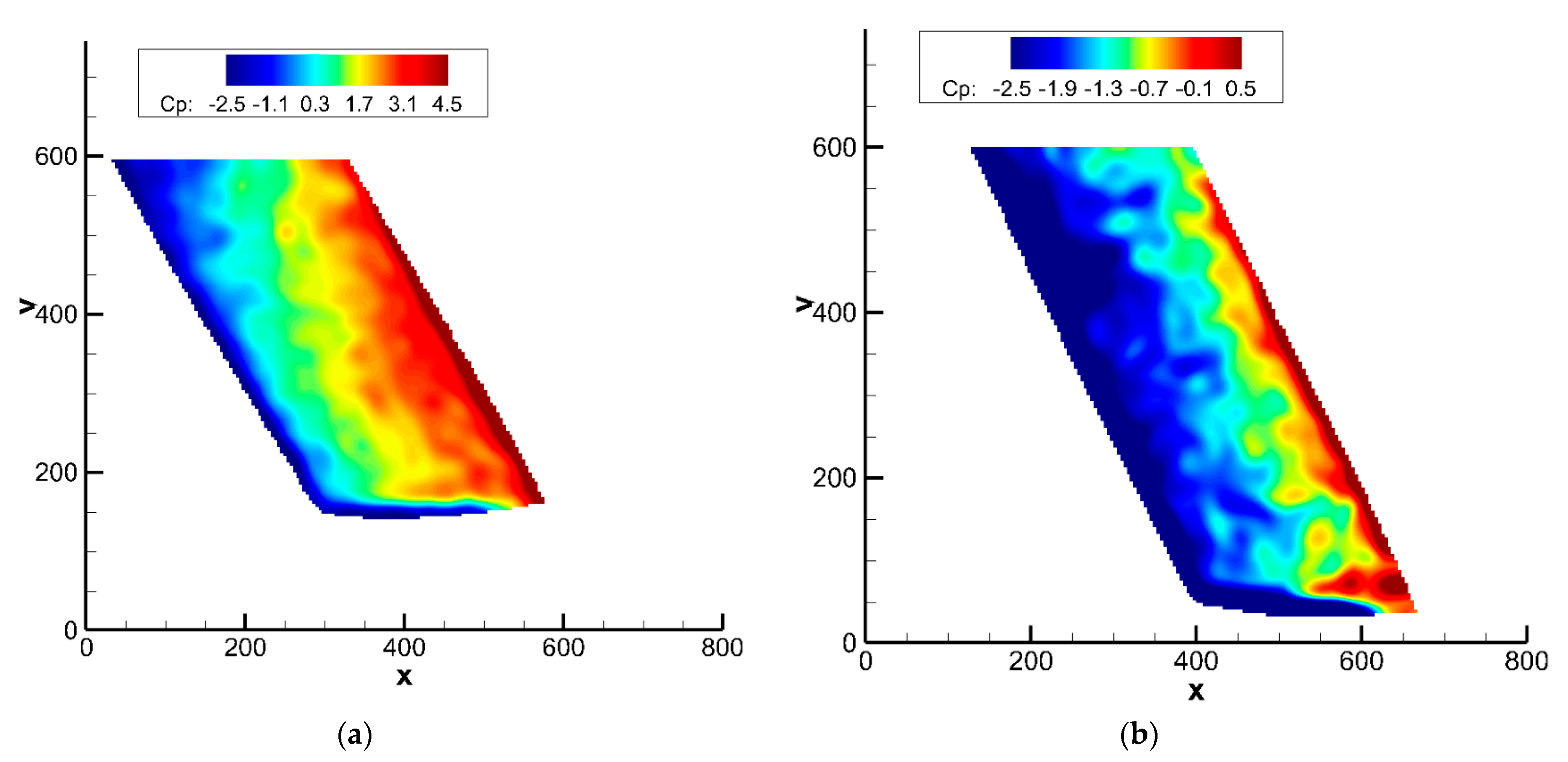
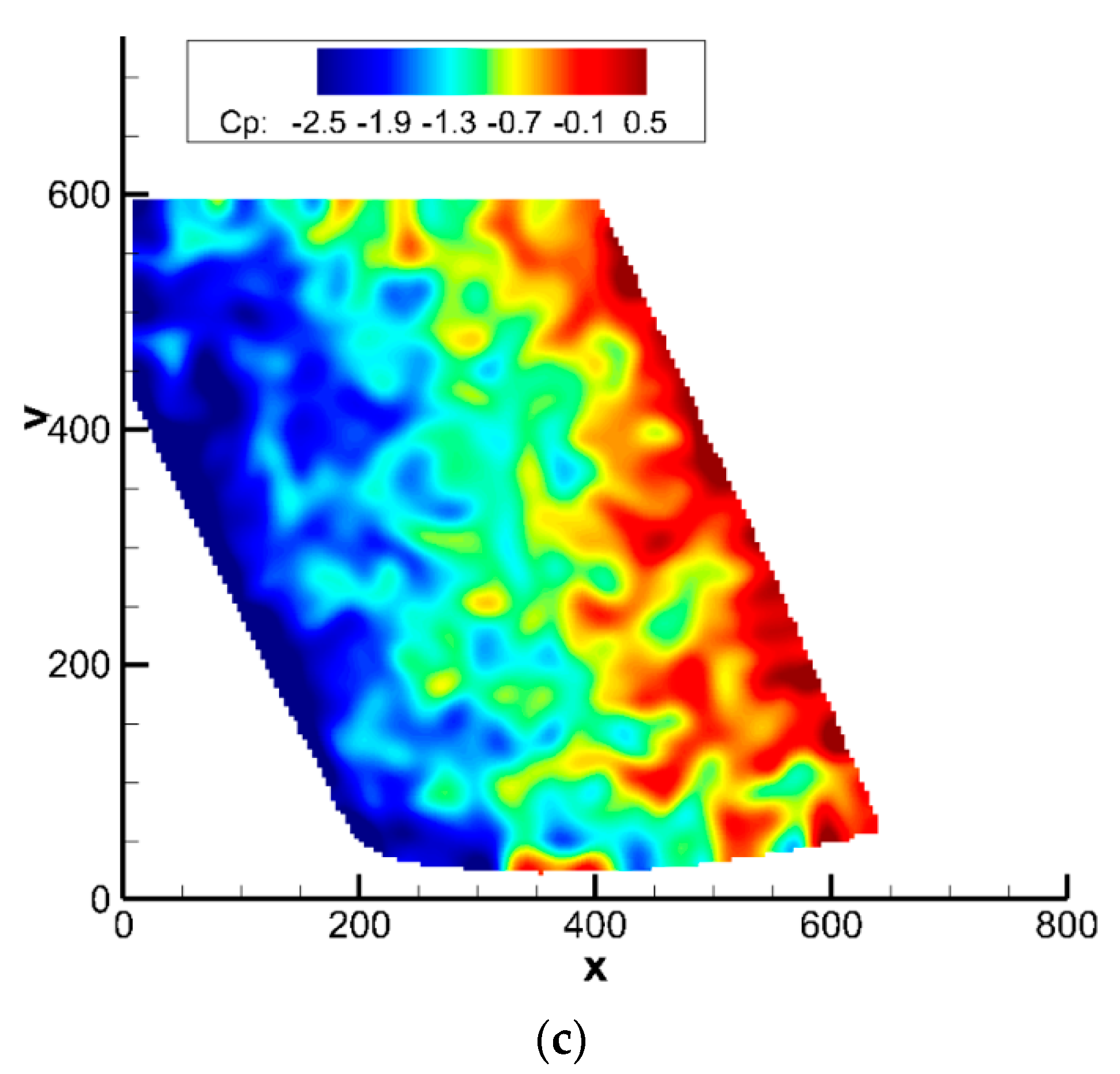
3.5. Turbo PSP Results
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McAlister, K.W.; Carr, L.W.; McCroskey, W.J. Dynamic Stall Experiments on the NACA 0012 Airfoil; NASA: Washington, DC, USA, 1978.
- Carta, F.; Fink, M.; Jepson, W. The Influence of Sweep on the Aerodynamic Loading of an Oscillating NACA 0012 Airfoil; Volume 1: Technical Report; 1979. Available online: https://ntrs.nasa.gov/api/citations/19790013881/downloads/19790013881.pdf (accessed on 2 December 2021).
- Visbal, M.R.; Garmann, D.J. Dynamic stall of a finite-aspect-ratio wing. AIAA J. 2019, 57, 962–977. [Google Scholar] [CrossRef]
- Visbal, M.R.; Shang, J. Investigation of the flow structure around a rapidly pitching airfoil. AIAA J. 1989, 27, 1044–1051. [Google Scholar] [CrossRef]
- Kuchemann, D.; Weber, J. The Subsonic Flow Past Swept Wings at Zero Lift without and with Body; Aeronautical Research Council: London, UK, 1953. [Google Scholar]
- Houghton, E.L.; Carpenter, P.W. Aerodynamics for Engineering Students, 5th ed.; Elsevier: Oxford, UK, 2003. [Google Scholar]
- Rumsey, C. 2DN00: 2D NACA 0012 Airfoil Validation Case; Langley Research Center: Hampton, VA, USA, 2018.
- Gursul, I.; Wang, Z.; Vardaki, E. Review of flow control mechanisms of leading-edge vortices. Prog. Aerosp. Sci. 2007, 43, 246–270. [Google Scholar] [CrossRef] [Green Version]
- Visbal, M.R.; Garmann, D.J. High-fidelity simulations of dynamic stall over a finite-aspect-ratio wing. In Proceedings of the 8th AIAA Flow Control Conference, Washington, DC, USA, 13–17 June 2016; p. 4243. [Google Scholar] [CrossRef]
- Visbal, M.R.; Garmann, D.J. Analysis of dynamic stall on a pitching airfoil using high-fidelity large-eddy simulations. AIAA J. 2018, 56, 46–63. [Google Scholar] [CrossRef]
- Visbal, M.R.; Garmann, D.J. Effect of sweep on dynamic stall of a pitching finite-aspect-ratio wing. AIAA J. 2019, 57, 3274–3289. [Google Scholar]
- Ericsson, L.; Reding, J. Fluid dynamics of unsteady separated flow. Part II. Lifting surfaces. Prog. Aerosp. Sci. 1987, 24, 249–356. [Google Scholar] [CrossRef]
- Visbal, M. On some physical aspects of airfoil dynamic stall. In the International Symposium on Non-Unsteady Fluid Dynamics; American Society of Mechanical Engineers: Fairfield, NJ, USA, 1990; Volume 92, pp. 127–147. [Google Scholar]
- Ekaterinaris, J.A.; Platzer, M.F. Computational prediction of airfoil dynamic stall. Prog. Aerosp. Sci. 1998, 33, 759–846. [Google Scholar] [CrossRef]
- Visbal, M.R. Analysis of the Onset of Dynamic Stall Using High-Fidelity Large-Eddy Simulations. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; p. 591. [Google Scholar]
- Visbal, M.R. Numerical Exploration of Flow Control for Delay of Dynamic Stall on a Pitching Airfoil. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2044. [Google Scholar]
- Visbal, M.R. Control of Dynamic Stall on a Pitching Airfoil Using High-frequency Actuation. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; Volume 1267. [Google Scholar] [CrossRef]
- Chandrasekhara, M.S.; Carr, L.W.; Wilder, M.C. Interferometric Investigations of Compressible Dynamic Stall over a Transiently Pitching Airfoil. AIAA J. 1994, 32, 586–593. [Google Scholar] [CrossRef] [Green Version]
- Ullah, A.H.; Fabijanic, C.; Refling, W.; Estevadeordal, J. Experimental Investigation of the Effect of Sweep on a Pitching Finite-Aspect-Ratio Wing. In Proceedings of the AIAA Scitech 2021 Forum, Orlando, FL, USA, 11–15 & 19–21 January 2021; p. 1733. [Google Scholar]
- Tomek, K.L.; Ullah, A.H.; Fabijanic, C.; Estevadeordal, J. Experimental Investigation of Dynamic Stall on Pitching Swept Finite-Aspect-Ratio Wings. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1980. [Google Scholar]
- Rockwood, M.; Medina, A.; Garmann, D.J.; Visbal, M.R. Dynamic Stall of a Swept Finite Wing for a Range of Reduced Frequencies. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Stolt, A.J.; Ullah, A.H.; Estevadeordal, J. Study of leading-edge dimple effects on airfoil flow using tomographic PIV and temperature sensitive paint. Fluids 2019, 4, 184. [Google Scholar] [CrossRef] [Green Version]
- Watkins, N.; Leighty, B.; Lipford, W.; Wong, O.; Goodman, K.; Crafton, J.; Forlines, A.; Goss, L.; Gregory, J.; Juliano, T. Deployment of a pressure sensitive paint system for measuring global surface pressures on rotorcraft blades in simulated forward flight. In Proceedings of the 28th Aerodynamic Measurement Technology, Ground Testing, and Flight Testing Conference including the Aerospace T&E Days Forum, New Orleans, LA, USA, 25–28 June 2012; p. 2756. [Google Scholar]
- Gregory, J.; Asai, K.; Kameda, M.; Liu, T.; Sullivan, J. A review of pressure-sensitive paint for high-speed and unsteady aerodynamics. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2008, 222, 249–290. [Google Scholar] [CrossRef]
- Gardner, A.D.; Klein, C.; Sachs, W.; Henne, U.; Mai, H.; Richter, K. Investigation of three-dimensional dynamic stall on an airfoil using fast-response pressure-sensitive paint. Exp. Fluids 2014, 55, 1807. [Google Scholar] [CrossRef]
- Disotell, K.J.; Nikoueeyan, P.; Naughton, J.W.; Gregory, J.W. Global surface pressure measurements of static and dynamic stall on a wind turbine airfoil at low Reynolds number. Exp. Fluids 2016, 57, 82. [Google Scholar] [CrossRef]
- Ullah, A.H.; Rostad, B.L.; Estevadeordal, J. Three-cylinder rotating system flows and their effects on a downstream dimpled airfoil. Exp. Therm. Fluid Sci. 2021, 124, 110343. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]











| Experimental Parameters | |
|---|---|
| Wind tunnel test area dimensions (Height × Width × Length) | 304.8 mm × 304.8 mm × 1828.8 mm |
| Wing | NACA0012 |
| Chord length | 76.2 mm |
| Free stream Mach number | M∞ = 0.1 |
| Chord Reynolds number | Rec = 2 × 105 |
| Actuation angle range | α = 4° and 22° |
| Sweep angles | Λ = 0°, 15°, and 30° |
| Reduced frequency k = πfc/U∞ | 0.2 (PIV) and 0.1 (PSP) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, A.H.; Tomek, K.L.; Fabijanic, C.; Estevadeordal, J. Dynamic Stall Characteristics of Pitching Swept Finite-Aspect-Ratio Wings. Fluids 2021, 6, 457. https://doi.org/10.3390/fluids6120457
Ullah AH, Tomek KL, Fabijanic C, Estevadeordal J. Dynamic Stall Characteristics of Pitching Swept Finite-Aspect-Ratio Wings. Fluids. 2021; 6(12):457. https://doi.org/10.3390/fluids6120457
Chicago/Turabian StyleUllah, Al Habib, Kristopher L. Tomek, Charles Fabijanic, and Jordi Estevadeordal. 2021. "Dynamic Stall Characteristics of Pitching Swept Finite-Aspect-Ratio Wings" Fluids 6, no. 12: 457. https://doi.org/10.3390/fluids6120457
APA StyleUllah, A. H., Tomek, K. L., Fabijanic, C., & Estevadeordal, J. (2021). Dynamic Stall Characteristics of Pitching Swept Finite-Aspect-Ratio Wings. Fluids, 6(12), 457. https://doi.org/10.3390/fluids6120457





