Cross-Flow-Induced Vibration of an Elastic Plate
Abstract
:1. Introduction
2. Methods
2.1. Problem Definition
2.2. Governing Equations
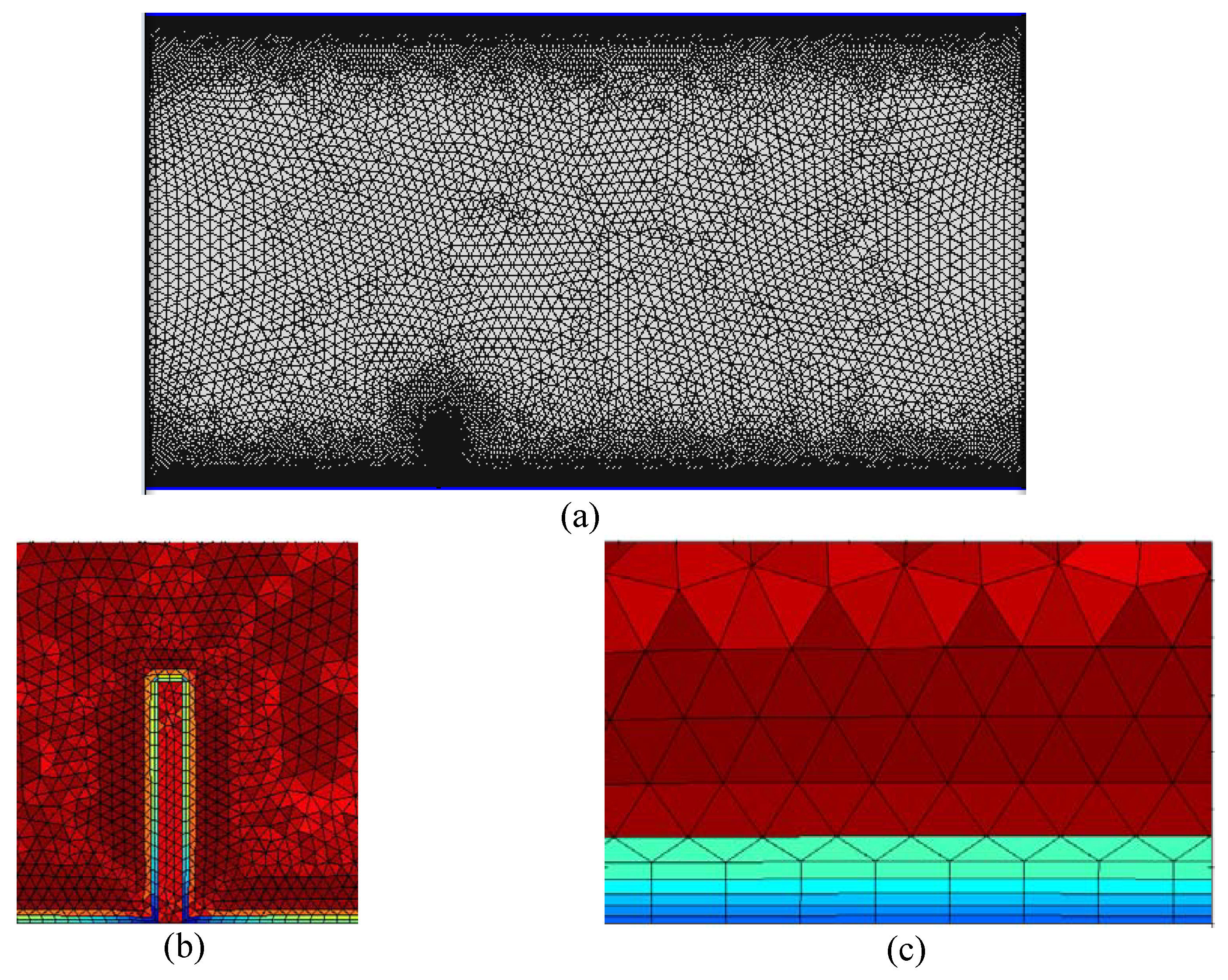
2.3. Solver, Mesh, and Parameters
3. Results
3.1. Rigid Plate
3.2. Elastic Plate with
3.3. Effect of Solid Elasticity and Density
4. Discussion
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Langre, E. Effects of Wind on Plants. Annu. Rev. Fluid Mech. 2008, 40, 141–168. [Google Scholar] [CrossRef] [Green Version]
- Tadrist, L.; Julio, K.; Saudreau, M.; de Langre, E. Leaf flutter by torsional galloping: Experiments and model. J. Fluids Struct. 2015, 56, 1–10. [Google Scholar] [CrossRef]
- Song, Z.; Borazjani, I. The Role of Shape and Heart Rate on the Performance of the Left Ventricle. J. Biomech. Eng. 2015, 137, 114501. [Google Scholar] [CrossRef]
- Borazjani, I. Numerical Simulations of Flow around Copepods: Challenges and Future Directions. Fluids 2020, 5, 52. [Google Scholar] [CrossRef] [Green Version]
- Blevins, R.D. Flow-Induced Vibration; Krieger Publishing Company: Malabar, FL, USA, 2001. [Google Scholar]
- Païdoussis, M.P.; Price, S.J.; de Langre, E. Fluid-Structure Interactions: Cross-Flow-Induced Instabilities; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Triantafyllou, M.S.; Triantafyllou, G.S.; Yue, D.K.P. Hydrodynamics of Fishlike Swimming. Annu. Rev. Fluid Mech. 2000, 32, 33–53. [Google Scholar] [CrossRef]
- Shi, G.; Xiao, Q.; Zhu, Q. Effects of time-varying flexibility on the propulsion performance of a flapping foil. Phys. Fluids 2020, 32, 121904. [Google Scholar] [CrossRef]
- Borazjani, I. Fluid–structure interaction, immersed boundary-finite element method simulations of bio-prosthetic heart valves. Comput. Methods Appl. Mech. Eng. 2013, 257, 103–116. [Google Scholar] [CrossRef]
- Borazjani, I. A Review of Fluid-Structure Interaction Simulations of Prosthetic Heart Valves. J. Long-Term Eff. Med Implant. 2015, 25, 75–93. [Google Scholar] [CrossRef]
- Akaydin, H.D.; Elvin, N.; Andreopoulos, Y. The performance of a self-excited fluidic energy harvester. Smart Mater. Struct. 2012, 21, 025007. [Google Scholar] [CrossRef]
- Soti, A.K.; Bhardwaj, R.; Sheridan, J. Flow-induced deformation of a flexible thin structure as manifestation of heat transfer enhancement. Int. J. Heat Mass Transf. 2015, 84, 1070–1081. [Google Scholar] [CrossRef] [Green Version]
- Dong, D.; Chen, W.; Shi, S. Coupling Motion and Energy Harvesting of Two Side-by-Side Flexible Plates in a 3D Uniform Flow. Appl. Sci. 2016, 6, 141. [Google Scholar] [CrossRef] [Green Version]
- Gutierrez-Amo, R.; Fernandez-Gamiz, U.; Errasti, I.; Zulueta, E. Computational Modelling of Three Different Sub-Boundary Layer Vortex Generators on a Flat Plate. Energies 2018, 11, 3107. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Kim, J.T.; Hong, L.; Chamorro, L.P. Flow-induced oscillations of low-aspect-ratio flexible plates with various tip geometries. Phys. Fluids 2018, 30, 097102. [Google Scholar] [CrossRef]
- Allen, J.; Smits, A. Energy Harvesting Eel. J. Fluids Struct. 2001, 15, 629–640. [Google Scholar] [CrossRef] [Green Version]
- Young, J.; Lai, J.C.; Platzer, M.F. A review of progress and challenges in flapping foil power generation. Prog. Aerosp. Sci. 2014, 67, 2–28. [Google Scholar] [CrossRef]
- McCarthy, J.; Watkins, S.; Deivasigamani, A.; John, S. Fluttering energy harvesters in the wind: A review. J. Sound Vib. 2016, 361, 355–377. [Google Scholar] [CrossRef]
- Sun, H.; Ma, C.; Bernitsas, M.M. Hydrokinetic power conversion using Flow Induced Vibrations with cubic restoring force. Energy 2018, 153, 490–508. [Google Scholar] [CrossRef]
- Sun, H.; Bernitsas, M.M. Bio-Inspired adaptive damping in hydrokinetic energy harnessing using flow-induced oscillations. Energy 2019, 176, 940–960. [Google Scholar] [CrossRef] [Green Version]
- Binyet, E.M.; Chang, J.Y.; Huang, C.Y. Flexible Plate in the Wake of a Square Cylinder for Piezoelectric Energy Harvesting—Parametric Study Using Fluid–Structure Interaction Modeling. Energies 2020, 13, 2645. [Google Scholar] [CrossRef]
- Malefaki, I.; Konstantinidis, E. Assessment of a Hydrokinetic Energy Converter Based on vortex Induced Angular Oscillations of a Cylinder. Energies 2020, 13, 717. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Yang, M.; Wang, E.; Sun, H. Performance of single-cylinder VIVACE converter for hydrokinetic energy harvesting from flow-induced vibration near a free surface. Ocean. Eng. 2020, 218, 108168. [Google Scholar] [CrossRef]
- Shelley, M.J.; Zhang, J. Flapping and Bending Bodies Interacting with Fluid Flows. Annu. Rev. Fluid Mech. 2011, 43, 449–465. [Google Scholar] [CrossRef] [Green Version]
- Cisonni, J.; Lucey, A.D.; Elliott, N.S.; Heil, M. The stability of a flexible cantilever in viscous channel flow. J. Sound Vib. 2017, 396, 186–202. [Google Scholar] [CrossRef] [Green Version]
- Tavallaeinejad, M.; Païdoussis, M.P.; Legrand, M.; Kheiri, M. Instability and the post-critical behaviour of two-dimensional inverted flags in axial flow. J. Fluid Mech. 2020, 890, A14. [Google Scholar] [CrossRef]
- Tavallaeinejad, M.; Salinas, M.F.; Païdoussis, M.P.; Legrand, M.; Kheiri, M.; Botez, R.M. Dynamics of inverted flags: Experiments and comparison with theory. J. Fluids Struct. 2021, 101, 103199. [Google Scholar] [CrossRef]
- Alben, S.; Shelley, M.; Zhang, J. Drag reduction through self-similar bending of a flexible body. Nature 2002, 420, 479–481. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Liu, M.; Peng, S. Smoothed particle hydrodynamics and element bending group modeling of flexible fibers interacting with viscous fluids. Phys. Rev. E 2014, 90, 063011. [Google Scholar] [CrossRef] [Green Version]
- Henriquez, S.; Barrero-Gil, A. Reconfiguration of flexible plates in sheared flow. Mech. Res. Commun. 2014, 62, 1–4. [Google Scholar] [CrossRef]
- Leclercq, T.; de Langre, E. Drag reduction by elastic reconfiguration of non-uniform beams in non-uniform flows. J. Fluids Struct. 2016, 60, 114–129. [Google Scholar] [CrossRef]
- Barois, T.; de Langre, E. Flexible body with drag independent of the flow velocity. J. Fluid Mech. 2013, 735, R2. [Google Scholar] [CrossRef] [Green Version]
- Barsu, S.; Doppler, D.; Jerome, J.J.S.; Rivière, N.; Lance, M. Drag measurements in laterally confined 2D canopies: Reconfiguration and sheltering effect. Phys. Fluids 2016, 28, 107101. [Google Scholar] [CrossRef] [Green Version]
- Tian, F.B.; Dai, H.; Luo, H.; Doyle, J.F.; Rousseau, B. Fluid–structure interaction involving large deformations: 3D simulations and applications to biological systems. J. Comput. Phys. 2014, 258, 451–469. [Google Scholar] [CrossRef] [Green Version]
- Basting, S.; Quaini, A.; Čanić, S.; Glowinski, R. Extended ALE Method for fluid–structure interaction problems with large structural displacements. J. Comput. Phys. 2017, 331, 312–336. [Google Scholar] [CrossRef] [Green Version]
- Bano, T.; Hegner, F.; Heinrich, M.; Schwarze, R. Investigation of Fluid-Structure Interaction Induced Bending for Elastic Flaps in a Cross Flow. Appl. Sci. 2020, 10, 6177. [Google Scholar] [CrossRef]
- Dey, A.A.; Modarres-Sadeghi, Y.; Rothstein, J.P. Viscoelastic flow-induced oscillations of a cantilevered beam in the crossflow of a wormlike micelle solution. J. Non-Newton. Fluid Mech. 2020, 286, 104433. [Google Scholar] [CrossRef]
- Plate, E.J. The aerodynamics of shelter belts. Agric. Meteorol. 1971, 8, 203–222. [Google Scholar] [CrossRef]
- Raine, J.; Stevenson, D. Wind protection by model fences in a simulated atmospheric boundary layer. J. Wind. Eng. Ind. Aerodyn. 1977, 2, 159–180. [Google Scholar] [CrossRef]
- Perera, M. Shelter behind two-dimensional solid and porous fences. J. Wind. Eng. Ind. Aerodyn. 1981, 8, 93–104. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, H.B. Laboratory measurements of velocity and turbulence field behind porous fences. J. Wind. Eng. Ind. Aerodyn. 1999, 80, 311–326. [Google Scholar] [CrossRef]
- Dong, Z.; Luo, W.; Qian, G.; Lu, P.; Wang, H. A wind tunnel simulation of the turbulence fields behind upright porous wind fences. J. Arid. Environ. 2010, 74, 193–207. [Google Scholar] [CrossRef]
- Liu, B.; Qu, J.; Zhang, W.; Tan, L.; Gao, Y. Numerical evaluation of the scale problem on the wind flow of a windbreak. Sci. Rep. 2014, 4, 6619. [Google Scholar] [CrossRef] [Green Version]
- Pieris, S.; Tuna, B.; Yarusevych, S.; Peterson, S. Flow development upstream of a fence. Int. J. Heat Fluid Flow 2020, 82, 108565. [Google Scholar] [CrossRef]
- Fang, F.M.; Hsieh, W.D.; Jong, S.W.; She, J.J. Unsteady Turbulent Flow Past Solid Fence. J. Hydraul. Eng. 1997, 123, 560–565. [Google Scholar] [CrossRef]
- Hwang, R.R.; Chow, Y.; Peng, Y. Numerical study of turbulent flow over two-dimensional surface-mounted ribs in a channel. Int. J. Numer. Methods Fluids 1999, 31, 767–785. [Google Scholar] [CrossRef]
- Fragos, V.; Psychoudaki, S.; Malamataris, N. Two-dimensional numerical simulation of vortex shedding and flapping motion of turbulent flow around a rib. Comput. Fluids 2012, 69, 108–121. [Google Scholar] [CrossRef]
- Siller, H.; Fernholz, H. Control of the separated flow downstream of a two-dimensional fence by low-frequency forcing. Appl. Sci. Res. 1996, 57, 309–318. [Google Scholar] [CrossRef]
- Orellano, A.; Wengle, H. Numerical simulation (DNS and LES) of manipulated turbulent boundary layer flow over a surface-mounted fence. Eur. J. Mech. B/Fluids 2000, 19, 765–788. [Google Scholar] [CrossRef]
- Blevins, R.D. Formulas for Dynamics, Acoustics and Vibration; John Wiley & Sons, Ltd.: Chichester, UK, 2016. [Google Scholar] [CrossRef]
- Eloy, C.; Souilliez, C.; Schouveiler, L. Flutter of a rectangular plate. J. Fluids Struct. 2007, 23, 904–919. [Google Scholar] [CrossRef]
- Launder, B.; Spalding, D. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Basnet, K. Flow around Porous Barriers: Fundamental Flow Physics and Applications. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 2015. Available online: http://ir.uiowa.edu/etd/1824 (accessed on 28 November 2016).
- Chen, G.; Alam, M.M.; Zhou, Y. Dependence of added mass on cylinder cross-sectional geometry and orientation. J. Fluids Struct. 2020, 99, 103142. [Google Scholar] [CrossRef]
- Okajima, A.; Nakamura, A.; Kosugi, T.; Uchida, H.; Tamaki, R. Flow-induced in-line oscillation of a circular cylinder. Eur. J. Mech. B Fluids 2004, 23, 115–125. [Google Scholar] [CrossRef]
- Sherwood, J.; Dusting, J.; Konstantinidis, E.; Balabani, S. Flow-Induced Streamwise Vibration of a Flexibly-Mounted Cantilevered Cylinder in Steady and Pulsating Crossflow. In Proceedings of the ASME 2009 Pressure Vessels and Piping Conference, Prague, Czech Republic, 26–30 July 2009; Volume 4: Fluid-Structure Interaction, pp. 203–210. [Google Scholar] [CrossRef]
- Konstantinidis, E. On the response and wake modes of a cylinder undergoing streamwise vortex induced vibration. J. Fluids Struct. 2014, 45, 256–262. [Google Scholar] [CrossRef]
- Jin, Y.; Kim, J.T.; Fu, S.; Chamorro, L.P. Flow-induced motions of flexible plates: Fluttering, twisting and orbital modes. J. Fluid Mech. 2019, 864, 273–285. [Google Scholar] [CrossRef]
- Tavallaeinejad, M.; Païdoussis, M.P.; Flores Salinas, M.; Legrand, M.; Kheiri, M.; Botez, R.M. Flapping of heavy inverted flags: A fluid-elastic instability. J. Fluid Mech. 2020, 904, R5. [Google Scholar] [CrossRef]




| Fluid | Density, | 1000 kg/m |
| Viscosity, | 0.001 Pa·s | |
| Velocity, | 0.25 m/s | |
| Solid | Height, H | 0.1 m |
| Thickness | 0.01 m | |
| Poisson’s ratio, | 0.33 | |
| Density, | 3000–7000 kg/m | |
| Young’s modulus, E | 0.2–1.0 GPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konstantinidis, E. Cross-Flow-Induced Vibration of an Elastic Plate. Fluids 2021, 6, 82. https://doi.org/10.3390/fluids6020082
Konstantinidis E. Cross-Flow-Induced Vibration of an Elastic Plate. Fluids. 2021; 6(2):82. https://doi.org/10.3390/fluids6020082
Chicago/Turabian StyleKonstantinidis, Efstathios. 2021. "Cross-Flow-Induced Vibration of an Elastic Plate" Fluids 6, no. 2: 82. https://doi.org/10.3390/fluids6020082
APA StyleKonstantinidis, E. (2021). Cross-Flow-Induced Vibration of an Elastic Plate. Fluids, 6(2), 82. https://doi.org/10.3390/fluids6020082






