A Computational Model for Tail Undulation and Fluid Transport in the Giant Larvacean
Abstract
:1. Introduction
2. Materials and Methods
2.1. Field Quantification of Larvacean Kinematics
2.2. Fluid–Structure Interaction Model
2.3. Material Model
2.4. Computational Implementation
3. Results
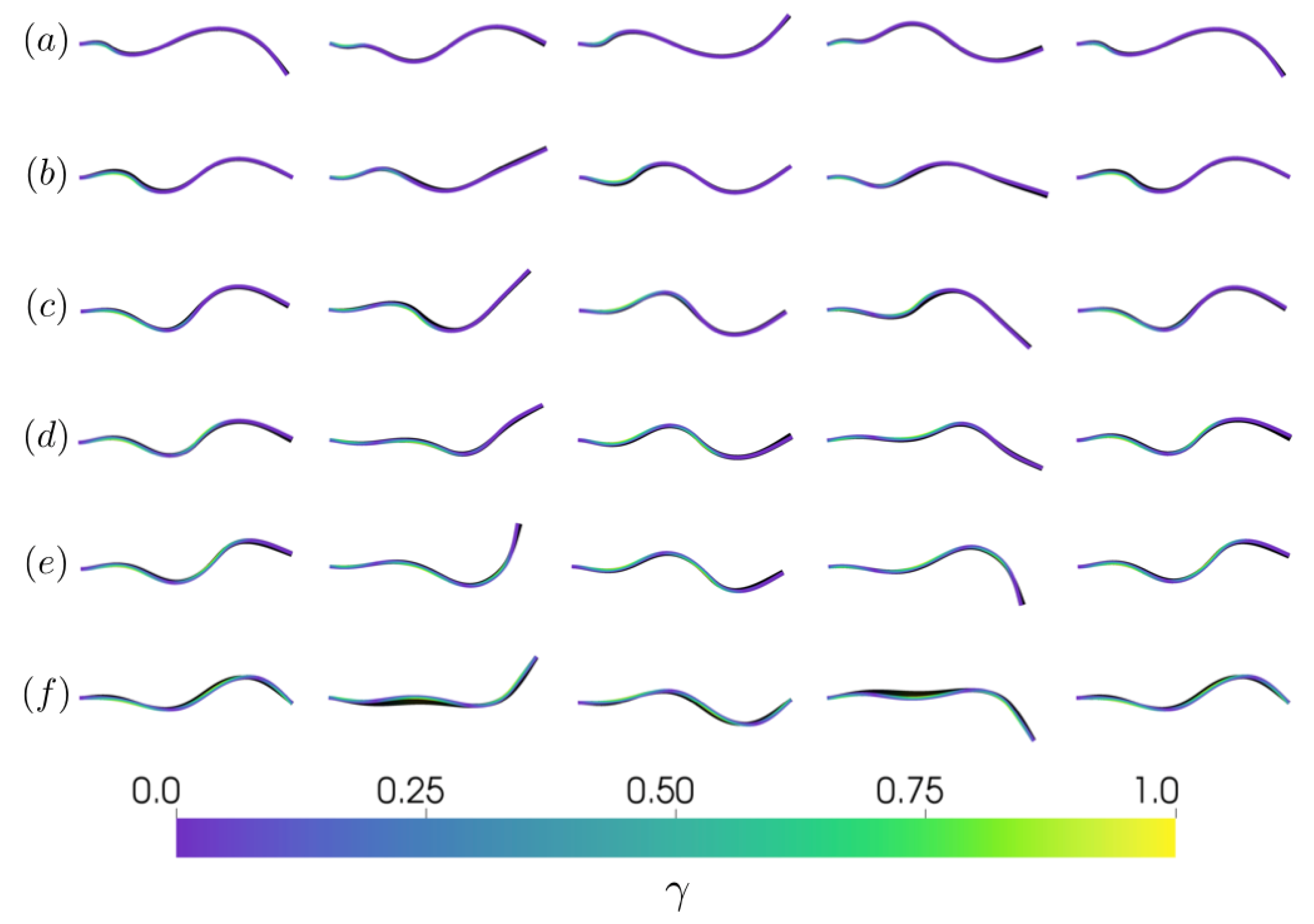
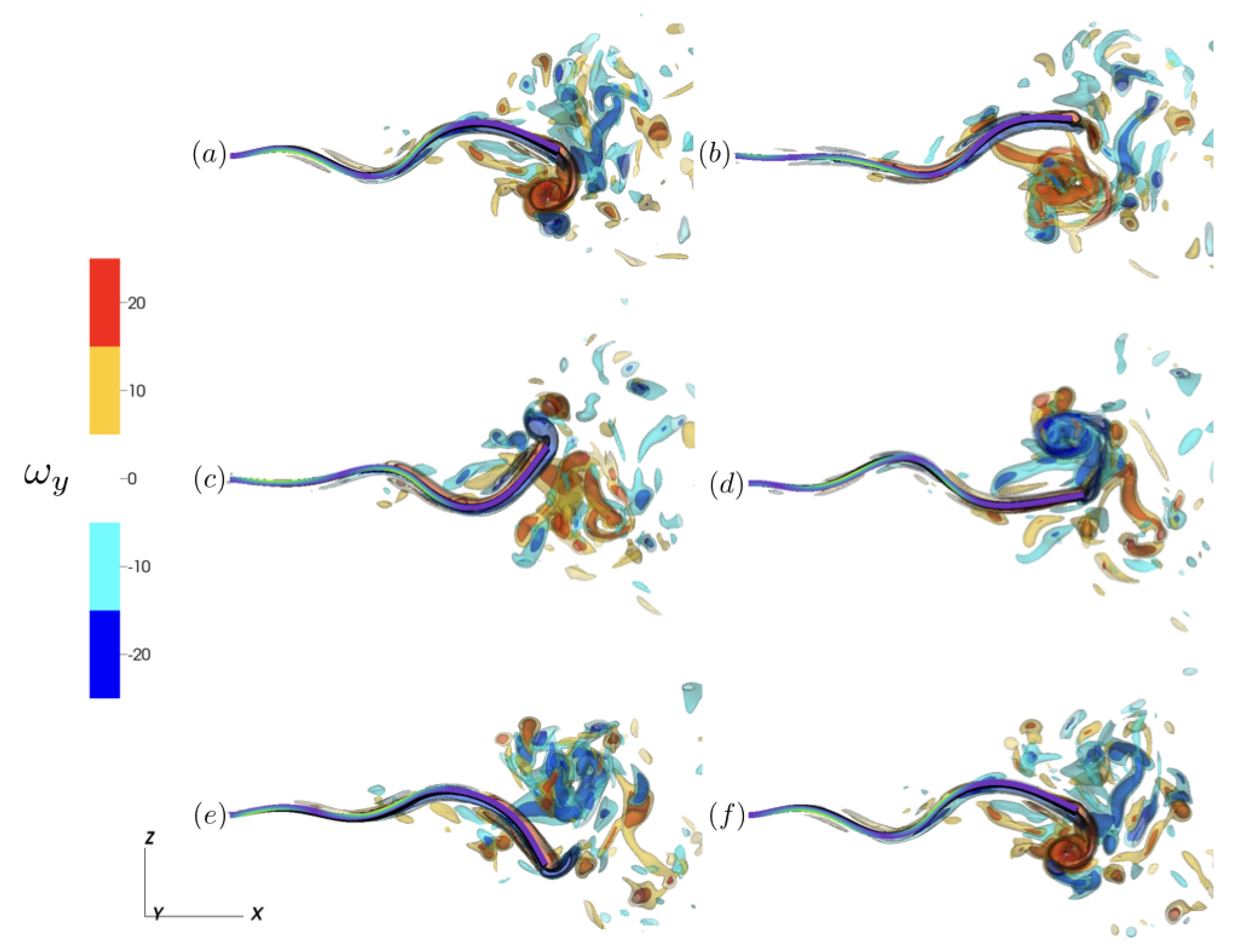
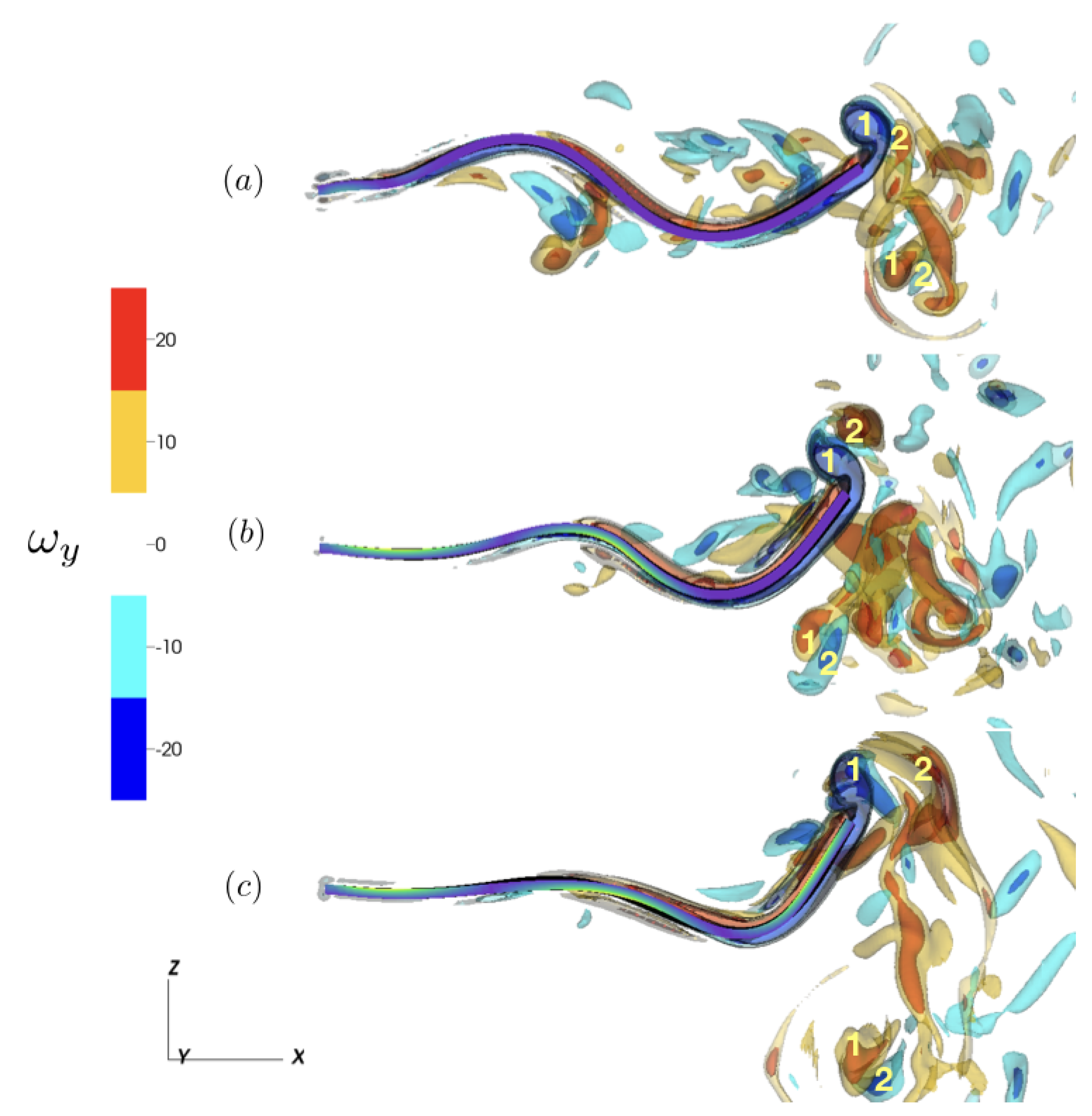
3.1. Kinematics and Fluid Flow of Larvacean Tail Beat
3.2. Model Schematic and Results
3.2.1. Reference Case
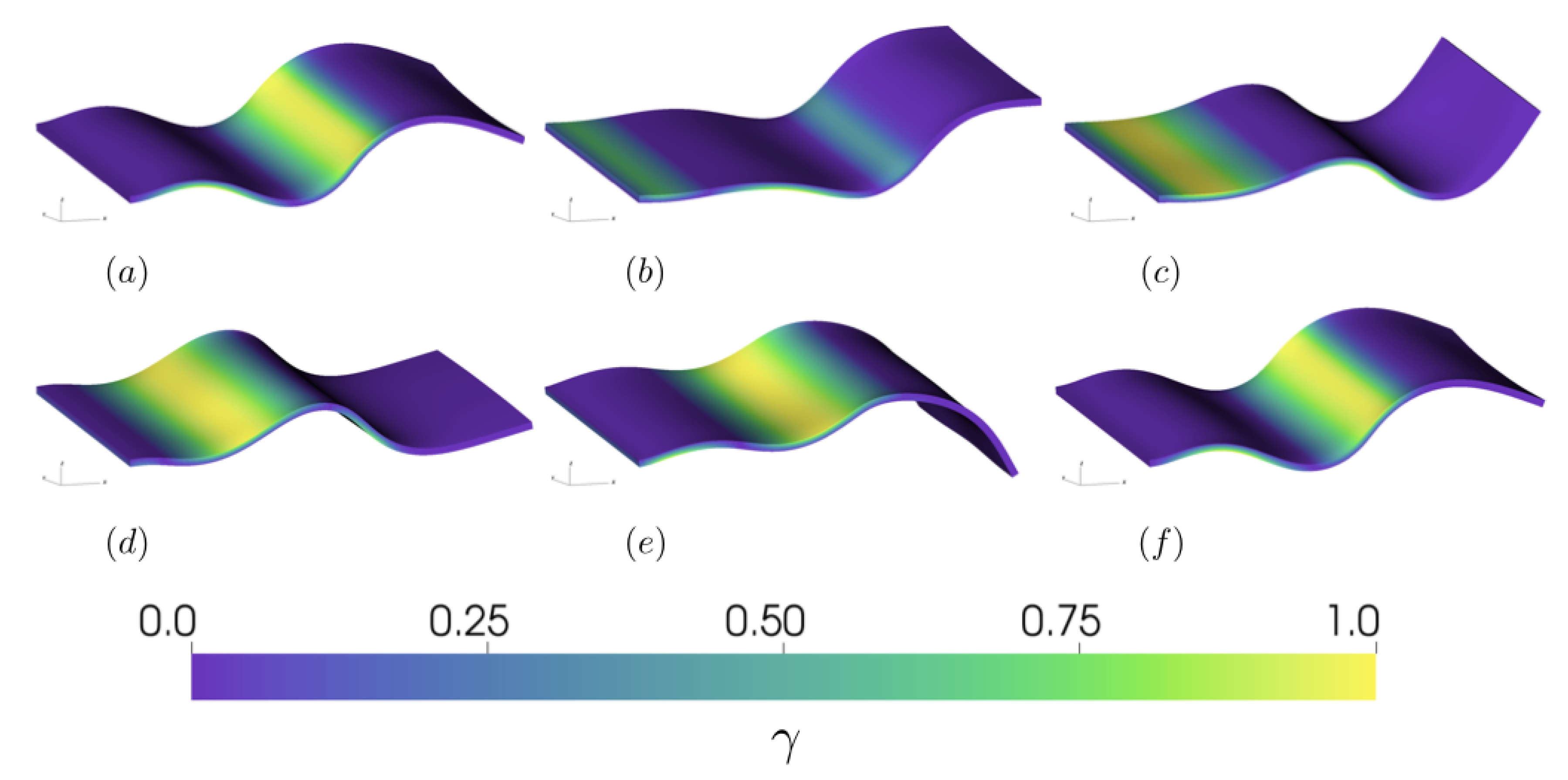
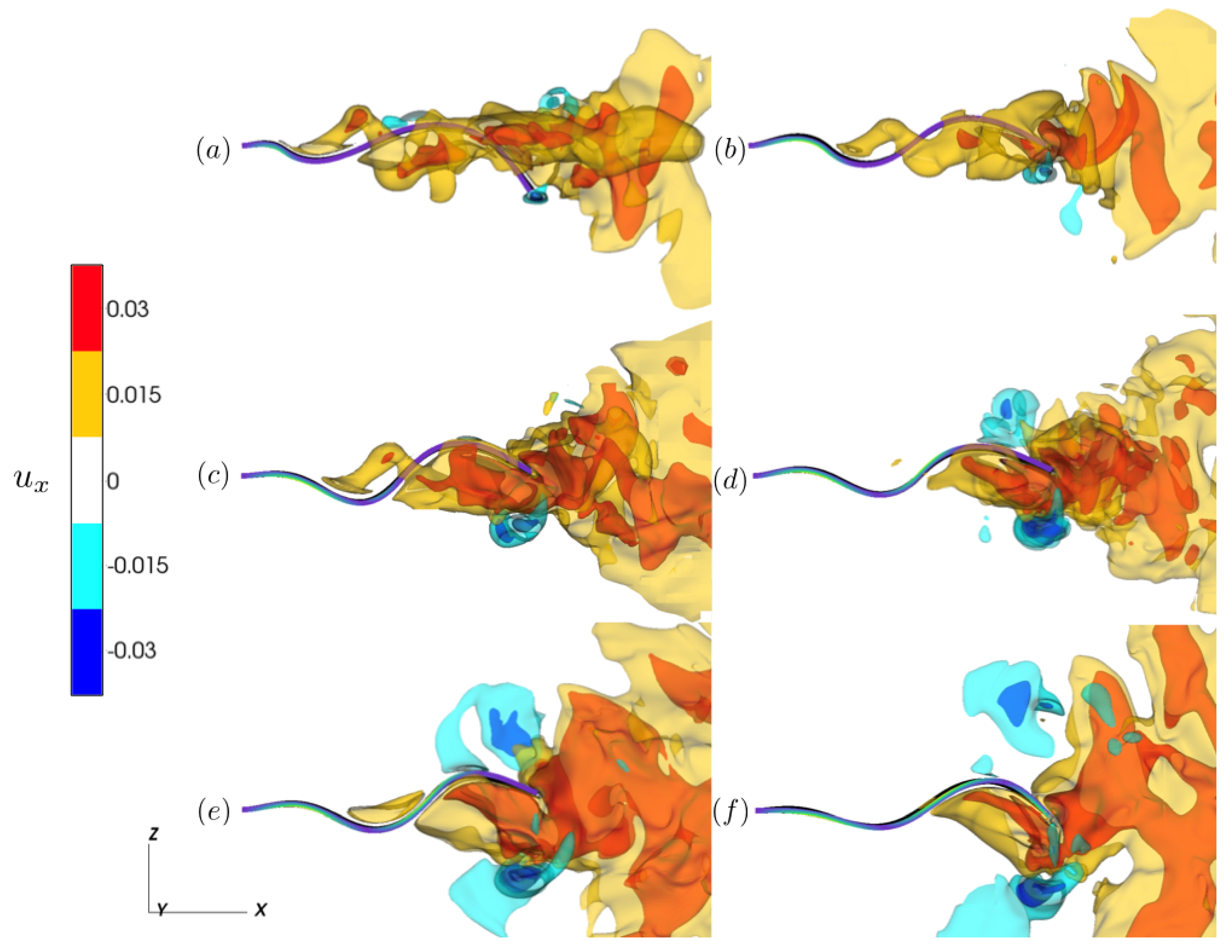
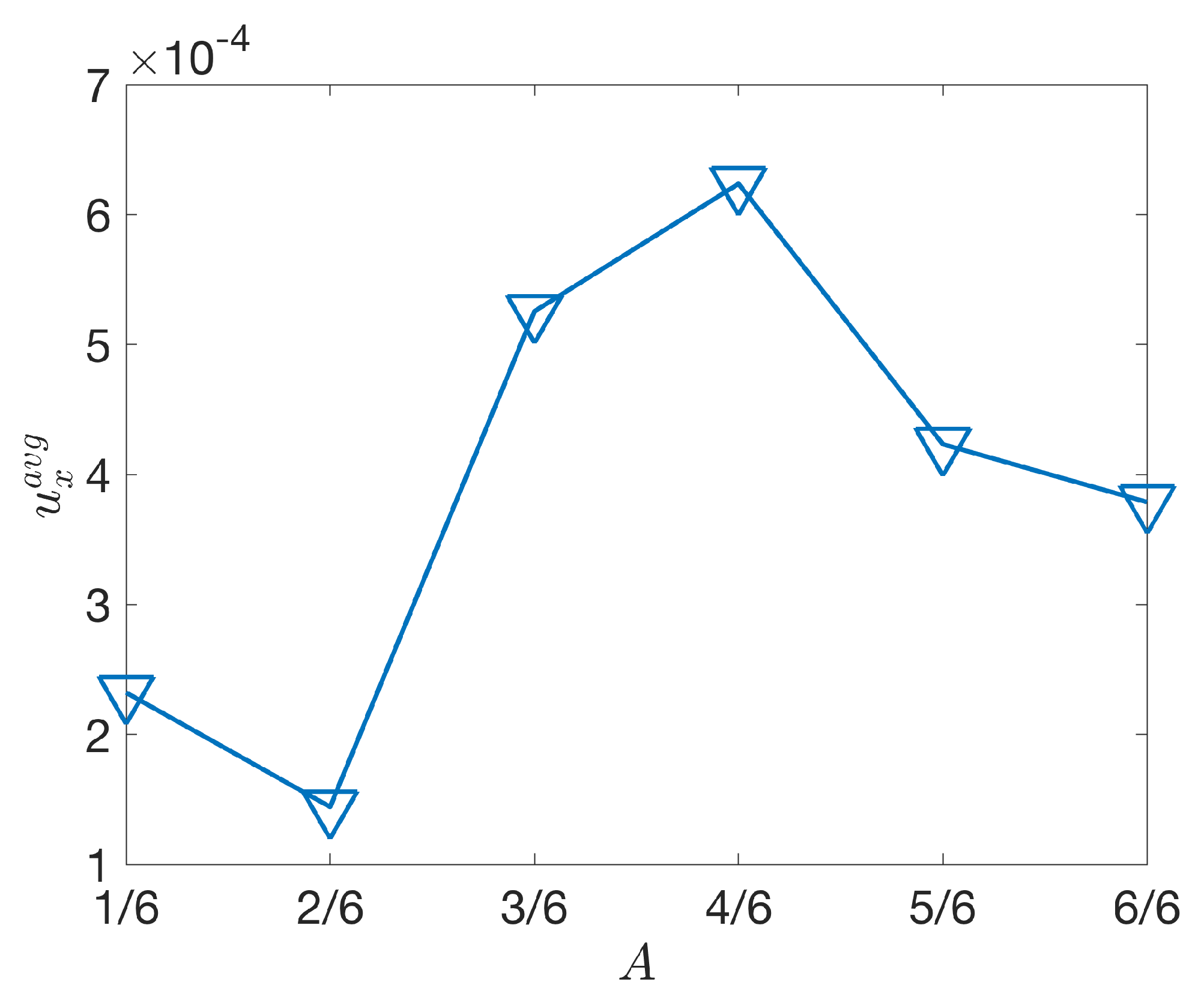
3.2.2. Varying the Activation Region
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chu, W.S.; Lee, K.T.; Song, S.H.; Han, M.W.; Lee, J.Y.; Kim, H.S.; Kim, M.S.; Park, Y.J.; Cho, K.J.; Ahn, S.H. Review of Biomimetic Underwater Robots Using Smart Actuators. Int. J. Precis. Eng. Manuf. 2012, 13, 1281–1292. [Google Scholar] [CrossRef]
- Robison, B.H.; Reisenbichler, K.R.; Sherlock, R.E. The coevolution of midwater research and ROV technology at MBARI. Oceanography 2017, 30, 26–37. [Google Scholar] [CrossRef]
- Katija, K.; Sherlock, R.E.; Sherman, A.D.; Robison, B.H. New technology reveals the role of giant larvaceans in oceanic carbon cycling. Sci. Adv. 2017, 3, e1602374. [Google Scholar] [CrossRef] [Green Version]
- Yoerger, D.R.; Curran, M.; Fujii, J.; German, C.R.; Gomez-Ibanez, D.; Govindarajan, A.F.; Howland, J.C.; Llopiz, J.K.; Wiebe, P.H.; Hobson, B.W.; et al. Mesobot: An autonomous underwater vehicle for tracking and sampling midwater targets. In Proceedings of the 2018 IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018; pp. 1–7. [Google Scholar]
- Katija, K.; Troni, G.; Daniels, J.; Lance, K.; Sherlock, R.E.; Sherman, A.D.; Robison, B.H. Revealing enigmatic mucus structures in the deep sea using DeepPIV. Nature 2020, 583, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Katija, K.; Roberts, P.L.; Daniels, J.; Lapides, A.; Barnard, K.; Risi, M.; Ranaan, B.Y.; Woodward, B.G.; Takahashi, J. Visual tracking of deepwater animals using machine learning-controlled robotic underwater vehicles. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 5–9 January 2021; pp. 860–869. [Google Scholar]
- Drucker, E.G.; Lauder, G.V. Locomotor forces on a swimming fish: Three-dimensional vortex wake dynamics quantified using digital particle image velocimetry. J. Exp. Biol. 1999, 202, 2393–2412. [Google Scholar]
- Dickinson, M.H.; Farley, C.T.; Full, R.J.; Koehl, M.A.R.; Kram, R.; Lehman, S. How animals move: An integrative view. Science 2000, 288, 100–106. [Google Scholar] [CrossRef] [Green Version]
- Fish, F.E. Balancing requirements for stability and maneuverability in cetaceans. Integr. Comp. Biol. 2002, 42, 85–93. [Google Scholar] [CrossRef]
- Oeffner, J.; Lauder, G.V. The hydrodynamic function of shark skin and two biomimetic applications. J. Exp. Biol. 2012, 215, 785–795. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moored, K.W.; Dewey, P.A.; Smits, A.; Haj-Hariri, H. Hydrodynamic wake resonance as an underlying principle of efficient unsteady propulsion. J. Fluid Mech. 2012, 708, 329–348. [Google Scholar] [CrossRef]
- Tytell, E.D.; Carr, J.A.; Danos, N.; Wagenbach, C.; Sullivan, C.M.; Kiemel, T.; Cowan, N.J.; Ankarali, M.M. Body stiffness and damping depend sensitively on the timing of muscle activation in lampreys. Integr. Comp. Biol. 2018, 58, 860–873. [Google Scholar] [CrossRef] [PubMed]
- Beal, D.; Hover, F.; Triantafyllou, M.; Liao, J.; Lauder, G.V. Passive propulsion in vortex wakes. J. Fluid Mech. 2006, 549, 385–402. [Google Scholar] [CrossRef] [Green Version]
- Costello, J.H.; Colin, S.P.; Dabiri, J.O.; Gemmell, B.J.; Lucas, K.N.; Sutherland, K.R. The hydrodynamics of jellyfish swimming. Annu. Rev. Mar. Sci. 2020, 13, 375–396. [Google Scholar] [CrossRef] [PubMed]
- Gemmell, B.J.; Costello, J.H.; Colin, S.P.; Stewart, C.J.; Dabiri, J.O.; Tafti, D.; Priya, S. Passive energy recapture in jellyfish contributes to propulsive advantage over other metazoans. Proc. Natl. Acad. Sci. USA 2013, 110, 17904–17909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Costello, J.H.; Colin, S.P.; Dabiri, J.O. Medusan morphospace: Phylogenetic constraints, biomechanical solutions, and ecological consequences. Invertebr. Biol. 2008, 127, 265–290. [Google Scholar] [CrossRef] [Green Version]
- Matsumoto, G. Swimming movements of ctenophores, and the mechanics of propulsion by ctene rows. In Hydrobiologia; Springer: Berlin/Heidelberg, Germany, 1991; Volume 216, pp. 319–325. [Google Scholar]
- Goebel, W.L.H.; Colin, S.P.; Costello, J.H.; Gemmell, B.J.; Sutherland, K.R. Scaling of ctenes and consequences for swimming performance in the ctenophore Pleurobrachia bachei. Invertebr. Biol. 2020, 139, e12297. [Google Scholar]
- Colin, S.P.; Costello, J.H.; Hansson, L.J.; Titelman, J.; Dabiri, J.O. Stealth predation and the predatory success of the invasive ctenophore Mnemiopsis leidyi. Proc. Natl. Acad. Sci. USA 2010, 107, 17223–17227. [Google Scholar] [CrossRef] [Green Version]
- Murphy, D.W.; Webster, D.R.; Kawaguchi, S.; King, R.; Yen, J. Metachronal swimming in Antarctic krill: Gait kinematics and system design. Mar. Biol. 2011, 158, 2541–2554. [Google Scholar] [CrossRef]
- Catton, K.B.; Webster, D.R.; Kawaguchi, S.; Yen, J. The hydrodynamic disturbances of two species of krill: Implications for aggregation structure. J. Exp. Biol. 2011, 214, 1845–1856. [Google Scholar] [CrossRef] [Green Version]
- Murphy, D.W.; Olsen, D.; Kanagawa, M.; King, R.; Kawaguchi, S.; Osborn, J.; Webster, D.R.; Yen, J. The three dimensional spatial structure of Antarctic krill schools in the laboratory. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Dabiri, J.O.; Colin, S.P.; Gemmell, B.J.; Lucas, K.N.; Leftwich, M.C.; Costello, J.H. Jellyfish and fish solve the challenges of turning dynamics similarly to achieve high maneuverability. Fluids 2020, 5, 106. [Google Scholar] [CrossRef]
- Bhalla, A.P.S.; Griffith, B.E.; Patankar, N.A. A forced damped oscillation framework for undulatory swimming provides new insights into how propulsion arises in active and passive swimming. PLoS Comput. Biol. 2013, 9, e1003097. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bale, R.; Hao, M.; Bhalla, A.P.S.; Patankar, N.A. Energy efficiency and allometry of movement of swimming and flying animals. Proc. Natl. Acad. Sci. USA 2014, 111, 7517–7521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoover, A.P.; Xu, N.W.; Gemmell, B.J.; Colin, S.P.; Costello, J.H.; Dabiri, J.O.; Miller, L.A. Neuromechanical wave resonance in jellyfish swimming. Proc. Natl. Acad. Sci. USA 2021. to appear. [Google Scholar]
- Lucas, K.N.; Johnson, N.; Beaulieu, W.T.; Cathcart, E.; Tirrell, G.; Colin, S.P.; Gemmell, B.J.; Dabiri, J.O.; Costello, J.H. Bending rules for animal propulsion. Nat. Commun. 2014, 5, 3293. [Google Scholar] [CrossRef] [Green Version]
- Taylor, G.K.; Nudds, R.L.; Thomas, A.L. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef] [PubMed]
- Floryan, D.; Van Buren, T.; Smits, A.J. Efficient cruising for swimming and flying animals is dictated by fluid drag. Proc. Natl. Acad. Sci. USA 2018, 115, 8116–8118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alldredge, A. Appendicularians. Sci. Am. 1976, 235, 94–105. [Google Scholar] [CrossRef]
- Flood, P.R.; Deibel, D. The appendicularian house. In The Biology of Pelagic Tunicates; Oxford University Press: Oxford, UK, 1998; pp. 105–125. [Google Scholar]
- Sherlock, R.; Walz, K.; Schlining, K.; Robison, B. Morphology, ecology, and molecular biology of a new species of giant larvacean in the eastern North Pacific: Bathochordaeus mcnutti sp. nov. Mar. Biol. 2017, 164, 20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sutherland, K.R.; Madin, L.P.; Stocker, R. Filtration of submicrometer particles by pelagic tunicates. Proc. Natl. Acad. Sci. USA 2010, 107, 15129–15134. [Google Scholar] [CrossRef] [Green Version]
- Stach, T.; Winter, J.; Bouquet, J.M.; Chourrout, D.; Schnabel, R. Embryology of a planktonic tunicate reveals traces of sessility. Proc. Natl. Acad. Sci. USA 2008, 105, 7229–7234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Razy-Krajka, F.; Stolfi, A. Regulation and evolution of muscle development in tunicates. EvoDevo 2019, 10, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Bone, Q. On the locomotion of ascidian tadpole larvae. J. Mar. Biol. Assoc. UK 1992, 72, 161–186. [Google Scholar] [CrossRef]
- Torrence, S.A.; Cloney, R.A. Nervous system of ascidian larvae: Caudal primary sensory neurons. Zoomorphology 1982, 99, 103–115. [Google Scholar] [CrossRef]
- Conley, K.R.; Gemmell, B.J.; Bouquet, J.M.; Thompson, E.M.; Sutherland, K.R. A self-cleaning biological filter: How appendicularians mechanically control particle adhesion and removal. Limnol. Oceanogr. 2018, 63, 927–938. [Google Scholar] [CrossRef]
- Smits, A.J. Undulatory and oscillatory swimming. J. Fluid Mech. 2019, 874. [Google Scholar] [CrossRef] [Green Version]
- Spagnolie, S.E.; Moret, L.; Shelley, M.J.; Zhang, J. Surprising behaviors in flapping locomotion with passive pitching. Phys. Fluids 2010, 22, 041903. [Google Scholar] [CrossRef] [Green Version]
- Alben, S. Optimal flexibility of a flapping appendage in an inviscid fluid. J. Fluid Mech. 2008, 614, 355–380. [Google Scholar] [CrossRef] [Green Version]
- Alben, S.; Witt, C.; Baker, T.V.; Anderson, E.; Lauder, G.V. Dynamics of freely swimming flexible foils. Phys. Fluids 2012, 24, 051901. [Google Scholar] [CrossRef] [Green Version]
- Moore, M.N.J. A fast Chebyshev method for simulating flexible-wing propulsion. J. Comput. Phys. 2017, 345, 792–817. [Google Scholar] [CrossRef] [Green Version]
- Tytell, E.D.; Hsu, C.Y.; Williams, T.L.; Cohen, A.H.; Fauci, L.J. Interactions between internal forces, body stiffness, and fluid environment in a neuromechanical model of lamprey swimming. Proc. Natl. Acad. Sci. USA 2010, 107, 19832–19837. [Google Scholar] [CrossRef] [Green Version]
- Hamlet, C.; Fauci, L.J.; Tytell, E.D. The effect of intrinsic muscular nonlinearities on the energetics of locomotion in a computational model of an anguilliform swimmer. J. Ther. Biol. 2015, 385, 119–129. [Google Scholar] [CrossRef] [Green Version]
- Hoover, A.P.; Griffith, B.E.; Miller, L.A. Quantifying performance in the medusan mechanospace with an actively swimming three-dimensional jellyfish model. J. Fluid Mech. 2017, 813, 1112–1155. [Google Scholar] [CrossRef]
- Hoover, A.P.; Porras, A.J.; Miller, L.A. Pump or coast: The role of resonance and passive energy recapture in medusan swimming performance. J. Fluid Mech 2019, 863, 1031–1061. [Google Scholar] [CrossRef] [Green Version]
- Katija, K.; Beaulieu, W.T.; Regula, C.; Colin, S.P.; Costello, J.H.; Dabiri, J.O. Quantification of flows generated by the hydromedusa Aequorea victoria: A Lagrangian coherent structure analysis. Mar. Ecol. Prog. Ser. 2011, 435, 111–123. [Google Scholar] [CrossRef]
- Katija, K.; Colin, S.P.; Costello, J.H.; Dabiri, J.O. Quantitatively measuring in situ flows using a self-contained underwater velocimetry apparatus (SCUVA). JoVE 2011, 56, e2615. [Google Scholar] [CrossRef]
- Brown, E.R.; Nishino, A.; Bone, Q.; Meinertzhagen, I.; Okamura, Y. GABAergic synaptic transmission modulates swimming in the ascidian larva. Eur. J. Neurosci. 2005, 22, 2541–2548. [Google Scholar] [CrossRef] [PubMed]
- Peskin, C.S. The Immersed Boundary Method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef] [Green Version]
- Mittal, R.; Iaccarino, G. Immersed Boundary Methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef] [Green Version]
- Griffith, B.E.; Patankar, N.A. Immersed methods for fluid–structure interaction. Annu. Rev. Fluid Mech. 2020, 52, 421–448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Griffith, B.E.; Luo, X. Hybrid finite difference/finite element immersed boundary method. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2888. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Zheng, H.; Poh, P.S.; Machens, H.G.; Schilling, A.F. Hydrogels for engineering of perfusable vascular networks. Int. J. Mol. Sci. 2015, 16, 15997–16016. [Google Scholar] [CrossRef] [PubMed]
- Quinn, D.B.; Lauder, G.V.; Smits, A.J. Scaling the propulsive performance of heaving flexible panels. J. Fluid Mech. 2014, 738, 250–267. [Google Scholar] [CrossRef] [Green Version]
- Hoover, A.P.; Cortez, R.; Tytell, E.D.; Fauci, L.J. Swimming performance, resonance and shape evolution in heaving flexible panels. J. Fluid Mech. 2018, 847, 386–416. [Google Scholar] [CrossRef] [Green Version]
- Griffith, B.E. IBAMR: An Adaptive and Distributed-Memory Parallel Implementation of the Immersed Boundary Method. Available online: https://github.com/IBAMR/IBAMR (accessed on 8 February 2021).
- Griffith, B.E.; Hornung, R.D.; McQueen, D.M.; Peskin, C.S. An adaptive, formally second order accurate version of the immersed boundary method. J. Comput. Phys. 2007, 223, 10–49. [Google Scholar] [CrossRef]
- Dewey, P.A.; Boschitsch, B.M.; Moored, K.W.; Stone, H.A.; Smits, A.J. Scaling laws for the thrust production of flexible pitching panels. J. Fluid Mech. 2013, 732, 29–46. [Google Scholar] [CrossRef]
- Quinn, D.B.; Lauder, G.V.; Smits, A.J. Flexible propulsors in ground effect. Bioinspiration Biomimetics 2014, 9, 036008. [Google Scholar] [CrossRef] [Green Version]
- Williamson, C.; Roshko, A. Vortex Formation in the Wake of an Oscillating Cylinder. J. Fluids Struct. 1988, 2, 355–381. [Google Scholar] [CrossRef]
- Park, S.J.; Gazzola, M.; Park, K.S.; Park, S.; Di Santo, V.; Blevins, E.L.; Lind, J.U.; Campbell, P.H.; Dauth, S.; Capulli, A.K.; et al. Phototactic guidance of a tissue-engineered soft-robotic ray. Science 2016, 353, 158–162. [Google Scholar] [CrossRef] [Green Version]
- Nawroth, J.C.; Lee, H.; Feinberg, A.W.; Ripplinger, C.M.; McCain, M.L.; Grosberg, A.; Dabiri, J.O.; Parker, K.K. A tissue-engineered jellyfish with biomimetic propulsion. Nat. Biotechnol. 2012, 30, 792–797. [Google Scholar] [CrossRef]
- Nawroth, J.C.; Scudder, L.L.; Halvorson, R.T.; Tresback, J.; Ferrier, J.P., Jr.; Sheehy, S.P.; Cho, A.; Kannan, S.; Sunyovszki, I.; Goss, J.A.; et al. Automated fabrication of photopatterned gelatin hydrogels for organ-on-chips applications. Biofabrication 2018, 10, 025004. [Google Scholar] [CrossRef]
- Michelin, S.; Llewellyn Smith, S.G. Resonance and propulsion performance of a heaving flexible wing. Phys. Fluids 2009, 21, 071902. [Google Scholar] [CrossRef] [Green Version]
- Eldredge, J.D.; Toomey, J.; Medina, A. On the roles of chord-wise flexibility in a flapping wing with hovering kinematics. J. Fluid Mech. 2010, 659, 94–115. [Google Scholar] [CrossRef]
- Ramananarivo, S.; Godoy-Diana, R.; Thiria, B. Rather than resonance, flapping wing flyers may play on aerodynamics to improve performance. Proc. Natl. Acad. Sci. USA 2011, 108, 5964–5969. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lehn, A.M.; Thornycroft, P.J.; Lauder, G.V.; Leftwich, M.C. Effect of input perturbation on the performance and wake dynamics of aquatic propulsion in heaving flexible foils. Phys. Rev. Fluids 2017, 2, 023101. [Google Scholar] [CrossRef]
- Paraz, F.; Eloy, C.; Schouveiler, L. Experimental Study of the Response of a Flexible Plate to a Harmonic Forcing in a Flow. C. R. Mécanique 2014, 342, 532–538. [Google Scholar] [CrossRef]
- Buchholz, J.H.; Smits, A.J. The Wake Structure and Thrust Performance of a Rigid Low-Aspect-Ratio Pitching Panel. J. Fluid Mech. 2008, 603, 331–365. [Google Scholar] [CrossRef] [Green Version]
- Green, M.A.; Rowley, C.W.; Smits, A.J. The Unsteady Three-Dimensional Wake Produced by a Trapezoidal Pitching Panel. J. Fluid Mech. 2011, 685, 117–145. [Google Scholar] [CrossRef] [Green Version]
- Quinn, D.B.; Lauder, G.V.; Smits, A.J. Maximizing the Efficiency of a Flexible Propulsor Using Experimental Optimization. J. Fluid Mech. 2015, 767, 430–448. [Google Scholar] [CrossRef] [Green Version]
- Lucas, K.N.; Thornycroft, P.J.; Gemmell, B.J.; Colin, S.P.; Costello, J.H.; Lauder, G.V. Effects of Non-Uniform Stiffness on the Swimming Performance of a Passively-Flexing, Fish-like Foil Model. Bioinspiration Biomimetics 2015, 10, 056019. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vogel, S. Glimpses of Creatures in Their Physical Worlds; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Asadzadeh, S.S.; Larsen, P.S.; Riisgård, H.U.; Walther, J.H. Hydrodynamics of the leucon sponge pump. J. R. Soc. Interface 2019, 16, 20180630. [Google Scholar] [CrossRef] [Green Version]
- Mapstone, G.M. Global diversity and review of Siphonophorae (Cnidaria: Hydrozoa). PLoS ONE 2014, 9, e87737. [Google Scholar] [CrossRef] [PubMed]
- Dunn, C.W.; Leys, S.P.; Haddock, S.H. The hidden biology of sponges and ctenophores. Trends Ecol. Evol. 2015, 30, 282–291. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- St. John, M.A.; Borja, A.; Chust, G.; Heath, M.; Grigorov, I.; Mariani, P.; Martin, A.P.; Santos, R.S. A dark hole in our understanding of marine ecosystems and their services: Perspectives from the mesopelagic community. Front. Mar. Sci. 2016, 3, 31. [Google Scholar] [CrossRef] [Green Version]
- Brito-Morales, I.; Schoeman, D.S.; Molinos, J.G.; Burrows, M.T.; Klein, C.J.; Arafeh-Dalmau, N.; Kaschner, K.; Garilao, C.; Kesner-Reyes, K.; Richardson, A.J. Climate velocity reveals increasing exposure of deep-ocean biodiversity to future warming. Nat. Clim. Chang. 2020, 10, 576–581. [Google Scholar] [CrossRef]

| Quantity | Symbol | Reference Value |
|---|---|---|
| Elastic Modulus | E | 10 kPa |
| Poisson ratio | ||
| Target spring constant | Pa | |
| Max reference tension magnitude | 4000 N | |
| Tail length | L | 6.1 cm |
| Wavelength | 5 cm | |
| Tether transition parameter | 10,000 | |
| Activation transition parameter | 500 |
| Quantity | Symbol | Reference Value |
|---|---|---|
| Numerical timestep | ||
| Domain width | W | 0.2 m |
| Grid stepsize | h |
| Tail | Tail Wave | |||||
|---|---|---|---|---|---|---|
| W | L | a | f | N | ||
| cm | cm | cm | cm | s | ||
| BM1 | 3.2 | 6.1 | 1.4 | 5.5 | 0.59 ± 0.02 | 3 |
| BM2 | 3.1 | 6.6 | 2.0 | 5.2 | 0.68 ± 0.05 | 5 |
| BM3 | 2.7 | 5.8 | 1.7 | 5.2 | 1.04 ± 0.09 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoover, A.P.; Daniels, J.; Nawroth, J.C.; Katija, K. A Computational Model for Tail Undulation and Fluid Transport in the Giant Larvacean. Fluids 2021, 6, 88. https://doi.org/10.3390/fluids6020088
Hoover AP, Daniels J, Nawroth JC, Katija K. A Computational Model for Tail Undulation and Fluid Transport in the Giant Larvacean. Fluids. 2021; 6(2):88. https://doi.org/10.3390/fluids6020088
Chicago/Turabian StyleHoover, Alexander P., Joost Daniels, Janna C. Nawroth, and Kakani Katija. 2021. "A Computational Model for Tail Undulation and Fluid Transport in the Giant Larvacean" Fluids 6, no. 2: 88. https://doi.org/10.3390/fluids6020088
APA StyleHoover, A. P., Daniels, J., Nawroth, J. C., & Katija, K. (2021). A Computational Model for Tail Undulation and Fluid Transport in the Giant Larvacean. Fluids, 6(2), 88. https://doi.org/10.3390/fluids6020088






